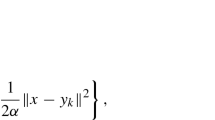Abstract
We focus on a special nonconvex and nonsmooth composite function, which is the sum of the smooth weakly convex component functions and a proper lower semi-continuous weakly convex function. An algorithm called the proximal-like incremental aggregated gradient (PLIAG) method proposed in Zhang et al. (Math Oper Res 46(1): 61–81, 2021) is proved to be convergent and highly efficient to solve convex minimization problems. This algorithm can not only avoid evaluating the exact full gradient which can be expensive in big data models but also weaken the stringent global Lipschitz gradient continuity assumption on the smooth part of the problem. However, under the nonconvex case, there is few analysis on the convergence of the PLIAG method. In this paper, we prove that the limit point of the sequence generated by the PLIAG method is the critical point of the weakly convex problems. Under further assumption that the objective function satisfies the Kurdyka–Łojasiewicz (KL) property, we prove that the generated sequence converges globally to a critical point of the problem. Additionally, we give the convergence rate when the Łojasiewicz exponent is known.
Similar content being viewed by others
References
Attouch, H., Bolte, J.: On the convergence of the proximal algorithm for nonsmooth functions involving analytic features. Math. Program. 116(1), 5–16 (2009)
Attouch, H., Bolte, J., Redont, P., Soubeyran, A.: Proximal alternating minimization and projection methods for nonconvex problems: An approach based on the kurdyka-łojasiewicz inequality. Math. Oper. Res. 35(2), 438–457 (2010)
Aytekin, A., Feyzmahdavian, H.R., Johansson, M.: Analysis and implementation of an asynchronous optimization algorithm for the parameter server. arXiv preprint arXiv:1610.05507 (2016)
Bauschke, H.H., Bolte, J., Teboulle, M.: A descent lemma beyond lipschitz gradient continuity: first-order methods revisited and applications. Math. Oper. Res. 42(2), 330–348 (2017)
Beck, A., Teboulle, M.: Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans. Image Process. 18(11), 2419–2434 (2009)
Beck, A., Teboulle, M.: Gradient-based algorithms with applications to signal recovery problems. In: Palomar, D., Eldar, Y.C. (eds.) Convex Optimization in Signal Processing and Communications, pp. 139–162. Cambridge University Press, Cambridge (2009)
Bolte, J., Sabach, S., Teboulle, M.: Proximal alternating linearized minimization for nonconvex and nonsmooth problems. Math. Program. 146(1), 459–494 (2014)
Bolte, J., Sabach, S., Teboulle, M., Vaisbourd, Y.: First order methods beyond convexity and lipschitz gradient continuity with applications to quadratic inverse problems. SIAM J. Optim. 28(3), 2131–2151 (2018)
Boţ, R.I., Csetnek, E.R., László, S.C.: An inertial forward-backward algorithm for the minimization of the sum of two nonconvex functions. EURO J. Comput. Optim. 4(1), 3–25 (2016)
Bregman, L.M.: The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming. USSR Comput. Math. Math. Phys. 7(3), 200–217 (1967)
Chen, G., Teboulle, M.: Convergence analysis of a proximal-like minimization algorithm using bregman functions. SIAM J. Optim. 3(3), 538–543 (1993)
Jia, Z.H., Wu, Z.M., Dong, X.M.: An inexact proximal gradient algorithm with extrapolation for a class of nonconvex nonsmooth optimization problems. J. Inequal. Appl. 2019(1), 125 (2019)
Kurdyka, K.: On gradients of functions definable in o-minimal structures. Annal. de l’Institut Fourier 48(3), 769–783 (1998)
Li, H., Lin, Z.C.: Accelerated proximal gradient methods for nonconvex programming. In: Advances in neural information processing systems, pp. 379-387 (2015)
Lions, P.L., Mercier, B.: Splitting algorithms for the sum of two nonlinear operators. SIAM J. Numer. Anal. 16(6), 964–979 (1979)
Lojasiewicz, S.: Une propriété topologique des sous-ensembles analytiques réels. Les Équations aux Dérivées Partielles 117, 87–89 (1963)
Mordukhovich, B.S.: Variational analysis and generalized differentiation I: Basic theory. Grundlehren der Mathematischen Wissenschaften, vol. 330. Springer, Berlin (2006)
Peng, W., Zhang, H., Zhang, X.Y.: Nonconvex proximal incremental aggregated gradient method with linear convergence. J. Optim. Theory Appl. 183(1), 230–245 (2019)
Rockafellar, R.T., Wets, R.J.-B.: Variational analysis. Fundamental Principles of Mathematical Science, vol. 317. Springer, Berlin (1998)
Vanli, N.D., Gurbuzbalaban, M., Ozdaglar, A.: Global convergence rate of proximal incremental aggregated gradient methods. SIAM J. Optim. 28(2), 1282–1300 (2018)
Vanli, N.D., Gurbuzbalaban, M., Ozdaglar, A.: A stronger convergence result on the proximal incremental aggregated gradient method. arXiv preprint arXiv:1611.08022, (2016)
Zhang, H., Dai, Y.H., Guo, L., Peng, W.: Proximal-like incremental aggregated gradient method with linear convergence under bregman distance growth conditions. Math. Oper. Res. 46(1), 61–81 (2021)
Zhang, X.Y., Zhang, H., Peng, W.: Inertial bregman proximal gradient algorithm for nonconvex problem with smooth adaptable property. arXiv preprint arXiv:1904.04436, (2019)
Acknowledgements
This work is supported by National Natural Science Foundation of China (Grant No. 11801279 and 11871279), Natural Science Foundation of Jiangsu Province (Grant No. BK20180782), and the Startup Foundation for Introducing Talent of NUIST (Grant No. 2017r059).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Proof of Lemma 3.1
Considering the \(L_j\)-smooth of the pair \(( f_j,\omega )\) according to Assumption 2(a), we can obtain that
where the second inequality follows from the convexity of \(f_j(\cdot )+\frac{\beta _j}{2}\Vert \cdot \Vert ^2\) according to Assumption 2(b). Summing (31) over all \(j\in {\mathcal {J}}_k\), we can get
where \(\gamma _1\) is defined in Assumption 2 as \(\gamma _1{:}{=}\sum _{n=1}^N\beta _n\). By the optimality of \(x_{k+1}\), we have
Using the subgradient inequality for the convex function \(h(x)+\sum \limits _{i\in {\mathcal {I}}_{k}}f_i (x)+\frac{\gamma _1+\gamma _2}{2}\Vert x\Vert ^2\) at \(x_{k+1}\), we have
where the last equality follows from the three-point identity of the Bregman distance. Adding (34) to (32), we get
According to Assumption 1(d), we deduce
where the second inequality is due to the fact that \(\tau _k^i\) is bounded above by \(\tau \) and the last inequality follows from \(L{:}{=}\sum _{j=1}^N L_j\). Together with the above inequality, (35) can be rewritten as
Invoking (36) with \(x=x_k\) implies
The component \(\sum _{j=k-\tau }^{k}D_{\omega }(x_{j+1},x_{j})\) in (37) can be written as
and the component \(\Vert x_k-x_{k-\tau _{k}^{j}}\Vert ^{2}\) in (37) has the following inequality
Using the above inequaity, we have
Plugging (38) and (39) into (37) and minusing \(\upsilon ({\mathcal {P}})\) on both sides of the inequality, we can get
Recalling the definition of \(T_k\), \(C_1\) and \(C_2\), (40) can be rewritten as
thus complete the proof. \(\square \)
Rights and permissions
About this article
Cite this article
Jia, Z., Huang, J. & Cai, X. Proximal-like incremental aggregated gradient method with Bregman distance in weakly convex optimization problems. J Glob Optim 80, 841–864 (2021). https://doi.org/10.1007/s10898-021-01044-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10898-021-01044-9