Cooperative multiobjective optimization with bounds on objective functions

Abstract

When solving large-scale multiobjective optimization problems, solvers can get stuck because of memory and/or time limitations. In such cases, one is left with no information on the distance to the best feasible solution, found before the optimization process has stopped, to the true Pareto optimal solution. In this work, we show how to provide such information. To this aim we make use of the concept of lower shells and upper shells, developed in our earlier works. No specific assumptions about the problems to be solved are made. We illustrate the proposed approach on biobjective multidimensional knapsack problems derived from single-objective multidimensional knapsack problems in the Beasley OR Library. We address cases when a top-class commercial mixed-integer linear solver fails to provide Pareto optimal solutions attempted to be derived by scalarization.

1 Introduction

The ubiquitous access to more and more powerful computing platforms stimulates the appetite to solve more and more large optimization problems. However, various barriers (time and/or memory limits, ”the curse of dimensionality” in combinatorial problems) are the cause that in practice one is often left with suboptimal solutions. In such cases, the existence of lower and upper bounds on the exact solution is essential. The multiobjective optimization literature is rich with various approaches to this issue, cf. [14, 15] for brief overviews.

This work has been inspired by the fact that when solving large-scale multiobjective optimization (MO) problems, it can happen that Pareto optimal (efficient) solutions are not derived. The reasons for that can be twofold. When making use of heuristics, such as Evolutionary Multiobjective Optimization (EMO), or other, Pareto optimality of derived solutions is not guaranteed. When making use of exact methods, such as mixed-integer programming (MIP), solvers can reach memory limits, and, less often, time limits, before the optimal solution is found. In both cases, one is left with a feasible solution which may be believed to be Pareto optimal or close to Pareto optimality, but no information is offered about how wide the actual gap is (the Pareto suboptimality gap) between the image (in the objective space) of the feasible solution derived and the image (in the objective space) of the set of Pareto optimal solutions (the Pareto front).

To cope with such unfavorable situations and to provide the lacking information, here we employ the general methodology developed for calculating bounds on objective function values of implicit Pareto optimal solutions [12, 14, 15, 17, 18]. The central concept of this methodology is to built two-sided approximations of the Pareto front (PF). To this aim, two sets of elements are produced, one composed of feasible solutions, called lower shell, and another composed of feasible or infeasible solutions, called upper shell. The images of these sets form, respectively, an internal and an external approximation of the PF. No element of the lower shell needs to be Pareto optimal.

Lower and upper shells which we make use of are composed of just elements (points, solutions). No relationship between them (in the form of constructing lines, triangles, polygons, etc.), except nondominancy, is assumed. Following the terminology introduced by Ruzika and Wiecek [28], they are 0-order approximations of PFs, whereas, e.g., the bound sets [8] or the attainment function [9] are of an order higher than 0.

In the literature, two general approaches to approximate the PF are present. The first approach, based on exact optimization methods, aims at building approximating constructs starting from a number of efficient solutions derived by an exact optimization method. From a vast literature on that approach one can quote [28] (a survey paper), [1, 8, 11] and [20].

The second approach, based on inexact, mostly population type optimization methods (cf., e.g., [2, 4,5,6, 10, 25,26,27, 29, 30]), aims at producing discrete feasible approximations (lower shells) of Pareto fronts. In the second approach, no guarantee is offered that the resulting approximations include actual elements of the PF. In consequence, the actual behavior of such methods can be only observed on test problems with known sets of Pareto optimal solutions.

The methodology we refer to [12, 15, 17, 24] follows the second approach. However, in contrast to other methods consistent with that approach, the said methodology provides for two-sided, lower and upper bounds on objective functions values of Pareto optimal solutions. By this, the behavior of inexact methods can be put under control. Moreover, responding to the needs of Multiple Criteria Decision Making, the methodology abstains from approximating the whole Pareto front and takes a more pragmatic course. Namely, it produces ad hoc local approximations of the Pareto front, only in regions of the explicit decision maker’s interest. This provides for large savings by forgoing vain computations.

As the said methodology works only for a special case (see Sect. 4), in this work, we extend this methodology to the general MO setting.

The outline of the work is as follows. In Sect. 2, we recall the multiobjective problem formulation in its most general form and recall a method for Pareto optimal solution derivation, which is instrumental for the subsequent development. In Sect. 3, we present our development of general lower and upper bounds and in Sect. 4, we discuss a special case. Section 5 addresses the issue of derivation of upper shells. We illustrate the development in Sect. 6 on large-scale biobjective multidimensional knapsack problems. Section 7 concludes.

2 Preliminaries

Let x denote a solution, X a space of solutions, $X \subseteq {{\mathbb {R}}}^n$, $X_0$ a set of feasible solutions, $X_0 \subseteq X$. Then the general multiobjective optimization problem is defined as:

$$\begin{aligned}&vmax f(x) \nonumber \\&\text {subject to: }\, x \in X_0 \,, \end{aligned}$$

(1)

where $f : X \rightarrow {{\mathbb {R}}}^k$, $f = (f_1,\ldots ,f_k)$, $f_l : \rightarrow {{\mathbb {R}}}, \ l=1,\ldots ,k, \ k \ge 2$, are objective functions, and vmax denotes the operator of deriving all Pareto optimal solutions in $X_0$. ${{\mathbb {R}}}^k$ is called the objective space.

Solution ${\bar{x}}$ is Pareto optimal (or: efficient) if $f_l(x) \ge f_l({\bar{x}}), \ l = 1,\ldots ,k$, implies $f(x) = f({\bar{x}})$. If $f_l(x) \ge f_l({\bar{x}}), \ l = 1,\ldots ,k$, and $f(x) \not = f({\bar{x}})$, then we say that x dominates ${\bar{x}}$ and we write ${\bar{x}} \prec x$. Solution ${\bar{x}}$ is weakly Pareto optimal (or: weakly efficient) if there is no such x that $f_l(x)>f_l({\bar{x}}), \ l=1,\ldots ,k$. Below, we shall denote the set of Pareto optimal solutions (or: efficient set) to (1) by N. Set f(N) is called the Pareto front (PF).

It is a well-established result (cf. [7, 12, 23]) that solution x is Pareto optimal (actually, this solution is properly Pareto optimal, for a formal treatment of this issue cf., e.g., [12], pp. 36-37, [7], p. 121, [23], p. 103) if and only if it solves the Chebyshev weighted optimization problem

$$\begin{aligned} \min \limits _{x \in X_0} \max \limits _{l} [\lambda _l (y^*_l - f_l(x)) + \rho e^k(y^* - f(x))] \,, \end{aligned}$$

(2)

where weights $\lambda _l > 0, \ l=1,\ldots ,k$, $e^k = (1,1,\ldots ,1)$, $y^*_l = {\hat{y}}_l + \varepsilon$, ${\hat{y}}_l = \max _{x \in X_0} f_l(x) < \infty , \ l=1,\ldots ,k$, $\varepsilon > 0$ ($\hat{y}$ is called the ideal point), and $\rho$ is a positive ”sufficiently small” number. By solving problem (2) with $\rho =0$ weakly Pareto optimal solutions are derived (cf., e.g., [23], p. 98).

By the ”only if” part of this result, no Pareto optimal solution is a priori excluded from being derived by solving an instance of optimization problem (2). In contrast to that, maximization of a weighted sum of objective functions over $X_0$ does not possess, in general (and especially in the case of problems with discrete variables), this property (cf., e.g., [12], pp. 37-38, [19], pp. 54-56, [7], p. 121, [23], p. 78).

On the first glance, the objective function in (2) seems to be difficult to handle. However, problem (2) is equivalent to

$$\begin{aligned}&\min \limits _{x \in X_0} s \nonumber \\&\text {subject to: }\, s \ge \lambda _l (y^*_l - f_l(x)) + \rho e^k(y^* - f(x)), \ \ l=1,\ldots ,k. \end{aligned}$$

(3)

In the sequel, we will assume that Pareto optimal solutions are derived by solving problem (2) with varying $\lambda _l, l=1,\ldots ,k$.

3 Development of general lower and upper bounds

Given $\lambda =(\lambda _1,\ldots ,\lambda _k)$, let $x^{P_{opt}}(\lambda )$ denote a Pareto optimal solution to problem (2), which would be derived if this problem were solved to optimality (the implicit Pareto optimal solution). By the definition of ${\hat{y}}$, $f(x^{P_{opt}}(\lambda )) \in Y = \{ y \in {{\mathbb {R}}}^k \,|\, y_l \le {\hat{y}}_l, \, l=1,\ldots ,k \}$.

3.1 Lower bounds

The lower bound we developed in our earlier works [12] is general, i.e., it is valid for any problem of the form (1). Here, for completeness sake, we present the underlying arguments. To simplify the presentation, we assume here $\rho = 0$ (cf. [16], pp. 13-15, for the derivation of the formula for lower bounds with $\rho > 0$). In this case, $x^{P_{opt}}(\lambda )$ can be weakly efficient.

In contrast to single-objective problems, where any feasible solution yields a lower bound for the optimal value of the objective function, in MO, where the notion of Pareto optimal solutions (elements of N) replaces the notion of optimal solutions and set f(N) is not a singleton, this is not the case. Suppose for a while $k=2$. Since $x^{P_{opt}}(\lambda )$ is a solution to (2) and thus it is Pareto optimal, for a given solution ${\bar{x}}$ of $X_0$, $f(x^{P_{opt}}(\lambda ))$ is neither in the set $\{ f(x) \in Y \, | \, x \in X_0, \ f_1(x) \le f_1({\bar{x}})$ AND $f_2(x) < f_2({\bar{x}}) \}$ nor in the set $\{ f(x) \in Y \, | \, x \in X_0, \ f_1(x) < f_1({\bar{x}})$ AND $f_2(x) \le f_2({\bar{x}}) \}$, but it is in the set $\{ f(x) \in Y \, | \, x \in X_0, \ f_1(x) \ge f_1({\bar{x}})$ OR $f_2(x) \ge f_2({\bar{x}}) \}.$ Similar observations are valid for any $k \ge 2$. Lower bounds provided on $f(x^{P_{opt}}(\lambda ))$ by elements of $X_0$ are of disjunctive type and therefore not constructive.

To propose constructive, i.e., conjunctive bounds, one has to exploit the fact that Pareto optimal solutions are derived, as assumed, by solving problem (2).

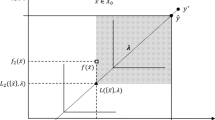
Again, let ${\bar{x}}$ be a solution, ${\bar{x}} \in X_0$. The contours of the objective function in (2) are borders of shifted cones $\{ y \,|\, y_l \ge 0, \ l=1,\ldots ,k \}$ with cone apexes on the compromise half line $\{ y \,|\, y_l = y^*_l - \frac{1}{\lambda _l} t, t\ge 0, \ l=1,\ldots ,k \}$ (cf. [12], pp. 59-62, [17], p. 191, [19], pp. 65-69). Given $\lambda$, no solution from subset $\{ x \, | \, x \in X_0, \ f_1(x) < L_1(\lambda ,\{ {\bar{x}} \})$ OR $f_2(x) < L_2(\lambda ,\{ {\bar{x}} \})$ ...OR $f_k(x) < L_k(\lambda ,\{ {\bar{x}} \})\}$, where $L_l(\lambda ,\{ {\bar{x}} \}), \ l=1,\ldots ,k$, are components of the element at which the compromise half line intercepts $\{ y \, | \, y \in R^k, \ y_l \le f_l({\bar{x}}), \ l=1,\ldots ,k \}$ (as illustrated in Fig. 1 for $k=2$) can be solution to (2) since any such solution yields a greater value of the objective function of (2) than $f({\bar{x}})$. Thus, $L(\lambda , \{ {\bar{x}} \})$ is the vector of lower bounds for the corresponding components of $f(x^{P_{opt}}(\lambda ))$.

Fig. 1

Lower bounds $L_l(\lambda , \{ {\bar{x}} \})$ on $f_l(x^{P_{opt}}(\lambda ))$ provided by element ${\bar{x}} \in X_0$ are constructive: $L_1(\lambda , \{{\bar{x}} \}) \le f_1(x^{P_{opt}}(\lambda ))$ AND $L_2(\lambda , \{{\bar{x}} \}) \le f_2(x^{P_{opt}}(\lambda ))$. With this lower bound, $f(x^{P_{opt}}(\lambda ))$ is located somewhere in the dotted area

Given multiple solutions of ${\bar{x}} \in X_0$, for each coordinate the maximal lower bound is selected. Solutions which are dominated by another elements of $X_0$ clearly provide lower bounds which are lower than or equal to lower bounds provided by dominating solutions. Therefore, to avoid redundancy, it is reasonable to work with solutions which do not dominate one another and this is formalized by the notion of lower shell.

Lower shell to problem (1) is a finite nonempty set $S_L \subseteq X_0$, elements of which satisfy

$$\begin{aligned} \forall \, x \in S_L \ \ \not \exists \, x' \in S_L \ \ x \prec x' \,. \end{aligned}$$

(4)

The formula for lower bounds with $\rho \ge 0$ ([12], pp. 92–94, [16], pp. 13–15) is

$$\begin{aligned}&f_l(x^{P_{opt}}(\lambda )) \ge L_l(\lambda , S_L) \nonumber \\&\quad := \max \{\max \limits _{x \in S_L}\{y^*_l - (\lambda _l + \rho )^{-1} [ \max \limits _{j=1,\ldots ,k} \ \lambda _j((y^*_j - f_j(x)) \nonumber \\&\qquad +\, \rho e^k(y^* - f(x))) ] + \frac{\rho }{\lambda _l + \rho }\mathop {\sum }\nolimits ^k_{j \ne l} (y^*_j - U_j(\lambda ))\}, {\bar{L}}_l \}, \ l =1,\ldots ,k, \end{aligned}$$

(5)

where ${\bar{L}}_l$ are lower bounds implied by some a priori information on $f_l(x^{P_{opt}}(\lambda ))$, if available. If such lower bounds are not available, then one can simply set ${\bar{L}}_l=-\infty$. $U_l(\lambda )$ are known upper bounds on $f_l(x^{P_{opt}}(\lambda ))$ (e.g., when one can infer these bounds basing on properties of problem (1)). If $U_l(\lambda )$ are not known, then one can simply set $U_l(\lambda )=y_l^*$.

3.2 Upper bounds

Upper shell¹ is a finite nonempty set $S_U \subseteq {{\mathbb {R}}}^n$, elements of which satisfy

$$\begin{aligned}&\forall \, x \in S_U \ \ \not \exists \, x' \in S_U \ \ x' \prec x \,, \end{aligned}$$

(6)

$$\begin{aligned}&\forall \, x \in S_U \ \ \not \exists \, x' \in N \ \ x \prec x' \,, \end{aligned}$$

(7)

Not every element of an upper shell provides an upper bound on a component of $f(x^{P_{opt}}(\lambda ))$. To be so, elements of upper shell have to be appropriately located with respect to a lower bound $L(\lambda ,S_L)$.

Let $S_U$ be an upper shell to problem (1).

Proposition 1

$x \in S_U$ provides an upper bound for some $f_l(x^{P_{opt}}(\lambda ))$ only if for at least one l, $L_l(\lambda ,S_L) \ge f_l(x)$.

Proof

$x \in S_U$ provides no upper bound for $f_l(x^{P_{opt}}(\lambda ))$ if for all $l, \ l=1,\ldots ,k$, $L_l(\lambda ,S_L)) < f_l(x)$, as in this case nothing precludes $f_l(x^{P_{opt}}(\lambda )) \ge f_l(x)$ for one or several l. $\square$

Remark 1

It is worth observing that also some Pareto optimal solutions can satisfy conditions of Proposition 1. This relates to the development of [12] where lower and upper bounds were proposed with shells (subsets of Pareto optimal solutions), the concept in which lower and upper shells coincide. Later on, with applications to space sampling algorithms (e.g., evolutionary) in mind [14, 17, 24], to clearly delineate feasible and infeasible sampling spaces, we have adopted the condition $S_U \subseteq {{\mathbb {R}}}^n \setminus X_0$. However, for the sake of generality, here we stick to the definition of upper shell as that given above.

Proposition 2

Suppose $x \in S_U$ and $L_{\,{\bar{l}}\,}(\lambda ,S_L) \le f_{\,{\bar{l}}\,}(x)$ for some ${\bar{l}}$ and $L_l(\lambda ,S_L) \ge f_l(x)$ for all $l=1,\ldots ,k, \ l \ne {\bar{l}}$. Then x provides an upper bound for $f_{\,{\bar{l}}\,}(x^{P_{opt}}(\lambda ))$, namely $f_{\,{\bar{l}}\,}(x^{P_{opt}}(\lambda )) \le f_{\,{\bar{l}}\,}(x)$.

Proof

By assumption, $f_l(x^{P_{opt}}(\lambda )) \ge L_l(\lambda ,S_L) \ge f_{l}(x)$ for all $l=1,\ldots ,k, \ l \ne {\bar{l}}$. Since $x \in S_U$ and hence x is not dominated by $f(x^{P_{opt}}(\lambda ))$, the condition $f_{\,{\bar{l}}\,}(x^{P_{opt}}(\lambda )) \le f_{\,{\bar{l}}\,}(x)$ must hold $\square$

4 The special case

Lower and upper bounds were originally developed ([12], pp. 92–102, [16], pp. 13–17) for the special case when at $x^{P_{opt}}(\lambda )$, the optimal solution to (3) (and hence, also to (2)), the following holds

$$\begin{aligned} s = \lambda _l (y^*_l - f_l(x^{P_{opt}}(\lambda ))) + \rho e^k(y^* - f(x^{P_{opt}}(\lambda ))), \ \ l=1,\ldots ,k\,. \end{aligned}$$

(8)

In other words, $f(x^{P_{opt}}(\lambda ))$ lies at the apex of the contour of the objective function of (2).

As said, lower bounds developed in three references cited above are valid for the general case, and only upper bounds are case specific.

Given ${\bar{x}} \in S_U$, by the definition of $S_U$, the part of the half line emanating from $y^*$ (the locus of apexes of the objective function of (2)) belonging to $\{f(x) \, | \, f(x) \ge f({\bar{x}}) \}$ cannot contain $f(x^{P_{opt}}(\lambda ))$. Thus, the intercept point of this half line with $\{f(x) \, | \, f(x) \ge f({\bar{x}}) \}$ defines upper bounds for some components of $f(x^{P_{opt}}(\lambda ))$. For $k=2$, this is illustrated in Fig. 2. The formula for upper bounds for this case can be found in three references cited above.

Fig. 2

${\bar{x}} \in S_U$ provides a constructive upper bound for $f(x^{P_{opt}}(\lambda ))$ (hypothetical location), namely $f_2({\bar{x}})$, as indicated by $\circ$. Since ${\bar{x}} \in S_U$, $f(x^{P_{opt}}(\lambda ))$ cannot belong to the dotted area

5 Derivation of upper shells

To make use of Proposition 2 we need $S_U$. Usually it is not known which part of ${\mathbb {R}}^n$ should be searched for elements of $S_U$. However, upper shells can be derived from some relaxations of problem (1), as shown by Proposition 3.

Let $X_0 \subset X_0' \subseteq {\mathbb {R}}^n$. Consider the problem

$$\begin{aligned}&vmax f(x) \nonumber \\&\text {subject to: \,} x \in X_0' \,, \end{aligned}$$

(9)

with the set of efficient elements $N'$.

Proposition 3

Any subset of $N'$ is an upper shell to problem 1.

Proof

Since

$$\begin{aligned} \forall \, x \in N' \not \exists \, x' \in N' \ \ x' \prec x, \end{aligned}$$

for any $A \subseteq N'$ we have

$$\begin{aligned} \forall \, x \in A \not \exists \, x' \in A \ \ x' \prec x, \end{aligned}$$

thus A satisfies condition (6).

Since

$$\begin{aligned} X_0 \subset X', \end{aligned}$$

we have

$$\begin{aligned} \forall \, x \in N' \not \exists \, x' \in X_0 \ \ x \prec x'. \end{aligned}$$

Hence,

$$\begin{aligned} \forall \, x \in N' \not \exists \, x' \in N \ \ x \prec x', \end{aligned}$$

and

$$\begin{aligned} \forall \, x \in A \not \exists \, x' \in N \ \ x \prec x', \end{aligned}$$

thus A satisfies condition (7).

In consequence, A is an upper shell. $\square$

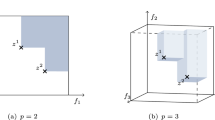
Figure 3 gives a schematic illustration to Proposition 3. The significance of Proposition 3 is in that it paves a way to derive upper shells in an algorithmic way. Its practical usefulness depends on whether the relaxed problems can be solved to optimality in fractions of times spent on deriving incumbents of the original problems unsolved to optimality.

Fig. 3

An illustration to Proposition 3–a case when $N' \ne N$

6 Numerical experiments

We apply the development of Sect. 5 to the case where large-scale multiobjective multidimensional knapsack problems solved by an optimization solver have been not solved to optimality. It is well known (see, e.g., [21]) that the knapsack problem is ${{\mathcal {N}}}{{\mathcal {P}}}$-hard. The multidimensional knapsack problem, being its generalization, is also ${{\mathcal {N}}}{{\mathcal {P}}}$-hard, so the multiobjective multidimensional knapsack problem is as well. It is also known that the difficulty of solving this problem by an MIP solver depends on the number of decision variables as well as the structure of the constraint set (see, e.g., [3]).

In this work, we say that the multiobjective multidimensional knapsack problem is a large-scale problem if it cannot be solved to optimality by a highly specialized MIP solver within a reasonable memory or time limit. We show how in such cases the lacking information about the size of the Pareto suboptimality gap can be retrieved.

The multiobjective multidimensional knapsack problem is formulated as follows.

$$\begin{aligned} \begin{array}{rl} vmax &{} \left\{ \begin{array}{r} \sum ^n_{j=1} c_{1,j}x_j \\ \dots \\ \sum ^n_{j=1} c_{k,j}x_j \end{array} \right. \\ &{} \text {subject to: }\, x \in X_0, \end{array} \end{aligned}$$

(10)

where $X_0 = \{ x \, | \, \sum ^n_{j=1} a_{i,j}x_j \le b_i, \ i=1,\ldots ,m, \, x_j \in \{ 0,1 \} \,, \ j=1,\ldots ,n\}$, and all $a_{i,j}\,, \ c_{i,j}$ are nonnegative.

6.1 Solving multidimensional knapsack problems on the NEOS platform

To solve multiobjective mixed-integer linear problems (3) (weights $\lambda _l$ are real numbers, hence variable s, the objective function in (3), assumes real values) we have to rely on MIP solvers. Our choice was CPLEX, because it is renown as an effective and robust MIP optimizer. Moreover, it is accessible free of charge, e.g., via NEOS platform (https://neos-server.org/neos/solvers/lp:CPLEX/LP.html). Running optimization problems on an open access platform ensures perfect result reproducibility. At the time of numerical experiments, this platform run CPLEX version 12.6.2.0. With NEOS, jobs are terminated whenever time limit of 8 hours of CPU or memory limit of 3 GB is reached. However, as NEOS reaching one of these limits provides no output log, we put the memory limit to 2.048 GB ².

6.2 Multidimensional knapsack test problems

For test problems we selected single-objective multidimensional knapsack problems from Beasley OR Library (http://people.brunel.ac.uk/mastjjb/jeb/info.html), collected in [3], and we extend them to biobjective problems (cf. Sect. 6.3). The library contains 270 problems grouped in 9 groups (the first number indicates the number of constraints, the second indicates the number of variables): (5, 100), (5, 250), (10, 100), (5, 500), (10, 250), (10, 500), (30, 100), (30, 250), (30, 500). Each group contains three subgroups, each with different right hand side coefficients

$$\begin{aligned} b_i = \alpha \sum _{j=1}^n a_{i,j} \end{aligned}$$

where $\alpha$ is the tightness ratio, equal to 0.25 for the first ten, 0.50 for the next ten, and 0.75 for the remaining ten problems in a group.

To prepare input data for CPLEX we converted all the 270 knapsack problems in the Beasley OR Library to the LP format. We made the converted problems publicly available via the web ³.

With CPLEX running on NEOS, we were able to solve to optimality almost all single-objective problems from (5, 500) and (30, 100) groups, a few problems from (10, 250) group and no problem from (10, 500), (30, 250) and (30, 500) groups. The detailed results are given in [13]. In each case, the suboptimality gap ⁴ is defined by the following formula

$$\begin{aligned} \hbox {subopt. gap} = 100*\frac{\hbox {current MIP best bound - objective funct. value for incumbent}}{\hbox {objective funct. value for incumbent}} , \end{aligned}$$

and all those values are provided in CPLEX logs (where the suboptimality gap is termed gap).

6.3 Biobjective multidimensional knapsack problems

We generated biobjective multidimensional knapsack (BMK) problems (10) from Chu and Beasley problems. For each original Chu and Beasley problem we added the second objective function obtained by permuting the coefficients of the first.

To solve BMK problems constructed in that manner, we made use of transformation (3). In case of knapsack problems, the resulting problems are MIP problems, thus they can be handled by CPLEX.

To simplify modifications of the input LP files, reflecting varying weights $\lambda _l$, we introduced two unconstrained (free) variables $f_1$ and $f_2$, equal to the first and the second objective function, respectively,

$$\begin{aligned}&-f_1 + \sum ^n_{j=1} c_{1,j}x_j = 0 \,, \\&-f_2 + \sum ^n_{j=1} c_{2,j}x_j = 0\,. \end{aligned}$$

Both variables $f_1$ and $f_2$ are clearly nonnegative. With that convention, the transformed problems have the following form, consistent with the LP format:

$$\begin{aligned} \begin{array}{c} \min s \\ \begin{array}{cc} \hbox {subject to:} &{} \left\{ \begin{array}{l} s + (\lambda _1 + \rho )f_1 + \rho f_2 \ge \lambda _1 y^*_1 + \rho (y^*_1 + y^*_2), \\ s + \rho f_1 + (\lambda _2 + \rho )f_2 \ge \lambda _2 y^*_2 + \rho (y^*_1 + y^*_2), \\ -f_1 + \sum ^n_{j=1} c_{1,j}x_j = 0 \,, \\ -f_2 + \sum ^n_{j=1} c_{2,j}x_j = 0\,, \\ \sum ^n_{i,j} a_{i,j}x_j \le b_i, \ i=1,\ldots ,m, \\ x_j \in \{ 0,1 \} \,. \end{array} \right. \end{array} \end{array} \end{aligned}$$

(11)

We set $\rho = 0.001$. In order to make $y^*$ a relatively good approximation of ${{{\hat{y}}}}$, we maximized each objective function of problem (10) separately, setting the relative MIP gap tolerance to $1\%$. We set $y^*_l$ to the optimal values of the respective objective functions derived with this tolerance. All these problems were solved in seconds. Obviously, ${{{\hat{y}}}}_l \le y^*_l$. Hence, the use of $y^*$ was legitimate.

We made all 270 transformed BMK problems (in the LP format) publicly available via the web ⁵. For each problem in the set, $\lambda _1$ and $\lambda _2$ were set to default values 0.5. For different settings of $\lambda _l$ , only the first two constraints in (11) have to be modified accordingly.

6.4 Solving biobjective multidimensional knapsack problems on the NEOS platform

We attempted to solve selected biobjective multidimensional problems (in the form (11) and with $\lambda _1 = \lambda _2 = 0.5$), namely the first, the eleventh and the twenty-first problem in group: (10, 500), (30, 100), (30, 250) and (30, 500), respectively. Given problem, let $x^{inc}(\lambda )$ denote an incumbent for a given $\lambda$. The results are given in Table 1. In all problems not solved to optimality the memory limit was reached.

We also attempted to solve one of these problems with as much memory as it was available on NEOS. We selected for that the first problem from the (10, 500) group and we set memory limit to 10 GB ⁶. Even in this case the problem was not solved to optimality, but a better (in terms of the value of the objective function s) incumbent was found, see results in Table 2.

Table 1 Results of solving selected BMK problems; (o) denotes problems solved to optimality, $x^{inc}\hbox { time}$—conservative estimate of time to reach the incumbent, read from the CPLEX logs, $\lambda =(0.5,0.5)$

Table 2 Results of solving the first problem from the (10, 500) group with the extended memory limit 10 GB; $x^{inc}\hbox { time}$—conservative estimate of time to reach the incumbent, read from the CPLEX logs, $\lambda =(0.5,0.5)$

6.5 Bounds at work

In this section, we consider BMK problems, formulated as in (11), which we were not able to solve to optimality because CPLEX reached the memory limit. For example, this is the case of biobjective multidimensional knapsack problems from group (10, 500) of single-objective problems. It is the first group of BMK problems (counting from low dimensions up) in which we were not able to solve to optimality any BMK problem formulated as in (11) with CPLEX run on NEOS, because of the memory limit (we checked this for $\lambda _1 = \lambda _2 = 0.5$, cf. Sect. 6.4). Hence, for problems within this range of dimensions or higher, complementing CPLEX (or any other MIP solver) with a method to derive a kind of lower and upper bound information on Pareto optimal solutions is of utmost importance. However, having no access to CPLEX code, we can do this only in the form of an external procedure.

Moreover, it is well known that MIP solvers derive relatively quickly incumbents close to optimal solutions (in terms of the objective function values) or even optimal solutions but without the proof of optimality. Small incremental improvements or proving (by implicit enumeration) optimality of the incumbent usually consumes the majority of computing time. Existence of lower and upper bounds on objective function values of Pareto optimal solutions allows one to decide if a satisfactory solution within an acceptability range has been already derived and, in consequence, allows to stop the optimization process early.

We applied lower bounds (formula (5)) and upper bounds (Proposition (2)) to selected BMK problems which were not solved on the NEOS platform to optimality because of the memory limit reached. In formula (5), we set ${\bar{L}}_l=0$, (as the absolute lower bound on values of all objective functions of problem (10) is 0), $U_l(\lambda )=y_l^*, \ l=1,2$. The values of $y^{*}_l$ for considered problems are shown in Table 3.

At first glance, it seems impossible to populate upper shells since the effcient set (N), the object to determined, is unknown. However, this can be done with the help of relaxations of problem (1) (see [15]). In this work, we take advantage of the fact that an MIP solver, when solving problem (11), solves also a series of its relaxations. To populate $S_U$, we used the MIP best bound on the objective function s (resulting from a problem relaxation), provided by CPLEX, and we derived corresponding values of objective functions $f_1$ and $f_2$, denoted $f_1^{bb}(\lambda )$ and $f_2^{bb}(\lambda )$, by solving two equations (cf. (3))

$$\begin{aligned} s^{bb}(\lambda )= & {} \lambda _1(y^*_1 - f_1^{bb}(\lambda )) + \rho e^k(y^* - f^{bb}(\lambda )), \nonumber \\ s^{bb}(\lambda )= & {} \lambda _2(y^*_2 - f_2^{bb}(\lambda )) + \rho e^k(y^* - f^{bb}(\lambda )), \end{aligned}$$

(12)

where $s^{bb}(\lambda )$ is the current MIP best bound and $f^{bb}(\lambda )=(f_1^{bb}(\lambda ),f_2^{bb}(\lambda ))$.

Remark 2

Let $x^{bb} \in {{\mathbb {R}}}^n$ be such that $f(x^{bb}) = f^{bb}(\lambda )$. No element of N dominates $x^{bb}$. Indeed, if an element of N dominated $x^{bb}$, then it is immediate to show that this element would produce s smaller than $s^{bb}(\lambda )$ corresponding to $f^{bb}(\lambda )$, a contradiction to $x^{bb}$ defining the MIP best bound. If so, $x^{bb}$ is a valid upper shell element.

At this point, we have no method to ensure condition (7) other than requesting elements x of an upper shell to satisfy $f_1^{bb}(\lambda ) \le f_1(x)$, $f_2^{bb}(\lambda ) \le f_2(x)$ with $x^{bb}$ being clearly the best choice.

By Remark 2, it is guaranteed that $x^{bb}$ is a legitimate element of an upper shell, e.g., one-element upper shell $\{x^{bb}\}$, but it may or may not satisfy conditions of Proposition 2. However, $x^{bb}$ may satisfy these conditions for $x^{P_{opt}}(\lambda ')$ derived with $\lambda ' \not = \lambda$. Along this line, for problems not solved to optimality for given ${\tilde{\lambda }}$ and conditions of Proposition 2 not satisfied, one should attempt to solve another two problems with $\lambda ', \ \lambda ''$, $\lambda '_1 > {\tilde{\lambda }}_1, \ \lambda '_2 < {\tilde{\lambda }}_2$ and $\lambda ''_1 < {\tilde{\lambda }}_1, \ \lambda ''_2 > {\tilde{\lambda }}_2$. These two problems, even if not solved to optimality, produce $(f^{bb}_1(\lambda '), f^{bb}_2(\lambda '))$ and $(f^{bb}_1(\lambda ''), f^{bb}_2(\lambda ''))$ which may yield valid upper bounds for $f(x^{P_{opt}}(\lambda ))$. If successful, these actions can be repeated with another two values of $\lambda$ closer to ${\tilde{\lambda }}$, in the hope to get tighter upper bounds. However, since the problems being solved are discrete, there is a range of $\lambda$ around ${\tilde{\lambda }}$ where all elements of the range yield the same $f(x^{P_{opt}}(\lambda ))$. Thus, there is a limit of upper bound tightness, specific for each individual problem.

It is clear that if $f^{bb}_1(\lambda ')$ is an upper bound for $f_1(x^{P_{opt}}(\lambda ))$ and $f^{bb}_2(\lambda '')$ is an upper bound for $f_2(x^{P_{opt}}(\lambda ))$, then $f^{bb}_1(\lambda ')$ is an upper bound for $f^{bb}_1(\lambda '')$ and $f^{bb}_2(\lambda '')$ is an upper bound for $f^{bb}_2(\lambda ')$. However, the last observation does not apply to problems with $k \ge 3$.

We experimented with the first problems (formulated as in (11)) from (10, 500), (30, 250) and (30, 500) group (as seen in Table 1, the first problem from (30, 100) group was solved to optimality). The results of computations are presented in Table 4. Pareto suboptimality gap is defined as vector $G_{Psub}=(G_{Psub,1},\ldots ,G_{Psub,k})$, where $G_{Psub,l}=100*\frac{U_{l}(\lambda ,S_U) - L_{l}(\lambda ,S_L)}{U_{l}(\lambda ,S_U)}, \ l=1,\ldots ,k$.

Table 3 Results of deriving $y^*$ for selected BMK problems

Table 4 Lower bounds, upper bounds and Pareto suboptimality gaps for selected BMK problems; $x^{inc}\hbox { time}$—conservative estimate of time to reach the incumbent, read from the CPLEX logs

For each problem in Table 4, lower shell $S_L$ was expanded after each new incumbent was derived. After deriving $x^{inc}((0.5,0.5))$, $S_L=\{x^{inc}((0.5,0.5))\}$. After deriving $x^{inc}((0.45,0.55))$, $S_L=S_L\cup \{x^{inc}((0.45,0.55))\}$. After deriving $x^{inc}((0.55,0.45))$, $S_L=S_L\cup \{x^{inc}((0.55,0.45))\}$. We used this workflow (by changing $\lambda$ vectors accordingly) to calculate bounds for the problem, as shown in Table 4 and Table 5.

As seen in Table 4, upper bounds on components of $f(x^{P_{opt}}(\lambda ))$, $\lambda =(0.5,0.5)$, are undefined for the first problem from group (30, 500). This is because elements of upper shells derived for $\lambda '=(0.45,0.55)$ and $\lambda ''=(0.55,0.45)$ do not satisfy conditions of Proposition 2. However, by taking another $\lambda$ vectors, namely ${{\tilde{\lambda }}}'=(0.4,0.6)$ and ${{\tilde{\lambda }}}''=(0.6,0.4)$, one can derive upper shells’ elements being a valid source of upper bounds on components of $f(x^{P_{opt}}(\lambda ))$ (see Table 5).

In Fig. 4 (for the first problem from group (30, 500)), one can see images (in the objective space) of incumbents (marked by rectangles) derived for set of lambda vectors ${\varLambda }=\{\lambda ,\lambda ',\lambda ''\}$. Circles represent images of upper shells derived for set ${\varLambda }$. Filled rectangles represent images of incumbents derived for set of lambda vectors ${{\tilde{{\varLambda }}}}=\{{{\tilde{\lambda }}}',{{\tilde{\lambda }}}''\}$, and bullets—images of upper shells derived for set ${{\tilde{{\varLambda }}}}$. The bottom left corner of the dashed rectangle determines the vector of lower bounds on components of $f(x^{P_{opt}}(\lambda ))$, and the upper right corner—the vector of upper bounds on components of $f(x^{P_{opt}}(\lambda ))$. One can also see that the set of incumbents derived for $\lambda \in {\varLambda }\cup {{\tilde{{\varLambda }}}}$ forms a lower shell. The union of one-element upper shells derived for $\lambda \in {\varLambda }\cup {{\tilde{{\varLambda }}}}$ forms, in turn, an upper shell.

Fig. 4

$\lambda =(0.5,0.5)$. Element $f(x^{P_{opt}}(\lambda ))$ for the first problem of group (30, 500) is bounded by the left lower corner of the rectangle (the vector of lower bounds) and its right upper corner (the vector of upper bounds)

It is worth noting here that the ”branch and bound”-based method for deriving approximations of the efficient set (hence—lower shells) of the multiobjective multidimensional knapsack problem presented in [22], also exploits the concept of relaxation to derive upper shells. However, in that approach, elements of an upper shell are used to control the derivation of elements of the efficient set approximation only.

Table 5 Lower bounds, upper bounds and Pareto suboptimality gaps for the selected problem of group (30, 500); $x^{inc} \text{ time }$ – conservative estimate of time to reach the incumbent, read from the CPLEX logs

7 Final remarks

When it comes to solving large-scale optimization problems, the concept of deriving the whole Pareto front looses its appeal and becomes just impractical. At most, the Pareto front can be navigated by solving instances of problem (2) with various $\lambda$ (the method to interpret $\lambda$ in decision making terms was given in [12, 17, 19]). Then, as suggested by Proposition 2, a number of upper shell elements can mutually and cooperatively provide upper bounds, and these bounds can be strengthened by deriving new upper shell elements.

In this work, we illustrated the proposed approach with pure combinatorial optimization problems. However, it can be applied to other class of problems, e.g., to mixed-integer quadratic programming problems. The cardinality constrained Markowitz portfolio selection problem is an another example of a practical decision-making problem which large-scale instances can be treated with the help of the proposed approach.

The strength of the proposed development, as well as its weakness, lies it its generality (no assumption about problem (1) has been used). Though we present here experiments with biobjective problems, the very principle applies to any number of objectives. However, working efficiently with more than two objectives requires more sophisticated methods to populate upper shells. This will be the subject for further research.