Introduction

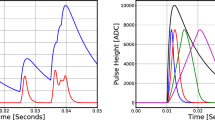
When scintillation crystals coupled to light collectors are employed as gamma-ray spectrometers, one of the primary obstacles faced under high counting rates is pile-up [1,2,3,4,5]. More generally, this is an issue to be taken into account with every spectrometer. With such detectors, each event corresponds to a pulse in the output signal. In order to trace it back to the gamma-rays energy, each pulse amplitude is generally computed as the waveform maximum or area: the higher the pulse amplitude, the higher the energy of the incoming particle. When pile-up occurs, though, two or more events are detected within a timelapse short enough to result in a superposition of their pulses, making the determination of the individual event amplitudes non-trivial. A schematic example of pile-up is shown in Fig. 1).

Fig. 1
figure 1

Schematic example of consecutive events in a spectrometer output signal: a no pile-up occurs; b the two waveforms overlap but they are still clearly distinguishable; c degenerate pile-up: the two events are so close that they appear as a single larger event

Full size image

Traditionally and still in most recently developed algorithms, piled-up events are typically identified and resolved using dedicated Pile-Up Recovery Algorithms (PURA), which restore the constituents waveforms and their amplitudes working directly on the overlapped waveforms [1,2,3,4,5]. However, there are instances in which the pulses overlap so closely that it is impossible to even identify the occurrence of pile-up, resulting in the integration of the pulses into a single spurious event. This phenomenon is known as degenerate pile-up. The consequence of degenerate pile-up – as for pile-up in general – is a general loss of events in the low-energy-side of the pulse-height-spectrum (PHS) and a surplus of spurious events in the high-energy one.

A Degenerate pile-Up Correction Algorithm (DUCA) was developed to rectify the incorrect reconstruction of degenerate pile-up events. The algorithm is based on a statistical approach and can be directly applied to the PHS, based only on its acquisition time, without any direct connection with the piled-up waveforms. The algorithm description will follow in section "Correction Algorithm", divided into basic assumptions in section "Basic Assumptions", the actual spectrum correction in section "Spectrum Correction". Tests of the algorithm with synthetic data follow in section "Algorithm Tests". A discussions on the algorithm stability is then presented in section "Algorithm Stability", before getting to the conclusions in section "Conclusion".

Correction Algorithm

Basic Assumptions

DUCA relies on the assumption that the process of events detection is random enough to follow a Poisson distribution. This assumption allows to compute the probability of detecting two events closer than a certain time \(\tau\) based only on a single parameter, which is the average events rate R, according to Eq. 1 [6]. DUCA could hence also be extended to other time distributions, prior this probability is known or can be computed based on some known parameters.

$$\begin{aligned} P_{\text {pu}} = \text {e}^{-R \cdot \tau } \left( 1 - \text {e}^{-R \cdot \tau } \right) \end{aligned}$$
(1)

If, instead of a generic time window, \(\tau\) is the effective time below which the employed PURA is unable to recover events, then \(P_{\text {pu}}\) is the probability of having degenerate pile-up. The threshold time \(\tau\) can be determined through the application of DUCA itself. For the moment, \(\tau\) is assumed to be a known value non-depending on the overlapped pulses energies. This assertion will be justified in section "Algorithm Stability".

Precisely because of pile-up, though, the measured rate \(R_{m}\) is lower than the true one R. Luckily, it is possible to compute it by solving a transcendental equation:

$$\begin{aligned} R = - \frac{W \left[ -\tau \left( R_m + ( N_r / T ) \right) \right] }{\tau } \end{aligned}$$
(2)

where \(\text {W}\) is the Lambert W function [7], T is the acquisition time and \(N_r\) is the number of events which could have eventually been rejected by PURA.

DUCA relies on an other further assumption: it assumes that each time two events overlap, they result in the spectrum as a single event having as amplitude the sum on their amplitudes. This entails that DUCA works better if the PURA integrates the pulses areas for getting their amplitudes instead of using their maxima or performing fits on the pulse shape. The results here discussed were obtained with a PURA [5] using a sort of a middle-way between pulses areas and fits on the waveforms.

Spectrum Correction

Consider a PHS obtained as a PURA output, with measured bins contents {\(m_i\)}. Once normalised to unity, the new bins contents {\(h_i\)} can be interpreted as a probability distribution function. DUCA works on it bin-wisely. For the \(i^{\text {th}}\) bin, it computes the probability of getting spurious events \(P_i^{\text {in}}\) and that of losing true events \(P_i^{\text {out}}\). Then it corrects consequently:

$$\begin{aligned} h^*_i = h_i + P^{\text {out}}_i - P^{\text {in}}_i \end{aligned}$$
(3)

where \(h^*_i\) is the correct bin probability.

\(P^{\text {out}}_i\) is the probability of simultaneously getting an event in the \(i^{\text {th}}\) bin and having it piled-up with at least an other event, which means:

$$\begin{aligned} P^{\text {out}}_i = h^*_i \, P_{\text {pu}} \end{aligned}$$
(4)

The first bin can not gain spurious events and hence \(P^{\text {in}}_1 = 0\). This allows to correct it as:

$$\begin{aligned} h^*_1 = \frac{h_1}{1 - P_{\text {pu}}} \end{aligned}$$
(5)

For every other bin, on the other hand, computing \(P_i^{\text {in}}\) requires some math. In addition, it also requires to put an arbitrary threshold on the number of possible piled-up events taken into account. Suppose, for example, that only single pile-up is considered. Then a sum has to be performed over all possible couples of events whose areas sum is equivalent to the current bin and require them to be piled-up. Note that swapping the order of two piled-up events corresponds to consider a different case of pile-up and that both have to be taken into account in the sum.

$$\begin{aligned} P^{\text {in}}_i = \sum _{j < i} \, h^*_j \, h^*_{i - j} \, P_{\text {pu}} \end{aligned}$$
(6)

A note should be pointed out about the finite width of the bins. This point can be better explained with an example. Consider the case in which \(i = 7\) and \(j = 3\) in Eq. 6. In a not-rebinned spectrum, the j-th bin edges would be 2 and 3 and the \((i - j)\)-th bin edges would be 3 and 4. This means that the sum of two of these events could range from 5 to 7, hence covering the i-th bin itself but also the \((i - 1)\)-th one. Similarly, when considering \(i = 6\) in the previous step, the probability would be shared with the \(i = 5\) bin. In DUCA, the bins width is considered narrow enough to neglect this effect.

If, for example, double and triple pile-up are also taken into account, the formula gets recursively more complicated, since the second and third event can in turn be the result of degenerate pile-up. Equation 7 shows how Eq. 6 changes in case both double and triple pile-up are taken into account.

$$\begin{aligned} \begin{aligned} P^{\text {in}}_i = \sum _{j< i} \, h^*_j \, \Bigg [&h^*_{i - j} (P_{\text {pu}} - P^2_{\text {pu}} - P^3_{\text {pu}}) \, \\&+ \sum _{k< i - j} \, h^*_k \bigg ( h^*_{i - j - k} \, (P^2_{\text {pu}} - P^3_{\text {pu}}) \, \\&+ \sum _{l < i - j - k} \, h^*_l \, h^*_{i - j - k - l} \, P^3_{\text {pu}} \bigg ) \Bigg ] \end{aligned} \end{aligned}$$
(7)

Note that \(P^{\text {in}}_i\) always depends only on the bins corresponding to lower amplitudes with respect to the \(i^{\text {th}}\) itself. Therefore, the correction of the spectrum starts from the \(1^{\text {st}}\) bin and moves toward higher amplitudes, one bin at a time.

Once \(P^{\text {in}}_i\) is known, the \(i^{\text {th}}\) bin can be corrected according to Eq. 8.

$$\begin{aligned} h^*_i = \frac{h_i - P^{\text {in}}_i}{1 - P_{\text {pu}}} \end{aligned}$$
(8)

Lastly, it is sufficient to multiply {\(h^*_i\)} for the acquisition time and the acquisition rate R to get the correct bins content {\(m^*_i\)}.

If N is the number of piled-up events, DUCA has a O(\(n^N\)) time complexity and hence it could be convenient to perform a moderate rebinning of the spectrum before its application. So, a trade-off is to be considered between running time and accuracy of the reconstructed spectrum.

Algorithm Tests

Synthetic Gaussian Spectrum

A synthetic spectrum with a Gaussian distribution was used to check DUCA behaviour on bins with decreasing content within different orders of magnitude and find its working limits.

One billion waveforms 150 ns long were generated, with 5 ns sampling frequency (30 points each) and double floating points amplitude precision, according to a Poisson distribution in time with \(R = {1\,\textrm{MHz}}\) average rate. A Gaussian centered in zero and with 3000 channels as standard deviation was employed as probability distribution.

For the used PURA [5], the effective threshold time \(\tau\) was 35 ns (see section "Algorithm Stability"), entailing a degenerate pile-up probability of \(p_{\text {pu}} = {}{3.3}{}\%\), according to Eq. 1. The output spectrum was then rebinned by a factor 32 before DUCA application.

No source of noise was added in order to not introduce further sources of discrepancies between the true spectrum and the reconstructed one, so that any difference would have only been due to a mis-reconstruction of the spectrum by PURA and DUCA.

In Fig. 2, the true synthetic spectrum is shown together with PURA and DUCA outputs. DUCA was run both considering up to 2 (level 1) or 3 (level 2) simultaneously piled-up events. As expected, the PURA underestimates the number of events in the low-energy-side of the spectrum and finds a surplus in the high-energy one. DUCA, on the other hand, is capable of restoring the original shape if run at the second level. The third level (4 piled-up events) leads to a negligible difference and was hence not even shown in the plot.

Fig. 2
figure 2

Synthetic Gaussian spectrum. Comparison between the true one (filled area) and those obtained as PURA (red line) and DUCA outputs (gray and black lines). Linear scale on the left and log10 scale on the right. See the text for description

Full size image

Some events are missing in the low energy range of the spectrum because they were below the PURA trigger and not because of not recovered pile-up.

The level 2 DUCA histogram is close to the original one up to around channel 6000, so it can be concluded that DUCA is capable of restoring the correct bins content down to \(2 \cdot 10^{-5}\) order of magnitude compared to the most populated bin in the spectrum.

Synthetic Uniform Spectra and Varying Count Rates

In order to quantify the quality of DUCA corrected spectra as a function of the events rate, nine synthetic, uniform spectra one billion events each were generated, each corresponding to a different rate R, ranging from 20 kHz to 1 MHz. The maximum generated event amplitude was 500. The waveforms characteristics were the same of the Gaussian spectrum. This way, the degenerate pile-up probability ranged between 0.07 to 3.3%. Even this time, the pulses were produced without adding electrical noise. In addition, DUCA was run at its first level (2 piled-up events at most) to fasten the analysis.

For each spectrum, DUCA was applied after PURA and and a 32-bin rebinning of the histogram, then both algorithms outputs were compared to the true synthetic spectrum. For the comparison, a simplified version of the Earth Mover’s Distance (EMD) was employed [8]. This figure of merit is a measure of the dissimilarity between two histogram distributions, which in this case was computed simply as the sum of the absolute differences between the bins contents of the two histograms, normalized to the original total number of events:

$$\begin{aligned} \text {EMD} = \frac{1}{N} \sum _i \left| {h_i}_1 - {h_i}_2 \right| \end{aligned}$$
(9)

where N is the original total number of events and \(\{ h_i \}_1\) and \(\{ h_i \}_2\) are the two histograms under consideration. In short, its value corresponds to the fraction of events out of place in a distribution with respect to a reference one. Since pile-up is a concern when the high-energy-side of the PHS is under study, the out of place events were only considered if in the high-energy-side itself, after the last non-empty bin of the original uniform distribution.

Figure 3 shows the percentage EMD both for PURA and DUCA in the plot above and their percentage ratio in the plot below, as functions of the events rate R. In particular, the metric in Eq. 10 was used for the EMDs comparison.

$$\begin{aligned} \text {EMDs ratio} = \frac{\text {EMD}_{\text {DUCA}} - \text {EMD}_{\text {PURA}}}{\text {EMD}_{\text {PURA}}} \end{aligned}$$
(10)

The fraction of out of place events for PURA increases with the events rate up to 1.5% at 1 MHz, while DUCA EMD also increases but its absolute value with respect to PURA EMD saturates down to 80%. It could be useful to point out that the PURA fraction of out-of-place events is lower than the expected fraction of piled-up because only the high-energy-side of the spectrum is taken into account.

Fig. 3
figure 3

Percentage Earth Mover’s Distances for PURA and DUCA on uniform spectra with varying events rate in the plot above. DUCA percentage improvement with respect to PURA in the plot below

Full size image

Algorithm Stability

As already mentioned in section "Basic Assumptions", the effective threshold time \(\tau\) of a certain PURA can be estimated with DUCA itself. In principle, because of noise, \(\tau\) could depend on the amplitudes of the pulses at stake: the higher the amplitudes of the pulses, the higher the probability for PURA to success. Though, it is still possible to identify an effective \(\tau\) which minimizes the DUCA output EMD with respect to the original spectrum. This stresses out the importance of simulating a measurement before applying DUCA, if the threshold time is not known a priori.

The first bins of a measured PHS are always empty, being a trigger employed to assess the presence of an event in the signal oscillogram. At most, they may contain events as piled-up events recovered by the PURA@. Though, this is not a concern at all for DUCA. This was proven with a 1 MHz uniformly distributed synthetic spectrum, by setting the first 50 bins to zero. Whether these events were present or not in the spectrum did not affect the high-energy-side if not for less than 1% of the events removed by DUCA.

Regarding the maximum working rate, DUCA limitations are due to its intrinsic probability nature. Whenever the probability of multiple pile-up is very high (at least more than some MHz), also the total number of events would have to be high enough to guarantee the reliability of DUCA application. By the way, DUCA limitations do not represent a concern, since the main restriction is linked to the former PURA application. Whenever the events rate is so high that the probability of getting more than three piled-up events is not negligible, any PURA capability of restoring non-degenerate piled-up events would not be reliable anymore.

Lastlty, the algorithm stability with respect to the possible misplacement of some events in the spectrum was tested by changing the seed of the synthetic spectrum random number generator. This lead to a \(\pm 4\%\) variation in the EMDs ratio at 1 MHz, thus prooving the robustness of DUCA.

Conclusions

Pile-up represents a concern for spectrometers operating at high counting rates. In case of degenerate pile-up, current Pile-Up Recovery Algorithms (PURA) can not identify the occurrence of pile-up.

A Degenerate pile-Up Correction Algorithm (DUCA) was developed to correct PHS for degenerate pile-up. DUCA corrects the spectra bin-wisely and relies on a single parameter, which is the PURA pile-up discrimination threshold time. In case it is not known, this threshold time can be estimated with DUCA itself with the aid of synthetic spectra.

DUCA is based on two assumptions: the detected events follow a Poisson distribution in time; in case of degenerate pile-up, the spurious event amplitude corresponds to the sum of the piled-up events amplitudes. The algorithm does not intrinsically present concerning rate working limits, nor is affected by the presence of a trigger at low energies.

It was tested on synthetic uniform spectra ranging from 20 kHz up to 1 MHz, always improving the Earth Mover’s Distance with respect to the original one down to -80% at 1 MHz.

DUCA can hence be employed to correct high-counting-rates spectra from degenerate pile-up at least up to 1 MHz.