1 Introduction

In the late 1990’s, M. Gromov introduced the notion of mean topological dimension for a continuous map \( \phi : X\rightarrow X\), which is denoted by \(\text {mdim}(X,\phi )\), where X is a compact topological space. The mean topological dimension is an invariant under conjugacy. Furthermore, this is a useful tool in order to characterize dynamical systems that can be embedded in \((([0,1]^m)^{{\mathbb {Z}}},\sigma )\), where \(\sigma \) is the left shift map on \(([0,1]^m)^{{\mathbb {Z}}} \) (see [12, 13]). In [8], Lindenstrauss and Weiss proved that any homeomorphism \(\phi : X\rightarrow X\) that can be embedded in \((([0,1]^m)^{{\mathbb {Z}}},\sigma )\) must satisfy that \(\text {mdim}(X,\phi )\le m\). In [6], Gutman and Tsukamoto showed that, if \((X, \phi )\) is a minimal system with \(\text {mdim}(X, \phi ) <m/ 2\), then we can embed it in \((([0, 1]^{m})^{{\mathbb {Z}}},\sigma )\). In [11], Lindenstrauss and Tsukamoto presented an example of a minimal system with mean topological dimension equal to m/2 that cannot be embedded into \((([0, 1]^{m})^{{\mathbb {Z}}},\sigma )\), which show the constant m/2 is optimal. Some applications in information theory can be found in [10] and [9].

The mean topological dimension is difficult to calculate. Therefore, Lindenstrauss and Weiss in [8] introduced the notion of metric mean dimension, which is an upper bound for the mean topological dimension. The metric mean dimension is a metric-dependent quantity (this dependence is not continuous, as we can see in [3]), therefore, it is not an invariant under topological conjugacy.

1.1 Metric mean dimension

Let X be a compact metric space endowed with a metric d. For any \(n\in {\mathbb {N}}\), we define \(d_n:X\times X\rightarrow [0,\infty )\) by

$$\begin{aligned} d_n(x,y)=\max \{d(x,y),d(\phi (x),\phi (y)),\dots ,d(\phi ^{n-1}(x),\phi ^{n-1}(y))\}. \end{aligned}$$

Fix \(\varepsilon >0\). We say that \(A\subset X\) is an \((n,\phi ,\varepsilon )\)-separated set if \(d_n(x,y)>\varepsilon \), for any two distinct points \(x,y\in A\). We denote by \(\text {sep}(n,\phi ,\varepsilon )\) the maximal cardinality of any \((n,\phi ,\varepsilon )\)-separated subset of X. Set

$$\begin{aligned} \text {sep}(\phi ,\varepsilon )=\underset{n\rightarrow \infty }{\limsup }\frac{1}{n}\log \text {sep}(n,\phi ,\varepsilon ). \end{aligned}$$

We say that \(E\subset X\) is an \((n,\phi ,\varepsilon )\)-spanning set for X if for any \(x\in X\) there exists \(y\in E\) such that \(d_n(x,y)<\varepsilon \). Let \(\text {span}(n,\phi ,\varepsilon )\) be the minimum cardinality of any \((n,\phi ,\varepsilon )\)-spanning subset of X. Set

$$\begin{aligned} \text {span}(\phi ,\varepsilon )=\underset{n\rightarrow \infty }{\limsup }\frac{1}{n}\log \text {span}(n,\phi ,\varepsilon ). \end{aligned}$$

Definition 1.1

The topological entropy of \(\phi :X\rightarrow X\) is defined by

$$\begin{aligned} h_{\text {top}}(\phi )=\lim _{\varepsilon \rightarrow 0} \text {sep}(\phi ,\varepsilon )=\lim _{\varepsilon \rightarrow 0} \text {span}(\phi ,\varepsilon ). \end{aligned}$$

Definition 1.2

We define the lower metric mean dimension and the upper metric mean dimension of \((X,d,\phi )\) by

$$\begin{aligned} \underline{\text {mdim}}_{\text {M}}(X,d,\phi )&=\liminf _{\varepsilon \rightarrow 0} \frac{\text {sep}(\phi ,\varepsilon )}{|\log \varepsilon |}= \liminf _{\varepsilon \rightarrow 0} \frac{\text {span}(\phi ,\varepsilon )}{|\log \varepsilon |}\\ \text {and }\quad \overline{\text {mdim}}_{\text {M}}(X,d,\phi )&=\limsup _{\varepsilon \rightarrow 0} \frac{\text {sep}(\phi ,\varepsilon )}{|\log \varepsilon |}=\limsup _{\varepsilon \rightarrow 0} \frac{\text {span}(\phi ,\varepsilon )}{|\log \varepsilon |}, \end{aligned}$$

respectively.

Remark 1.3

Throughout the paper, we will omit the underline and the overline on the notations \(\underline{\text {mdim}}_{\text {M}}\) and \(\overline{\text {mdim}}_{\text {M}}\) when the result be valid for both cases, that is, we will use \(\text {mdim}_{\text {M}}\) for the both cases.

In recent years, the metric mean dimension has been the subject of multiple investigations, which can be verified in the bibliography of the present work. The purpose of this manuscript is to complete the research started in [5, 14] and [2], concerning to the topological properties of the level sets of the metric mean dimension map.

In [5], Theorem C, the authors proved the set consisting of continuous maps \(\phi :[0,1]\rightarrow [0,1]\) such that \(\underline{\text {mdim}}_\text {M}([0,1], |\cdot |,\phi )=\overline{\text {mdim}}_\text {M}([0,1], |\cdot |,\phi )=\alpha \), for a fixed \(\alpha \in [0,1]\), is dense in \(C^{0}([0,1])\) (see also [2], Theorem 4.1). Furthermore, in Theorem A they showed if N is an n-dimensional compact riemannian manifold, with \(n\ge 2\), and riemannian metric d, the set of homeomorphisms \(\phi :N\rightarrow N\) such that \(\overline{\text {mdim}}_\text {M}(N, d,\phi )=n\) contains a residual set in \(\text {Hom}(N)\) (see a particular case of this fact in [14], Proposition 10). Next, for any \(n\ge 1\), the set consisting of continuous maps \(\phi :N\rightarrow N\) such that

$$\begin{aligned} \underline{\text {mdim}}_\text {M}(N, d,\phi )=\overline{\text {mdim}}_\text {M}(N, d,\phi )=\alpha \end{aligned}$$

is dense in \(C^{0}(N)\), for a fixed \(\alpha \in [0,n]\) (see [2], Theorem 4.5, and [1], Theorem 3.6).

We consider the next level sets of the metric mean dimension for homeomorphisms:

Definition 1.4

For \(\alpha ,\beta \in [0,n]\), with \(\alpha \le \beta \), we will set

$$\begin{aligned} {H}_{\alpha }^{\beta }(N)=\{\phi \in \text {Hom}(N): \underline{\text {mdim}}_\text {M}(N, d,\phi )=\alpha \, \, \text {and} \, \, \overline{\text {mdim}}_\text {M}(N, d,\phi )=\beta \}. \end{aligned}$$

If \(\alpha =\beta \), we denote \({H}_{\alpha }^{\alpha }(N)\) by \({H}_{\alpha }(N)\).

If \(n=1\), then \({H}_{\alpha }^{\beta }(N)=\emptyset \) for \(0<\alpha \le \beta \le 1\). This is due to the fact that any homeomorphism on a one-dimensional compact Riemannian manifold has zero topological entropy, leading to zero metric mean dimension. Our initial result is presented in the following theorem, proved in [1], Theorem 3.6, specifically for continuous maps on the interval.

Theorem 1.5

Let \(n\ge 2\). For any \(\alpha ,\beta \in [0,n]\), with \(\alpha \le \beta \), the set \({H}_{\alpha }^{\beta }(N)\) is dense in \(Hom (N)\).

Using the techniques employed to prove Theorem 1.5, we will provide a new proof of Theorem A in [5], that is:

Theorem 1.6

The set \({\overline{H}}(N)=\{\phi \in Hom (N):\overline{mdim }_{M }(N,d,\phi )=n\}\) contains a residual set in \(Hom (N)\).

Yano, in [15], defined a kind of horseshoe in order to prove the set consisting of homeomorphisms \(\phi :N\rightarrow N\) with infinite entropy is generic in \(\text {Hom}(N)\), where N is an n dimensional compact manifold, with \(n\ge 2\). If we want to construct a continuous map with infinite entropy we can consider an infinite sequence of horseshoes such that the number of legs is unbounded. For the metric mean dimension case, in [5] and [14] the authors used horseshoe in order to prove the set consisting of homeomorphisms \(\phi :N\rightarrow N\) with upper metric mean dimension equal to n (which is the maximal value of the metric mean dimension for any map defined on N) is generic in \(\text {Hom}(N)\). To get metric mean dimension equal to n we must construct a sequence of horseshoes such that the number of legs increases very quickly compared to the decrease in their diameters.

Estimating the precise value of the metric mean dimension for a homeomorphism, and hence to obtain a homeomorphism with metric mean dimension equal to a fixed \(\alpha \in (0,n)\), is harder and not trivial sake. We need to establish a precise relation between the sizes of the horseshoes together with the number of appropriated legs to control the metric mean dimension. This is our main tool (see Lemma 2.3).

The paper is organized as follows: In Sect. 2, we will construct homeomorphisms, defined on an n-cube, with metric mean dimension equal to \(\alpha \), for a fixed \(\alpha \in (0,n]\). Furthermore, given \(\alpha ,\beta \in [0,n]\), with \(\alpha \le \beta \), we will construct examples of homeomorphisms \(\phi :[0,1]^{n}\rightarrow [0,1]^{n}\) such that \( \underline{\text {mdim}}_{\text {M}}([0,1]^{n},d,\phi )=\alpha \) and \( \overline{\text {mdim}}_{\text {M}}([0,1]^{n},d,\phi )=\beta .\) In Sect. 3, we will prove Theorem 1.5. Finally, in Sect. 4, we will show Theorem 1.6.

2 Homeomorphisms on the n-cube with positive metric mean dimension

Let \(n\ge 2\). Given \(\alpha , \beta \in [0,n]\), \(\alpha \le \beta \), in this section we will construct a homeomorphism \(\phi _{\alpha , \beta }\), defined on an n-cube, with lower metric mean dimension equal to \(\alpha \) and upper metric mean dimension equal to \(\beta \) (see Lemma 2.4). This construction will be the main tool to prove the Theorem 1.5, since if a homeomorphism present a periodic orbit, then we can glue, in the \(C^0\)-topology, along this orbit the dynamic of \(\phi _{\alpha ,\beta }\).

The construction of \(\phi _{\alpha , \beta }\) requires a special type of horseshoe. So, let us present the first definition.

Definition 2.1

(n-dimensional \((2k+1)^{n-1}\)-horseshoe) Fix \(n\ge 2\). Take \(E=[a,b]^{n}\) and set \(|E|=b-a\). For a fixed natural number \(k>1\), take the sequence \(a=t_0<t_{1}<\cdots<t_{4k}<t_{4k+1}=b \), with \(|t_{i}-t_{i-1}|=\frac{b-a}{4k+1}\), and consider

$$\begin{aligned} H_{i_{1},i_{2},\dots ,i_{n-1}}=[a,b]\times [t_{i_{1}-1},t_{i_{1}}]\times \cdots \times [t_{i_{n-1}-1}, t_{i_{n-1}}],\quad \text {for }i_{j}\in \{1,\dots , 4k+1\}. \end{aligned}$$

Take \(a=s_0<s_{1}<\cdots<s_{2(2k+1)^{n-1}-2}<s_{2(2k+1)^{n-1}-1}=b \), with \(|s_{i}-s_{i-1}|=\frac{b-a}{2(2k+1)^{n-1}-1}\), and consider

$$\begin{aligned} V_{l}=[s_{l-1}, s_{l}]\times [a,b]^{n-1},\quad \text {for } l=1, 2, \dots , 2(2k+1)^{n-1}-1. \end{aligned}$$

We say that \(E\subseteq A\subseteq {\mathbb {R}}^{n}\) is an n-dimensional \((2k+1)^{n-1}\)-horseshoe for a homeomorphism \(\phi :A\rightarrow A\) if:

  • \(\phi (a,a,\dots ,a,b)=(a,a,\dots ,a,b)\) and \(\phi (b,b,\dots ,b,a)=(b,b,\dots ,b,a)\);

  • For any \(H_{i_{1},i_{2},\dots ,i_{n-1}}\), with \(i_{j}\in \{1,3,\dots , 4k+1\}\), there exists some \(l\in \{1,3,\dots , 2(2k+1)^{n-1}-1\}\) with

    $$\begin{aligned} \phi (V_{l})=H_{i_{1},i_{2},\dots ,i_{n-1}} \quad \text {and}\quad \phi |_{V_{l}}:V_{l}\rightarrow H_{i_{1},i_{2},\dots ,i_{n-1}} \quad \text {is linear}. \end{aligned}$$

  • For any \(l=2,4,\dots , 2(2k+1)^{n-1}-2\), \(\phi (V_{l})\subseteq A{\setminus } E\).

In that case, the sets \(H_{i_{1},i_{2},\dots ,i_{n-1}}\), with \(i_{j}\in \{1,3,\dots , 4k+1\}\) are called the legs of the horseshoe.

Fig. 1
figure 1

2-dimensional 5-horseshoe

Full size image
Fig. 2
figure 2

3-dimensional 9-horseshoe

Full size image

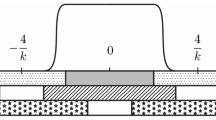
In Fig. 1 we present an example of a 2-dimensional 5-horseshoe. In that case, \(k=2\), we have \(2(2k+1)-1\) divisions \(V_{i}\) of \([a,b]^{2}\), and \(2k+1\) legs \(H_{i}\), for \(i=1,3,5,7,9\). In Fig. 2 we have a 3-dimensional 9-horseshoe (we only show \(\phi (E)\cap E\) in that figure). In that case, \(k=1\), we have \(2(2k+1)^{2}-1\) divisions \(V_{i}\) of \([a,b]^{3}\), and \((2k+1)^{2}\) legs \(H_{i,j}\), for \(i,j=1,3,5\).

Note if \(E=[a,b]^{n}\) is an n-dimensional \((2k+1)^{n-1}\)-horseshoe for \(\phi \), then

$$\begin{aligned} \phi ^{2}(V_{l_{1}}\cap H_{i_{1}^{(1)},\dots ,i_{n-1}^{(1)}})\cap V_{l_{2}}\cap H_{i_{1}^{(2)},\dots ,i_{n-1}^{(2)}}\ne \emptyset , \end{aligned}$$

for any \(l_{1},l_{2}\in \{1,3\dots , 2(2k+1)^{n-1}\}\) and \(i_{1}^{(1)},\dots ,i_{n-1}^{(1)},i_{1}^{(2)},\dots ,i_{n-1}^{(2)}\in \{1,3,\dots , 4k+1\}\) (see Fig. 3).

Fig. 3
figure 3

E is the first square, is a 2-dimensional 3-horseshoe for \(\phi \)

Full size image

The assumptions \(\phi (a,a,\dots ,a,b)=(a,a,\dots ,a,b)\) and \(\phi (b,b,\dots ,b,a)=(b,b,\dots ,b,a)\) is just to be able to extend \(\phi \) to a homeomorphism \(\tilde{\phi }:E^{\prime }\rightarrow E^{\prime }\), where \(E^{\prime }\) is an n-cube with \(E\subset E^{\prime }\), such that \(\tilde{\phi }|_{\partial E^{\prime }}\equiv Id\) and \(h_{\text {top}}(\phi ^{\prime })=h_{\text {top}}(\phi |_{E\cap \phi (E )})\) (see Lemma 2.2). Thus, our strategy to prove the Theorem 1.5 will be to use local charts to glue such horseshoes along of periodic orbits of a homeomorphism.

Lemma 2.2

Let \(E, E^{\prime }\subseteq {\mathbb {R}}^n\) be closed n-cubes with \(E \subsetneqq (E^{\prime })^{\circ }\) and fix \(k\in {\mathbb {N}}\). There exists a homeomorphism \(\phi : E^{\prime }\longrightarrow E^{\prime }\) such that \(\phi |_{E}: E \longrightarrow E\) is an n-dimensional \((2k+1)\)-horseshoe, \(\phi |_{\partial E^{\prime }}\equiv Id\) and \(h_{top }(\phi )=h_{top }(\phi |_{E\cap \phi (E )})\).

Inspired by the results shown in [5] and [14] to obtain a homeomorphism \(\phi :N\rightarrow N\) with upper metric mean dimension equal to \(\text {dim}(N)\), we present the next lemma, which proves for any \(\alpha \in (0,n]\), there exists a homeomorphism \(\phi :\mathcal {\mathcal {C}}:= [0,1]^n\rightarrow \mathcal {\mathcal {C}}\), with (upper and lower) metric mean dimension equal to \(\alpha \).

On any n-cube \(E\subseteq {\mathbb {R}}^{n}\), we will consider the metric inherited from \({\mathbb {R}}^{n}\), \(\Vert \cdot \Vert \), given by

$$\begin{aligned} \Vert (x_{1},\dots ,x_{n})-(y_{1},\dots ,y_{n})\Vert = \sqrt{(x_{1}-y_{1})^{2}+\cdots +(x_{n}-y_{n})^{2}}. \end{aligned}$$

Lemma 2.3

Let \(\phi : {\mathcal {C}}\rightarrow {\mathcal {C}}\) be a homeomorphism, \(E_{k}=[a_k, b_k]^{n}\) and \(E_{k}^{\prime }\) sequences of cubes such that:

C1.:

\( E_{k}\subset (E_{k}^{\prime })^{\circ }\) and \((E_{k}^{\prime })^{\circ }\cap (E_{s}^{\prime })^{\circ }=\emptyset \) for \(k\ne s\).

C2.:

\(S:=\cup _{k=1}^{\infty }E^{\prime }_{k}\subseteq {\mathcal {C}}\).

C3.:

each \(E_{k}\) is an n-dimensional \(3^{k(n-1)}\)-horseshoe for \(\phi \);

C4.:

For each k, \(\phi |_{E_{k}^{\prime }}: E_{k}^{\prime }\rightarrow E_{k}^{\prime }\) satisfies the properties in Lemma 2.2;

C5.:

\(\phi |_{{\mathcal {C}}{\setminus } S}: {\mathcal {C}}{\setminus } S\rightarrow {\mathcal {C}}{\setminus } S\) is the identity.

We have:

  1. (i)

    For a fixed \(r\in (0,\infty )\), if \(|E_{k}|=\frac{B}{3^{kr}}\) for each \(k\in {\mathbb {N}}\), where \(B>0\) is a constant, then

    $$\begin{aligned} mdim _{M }({\mathcal {C}},\Vert \cdot \Vert ,\phi ^{2}) =\frac{n}{r+1}. \end{aligned}$$
  2. (ii)

    If \(|E_{k}|=\frac{B}{k^{2}}\) for each \(k\in {\mathbb {N}}\), where \(B>0\) is a constant, then

    $$\begin{aligned} mdim _{M }( {\mathcal {C}},\Vert \cdot \Vert ,\phi ^{2}) =n. \end{aligned}$$

Proof

We will prove (i), since (ii) can be proved analogously. Set \(\varphi =\phi ^{2}\). Note that

$$\begin{aligned} {{\text {mdim}}_{\text {M}}}( {\mathcal {C}},\Vert \cdot \Vert ,\varphi ) ={{\text {mdim}}_{\text {M}}}(S,\Vert \cdot \Vert ,\varphi |_{S} ). \end{aligned}$$

Take any \(\varepsilon \in (0,1)\). For any \(k\ge 1\), set \( \varepsilon _k= \frac{|E_{k}|}{2(3^{k})-1} =\frac{B}{(2(3^{k})-1)3^{kr}} \). There exists \(k\ge 1\) such that \(\varepsilon \in [\varepsilon _{k+1}, \varepsilon _{k}]\). We have

$$\begin{aligned} \text {sep}( n, \varphi , \varepsilon )\ge \text {sep}( n, \varphi , \varepsilon _{k})\ge \text {sep}( n, \varphi |_{E_{k}\cap \phi (E_{k})}, \varepsilon _{k}) \quad \text {for any }n\ge 1. \end{aligned}$$

Since \(E_{k}\) is an n-dimensional \(3^{k(n-1)}\)-horseshoe for \(\phi \), for each \(k\ge 1\), consider

$$\begin{aligned} {H}^{k}_{i_{1},i_{2},\dots ,i_{n-1}}=[a_{k},b_{k}]\times [t_{i_{1}-1},t_{i_{1}}]\times \cdots \times [t_{i_{n-1}-1}, t_{i_{n-1}}],\quad \text {for }i_{j}=1,\dots , 2(3^{k}) -1, \end{aligned}$$

and

$$\begin{aligned} V_{l}^{k}=[s_{l-1}, s_{l}]\times [a_{k},b_{k}]^{n-1},\quad \text {for }l=1,\dots , 2(3^{k})^{n-1}-1, \end{aligned}$$

as in Definition 2.1. For each \(j=1,\dots , n-1\), let \(i_{j}\in \{1,3,5,\dots , 2(3^{k})-1\}\) and take

$$\begin{aligned} C^{k}_{l,i_{1},\dots ,i_{n-1}} = H^{k}_{i_{1},i_{2},\dots ,i_{n-1}}\cap V^{k}_{l} \quad \text {for each }l\in \{1,3,\dots , 2(3^{k})^{n-1}-1\}. \end{aligned}$$

For \(t=1,\dots ,m\), let \(i_{1}^{(t)},\) \( \dots ,i_{n-1}^{(t)}\in \{1,3,\dots , 2(3^{k}) -1\}\), \(l_{j_{t}}\in \{1,3,\dots , 2(3^{k})^{n-1}-1\}\) and set

$$\begin{aligned} C^{k}_{l_{j_{2}}, i_{1}^{(2)},\dots , i_{n-1}^{(2)},l_{j_{1}},i_{1}^{(1)},\dots , i_{n-1}^{(1)}}&=\varphi ^{-1}\left[ \varphi \left( C^{k}_{ l_{j_{2}},i_{1}^{(2)},\dots , i_{n-1}^{(2)}}\right) \cap C^{k}_{l_{j_{1}},i_{1}^{(1)},\dots ,i_{n-1}^{(1)}}\right] \\&\vdots \\ C^{k}_{l_{j_{m}}, i_{1}^{(m)},\dots ,i_{n-1}^{(m)}, \dots , l_{j_{1}},i_{1}^{(1)}, i_{1}^{(1)},\dots , i_{n-1}^{(1)}}&=\varphi ^{-(m-1)}\\&\left[ \varphi ^{m-1}\left( C^{k}_{l_{j_{m}},i_{1}^{(m)},\dots ,i_{n-1}^{(m)}, \dots ,l_{j_{2}}, i_{1}^{(2)},\dots ,i_{n-1}^{(2)}}\right) \cap C^{k}_{l_{j_{1}},i_{1}^{(1)},\dots ,i_{n-1}^{(1)}}\right] \end{aligned}$$

From the definition of \(\varphi \), these sets are non-empty. Furthermore, we can choose a sequence \(s_{1},\dots ,s_{3^{k}}\in \{1,3,\dots , 2(3^{k})^{n-1}-1\}\) such that, if x and y belong to different sets \( C^{k}_{s^{(m)},i_{1}^{(m)},\dots ,i_{n-1}^{(m)}, \dots ,s_{(m)}, i_{1}^{(1)},\dots , i_{n-1}^{(1)}} \), where \(s^{(j)}\in \{s_{1},\dots ,s_{3^{k}}\}\), then \(d_{m}(x,y)>\varepsilon _{k}\). Note that we have \(3^{km}3^{k(n-1) m}= 3^{knm}\) sets of this form. Hence,

$$\begin{aligned} \text {sep}(m, \varphi , \varepsilon _{k}) \ge 3^{knm} \quad \text {and thus}\quad \text {sep}(\varphi , \varepsilon )\ge \log {3^{kn}}. \end{aligned}$$

Therefore,

$$\begin{aligned} {\underline{\text {mdim}}_{\text {M}}}(S ,\Vert \cdot \Vert ,\varphi |_{S} )&= \liminf _{\varepsilon \rightarrow 0} \frac{\text {sep}(\varphi ,\varepsilon )}{|\log {\varepsilon }|} \ge \lim _{k\rightarrow \infty }\frac{\log 3^{kn}}{|\log \varepsilon _{k+1}|} \\&=\lim _{k\rightarrow \infty }\frac{\log 3^{kn}}{\log [(2(3^{k+1})-1)3^{(k+1)r}B^{-1}]} = \lim _{k\rightarrow \infty }\frac{\log 3^{kn}}{\log [3^{(k+1)+(k+1)r} ]} \\&=\frac{n}{r+1}. \end{aligned}$$

On the other hand, note that \( \frac{\log 3^{kn}}{\log [4(2(3^{k})-1)3^{kr}B^{-1}]} \rightarrow \frac{n}{1+r}\) as \(k\rightarrow \infty \). Hence, for any \(\delta >0\), there exists \(k_{0}\ge 1\), such that, for any \(k> k_{0}\), we have \( \frac{\log 3^{kn}}{\log [4(2(3^{k})-1)3^{kr}B^{-1}]} <\frac{n}{1+r}+\delta \). Hence, suppose that \(\varepsilon >0\) is small enough such that \(\varepsilon <\epsilon _{k_{0}}\). Set \( \tilde{\Omega }_{k}=\underset{n\in {\mathbb {Z}}}{\bigcap }\varphi ^{n}(E_{k})\) and take \(\tilde{\Omega }=\underset{k\in {\mathbb {N}}}{\bigcup }\Omega _{k}\). We have

$$\begin{aligned} {{\text {mdim}}_{\text {M}}}( {\mathcal {C}},\Vert \cdot \Vert ,\varphi ) ={{\text {mdim}}_{\text {M}}}(\tilde{\Omega },\Vert \cdot \Vert ,\varphi |_{\tilde{\Omega }} ). \end{aligned}$$

If \(x\in \tilde{\Omega }\), then x belongs to some \(C^{k}_{l_{j_{m}},i_{1}^{(m)},\dots ,i_{n-1}^{(m)}, \dots ,l_{j_{1}}, i_{1}^{(1)},\dots , i_{n-1}^{(1)}}\). Take \(s^{(j_{1})},\dots s^{(j_{m})} \in \{s_{1},\dots , s_{3^{k}}\}\) with

$$\begin{aligned} |s^{(j_{i})}-l_{j_{i}}|=\underset{t=1,\dots ,m}{\min }|s^{(t)}-l_{j_{i}}|,\quad \text {fot each }i=1,\dots ,m, \end{aligned}$$

and furthermore \(d_{m}(x,y)\le 4 \varepsilon _{k}\) for any \(y\in C^{k}_{s^{(j_{m})},i_{1}^{(m)},\dots ,i_{n-1}^{(m)}, \dots ,s^{(j_{1})}, i_{1}^{(1)},\dots , i_{n-1}^{(1)}}\). Hence, if \(Y_{k}=\cup _{j=1}^{k}E_{j}\), for every \( m\ge 1\), we have

$$\begin{aligned} \text {span}(m,\varphi |_{Y_{k}}, 4\varepsilon )&\le \sum _{j=1}^{k} \frac{3^{jnm}}{\varepsilon } \le k\frac{3^{knm}}{\varepsilon } . \end{aligned}$$

Therefore,

$$\begin{aligned} \frac{\text {span}(\varphi |_{Y_{k}} ,4 \varepsilon )}{|\log 4\varepsilon |}&\le \limsup _{m\rightarrow \infty } \frac{\log \left[ k\frac{3^{knm}}{\varepsilon } \right] }{m |\log 4\varepsilon _{k}|} = \frac{\log 3^{kn}}{\log [4(2(3^{k})-1)3^{kr}B^{-1}]} <\frac{n}{1+r}+\delta . \end{aligned}$$

This fact implies that for any \(\delta >0\) we have

$$\begin{aligned} {\overline{\text {mdim}}_{\text {M}}}(S ,\Vert \cdot \Vert ,\varphi |_{S} )<\frac{n}{r+1}+\delta \quad \text {and hence }\quad {\overline{\text {mdim}}_{\text {M}}}(S ,\Vert \cdot \Vert ,\varphi |_{S})\le \frac{n}{r+1}.\end{aligned}$$

The above facts prove that \({ {\text {mdim}}_{\text {M}}}(\mathcal {C},\Vert \cdot \Vert ,\varphi )=\frac{n}{r+1}. \) \(\square \)

Given \(\alpha ,\beta \in [0,n]\), with \(\alpha \le \beta \), in the next lemma we construct an homeomorphism \(\phi :[0,1]^{n}\rightarrow [0,1]^{n}\) such that

$$\begin{aligned} \underline{\text {mdim}}_{\text {M}}([0,1]^{n},\Vert \cdot \Vert ,\phi )=\alpha \quad \text {and}\quad \overline{\text {mdim}}_{\text {M}}([0,1]^{n},\Vert \cdot \Vert ,\phi )=\beta . \end{aligned}$$

Lemma 2.4

For every \(\alpha ,\beta \in [0,n]\), with \(\alpha <\beta \), there exists a homeomorphism \(\phi _{\alpha ,\beta }:[0,1]^{n}\rightarrow [0,1]^{n}\) such that

$$\begin{aligned} \alpha = \underline{mdim }_{M }([0,1]^{n},\Vert \cdot \Vert ,\phi _{\alpha ,\beta })< \overline{mdim }_{M }([0,1]^{n},\Vert \cdot \Vert ,\phi _{\alpha ,\beta })=\beta . \end{aligned}$$

Proof

We will prove the case \(\beta <n\). First, we will show there exists a homeomorphism \(\phi _{0,\beta }:[0,1]^{n}\rightarrow [0,1]^{n}\) such that

$$\begin{aligned} 0= \underline{\text {mdim}}_{\text {M}}([0,1]^{n},\Vert \cdot \Vert ,\phi _{0,\beta })< \overline{\text {mdim}}_{\text {M}}([0,1]^{n},\Vert \cdot \Vert ,\phi _{0,\beta })=\beta . \end{aligned}$$

Fix \(r>0\) and set \( b=\frac{n}{r+1}\). Set \(a_{0}=0\) and \(a_{n}= \sum _{i=0}^{n-1}\frac{C}{3^{ir}}\) for \(n\ge 1\), where \(C=\frac{1}{\sum _{i=0}^{\infty }\frac{1}{3^{ir}}}= \frac{3^{r}-1}{3^{r}}\). Let \(E_{k}=[a_{k},b_{k}]^{n}\) and \(E_{k}^{\prime }\) satisfying the conditions C1 and C2, C4 and C5 in Lemma 2.3, with \(|E_{k}|=\frac{B}{3^{kr}}\), and such that each \(E_{k^{k}}\) is an n-dimensional \(3^{nk^{k}}\)-horseshoe for \(\phi _{0,\beta }\) and otherwise \(\phi _{0,\beta }|_{E_{k}}\) is the identity on \(E_{k}\). We can prove \( \underline{\text {mdim}}_{\text {M}}([0,1]^{n},\Vert \cdot \Vert ,\phi _{0,\beta })=0\) and \( \overline{\text {mdim}}_{\text {M}}([0,1]^{n},\Vert \cdot \Vert ,\phi _{0,\beta })=\beta .\)

Now consider \(\alpha <\beta \). From Lemma  2.3(i), we have there exists \(\phi _{\alpha }\in \text {Hom}([0,1]^{n})\) such that

$$\begin{aligned} {\underline{\text {mdim}}_{\text {M}}}([0,1]^{n},\Vert \cdot \Vert ,\phi _{\alpha })={\overline{\text {mdim}}_{\text {M}}}([0,1] ^{n},\Vert \cdot \Vert ,\phi _{\alpha })=\alpha . \end{aligned}$$

Set \( {\phi }_{\alpha ,\beta }\in \text {Hom}([0,1]^{n})\) be defined by

$$\begin{aligned} {\phi }_{\alpha ,\beta } (x) ={\left\{ \begin{array}{ll} T_{1}^{-1}\circ \phi _{0,\beta }\circ T_{1}(x) &{} \text {if }x\in [0,\frac{1}{2}]^{n},\\ T_{2}^{-1}\circ \phi _{\alpha }\circ T_{2} (x)&{} \text {if }x\in [\frac{1}{2},1]^{n},\\ x &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

where \(T_{1}:[0,\frac{1}{2}]^{n}\rightarrow [0,1]^{n}\) and \(T_{2}:[\frac{1}{2},1]^{n}\rightarrow [0,1]^{n}\) are bi-lipchitsz maps. We have

$$\begin{aligned}&{\underline{\text {mdim}}_{\text {M}}}([0,1]^{n} ,\Vert \cdot \Vert , {\phi }_{\alpha ,\beta })\\&\quad =\max \{{\underline{\text {mdim}}_{\text {M}}}([0,{1}/{2}]^{n} ,\Vert \cdot \Vert , {\phi }_{\alpha ,\beta }|_{[0,\frac{1}{2}]^{n} }),{\underline{\text {mdim}}_{\text {M}}}([{1}/{2},1]^{n} ,\Vert \cdot \Vert , {\phi }_{\alpha ,\beta }|_{[\frac{1}{2},1]^{n}})\}\\&\quad =\max \{{\underline{\text {mdim}}_{\text {M}}}([0,1]^{n} ,\Vert \cdot \Vert , \phi _{0,\beta }),{\underline{\text {mdim}}_{\text {M}}}([0,1]^{n} ,\Vert \cdot \Vert ,\phi _{\alpha })\}\\&\quad = {\underline{\text {mdim}}_{\text {M}}}([0,1]^{n} ,\Vert \cdot \Vert ,\phi _{\alpha })=\alpha . \end{aligned}$$

Analogously, we prove \( {\overline{\text {mdim}}_{\text {M}}}([0,1]^{n},\Vert \cdot \Vert ,\phi _{\alpha ,\beta })={\overline{\text {mdim}}_{\text {M}}}([0,1]^{n},\Vert \cdot \Vert , \phi _{0,\beta })=\beta .\) \(\square \)

3 Homeomorphisms on manifolds with positive metric mean dimension

Throughout this section, N will denote an n dimensional compact riemannian manifold with \(n\ge 2\) and d a riemannian metric on N. On \(\text {Hom}(N)\) we will consider the metric

$$\begin{aligned} {\hat{d}}(\phi ,\varphi )=\max _{p\in N}\{d(\phi (p),\varphi (p)),d(\phi ^{-1}(p),\varphi ^{-1}(p))\}\quad \quad \text { for any }\phi , \varphi \in \text {Hom}(N). \end{aligned}$$

It is well-known \((\text {Hom}(N),{\hat{d}})\) is a complete metric space. The main goal of this section is to prove Theorem 1.5.

Good Charts For each \(p\in N\), consider the exponential map

$$\begin{aligned} \text {exp}_{p}: B_{\delta ^{\prime }}(0_{p})\subseteq T_{p}N\rightarrow B_{\delta ^{\prime }}(p)\subseteq N, \end{aligned}$$

where \(0_{p}\) is the origin in the tangent space \(T_{p}N\), \(\delta ^{\prime }\) is the injectivity radius of N and \(B_{\epsilon }(x)\) denote the open ball of radius \(\epsilon >0\) with center x. We will take \( {\delta }_{N}=\frac{\delta ^{\prime }}{2}\). The exponential map has the following properties:

  • Since N is compact, \(\delta ^{\prime }\) does not depends on p.

  • \( \text {exp}_{p}(0_{p}) = p\) and \( \text {exp}_{p}[ B_{\delta _{N}}(0_{p})] = B_{\delta _{N}}({p})\);

  • \(\text {exp}_{p}: B_{\delta _{N}}(0_{p})\rightarrow B_{\delta _{N}}({p})\) is a diffeomorphism;

  • If \(v\in B_{\delta _{N}}(0_{p})\), taking \(q=\text {exp}_{p}(v)\) we have \(d(p,q)=\Vert v\Vert \).

  • The derivative of \(\text {exp}_{p}\) at the origin is the identity map:

    $$\begin{aligned} D (\text {exp}_{p})(0) = \text {id}: T_{p}N \rightarrow T_{p}N. \end{aligned}$$

Since \(\text {exp}_{p}: B_{\delta _{N}}(0_{p})\rightarrow B_{\delta _{N}}({p})\) is a diffeomorphism and \(D (\text {exp}_{p})(0) = \text {id}: T_{p}N \rightarrow T_{p}N,\) we have \(\text {exp}_{p}: B_{\delta _{N}}(0_{p})\rightarrow B_{\delta _{N}}({p})\) is a bi-Lipschitz map with Lipschitz constant close to 1. Therefore, we can assume that if \(v_{1},v_{2}\in B_{\delta _{N}}(0_{p})\), taking \(q_{1}=\text {exp}_{p}(v_{1})\) and \(q_{2}=\text {exp}_{p}(v_{2})\), we have \(d(q_{1},q_{2})=\Vert v_{1} -v_{2}\Vert \). Furthermore, we will identify \(B_{\delta _{N}}(0_{p})\subset T_{p}N\) with \(B_{\delta _{N}}(0)=\{x\in {\mathbb {R}}^{n}:\Vert x\Vert <\delta _{N}\}\subseteq {\mathbb {R}}^{n}\).

Recall that if \(\alpha =\beta \in [0,n]\), then

$$\begin{aligned} {H_{\alpha }^{\alpha }}(N): ={H}_{\alpha }(N)=\{\phi \in \text {Hom}(N): \underline{\text {mdim}}_\text {M}(N, d,\phi )=\overline{\text {mdim}}_\text {M}(N, d,\phi )=\alpha \}. \end{aligned}$$

Theorem 3.1

For any \(\alpha \in [0,n]\), the set \(H_{\alpha }(N) \) is dense in \(Hom (N)\).

Proof

Let \(P^{r}(N)\) be the set of \(C^{r}\)-diffeomorphisms on N with a periodic point. This set is \(C^{0}\)-dense in \(\text {Hom}(N)\) (see [4, 7]). Hence, in order to prove the theorem, it is sufficient to show that \(H_{\alpha }(N)\) is dense in \(P^r(N)\). Fix \(\psi \in P^{r}(N)\) and take any \(\varepsilon \in (0,\delta _{N})\). Suppose that \(p\in N\) is a periodic point of \(\psi \), with period k. Let \(\beta >0\), small enough, such that \([-\beta , \beta ]^n\subset B_{\frac{\varepsilon }{4}}(0)\). For each \(i=0,\dots , k-1\), \(N{\setminus } \psi (\exp _{\psi ^{i}(p)}\partial [-\beta ,\beta ]^n)\) has two connected components. We denote by \(C_{i}\) the connected component that contains \(\psi ^{i}(p)\). Consider the positive number

$$\begin{aligned} \gamma =\min _{i=0,\dots , k-1}d(\psi ^{i+1}(p), \psi (\exp _{\psi ^{i}(p)}\partial [-\beta ,\beta ]^n))>0. \end{aligned}$$

Let \(\lambda \in (0, \min \{\gamma /2, \beta \}),\) such that

$$\begin{aligned} \exp _{\psi ^{i+1}(p)} [-\lambda ,\lambda ]^n\subset C_{i+1}\quad \text {for each }i=0,\dots , k-1. \end{aligned}$$

The regions \([-\beta ,\beta ]^n{\setminus } (-\lambda , \lambda )^n \) and \( C_{i+1}{\setminus } \exp _{\psi ^{i}(p)}(-\lambda , \lambda )^n \) are homeomorphic. For each \(i=0,\dots , k-1, \) take

$$\begin{aligned} h_i: \partial [-\beta ,\beta ]^n&\rightarrow \exp ^{-1}_{\psi ^{i+1}(p)} \left( \partial {C}_{i+1}\right) \\ u&\mapsto \exp ^{-1}_{\psi ^{i+1}(p)}\circ \psi \circ \exp _{\psi ^{i}(p)}(u) . \end{aligned}$$

Then, there exists a homeomorphism

$$\begin{aligned} H_i: [-\beta ,\beta ]^n\setminus (-\lambda , \lambda )^n \rightarrow \exp ^{-1}_{\psi ^{i+1}(p)}[C_{{i+1}}\setminus \exp _{\psi ^{i+1}(p)}(-\lambda , \lambda )^n], \end{aligned}$$

such that

$$\begin{aligned} H_{i}|_{\partial [-\lambda ,\lambda ]^n}=Id\ \ \text {and}\ \ H_{i}|_{\partial [-\beta ,\beta ]^n}=h_i. \end{aligned}$$

If \(q\in R_i=\exp _{\psi ^{i}(p)} \left( [-\beta ,\beta ]^n{\setminus } (-\lambda ,\lambda )^n \right) \), we can write

$$\begin{aligned} q=\exp _{\psi ^{i}(p)}(z), \quad \text {for some } z\in [-\beta ,\beta ]^n\setminus (-\lambda ,\lambda )^n. \end{aligned}$$

Set \(\varphi _{\alpha }: N\rightarrow N\), given by

$$\begin{aligned} \varphi _{\alpha }(q)={\left\{ \begin{array}{ll}\exp _{\psi ^{i+1}(p)}H_i(z), &{}\text {if }q\in R_i=\exp _{\psi ^{i}(p)} \left( [-\beta ,\beta ]^n\setminus (-\lambda ,\lambda )^n \right) \\ \exp _{\psi ^{i+1}(p)}\phi _{\alpha }(\exp _{\psi ^{i}(p)}^{-1}(q)), &{}\text {if }q\in D_i:=\exp _{\psi ^{i}(p)} \left( [ -\lambda ,\lambda ]^n \right) \\ \psi (q), &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

where \(\phi _{\alpha }:[ -\lambda ,\lambda ]^n \rightarrow [ -\lambda ,\lambda ]^n\) is a homeomorphism which satisfies \(\phi _{\alpha }|_{\partial [ -\lambda ,\lambda ]^n }=Id\) and

$$\begin{aligned} {{\text {mdim}}_{\text {M}}}([ -\lambda ,\lambda ]^n,\Vert \cdot \Vert ,\phi _{\alpha })=\alpha , \end{aligned}$$

(see Lemma 2.3). Set \(K:=\cup _{i=0}^{k-1}D_{i}\). Note that \(N\setminus K\) is \(\varphi _{\alpha }\) invariant and

$$\begin{aligned} \text {mdim}_\text {M}(N\setminus K,d,\varphi _{\alpha }|_{N\setminus K})=0. \end{aligned}$$

Hence,

$$\begin{aligned} \text {mdim}_\text {M}(N,d,\varphi _{\alpha })= \text {mdim}_\text {M}(K,d,\varphi _{\alpha }|_{K}). \end{aligned}$$

Note if \(q\in D_{i}\), we have

$$\begin{aligned}{} & {} (\varphi _{\alpha })^{s}(q) = \text {exp}_{\psi ^{(i+s)\text { mod }k}(p)}\circ (\phi _{\alpha })^{s}\circ \text {exp}^{-1}_{\psi ^{i}(p)}(q)\\{} & {} \quad \text {and}\quad (\varphi _{\alpha })^{k}(q) = \text {exp}_{\psi ^{i}(p)}\circ (\phi _{\alpha })^{k}\circ \text {exp}^{-1}_{\psi ^{i}(p)}(q). \end{aligned}$$

Hence, \(D\subseteq D_{i}\) is an \((s,\phi _{\alpha },\epsilon )\)-separated set if and only if \(\text {exp}_{\psi ^{i}(p)}(D)\subseteq N\) is an \((s,\varphi _{\alpha },\epsilon )\)-separated set for any \(\epsilon >0\). Therefore, \(\text {sep}(s,\varphi _{\alpha }|_{K},\epsilon )=k\,\text {sep}(s,\phi _{\alpha },\epsilon ).\) Therefore,

$$\begin{aligned} \text {mdim}_\text {M}( K,d,\varphi _{\alpha }|_{K})= \text {mdim}_\text {M}([-\lambda ,\lambda ]^{n},\Vert \cdot \Vert ,\phi _{\alpha }), \end{aligned}$$

which proves the theorem. \(\square \)

The last theorem proved Theorem 1.5 in the case \(\alpha =\beta =n\). The proof of the general case will be a consequence of the above arguments, in fact:

Proof of the Theorem 1.5

The proof follows similarly to the proof of Theorem 3.1, changing \(\phi _{\alpha }\) by a continuous map \(\phi _{\alpha ,\beta }:[-\lambda , \lambda ]^n \rightarrow [-\lambda , \lambda ]^n\) such that

$$\begin{aligned} {\underline{\text {mdim}}_{\text {M}}}([-\lambda , \lambda ]^{n},\Vert \cdot \Vert , {\phi }_{\alpha ,\beta })=\alpha \quad \text {and}\quad {\overline{\text {mdim}}_{\text {M}}}([-\lambda , \lambda ]^{n},\Vert \cdot \Vert ,\phi _{\alpha ,\beta })=\beta , \end{aligned}$$

as in the Lemma 2.4. \(\square \)

4 Tipical homeomorphism has maximal metric mean dimension

To complete this work, in this section we show Theorem 1.6, which was proved in Theorem A in [5], however, we will present an alternative proof of this fact using the techniques of Sects. 2 and 3.

Definition 4.1

(n-dimensional strong horseshoe) Let \(E=[a,b]^{n}\) and set \(|E|=b-a\). For a fixed natural number \(k>1\), set \(\delta _{k}= \frac{b-a}{4k+1}\) and \(\epsilon _{k}=\frac{b-a}{2(2k+1)^{n-1}-1}\). For \(i=0,1, 2, \dots , 4k+1\), set \(t_i= a+i\delta _{k} \) and consider

$$\begin{aligned} H_{i_{1},i_{2},\dots ,i_{n-1}}=[a,b]\times [t_{i_{1}-1},t_{i_{1}}]\times \cdots \times [t_{i_{n-1}-1}, t_{i_{n-1}}], \end{aligned}$$

for \(i_{j}\in \{1,\dots , 4k+1\}.\) For \(l=0,1, 2, \dots , 2(2k+1)^{n-1}-2\), set \(s_l= a+l\epsilon _{k} \) and consider

$$\begin{aligned} V_{l+1}=[s_l, s_{l+1}]\times [a,b]^{n-1}. \end{aligned}$$

We say that \(E\subseteq A\subseteq {\mathbb {R}}^{n}\) is an n-dimensional strong \((\epsilon ,(2k+1)^{n-1})\)-horseshoe for a homeomorphism \(\phi :A\rightarrow A\) if \(|E|>\epsilon \) and furthermore:

  • For any \(H_{i_{1},i_{2},\dots ,i_{n-1}}\), with \(i_{j}\in \{1,3,\dots , 4k+1\}\), there exists \(l\in \{1,3,\dots , 2(2k+1)^{n-1}-1\}\) with

    $$\begin{aligned} H_{i_{1},i_{2},\dots ,i_{n-1}}\subseteq \phi (V_{l})^{\circ }. \end{aligned}$$

  • For any \(l=2,4,\dots , 2(2k+1)^{n-1}-2\), \(\phi (V_{l})\subseteq A{\setminus } E\).

Remark 4.2

Note if \(\epsilon ^{\prime }>\epsilon \), then any n-dimensional strong \((\epsilon ^{\prime },(2k+1)^{n-1})\)-horseshoe for \( \phi \) is an n-dimensional strong \((\epsilon ,(2k+1)^{n-1})\)-horseshoe for \( \phi \).

Using local charts, the last definition can be done on the manifold N.

Definition 4.3

Let N be an n-dimensional riemannian manifold and fix \(k\ge 1\). We say that \(\phi \in \text {Hom}(N)\) has an n-dimensional strong \(( \epsilon , (2k+1)^{n-1})\)-horseshoe \(E=[a,b]^{n}\), if there is s and an exponential charts \(\text {exp}_{i}: B_{\delta _{N}}(0)\rightarrow N\), for \(i=1,\dots ,s\), such that:

  • \(\phi _{i}=\text {exp}_{(i+1)\text {mod}\, s}\circ \phi \circ \text {exp}^{-1}_{i}: B_{\delta }(0 )\rightarrow B_{\delta _{N}}(0)\) is well defined for some \(\delta \le \delta _{N}\);

  • E is an n-dimensional strong \((\epsilon , (2k+1)^{n-1})\)-horseshoe for \(\phi _{i} \).

To simplify the notation, we will set \(\phi _{i}=\phi \) for each \(i=1,\dots , s\).

For \(\epsilon >0\) and \(k\in {\mathbb {N}}\), we consider the sets

$$\begin{aligned}&H(\epsilon , k)=\{\phi ^{2} \in \text {Hom}(N): \phi \text { has a strong }(\epsilon ,k) \text {-horseshoe} \} \\&H(k)=\bigcup _{i\in {\mathbb {N}}}H\left( \frac{1}{ i^{2}},3^{ki(n-1)} \right) \\&\mathcal {H}=\overset{\infty }{\underset{k=1}{\bigcap }} H(k). \end{aligned}$$

Lemma 4.4

The set \(\mathcal {H}\) is residual.

Proof

Clearly, for any \(\epsilon \in (0,\delta _{N})\) and \(k\in {\mathbb {N}}\), the set \( H(\epsilon , k)\) is open and nonempty.

We claim that the set H(k) is dense in \(\text {Hom}(N)\). In fact: fix \(\psi \in P^{r}(N)\) with a s-periodic point. In the same way as the proof of the Theorem 3.1, every small neighborhood of the orbit of this point can be perturbed in order to obtain a strong \(\left( \frac{1}{i^{2}},3^{n k i}\right) \) horseshoe for a \(\phi \) such that \(\phi ^{2}\) be close to \(\psi \) for a large enough i. Thus H(k) is a dense set, and a fortiori \(\mathcal {H}=\overset{\infty }{\underset{k=1}{\bigcap }} H(k) \) is residual in \(\text {Hom}(N)\). \(\square \)

Finally, we prove Theorem 1.6.

Proof of the Theorem 1.6

It is sufficient to prove that \(\overline{\text {mdim}}_{\text {M}}(N,d,\phi )=n\) for any \(\phi \in \mathcal {H}\). For this sake, take \(\varphi =\phi ^{2}\in \mathcal {H}\). We have \(\varphi \in H(k)\) for any \(k\ge 1\). Therefore, for any \(k\in {\mathbb {N}}\), there exists \(i_{k}\), with \(i_{k}<i_{k+1}\), such that \(\phi \) has a strong \(\left( \frac{1}{i_{k}^{2}},3^{n\,k\, i_{k}} \right) \)-horseshoe \(E_{{k}}=[a_{k},b_{k}]^{n}\), such that \(|E_{{k}}|>\frac{1}{i_{k}^{2}}\), consisting of rectangles

$$\begin{aligned}{} & {} H^{i_{k}}_{j_{1},j_{2},\dots ,j_{n-1}}=[a_{k},b_{k}]\times [t^{{k}}_{j_{1}-1},t^{{k}}_{j_{1}}]\times \cdots \times [t^{{k}}_{j_{n-1}-1}, t^{{k}}_{j_{n-1}}],\\{} & {} \quad \text {with}\quad j_{t}\in \{1,3,\dots , 2(3^{k \,i_{k}})-1\}, \end{aligned}$$

and

$$\begin{aligned} V^{{k}}_{l}=[s^{k}_{l-1}, s^{k}_{l}]\times [a_{k},b_{k}]^{n-1},\quad \text { for }l\in \{1,3,\dots , 2( {3^{k i_{k}(n-1)}})-1\}, \end{aligned}$$

with

$$\begin{aligned} H^{{k}}_{j_{1},j_{2},\dots ,j_{n-1}}\subseteq \phi (V^{{k}}_{l})^{\circ }\quad \text {for some } l. \end{aligned}$$

For \(i_{j}\in \{1,\dots , 2(3^{ki_{k}})-1\}\) and \(l=1,\dots , 2(3^{ki_{k}})^{n-1}-1,\) take

$$\begin{aligned} E^{k}_{l,i_{1},\dots ,i_{n-1}} =[s^{k}_{l-1},s^{k}_{l}]\times [t^{k}_{i_{1}-1},t^{k}_{i_{1}}]\times \cdots \times [t^{k}_{i_{n-1}-1}, t^{k}_{i_{n-1}}]. \end{aligned}$$

For \(t=1,\dots ,m\), let \(i_{1}^{(t)},\) \( \dots ,i_{n-1}^{(t)}\in \{1,3,\dots , 2(3^{ki_{k}})-1\}\) and for \(l_{t}\in \{1,\dots , 2(3^{ki_{k}})^{n-1}-1\},\) set

$$\begin{aligned} C^{k}_{l_{1}, i_{1}^{(1)},\dots , i_{n-1}^{(1)}}&= E^{k}_{l_{1},i_{1}^{(1)},\dots ,i_{n-1}^{(1)}}\\ C^{k}_{l_{2},i_{1}^{(2)},\dots , i_{n-1}^{(2)},l_{1},i_{1}^{(1)},\dots , i_{n-1}^{(1)}}&=\varphi ^{-1}\left[ \varphi \left( C^{k}_{l_{2}, i_{1}^{2},\dots , i_{n-1}^{2}}\right) \cap E^{k}_{l_{1},i_{1}^{(1)},\dots ,i_{n-1}^{(1)}}\right] \\&\vdots \\ C^{k}_{l_{m},i_{1}^{(m)},\dots ,i_{n-1}^{(m)}, \dots ,l_{1}, i_{1}^{(1)},\dots , i_{n-1}^{(1)}}&=\varphi ^{-(m-1)}\left[ \varphi ^{m-1}\left( C^{k}_{l_{m},i_{1}^{(m)},\dots ,i_{n-1}^{(m)}, \dots ,l_{2}, i_{1}^{(2)},\dots ,i_{n-1}^{(2)}}\right) \cap E^{k}_{l_{1},i_{1}^{(1)},\dots ,i_{n-1}^{(1)}}\right] \end{aligned}$$

Furthermore, set

$$\begin{aligned} {\tilde{C}}^{k}_{l_{m},i_{1}^{(m)},\dots ,i_{n-1}^{(m)}, \dots ,l_{1}, i_{1}^{(1)},\dots , i_{n-1}^{(1)}}:=\text {exp}\left[ C^{k}_{l_{m},i_{1}^{(m)},\dots ,i_{n-1}^{(m)}, \dots ,l_{1}, i_{1}^{(1)},\dots , i_{n-1}^{(1)}} \right] . \end{aligned}$$

For any \(k\ge 1\), take \(\varepsilon _{k}=\frac{1}{4i_{k}^{2}(2(3^{k \,i_{k} })-1)}\). We can choose at least \(3^{ki_{k}}\) sub-indices \(p_{1},\dots ,p_{3^{ki_{k}}}\) in \(\{1,\dots , 2(3^{ki_{k}})^{n-1}-1\}\) such that if \(x\in {\tilde{C}}_{p_{s}, i_{1},\dots , i_{n-1}}\) and \(y\in {\tilde{C}}_{p_{t}, i_{1},\dots , i_{n-1}}\), with \(s\ne t\), then \(d_{1}(x,y)>\varepsilon _{k}\). Hence, if x and y belong to different sets \( {\tilde{C}}^{k}_{p^{(m)},i_{1}^{(m)},\dots ,i_{n-1}^{(m)}, \dots ,p^{(1)}, i_{1}^{(1)},\dots , i_{n-1}^{(1)}},\) with \(p^{(t)}\in \{p_{1},\dots ,p_{3^{ki_{k}}}\}\) and \(i_{1}^{(t)},\) \( \dots ,i_{n-1}^{(t)}\in \{1,3,\dots , 2(3^{ki_{k}})-1\}\), we have that \(d_{m}(x,y)>\varepsilon _{k}\). Hence,

$$\begin{aligned} \text {sep}(m, \varphi , \varepsilon _{k}) \ge 3^{ki_{k}nm} \quad \text {and thus}\quad \text {sep}(\varphi , \varepsilon _{k})\ge \log {3^{nki_{k}}}. \end{aligned}$$

Therefore,

$$\begin{aligned} {\overline{\text {mdim}}_{\text {M}}}(N ,d,\varphi )&= \limsup _{k\rightarrow \infty } \frac{\text {sep}(\varphi ,\varepsilon _{k} )}{|\log {\varepsilon _{k}}|} \ge \lim _{k\rightarrow \infty }\frac{ \log 3^{nki_{k}}}{|\log \varepsilon _{k}|} =\limsup _{k\rightarrow \infty }\frac{\log 3^{nki_{k}}}{\log [4i_{k}^{2}(2(3^{ki_{k}})-1)]} =n. \end{aligned}$$

This fact proves the theorem, since for any \(\psi \in \text {Hom}(N)\), the inequality \( \overline{\text {mdim}}_{\text {M}}(N,d,\phi )\le n\) always holds (see [14], Remark 4). \(\square \)