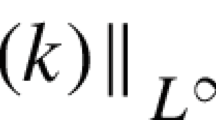Rayleigh–Bénard Convection with Stochastic Forcing Localised Near the Bottom

Abstract

We prove stochastic stability of the three-dimensional Rayleigh–Bénard convection in the infinite Prandtl number regime for any pair of temperatures maintained on the top and the bottom. Assuming that the non-degenerate random perturbation acts in a thin layer adjacent to the bottom of the domain, we prove that the law of the random flow periodic in the two infinite directions stabilises to a unique stationary measure, provided that there is at least one point accessible from any initial state. We also prove that the latter property is satisfied if the amplitude of the noise is sufficiently large.

Appendix

1.1 Sufficient Condition for Exponential Mixing

In this section we state an abstract result that guarantee mixing and uniqueness of the invariant measure. We also use notation from Sect. 1.

Let X be a compact subset of a closed affine subspace ${{\mathcal {H}}}$ in a separable Hilbert space H. Let $(T_k,{{\mathbb {P}}}_T)$ be a discrete-time Markov process in X with a transition function $P_k(T,\Gamma )$ (where $T\in X$ and $\Gamma \in {{\mathcal {B}}}(X)$) and the corresponding Markov operators ${{\mathfrak {P}}}_k$ and ${{\mathfrak {P}}}_k^*$ acting in the spaces C(X) and ${{\mathcal {P}}}(X)$, respectively. We assume that the Markov process is generated by a random dynamical system of the form (3.2), where $\{\eta _k\}_{k\ge 1}$ is a sequence of i.i.d. random variables in a separable Hilbert space E, and ${{\mathcal {S}}}:{{\mathcal {H}}}\times E\rightarrow {{\mathcal {H}}}$ is a continuous map. We denote by ${{\mathcal {K}}}$ the support of the law for $\eta _k$ and assume that ${{\mathcal {S}}}(X\times {{\mathcal {K}}})\subset X$. A proof of the following result can be found in [35, 49].

Theorem 6.1

Let us assume that the random dynamical system (3.2) satisfies the following four hypotheses.

(H$_1$):

There is a Hilbert space V compactly embedded into H such that the map ${{\mathcal {S}}}$ is twice continuously differentiable from ${{\mathcal {H}}}\times E$ to V, and its derivatives are bounded on bounded subsets.

(H$_2$):

There is a function ${\widehat{T}}\in X$ such that, for any $\varepsilon >0$, there exists an integer $m\ge 1$ with the following property: for any $T_0\in X$ one can find $\zeta _1,\dots ,\zeta _m\in {{\mathcal {K}}}$ such that

$$\begin{aligned} \Vert {{\mathcal {S}}}^m(T_0;\zeta _1,\dots ,\zeta _m)-{\widehat{T}}\Vert _H\le \varepsilon , \end{aligned}$$

(6.1)

where ${{\mathcal {S}}}^k(T_0;\eta _1,\dots ,\eta _k)$ denotes the trajectory of (3.2) at time k.

(H$_3$):

For any $T\in X$ and $\eta \in {{\mathcal {K}}}$, the derivative $(D_\eta {{\mathcal {S}}})(T,\eta ):E\rightarrow H$ has a dense image.

(H$_4$):

There is an orthonormal basis $\{e_j\}$ such that the random variables $\eta _k$ can be written in the form

$$\begin{aligned} \eta _k=\sum _{j=1}^\infty b_j\xi _{jk}e_j, \end{aligned}$$

where $b_j$ are non-zero numbers such that $\sum _jb_j^2<\infty$, and $\xi _{jk}$ are independent random variables whose law $\ell _j$ possess densities $\rho _j\in C^1({\mathbb {R}})$ supported in the interval $[-1,1]$.

Then the Markov process $(T_k,{{\mathbb {P}}}_T)$ has a unique stationary measure $\mu \in {{\mathcal {P}}}(X)$, and there are positive numbers C and $\gamma$ such that, for any $\lambda \in {{\mathcal {P}}}(X)$,

$$\begin{aligned} \Vert {{\mathfrak {P}}}_k^*\lambda -\mu \Vert _L^*\le Ce^{-\gamma k}\quad \text{ for } \text{ all } k\ge 0, \end{aligned}$$

(6.2)

where $\Vert \cdot \Vert _L^*$ stands for the dual-Lipschitz norm on ${{\mathcal {P}}}(X)$.

1.2 Proof of Lemma 4.1

Step 1: Preliminary estimates. Given a function $f:{\mathbb {R}}_+\times D\rightarrow {\mathbb {R}}$ and number $s\ge 0$, we shall write $\theta _sf$ for the restriction of its translation $t\mapsto f(s+t,x)$ to the domain $J\times D$. Let us first consider the equation

$$\begin{aligned} \partial _t v-\Delta v+\langle M(v),\nabla \rangle v=g(t,x), \end{aligned}$$

(6.3)

supplemented with the initial and boundary conditions (4.11). Using energy estimates, it is standard to prove that (6.3) is well posed in $H_0^1(D)$ for any $g\in L_\mathrm{{loc}}^2({\mathbb {R}}_+\times D)$. We claim that if $\delta >0$ is sufficiently small and

$$\begin{aligned} \sup _{t\ge 0}\Vert \theta _t g\Vert _{L^2(J\times D)}\le \delta , \end{aligned}$$

(6.4)

then, for any $R>0$ and a sufficiently large $c(R)>0$, the following properties hold:

(a):

If $v_0\in H_0^1(D)$ is such that $\Vert v_0\Vert _{H^1}\le R$, then the solution v of (6.3), (4.11) satisfies the inequality

$$\begin{aligned} \sup _{t\ge 0}\Vert \theta _tv\Vert _{{\mathcal {X}}}\le c(R). \end{aligned}$$

(6.5)

(b):

If $v_0^1, v_0^2\in H_0^1(D)$ are two initial conditions such that $\Vert v_0^i\Vert _{H^1}\le R$, $i=1,2$, and $g_i\in L_{\textrm{loc}}^2({\mathbb {R}}_+\times D)$ are two functions for which (6.4) holds, then the corresponding solutions satisfy the inequality

$$\begin{aligned} \Vert \theta _t v^1-\theta _t v^2\Vert _{{\mathcal {X}}}\le c(R)e^{-\gamma t}\Bigl (\Vert v_0^1-v_0^2\Vert _{H^1}+\sup _{0\le s\le t}\bigl (e^{\gamma s}\Vert \theta _s g_1-\theta _s g_2\Vert _{L^2}\bigr )\Bigr ), \end{aligned}$$

(6.6)

where $t\ge 0$ is arbitrary, $\gamma >0$ is a number not depending on R, the initial conditions $v_0^i$, $i = 1, 2$, or the right-hand sides $g_i$, $i = 1, 2$, and the $L^2$ norm is taken on the domain $J\times D$.

These properties are well known for the 2D Navier–Stokes equations (cf. [13, Chaps. I and II]). For (6.3), the proof is similar and can be completed with the help of the arguments used for Propositions 2.2 and 2.3.

Step 2: Uniqueness. Let $v^1, v^2$ be two solutions of (4.10), (4.11) satisfying (4.12). Since ${{\mathcal {X}}}$ is continuously embedded into $L^\infty (J, H^1(D))$, we see that

$$\begin{aligned} \Vert v^i(0)\Vert _{H^1}\le R, \quad i=1,2, \end{aligned}$$

(6.7)

where R depends only on r. The functions $v_i$ can be regarded as solutions of (6.3) with the right-hand sides

$$\begin{aligned} g_i(t)=(I-\Pi _l)(\chi ''-M_3(v^i)\chi '). \end{aligned}$$

(6.8)

Since $v_i$, $i = 1, 2$ satisfies (4.12), we can find an integer $l_0\ge 1$ depending only on r such that (6.4) holds for $g_i$ from (6.8), provided that $l\ge l_0$. Setting $v=v^1-v^2$ and $g=g_1-g_2$, we use assertion (b) to write

$$\begin{aligned} \sup _{t\ge 0}\Vert \theta _tv\Vert _{{\mathcal {X}}}\le c(R)\sup _{t\ge 0}\Vert \theta _tg\Vert _{L^2(J\times D)}, \end{aligned}$$

(6.9)

where the suprema on both sides are taken over all non-negative integers t. Since $g=-(I-\Pi _l)M_3(v)\chi '$, it follows that

$$\begin{aligned} \sup _{t\ge 0}\Vert \theta _tg\Vert _{L^2(J\times D)}\le \delta _l\sup _{t\ge 0}\Vert \theta _tv\Vert _{{\mathcal {X}}}, \end{aligned}$$

(6.10)

where $\{\delta _l\}$ is a sequence converging to zero as $l\rightarrow \infty$. Combining (6.9) and (6.10), and choosing $l\ge 1$ so large that $\delta _lc(R)\le \frac{1}{2}$, we see that $v\equiv 0$.

Step 3: Existence. Let us fix an integer n and an initial condition $v_0\in H_0^1(D)$ such that $\Vert v_0\Vert _{H^1}\le r_0$. We use a fixed point argument to construct a solution v of (4.10), (4.11) on every time interval $J_n=[0,n]$ with integer $n \ge 1$ such that (4.12) holds for $\theta _kv=v_k$ with $0\le k\le n-1$ and a number $r>0$ not depending on n. Then, the existence of the global solution follows from the uniqueness proved in Step 2.

For each $r > 0$, denote

$$\begin{aligned} {{\mathcal {F}}}_n(r) = \{w\in L^2(J_n \times D): \Vert \theta _kw\Vert _{L^2(J \times D)}\le r \text { for all integers } 0\le k\le n-1 \} \end{aligned}$$

and note that ${{\mathcal {F}}}_n(r)$ is a closed subset in the Hilbert space $L^2(J_n \times D)$. For any $w \in {{\mathcal {F}}}_n(r)$, we define⁵$g=g_w:=(I-\Pi _l)(\chi ''-M_3(w)\chi ')$. By the smoothing of M, smoothness of $\chi$, the inverse Poincaré inequality, for every $\delta > 0$ implies that there is $l=l(r) \ge 0$ such that (6.4) holds. By Step 1, there exists a map $R_{v_0}:{{\mathcal {F}}}_n(r)\rightarrow {{\mathcal {X}}}_n^0$ taking $w \in {{\mathcal {F}}}_n(r)$ to the solution $v\in {{\mathcal {X}}}_n^0$ of problem (6.3), (4.11). Since the embedding ${{\mathcal {X}}}_n^0 \hookrightarrow L^2(J_n \times D)$ is compact, the map $R_{v_0}:{{\mathcal {F}}}_n(r)\rightarrow L^2(J_n \times D)$ is compact. In addition, by (6.5), if $r \ge c(r_0)$ is sufficiently large, then $R_{v_0}$ maps the set ${{\mathcal {F}}}_n(r)$ into itself. The Leray–Schauder theorem now implies that $R_{v_0}$ has a fixed point, which is the required solution of (4.10), (4.11) on $J_n$.

Step 4: Exponential stability. Let $v^1$ and $v^2$ be two solutions of (4.10), (4.11), (4.12) associated with some initial functions $v_0^1,v_0^2\in B_{H_0^1}(r_0)$. Regarding $v^i$ as solutions of (6.3) with $g_i$ given by (6.8), we can write inequality (6.6) for the difference $v=v^1-v^2$ as

$$\begin{aligned} \sup _{0\le s\le t}\bigl (e^{\gamma s}\Vert \theta _s v\Vert _{{\mathcal {X}}}\bigr ) \le c(R)\Vert v_0\Vert _{H^1}+c(R) \sup _{0\le s\le t}\bigl (e^{\gamma s}\Vert \theta _s g\Vert _{L^2(J\times D)}\bigr ), \end{aligned}$$

(6.11)

where $g=g_1-g_2$, $v_0=v_0^1-v_0^2$, $t\ge 0$ is any integer, and the supremums on both sides are taken over all integers $s\in [0,t]$. Exactly the same argument as in Step 2 allows one to absorb the second term on the right-hand side of (6.11) by the left-hand side if l is sufficiently large. We thus obtain

$$\begin{aligned} \sup _{0\le s\le t}\bigl (e^{\gamma s}\Vert \theta _s v\Vert _{{\mathcal {X}}}\bigr )\le C\Vert v_0\Vert _{H^1}, \end{aligned}$$

provided that l is sufficiently large. This implies the required inequality (4.13).

Step 5: Periodic solution. Let us fix any $r_0>0$. To construct a periodic solution with an ${{\mathcal {X}}}$-norm smaller than $r_0/2$, we first show that if $r>0$ is sufficiently large, then there is an integer $l_r\ge 1$ such that, for any $l\ge l_r$, the Eq. (4.10) has a unique 1-periodic solution ${\bar{v}}^l$ such that (4.12) holds for it. The uniqueness follows immediately from (4.13), so that we only prove the existence.

If l is sufficiently large, there is ${\tilde{r}} > 0$ and  $\tilde{v}$ the solution of (4.10), (4.11) with $v_0=0$ such that $\Vert \theta _k {\tilde{v}}\Vert _{{\mathcal {X}}}\le {\tilde{r}}$ for any $k\ge 1$. Then by (4.13), for any $r>0$, there is an integer $l_r\ge 1$ such that, for any $v_0\in B_{H_0^1}(r)$ and any integer $l\ge l_r$, the unique solution of (4.10), (4.11) constructed in Steps 2 and 3 satisfies the inequality

$$\begin{aligned} \Vert v(t)-{\tilde{v}}(t)\Vert _{H^1}\le Ce^{-\gamma t}\Vert v_0\Vert _{H^1}\le Ce^{-\gamma t}r. \end{aligned}$$

(6.12)

In particular, if $r\ge 2{\tilde{r}}$ and $t=n\ge 1$ is a large integer, then $\Vert v(n)\Vert _{H^1}\le r$. Denoting by ${{\mathcal {R}}}_t:B_{H_0^1}(r)\rightarrow H_0^1$ the map taking $v_0$ to the value of the corresponding solution of (4.10), (4.11) at time t, we conclude that ${{\mathcal {R}}}_n$ maps the ball $B_{H_0^1}(r)$ into itself. Using again (4.13), we see that ${{\mathcal {R}}}_n$ is a contraction for any $n\ge n_r$, where $n_r$ is a sufficiently large integer. By the Banach fixed point theorem, there exists the unique fixed point $w^n\in B_{H_0^1}(r)$. If $w^n$ and $w^{n+1}$ are the fixed points corresponding for ${\mathcal {R}}_n$ and ${\mathcal {R}}_{n+1}$, then both of them are fixed points corresponding to ${\mathcal {R}}_{n(n+1)}$. However, since the latter is unique, we obtain $w^n = w^{n+1}$. Therefore ${\mathcal {R}}_1(w^n) = w^{n+1}(n+1)=w^{n+1}(0)=w^n$, so that ${{\mathcal {R}}}_t(w^n)$ is a 1-periodic solution of (4.10), which will be denoted by ${\bar{v}}^l$.

To complete the construction of the required periodic solution of (4.10), it suffices to show that

$$\begin{aligned} \Vert {\bar{v}}^l\Vert _{{{\mathcal {X}}}}\rightarrow 0\quad \text{ as } l\rightarrow \infty . \end{aligned}$$

(6.13)

Once this is proved, we can choose l so large that $\Vert \bar{v}^l\Vert _{{\mathcal {X}}}\le r_0/2$.

To prove (6.13), we view ${\bar{v}}^l$ as a solution of (6.3) and use inequality (6.6) with $v^2\equiv 0$ and the periodicity of ${\bar{v}}^l$ to write

$$\begin{aligned} \Vert {\bar{v}}^l\Vert _{{\mathcal {X}}}=\Vert \theta _n{\bar{v}}^l\Vert _{{\mathcal {X}}}\le Ce^{-\gamma n}\Vert \bar{v}^l(0)\Vert _{H^1} +C\Vert g^l\Vert _{L^2(J\times D)}, \end{aligned}$$

where $g^l$ is given by relation (6.8) in which $v^i$ is replaced by ${\bar{v}}^l$. Since $n\ge 1$ is arbitrary and $\Vert g^l\Vert _{L^2(J\times D)}\rightarrow 0$ as $l\rightarrow \infty$, the above inequality readily implies (6.13). This completes the proof of the lemma.

1.3 Proof of Lemma 4.3

We follow a standard argument based on backward uniqueness for (4.17); cf. [36, Sect. 7.2]. For the rest of the proof, we fix any $T_0 \in X$ and $\eta \in E$ and denote by $T \in {{\mathcal {X}}}$ the solution of (2.1) constructed in Proposition 2.2. Recall that $R(t,\tau )$ denotes the resolving operator for Eq. (4.17) with $\zeta \equiv 0$ and an initial condition specified at time $t=\tau$. Specifically, for given $\tau , t \in {\mathbb {R}}$ satisfying the inequality $\tau <t$ and for any $\theta _\tau \in H^1_0(D)$, we have $R(t,\tau )\theta _\tau = \theta (t)$, where $\theta \in {{\mathcal {X}}}$ is a solution of (4.17) with $\theta (\tau ) = \theta _\tau$. It is well known (cf. Proposition 2.2) that $R(t,\tau ): H^{1}_0 \rightarrow H^{1}_0$ is well-defined continuous linear map.

Suppose that ${{\mathcal {L}}}_1$ is not dense in $H_0^1$. Then, there is a non-zero $\psi _1\in H^{-1}$ such that

$$\begin{aligned} \bigl (R(1,0)\theta _0,\psi _1\bigr )=0 \quad \text{ for } \text{ any } \theta _0\in H_0^1, \end{aligned}$$

(6.14)

where $(\cdot , \cdot )$ is understood as the duality pairing between $H_0^1$ and $H^{-1}$. Following a well-known idea, let us consider the dual problem (5.3), (5.6). We claim that it has a unique solution $\psi$ of the form

$$\begin{aligned} \psi (t)={\bar{\psi }}(t)+\xi (t), \quad {\bar{\psi }}(t):=e^{(1-t)\Delta }\psi _1, \end{aligned}$$

(6.15)

where $\xi \in L^2(J,H^1)\cap H^1(J,H^{-1})$. Indeed, the uniqueness is standard and follows from energy estimates. To prove the existence, we substitute (6.15) into (5.3) and (5.6) and derive the following problem for $\xi$:

$$\begin{aligned} \partial _t \xi + \Delta \xi +\mathop {\textrm{div}}\nolimits (\xi M(T))-M^*(\xi \nabla T)=g, \quad \xi (1)=0 , \end{aligned}$$

(6.16)

where $g:=M^*({\bar{\psi }}\nabla T)-\mathop {\textrm{div}}\nolimits ({\bar{\psi }} M(T))$. By the regularising property of M and Sobolev embeddings, we have $g\in L^2(J,H_0^1)+L^2(J,H^{-1})$. Then, by a fixed point argument (cf. proof of Lemma 4.1), it follows that we can find a unique solution $\xi$ of (6.16) in the space $L^2(J,H_0^1) \cap H^1(J,H^{-1})$.

Now note that $\frac{{\text {d} }}{{\text {d} }t}(\theta (t),\psi (t))=0$ for $t\in (0,1)$, so that the function $(\theta (t),\psi (t))$ does not depend on $t\in [0,1]$. Combining this with (6.14), we see that

$$\begin{aligned} 0=\bigl (R(1,0)\theta _0,\psi _1\bigr ) =\bigl (\theta (1),\psi (1)\bigr ) =\bigl (\theta _0,\psi (0)\bigr ) \end{aligned}$$

for any $\theta _0\in H_0^1$. It follows that $\psi (0)=0$. By the backward uniqueness for (5.3) (see e.g. [13, Sect. II.8]), we conclude that $\psi _1=0$. This contradicts the hypothesis that $\psi _1\ne 0$ and completes the proof of the lemma.

1.4 Carleman Estimates of Fabre–Lebeau

In what follows, we denote by $|\cdot |$ the maximum norm on Euclidean spaces, and given $r>0$, we write $B_r=\{x\in {\mathbb {R}}^3:|x|<r\}$. For positive numbers $t_0$, $r_0$, N, and $\delta$ define

$$\begin{aligned} W(t_0,r_0)&=\{(t,x)\in {\mathbb {R}}^4:|t|\le t_0,|x|\le r_0\}, \end{aligned}$$

(6.17)

$$\begin{aligned} \varphi (t,x)&=\bigl (x_3+N(x_1^2+x_2^2+t^2)-\delta \bigr )^2\varkappa (t,x), \end{aligned}$$

(6.18)

where $\varkappa$ is a smooth function with compact support that is equal to 1 on W(1, 1). If we consider $\varphi$ as a function of x and regarding t as a parameter, we write $\varphi _t(x)$ instead of $\varphi (t, x)$. We recall two Carleman-type estimates for elliptic and parabolic problems established by Fabre and Lebeau [29] (see also [42] for some related results).

1.4.1 Heat Operator

The following result is [29, Lemma 4.3] applied to the weight function $\varphi$ given by (6.18). The fact that $\varphi$ satisfies the required hypotheses is established in [29, Lemma 4.5] when $N=1$. The general case follows by a similar argument.

Proposition 6.2

For any $N>0$ and sufficiently small $\delta >0$, there are positive numbers $t_1$, $r_1$, $C_1$, and $h_1$ such that, for any function

$$\begin{aligned} z\in L^2\bigl ([-t_1,t_1],H_0^2(B_{r_1})\bigr )\cap H_0^1\bigl ([-t_1,t_1],L^2(B_{r_1})\bigr ), \end{aligned}$$

and for any $0<h\le h_1$ one has

$$\begin{aligned} \bigl \Vert e^{\varphi /h}z\bigr \Vert ^2+h^2\bigl \Vert e^{\varphi /h}\nabla _xz\bigr \Vert ^2\le C_1h^3\bigl \Vert e^{\varphi /h}(\partial _t-\Delta )z\bigr \Vert ^2, \end{aligned}$$

(6.19)

where $\Vert \cdot \Vert$ stands for the $L^2$-norm taken over ${\mathbb {R}}^4$.

Remark 6.3

Inequality (6.19) is invariant under the time reversal, so that the heat operator entering its right-hand side can be replaced by the backward heat operator $\partial _t+\Delta$.

1.4.2 Elliptic Operators with Constant Coefficients

We now focus on Stokes-type systems satisfied by the velocity field in the Boussinesq system. Since we investigate stationary solutions, we regard t as a parameter. Let L be a first-order differential operator acting on vector functions:

$$\begin{aligned} Lf=\sum _{j=1}^3\sum _{k=1}^n a_{jk}\partial _j f_k, \quad f=(f_1,\dots ,f_n), \end{aligned}$$

where $a_{jk}$ are given real numbers. The following result is a consequence of [29, Theorem 3.1] applied to the function $\varphi _t$ defined in (6.18) with a sufficiently small t.

Proposition 6.4

For any $N>0$ and sufficiently small $\delta >0$, there are positive numbers $t_2$, $r_2$, $C_2$, and $h_2$ such that for any functions $y\in H_0^1(B_{r_2})$ and $f\in L^2({\mathbb {R}}^3)^n$ satisfying

$$\begin{aligned} \mathop {\textrm{supp}}\nolimits f\subset B_{r_2},\quad \Delta y-Lf\in L^2(B_{r_2}),\quad \mathop {\textrm{supp}}\nolimits (\Delta y-Lf)\subset B_{r_2}, \end{aligned}$$

the following inequality holds for $0<h\le h_2$ and $|t|\le t_2:$

$$\begin{aligned} \bigl \Vert e^{\varphi _t/h}y\bigr \Vert ^2+h^2\bigl \Vert e^{\varphi _t/h}\nabla _xy\bigr \Vert ^2 \le C_2\Bigl (h\bigl \Vert e^{\varphi _t/h}f\bigr \Vert ^2+h^3\bigl \Vert e^{\varphi _t/h}(\Delta y-Lf)\bigr \Vert ^2\Bigr ), \end{aligned}$$

(6.20)

where $\Vert \cdot \Vert$ stands for the $L^2$-norm taken over ${\mathbb {R}}^3$.

Proof

Let us set

$$\begin{aligned} a_t(x,\xi )=|\xi |^2-|\nabla \varphi _t(x)|^2, \quad b_t(x,\xi )=2\langle \xi ,\nabla \varphi _t(x)\rangle . \end{aligned}$$

Recall that the Poisson bracket of $a_t$ and $b_t$ is defined by

$$\begin{aligned} \{a_t,b_t\}(x,\xi )=\sum _{j=1}^3 \biggl (\frac{\partial a_t}{\partial \xi _j}\frac{\partial b_t}{\partial x_j}-\frac{\partial a_t}{\partial x_j}\frac{\partial b_t}{\partial \xi _j}\biggr ). \end{aligned}$$

By [29, Theorem 3.1], it suffices to prove that, for any $(t,x,\xi )\in {\mathbb {R}}^7$ such that $|t|+|x|\ll 1$, the relations $a_t(x,\xi )=0$ and $b_t(x,\xi )=0$ imply the inequality

$$\begin{aligned} \{a_t,b_t\}(x,\xi )\ge c, \end{aligned}$$

(6.21)

where $c>0$ does not depend on $(t,x,\xi )$. To this end, assume that $\delta > 0$ in the definition of $\varphi _t$ is small and $|x|+|t|\le \delta /2$. For such (x, t) we have $\varphi _t \approx \delta ^2$ which means $C^{-1} \delta ^2 \le \varphi _t(x, t) \le C\delta ^2$ for some universal constant $C>1$. It is straightforward to check that

$$\begin{aligned} \{a_t,b_t\}(x,\xi )=4\sum _{j,k=1}^3\partial _j\partial _k\varphi _t\bigl (\xi _j\xi _k+\partial _j\varphi _t \partial _k\varphi _t \bigr ). \end{aligned}$$

(6.22)

Next, note that

$$\begin{aligned} \partial _j\varphi _t(x)=2(x_3-\delta )\delta _{j3} + O(\delta ^2), \quad \partial _j\partial _k\varphi _t(x)=2\delta _{j3}\delta _{k3}+O(\delta ), \end{aligned}$$

where $\delta _{jk}$ is Kronecker’s symbol. It follows that $|\xi |=|\nabla \varphi _t(x)| \approx \delta$ whenever $a_t(x,\xi )=0$. In addition, if $b_t(x,\xi )=0$, then

$$\begin{aligned} \xi _3\partial _3\varphi _t= - \xi _1\partial _1\varphi _t - \xi _2\partial _2\varphi _t= O(\delta ^3). \end{aligned}$$

Since $\partial _3\varphi _t \approx \delta$, we conclude that $\xi _3=O(\delta ^2)$. After substitution into (6.22) it follows that

$$\begin{aligned} \{a_t,b_t\}(x,\xi )= 32 \delta ^2+O(\delta ^3). \end{aligned}$$

Hence, for $\delta \ll 1$ the required inequality (6.21) is satisfied with $c=16\delta ^2$. $\square$