Variable Time Step Dynamics with Choice

Abstract

We are interested in systems that can and possibly do switch between different regimes; the durations of staying in each regime (dwell times) may vary. We work with the deterministic picture and study global attractors both in the state space and, one of the novelties, in the hyperspace. We give an example of a simple ODE system where the existence or non-existence of attractors depends on the intervals from which the dwell times are chosen. Another novelty is the description of restricted iterated function systems and their attractors. An unexpected corollary is that for the restricted to a subshift hyperbolic IFS, its attractor is the image under Hutchinson’s map $p$ of a different, in general, subshift (we call it dual to the original one).

Appendix

In this section we collect a few useful facts about the space $X^\sharp$ and convergence of sets in $X$ and in $X^\sharp$. Also, we present some results on the global attractors of systems arising from iterations of a single multi-valued map.

The notation convention is the same as in Sect. 3. As in the main part of the paper, the space $(X, d)$ is complete. Then $(X^\sharp , d^\sharp )$ is also complete, [22, §33, IV].

Lemma 26

• (1) $d^\sharp (A, B) = d^\sharp (A, \overline{B})$; if $d^\sharp (A, B) = 0$, then $\overline{A} = \overline{B}$.

• (2) If $B$ is a nonempty, closed, bounded set in $X$, then $B^\sharp$, the family of all nonempty, closed subsets of $B$, is a bounded set in $X^\sharp$ (it need not be closed).

• (3) If ${\fancyscript{A}}$ is a nonempty, bounded subset of $X^\sharp$, then ${\fancyscript{A}}^\flat = \bigcup _{C\in {\fancyscript{A}}} C$ is a bounded subset of $X$.

• (4) If $A\subset X$ is compact, then $A^\sharp$ is compact in $X^\sharp$.

The proof is an easy exercise. $\square$

• We say that a set $A$ attracts the sets $A_n$ if $\lim _n e(A_n, A) = 0$.

The following observation proves to be quite useful.

Lemma 27

Let $A\subset X$ be a compact set. Let $B_n$ be a sequence of sets attracted by $A$. Then the sequence $\overline{B_n}$ has a subsequence converging in the Hausdorff metric. Its limit is a compact subset of $A$.

Proof

Choose a sequence $n_k\nearrow +\infty$ such that $\overline{B_{n_k}}\subset \mathcal{O}_{2^{-k}}(A)$. Because $A$ is compact, we can define the sets

$$\begin{aligned} A_k = \{y\in A\,:\, \exists x\in B_{n_k} \;\hbox {such that}\; d(x, y) = d(x,A)\}. \end{aligned}$$

Obviously, $d^\sharp (B_{n_k},A_k)\le 2^{-k}$. Since $A^\sharp$ is compact in $X^\sharp$, the sequence $\overline{A_k}$ has a convergent subsequence with a limit in $A^\sharp$. The corresponding subsequence of $B_{n_k}$ will have the same limit. $\square$

The limit of a Cauchy sequence, $A_n$, in the hyperspace $X^\sharp$ can be described with the help of the formula due to Hausdorff, [22, §29, IV(8)]:

$$\begin{aligned} A_n\rightarrow {A} = \bigcap _n \overline{\bigcup _{m\ge n} A_m} = \{x\in X: \,\exists n_k\nearrow \infty \,\exists x_k\in A_{n_k} \;\text {such that}\; x = \lim x_k\}. \end{aligned}$$

(66)

The basic convergence results stem from a generalization of the Cantor nested intervals theorem. The following theorem is a version of the Kuratowski generalization of Cantor’s result, [22, §34]. The first part is in [34, Theorem 3.1] and the second follows from [26, Prop. 3(viii)].

Theorem 28

Assume $A_1\supset A_2\supset \dots$ is a nested sequence of nonempty, closed, bounded subsets in $X$. Assume that $\psi (A_n)\rightarrow 0$ for some mnc $\psi$. Then,

• (1) the set $A = \bigcap _n A_n$ is nonempty and compact;

• (2) $A_n\rightarrow A$ in $X^\sharp$.

Combining this with Lemma 27, we obtain the following corollary.

Corollary 29

Suppose $A_1\supset A_2\supset \dots$ is a nested sequence of non-empty, closed, and bounded sets, and assume that $\lim _n\psi (A_n) = 0$. Then any sequence of closed subsets $B_n\subset A_n$ has a convergent in the Hausdorff metric subsequence (with the limit a subset of $A$).

The implications of convergence to a compact set are as follows.

Lemma 30

Assume $A_n\rightarrow A$ in $X^\sharp$ and $A$ is compact. Then

• (1) any sequence $C_k$ of nonempty, closed subsets of $A_{n_k}$, where $n_k\nearrow \infty$, has a convergent in $X^\sharp$ subsequence, and its limit is a compact subset of $A$;

• (2) $\psi (A_n) \rightarrow 0\,;$

• (3) $\overline{\bigcup _{m\ge n} A_m} \rightarrow A\,;$

• (4) $\psi (\overline{\bigcup _{m\ge n} A_m})\rightarrow 0.$

Proof

The first statement follows from Lemma 27. For the second observe that $\psi (A_n) = \psi (A_n) - \psi (A) \le c_\psi d^\sharp (A_n, A)\rightarrow 0$. The third statement is a consequence of the first and formula (66). Finally, the fourth statement follows from the second. $\square$

It is convenient to have a different description of the condition $\lim _n\psi (A_n) = 0$.

Lemma 31

Let $A_1\supset A_2\supset \dots$ be a nested sequence of nonempty, closed, and bounded sets. The following conditions are equivalent:

• (1) $\lim _n\psi (A_n) = 0$.

• (2) Every sequence $x_k$, where $x_k\in A_{n_k}$, $n_k\nearrow +\infty$, has a convergent subsequence.

Proof

Let the first condition be satisfied. For any $n$, $\{x_k\}\subset A_n$ except for at most a finite number of $x_k$’s. Hence, $\psi (\{x_k\})\le \psi (A_n)$, and therefore $\psi (\{x_k\})=0$, which implies the second condition.

Now suppose the second condition is satisfied. Note that if a set $C$ has a finite $\epsilon$-net $Q\subset C$, then $d^\sharp (C, Q)\le \epsilon$, and therefore, by the property mnc(iv),

$$\begin{aligned} \psi (C) \le c_\psi \;\epsilon . \end{aligned}$$

If $\psi (A_n)$ does not converge to $0$, then there is subsequence $n_k$ and an $\epsilon > 0$ such that

$$\begin{aligned} \psi (A_{n_k}) > c_\psi \,\epsilon . \end{aligned}$$

Hence, the sets $A_{n_k}$ do not have finite $\epsilon$-nets. Take a point $x_1\in A_{n_1}$. There exists $x_2\in A_{n_2}$ such that $d(x_1, x_2) > \epsilon /2$. There exists $x_3\in A_{n_3}$ such that $d(x_3, \{x_1, x_2\}) > \epsilon /2$, and so on. The sequence $\{x_n\}$ is not totally bounded. However, by construction, $x_k \in A_{n_k}$, and by assumption, the sequence $\{x_k\}$ must have a convergent subsequence. A contradiction. $\square$

Consider now a map $\Phi$ defined on nonempty bounded subsets of $X$ with values also bounded subsets of $X$. The first two assumptions on $\Phi$ are these:

• $\mathbf \Phi 1$: $\Phi$ maps $X^\sharp$ into itself.

• $\mathbf \Phi 2$: If $A\subset B$, then $\Phi (A)\subset \Phi (B)$.

We do not assume that $\Phi$ is a multi-valued map in the traditional sense. In our considerations the set $\Phi (A)$ may be larger than the union of the sets $\Phi (x)$ over all $x\in A$ (where $\Phi (x)$ is $\Phi (\{x\})$, of course).

The iterations $\Phi ^n$ satisfy the conditions of Definition 17. They generate the dynamics of sets on $X$ and on $X^\sharp$. These are the systems $\left( \{\Phi ^n\}, X\right)$ and $\left( \{\Phi ^n\}, X^\sharp \right)$ in the notation of Sect. 5. We are interested in the global attractors of these systems. Here is a corollary of Theorems 18, 20, and Lemma 31.

Theorem 32

• (1) For the system $\left( \{\Phi ^n\}, X\right)$ to possess a global attractor it is necessary and sufficient that the following two conditions hold.

  • (a) There is a bounded global absorbing set;

  • (b) For some mnc $\psi$, $\psi (\Phi ^n(A))\rightarrow 0$ for every bounded set $A$.

• (2) If both conditions (a) and (b) are satisfied, the system $\left( \{\Phi ^n\}, X^\sharp \right)$ possesses a global attractor. If $K$ is the global attractor of $\left( \{\Phi ^n\}, X\right)$ and ${\fancyscript{K}}$ is the global attractor of $\left( \{\Phi ^n\}, X^\sharp \right)$, then ${\fancyscript{K}}^\flat = K$.

• (3) Assume both conditions (a) and (b) are satisfied. Let $B$ be a bounded global absorbing set. Then

  

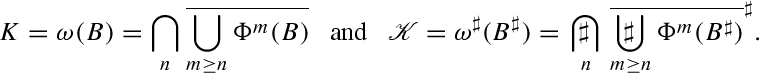
In the third statement, the formula for $K$ follows from [6, Corollary 19], and the formula for ${\fancyscript{K}}$ uses a similar argument.

We call the maps $\Phi$ satisfying the condition (b) asymptotically $\psi$-condensing. If $\Phi$ originates from a map $\Phi : X\rightarrow 2^X$ so that $\Phi (A) = \bigcup _{x\in A} \Phi (x)$, then $\Phi$ is asymptotically $\psi$-condensing if it is $\psi$-condensing (this requires a proof, see [34]). Recall that $\Phi$ is $\psi$-condensing with respect to some mnc $\psi$ with the properties mnc(i)–(iv) iff $\psi (\Phi (B))\le \psi (B)$ for any bounded $B$, and the inequality is strict if $\psi (B) > 0$. The condition $\Phi (A) = \bigcup _{x\in A} \Phi (x)$ can be weakened as follows, see [34, Theorems 4.1 and 4.2]. Consider the following two properties (“compact sets” in $\mathbf{\Phi 4a}$ are replaced by “finite sets” in $\mathbf{\Phi 4b}$).

$\mathbf \Phi 4a(b)$::

For every $D\in X^\sharp$, there is a sequence of sets $B_n\subset \Phi ^n(D)$, $n = 1, 2,\dots$, such that

(1):

$d^\sharp (B_n, \Phi ^n(D))\rightarrow 0$;

(2):

for $n = 1, 2,\dots$, for every compact set ($\mathbf{b:}$ finite set) $L\in B_n$ there is a compact set ($\mathbf{b:}$ finite set) $L^\prime \subset B_{n-1}$ such that

$$\begin{aligned} L\subset \Phi \left( L^\prime \right) . \end{aligned}$$

(67)

[The reason assumption $\mathbf{\Phi 4}$ precedes $\mathbf{\Phi 3}$ is that we would like to have the same names for the properties of $\Phi$ here as in [18].] An example of a map that satisfies $\mathbf{\Phi 4b}$ is the Hutchinson-Barnsley map (13). The following result is due essentially to Massatt, [34].

Proposition 33

Let $\Phi$ satisfy the assumptions $\mathbf{\Phi 1}$, $\mathbf{\Phi 2}$, and $\mathbf{\Phi 4a}$ or $\mathbf{\Phi 4b}$. In addition, let there be a bounded global absorbing set for the iterations of $\Phi$ in $X$. Then, if $\Phi$ is $\psi$-condensing, it is asymptotically $\psi$-condensing. As a result, both $\left( \{\Phi ^n\}, X\right)$ and $\left( \{\Phi ^n\}, X^\sharp \right)$ have global attractors.

It is easier to check that a map is condensing than that it is asymptotically condensing. For example, $\Phi$ is condensing if it is compact (i.e., it maps bounded sets into relatively compact sets). For another example, assume $\Phi (A) = \bigcup _{x\in A}S(x)$ and $S$ is a single-valued map. Then $\Phi$ is condensing if $S$ is a contraction, or if $S$ is compact. If $X$ is a Banach space and $\psi$ is the Kuratowski, or the Hausdorff, or any other mnc with the additional property that $\psi (A + B) \le \psi (A) + \psi (B)$ for any pair of bounded sets, then if $S$ is a sum of a finite number of $\psi$-condensing maps, $\Phi$ is $\psi$-condensing.

The invariance of attractors $K$ and ${\fancyscript{K}}$ does not come free, some form of continuity of $\Phi$ is needed. For example, the following assumption will do:

$\mathbf{\Phi 3a:}$ If $A_k, A\in X^\sharp$ and $A$ is compact, then

$$\begin{aligned} A_k\rightarrow A \quad \implies \quad \Phi (A_k)\rightarrow \Phi (A). \end{aligned}$$

Proposition 34

Assume $\left( \{\Phi ^n\}, X\right)$ has a global attractor. Let $K$ be this attractor and let ${\fancyscript{K}}$ be the global attractor of $\left( \{\Phi ^n\}, X^\sharp \right)$. Assume $\Phi$ has the property $\mathbf{\Phi 3a}$. Then $K = \Phi (K)$ and ${\fancyscript{K}} = \Phi ({\fancyscript{K}})$. This, in turn, implies that $K$ is the union in $X$ of bounded two-sided set-trajectories of $\Phi$. [A two-sided trajectory is a sequence of bounded, closed sets $A_n$, $n\in \mathbb Z$, such that $\Phi (A_n) = A_{n+1}$. It is bounded if $\{A_n\}$ is bounded in $X^\sharp$.] The attractor ${\fancyscript{K}}$ is the union (in $X^\sharp$) of bounded two-sided point-trajectories of $\Phi$. Also, $K$ is the maximal compact $\Phi$-invariant subset of $X$ and ${\fancyscript{K}}$ is the maximal $\Phi$-invariant compact subset of $X^\sharp$.