Abstract
We generalize Gehrig-Kawski theorem connecting the adjoint of the Eulerian idempotent with the logarithm of identity operator in the convolution product algebra  . This has application in dynamical systems, control theory, coordinates of the first kind, generalized BCH-formula, Magnus expansion, etc., and is connected with iterated integrals and the signature of a path. We also show certain algebraic identities, which are meaningful in context of control and path-signature theory.
. This has application in dynamical systems, control theory, coordinates of the first kind, generalized BCH-formula, Magnus expansion, etc., and is connected with iterated integrals and the signature of a path. We also show certain algebraic identities, which are meaningful in context of control and path-signature theory.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Eulerian idempotent  can be explicitly defined as a linear endomorphism satisfying
can be explicitly defined as a linear endomorphism satisfying

for all \(w\in {\mathrm {A}^*}\). Its importance comes, however, from a more implicate (but natural) definition \(\pi _{1} = \log \operatorname {Id}\), where the logarithm is taken in the algebra  with the convolution product \(*\). The name “Eulerian idempotent” emanates from the Eulerian numbers, which are related with coefficients (in symmetric group algebras) of higher order Eulerian idempotents \(\pi _{n} = \frac 1 {n!} \pi _{1}^{* n}\) [1]. \(\pi _{1}\) is interesting from many points of view. Purely mathematical aspects concern free Lie algebras, symmetric algebras, Solomon algebras, preLie algebras, etc. In this article, we focus our attention on algebraic applications in dynamical systems, control theory, coordinates of the first kind, generalized BCH-formula, Magnus expansion, etc., which are connected with iterated integrals, the signature of a path and so on. In detail, Sussmann [22] showed a product expansion for the solution of a non-linear control-affine system in terms of Lyndon basis of the free Lie algebra on words assigned to the controls. Then Melançon and Reutenauer [16] discovered the same expansion in purely algebraic context, and Reutenauer [20] generalized it to a Hall basis setting. This was rewritten in control-theoretic setting by Kawski and Sussmann [11]. The generalized algebraic version of these results is as follows:
with the convolution product \(*\). The name “Eulerian idempotent” emanates from the Eulerian numbers, which are related with coefficients (in symmetric group algebras) of higher order Eulerian idempotents \(\pi _{n} = \frac 1 {n!} \pi _{1}^{* n}\) [1]. \(\pi _{1}\) is interesting from many points of view. Purely mathematical aspects concern free Lie algebras, symmetric algebras, Solomon algebras, preLie algebras, etc. In this article, we focus our attention on algebraic applications in dynamical systems, control theory, coordinates of the first kind, generalized BCH-formula, Magnus expansion, etc., which are connected with iterated integrals, the signature of a path and so on. In detail, Sussmann [22] showed a product expansion for the solution of a non-linear control-affine system in terms of Lyndon basis of the free Lie algebra on words assigned to the controls. Then Melançon and Reutenauer [16] discovered the same expansion in purely algebraic context, and Reutenauer [20] generalized it to a Hall basis setting. This was rewritten in control-theoretic setting by Kawski and Sussmann [11]. The generalized algebraic version of these results is as follows:
In this formula, it is crucial that \(\exp \) is taken with respect to a product \(\operatorname {sh}\otimes \operatorname {conc}\) (see Section 2.2 for the definitions), and \(\mathcal {H}\) is a Hall set (see Section 2.4 for the definitions of \(\mathcal {H}\), \(\mathcal {P}_{h}\), \(\mathcal {S}_{h}\)). After a decade, Gehrig [8] and Kawski with Gehrig [7] proved that the adjoint homomorphism  gives rise to another formula as follows:
gives rise to another formula as follows:
with the same data as previously. They work in a context of control theory. Namely, for a control system with the following:

the above formula gives solution as follows:
where \(\phi ^{t}\) is a linear mapping defined for \(a_{1}{\cdots } a_{k} \in \mathrm {A}^*_{k}\) by
and \(X_{h}\) are appropriate vector fields. In particular, for fixed controls \(u_{i}\) and a fixed \(t>0\), the solution \(x(t)\) is an image of \(x(0)\) under the t-time flow of a certain vector field. For varying t, the vector field is also t-varying. This is also connected with the theory of rough paths [12,13,14]. Namely, for a basis \((e_{i})\) of  , take an alphabet \(\mathrm {A} = \left \{ e_{i} \right \}\); define a linear isomorphism
, take an alphabet \(\mathrm {A} = \left \{ e_{i} \right \}\); define a linear isomorphism  by \(\iota _{\otimes }(e_{i_{1}}{\cdots } e_{i_{k}}) = e_{i_{1}}\otimes {\cdots } \otimes e_{i_{k}}\). The signature of a path
by \(\iota _{\otimes }(e_{i_{1}}{\cdots } e_{i_{k}}) = e_{i_{1}}\otimes {\cdots } \otimes e_{i_{k}}\). The signature of a path  is as follows:
is as follows:

and Gehrig-Kawski formula gives the logarithm of the signature as follows:
where  is a homomorphism defined by ϕγ(P) = (X(γ)|ι⊗(P)).
is a homomorphism defined by ϕγ(P) = (X(γ)|ι⊗(P)).
In this article, we firstly generalize Gehrig-Kawski’s result to a non-Hall basis (which means to all basis) of free Lie algebra \(\text {Lie}(\mathrm {A})\) (this is a more general answer to the Problem 1 stated in [10]). We prove that for a basis \(\left \{ P_{h} \ | \ h\in \mathrm {B} \right \}\) in \(\text {Lie}(\mathrm {A})\) and a projection  , there exist the canonical subspace
, there exist the canonical subspace  and its basis \(\left \{ S_{h} \ | \ h\in \mathrm {B} \right \}\) for which is as follows:
and its basis \(\left \{ S_{h} \ | \ h\in \mathrm {B} \right \}\) for which is as follows:
We state this result in Theorem 1. After this, we give examples for this theorem choosing different basis in \(\text {Lie}(\mathrm {A})\) and a projection \(\rho \). In particular, we obtain the Gehrig-Kawski formula for a Hall basis.
In the second part of the article, we focus on the aforementioned mappings \(\phi ^{t}\circ \pi _{1}^{\prime }\) and \(\phi _{\gamma }\circ \pi _{1}^{\prime }\) as particular cases of a mapping \(\phi \circ \pi _{1}^{\prime },\) with  an algebra homomorphism (R is a
an algebra homomorphism (R is a  ). We show in Theorem 3 that for \(w\in \mathrm {A}^*_{m}\), it follows:
). We show in Theorem 3 that for \(w\in \mathrm {A}^*_{m}\), it follows:
where \(\phi _{n}(w) = {\sum }_{w_{1}{\cdots } w_{k} = w} \phi (w_{1})\cdots \phi (w_{k})\). From this theorem, we deduce that for a path \(\gamma \), the homogeneous components of the logarithmic signature of \(\gamma \) can be expressed through the following:
defined for \(w\in \mathrm {A}^*_{m}\). This formula explicitly connects the m-homogeneous component of \(\log X(\gamma )\) with the signatures \(X(\gamma ^{\star n})\) (n = 1,…,m) of the n th powers concatenation of \(\gamma \).
2 Preliminary
In the article, we assume  to be the set of natural numbers beginning from 1,
to be the set of natural numbers beginning from 1,  to be a field of characteristic 0. For a unitary associative
to be a field of characteristic 0. For a unitary associative  with unit \(1,\) we use standard notations as follows:
with unit \(1,\) we use standard notations as follows:
for any \(Q \in {\text {Alg}}\), for which it makes sense. Here, \(Q^{\bullet k}\) is defined recursively by \(Q^{\bullet 0} = 1\), and \(Q^{\bullet k} = Q \bullet Q^{\bullet k-1}\) for  .
.
2.1 Tensor Algebra
Let V be a finite dimensional linear space over  . For
. For  , denote by \(V^{\otimes {k}}\) the k th tensor product of
, denote by \(V^{\otimes {k}}\) the k th tensor product of  . Let \(T^{\otimes } V = \bigoplus _{k = 0}^{\infty } V^{\otimes {k}}\) and \(T^{\bar \otimes }V\) be its algebraic closure. Consider \(\otimes : T^{\bar \otimes }V \times T^{\bar \otimes } V \to T^{\bar \otimes } V\) as a product, i.e., V⊗k × V⊗l ∋ (x,y)↦x ⊗ y ∈ V⊗k + l. Then \((T^{\otimes } V,\otimes )\) and \((T^{\bar \otimes } V,\otimes )\) are associative \(\mathit {K}\)-algebras with
. Let \(T^{\otimes } V = \bigoplus _{k = 0}^{\infty } V^{\otimes {k}}\) and \(T^{\bar \otimes }V\) be its algebraic closure. Consider \(\otimes : T^{\bar \otimes }V \times T^{\bar \otimes } V \to T^{\bar \otimes } V\) as a product, i.e., V⊗k × V⊗l ∋ (x,y)↦x ⊗ y ∈ V⊗k + l. Then \((T^{\otimes } V,\otimes )\) and \((T^{\bar \otimes } V,\otimes )\) are associative \(\mathit {K}\)-algebras with  as the unit.
as the unit.
2.2 Shuffle Algebra
Let \(\mathrm {A}\) be a certain finite set of cardinality \(\geq 2\), called the alphabet. Denote by  , the set of words of length n, the set of all words, the \(\mathit {K}\)-algebras of non-commutative polynomials, and series in the letters \(\mathrm {A}\), respectively; by \(\mathrm {1} \in \mathrm {A}^*_{0}\), we denote the empty word; by
, the set of words of length n, the set of all words, the \(\mathit {K}\)-algebras of non-commutative polynomials, and series in the letters \(\mathrm {A}\), respectively; by \(\mathrm {1} \in \mathrm {A}^*_{0}\), we denote the empty word; by  , the subset of non-trivial (non-empty) words, the submodule spanned on non-trivial words, and its algebraic closure, respectively. The module
, the subset of non-trivial (non-empty) words, the submodule spanned on non-trivial words, and its algebraic closure, respectively. The module  is dual to
is dual to  , and we identify
, and we identify  with the
with the  functional
functional  by writing \(P={\sum }_{w\in \mathrm {A}^{*}_{}}({P}|{w}) w\). The product of two series
by writing \(P={\sum }_{w\in \mathrm {A}^{*}_{}}({P}|{w}) w\). The product of two series  is therefore defined by \(({\text {PQ}}|{w}) := {\sum }_{\text {uv}=w} ({P}|{u})({Q}|{v})\). Since
is therefore defined by \(({\text {PQ}}|{w}) := {\sum }_{\text {uv}=w} ({P}|{u})({Q}|{v})\). Since  is a finite-free generated algebra, the module
is a finite-free generated algebra, the module  is dual to
is dual to  , and we also identify
, and we also identify  with
with  by \(Q={\sum }_{w\in \mathrm {A}^*_{}}({Q}|{w}) w\). Clearly, \((P| Q)_{} = (Q| P)_{}\), and it also plays a role of a scalar product in
by \(Q={\sum }_{w\in \mathrm {A}^*_{}}({Q}|{w}) w\). Clearly, \((P| Q)_{} = (Q| P)_{}\), and it also plays a role of a scalar product in  . For a
. For a  , we denote by
, we denote by  the module of series representing functionals vanishing on Y. If
the module of series representing functionals vanishing on Y. If  are
are  then for an endomorphism \(\rho : X\to Y\), we denote \(\ker ^{\perp }\rho := (\ker \rho )^{\perp }\).
then for an endomorphism \(\rho : X\to Y\), we denote \(\ker ^{\perp }\rho := (\ker \rho )^{\perp }\).
Since  , and
, and  is the algebraic closure of
is the algebraic closure of  , we define all objects in the larger algebra. The concatenation product in
, we define all objects in the larger algebra. The concatenation product in  has its tensorial version which we denote by
has its tensorial version which we denote by  , i.e., \(\operatorname {conc}(P\otimes Q) = \text {PQ}\). Introduce another—shuffle—product
, i.e., \(\operatorname {conc}(P\otimes Q) = \text {PQ}\). Introduce another—shuffle—product  defined recursively for words by
defined recursively for words by  for any \(w\in \mathrm {A}^*_{}\), and
for any \(w\in \mathrm {A}^*_{}\), and

for all \(a_{1},a_{2}\in \mathrm {A}\) and \(w_{1}, w_{2}\in \mathrm {A}^*_{}\). In what follows, we will use another standard notation for the shuffle product  , i.e.,
, i.e.,  , and its generalized version
, and its generalized version  given by the following:
given by the following:

for \(w_{1},\ldots , w_{k}\in \mathrm {A}^*_{}\). We denote by  (resp.
(resp.  ) the commutative
) the commutative  of non-commutative polynomials (resp. series) in the letters \(\mathrm {A}\) with
of non-commutative polynomials (resp. series) in the letters \(\mathrm {A}\) with  as the product. The adjoint coproduct of the shuffle product
as the product. The adjoint coproduct of the shuffle product  and its generalized version
and its generalized version  are defined by the following:
are defined by the following:

Similarly, we define the adjoint coproduct of the concatenation  and its generalized version
and its generalized version  by the following;
by the following;
where the sum is taken over all \(w_{i}\in {\mathrm {A}^*}\). Note that  and
and  are mutually adjoint bialgebras [20, Prop. 1.9].
are mutually adjoint bialgebras [20, Prop. 1.9].
2.3 Free Lie Algebra on A
Let  be the standard Lie bracket, i.e., a bilinear mapping given by \([P,Q] := \text {PQ} - \text {QP}\). We denote by \(\text {Lie}(\mathrm {A})\) the smallest
be the standard Lie bracket, i.e., a bilinear mapping given by \([P,Q] := \text {PQ} - \text {QP}\). We denote by \(\text {Lie}(\mathrm {A})\) the smallest  of
of  , which contains \(\mathrm {A}\), and is closed under the Lie bracket, i.e., the free Lie algebra generated by \(\mathrm {A}\), and by \(\text {Lie}((\mathrm {A}))\) its algebraic closure. By \(\text {Lie}^{*}(\mathrm {A})\), we denote the module of
, which contains \(\mathrm {A}\), and is closed under the Lie bracket, i.e., the free Lie algebra generated by \(\mathrm {A}\), and by \(\text {Lie}((\mathrm {A}))\) its algebraic closure. By \(\text {Lie}^{*}(\mathrm {A})\), we denote the module of  functionals
functionals  . Denote by \((S \lfloor X){}\) the action of a
. Denote by \((S \lfloor X){}\) the action of a  on an element \(X\in \text {Lie}(\mathrm {A})\). Let \(\mathrm {B}\) be an totally ordered set, and \(\left \{ P_{h} \ | \ h\in \mathrm {B} \right \}\) be a basis in \(\text {Lie}(\mathrm {A})\). Let \(\left \{ S_{h} \ | \ h\in \mathrm {B} \right \}\) be the dual basis of \(\text {Lie}^{*}(\mathrm {A})\), i.e., the one defined by the following:
on an element \(X\in \text {Lie}(\mathrm {A})\). Let \(\mathrm {B}\) be an totally ordered set, and \(\left \{ P_{h} \ | \ h\in \mathrm {B} \right \}\) be a basis in \(\text {Lie}(\mathrm {A})\). Let \(\left \{ S_{h} \ | \ h\in \mathrm {B} \right \}\) be the dual basis of \(\text {Lie}^{*}(\mathrm {A})\), i.e., the one defined by the following:
for any \(X\in \text {Lie}(\mathrm {A})\).
2.4 Hall Sets & Basis
Let \(\mathcal {M}(\mathrm {A})\) be the set of binary, complete, planar, rooted trees with leaves labeled by \(\mathrm {A}\). Each such tree can be naturally identified with the unique expression in the set \(\mathcal {E}(\mathrm {A})\) defined by the following two conditions: (i) if \(a\in \mathrm {A}\), then \(a\in \mathcal {E}(\mathrm {A})\), and (ii) if \(t,t^{\prime }\in \mathcal {E}(\mathrm {A})\), then \((t,t^{\prime })\in \mathcal {E}(\mathrm {A})\). In the sequel, we will not distinguish between these sets, i.e., we assume \(\mathcal {M}(\mathrm {A}) = \mathcal {E}(\mathrm {A})\). Define the mapping \(\mathcal {F}(\cdot ):\mathcal {M}(\mathrm {A})\to \mathrm {A}^*_{}\), which assigns to a tree \(t\in \mathcal {M}(\mathrm {A})\), the word given by dropping all brackets in it, i.e., \(\mathcal {F}(a) = a\) for all \(a\in \mathrm {A}\), and \(\mathcal {F}((t,t^{\prime })) = \mathcal {F}(t)\mathcal {F}(t^{\prime })\) for all \(t,t^{\prime }\in \mathcal {M}(\mathrm {A})\). The word \(\mathcal {F}(t)\) is called the foliage of \(t\in \mathcal {M}(\mathrm {A})\). Define also the mapping \(\mathcal {P}_{\cdot }:\mathcal {M}(\mathrm {A})\to \text {Lie}(\mathrm {A})\), which changes the rounded brackets into the Lie brackets, i.e., \(\mathcal {P}_{a} = a\) for all a ∈A, and \(\mathcal {P}_{(t,t^{\prime })} := [\mathcal {P}_{t},\mathcal {P}_{t^{\prime }}]\) for all \(t,t^{\prime }\in \mathcal {M}(\mathrm {A})\). We will generalize this definition in the sequel. A Hall set \(\mathcal {H}\) on the letters \(\mathrm {A}\) [9]Footnote 1, is a subset of \(\mathcal {M}(\mathrm {A})\) totally ordered by \(\leq \) and satisfying:
-
(I)
\(\mathrm {A} \subset \mathcal {H}\);
-
(II)
if \(h = (h^{\prime },h^{\prime \prime })\in \mathcal {H}\setminus \mathrm {A}\), then \(h^{\prime \prime } \in \mathcal {H}\) and \(h < h^{\prime \prime }\);
-
(III)
for all \(h = (h^{\prime },h^{\prime \prime })\in \mathcal {M}(\mathrm {A})\setminus \mathrm {A}\) we have \(h\in \mathcal {H}\) iff
-
\(h^{\prime }, h^{\prime \prime } \in \mathcal {H}\) and \(h^{\prime } < h^{\prime \prime }\), and
-
\(h^{\prime } \in \mathrm {A}\) or \(h^{\prime } = (x,y)\) such that \(y \geq h^{\prime \prime }\).
-
Fix a Hall set \(\mathcal {H}\) on the letters \(\mathrm {A}\) totally ordered by \(\leq \). Each Hall tree \(h\in \mathcal {H}\) corresponds to a word \(\mathcal {F}(h)\in \mathrm {A}^*_{}\) called a Hall word. Denote by \(\mathcal {W}\), the set of Hall words with ordering \(\leq \) inherited from the ordering on \(\mathcal {H}\) in the natural way. Each word w ∈A∗, is the unique concatenation of a unique non-increasing series of Hall words, that is, \(w=h_{1}{\cdots } h_{k}\) for some unique  , and \(h_{i}\in \mathcal {W}\) such that \(h_{1} \geq \cdots \geq h_{k}\). Let
, and \(h_{i}\in \mathcal {W}\) such that \(h_{1} \geq \cdots \geq h_{k}\). Let  be the mapping defined by the following
be the mapping defined by the following
-
(i)
\(\mathcal {P}_{\mathrm {1}} := 1\);
-
(ii)
\(\mathcal {P}_{a} := a\) for \(a\in \mathrm {A}\);
-
(iii)
\(\mathcal {P}_{h} := \mathcal {P}_{t}\in \text {Lie}(\mathrm {A})\) for \(h\in \mathcal {W}\) such that \(h=\mathcal {F}(t)\), \(t\in \mathcal {H}\subset \mathcal {M}(\mathrm {A})\);
-
(iv)
 for \(w = h_{1}{\cdots } h_{k}\), where
for \(w = h_{1}{\cdots } h_{k}\), where 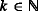 and \(h_{i}\in \mathcal {W}\) such that \(h_{1} \geq \cdots \geq h_{k}\).
and \(h_{i}\in \mathcal {W}\) such that \(h_{1} \geq \cdots \geq h_{k}\).
The set \(\left \{ \mathcal {P}_{h}\in \text {Lie}(\mathrm {A}) \ | \ h\in \mathcal {W} \right \}\) is the Hall basis of \(\text {Lie}(\mathrm {A})\) corresponding to the Hall set \(\mathcal {H}\). By the Poincaré-Birkhoff-Witt theorem, the set of ordered products \(\mathcal {P}_{h_{1}}{\cdots } \mathcal {P}_{h_{k}}\), where \(h_{1} \geq {\cdots } \geq h_{k}\) are Hall words, creates a basis for the enveloping algebra of \(\text {Lie}(\mathrm {A})\), which in the free case is isomorphic to  . Therefore, \(\left \{ \mathcal {P}_{w} \ | \ w\in \mathrm {A}^*_{} \right \}\) is a basis in
. Therefore, \(\left \{ \mathcal {P}_{w} \ | \ w\in \mathrm {A}^*_{} \right \}\) is a basis in  . Consider the dual basis \(\left \{ \mathcal {S}_{w} \ | \ w\in \mathrm {A}^*_{} \right \}\) in
. Consider the dual basis \(\left \{ \mathcal {S}_{w} \ | \ w\in \mathrm {A}^*_{} \right \}\) in  .
.
Proposition 1 ([20, Theorem 5.3])
-
(i)
\(\mathcal {S}_{1} = 1\) ;
-
(ii)
If \(h = av \in \mathcal {W}\) is a Hall word, where \(a\in \mathrm {A}, v\in \mathrm {A}^*_{}\) , then \(\mathcal {S}_{h} = a\mathcal {S}_{v}\) ;
-
(iii)
If\(w = h_{1}^{i_{1}}{\cdots } h_{k}^{i_{k}} \in \mathrm {A}^*_{}\)isany word, where\(h_{1} > {\cdots } > h_{k}\)areHall words and
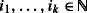 , then
, then
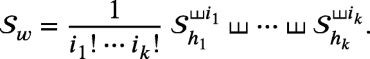
One of the consequences of this proposition is that  is the algebraic closure of the free commutative algebra over \(\left \{ \mathcal {S}_{h} \ | \ h\in \mathcal {W} \right \}\). In particular,
is the algebraic closure of the free commutative algebra over \(\left \{ \mathcal {S}_{h} \ | \ h\in \mathcal {W} \right \}\). In particular,  , where \(h_{1} \geq {\cdots } \geq h_{k}\) are Hall words, creates a basis for
, where \(h_{1} \geq {\cdots } \geq h_{k}\) are Hall words, creates a basis for  .
.
2.5 Algebra of Endomorphisms 
Consider  —the
—the  of linear endomorphisms from
of linear endomorphisms from  to
to  . For
. For  define their convolution product as follows:
define their convolution product as follows:

Let  be a projection \(\epsilon (Q) = (Q| 1)_{} \mathrm {1}\). Then,
be a projection \(\epsilon (Q) = (Q| 1)_{} \mathrm {1}\). Then,  is an associative
is an associative  with unit \(\epsilon \). Introduce the complete tensor product as follows:
with unit \(\epsilon \). Introduce the complete tensor product as follows:

and a product \(\bar * = \operatorname {sh}\otimes \operatorname {conc} : \mathcal {A}\otimes \mathcal {A} \to \mathcal {A}\), i.e.,
for  Then, \((\mathcal {A},\bar *)\) is an associative
Then, \((\mathcal {A},\bar *)\) is an associative  with unit \(\bar 1 = 1\otimes 1\). The canonical isomorphism of modules
with unit \(\bar 1 = 1\otimes 1\). The canonical isomorphism of modules  given by the following:
given by the following:
is a homomorphism of algebras  and \((\mathcal {A},\bar *)\), i.e.,
and \((\mathcal {A},\bar *)\), i.e.,
Note that in the definition of \(\operatorname {Im}\), we choose the most natural basis \(\left \{ u \ | \ u\in {\mathrm {A}^*} \right \}\) in  and its dual basis \(\left \{ u \ | \ u\in {\mathrm {A}^*} \right \}\) in
and its dual basis \(\left \{ u \ | \ u\in {\mathrm {A}^*} \right \}\) in  , but in general one can take a different basis and its dual.
, but in general one can take a different basis and its dual.
3 Eulerian Idempotent and its Adjoint
Let  be a projection given by \( I(Q) = Q - \epsilon (Q)\). We are particularly interested in an endomorphism
be a projection given by \( I(Q) = Q - \epsilon (Q)\). We are particularly interested in an endomorphism 
called the Eulerian idempotent. A straightforward calculation shows that \(\operatorname {Im}(\pi _{1})\) equals
It is known that \(\pi _{1}\) is a projection,  , and
, and  for all
for all  . The second statement means
. The second statement means  . From Proposition 1, we conclude that
. From Proposition 1, we conclude that

is a basis of this space. The kernel of \(\pi _{1}\) have another characterization:  , where
, where  [20, Thm. 3.7].
[20, Thm. 3.7].
The main results in this article concern  —the adjoint endomorphism to \(\pi _{1}\), i.e., the one defined by the following;
—the adjoint endomorphism to \(\pi _{1}\), i.e., the one defined by the following;
for all  . A straightforward calculation using adjointness of \(\operatorname {conc}_{k}\) and \(\delta _{k}^{\prime }\), adjointness of \(\operatorname {sh}_{k}\) and \(\delta _{k}\), and self-adjointness of I, brings to the following formula
. A straightforward calculation using adjointness of \(\operatorname {conc}_{k}\) and \(\delta _{k}^{\prime }\), adjointness of \(\operatorname {sh}_{k}\) and \(\delta _{k}\), and self-adjointness of I, brings to the following formula
Since \(\pi _{1}\) is a projection, the same is true for \(\pi _{1}^{\prime }\). In particular,  and
and  , which we denote by \(\text {Lie}^{\perp }(\mathrm {A})\).
, which we denote by \(\text {Lie}^{\perp }(\mathrm {A})\).
Since \(\pi _{1}\) is onto \(\text {Lie}(\mathrm {A})\), we also consider its adjoint as an epimorphism. Namely, for  , we introduce its adjoint endomorphism
, we introduce its adjoint endomorphism  . It is a
. It is a  monomorphism onto \(\ker ^{\perp } \pi _{1}\) satisfying the following:
monomorphism onto \(\ker ^{\perp } \pi _{1}\) satisfying the following:
for all  .
.
Proposition 2
Let\(\left \{ P_{h} \ | \ h\in \mathrm {B} \right \}\)and\(\left \{ S_{h} \ | \ h\in \mathrm {B} \right \}\)bebases in\(\text {Lie}(\mathrm {A})\)and its dual inLie∗(A), respectively. It followsthat
Proof
We prove that
Since  it follows that
it follows that
This ends the proof. □
Choose a basis \(\left \{ P_{h} \ | \ h\in \mathrm {B} \right \}\) in \(\text {Lie}(\mathrm {A})\), and a projection  on \(\text {Lie}(\mathrm {A})\). Then, \(\text {Lie}^{*}(\mathrm {A})\) is naturally identified with
on \(\text {Lie}(\mathrm {A})\). Then, \(\text {Lie}^{*}(\mathrm {A})\) is naturally identified with  by the isomorphism \(\iota _{\rho } : \text {Lie}_{\rho }^{*}(\mathrm {A}) \to \text {Lie}^{*}(\mathrm {A})\) given by \((\iota _{\rho } (S) \lfloor P){} = (S| P)_{}\). In \(\text {Lie}_{\rho }^{*}(\mathrm {A})\), there exists the dual basis \(\left \{ S_{h} \ | \ h\in \mathrm {B} \right \}\) to the one in \(\text {Lie}(\mathrm {A})\) given by the following:
by the isomorphism \(\iota _{\rho } : \text {Lie}_{\rho }^{*}(\mathrm {A}) \to \text {Lie}^{*}(\mathrm {A})\) given by \((\iota _{\rho } (S) \lfloor P){} = (S| P)_{}\). In \(\text {Lie}_{\rho }^{*}(\mathrm {A})\), there exists the dual basis \(\left \{ S_{h} \ | \ h\in \mathrm {B} \right \}\) to the one in \(\text {Lie}(\mathrm {A})\) given by the following:
Theorem 1
Let\(\left \{ P_{h} \ | \ h\in \mathrm {B} \right \}\)abasis in\(\text {Lie}(\mathrm {A})\), a projection on \(\text {Lie}(\mathrm {A})\), and \(\left \{ S_{h} \ | \ h\in \mathrm {B} \right \}\) the basis in \(\text {Lie}_{\rho }^{*}(\mathrm {A})\) given by (4). It follows that
a projection on \(\text {Lie}(\mathrm {A})\), and \(\left \{ S_{h} \ | \ h\in \mathrm {B} \right \}\) the basis in \(\text {Lie}_{\rho }^{*}(\mathrm {A})\) given by (4). It follows that
Proof
Using Proposition 2 for \(\left \{ P_{h} \ | \ h\in \mathrm {B} \right \}\) and \(\left \{ \iota _{\rho }(S_{h}) \ | \ h\in \mathrm {B} \right \}\) we get
Since \((\iota _{\rho }(\alpha ) \lfloor \pi _{1}(Q)){} = (\alpha | \pi _{1}(Q))_{}\) for all  , we have \({\bar \pi }_{1}^{\prime }\circ \iota _{\rho } = \pi _{1}^{\prime }\) on \(\text {Lie}_{\rho }^{*}(\mathrm {A})\). This ends the proof. □
, we have \({\bar \pi }_{1}^{\prime }\circ \iota _{\rho } = \pi _{1}^{\prime }\) on \(\text {Lie}_{\rho }^{*}(\mathrm {A})\). This ends the proof. □
A few remarks are in order. First of all, we recall that in the algebra \(\mathcal {A}\) the product is \(\operatorname {sh}\otimes \operatorname {conc}\), so the shuffle product is used to compute the left side of the tensor product. It means that good properties of \(\pi _{1}^{\prime }(S_{h})\) with respect to \(\operatorname {sh}\) are welcome. Secondly, the proved formula is similar to the quite clear formula (6.2.1) in Reutenauer’s book [20] (in which the sum is taken over all words). In our case, however, the sum is taken over the basis of the Lie algebra, which contains essential information about the logarithm of a series [4, 18]. Therefore, this theorem generalizes the Gehrig-Kawski theorem (see Theorem 2 beneath) to its most extent. The advantage of the theorem is that it can be used to compute BCH-formula, Magnus expansion, logarithm of the signature, coordinates of the second kind, etc., both in general case, as well as for particular situations. In each case, one can try to choose a basis in Lie(A) and \(\rho \) to utilize specific features of a given problem.
There are several natural choices for \(\rho \). The first one is \(\rho = \pi _{1}\). Recall that  and
and  in which there are natural basis
in which there are natural basis

written in terms of the dual elements to a Hall basis in \(\text {Lie}(\mathrm {A})\) [17, Th. 3.1.1]. The description of its dual in \(\text {Lie}(\mathrm {A})\) is unknown.
The second one is to take \(\rho = \rho _{\perp }\) as the orthogonal projection with respect to the scalar product \((\cdot | \cdot )_{}\) in  (for more details about this projection see [5]). In this case, \(\text {Lie}_{\rho _{\perp }}^{*}(\mathrm {A}) = \ker ^{\perp }\rho _{\perp } = \text {Lie}((\mathrm {A}))\). In particular, \(\rho _{\perp } \neq \pi _{1}\). Take a basis \(\left \{ P_{h} \ | \ h\in \mathrm {B} \right \}\) in \(\text {Lie}(\mathrm {A})\) on a well-ordered set \(\mathrm {B}\). Using Gram-Schmidt process obtain the orthonormal basis \(\left \{ \hat P_{h} \ | \ h\in \mathrm {B} \right \}\). Then, this is also the dual basis in \(\text {Lie}(\mathrm {A})\). Therefore, from the above theorem, we get \(\operatorname {Im}(\operatorname {Id}) = \exp \left ({\sum }_{h\in \mathrm {B}} \pi _{1}^{\prime }(\hat P_{h})\otimes \hat P_{h} \right ). \) The same is clearly true for any orthonormal basis in \(\text {Lie}(\mathrm {A})\).
(for more details about this projection see [5]). In this case, \(\text {Lie}_{\rho _{\perp }}^{*}(\mathrm {A}) = \ker ^{\perp }\rho _{\perp } = \text {Lie}((\mathrm {A}))\). In particular, \(\rho _{\perp } \neq \pi _{1}\). Take a basis \(\left \{ P_{h} \ | \ h\in \mathrm {B} \right \}\) in \(\text {Lie}(\mathrm {A})\) on a well-ordered set \(\mathrm {B}\). Using Gram-Schmidt process obtain the orthonormal basis \(\left \{ \hat P_{h} \ | \ h\in \mathrm {B} \right \}\). Then, this is also the dual basis in \(\text {Lie}(\mathrm {A})\). Therefore, from the above theorem, we get \(\operatorname {Im}(\operatorname {Id}) = \exp \left ({\sum }_{h\in \mathrm {B}} \pi _{1}^{\prime }(\hat P_{h})\otimes \hat P_{h} \right ). \) The same is clearly true for any orthonormal basis in \(\text {Lie}(\mathrm {A})\).
The third one is to take \(\rho = \rho _{\operatorname {PBW}}\) as the projection with kernel derived from Poincare-Birkhoff-Witt theorem. More precisely, universal enveloping algebra of the free Lie algebra \(\text {Lie}(\mathrm {A})\) is  . If \(\left \{ P_{h} \ | \ h\in \mathrm {B} \right \}\) is a basis in \(\text {Lie}(\mathrm {A})\) then, using Poincaré-Birkhoff-Witt theorem, the set of ordered products \(P_{h_{1}}{\cdots } P_{h_{k}}\), where \(h_{1} \geq {\cdots } \geq h_{k} \in \mathrm {B}\), is a basis for the enveloping algebra of \(\text {Lie}(\mathrm {A})\), i.e., in
. If \(\left \{ P_{h} \ | \ h\in \mathrm {B} \right \}\) is a basis in \(\text {Lie}(\mathrm {A})\) then, using Poincaré-Birkhoff-Witt theorem, the set of ordered products \(P_{h_{1}}{\cdots } P_{h_{k}}\), where \(h_{1} \geq {\cdots } \geq h_{k} \in \mathrm {B}\), is a basis for the enveloping algebra of \(\text {Lie}(\mathrm {A})\), i.e., in  . Denote by \(S_{h_{1},\ldots ,h_{k}}\), \(h_{1} \geq {\cdots } \geq h_{k}\in \mathrm {B}\), the elements of the dual basis in
. Denote by \(S_{h_{1},\ldots ,h_{k}}\), \(h_{1} \geq {\cdots } \geq h_{k}\in \mathrm {B}\), the elements of the dual basis in  . We define \(\rho _{\operatorname {PBW}}\) as a projection on \(\text {Lie}(\mathrm {A})\) with the kernel
. We define \(\rho _{\operatorname {PBW}}\) as a projection on \(\text {Lie}(\mathrm {A})\) with the kernel  . From PBW theorem, the elements written in this formula are linearly independent, hence creates a basis of \(\ker \rho _{\operatorname {PBW}}\). On the dual side, \(\ker ^{\perp }\rho _{\operatorname {PBW}} = \operatorname {span}\left \{ S_{h} \ | \ h\in \mathrm {B} \right \}\), but in general case, there is not known explicit formulas for \(S_{h}\). It follows that \(\ker \rho _{\operatorname {PBW}} \neq \ker \pi _{1}\), because for \(h > h^{\prime } \in \mathrm {B}\), we have \(\ker \pi _{1} \ni (P_{h} + P_{h^{\prime }})^{2} = {P_{h}^{2}} + P_{h^{\prime }}^{2} + 2P_{h}P_{h^{\prime }} - [P_{h},P_{h^{\prime }}]\), but \(\rho _{\operatorname {PBW}}((P_{h} + P_{h^{\prime }})^{2}) = - [P_{h},P_{h^{\prime }}]\). Therefore, \(\rho _{\operatorname {PBW}} \neq \pi _{1}\). It also follows that \(\ker ^{\perp }\rho _{\operatorname {PBW}} \neq \ker ^{\perp }\rho _{\perp }\), because for \(h > h^{\prime } \in \mathrm {B}\), we have \((P_{h} P_{h^{\prime }}| [P_{h},P_{h^{\prime }}])_{} = (P_{h} P_{h^{\prime }}| P_{h} P_{h^{\prime }})_{} - (P_{h} P_{h^{\prime }}| P_{h^{\prime }}P_{h})_{} > 0\), since \(P_{h} P_{h^{\prime }},P_{h^{\prime }}P_{h}\) are linearly independent and have the same norm. Therefore, \(\rho _{\operatorname {PBW}} \neq \rho _{\perp }\). Note that each choice of the basis in \(\text {Lie}(\mathrm {A})\) gives a different projection \(\rho _{\operatorname {PBW}}\), so in this case, we actually define a class of examples.
. From PBW theorem, the elements written in this formula are linearly independent, hence creates a basis of \(\ker \rho _{\operatorname {PBW}}\). On the dual side, \(\ker ^{\perp }\rho _{\operatorname {PBW}} = \operatorname {span}\left \{ S_{h} \ | \ h\in \mathrm {B} \right \}\), but in general case, there is not known explicit formulas for \(S_{h}\). It follows that \(\ker \rho _{\operatorname {PBW}} \neq \ker \pi _{1}\), because for \(h > h^{\prime } \in \mathrm {B}\), we have \(\ker \pi _{1} \ni (P_{h} + P_{h^{\prime }})^{2} = {P_{h}^{2}} + P_{h^{\prime }}^{2} + 2P_{h}P_{h^{\prime }} - [P_{h},P_{h^{\prime }}]\), but \(\rho _{\operatorname {PBW}}((P_{h} + P_{h^{\prime }})^{2}) = - [P_{h},P_{h^{\prime }}]\). Therefore, \(\rho _{\operatorname {PBW}} \neq \pi _{1}\). It also follows that \(\ker ^{\perp }\rho _{\operatorname {PBW}} \neq \ker ^{\perp }\rho _{\perp }\), because for \(h > h^{\prime } \in \mathrm {B}\), we have \((P_{h} P_{h^{\prime }}| [P_{h},P_{h^{\prime }}])_{} = (P_{h} P_{h^{\prime }}| P_{h} P_{h^{\prime }})_{} - (P_{h} P_{h^{\prime }}| P_{h^{\prime }}P_{h})_{} > 0\), since \(P_{h} P_{h^{\prime }},P_{h^{\prime }}P_{h}\) are linearly independent and have the same norm. Therefore, \(\rho _{\operatorname {PBW}} \neq \rho _{\perp }\). Note that each choice of the basis in \(\text {Lie}(\mathrm {A})\) gives a different projection \(\rho _{\operatorname {PBW}}\), so in this case, we actually define a class of examples.
The fourth one, a subclass of the previous one, is to take \(\rho = \rho _{\operatorname {Hall}}\), the projection derived as above taking a Hall basis in \(\text {Lie}(\mathrm {A})\). Recall that we described these basis in Section 2.4. In this case, Theorem 1 is equivalent to the following Gehrig-Kawski theorem.
Theorem 2 (8 Theorem 28)
Let \(\mathcal {W}\) be a set of Hall words on the letters \(\mathrm {A}\) . It follows that
In Tables 1 and 2, we gather known informations about \(\ker \rho , \ker ^{\perp }\rho = \text {Lie}_{\rho }^{*}(\mathrm {A})\) and basis in \(\text {Lie}(\mathrm {A})\) and its dual in \(\text {Lie}_{\rho }^{*}(\mathrm {A})\) associated with projections \(\rho \) just described.
4 Computing \(\phi \circ \pi _{1}^{\prime }\)
Let \((R, \mu )\) be a  with a multiplication \(\mu :R\otimes R \to R\). If there is no confusion, we will use standard notation \(\text {ab} = \mu (a\otimes b)\). We also recursively introduce \(\mu _{k} : R^{\otimes k} \to R\) by \(\mu _{1}(a) = a\), \(\mu _{2} = \mu \), \(\mu _{k + 1} = \mu \circ (\mu _{k}\otimes \mu _{1})\). Let \((R^{\prime }, \cdot )\) be an K-algebra with a multiplication \(\cdot : R^{\prime }\times R^{\prime } \to R^{\prime }\) (we use simpler definition of this product, because we will not use its tensorial properties).
with a multiplication \(\mu :R\otimes R \to R\). If there is no confusion, we will use standard notation \(\text {ab} = \mu (a\otimes b)\). We also recursively introduce \(\mu _{k} : R^{\otimes k} \to R\) by \(\mu _{1}(a) = a\), \(\mu _{2} = \mu \), \(\mu _{k + 1} = \mu \circ (\mu _{k}\otimes \mu _{1})\). Let \((R^{\prime }, \cdot )\) be an K-algebra with a multiplication \(\cdot : R^{\prime }\times R^{\prime } \to R^{\prime }\) (we use simpler definition of this product, because we will not use its tensorial properties).
Let  and
and  be algebra homomorphisms. Then, it is easy to see that
be algebra homomorphisms. Then, it is easy to see that
From Theorem 1, we conclude that
Our aim is to give expression for \(\phi \circ \pi _{1}^{\prime }\). For  , let us define a linear mapping
, let us define a linear mapping  , for \(v\in {\mathrm {A}^*}\) given by the following:
, for \(v\in {\mathrm {A}^*}\) given by the following:
where the sum is taken over all \(v_{i}\in {\mathrm {A}^*}\). We emphasize the existence of the empty word \(\mathrm {1} \in {\mathrm {A}^*}\). In particular \(\phi _{1}(v) = \phi (v)\).
Recall  , and
, and
where \(\operatorname {sh}_{k}\) and \(\delta _{k}^{\prime }\) are defined by (2) and (3), respectively. Therefore,
For  , let us define linear mappings
, let us define linear mappings  , for \(v\in {\mathrm {A}^*}\) given by the following:
, for \(v\in {\mathrm {A}^*}\) given by the following:
where the sum is taken over all \(u_{i}\in {\mathrm {A}^*_{+}}\)—the set of non-trivial words. Since I annihilates empty word, it is easy to see that
We conclude that
In the following lemma, we derive \({\tilde \phi }_{k}\)’s in terms of \(\phi _{k}\)’s.
Lemma 4.1
It follows that
Proof
Since in the definition of \(\phi _{k}\)’s, we sum over all words and in the definition of \({\tilde \phi }_{k}\)’s, we sum over all non-empty words, we see that
Now, we use induction on k to prove the hypothesis. For \(k = 1\), this is clear. Then, using (6) and then induction hypothesis, we have the following:
Since \(\binom {k + 1}{m} \binom {k + 1 -m}{n} = \binom {k + 1}{n} \binom {k + 1 -n}{m}\), and changing the order of summation, we have the following:
The expression in the square brackets equals \(-1\), and we are done. □
Using this lemma, we see that
If \(v_{m} \in \mathrm {A}^*_{m}\), then clearly \({\tilde \phi }_{n}(v_{m}) = 0 \) for all \(n > m\) (since we can not divide m-letter word on n non-trivial words). It means that
After changing the order of summation, we get
A simple induction on m shows that
and therefore
The above reasoning brings us to the following theorem.
Theorem 3
Let , and assume \(S = {\sum }_{m \geq 1} S_{m}\), where \(S_{m}\) is the homogeneous part spanned by words of length m, i.e., \( S_{m} = {\sum }_{v \in \mathrm {A}^*_{m}} (S| v)_{} v\). Then,
, and assume \(S = {\sum }_{m \geq 1} S_{m}\), where \(S_{m}\) is the homogeneous part spanned by words of length m, i.e., \( S_{m} = {\sum }_{v \in \mathrm {A}^*_{m}} (S| v)_{} v\). Then,
5 Signature of a Path
Let \(\gamma \) be a continuous path with finite variation in a finite dimensional linear space V over  equipped with the metric \(d_{V}\). More precisely, take \(T >0\) and let \(\mathit {t} = (t_{1},\ldots ,t_{r})\), such that \(0 = t_{0} < t_{1} < {\cdots } < t_{r} \leq T\) and
equipped with the metric \(d_{V}\). More precisely, take \(T >0\) and let \(\mathit {t} = (t_{1},\ldots ,t_{r})\), such that \(0 = t_{0} < t_{1} < {\cdots } < t_{r} \leq T\) and  . Denote the set off all such tuples by \(\mathcal {P}\). For a continuous mapping \(\gamma _{\cdot }: [0,T]\to V\) its length is defined by the following:
. Denote the set off all such tuples by \(\mathcal {P}\). For a continuous mapping \(\gamma _{\cdot }: [0,T]\to V\) its length is defined by the following:
If \(|\gamma | < +\infty \), then it is of finite variation. In particular, this implies that \(\gamma \) is differentiable almost everywhere and
for \(t\in [0,T]\). Recursively define \({X_{k}^{t}}(\gamma )\in V^{\otimes {k}}\) for  , \(t\in [0,T]\), by
, \(t\in [0,T]\), by
Denote \(X_{k}(\gamma ) = {X_{k}^{T}}(\gamma )\) for \(k >0\), and \(X_{0}(\gamma ) = {1}\) the neutral element in \(T^{\otimes } V\). The signature of the path [13] γ is
in the tensor algebra \(T^{\bar \otimes } V\).
In the space of continuous paths with finite variation, we introduce a natural concatenation product. Namely, for two paths \(\gamma : [0,T]\to V, \tilde \gamma : [0,\tilde T] \to V\), we define the concatenation of these paths \(\gamma \star \tilde \gamma :[0,T + \tilde T] \to V\) by
It follows from [2] that
for any paths \(\gamma ,\tilde \gamma \). In particular, this means that for each 
Clearly, this can be generalized to \(X(\gamma \star {\cdots } \star \tilde \gamma ) = X(\gamma ) \otimes {\cdots } \otimes X(\tilde \gamma )\). We are particularly interested in a case \(\gamma = {\ldots } = \tilde \gamma \), in which we use a notation \(\gamma \star {\cdots } \star \gamma = \gamma ^{\star k}\) for the k-times concatenation of \(\gamma \).
Take a basis \((e_{i})\) of V and take an alphabet \(\mathrm {A}\) consisting of the basis elements, i.e., \(\mathrm {A} = \left \{ e_{i} \right \}\). Define a natural algebra homomorphism  given by \(\iota _{\otimes }(e_{i_{1}}{\cdots } e_{i_{k}}) = e_{i_{1}}\otimes {\cdots } \otimes e_{i_{k}}\). Introduce a scalar product
given by \(\iota _{\otimes }(e_{i_{1}}{\cdots } e_{i_{k}}) = e_{i_{1}}\otimes {\cdots } \otimes e_{i_{k}}\). Introduce a scalar product  for which \(\left \{ \iota _{\otimes }(w) \ | \ w\in {\mathrm {A}^*} \right \}\) is an orthonormal basis. and define a linear homomorphism
for which \(\left \{ \iota _{\otimes }(w) \ | \ w\in {\mathrm {A}^*} \right \}\) is an orthonormal basis. and define a linear homomorphism  given by \(\phi _{\gamma }(e_{i_{1}}{\cdots } e_{i_{k}}) = (X(\gamma )| e_{i_{1}}\otimes {\cdots } \otimes e_{i_{k}})_{}\) and \(\phi _{\gamma }(\mathrm {1}) = 1\).
given by \(\phi _{\gamma }(e_{i_{1}}{\cdots } e_{i_{k}}) = (X(\gamma )| e_{i_{1}}\otimes {\cdots } \otimes e_{i_{k}})_{}\) and \(\phi _{\gamma }(\mathrm {1}) = 1\).
Assuming \(\gamma _{t} = {\sum }_{i} {\gamma _{t}^{i}} e_{i}\) we see that
Chen [3] proved that \(\phi _{\gamma }\) is a shuffle algebra homomorphism, i.e.,  for \(v,w\in {\mathrm {A}^*}\). This means we can apply Theorem 2 in which we express \(\phi _{\gamma }\circ \pi ^{\prime }\) in terms of \((\phi _{\gamma })_{k}\) (defined in (5)). Now observe that
for \(v,w\in {\mathrm {A}^*}\). This means we can apply Theorem 2 in which we express \(\phi _{\gamma }\circ \pi ^{\prime }\) in terms of \((\phi _{\gamma })_{k}\) (defined in (5)). Now observe that
Finally, Theorem 3 states that
where \(S_{m} = {\sum }_{v \in \mathrm {A}^*_{m}} (S| v)_{} v\).
Let us also look what is the meaning of Theorem 2 in this context. Using canonical identification  and the definition of ϕγ we see that
and the definition of ϕγ we see that
Since \(\phi _{\gamma }\) is a shuffle algebra homomorphism, \(\iota _{\otimes }\) a concatenation algebra homomorphism, and using Theorem 2, we conclude that
If for all \(h\in \mathrm {B}\), \(S_{h}\) is homogeneous of order \(\# h\), i.e., \(S_{h} \in \operatorname {span} \left \{ w\in \mathrm {A}^*_{\# h} \right \}\) (this is the case for Hall bases), then
This means that having got the signature of a path, the logarithm of this signature can be computed in terms of the signatures of concatenations of the path. For more information about log signature (see [6, 15, 19]).
References
Chapoton F, Patras F. Enveloping algebras of preLie algebras, Solomon idempotents and the Magnus formula. International Journal of Algebra and Computation 2013;23(04):853–61.
Chen K-T. Iterated integrals and exponential homomorphisms. Proc London Math Soc 1954;4(3):502–12.
Chen K-T. Algebraic paths. J Algebra 1968;10:8–36.
Chow W-L. ÜBer Systeme von linearen partiellen Differentialgleichungen erster Ordnung. Math Ann 1939;117(1):98–105.
Duchamp G. Orthogonal projection onto the free Lie algebra. Theor Comput Sci 1991;79(1):227–39.
Friz PK, Victoir NB. Multidimensional stochastic processes as rough paths: theory and applications. Cambridge: Cambridge University Press; 2010.
Gehrig E, Kawski M. A Hopf-algebraic formula for compositions of noncommuting flows. 47th IEEE conference on decision and control, 2008. CDC 2008, IEEE; 2008. p. 1569–74.
Gehrig ET. Hopf algebras, projections, and coordinates of the first kind in control theory. Arizona: Arizona State University; 2007.
Hall M. A basis for free Lie rings and higher commutators in free groups. Proc Am Math Soc 1950;1(5):575–81.
Kawski M. Bases for Lie algebras and a continuous CBH formula. Unsolved problems in mathematical systems and control theory. In: Blondel VD and Megretski A, editors. Princeton: Princeton University Press; 2004.
Kawski M, Sussmann HJ. Noncommutative power series and formal Lie-algebraic techniques in nonlinear control theory. Operators, systems, and linear algebra (Kaiserslautern, 1997), European Consort. Math. Indust. Teubner, Stuttgart; 1997. p. 111–28.
Lyons T, Qian Z. System control and rough paths. Oxford: Oxford University Press; 2002.
Lyons TJ. Differential equations driven by rough signals. Revista Matemática Iberoamericana 1998;14(2):215–310.
Lyons TJ, Caruana M, Lévy T. Differential equations driven by rough paths. Berlin: Springer; 2007.
Lyons TJ, Sidorova N, et al. On the radius of convergence of the logarithmic signature. Ill J Math 50 2006;1-4:763–90.
Melançon G, Reutenauer C. Lyndon words, algebras, free and shuffles. Canad J Math 1989;41(4):577–91.
Radford DE. A natural ring basis for the shuffle algebra and an application to group schemes. Journal of Algebra 1979;58(2):432–54.
Rashevskii PK. About connecting two points of complete non-holonomic space by admissible curve (in Russian). Uch Zapiski ped inst Libknexta 1938;2:83–94.
Reizenstein J, Graham B. 2018. The iisignature library: efficient calculation of iterated-integral signatures and log signatures. arXiv:1802.08252.
Reutenauer C. Free Lie algebras, vol. 7 of London mathematical society monographs. New Series. New York: The Clarendon Press Oxford University Press; 1993. Oxford Science Publications.
Shirshov A. On the bases of a free Lie algebra. Algebra Logika 1962;1(1):14–9.
Sussmann HJ. A product expansion for the Chen series. Theory and applications of nonlinear control systems (Stockholm, 1985), North-Holland, Amsterdam; 1986. p. 323–35.
Viennot G. Algèbres de Lie libres et monoïdes libres, vol. 691 of Lecture Notes in Mathematics. Berlin: Springer; 1978. Bases des algèbres de Lie libres et factorisations des monoïdes libres.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Pietrzkowski, G. On the Adjoint of the Eulerian Idempotent in an Analytic Context. J Dyn Control Syst 25, 535–549 (2019). https://doi.org/10.1007/s10883-018-9421-z
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10883-018-9421-z



 for
for 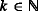 and
and 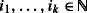 , then
, then