1 Introduction

In many real-world scheduling problems one cannot assume that job processing times are fixed. Wright (1936) noticed that the time required to perform an aircraft production task decreases in conjunction with the worker’s experience. Today, it is widely observed that the processing time of a job may vary in reaction to different environmental factors, such as the amounts of resources available, the starting time of the job, or the set of jobs performed earlier. In the latter case, it is often assumed that the actual processing time of a job depends either on its position in a schedule, or on the sum of basic processing times of jobs that have been already executed. If all the jobs are assumed to be identical, both these approaches are, in some sense, exchangeable. In this paper, the actual processing time of a job is described by a positive function of at most three arguments: the index of the job, the machine to which the job is assigned, and the position it holds on this machine. We also assume that the jobs are either independent, or they need to be processed in a given order, i.e. the precedence constraints take form of a single chain.

Recently, one can observe a growing number of papers related to scheduling problems with the learning effect, where the processing time of a job decreases as the set of already executed jobs grows (see, e.g., Wang et al. 2020). A dual group of problems with the aging effect is also widely considered in literature (see, e.g., Lu et al. 2018; Liu et al. 2018). Having this in mind, we analyze a number of general scheduling problems where job processing times may, but do not have to give in to such a monotonic impact. In particular, we show polynomial algorithms for scheduling problems in which job processing times are described by any arbitrary positive and discrete function. The analyzed problems vary in: the set of factors that impact actual processing times of jobs (position, position and machine, position and job, or all the factors together), the precedence constraints among jobs (independent or chained jobs), and the objective function (maximum completion time or the total completion time).

In practice, it is often assumed that job processing times vary among jobs. As the machines may have different capabilities, the processing time may also depend on the machine chosen (scheduling on unrelated machines). However, the assumption that the actual processing time of a job freely depends on the position it holds on a machine, may seem artificial and impractical. As indicated above and further discussed in Sect. 2, position-dependent models are usually monotonic with respect to the job position. By assuming that job processing time may freely depend on its position, we obtain general results that can be successfully applied both for learning and aging models.

The contribution of the paper is two-fold. First, we analyze various parallel-machine scheduling problems where the actual processing times of independent jobs may freely depend on the three factors: machine, job, and its position on a machine. We present the full classification of computational complexity for these problems and their subproblems. It can be shown that most of such problems can be solved in polynomial time. Second, we show that although the case of single-chained jobs is not easier in general, some of the corresponding problems in this group can also be solved in polynomial time.

This paper is organized as follows. In Sect. 2, we briefly review main position-dependent learning and aging models. We also present main results in the area of job- and machine-dependent processing times. In Sect. 3, we formalize the problem considered in this paper. In Sect. 4, we present the full classification of the complexity of problems with independent jobs. Then, in Sect. 5, we show how the assumption that the jobs are chained influences the analyzed problems. We complete the paper by Sect. 6 which includes conclusions and remarks on future research.

2 Literature review

To the best of our knowledge, the first position-dependent model, where the actual job processing time depends on the number of jobs executed earlier, was proposed by Gawiejnowicz (1996). In this model, the actual processing time of the i-th job scheduled on the r-th position, \(p_{i,r}\), depends on its basic processing time, \(\bar{p}_i\), and the value of \(\nu (r) \in [0, 1]\). In particular, Gawiejnowicz focused on makespan minimization on a single machine within the general \(p_{i,r} = \bar{p}_i/\nu (r)\) model. Similar results—limited to the learning effect—were presented by Biskup (1999), who introduced the \(p_{i,r} = \bar{p}_ir^a\) model, where \(a < 0\) is a constant learning index. He considered single-machine scheduling problems to minimize the total flow time and the maximum deviation from the common due date. A few years later, Mosheiov and Sidney (2003) analyzed a more general case where the learning indices are job-dependent, that is \(p_{i,r} = \bar{p}_ir^{a_i}\). All these results constituted a base for rich research in the area of position-dependent scheduling.

Another popular approach to position-dependent scheduling is based on the paper by DeJong (1957). Okołowski and Gawiejnowicz (2010) considered a group of parallel-machine scheduling problems within the model of generalized DeJong’s learning effect. In this model, it is assumed that \(p_{i,r} = \bar{p}_i[M + (1-M)r^a]\), where \(0 \le M < 1\) is called the incompressibility factor. The same model was analyzed later by Ji et al. (2015).

The list of models, where job processing time depends on the number of jobs executed earlier, is still expanding. There are a few models that take into account that job processing times may be affected simultaneously by factors of different kind. For example, a number of models in which time-dependent job deterioration and DeJong’s learning effect are mixed were analyzed by Zhang et al. (2018) and Sun et al. (2020). We refer the reader to Agnetis et al. (2014), Strusevich and Rustogi (2017), Azzouz et al. (2017), and Gawiejnowicz (2020) for more details on different scheduling models of the kind discussed in this section.

There are two main limitations of the models of scheduling with variable job processing times, especially those that are position-dependent. First, the majority of results are related to single-machine scheduling (see, e.g., Wang 2010; Wang and Wang 2013; Debczynski and Gawiejnowicz 2013 or Huang and Wang 2014). At the same time, one can find only limited number of polynomial results on parallel-machine scheduling of position-dependent jobs (see, e.g., Mosheiov and Sidney 2003; Mosheiov 2008 or Przybylski 2017). Second, most papers related to position-dependent scheduling focus on particular learning or aging models. In fact, there are only individual results independent of the form of the function describing the actual processing time of a job (e.g. Mosheiov 2008). Inspired by the latter paper, we assume that the actual processing time of a job may freely depend on the position it holds on a machine. In particular, we do not make any assumption on the form of such a relation, including its monotonicity. This way, our results can be successfully applied to almost all position-dependent models discussed in literature.

For many practical applications it is also justified to assume that the actual processing time of a job freely depends on a machine it is assigned to. The general problems of scheduling fixed-time jobs on unrelated machines to minimize the makespan or the total weighted completion time are known to be \({{\mathcal {N}}}\!{{\mathcal {P}}}\)-Hard. For this reason, approximation algorithms are proposed (see, e.g., Lenstra et al. 1990; Schulz and Skutella 2002 or Bansal et al. 2019). On the other hand, Bruno et al. (1974) showed that there exists a polynomial algorithm for the case of total completion time as the objective. Having this in mind, we also assume that the actual processing time of a job may depend on a machine it is being assigned to. In the next section, we present the formal definition of this dependency.

3 Problem formulation

In this section, we formulate the set of parallel-machine scheduling problems with job-, machine-, and position-dependent processing times which are going to be discussed henceforth. Let us be given m parallel machines, \(P_1, P_2, \dots , P_m\), and n non-preemptable jobs, \(J_1, \dots , J_n\). The processing time of job \(J_i\) assigned to a given machine \(P_j\) is described by the \(\varphi ^j_i :{\mathbb {N}}_+ \rightarrow {\mathbb {Q}}_+\) function. The value of the function freely depends on the position r the job holds on the j-th machine. In other words, the processing time of the i-th job holding the r-th position on the j-th machine is equal to \(p_{i,j,r} = \varphi ^j_i(r)\). If the values of the functions are job-independent, they will be denoted by \(\varphi ^j\), and then it holds that \(p_{j,r} = \varphi ^j(r)\) for each job \(J_i\). Similarly, if the values of the functions are machine-independent, they will be denoted by \(\varphi _i\), and then it holds that \(p_{i,r} = \varphi _i(r)\) for each feasible i. If the values of the functions are job- and machine-independent, they will be denoted by \(\varphi \), and then it holds that \(p_{r} = \varphi (r)\). The jobs may be either independent (i.e. with no precedence constraints), or chained. Our aim is to find an optimal schedule in the sense of at least one of the following objective functions: maximum completion time or total completion time. Using the traditional three-field notation (see Gawiejnowicz 2020 for a concise description), we can denote these problems by \(\text {P}m|p_{i,j,r} = \varphi ^j_i(r)|C_{\mathrm{max}}\), \(\text {P}m|p_{i,j,r} = \varphi ^j_i(r)|\sum C_i{}\), \(\text {P}m|\text {chain}, p_{i,j,r} = \varphi ^j_i(r)|C_{\mathrm{max}}\), and \(\text {P}m|\text {chain}, p_{i,j,r} = \varphi ^j_i(r)|\sum C_i{}\).

Throughout the paper we will assume that the set of \(\varphi ^j_i\) functions is a part of the problem description, not the input, and that the values of such \(\varphi ^j_i\) functions are precomputed and thus obtainable in constant time. This assumption helps us focus on the essence of the presented results. However, if the values of the \(\varphi ^j_i\) functions were computed on the fly and could be obtained in polynomial time, then all the polynomial algorithms presented henceforth would remain polynomial.

4 Independent jobs

In this section, we consider problems in which position-dependent actual processing times are additionally job-dependent, machine-dependent, or mixed job- and machine-dependent, i.e. \(p_{i,r} = \varphi _i(r)\), \(p_{j,r} = \varphi ^j(r)\), or \(p_{i,j,r} = \varphi _i^j(r)\), respectively. However, we assume that there are no precedence constraints among jobs.

Let us start this section by observing that the \(\text {P}m|p_{r} = \varphi (r)|C_{\mathrm{max}}\) and \(\text {P}m|p_{r} = \varphi (r)|\sum C_i{}\) problems can be easily solved by assigning at most \(\lceil n / m \rceil \) jobs to each of the machines in such a way that the numbers of jobs executed on any pair of machines do not differ by more than one. As it will be shown, in case of machine-dependent processing times, some of the problems can still be solved in polynomial time even if chain precedence constraints are defined. However, if the actual processing times are job-dependent, then they might be—as a special case—constant. As, for \(m=2\), this leads to the \(\text {P}2||C_{\mathrm{max}}\) problem, the following proposition holds.

Proposition 1

The \(\text {P}2|p_{i,r} = \varphi _i(r)|C_{\mathrm{max}}\) problem is \({{\mathcal {N}}}\!{{\mathcal {P}}}\)-Hard.

It is worth noticing that although the \(\text {P}2|p_{i,r} = \varphi _i(r)|C_{\mathrm{max}}\) problem is \({{\mathcal {N}}}\!{{\mathcal {P}}}\)-Hard, the \(1|p_{i,r} = \varphi _i(r)|C_{\mathrm{max}}\) problem can be rewritten as the following balanced Assignment problem.

$$\begin{aligned} \text {min}\quad&\sum _{i=1}^n \sum _{r=1}^n \varphi _i(r)\cdot x_{i,r} \end{aligned}$$
(1)
$$\begin{aligned} \text {s.t.}\quad&\sum _{i=1}^{n} x_{i,r} = 1 \qquad \text { for } r = 1, 2, \dots , n \end{aligned}$$
(2)
$$\begin{aligned}&\sum _{r=1}^{n} x_{i,r} = 1 \qquad \text { for } i = 1, 2, \dots , n\nonumber \\&x_{i,r} \in \{0, 1\}. \end{aligned}$$
(3)

Here, \(x_{i, r}\) is an indicator variable that is equal to 1 if and only if job \(J_i\) holds the r-th position in a schedule. Condition (2) guarantees that only one job will be assigned to each of the positions, from 1 to n. Similarly, condition (3) ensures us that each job will be assigned to exactly one position. Finally, (1) represents the value of the \(C_{\mathrm{max}}\) objective function for a given job-to-position assignment. As shown by Fredman and Tarjan (1987), a balanced Assignment problem can be solved in \(O(n^3)\). We refer the reader to a book by Burkard et al. (2012) for a wide review on the Assignment problem.

The \(1|p_{i,r} = \varphi _i(r)|\sum C_i{}\) problem can also be rewritten as a variant of the Assignment problem. Assume that n jobs are executed on a single machine, one after another, with their processing times equal to \(p_1, p_2, \dots , p_n\), respectively. Then,

$$\begin{aligned} \sum C_i{}&= p_1 + (p_1 + p_2) + \dots + (p_1 + p_2 + \dots + p_n)\\&= n\cdot p_1 + (n - 1) \cdot p_2 + \dots + 2\cdot p_{n-1} + p_n. \end{aligned}$$

For this reason, the objective takes form of

$$\begin{aligned} \text {min} \quad \sum _{i=1}^n \sum _{r=1}^n (n-r+1) \cdot \varphi _i(r)\cdot x_{i,r}. \end{aligned}$$
(4)

As n is a constant, one can introduce a new function, \(\bar{\varphi }_i(r) = (n-r+1)\cdot \varphi _i(r)\), and rewrite the objective as

$$\begin{aligned} \text {min} \quad \sum _{i=1}^n \sum _{r=1}^n \bar{\varphi }_i(r)\cdot x_{i,r}. \end{aligned}$$

which is equivalent to (1). Thus, the \(1|p_{i,r} = \varphi _i(r)|\sum C_i{}\) problem can be solved in polynomial time, too. What is more interesting, the latter result can be generalized to a case of parallel machines, mixed position-, job- and machine-dependent processing times, and \(\sum C_i\) objective function as follows.

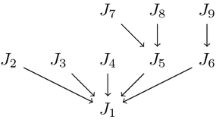
Let us start with a two-machine case in which \(p_{i,j,r} = \varphi _i^j(r)\). Consider an instance of the Assignment problem, denoted by \(I_c\). In this instance, we are given n jobs which should be assigned to both a position and a machine. However, we assume a priori that exactly c jobs will be assigned to the first machine. This means that the remaining \(n-c\) jobs will be assigned to the second machine. Given an instance \(I_c\) and any corresponding feasible schedule \(T_c\) with no idle times between jobs, we have

$$\begin{aligned} \sum C_i{}(T_c)&= \sum _{r=1}^{c}\sum _{q=1}^{r}\varphi _{[q]}^1(q) +\sum _{r=1}^{n-c}\sum _{q=1}^{r}\varphi _{[q]}^2(q)\nonumber \\&= \sum _{r=1}^{c}(c - r + 1)\cdot \varphi _{[r]}^1(r) +\sum _{r=1}^{n-c}(n - c - r + 1)\cdot \varphi _{[r]}^2(r) \end{aligned}$$
(5)

where \(\varphi _{[r]}^j\) is a function associated with the job holding the r-th position on the j-th machine. Figure 1 shows an example of a corresponding bipartite graph for \(n = 5\) and \(c = 2\). The weights of the edges correspond to the impact of a job-to-machine-to-position assignment on the final value of the \(\sum C_i\) objective function, based on (5). With the reasoning similar to the one presented for (4), instance \(I_c\) can be formulated as the following ILP program for the Assignment problem.

$$\begin{aligned} \text {min}\quad&\sum _{i=1}^n \Bigg [\sum _{r=1}^c (c-r+1) \cdot \varphi _i^1(r)\cdot x_{i,1,r}+ \sum _{r=1}^{n-c} (n-c-r+1) \cdot \varphi _i^2(r)\cdot x_{i,2,r} \Bigg ] \end{aligned}$$
(6)
$$\begin{aligned} \text {s.t.}\quad&\sum _{i=1}^{n} x_{i,1,r} = 1 \qquad \text { for } r = 1, 2, \dots , c \end{aligned}$$
(7)
$$\begin{aligned}&\sum _{i=1}^{n} x_{i,2,r} = 1 \qquad \text { for } r = 1, 2, \dots , n-c \end{aligned}$$
(8)
$$\begin{aligned}&\sum _{r=1}^{c} x_{i,1,r} + \sum _{r=1}^{n-c} x_{i,2,r} = 1 \qquad \text { for } i = 1, 2, \dots , n \end{aligned}$$
(9)
$$\begin{aligned}&x_{i,j,r} \in \{0, 1\}. \end{aligned}$$
(10)
Fig. 1
figure 1

The \(I_2\) instance with 5 jobs

Full size image

Here, conditions (7–8) guarantee that exactly one job will be assigned to each of the c positions on the first machine, and each of the \(n - c\) positions on the second machine. Similarly, condition (9) ensures us that each job will be assigned to exactly one spot.

As we can now solve the case with fixed number of jobs assigned to the first machine, we may construct an enumerating algorithm for the general problem, presented as Algorithm 1.

figure a

Theorem 1

Algorithm 1 solves the \(\text {P}2|p_{i,j,r} = \varphi _i^j(r)|\sum C_i{}\) problem in \(O(n^4)\) time.

Proof

In order to find an optimal schedule for the \(\text {P}2|p_{i,j,r} = \varphi _i^j(r)|\sum C_i{}\) problem, we consider all the possible numbers of jobs c assigned to the first machine. Then, we select the \(c'\) value that guarantees the lowest value of the objective function. Thus, the algorithm must lead to an optimal schedule. Notice that the optimal \(c'\) may be any value between 0 to n, as the actual processing times of jobs are also machine-dependent. For example, if \(\varphi _i^1(r) < \frac{1}{n}\) and \(\varphi _i^2(r) \ge 1\) for each i and r, then \(c' = n\) (in the optimal schedule all n jobs are assigned to the first machine). Similarly, if \(\varphi _i^1(r) \ge 1\) and \(\varphi _i^2(r) < \frac{1}{n}\) for each i and r, then \(c' = 0\) (in the optimal schedule all n jobs are assigned to the second machine). Notice that if the processing times were machine-independent, then it would be enough to consider only the cases in which \(0 \le c \le \lfloor n/2\rfloor \). Indeed, given the optimal schedule \(T_c\) inside the for loop (line 3), one could immediately obtain the optimal schedule \(T_{n-c}\) with the same value of the objective function, simply by swapping the machines.

As the for loop (line 3) is executed \(n + 1\) times, and each time an optimal assignment for \(I_c\) is found in \(O(n^3)\), the total required number of operations is \(O(n^4)\). \(\square \)

Now, let us consider the general \(\text {P}m|p_{i,j,r} = \varphi _i^j(r)|\sum C_i{}\) problem. One can notice that the same approach can be applied here. Indeed, let AP(m, n) be a number of Assignment problems that need to be solved in order to find an optimal solution for m machines and n jobs. It holds that

$$\begin{aligned} {AP}(m, n) =\left\{ \begin{array}{lr} 1,&{} \text {for } m = 1 \\ 1 + \sum _{c = 0}^{n-1} {AP}(m - 1, n - c),&{} \text {for } m > 1 \end{array}\right\} = O(n^{m-1}). \end{aligned}$$

This means that the \(\text {P}m|p_{i,j,r} = \varphi _i^j(r)|\sum C_i{}\) problem can be solved in the time of \(O(n^{m-1}\cdot n^3) = O(n^{m+2})\). The same asymptotic result can be justified by the following reasoning. Given a fixed sequence of non-negative numbers of jobs \((n_1, n_2, \dots , n_m)\) that have to be assigned to each of the machines, one can find an optimal solution by solving the Assignment problem. The number of \((n_1, n_2, \dots , n_m)\) sequences such that \(\sum _{j=1}^m n_j = n\) is defined by \(\left( {\begin{array}{c}n + m - 1\\ n\end{array}}\right) = O(n^{m-1}/(m-1)!)\), for a fixed m. Thus, the \(\text {P}m|p_{i,j,r} = \varphi _i^j(r)|\sum C_i{}\) problem can be solved in \(O(n^{m+2})\).

We will finish this section by considering the \(\text {P}2|p_{j,r} = \varphi ^j(r)|C_{\mathrm{max}}\) and the \(\text {P}2|p_{j,r} = \varphi ^j(r)|\sum C_i{}\) problems. Let us observe that for any schedule T the values of \(C_{\mathrm{max}}(T)\) and \(\sum C_i{}(T)\) depend on the number of jobs executed on each of the machines only. For example, if in the \(T_c\) schedule there are c jobs assigned to machine \(P_1\) and \(n-c\) jobs assigned to machine \(P_2\), then

$$\begin{aligned} C_{\mathrm{max}}(T_c) = \max \left\{ \sum _{r=1}^{c} \varphi ^1(r), \sum _{r=1}^{n-c} \varphi ^2(r) \right\} \end{aligned}$$

and

$$\begin{aligned} \sum C_i{}(T_c) = \sum _{r=1}^{c} (c - r + 1)\cdot \varphi ^1(r) +\sum _{r=1}^{n-c} (n - c - r + 1)\cdot \varphi ^2(r). \end{aligned}$$

For this reason, the optimal schedule can be obtained enumeratively by finding, in O(n) time, the values of

$$\begin{aligned} c' = \mathop {\mathrm{arg}\,\mathrm{min}}\limits _{0 \le c \le n} \max \left\{ \sum _{r=1}^{c} \varphi ^1(r), \sum _{r=1}^{n-c} \varphi ^2(r) \right\} \end{aligned}$$

and

$$\begin{aligned} c'' = \mathop {\mathrm{arg}\,\mathrm{min}}\limits _{0 \le c \le n} \left\{ \sum _{r=1}^{c} (c - r + 1)\cdot \varphi ^1(r) +\sum _{r=1}^{n-c} (n - c - r + 1)\cdot \varphi ^2(r)\right\} , \end{aligned}$$

respectively, and then assigning any \(c'\) jobs to machine \(P_1\) and the remaining \(n-c'\) jobs to machine \(P_2\) in the case of the \(C_{\mathrm{max}}\) objective function, and any \(c''\) jobs to machine \(P_1\) and the remaining \(n-c''\) jobs to machine \(P_2\) in the case of the \(\sum C_i{}\) objective function.

In general, the \(\text {P}m|p_{j,r} = \varphi ^j(r)|C_{\mathrm{max}}\) and \(\text {P}m|p_{j,r} = \varphi ^j(r)|\sum C_i{}\) problems can be solved by greedily assigning each of n jobs to a machine that guarantees the lowest \(C_{\mathrm{max}}\) at the moment of assignment, as shown in Algorithm 2.

figure b

Theorem 2

Algorithm 2 solves the \(\text {P}m|p_{j,r} =\varphi ^j(r)|C_{\mathrm{max}}\) and \(\text {P}m|p_{j,r} = \varphi ^j(r)|\sum C_i{}\) problems in \(O(m + n\log m)\) time.

Proof

One can notice that for a single job it is optimal to select a machine that guarantees the lowest completion time of this job. Assume that \(n > 1\) is the lowest number of jobs for which Algorithm 2 leads to a suboptimal schedule.

Let \(T_n\) be a schedule generated by Algorithm 2 for n jobs and let \(T'_n\) be an optimal schedule for the same instance. It must hold that \(C_{\mathrm{max}}(T'_n) < C_{\mathrm{max}}(T_n)\), because \(T_n\) is suboptimal. Let us remove from schedule \(T_n\) any job for which the completion time is equal to \(C_{\mathrm{max}}(T_n)\). Call the resulting schedule \(T_{n-1}\).

By the construction of Algorithm 2, \(T_{n-1}\) is an optimal schedule of \(n - 1\) jobs. For that reason it must hold that \(C_{\mathrm{max}}(T_{n-1}) \le C_{\mathrm{max}}(T'_n) < C_{\mathrm{max}}(T_n)\). At the same time, there exists at least one machine \(P_j\) such that the number of jobs assigned to it in the \(T_{n-1}\) schedule is lower than in the \(T'_n\) schedule. After assigning a new job to that machine we obtain a new schedule, \(S_n\). Again, by the construction of the algorithm, it must hold that \(C_{\mathrm{max}}(T_{n}) \le C_{\mathrm{max}}(S_n)\). Consequently, \(C_{\mathrm{max}}(T_{n}) \le C_{\mathrm{max}}(S_n) \le C_{\mathrm{max}}(T'_n) < C_{\mathrm{max}}(T_n)\) which is a contradiction. A similar reasoning can be provided for the \(\sum C_i{}\) objective function.

Before the for loop (line 4), one needs to perform O(m) operations. In the for loop, the number of operations is bounded by O(nm). However, if one implements P as a priority queue using a strict Fibonacci heap (Brodal et al. 2012), this result can be improved. Building a heap P at the beginning would still require O(m) operations, but finding \(\min (P)\) could be done in O(1) time, and increasing a key in the P heap would require \(O(\log m)\) time. For that reason the number of operations required by the for loop (line 4) can be reduced to \(O(n\log m)\), and thus the total number of operations is \(O(m + n\log m)\). \(\square \)

We present a summary of the results discussed up to this moment in Table 1. The results proved in this section are printed in bold. Other results in the table follow either from their generalizations (if they are polynomial) or from their special cases (in case of \({{\mathcal {N}}}\!{{\mathcal {P}}}\)-Hardness).

Table 1 Complexity of considered problems with independent jobs
Full size table

5 Chained jobs

In the previous section, we analyzed the \(Pm|p_{i,j,r} = \varphi ^j_i(r)|C_{\mathrm{max}}\) and \(Pm|p_{i,j,r} = \varphi ^j_i(r)|\sum C_i{}\) problems of scheduling jobs with no precedence constraints. Now, we will assume that the jobs need to be executed in a given order, i.e. that they are chained.

It might be observed that when one schedules jobs with fixed processing times, the problems in which jobs are single-chained are usually easier than the ones with independent jobs. For example, the \(P||C_{\mathrm{max}}\) problem is \({{\mathcal {N}}}\!{{\mathcal {P}}}\)-Hard, while the \(P|\text {chain}|C_{\mathrm{max}}\) problem can be solved in linear time. It is also true for more general \(R||C_{\mathrm{max}}\) and \(R|\text {chain}|C_{\mathrm{max}}\) problems.

However, it seems that the case of chained jobs is generally harder than the case of independent jobs when it comes to mixed job-, machine- and position-dependent processing times. Despite this, in this section we will present polynomial algorithms for the \(Pm|\text {chain}, p_{j,r} = \varphi ^j(r)|C_{\mathrm{max}}\) and \(Pm|\text {chain}, p_{j,r} = \varphi ^j(r)|\sum C_i{}\) problems. We will analyze these problems one after another.

Let us begin with the \(P2|\text {chain}, p_{j,r} = \varphi ^j(r)|C_{\mathrm{max}}\) problem. Assume that we are given n chained jobs, i.e. \(J_1 \rightarrow J_2 \rightarrow , \dots \rightarrow J_n\). One can observe that in any optimal schedule related to the \(\text {P}2|\text {chain}, p_{j,r} = \varphi ^j(r)|C_{\mathrm{max}}\) problem jobs must be executed one after another, without unnecessary idleness. That means that the value of the \(C_{\mathrm{max}}\) objective function is basically the sum of the actual processing times of all jobs. Moreover, the objective value does not depend on the exact job-to-machine assignment, but rather on the number of jobs assigned to the first (and consequently, to the second) machine. If one assigns c jobs to the first machine, then the sum of their actual processing times is equal to \(\sum _{r=1}^c \varphi ^1(r).\) As there are n jobs in total, the remaining \(n-c\) jobs must be assigned to the second machine, with sum of their actual processing times equal to \(\sum _{r=1}^{n-c} \varphi ^2(r).\) This means that for any schedule \(T_c\) with exactly c jobs assigned to the first machine and with no idle times between consecutive jobs, we have

$$C_{\mathrm{max}}(T_c) = \sum _{r=1}^c \varphi ^1(r) + \sum _{r=1}^{n-c} \varphi ^2(r).$$

These considerations lead us to the linear algorithm for the \(\text {P}2|\text {chain}, p_{j,r} = \varphi ^j(r)|C_{\mathrm{max}}\) problem, presented as Algorithm 3.

figure c

Algorithm 3 is based on the observation, that there are only \(n + 1\) ways to write down a positive integer n as a sum of two non-negative integers. In general, for m machines, there are \(O(n^{m-1}/(m-1)!)\) ways to assign n identical jobs to m machines (see the discussion on the \(\text {P}m|p_{i,j,r} = \varphi _i^j(r)|\sum C_i{}\) problem). So, the \(O(n^{m-1}/(m-1)!)\) algorithm, presented as Algorithm 4, can be applied for the \(\text {P}m|\text {chain}, p_{j,r} = \varphi ^j(r)|C_{\mathrm{max}}\) problem.

figure d

Is is worth noticing, based on the results by Przybylski (2017), that if the \(\varphi \) function is non-increasing, then the \(\text {P}m|\text {chains}, p_{r} = \varphi (r)|C_{\mathrm{max}}\) problem with more than one chain of jobs to be scheduled can be solved in O(n).

In case of the \(\text {P}2|\text {chain}, p_{j,r} = \varphi ^j(r)|C_{\mathrm{max}}\) problem, one can find an optimal schedule by answering a simple question of how many jobs should be assigned to each of two machines? Given an optimal number \(c'\) of jobs that should be assigned to machine \(P_1\), one of \(\left( {\begin{array}{c}n\\ c'\end{array}}\right) \) optimal schedules can be obtained by choosing any \(c'\) jobs from the original chain of n jobs. However, in case of the \(\sum C_i\) objective function, there are two questions to be answered. First, how many jobs should be assigned to each of two machines, and second, which jobs should it be. Thus, the \(\text {P}2|\text {chain}, p_{i,j,r} = \varphi _i^j(r)|\sum C_i{}\) problem cannot be reformulated as the Assignment problem, even if we assume that the number of jobs executed on each of the machines is constant. This is so, because jobs need to be executed in a given order. As a consequence, the actual processing time of a job \(J_i\) in any feasible schedule directly depends on how many jobs from the \(\{J_1, J_2, \dots , J_{i-1}\}\) set were assigned to each of the machines.

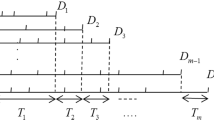
It turns out that the \(\text {P}m|\text {chain}, p_{j,r} = \varphi ^j(r)|\sum C_i{}\) problem can still be solved by a polynomial algorithm that uses, as a subroutine, a known algorithm for the \(1|\text {chains}|\sum C_i{}\) problem. For the latter case, assume that we are given a set of m chains of jobs, containing \(n_1, n_2, \dots , n_m\) jobs, respectively, where \(\sum _{j=1}^m n_j = n\). Denote those jobs as presented in Fig. 2. Without loss of generality, we may assume that if \(n_j = 0\) for some j, then the chain is empty and the index j is omitted.

Fig. 2
figure 2

Notation for a set of chains

Full size image

Given such a set of chains, one can find a single-machine schedule that is optimal in the sense of the \(\sum C_i\) objective function, based on Algorithm 5 by Conway et al. (1967). This algorithm requires \(O(n^2)\) time and is presented in its original form, i.e. as the list of steps.

figure e

Algorithm 5 can be adapted to the \(\text {P}m|\text {chain}, p_{j,r} = \varphi ^j(r)|\sum C_i{}\) problem in the following way. Given an instance of the latter problem, with a chain of length n, we imagine any feasible schedule. In such a schedule \(n_j\) jobs are executed on machine \(P_j\), with their actual processing times equal to \(\varphi ^j(1), \varphi ^j(2), \dots , \varphi ^j(n_j)\), respectively. This is so for each \(1 \le j \le m\). As no two jobs are executed at the same time, this can be viewed as a single-machine scheduling problem, in which we schedule m independent chains of jobs with fixed processing times to minimize the value of \(\sum C_i\).

Let us be given an instance of the \(\text {P}m|\text {chain}, p_{j,r} = \varphi ^j(r)|\sum C_i{}\) problem. Also, let \((n_1, n_2, \dots , n_m)\) be a sequence of non-negative integers such that \(\sum _{j=1}^m n_j = n\). For such a sequence, we generate an instance of the \(1|\text {chains}|\sum C_i{}\) problem, in which we have at most m chains of jobs. The j-th chain consists of \(n_j\) jobs, \(J_{j,1} {\rightarrow } J_{j,2} {\rightarrow } \dots {\rightarrow } J_{j,n_j}\), with their fixed processing times equal to \(\varphi ^j(1), \varphi ^j(2), \dots , \varphi ^i(n_j)\), respectively. Given a single-machine schedule that provides the lowest value of \(\sum C_i\) within all the \((n_1, n_2, \dots , n_m)\) sequences, a corresponding m-machine optimal schedule with the same value of \(\sum C_i\) can be generated, as shown in Algorithm 6.

figure f

Notice that inside of Algorithm 6, we perform Algorithm 5 \(O(n^{m-1}/(m-1)!)\) times. As the latter algorithm needs \(O(n^2)\) operations, the first for loop (line 4) requires \(O(n^{m+1}/(m-1)!)\) operations in total. The second for loop (line 15) can be performed in O(n) time. So, Algorithm 6 requires a total running time of \(O(n^{m+1})\).

6 Conclusions

We considered a set of parallel-machine scheduling problems with jobs that are position-dependent. However, the actual processing time of a job might also freely depend on the job itself and a machine it had been assigned to. We analyzed the cases of independent and chained jobs, with maximum completion time and total completion time as the objective functions.

As the \(Pm|p_{i,j,r} = \varphi _i^j(r)|C_{\mathrm{max}}\) problem is \({{\mathcal {N}}}\!{{\mathcal {P}}}\)-Hard in general, we proposed a number of polynomial algorithms that solve some of its special cases. Those special cases have been obtained by reducing the number of different \(\varphi \) functions. In case of the \(Pm|p_{i,j,r} = \varphi _i^j(r)|\sum C_i{}\) problem, we presented a full set of polynomial algorithms for it an its subproblems. Then, for the case of chained jobs, we presented a series of polynomial algorithms for the \(Pm|\text {chain}, p_{j,r} = \varphi ^j(r)|C_{\mathrm{max}}\) and \(Pm|\text {chain}, p_{j,r} = \varphi ^j(r)|\sum C_i{}\) problems.

Although the presented results are theoretical, they can be used in real life. As the analyzed model is very general, it covers various job-, machine-, and position-dependent models—including the ones that might have not been discussed yet. For example, the presented results are true for classic learning and aging models (e.g. \(p_{i,r} = p_i\cdot r^{a_i}\), where \(a_i < 0\) or \(a_i > 0\), respectively). They also remain valid when DeJong’s learning effect is considered. Our results can be a base for further research on parallel-machine scheduling of variable-time jobs for which no assumptions on the model of positional-dependency are made.

There are still some open questions related to the problems discussed in this paper. Namely, we now focus on answering the questions of whether the \(\text {P}m|\text {chain}, p_{i,j,r} = \varphi _i^j(r)|C_{\mathrm{max}}\) and \(\text {P}m|\text {chain}, p_{i,j,r} = \varphi _i^j(r)|\sum C_i{}\) problems are polynomially-solvable. It is known that the answer is positive for job processing times that are only job- and machine-dependent. However, for position-dependent jobs, the answer requires some further analysis.