Precedence constrained parallel-machine scheduling of position-dependent jobs

Abstract

We consider parallel-machine job scheduling problems with precedence constraints. Job processing times are variable and depend on positions of jobs in a schedule. The objective is to minimize the maximum completion time or the total weighted completion time. We specify certain conditions under which the problem can be solved by scheduling algorithms applied earlier for fixed job processing times.

1 Introduction

In many scheduling problems one cannot assume that job processing times are fixed. This may be caused by different factors that have influence on parameters related to the job processing. There are a few main forms of variable job processing times considered in literature. For example, the time needed to process a job may depend on the starting time of this job or its position in a schedule. The first case, called time-dependent scheduling, constitutes a great part of research focused on scheduling with variable job processing times. A good review of this domain is presented in the book by Gawiejnowicz [1]. The case of position-dependent scheduling, considered in this paper, has been surveyed by Biskup [2] and Agnetis et al. [3].

There are two limitations of the majority of papers on scheduling problems with variable processing times. First, results presented there are mainly related to scheduling on one machine (see, e.g., Wang et al. [4], Huang and Wang [5], Debczynski and Gawiejnowicz [6], Debczynski [7], Wang and Wang [8, 9]) or on parallel machines, but with empty precedence constraints among jobs (see, e.g., Mosheiov and Sidney [10], Mosheiov [11], Huang and Wang [12]). The second limitation is that most of the results related to scheduling problems with variable job processing times concern particular cases, not general ones. Recent examples of general results of this kind, concerning so-called isomorphic scheduling problems, are presented in the paper by Gawiejnowicz and Kononov [13].

In this paper, we consider a group of parallel-machine problems of non-preemptive scheduling of precedence constrained jobs with variable processing times that depend on their positions in a schedule. Based on some transformations between schedules with fixed job processing times and schedules with position-dependent job processing times, we show how to solve some of considered problems in polynomial time.

Remaining sections of the paper are organized as follows. In Sect. 2, we present some definitions and results related to a few new classes of schedules and transformations between them. In Sect. 3, we prove our main results based on properties of mentioned transformations. In Sect. 4, we consider a special case of the parallel-machine scheduling problem with position-dependent jobs and show that it is polynomially-solvable. In Sect. 5, we give conclusions and indicate the directions of further research.

2 Preliminaries

The problems analysed in this paper can be formulated as follows. We are given a number of parallel identical machines and n non-preemptable jobs with some precedence constraints. The processing time of each job is variable and depends on the position r of the job in a schedule. This dependency is described by a positive and non-increasing function $\phi$ of argument r. In other words, the processing time of the j-th job in position r is equal to $p_{j,r} = \phi (r)$, where $1 \le r, j \le n$. The aim is to find a schedule with minimal maximum completion time or minimal total weighted completion time. Using the commonly known scheduling notation (for a brief description see Gawiejnowicz [1]), we will denote these problems as P|$\text {prec}, p_{j,r} = \phi (r)$|f, where $f \in \left\{ C_{\mathrm{max}}{}{}, \sum w_{i}C_{i}{}{} \right\}$.

One of special cases of these problems, when $\phi (r) = 1$, is the P|$\text {prec}, p_{j,r} = 1$|f problem of scheduling jobs with unit processing times. Therefore, a natural question is whether some known algorithms for the latter problem can be applied to its counterpart with job processing times described by the $\phi$ function. We give an answer to this question applying a transformation of schedules with fixed job processing times into schedules with position-dependent job processing times, and specify certain conditions under which the P|$\text {prec}, p_{j,r} = \phi (r)$|f problem can be solved by appropriately modified algorithms for unit job processing times.

Let T be a non-preemptive schedule of n jobs and let $J_i \in \left\{ J_1, J_2, \ldots , J_n \right\}$. The starting time and the completion time of job $J_i$ will be denoted by $S_i(T)$ and $C_i(T)$, respectively. The value of the objective function of T will be denoted by $C_{\mathrm{max}}{}(T) = \max \left\{ C_i(T) :i\in \left\{ 1, 2, \ldots , n\right\} \right\}$ or $\sum w_iC_i(T) = \sum _{i=1}^n w_iC_i(T)$. If it does not lead to misunderstanding, the argument determining the schedule will be omitted.

Let $\phi :\mathbb {N}_+ \rightarrow \mathbb {Q}_+$ be any discrete function satisfying the condition $\phi (r) > 0$ for every $r \in \mathbb {N}_+$, where $\mathbb {N}_+=\mathbb {N}{\setminus } \{0\}$. Moreover, let $\Phi$ be a function defined as $\Phi (k) = \sum _{i=1}^{k} \phi (i)$, where $k \in \mathbb {N}$. Notice that $\Phi (0)=0$ and that the $\Phi$ function is a bijection between its domain and image.

A schedule of n jobs will be called a natural schedule if it satisfies the following two conditions:

• (1) there exists $i \in \left\{ 1, 2, \ldots , n\right\}$ such that $S_i = 0$,

• (2) for every $i \in \left\{ 1, 2, \ldots , n\right\}$ we have $S_i \in \mathbb {N}$ and $C_i \in \mathbb {N}_+$.

The immediate observation is that for any natural schedule T we have $C_{\mathrm{max}}{}(T) \in \mathbb {N}$ and $\sum C_{i}{}(T) \in \mathbb {N}$. A natural schedule of jobs with unit processing times will be called a simple schedule. Notice that in a simple schedule we have $C_i = S_i + 1$ for every $i \in \left\{ 1, 2, \ldots , n\right\}$.

A schedule of n jobs will be called a $\phi$ -natural schedule if it satisfies (1) and

• (3) for every $i \in \left\{ 1, 2, \ldots , n\right\}$ there exists some $k \in \mathbb {N}$ such that $S_i = \Phi (k)$ and $C_i = \Phi (l)$ for some natural $l > k$.

If every job started in a given $\phi$-natural schedule at time $\Phi (k)$ is completed at time $\Phi (k+1)$, then the schedule will be called a $\phi$ -simple schedule. Notice that every simple schedule is a natural schedule, and every $\phi$-simple schedule is a $\phi$-natural schedule. Moreover, if $\phi (r)=1$, then every $\phi$-natural schedule is a natural schedule. Similarly, every $\phi$-simple schedule is a simple schedule.

A schedule will be called a continuous schedule, if every machine starts the execution of jobs at the moment 0 and none of the machines is idle before finishing all the jobs assigned to this machine.

Let T be a schedule. A pair $(t_1, t_2)$ will be called a time slot $(t_1, t_2)$, if the following statement is true for every machine: if the machine executes at least one job in the $(t_1, t_2)$ interval of T, then there is exactly one job executed by this machine in a given interval, its processing starts at the moment $t_1$ and it completes at the moment $t_2$. Therefore, any simple schedule T can be divided into time slots $(k, k+1)$, where $k \in \left\{ 0, \ldots , \text {C}_\text {max}(T)-1\right\}$. Similarly, any $\phi$-simple schedule $T'$ can be divided into time slots $(\Phi (j), \Phi (j+1))$, where $j \in \left\{ 0, \ldots , \Phi ^{-1}(\text {C}_\text {max}(T'))-1\right\}$. Notice that in the second case the time slots corresponding to j are of the length of $\phi (j+1)$.

Now, we will define a bijective transformation between the set of natural schedules and the set of $\phi$-natural schedules. Let T be a natural schedule of n jobs. We construct a new schedule $T'$ such that

• (4) if $S_i(T) = s_i$, then $S_i(T') := \Phi (s_i)$ for every $i \in \left\{ 1, 2, \ldots , n\right\}$,

• (5) if $C_i(T) = c_i$, then $C_i(T') := \Phi (c_i)$ for every $i \in \left\{ 1, 2, \ldots , n\right\}$.

Notice that the $T'$ schedule is a $\phi$-natural schedule and that the transformation defined by (4) and (5) does not change the order of jobs executed on any machine. We will denote this transformation by $\Lambda _\phi$, i.e. $T'=\Lambda _\phi (T)$.

Property 1

The following two properties arise immediately from the definitions given above.

• (a) If T is a (continuous) simple schedule, then $\Lambda _\phi (T)$ is a (continuous) $\phi$-simple schedule.

• (b) If T is a simple schedule, $\Lambda _\phi (T)$ is a corresponding $\phi$-simple schedule and k is any natural number such that $0 \le k < C_\text {max}(T)$, then the sets of jobs executed in the $(k, k+1)$ time slot of the T schedule and in the $(\Phi (k), \Phi (k+1))$ time slot of the $\Lambda _\phi (T)$ schedule are equal.

Consider now a $\phi$-natural schedule of n jobs and denote it by $T'$. We can construct a natural schedule T applying the following rules:

• (6) if $S_i(T') = \Phi (s_i)$, then $S_i(T) := s_i$ for every $i \in \left\{ 1, 2, \ldots , n\right\}$,

• (7) if $C_i(T') = \Phi (c_i)$, then $C_i(T) := c_i$ for every $i \in \left\{ 1, 2, \ldots , n\right\}$.

The values $s_i$ and $c_i$ exist and are natural numbers, because the $\Phi$ function is a bijection and $T'$ is a $\phi$-natural schedule. Then, the schedule T is a natural schedule. We will denote the transformation defined by (6) and (7) by $\Lambda _\phi ^{-1}$, i.e. $T = \Lambda _\phi ^{-1}(T')$.

Property 2

If $T'$ is a (continuous) $\phi$-simple schedule, then $\Lambda ^{-1}_\phi (T')$ is a (continuous) simple schedule.

Notice that for any positive function $\phi$ the $\Lambda _\phi$ transformation defined as above is a bijection between the set of natural schedules and the set of $\phi$-natural schedules. Moreover, Properties 1(a) and 2 imply that the $\Lambda _\phi$ transformation limited to the sets of simple schedules and $\phi$-simple schedules is a bijection as well.

3 Results

In this section we will prove our main results. We start with two auxiliary lemmas.

Lemma 1

Let there be given a number of identical parallel machines able to execute each of available jobs. If algorithm A generates a continuous simple schedule T for job processing times in the form of $p_{j,r}=1$, then algorithm A generates also a continuous $\phi$-simple schedule $T'= \Lambda _\phi (T)$ for job processing times in the form of $p_{j,r} = \phi (r)$.

Proof

Assume that, in the case when $p_{j,r} = 1$, schedule T generated by algorithm A is a continuous simple schedule. Then, by Property 1(a), schedule $T' = \Lambda _\phi (T)$ is a continuous $\phi$-simple schedule. Because, by Property 1(b), the $\Lambda _\phi$ transformation does not change the order of the jobs, $T'$ schedule is feasible and can be generated by scaling individual time slots of the T schedule. Finally, by definition of a continuous $\phi$-simple schedule, the processing time of the r-th job on each machine is equal to $\phi (r)$. $\square$

Lemma 2

Let $X_k = \left\{ (x_1, x_2, \ldots , x_k) :x_i \in \mathbb {N}_+, x_{i} \le i~\right\} ,$ where $k \in \mathbb {N}_+$. If $\phi$ is a positive and non-increasing discrete function, then

$$\begin{aligned} \min _{X_k}\left\{ \sum _{i=1}^k \phi (x_i) \right\} = \sum _{i=1}^k \phi (i) = \Phi (k). \end{aligned}$$

Proof

Let us notice that if $(x_1, x_2, \ldots , x_k) = (1, 2, \ldots , k)$, then $\sum _{i=1}^k \phi (x_i) = \Phi (k)$. This means that $\min _{X_k}\left\{ \sum _{i=1}^k \phi (x_i) \right\} \le \Phi (k).$ It remains to show that the reversed inequality is true. Let $(x_1, x_2, \ldots , x_k)$ be any series from $X_k$. It is easy to see that $\sum _{i=1}^k \phi (x_i) - \sum _{i=1}^k \phi (i) = \sum _{i=1}^k {(}\phi (x_i) - \phi (i){)}.$ Because the $\phi$ function is positive, non-increasing and $x_i \le i$, we conclude that $\phi (x_i) - \phi (i) \ge 0$. This means that $\sum _{i=1}^k {(}\phi ({x_i}) - \phi (i){)}$ is the sum of k non-negative elements, which proves that $\min _{X_k}\left\{ \sum _{i=1}^k \phi (x_i) \right\} \ge \Phi (k).$ $\square$

Based on Lemmas 1 and 2, we will now prove our main two results, specifying the conditions under which some known scheduling algorithms for unit job processing times may be adapted for corresponding problems with job processing times depending on positions of the jobs in a schedule.

The first of the results concerns the $C_{\mathrm{max}}$ objective function.

Theorem 1

Let $\phi$ be a positive and non-increasing discrete function and let I be an arbitrary instance of the P|$\text {prec}, p_{j,r} = 1$|$C_{\mathrm{max}}$ problem. If algorithm A generates an optimal schedule for I and it is a continuous simple schedule, then algorithm A generates also an optimal continuous $\phi$-simple schedule for the corresponding instance of the P|$\text {prec}, p_{j,r} = \phi (r)$|$C_{\mathrm{max}}$ problem.

Proof

Let T be a schedule generated by algorithm A for the case of unit job processing times. As we assumed, T is a continuous simple schedule. Denote its length by k. From the definition of a continuous simple schedule we conclude that there exists a series of k jobs executed continuously one after another on one of the machines, starting at the moment 0. Moreover, there is no feasible schedule shorter than k, because T is an optimal schedule with respect to the $C_{\mathrm{max}}{}$ objective function.

As we proved in Lemma 1, the $T' = \Lambda _\phi (T)$ schedule is a continuous $\phi$-simple schedule corresponding to the case when $p_{j,r} = \phi (r)$. The $\Lambda _\phi$ transformation does not change the order of the jobs, so the $T'$ schedule is feasible as well. Hence, to prove that $T'$ is optimal with respect to the $C_{\mathrm{max}}$ objective function when $p_{j,r} = \phi (r)$, it is sufficient to show that it is impossible to execute k position-dependent jobs one after another in time shorter than $\Phi (k)$.

Consider a series $(J_{i_1}, J_{i_2}, \ldots , J_{i_k})$ of jobs executed one after another in the $T'$ schedule. These jobs do not need to be executed on the same machine. Assume that there exists an index $j \in \left\{ 1, 2, \ldots , k \right\}$ such that the j-th job in the series is assigned to a machine on a position further than j. It means that there exists a series of $k+1$ jobs executed one after another in the $T'$ schedule. This implies, in turn, that $C_{\mathrm{max}}{}(T)$, where $T = \Lambda _\phi ^{-1}(T')$, is larger than k. A contradiction.

From the above we can conclude that every job of the considered series is assigned to a machine on a position less or equal to its position in the series. By Lemma 2 we conclude that if the discrete $\phi$ function is positive and non-increasing, the sum of processing times of jobs $J_{i_1}, J_{i_2}, \ldots , J_{i_k}$ executed one after another cannot be lower than $\Phi (k)$. $\square$

Now, we will show that a similar result holds also for the $\sum w_{i}C_{i}$ objective function.

Theorem 2

Let $\phi$ be a positive and non-increasing discrete function and let I be an arbitrary instance of the P|$\text {prec}, p_{j,r} = 1$|$\sum w_{i}C_{i}$ problem. If algorithm A generates an optimal schedule for I and it is a continuous simple schedule, then algorithm A generates also an optimal continuous $\phi$-simple schedule for the corresponding instance of the P|$\text {prec}, p_{j,r} = \phi (r)$|$\sum w_{i}C_{i}$ problem.

Proof

Let T be a schedule generated by algorithm A for the case of unit processing times. As it was assumed, T is a continuous simple schedule optimal with respect to the $\sum w_{i}C_{i}{}$ objective function. As we proved in Lemma 1, the $T' = \Lambda _\phi (T)$ schedule is a continuous $\phi$-simple schedule corresponding to the case when $p_{j,r} = \phi (r)$. The $\Lambda _\phi$ transformation does not change the order of jobs, so the $T'$ schedule is feasible.

Assume that $T'$ is not optimal with respect to the $\sum w_{i}C_{i}{}$ objective function. This means that at least one of two cases holds, Case 1 or Case 2.

In Case 1, we can swap, not violating precedence constraints, two jobs in $T'$ in such a way that the value of $\sum w_{i}C_{i}{}(T')$ will be lower than previously. Because job completion times are the values of increasing $\Phi$ function and the $\Lambda _\phi$ transformation does not change the order of jobs, this means that swapping the same jobs in T schedule would improve the value of $\sum w_{i}C_{i}{}(T)$ objective function. This leads to a contradiction, since schedule T is optimal.

In Case 2, there exists a job that can be completed earlier. By assumption, T is a continuous simple schedule optimal with respect to $\sum w_{i}C_{i}{}{}$. This means that starting from the first time slot, where at least one machine is idle, none of the jobs can be executed in any earlier time slot, and hence, completed earlier. It remains to show that if the completion time of job $J_i$ in T is equal to $C_i(T)$, then it is impossible to complete this job in $T'$ earlier than at the moment $\Phi (C_i(T))$. Applying the reasoning similar to the one from the proof of Theorem 1 and based on Lemma 2, we conclude that the statement of Theorem 2 is true. $\square$

As an immediate consequence of Theorem 2, we obtain the following result.

Corollary 1

Let $\phi$ be a positive and non-increasing discrete function and let I be an arbitrary instance of the P|$\text {prec}, p_{j,r} = 1$|$\sum C_{i}$ problem. If algorithm A generates an optimal schedule for I and it is a continuous simple schedule, then algorithm A generates also an optimal continuous $\phi$-simple schedule for the corresponding instance of the P|$\text {prec}, p_{j,r} = \phi (r)$|$\sum C_{i}$ problem.

We complete this section by a general remark. Notice that since the P|$\text {prec}, p_{j} = 1$|$C_{\mathrm{max}}$ and P|$\text {prec}, p_{j} = 1$|$\sum w_{i}C_{i}$ problems are $\textit{NP}$-hard, there are no polynomial algorithms solving these problems unless $P=\textit{NP}$. For that reason we have to consider some special cases for which such polynomial algorithms can be constructed. Theorems 1–2 and Corollary 1 can be applied to single instances and hence they can be used to analyse these cases. If we can calculate the value of the $\phi$ function in polynomial time and algorithm A specified in these theorems generates an optimal schedule for unit job processing times in polynomial time, then the algorithm A generates also in polynomial time an optimal schedule for job processing times given by the $\phi$ function.

4 A polynomial case

In this section, we will show one of applications of our results. Namely, we will show how to use Theorem 1 in a proof that one of special cases of parallel-machine problems considered in Sect. 3 is polynomially-solvable.

Recall that for the P|$\text {in-tree}, p_{j} = 1$|$C_{\mathrm{max}}$ problem of parallel-machine scheduling of unit-time jobs with precedence constraints in the form of in-tree, Hu [14] proposed a polynomial algorithm and proved its optimality. The main idea of the algorithm is as follows:

At the moment, when any of the machines becomes idle, assign to it a non-executed job furthest away from the tree-root and which predecessors have been all finished.

Now, we want to show how to solve the counterpart of the P|$\text {in-tree}, p_{j} = 1$|$C_{\mathrm{max}}$ problem with position-dependent job processing times in the form of $p_{j,r} = \phi (r)$.

We will start by a property of schedules generated by Hu’s algorithm. We assume that if there is more than one machine available, Hu’s algorithm allocates jobs to the machine with the lowest index. Notice also that for any instance of the P|$\text {in-tree}, p_{j} = 1$|$C_{\mathrm{max}}$ problem, the schedule generated by Hu’s algorithm is a simple schedule. Therefore, we may use the time slots defined in Sect. 2.

Property 3

For any instance of the P|$\text {in-tree}, p_{j} = 1$|$C_{\mathrm{max}}$, the number of jobs allocated to the machines in individual time slots of a schedule generated by the Hu’s algorithm is non-increasing.

Proof

This property is a natural consequence of the observation that the precedence constraints are given by an in-tree. That means that every job has at most one immediate successor. In other words, if in the $(k, k+1)$ time slot, where $k \in \mathbb {N}$, there are q jobs ready to execute, then in $(k+1, k+2)$ time slot there are at most q such jobs. Applying mathematical induction with respect to k, the property follows. $\square$

We assumed that in the case when there is more than one machine available, jobs will be assigned to the machine with the lowest index. This leads to the conclusion that a schedule generated by Hu’s algorithm is a continuous simple schedule for any instance of the P|$\text {in-tree}, p_{j} = 1$|$C_{\mathrm{max}}$ problem. This conclusion together with Theorem 1 lead to the following result.

Theorem 3

If $\phi$ is a positive and non-increasing discrete function of r, then Hu’s algorithm solves the P|$\text {in-tree}, p_{j,r} = \phi (r)$|$C_{\mathrm{max}}$ problem.

The natural question is whether Theorem 3 can be extended to more general cases. In fact, it is easy to show that neither Theorem 1 nor Hu’s algorithm work in the case where there is at least one job with processing time described by another function than remaining jobs. Consider the following example.

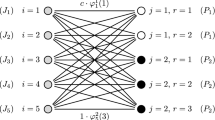
We are given the set of jobs $\left\{ J_1, J_2, \ldots , J_9\right\}$ with job precedence constraints represented by the digraph presented in Fig. 1. Let $\phi _1$ denote the function describing the processing times of jobs $J_1$ to $J_8$, while $\phi _2$ denotes the function describing the processing time of job $J_9$. The first four values of $\phi _1$ and $\phi _2$ functions are equal to those presented in Table 1. Then the schedule generated by Hu’s algorithm, presented in Fig. 2, is not optimal, while an optimal schedule is in the form given in Fig. 3.

Fig. 1

The digraph of precedence constraints for the example considered in Sect. 4

Table 1 The first four values of $\phi _1$ and $\phi _2$ functions for the example considered in Sect. 4

Fig. 2

The schedule generated by Hu’s algorithm for the example considered in Sect. 4

Fig. 3

The optimal schedule for the example considered in Sect. 4

Since similar examples can be constructed for $\sum w_{i}C_{i}{}$ and $\sum C_{i}{}$ objective functions, assumptions of Theorems 1–2 cannot be made weaker.

5 Conclusions

We considered a few parallel-machine scheduling problems with non-empty precedence constraints and position-dependent job processing times. We defined a new class of continuous simple schedules, and proved that if algorithm A generates a continuous simple schedule optimal with respect to the $C_{\mathrm{max}}$ or $\sum w_{i}C_{i}$ objective function in the case of unit job processing times, then it also generates an optimal schedule in the case when the processing time of each job is described by a positive and non-increasing function $\phi$ depending on a position of the job in a sequence. As one of possible applications of the results we showed that Hu’s algorithm solves the P|$\text {in-tree}, p_{j,r} = \phi (r)$|$C_{\mathrm{max}}$ problem. Finally, we showed by an example that it is difficult to extend the latter result to the case when at least one job has a different processing time function.

Theorems 1–2 may be used to solve some problems of scheduling identical or very similar jobs in the environment susceptible to the process of learning. Moreover, our results can be a base for further research on the problem of adapting known algorithms for more general cases. For example, the future analysis may concern the question whether we can use some other transformations to solve different problems with variable and position-dependent processing times.