The average covering tree value for directed graph games

Abstract

We introduce a single-valued solution concept, the so-called average covering tree value, for the class of transferable utility games with limited communication structure represented by a directed graph. The solution is the average of the marginal contribution vectors corresponding to all covering trees of the directed graph. The covering trees of a directed graph are those (rooted) trees on the set of players that preserve the dominance relations between the players prescribed by the directed graph. The average covering tree value is component efficient, and under a particular convexity-type condition it is stable. For transferable utility games with complete communication structure the average covering tree value equals to the Shapley value of the game. If the graph is the directed analog of an undirected graph the average covering tree value coincides with the gravity center solution.

1 Introduction

In classical cooperative game theory it is assumed that any coalition of players may form. However, in many practical situations the collection of feasible coalitions that can be formed is restricted by some social, economical, hierarchical, communicational, or technical structure. The study of games with transferable utility and limited cooperation represented by means of an undirected communication graph, later on for brevity called graph games, was initiated by Myerson (1977). Assuming that only connected players can cooperate, the Myerson value for graph games is defined as the Shapley value (cf. Shapley 1953) of the so-called restricted game for which the worth of each coalition is equal to the sum of the worths of its connected components in the graph. The average tree solution for graph games, introduced by Herings et al. (2008) for cycle-free graph games and generalized by Herings et al. (2010) for the class of all graph games, assigns to each player the average of the player’s marginal contributions to his successors in all admissible spanning trees of the given communication graph. A spanning tree is admissible if every player has in each component in the subgraph on the set of his successors in the tree exactly one direct successor in the tree. Another solution concept applicable to graph games is the gravity center solution for games with restricted communication represented by an arbitrary collection of coalitions, developed in Koshevoy and Talman (2014). For graph games the gravity center solution assigns to each player the average of the player’s marginal contributions to the player’s successors with respect to all admissible trees, not necessarily spanning trees.

In this paper we consider transferable utility games with limited cooperation induced by restrictions represented by means of a directed graph (digraph) later on for brevity called digraph games. For a directed link in an arbitrary digraph there are two possible different basic interpretations. One interpretation is that a link is directed to indicate which player has initiated the communication but at the same time it represents a fully developed communication link where players are able to communicate in both directions with each other. In such a case, following Myerson (1977), it is natural to assume that there is no subordination of players and to focus on component efficient values. Another interpretation of a directed link is based on the assumption that a directed link represents a one-way relation between the players, which leads to two different possible interpretations of a digraph. The first possibility is when the communication between players is supposed to be feasible only along the directed paths in the digraph, for example a flow situation. This assumption is incorporated into the solution concepts of web values, in particular the tree value, and the average web value for cycle-free digraph games introduced in Khmelnitskaya and Talman (2014) and the covering values for cycle-free digraph games studied in Li and Li (2011). Another option is to assume that the digraph represents a subordination of players. An example of such a situation is a sequencing problem where the tasks that have to be performed are ordered according to some technological procedure, not necessarily linearly ordered but the ordering of the tasks is represented by some digraph. Another example can be taken from the following social choice situation. Consider a society consisting of individuals with different opinions, possibly incomplete preferences, about the importance of several proposals or tasks that need to be completed. If the preferences of the individuals are aggregated by using majority voting, then it is well known that the resulting structure will be a digraph on the set of tasks. In this digraph, a directed link from a task to another task means that the majority of the society thinks the first task is more important than the latter one. In both examples the digraph might not be cycle-free. In the first example directed cycles may appear in cases when the production process includes, as subprocesses, the production of for example power supply (e.g., electricity or fuel) needed both for the overall production and in particular for these subprocesses as well. In the second example directed cycles stand for the well known Condorcet paradox. In case when it is assumed that the digraph represents a subordination of players we again have several options. It might be that each player is followed by only one player not dominating him and this situation is analyzed in Khmelnitskaya et al. (2014) where the Shapley value for digraph games is introduced. Another option is when after each player several players may follow as long as this does not hurt the total subordination among the remaining players prescribed by the digraph.

In the paper we abide by the latter interpretation of a directed link and we introduce a new component efficient solution concept for digraph games. To define this solution we first introduce for any directed graph the set of so-called covering trees. The root of a covering tree of a digraph is one of the undominated players (nodes) of the digraph. The root has in every component of the set of remaining players one of its undominated players as immediate successor. On its turn, each of these latter players in every subcomponent of the set of remaining players in the component the player belongs to has one of the undominated players in this subcomponent as immediate successor, and so on. For instance, in the example considering a sequencing problem the unrelated tasks can be performed at the same time and once a task has been completed the remaining succeeding tasks can be split into groups of unrelated tasks and next in every group a task is performed that is not dominated by any other task in that group, and so on. Since every digraph on a finite set has at least one undominated node, the collection of covering trees defined in this way is nonempty. In every covering tree of a digraph, the dominance relation between the players in the digraph is preserved in the sense that each player is an undominated player in the the subgraph on the set of his successors in the tree together with himself. To every covering tree corresponds a unique marginal contribution vector in which every player receives as payoff what he contributes in worth as undominated player when joining all the components of the set of his successors in the tree. The average covering tree value of a digraph game is then the average of the marginal contribution vectors that correspond to all covering trees of the underlying digraph.

We also introduce a convexity-type condition under which the solution is an element of the core and therefore cannot be blocked by any subset of connected players. In case the digraph is a tree this condition is weaker than superadditivity. For this case there is only one covering tree, the tree itself, and the average covering tree value is equal to the tree value first introduced in Demange (2004) under the name of hierarchical outcome and later axiomatized in Khmelnitskaya (2010). For digraph games with complete communication structure the average covering tree value is equal to the Shapley value (cf. Shapley 1953) of the underlying game. The solution can also be applied to undirected graph games by taking the directed analog of the undirected graph, obtained by replacing each undirected link between two players by two directed links in both directions. For this class of games, the average covering tree value is equal to the gravity center solution. This allows to consider the average covering tree value for digraph games as a generalization of the gravity center solution for undirected graph games. When for the class of undirected graph games only the covering trees of the directed analog that are also spanning trees of the graph are considered, the average covering tree value coincides with the average tree solution. Besides, the average covering tree value coincides with the Shapley value for digraph games if all covering trees of the digraph are linear.

The structure of the paper is as follows. Basic definitions and notation are given in Sect. 2. Covering trees of a digraph and the average covering tree value are defined in Sect. 3. Section 4 studies properties of the average covering tree value and its stability. The application of the average covering tree value to undirected graph games is discussed in Sect. 5.

2 Preliminaries

A cooperative game with transferable utility, or TU game, is a pair (N, v), where $N=\{1,\ldots ,n\}$ is a finite set of $n\ge 2$ players and $v:2^N\rightarrow \mathrm{I\!R}$ is a characteristic function defined on the power set of N, satisfying $v(\emptyset )=0$. A subset $S\subseteq N$ is a coalition and the associated real number v(S) represents the worth of coalition S, which can be freely distributed amongst the members of S. We denote the set of TU games with fixed player set N by $\mathcal{G}_N$. For simplicity of notation and if no ambiguity appears we write v when we refer to a game $(N,v)\in \mathcal{G}_N$. A game $v\in \mathcal{G}_N$ is superadditive if $v(S\cup Q)\ge v(S)+v(Q)$ for all $S, Q\subseteq N$ such that $S\cap Q=\emptyset$, and $v\in \mathcal{G}_N$ is convex if $v(S\cup Q)+v(S\cap Q)\ge v(S)+v(Q)$ for all $S,Q\subseteq N$.

A payoff vector is a vector $x\in {\mathrm{I\!R}}^N$ with ith component $x_i$ being the payoff to player $i\in N$. A value on $\mathcal{G}_N$ is a function $\xi :\mathcal{G}_N\rightarrow {\mathrm{I\!R}}^N$ that assigns to every game $v\in \mathcal{G}_N$ a payoff vector $\xi (v)\in {\mathrm{I\!R}}^N$ with $\xi _i(v)$ as the payoff to player $i \in N$. In the sequel we use notation $x(S)=\sum _{i\in S}x_i$ for any $x\in {\mathrm{I\!R}}^N$ and $S\subseteq N$. |A| denotes the cardinality of a finite set A.

The cooperation structure on the player set N is specified by a graph, directed or undirected, on N. A graph on N consists of N as the set of nodes and for a directed graph, or digraph, a collection of ordered pairs $\Gamma \subseteq \{(i,j)\,|\,i,j\in N,\ i\ne j\}$ as the set of directed links (arcs) from one player to another player in N, and for an undirected graph a collection of unordered pairs $L\subseteq \{\{i,j\}\,|\,i,j\in N,\ i\ne j\}$ as the set of links (edges) between two players in N. An undirected graph L on N we identify with its directed analog, $\Gamma ^L=\{(i,j)\mid \{i,j\}\in L\}$. We say that a digraph $\Gamma$ on N contains an undirected link $\{i,j\}$, if both $(i,j)\in \Gamma$ and $(j,i)\in \Gamma$.

For a digraph $\Gamma$ on N,  a sequence of different players $(i_1,\ldots ,i_k)$, $k\ge 2$, is a path in $\Gamma$ between players $i_1$ and $i_k$ if $\{(i_h,i_{h+1}), (i_{h+1}, i_h)\}\cap \Gamma \ne \emptyset$ for $h\!=\!1,\ldots ,k\!-\!1$, and a directed path in $\Gamma$ from player $i_1$ to player $i_k$ if $(i_h,i_{h+1})\in \Gamma$ for $h\!=\!1,\ldots , k\!-\!1$. Players i and j in N are connected in ${\Gamma }$ if there exists a path in $\Gamma$ between i and j. $\Gamma$ is connected  if any two different nodes in N are connected in $\Gamma$. If there exists a directed path in $\Gamma$ from player $i\in N$ to player $j\in N$, then j is a successor of i and i is a predecessor of j in $\Gamma$. If $(i,j)\in \Gamma$, then player j is an immediate successor of player i and player i is an immediate predecessor of j in $\Gamma$. For $i\in N$, $S^\Gamma (i)$ is the set of successors of player i in $\Gamma$ and $\bar{S}^\Gamma (i)=S^\Gamma (i)\cup \{i\}$ is the set of successors of i in $\Gamma$ together with player i. A path $(i_1,\ldots ,i_{k})$, $k\ge 3$, in $\Gamma$ is a cycle in $\Gamma$ if $\{(i_{k},i_1), (i_1,i_{k})\}\cap \Gamma \ne \emptyset$, and a directed path $(i_1,\ldots ,i_{k})$, $k\ge 2$, in $\Gamma$ is a directed cycle in $\Gamma$ if $(i_{k},i_1)\in \Gamma$.¹ A digraph $\Gamma$ on N is cycle-free  if it contains no directed cycles, i.e., no node is a successor of itself, and $\Gamma$ is strongly cycle-free  if it is cycle-free and contains no cycles.

Given a digraph $\Gamma$ on N and coalition $S\subseteq N$, the subgraph of $\Gamma$ on S is the digraph $\Gamma |_{S}=\{(i,j)\in \Gamma \mid i,j\in S\}$ on S. A coalition $S\subseteq N$ is connected  in ${\Gamma }$ if $\Gamma |_S$ is connected. For $S\subseteq N$, $C^\Gamma (S)$ denotes the collection of subsets of S being connected in $\Gamma$, and $S/\Gamma$ is the collection of maximal connected subsets, the components, of S in ${\Gamma }$.

A digraph T on N is a tree if there is a unique player without predecessors, the root of the tree, denoted by r(T), and for every other player in N there is a unique directed path in T from r(T) to that player. Note that a tree is a connected strongly cycle-free digraph. A player in a tree having no successors is a leaf. A tree T on N is a spanning tree of a digraph $\Gamma$ on N if $T\subseteq \Gamma$. A digraph composed by a number of disjoint trees is a forest. A tree in which each player has at most one immediate successor is linear.

Given a digraph $\Gamma$ on N and coalition $S\subseteq N$, player $i\in S$dominates player $j\in S$ in S if $j\in S^{\Gamma |_S}(i)$ and $i\notin S^{\Gamma |_S}(j)$. Player $i\in S$ is an undominated player in $\Gamma |_S$ if $i\in S^{\Gamma |_S}(j)$ implies $j\in S^{\Gamma |_S}(i)$. Notice that an undominated player in $\Gamma |_S$ is either a node in S without predecessors in $\Gamma |_S$ or a member of at least one directed cycle in $\Gamma |_S$. For a digraph $\Gamma$ on N and coalition $S\subseteq N$, $U^\Gamma (S)$ denotes the set of players undominated in $\Gamma |_S$. Since N is assumed to be finite, $U^\Gamma (S)\ne \emptyset$ for any nonempty coalition $S\subseteq N$. A tree has precisely one undominated player, being the root of the tree.

A pair $(v,\Gamma )$ of a TU game $v\in \mathcal{G}_N$ and digraph $\Gamma$ on N constitutes a game with directed cooperation structure or digraph game on N. The set of all digraph games on a fixed player set N is denoted by $\mathcal{G}_N^{\varGamma }$. A digraph game $(v,\Gamma )\in \mathcal{G}_N^{\varGamma }$ is superadditive (convex) if the game v is superadditive (convex). A value on $\mathcal{G}_N^{\varGamma }$ is a function $\xi :\mathcal{G}_N^{\varGamma }\rightarrow \mathrm{I\!R}^N$ that assigns to every digraph game $(v,\Gamma )$ a vector of payoffs $\xi (v,\Gamma )\in {\mathrm{I\!R}}^N$ with $\xi _i(v,\Gamma )$ as the payoff to player $i\in N$.

Following the assumption of Myerson (1977) for undirected graph games, it is assumed that only in a connected coalition players are able to cooperate and obtain the total worth of the coalition. In the remaining of the paper it is assumed without loss of generality that the grand coalition of all players forms a connected set in the given communication digraph. If this is not the case, then each component in the digraph can be considered separately.

3 The average covering tree value

In this section we introduce a new solution concept for the class of digraph games which is defined as the average of the marginal contribution vectors corresponding to all of the so-called covering trees of the digraph. Given a digraph $\Gamma$ on N, for the construction of a covering treeT of $\Gamma$ we apply the following algorithm.

Algorithm 3.1

• 0. Choose $i\in U^\Gamma (N)$. Set $T=\emptyset$, $S_i=N{\setminus }\{i\}$, and $S_j=\emptyset$ for $j\in N{\setminus }\{i\}$.

• 1. Let $S_i/\Gamma =\{C_1,\ldots ,C_m\}$. For $k=1,\ldots ,m,$ choose $j_k\in U^\Gamma (C_k)$ and set $S_{j_k}=C_k{\setminus } \{j_k\}$. Set $T=T\cup \{(i,j_1),\ldots ,(i,j_m)\}$ and $S_i=\emptyset$.

• 2. If $S_j= \emptyset$ for all $j\in N$, then stop. Otherwise, choose $i\in N$ such that $S_i\ne \emptyset$ and return to Step 1.

In the initial step 0 one of the undominated players in $\Gamma$ is chosen as the root r(T) of the covering tree, i.e., $r(T)\in U^\Gamma (N)$. We arrive to the iterative step 1 with some player i selected in the previous step. Player i is an undominated player of some connected coalition in $\Gamma ,$ where $S_i$ is the set of remaining players in this connected coalition, in particular, when coming from the initial step player i is the root r(T) and $S_i=N{\setminus }\{r(T)\}$. The set of players in $S_i$ is the union of one or more components in $\Gamma$, denoted by $C_1,\ldots ,C_m$. In each component $C_k$, $k=1,\ldots ,m$, an undominated player $j_k$ is chosen, which then becomes an immediate successor of i in the tree T, and by $S_{j_k}$ we denote the set of remaining players in $C_k$, i.e., $S_{j_k}= C_k{\setminus } \{j_k\}$. If in step 2 all sets $S_j$, $j\in N$, are empty, then there are no players left and the construction of the covering tree T has been completed. Otherwise, some player i with nonempty set $S_i$ is chosen and the procedure with step 1 is repeated.

Remark 3.2

From Algorithm 3.1 for the construction of a covering tree it follows that a tree T on N is a covering tree of a digraph $\Gamma$ on N if and only if for all $(i,j) \in T$ it holds that $i\in U^\Gamma (\bar{S}^T(i))$ and $\bar{S}^T(j) \in S^T(i)/\Gamma$.

This means that a tree is a covering tree of a digraph if and only if any player $i\in N$ is an undominated player in the set consisting of himself and all his successors in the tree and that each of his immediate successors in the tree together with his successors in the tree is a component of i’s successor set in the digraph.

Since the set of all players in a digraph game is assumed to be a connected set in the digraph, the set of nodes in a covering tree of the digraph coincides with the set of players. A covering tree of a digraph may contain directed links that do not belong to the digraph, i.e., a covering tree is not necessarily a spanning tree of the digraph. For an arbitrary digraph the number of covering trees depends on the number of undominated players in each component of all subgraphs. In case the digraph is a tree, there exists only one undominated player in every component of any subgraph of the tree, so that the only covering tree is the tree itself. On the other hand, for the complete digraph there exists a directed link from any player to any other player, so that there is only one component in any subgraph and every player of a coalition is undominated. Hence, the number of covering trees of the complete graph $\Gamma ^c_N$ on N is equal to n! and every covering tree is linear.

Example 3.3

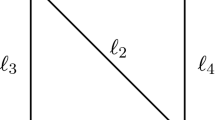
Consider the digraphs $\Gamma =\{(1,3),(2,3)\}$, $\Gamma '=\{(1,2),(2,3),(3,4),$$(4,1)\}$, and $\Gamma ''=\{(1,2),(1,4),(2,3),(3,2),(3,4),(3,5),(4,1)\}$, as depicted in Fig. 1.

Fig. 1

Digraphs of Example 3.3

The sets of undominated players in the digraphs $\Gamma$, $\Gamma '$, and $\Gamma ''$ are $\{1,2\}$, $\{1,2,3,4\}$, and $\{1,2,3,4\}$, respectively. Following Algorithm 3.1 we may construct the covering trees of digraphs $\Gamma$, $\Gamma ',$ and $\Gamma ''$, as depicted in Fig. 2.

Fig. 2

Covering trees corresponding to the digraphs of Example 3.3

We explain in detail the construction of the covering trees of the digraph $\Gamma$. In $\Gamma$ both players 1 and 2 are undominated and can be chosen as the root of a covering tree. If player 1 is taken as the root, the remaining players 2 and 3 form a connected coalition in $\Gamma$ with only player 2 being undominated, yielding covering tree $T_1=\{(1,2),(2,3)\}$. If player 2 is taken as the root, the remaining players 1 and 3 form a connected coalition in $\Gamma$ with only player 1 being undominated, yielding covering tree $T_2=\{(2,1),(1,3)\}$.

As we can see, covering trees may have different structures, in particular, some of them can be linear. The two covering trees of the digraph $\Gamma$ are linear but are not spanning trees of $\Gamma$. In fact, $\Gamma$ contains no spanning trees. On the other hand, all four covering trees of $\Gamma '$ are linear spanning trees. Among the covering trees of $\Gamma ''$ the trees $T''_1$, $T''_4$, $T''_5$, and $T''_7$ are spanning trees, while $T''_2$, $T''_3$, $T''_6$, and $T''_8$ are not.

The next proposition states that a covering tree of a directed graph preserves the subordination between players prescribed by the digraph.

Proposition 3.4

For every covering tree T of a digraph $\Gamma$ on N it holds that if $(i,j)\in \Gamma$ and $i\notin S^{\Gamma }(j)$ then $\bar{S}^{\Gamma }(j)\subseteq S^{T}(i)$.

Proof

Let $i,j\in N$ be such that $(i,j)\in \Gamma$ and $i\notin S^{\Gamma }(j)$. If $i=r(T),$ then $i\notin S^{\Gamma }(j)$ and $i\ne j$ imply $\bar{S}^{\Gamma }(j)\subseteq N{\setminus }\{i\}=S^{T}(i)$. Suppose $i\ne r(T)$. The set $\{i\}\cup \bar{S}^{\Gamma }(j)$ is a connected coalition in $\Gamma$ and for every $S\subseteq N$ such that $S\supseteq \{i\}\cup \bar{S}^{\Gamma }(j)$, player i dominates any player of $\bar{S}^{\Gamma }(j)$ in the subgraph $\Gamma |_S$. Take any $k\in N$ such that $i\in S^T(k)$. Then due to Algorithm 3.1 for constructing covering trees $S^T(k)\supseteq \{i\}\cup \bar{S}^{\Gamma }(j)$ and so any player of $\bar{S}^{\Gamma }(j)$ is dominated by i in the component of $S^T(k)$ in $\Gamma$ containing $\{i\}\cup \bar{S}^{\Gamma }(j)$. This also holds for the player $k'$ satisfying $(k',i)\in T$. Since $\bar{S}^T(i)$ is the component of $S^T(k')$ in $\Gamma$ containing $\{i\}\cup \bar{S}^{\Gamma }(j)$ and $i\notin S^{\Gamma }(j)$, it follows that $\bar{S}^{\Gamma }(j)\subseteq \bar{S}^T(i){\setminus }\{i\}=S^T(i)$. $\square$

The proposition says that if in a digraph $\Gamma$ player i directly dominates player j, i.e., $(i,j) \in \Gamma$ and $i\notin S^{\Gamma }(j)$, then in any covering tree of $\Gamma$ player i dominates both player j and any of his successors in the digraph.

A covering tree of a digraph possesses also the next useful properties.

Proposition 3.5

Let T be a covering tree of a digraph $\Gamma$ on N, then it holds that

(i) for all $i\in N$, $\bar{S}^T(i)\in C^\Gamma (N)$;

(ii) for all $i,j\in N$, if $\bar{S}^{T}(i)\cap \bar{S}^{T}(j)=\emptyset$, then $\bar{S}^{T}(i)\cup \bar{S}^{T}(j)\notin C^\Gamma (N)$.

Proof

(i) Let $i\in N$. If $i= r(T)$, then $\bar{S}^T(i)=N$ and by assumption N is a connected coalition in $\Gamma$. If $i\ne r(T)$, there exists $j\in N$ such that $(j,i)\in T$ which implies $\bar{S}^T(i)\in S^T(j)/\Gamma$. Hence, $\bar{S}^T(i)\in C^\Gamma (N)$.

(ii) Let $i,j\in N$ such that $\bar{S}^{T}(i)\cap \bar{S}^{T}(j)=\emptyset$. Since T is a covering tree, there exist unique $h,k,m\in N$ with $k\ne m$ satisfying $(h,k),(h,m)\in T$, $\bar{S}^T(i)\subseteq \bar{S}^T(k)$, and $\bar{S}^T(j)\subseteq \bar{S}^T(m)$. Since $\bar{S}^T(k)$ and $\bar{S}^T(m)$ are two different components of $S^T(h)$ in $\Gamma$, it holds that $\bar{S}^{T}(k)\cup \bar{S}^{T}(m)\notin C^\Gamma (N)$. Since $\bar{S}^T(i)\subseteq \bar{S}^T(k)$ and $\bar{S}^T(j)\subseteq \bar{S}^T(m)$, also $\bar{S}^{T}(i)\cup \bar{S}^{T}(j)\notin C^\Gamma (N)$. $\square$

Property (i) of Proposition 3.5 says that in every covering tree of a digraph each player together with all his successors forms a connected set in the digraph, while property (ii) states that the union of different branches of a covering tree is not connected in the digraph.

Given a digraph game $(v,\Gamma )\in \mathcal{G}_N^{\varGamma }$ and covering tree T of $\Gamma$, the marginal contribution vector$m^T (v,\Gamma )\in \mathrm{I\!R}^N$ corresponding to T is defined as the payoff vector

$$\begin{aligned} m_i^T(v,\Gamma )=v(\bar{S}^T(i))- \sum \limits _{C\in S^T(i)/\Gamma }v(C), \qquad \text{ for } \text{ all }i\in N. \end{aligned}$$

(1)

At the marginal contribution vector corresponding to a covering tree, any player receives as payoff the difference between the worth of the set composed by himself together with all his successors in the covering tree and the total worths of the components of the set of all his successors in the covering tree. This difference is the player’s contribution in worth when he joins his successors in the covering tree as undominated player to form a larger connected coalition.

Let $\mathcal {T}^{\Gamma }$ denote the collection of covering trees of a digraph $\Gamma$.

Definition 3.6

For a digraph game $(v,\Gamma )\in \mathcal{G}_N^{\varGamma }$, the average covering tree value (ACT value) is the average of the marginal contribution vectors corresponding to all covering trees of the digraph $\Gamma$, i.e.,

$$\begin{aligned} ACT(v,\Gamma )=\frac{1}{|\mathcal {T}^{\Gamma }|} \sum \limits _{T\in \mathcal {T}^{\Gamma }}m^T(v,\Gamma ). \end{aligned}$$

Example 3.7

Consider a 5-player digraph game with characteristic function $v(S)=|S|^2$, $S\subseteq N$, and digraph $\Gamma ''$ depicted in Fig. 1c). The marginal contribution vectors corresponding to the eight covering trees depicted in Fig. 2c are given by

$$\begin{aligned}&m^{T''_1}(v,\Gamma '')=(9,7,7,1,1),\ m^{T''_2}(v,\Gamma '')=(9,1,13,1,1),\\&m^{T''_3}(v,\Gamma '')=(3,9,11,1,1),\\&m^{T''_4}(v,\Gamma '')=(1,9,11,3,1),\ m^{T''_5}(v,\Gamma '')=(3,1,15,5,1),\\&m^{T''_6}(v,\Gamma '')=(7,1,15,1,1),\\&m^{T''_7}(v,\Gamma '')=(7,5,3,9,1),\ m^{T''_8}(v,\Gamma '')=(7,1,7,9,1). \end{aligned}$$

Whence we obtain that $ACT(v,\Gamma '')= (\frac{23}{4},\frac{17}{4},\frac{41}{4},\frac{15}{4},1)$.

When the digraph underlying a digraph game is a tree, there is only one covering tree, the tree itself, and the average covering tree value is equal to the tree value for forest digraph games first introduced in Demange (2004) under the name of hierarchical outcome and later axiomatized in Khmelnitskaya (2010). In case the digraph is a complete graph, the average covering tree value is the average of the marginal contribution vectors corresponding to n! covering trees, all of which are linear, and therefore, it coincides with the Shapley value of the underlying game. Besides, if all covering trees of the digraph are linear, the average covering tree value coincides with the Shapley value for digraph games. The particular case of the average covering tree value for undirected graph games is discussed in Sect. 5.

4 Properties and stability of the average covering tree value

In this section we show that the average covering tree value is (component) efficient and satisfies linearity, the null-player property, hierarchical efficiency, the weak player property, and is independent of inessential links. We also state conditions which guarantee the average covering tree value to be an element of the core.² The first three properties are well-known in the literature.

For a digraph game $(v,\Gamma )\in \mathcal{G}_N^{\varGamma }$, a payoff vector $x\in {\mathrm{I\!R}}^N$ is component efficient if $x(C)=v(C)$ for all $C\in N/\Gamma$, and x is efficient if $x(N)=v(N)$.

A value$\xi$ on $\mathcal{G} \subseteq \mathcal{G}_N^{\varGamma }$ is (component) efficient ((C)E) if for every $(v,\Gamma )\in \mathcal{G}$, $\xi (v,\Gamma )$ is (component) efficient.

A number of other values known in the literature, like the web values, in particular the tree value, and the average web value for digraph games introduced in Khmelnitskaya and Talman (2014) and the covering values for digraph games studied in Li and Li (2011), are not (component) efficient. Moreover, the latter values are defined only for cycle-free digraph games.

A value $\xi$ on $\mathcal{G}\subseteq \mathcal{G}_N^{\varGamma }$ is linear (L) if for every $(v,\Gamma ),(w,\Gamma )\in \mathcal{G}$ and $a,b\in \mathrm{I\!R}$, $\xi (av+bw,\Gamma )=a\xi (v,\Gamma )+b\xi (w,\Gamma )$, where $(av+bw)(S)=av(S)+ bw(S)$ for all $S\subseteq N$.

For a digraph game $(v,\Gamma )\in \mathcal{G}_N^{\varGamma }$, connected coalition $S\in C^\Gamma (N)$, and player $i\in S$, the marginal contribution of i to S is defined as

$$\begin{aligned} \Delta _i^{(v,\Gamma )}(S)=v(S)-\sum _{C\in (S{\setminus }\{i\})/\Gamma }v(C). \end{aligned}$$

A player $i\in N$ is a null-player in $(v,\Gamma )\in \mathcal{G}_N^{\varGamma }$ if $\Delta _i^{(v,\Gamma )}(S)=0$ for all $S\in C^\Gamma (N)$ such that $S\ni i$.

A value $\xi$ on $\mathcal{G}\subseteq \mathcal{G}_N^{\varGamma }$ satisfies the null-player property (NP) if for every $(v,\Gamma )\in \mathcal{G}$ and null-player i in $(v,\Gamma )$, $\xi _i(v,\Gamma )=0$.

Given a digraph $\Gamma$ on N, a coalition $S\subseteq N$ is a closed hierarchy in $\Gamma$ if it satisfies the following properties:

(i) $S=\bar{S}^{\Gamma }(i)$ for some $i\in N$;

(ii) $j\in N{\setminus } S$ and $h\in S{\setminus } U^\Gamma (S)$ imply $(j,h)\not \in \Gamma$.

A coalition is a closed hierarchy in a digraph if it consists of a player and all his successors in the digraph and, moreover, the only players in the coalition that are dominated by players outside the coalition are the undominated players in the coalition. Hence, any directed path from a player outside the coalition to a player inside the coalition contains an undominated player in the coalition.

A value $\xi$ on $\mathcal{G}\subseteq \mathcal{G}_N^{\varGamma }$ is hierarchically efficient (HE) if for every $(v,\Gamma )\in \mathcal G$ and closed hierarchy $S\subseteq N$ in $\Gamma$, $\sum \nolimits _{i\in S}\xi _i(v,\Gamma )=v(S)$.

Given a digraph game, a hierarchical efficient value assigns its worth to each closed hierarchy in the digraph. For a digraph game with the digraph being a tree, a hierarchically efficient value assigns to every coalition composed by a player together with all his successors in the tree exactly its worth.

Given a digraph $\Gamma$ on N, a player $i\in N$ is a weak player in $\Gamma$ if i has no successors in $\Gamma$, i.e., $S^{\Gamma }(i)=\emptyset$.

A value $\xi$ on $\mathcal{G}\subseteq \mathcal{G}_N^{\varGamma }$ possesses the weak player property (WP) if for every $(v,\Gamma )\in \mathcal{G}$ and weak player $i\in N$ in $\Gamma$, $\xi _i(v,\Gamma )=v(\{i\})$.

A value satisfying the weak player property assigns his own worth to every player without successors in the digraph. Such a player is not able to obtain any other payoff because this player cannot be an undominated player in any non-singleton coalition he belongs to. In case the digraph is a tree, the weak player property means that every player being a leaf of the tree receives his own worth. Note that every weak player forms a closed hierarchy in the digraph.

Given a digraph $\Gamma$ on N, a directed link $(i,j)\in \Gamma$ is inessential in $\Gamma$ if $i\notin S^{\Gamma }(j)$ and there exists $i'\in N$ such that $(i,i')\in \Gamma$, $i\notin S^{\Gamma }(i'),$ and $j\in S^{\Gamma }(i')$. A directed link $(i,j)\in \Gamma$ is inessential if it is possible to reach player j from i also by using a directed path different than link (i, j). The absence of an inessential link does not change the set of predecessors of a player.

A value $\xi$ on $\mathcal{G}\subseteq \mathcal{G}_N^{\varGamma }$ is independent of inessential links (IIL) if for every $(v,\Gamma )\!\in \!\mathcal{G}$ and inessential directed link $(i,j)\!\in \!\Gamma$ it holds that $\xi (v,\Gamma )\!=\!\xi (v,\Gamma \backslash \{(i,j)\})$.

A value being independent of inessential links assigns the same solution to a digraph game when inessential links are removed from (or added to) the digraph.

Theorem 4.1

The average covering tree value on $\mathcal{G}_N^{\varGamma }$ satisfies component efficiency, linearity, the null-player property, hierarchical efficiency, the weak player property, and independence of inessential links.

Proof

(CE) For a connected digraph game $(v,\Gamma )\in \mathcal{G}_N^{\varGamma }$, the average covering tree value is the average of the marginal contribution vectors corresponding to all covering trees of the digraph $\Gamma$. By (1) the marginal contribution vector corresponding to any covering tree of $\Gamma$ distributes the worth v(N) and is therefore efficient. If the digraph $\Gamma$ is not connected, then the average covering tree solution is applied separately to each component of N in $\Gamma$ and therefore distributes for every $C\in N/\Gamma$ the worth v(C) over all players in C. Whence the component efficiency of the average covering tree value follows.

(L) Given two digraph games $(v,\Gamma )$ and $(w,\Gamma )$ in $\mathcal{G}_N^{\varGamma }$ and real numbers $a,b\in \mathrm{I\!R}$, since the digraph representing the communication structure is the same for all three digraph games $(v,\Gamma )$, $(w,\Gamma )$ and $(av+bw,\Gamma )$, the collection of covering trees is the same for these three digraph games. Since the solution is a linear combination of the marginal contribution vectors induced by all covering trees and each of these marginal contribution vectors linearly depends on the worths of the coalitions, the ACT solution satisfies linearity.

(NP) Take any digraph game $(v,\Gamma )\in \mathcal{G}_N^{\varGamma }$ and null-player $i\in N$ for $(v,\Gamma )$. We show $m_i^T(v,\Gamma )=0$ for any $T\in \mathcal{T}^{\Gamma }$, which implies $ACT_i(v,\Gamma )=0$. Since i is a null-player for $(v,\Gamma )$, $i\in \bar{S}^{T}(i)$, and $\bar{S}^{T}(i)\in C^{\Gamma }(N)$, we have

$$\begin{aligned} \Delta _i^{(v, \Gamma )}(\bar{S}_{T}(i))=v(\bar{S}^T(i))-\displaystyle \sum \limits _{C\in (\bar{S}^T(i){\setminus }\{i\})/\Gamma }v(C)=0. \end{aligned}$$

Since $\bar{S}^T(i){\setminus }\{i\}=S^T(i)$, we obtain

$$\begin{aligned} v(\bar{S}^T(i))-\displaystyle \sum \limits _{C\in S^T(i)/\Gamma }v(C)=0, \end{aligned}$$

which implies

$$\begin{aligned} m_i^T(v,\Gamma )= v(\bar{S}^T(i))-\sum \limits _{C\in S^T(i)/\Gamma }v(C)=0. \end{aligned}$$

(HE / WP) Take any digraph game $(v,\Gamma )\in \mathcal{G}_N^{\varGamma }$ and let $S\subseteq N$ be a closed hierarchy. Clearly, $S=\bar{S}^\Gamma (u)$ for any $u\in U^\Gamma (S)$. Moreover, for all $Q\in C^\Gamma (N)$ with $Q\supsetneq S$ we have $U^\Gamma (Q)\cap S=\emptyset$ and for any $i\in Q{\setminus } S$ there exists $Q'\in (Q{\setminus }\{i\})/\Gamma$ such that $S\subseteq Q'$. Since the number of players is finite, for all $T\in \mathcal {T}^{\Gamma }$ we must have that $\bar{S}^{T}(u)=S$ for some $u\in U^\Gamma (S),$ which implies $\sum _{i\in S}ACT_i(v,\Gamma )=v(S)$. Since a weak player forms a closed hierarchy by its own, it holds that a value satisfying hierarchical efficiency also satisfies the weak player property.

(IIL) Take any digraph game $(v,\Gamma )\in \mathcal{G}_N^{\varGamma }$ and let $(i,j)\in \Gamma$ be an inessential directed link, so there exists $i'\in N$ such that $(i,i')\in \Gamma$, $i\notin S^{\Gamma }(i'),$ and $j\in S^{\Gamma }(i')$. Let $\Gamma '=\Gamma {\setminus }\{(i,j)\}$. We claim that $\mathcal {T}^{\Gamma }=\mathcal {T}^{\Gamma '}$.

Take any $T\in \mathcal {T}^{\Gamma }$. Since $(i,i')\in \Gamma$ and $i\notin S^{\Gamma }(i'),$ Proposition 3.4 implies $\bar{S}^{\Gamma }(i')\subseteq {S}^T(i)$. Hence, for all $S\supseteq S^T(i)$, $U^\Gamma (S)=U^{\Gamma '}(S)$ and $S/\Gamma =S/\Gamma '$. Moreover, $\Gamma |_{S^T(i)}=\Gamma '|_{S^T(i)}$, which implies that $T\in \mathcal {T}^{\Gamma '}$.

Conversely, take any $T'\in \mathcal {T}^{\Gamma '}$. The only difference between $\Gamma$ and $\Gamma '$ is the absence of the directed link (i, j). So, also for $\Gamma '$ we have that $(i,i')\in \Gamma '$ and $i\notin S^{\Gamma '}(i')$. Again from Proposition 3.4 it follows that $\bar{S}^{\Gamma '}(i')\subseteq S^{T'}(i).$ Hence, for all $S\supseteq S^{T'}(i)$, $U^{\Gamma '}(S)= U^\Gamma (S)$ and $S/\Gamma '=S/\Gamma$. Moreover, $\Gamma '|_{S^{T'}(i)}=\Gamma |_{S^{T'}(i)}$, which implies that $T'\in \mathcal {T}^{\Gamma }$. $\square$

Following Myerson, our basic assumption is that only connected players are able to cooperate. Whence the core of a digraph game $(v,\Gamma )\in \mathcal{G}_N^{\varGamma }$ is defined as the set of component efficient payoff vectors that are not blocked by any connected coalition, i.e.,

$$\begin{aligned} C(v,\Gamma )&=\{x\in \mathrm{I\!R}^N\mid x(C)=v(C)\ \text{ for } \text{ all }\ C\in N/\Gamma ;\ x(S)\\&\ge v(S)\ \text{ for } \text{ all }\ S\in C^\Gamma (N)\}. \end{aligned}$$

A value $\xi$ is stable on $\mathcal{G}\subseteq \mathcal{G}_N^{\varGamma }$ if for every $(v,\Gamma )\in \mathcal{G}$, $\xi (v,\Gamma )\in C(v,\Gamma )$.

In case the underlying digraph is a tree, it is shown in Demange (2004) that under the mild condition of superadditivity the corresponding unique marginal contribution vector, which coincides with the average covering tree value, is efficient and cannot be blocked by any connected coalition and, therefore, it belongs to the core of the digraph game. However, for digraph games with more general digraph structure superadditivity cannot guarantee even the nonemptiness of the core. Below we introduce a sufficient convexity-type condition that ensures the core stability of the average covering tree value.

Definition 4.2

Given a digraph $\Gamma$ on N, a connected coalition $S\in C^\Gamma (N)$ is hierarchical in $\Gamma$ if for any $i\in S$ and $j\in N$ such that $(i,j)\in \Gamma$ and $i\notin S^{\Gamma }(j)$ it holds that $\bar{S}^{\Gamma }(j)\subseteq S$.

A connected coalition is hierarchical in a digraph if whenever a player of the coalition dominates an immediate successor in the digraph then this immediate successor together with all his successors in the digraph also belong to the coalition. From Proposition 3.4 we immediately obtain the following corollary.

Corollary 4.3

Given a digraph $\Gamma$ on N, for any covering tree $T\in \mathcal {T}^{\Gamma }$ and $i\in N$ it holds that the coalition $\bar{S}^T(i)$ is hierarchical in $\Gamma$.

Definition 4.4

A digraph game $(v,\Gamma )\in \mathcal{G}_N^{\varGamma }$ is $\Gamma$-convex if

$$\begin{aligned} v(S)+v(Q)\le v(S\cup Q)+\sum \limits _{C\in (S\cap Q)/\Gamma }v(C) \end{aligned}$$

for every $S,Q\in C^\Gamma (N)$ that satisfy the following properties:

• (i) $S\cup Q \in C^\Gamma (N)$;

• (ii) S or Q is hierarchical in $\Gamma$;

• (iii) every $C\in (S\cap Q)/\Gamma$ is hierarchical in $\Gamma$.

On the class of digraph games with complete communication structure $\Gamma$-convexity reduces to convexity because for those games all subsets of N are hierarchical connected coalitions. If the digraph $\Gamma$ on N is not complete, then the condition of $\Gamma$-convexity of a digraph game $(v,\Gamma )\in \mathcal{G}_N^{\varGamma }$ is weaker than the condition of convexity of the TU game v. For convexity of a TU game v the convexity condition $v(S)+v(Q)\le v(S\cup Q)+v(S\cap Q)$ is required for all S and Q. However, for $\Gamma$-convexity this condition is only required for those S and Q such that both are connected coalitions, their union is a connected coalition, at least one of them is hierarchical, and each component of their intersection is hierarchical as well. Moreover, the worth of their intersection is replaced by the sum of the worths of the components of the intersection. For example, in case the digraph is a tree, the next proposition shows that $\Gamma$-convexity is weaker than $\Gamma$-superadditivity.

A digraph game $(v,\Gamma )\in \mathcal{G}_N^{\varGamma }$ is $\Gamma$-superadditive if $v(S)+v(Q)\le v(S\cup Q)$ for any disjoint connected coalitions S and Q such that $S\cup Q$ is a connected coalition.

Note that the condition of $\Gamma$-superadditivity for a digraph game $(v,\Gamma )$ is weaker than the condition of superadditivity for the game v.

Proposition 4.5

Any $\Gamma$-superadditive digraph game $(v,\Gamma )\in \mathcal{G}_N^{\varGamma }$ with digraph $\Gamma$ being a tree is $\Gamma$-convex.

Proof

Take a $\Gamma$-superadditive digraph game $(v,\Gamma )\in \mathcal{G}_N^{\varGamma }$ with $\Gamma$ being a tree. Let $S,Q \in C^\Gamma (N)$ be two distinct connected coalitions such that $S\cup Q$ is a connected coalition in $\Gamma$, Q is hierarchical in $\Gamma$, and each $C\in (S\cap Q)/\Gamma$ is hierarchical in $\Gamma$. We need to show that

$$\begin{aligned} v(S\cup Q)+\sum \limits _{C\in (S\cap Q)/\Gamma }v(C)\ge v(S)+v(Q). \end{aligned}$$

If $S\cap Q=\emptyset ,$ then $\Gamma$-superadditivity implies

$$\begin{aligned} v(S\cup Q)+\sum \limits _{C\in (S\cap Q)/\Gamma }v(C)=v(S\cup Q)\ge v(S)+v(Q). \end{aligned}$$

Suppose that $S\cap Q\ne \emptyset$ and $S{\setminus } Q\ne \emptyset$. Then $r(\Gamma |_Q)\in S\cap Q$ because $\Gamma$ is a tree. Since every $C\in (S\cap Q)/\Gamma$ must be a connected coalition hierarchical in $\Gamma$, it holds that $S\cap Q=Q,$ and so $Q\subset S$. This implies

$$\begin{aligned} v(S\cup Q)+\sum \limits _{C\in (S\cap Q)/\Gamma }v(C)= v(S\cup Q)+ v(S\cap Q)=v(S)+v(Q). \end{aligned}$$

Next, suppose $S\cap Q\ne \emptyset$ and $S{\setminus } Q=\emptyset .$ Then $r(\Gamma |_S)\in S\cap Q$ because $\Gamma$ is a tree. Since every $C\in (S\cap Q)/\Gamma$ must be a connected coalition hierarchical in $\Gamma$, it holds that $S\cap Q=S$ and S is also a connected coalition hierarchical in $\Gamma$, and so $S\subset Q$. This implies

$$\begin{aligned} v(S\cup Q)+\sum \limits _{C\in (S\cap Q)/\Gamma }v(C)= v(S\cup Q)+ v(S\cap Q)=v(Q)+v(S). \end{aligned}$$

$\square$

The next theorem shows that for any $\Gamma$-convex digraph game $(v,\Gamma )\in \mathcal{G}_N^{\varGamma }$ the average covering tree value is an element of the core, i.e., $ACT(v,\Gamma )\in C(v,\Gamma )$.

Theorem 4.6

The average covering tree value is stable on the class of $\Gamma$-convex digraph games.

Proof

Consider a $\Gamma$-convex digraph game $(v,\Gamma )\in \mathcal{G}_N^{\varGamma }$. We show that for every covering tree $T\in \mathcal{T}^\Gamma$ it holds that its corresponding marginal contribution vector $m^T(v,\Gamma )$ is an element of the core and therefore also its average must be. Take any $T\in \mathcal {T}^{\Gamma }$. Component efficiency of $ACT(v,\Gamma )$ follows from Theorem 4.1. To show that $\sum _{i\in S}{m_i}^T(v,\Gamma ) \ge v(S)$ for any $S\in C^\Gamma (N)$, consider the subgraph $T|_{S}$. It has components $S_1,\ldots ,S_{k'}$. Note that $T|_{S_1},\ldots , T|_{S_{k'}}$ are all subtrees of T. For $k=1,\ldots ,k'$, let $r_k$ denote the root of subtree $T|_{S_k}.$ Without loss of generality, let $r_1,\ldots ,r_{k'}$ be such that $k^1<k^2$ implies $\bar{S}^T({r_{k^1}})\subset \bar{S}^T({r_{k^2}})$ or $\bar{S}^T({r_{k^1}})\cap \bar{S}^T({r_{k^2}})=\emptyset$. For $k=1,\ldots ,k',$ let $G_{r_k}$ be the set of immediate successors of the players of $S_k$ in T that are not in S, i.e., $G_{r_k}=\{j\in N{\setminus } S\mid (i,j)\in T \text{ for } \text{ some } i\in S_k\}$. Let $R=\{r_1,\ldots ,r_{k'}\}$ and $I=\cup _{r\in R}G_r$. We define a tree $T^*$ with root $r_{k'}$ on the set of players $R\cup I$, where the set of immediate successors of a player $r\in R$ is given by $G_r$ and the set of immediate successors of a player $i\in I$ is given by the set

$$\begin{aligned} G_i=\{r\in R|~\bar{S}^T(r)\subset \bar{S}^T(i), \not \exists r'\in R{\setminus } \{r\} \text{ with } \bar{S}^T(r) \subset \bar{S}^T({r'})\subset \bar{S}^T(i)\}. \end{aligned}$$

Let $I=\{i_1,\ldots ,i_{l'}\}$. Without loss of generality, let $i_1,\ldots ,i_{l'}$ be such that $l^1 < l^2$ implies $k^1 \le k^2$ where $k^h$, $h=1,2$, is such that $(r_{k^h},i_{l^h})\in T^*$. For $l = 1,\ldots ,l'$ consider the sets $\bar{S}^T({i_l})$ and $B_{i_{l-1}}=S\cup (\bar{S}^T({i_1})\cup \cdots \cup \bar{S}^T({i_{l-1}}))$. By Corollary 4.3, $\bar{S}^T({i_l})$ is a connected coalition hierarchical in $\Gamma$ for any $l=1,\ldots ,l'$. To apply the induction argument on l in order to show that the set $B_{i_l}$ is a connected coalition, suppose that $B_{i_{l-1}}$ is a connected coalition. Notice that for $l=1$ the set $B_{i_{l-1}}=S$ is a connected coalition. Let $i\in N$ be the unique immediate predecessor of $i_l$ in T, then from the construction of $T^*$ it follows that $i\in S$ and from Remark 3.2 it follows that $\bar{S}^T(i_l)\in S^T(i)/\Gamma$. Due to (i) of Proposition 3.5$\bar{S}^T(i)$ is a connected coalition which implies that $(i,j)\in \Gamma$ for some $j\in \bar{S}^T(i_l).$ Because $j\in \bar{S}^T({i_l})$ and $i\in B_{i_{l-1}}$, $(i,j) \in \Gamma$ implies that their union, which is equal to $B_{i_{l}}$, is indeed a connected coalition. Moreover, by construction of $T^*$, the components of their possibly empty intersection are the hierarchical connected coalitions $\bar{S}^T(r),$$r\in G_{i_l}$. From $\Gamma$-convexity it then follows that

$$\begin{aligned}&v(S\cup (\bar{S}^T({i_1})\cup \cdots \cup \bar{S}^T({i_{l-1}}))) + v(\bar{S}^T({i_l})) \\&\quad \le v(S\cup (\bar{S}^T({i_1})\cup \cdots \cup \bar{S}^T({i_{l}}))) + \sum \limits _{r\in G_{i_l}}v(\bar{S}^T(r)). \end{aligned}$$

By repeated application of this inequality for $l=1,\ldots ,l'$ and since $S\cup (\bigcup \nolimits _{l=1}^{l'}\bar{S}^T(i_l))=\bar{S}^T(r_{k'})$ it follows that

$$\begin{aligned} v(S)+\displaystyle \sum _{l=1}^{l'} v(\bar{S}^T(i_l))\le v(\bar{S}^T(r_{k'})) + \displaystyle \sum _{l=1}^{l'}\displaystyle \sum \limits _{r\in G_{i_l}} v(\bar{S}^T(r)). \end{aligned}$$

Because $\{i_1,\ldots ,i_{l'}\}=\bigcup \nolimits _{k=1}^{k'}G_{r_k},$ the latter inequality can be rewritten as

$$\begin{aligned} v(S)+\sum \limits _{k=1}^{k'} \displaystyle \sum \limits _{i\in G_{r_k}}v(\bar{S}^T(i))\le v(\bar{S}^T({r_{k'}})) + \displaystyle \sum \limits _{k=1}^{k'}\sum \limits _{i\in G_{r_k}} \sum \limits _{r\in G_{i}}v(\bar{S}^T(r)). \end{aligned}$$

Since $T^*$ is a tree, every coalition $\bar{S}^T({r_k})$, $k=1,\ldots ,k'$, appears exactly once in the right hand side and we obtain

$$\begin{aligned} v(S)+\displaystyle \sum \limits _{k=1}^{k'} \displaystyle \sum \limits _{i\in G_{r_k}}v(\bar{S}^T(i))\le \displaystyle \sum \limits _{k=1}^{k'} v(\bar{S}^T({r_k})). \end{aligned}$$

Since for $k=1,\ldots ,k'$, $S_k=\bar{S}^T({r_k}){\setminus }(\bigcup \nolimits _{i\in G_{r_k}}\bar{S}^T(i))$, we have

$$\begin{aligned} \displaystyle \sum \limits _{i\in S}{m_i}^T(v,\Gamma )=\displaystyle \sum \limits _{k=1}^{k'}\left[ v(\bar{S}^T({r_k}))-\displaystyle \sum \limits _{i\in G_{r_k}}v(\bar{S}^T(i))\right] . \end{aligned}$$

From the last two equations it follows that $\sum _{i\in S}{m_i}^T(v,\Gamma )\ge v(S)$, which completes the proof. $\square$

5 Undirected graph games

In this section we consider the class of undirected (connected) graph games. As discussed in the preliminaries any undirected graph L on the player set N can be identified with its directed analog $\Gamma ^L$ by replacing each undirected link of L between two players by two directed links with opposite direction. In the directed analog of an undirected graph, every player in any connected coalition is undominated and therefore any connected coalition is hierarchical in the digraph. This follows from the fact that every successor of a player is also a predecessor of that player. Moreover, as it follows from Remark 3.2, if (i, j) is a link in a covering tree T of the directed analog of an undirected graph L, then the set consisting of j and all his successors in T is a component in L of the successor set of i in T.

In Koshevoy and Talman (2014) the Gravity Center or GC solution is introduced for TU games where the communication structure between players is represented by an arbitrary collection of coalitions which includes all singletons and the grand coalition. When applied to an undirected graph the collection of feasible coalitions is precisely the set of connected coalitions in the graph. In this setting a strictly nested set, denoted by $\mathcal N,$ is a subcollection of feasible coalitions where for each pair of feasible coalitions one is a subset of the other or their intersection is empty and the union of any number of disjoint feasible coalitions is not feasible. Each maximal strictly nested set induces a tree T on N such that for each $i\in N$ the set $\bar{S}^T(i)$ is the smallest coalition in $\mathcal N$ containing i and $(i,j)\in T$ if $\bar{S}^T(j)$ is the largest subset of $S^T(i)$ in $\mathcal N$ containing j. The GC solution is the average of the marginal contribution vectors that correspond to the trees that are induced by all maximal strictly nested sets of the set system. In case the collection of feasible coalitions is the set of connected coalitions of an undirected graph, the set of trees induced by the collection of maximal strictly nested sets is equal to the set of covering trees of the directed analog of the undirected graph. This is because for every covering tree the collection of sets consisting of any player and his successors is a maximal strictly nested set, and conversely every maximal strictly nested set induces a covering tree with the sets consisting of a player and his successors being the elements of the strictly nested set.

For an undirected graph game (v, L) on N, let GC(v, L) denote the GC solution of (v, L), i.e., GC(v, L) is the average of the marginal contribution vectors that correspond to all maximal strictly nested sets of the collection of connected coalitions of the graph L. Then the average covering tree value of the digraph game $(v,\Gamma ^L)$ is equal to the GC solution of the undirected graph game (v, L).

Proposition 5.1

For an undirected graph game (v, L) it holds that $ACT(v,\Gamma ^L)=GC(v,L)$.

To guarantee that the average covering tree value is core stable, in Definition 4.4 the concept of $\Gamma$-convexity is introduced for a digraph game $(v,\Gamma )$. In case of an undirected graph game (v, L) we may use $\Gamma ^L$-convexity of the game to obtain stability of the average covering tree solution. This stability condition coincides with the convexity-type condition given in Koshevoy and Talman (2014).

Corollary 5.2

For an undirected graph game (v, L), the average covering tree value $ACT(v,\Gamma ^L)$ is an element of the core if for any two connected coalitions S and Q in L such that $S\cup Q$ is a connected coalition in L it holds that

$$\begin{aligned} v(S)+v(Q)\le v(S\cup Q)+\sum \limits _{C\in (S\cap Q)/\Gamma ^L}v(C). \end{aligned}$$

(2)

Herings et al. (2008) introduce the average tree solution for TU games with cycle-free undirected graph communication structure. This solution is generalized for TU games with arbitrary undirected graph communication structure in Herings et al. (2010). The average tree solution is defined as the average of the marginal vectors that correspond to all spanning normal trees of the undirected graph. For an undirected graph L on N, a tree T on N is a spanning tree of L if $(i,j)\in T$ implies $\{i,j\}\in L$, and in Diestel (2005) a tree T on N is defined as a normal tree of L if the ends of every link in L are comparable in the tree order of T. A tree T on N is therefore a spanning normal tree of L if for every $(i,j)\in T$ it holds that $\{i,j\}\in L$ and $\bar{S}^T(j)\in S^T(i)/\Gamma ^L$. The collection of spanning normal trees of an undirected graph corresponds therefore one-to-one to the set of spanning covering trees of its directed analog.

Proposition 5.3

Let L be an undirected graph on N. A tree T on N is a spanning normal tree of L if and only if T is a spanning covering tree of $\Gamma ^L$.

On the class of undirected graph games the average tree solution is therefore equal to the average of the marginal contribution vectors that correspond to all covering trees that are also spanning trees of the directed analog of the graph. We remark that for a directed graph not being the directed analog of an undirected graph spanning covering trees may not exist. For example, the digraph $\Gamma$ of Example 3.3 has no spanning covering trees.

For undirected graph games, Myerson (1977) introduces the Myerson value. In order to find the Myerson value of an undirected graph game, the so-called Myerson restricted game and all permutations on N are considered. Every permutation yields a marginal contribution vector of the Myerson restricted game and the Myerson value is the average of all these n! marginal contribution vectors. If the communication structure of an undirected graph game is not complete, the same marginal contribution vector may correspond to different permutations. However, for the average covering tree value of the directed analog of an undirected graph game, all marginal contribution vectors will differ from each other, see Koshevoy and Talman (2014).

The next example illustrates for an undirected graph game the differences between the average covering tree value (or GC solution), the Myerson value, and the average tree solution.

Example 5.4

Consider the undirected graph game (v, L) with three players, where $L=\{\{1,2\},\{2,3\}\}$ and $v(S)=0$ if $|S|\le 1$ and $v(S)=|S|^2$ if $|S|\ge 2$. The graphical representation of the undirected graph L, its directed analog $\Gamma ^L,$ and the five covering trees of $\Gamma ^L$ are depicted in Fig. 3.

Fig. 3

Undirected graph and its directed analog with corresponding covering trees of Example 5.4

For each of the five covering trees of the digraph $\Gamma ^L$ shown in Fig. 3c, a different marginal contribution vector is obtained and their average is equal to the average covering tree value of the digraph game $(v,\Gamma ^L)$. The five marginal contribution vectors whose average is the GC solution of the undirected graph game (v, L) coincide with the marginal vectors corresponding to these covering trees. The covering trees $T_1,T_2,T_3$ are the spanning normal trees of the undirected graph L,  and their average is equal to the average tree solution of the undirected graph game (v, L). Those three trees are also the spanning covering trees of the digraph $\Gamma ^L$.

Fig. 4

Imputation set of the digraph game of Example 5.4

In Fig. 4, the imputation set of the directed graph game $(v,\Gamma ^L)$ is depicted. The shaded area in the figure shows the set of core allocations and each of the five extreme points of the core corresponds to a marginal contribution vector corresponding to one of the covering trees. The average covering tree solution for the directed graph game $(v,\Gamma ^L)$ and therefore also the GC solution for the undirected graph game (v, L) is the average of all five different marginal contribution vectors and is the gravity center of the core for this example. The average tree solution for the undirected graph game (v, L) is the average of the three marginal contribution vectors $m^{T_1}$, $m^{T_2},$$m^{T_3}.$ Since there are three players, there are six permutations with corresponding marginal contribution vectors that determine the Myerson value. Two permutations, (1, 3, 2) and (3, 1, 2),  yield the same marginal vector $m^{T_2}$. For the Myerson value, the vector $m^{T_2}$ is therefore counted twice as marginal contribution vector, while each of the other four vectors are counted once as marginal contribution vector.

To conclude, we have shown that based on the representation of an undirected graph via its directed analog, the gravity center solution for an undirected graph game coincides with the average covering tree value for the corresponding digraph game determined by the directed analog of the graph. Therefore, the average covering tree value for digraph games can be considered as a generalization of the gravity center solution for undirected graph games.