The two-step average tree value for graph and hypergraph games

Abstract

We introduce the two-step average tree value for transferable utility games with restricted cooperation represented by undirected communication graphs or hypergraphs. The solution can be considered as an alternative for both the average tree solution for graph games and the average tree value for hypergraph games. Instead of averaging players’ marginal contributions corresponding to all admissible rooted spanning trees of the underlying (hyper)graph, which determines the average tree solution or value, we consider a two-step averaging procedure, in which first, for each player the average of players’ marginal contributions corresponding to all admissible rooted spanning trees that have this player as the root is calculated, and second, the average over all players of all the payoffs obtained in the first step is computed. In general these two approaches lead to different solution concepts. Contrary to the average tree value, the new solution satisfies component fairness and the total cooperation equal treatment property on the entire class of hypergraph games. Moreover, the two-step average tree value is axiomatized on the class of semi-cycle-free hypergraph games, which is more general than the class of cycle-free hypergraph games by allowing the underlying hypergraphs to contain certain cycles. The two-step average tree value is also core stable on the subclass of superadditive semi-cycle-free hypergraph games.

1 Introduction

In classical cooperative game theory it is assumed that any coalition of players may form and realize its worth, and a fair distribution of total rewards among the players takes into account the worths of all coalitions. The most well-known solution of cooperative games with transferable utility, or TU games, the Shapley value, cf. (Shapley, 1953), assigns to each player as payoff the average of the player’s marginal contributions to his predecessors with respect to all possible linear orderings of the players. However, in many practical situations the collection of feasible coalitions is restricted by some social, economical, communication, or technical structure. The study of transferable utility games with limited cooperation introduced by means of an undirected communication graph, for brevity called graph games, is initiated in Myerson (1977). Assuming that only connected players can cooperate, the Myerson value for graph games is defined as the Shapley value of the so-called restricted game in which the worth of each coalition is equal to the sum of the worths of its connected components in the graph. Later several other solutions for graph games based also on this Myerson’s assumption have been proposed, in particular, the average tree solution introduced by Herings et al. (2008) for cycle-free graph games and generalized by Herings et al. (2010) for the class of all graph games. In comparison to the Myerson value the average tree solution is stable on the subclass of superadditive cycle-free graph games and for cycle-free graph games the order of computational complexity of the average tree solution is equal to n, the number of players, while the order of computational complexity of the Myerson value for all graph games is n!.

The idea of considering cooperative games with a communication structure that allows communication within sets of more than two players appears first in Myerson (1980), where NTU games with conference structure are investigated. In fact a conference in terms of Myerson coincides with a hyperlink of a hypergraph. TU games with hypergraph communication structure, for brevity called hypergraph games, are formally introduced by van den Nouweland et al. (1992). Recently the average tree value for hypergraph games, which generalizes the average tree value for graph games to hypergraph games, is introduced and investigated by Kang et al. (2021).

The goal of this paper is to introduce a two-step average tree value for hypergraph games, and in particular for graph games, which can be considered as an alternative with better properties to the average tree value. Similar to the average tree value for graph and hypergraph games, the new solution is based on the idea that the communication within every component of the underlying (hyper)graph can be represented by means of any of its admissible rooted spanning trees and the payoff to a player is determined by an averaging of the player’s marginal contributions with respect to all these trees on the component the player belongs to. In each such tree the player who is the root of the tree plays a particular role as the only player who is able to transmit by communication information to any other player in the component through a unique sequence of adjacent players. Since for distinct players the numbers of admissible rooted spanning trees having these players as the roots may differ, the simultaneous averaging in the definition of the average tree value over all admissible rooted spanning trees implies that the players participate in the game with weights determined by the numbers of admissible rooted spanning trees having them as their roots. The latter conflicts with the idea that in order to cooperate every player in a game is equally important. To eliminate this drawback we consider in the definition of the two-step average tree value a two-step averaging procedure, in which first for each player the average of all players’ marginal contributions corresponding to all admissible rooted spanning trees having this player as the root is calculated, and then the average over all players of the payoffs obtained in the first step is computed.

A comparative analysis of both solution concepts shows that the two-step average tree value satisfies component efficiency, component fairness, and the total cooperation equal treatment property on the entire class of hypergraph games, while the average tree value satisfies the latter two properties only on some particular subclasses. We also introduce a property called equal surplus of interactive players, which states that players that belong to the same set of hyperlinks receive the same payoff as surplus on their own worth. It is shown that both average tree values satisfy this property on the entire class of hypergraph games. Furthermore, an axiomatization of the two-step average tree value by component efficiency, component fairness, and equal surplus of interactive players on the class of so-called semi-cycle-free hypergraph games, which includes all cycle-free hypergraph games as a proper subclass, is provided. It is also shown that both average tree values are core stable on the subclass of superadditive semi-cycle-free hypergraph games.

The paper is organized as follows. Basic definitions and notation are given in Sect. 2. In Sect. 3 the two-step average tree value for (hyper)graph games is introduced and the cases of its coincidence with the average tree value are investigated. Section 4 studies several properties of the two-step average tree value and compares them with those of the average tree value. Section 5 provides an axiomatic characterization of the two-step average tree value. Section 6 examines the core stability.

2 Preliminaries

A cooperative game with transferable utility, or TU game, is a pair (N, v), where $N=\{1,2,\ldots ,n\}$ is a finite set of players and $v:2^N\rightarrow \mathrm{I\!R}$ is a characteristic function, with $v(\emptyset )=0$, assigning to every coalition $S\subseteq N$ its worth v(S), which can be freely distributed as payoff among the members of S. We denote by $\mathcal {G}_N$ the set of TU games with fixed player set N. For simplicity of notation and if no ambiguity appears we write v instead of (N, v). The subgame of $v\in \mathcal {G}_N$ on $Q\subseteq N$, $Q\ne \emptyset$, is the TU game $v|_Q\in \mathcal {G}_Q$ defined as $v|_Q(S)=v(S)$ for all $S\subseteq Q$. A game $v\in \mathcal {G}_N$ is superadditive if $v(S\cup Q)\ge v(S)+v(Q)$ for all $S, Q\subseteq N$ satisfying $S\cap Q=\emptyset$. The unanimity game determined by coalition $Q\subseteq N$, $Q\ne \emptyset$, is the TU game $u_Q\in \mathcal {G}_N$ defined as $u_Q(S)=1$ if $Q\subseteq S$ and $u_Q(S)=0$ otherwise. For a finite set S, |S| denotes the cardinality of S.

A communication structure on the set of players N is specified by a graph or hypergraph on N. A hypergraph on N is a set $H\subseteq \{e\in 2^N\mid |e|\ge 2\}$ of hyperlinks. A hypergraph H is r-uniform if $|e|=r$ for all $e\in H$. A 2-uniform hypergraph on N is an (undirected) graph on N and is denoted by a set of links $\Gamma \subseteq \Gamma ^N$, where $\Gamma ^N=\{\{i,j\}\mid i,j\in N, i\ne j\}$ is the complete graph on N. We denote by $\mathcal {H}_N$ ($\varGamma _N$) the set of hypergraphs (graphs) on N.

Let $H\in \mathcal {H}_N$. For $i\in N$, $H_i=\{e\in H\mid e\ni i\}$ is the set of hyperlinks in H containing i with $|H_i|$ the degree of i in H. A player i is connective in H if $|H_i|\ge 2$. Two players i and j are interactive in H if $H_i=H_j\ne \emptyset$. A player j is adjacent to player i in H if $i,j\in e$ for some $e\in H$. A sequence $C=(i_1,e_1,i_2,e_2,\ldots ,i_{k-1},e_{k-1},i_k)$, with $k\ge 2$, is a chain in H between player $i_1$ and player $i_k$ if it satisfies the following conditions: (i) $i_1,\ldots ,i_{k-1}$ are distinct players in N, (ii) $i_2,\ldots ,i_{k}$ are distinct players in N, (iii) $e_1, \ldots , e_{k-1}$ are distinct hyperlinks in H, and (iv) $i_h,i_{h+1}\in e_h$ for all $h\in \{1,\ldots , k-1\}$. For a chain $C=(i_1,e_1,i_2,e_2,\ldots ,i_{k-1},e_{k-1},i_k)$ in H, $N(C)=\bigcup _{h=1}^{k-1}e_h$ is the set of players contained in C and the sequence $(i_1,i_2,\ldots ,i_k)$ is a path in H between players $i_1$ and $i_k$. H is connected if n=1 or there exists a chain in H between every two distinct players in N. A chain $(i_1,e_1,i_2,e_2,\ldots ,i_{k-1},e_{k-1},i_k)$ in H with $k\ge 3$ is a cycle in H if $i_1=i_k$. H is cycle-free if there is no cycle in H. H is linear if $|e\cap e'|\le 1$ for every distinct $e, e'\in H$. When H is cycle-free, then H is linear, because distinct $i_1,i_2\in e_1\cap e_2$ for some $e_1,e_2\in H$, $e_1\ne e_2$, implies that $(i_1,e_1,i_2,e_2,i_1)$ is a cycle in H. H is a hypertree if H is connected and cycle-free. H is a cactus if H is connected and any two distinct cycles in H have at most one player in common, i.e., $|N(C)\cap N(C')|\le 1$ for every distinct cycles $C, C'$ in H. A hypertree is a linear cactus without cycles and a nonlinear cactus always contains cycles. For example, $H=\{e_1,e_2\}$ on $N=\{1,2,3,4\}$, where $e_1=\{1,2,3\}$ and $e_2=\{2,3,4\}$, is a nonlinear cactus with one cycle $(2,e_1,3,e_2,2)$.

For $S\subseteq N$, the hypergraph $H|_S=\{e\in H\mid e\subseteq S\}$ on S is the subhypergraph of H induced by S. A coalition $S\subseteq N$ is connected in H if $H|_S$ is connected, i.e., $|S|=1$ or there exists a chain in $H|_S$ between every two distinct players in S. $C^H(S)$ denotes the set of subsets of $S\subseteq N$ that are connected in H. For $S\subseteq N$, Q is a component of S in H, if Q is a maximal connected subset of S in H. S/H denotes the set of components of $S\subseteq N$ in H. A hyperlink $e\in H$ is a bridge in H if $|N/H|<|N/(H\backslash \{e\})|$. If H is cycle-free, then every $e\in H$ is a bridge in H.

A rooted tree on a component $K\in N/H$ of N in H is a set $T\subseteq \{(i,j)\mid i,j\in K,i\ne j\}$ of directed links with one player r(T), the root of T, satisfying that $(i,r(T))\notin T$ for all $i\in K$ and for every $i\in K$, $i \ne r(T)$, there is a unique directed path $(i_1,\ldots ,i_k)$ in T from $i_1$ to $i_k$, where $i_1=r(T)$, $i_k=i$, and $(i_h,i_{h+1})\in T$ for all $h\in \{1,\ldots ,k-1\}$. If there exists a directed path in T from i to j, then j is a successor of i and i is a predecessor of j in T, and if $(i,j)\in T$, then j is an immediate successor of i and i is an immediate predecessor of j in T. For $i\in K$, $S^T_i$ and ${\widehat{S}}^T_i$ denote the set of successors and the set of immediate successors of i in T, respectively, and ${\bar{S}}^T_i=S^T_i\cup \{i\}$. T is a rooted spanning tree of $H|_K$ if $(i,j)\in T$ implies $\{i,j\}\subseteq e$ for some $e\in H|_{{\bar{S}}^T_i}$. A rooted spanning tree T of $H|_K$ is admissible if $(i,j)\in T$ implies $\bar{S}_j^T\in S^T_i/H$. $\mathcal{T}^H(K)$ denotes the set of admissible rooted spanning trees of $H|_K$ and, for $r\in K$, ${{\mathcal {T}}}_r^H(K)$ denotes the set of admissible rooted spanning trees in $\mathcal{T}^H(K)$ having r as the root.

A game with hypergraph communication structure, or hypergraph game, is a triple (N, v, H), or in short (v, H), where $v \in \mathcal {G}_N$ is a TU game and $H \in \mathcal {H}_N$ is a hypergraph on N. When H is a graph $\Gamma$ on N, $(v,\Gamma )$ is a graph game. For fixed player set N, $\mathcal {G}_N^\mathcal{H}$ ($\mathcal {G}_N^{\varGamma }$) denotes the set of hypergraph (graph) games, $\mathcal {G}_N^{\mathcal{H}^{c}}$ ($\mathcal {G}_N^{{\varGamma }^{c}}$) the set of connected hypergraph (graph) games, and $\mathcal {G}_N^{\mathcal{H}^{cf}}$ ($\mathcal {G}_N^{{\varGamma }^{cf}}$) the set of cycle-free hypergraph (graph) games. A hypergraph game $(v,H)\in \mathcal{G}_N^\mathcal{H}$ is superadditive if for every $S\in C^H(N)$ and every partition of S into $S_1,\ldots ,S_k\in C^H(N)$, $k\ge 2$, it holds that $v(S)\ge \sum _{j=1}^k v(S_j)$. A payoff vector is a vector $x\in \mathrm{I\!R}^n$ that assigns payoff $x_i$ to player $i\in N$. For a subset of hypergraph games $\mathcal {G}\subseteq \mathcal {G}_N^\mathcal{H}$, a value on ${\mathcal {G}}$ is a mapping $\xi :\mathcal {G}\rightarrow \mathrm{I\!R}^n$ that assigns to every $(v,H)\in \mathcal {G}$ a payoff vector $\xi (v,H)\in \mathrm{I\!R}^n$ with $\xi _i(v,H)$ as the payoff to player $i\in N$.

Following Myerson (1980) it is assumed that in a game with hypergraph communication structure each player is able to communicate with himself and with all other players in a hyperlink he belongs to, moreover, all players of a hyperlink have to be present before communication between its members can take place. Therefore, only coalitions that are connected in the hypergraph are able to communicate in order to cooperate and realize their worth. A connected coalition in a hypergraph is either a singleton player or a single hyperlink or the connected union of two or more hyperlinks in the hypergraph. Note that distinct hypergraphs may have the same set of connected coalitions.

For a hypergraph game $(v,H)\in \mathcal {G}_N^\mathcal{H}$ and component $K\in N/H$, the marginal contribution of player $i\in K$ with respect to admissible rooted spanning tree $T\in \mathcal {T}^{H}(K)$ is given by

$$\begin{aligned} m_i^{T}(v,H)=v(\bar{S}^T_i)-\sum _{S\in S^T_i/H}v(S). \end{aligned}$$

Since $S^T_i/H=\{\bar{S}^T_j\}_{j\in {{\widehat{S}}^T_i}}$, for every $i \in K$ it holds that

$$\begin{aligned} m_i^{T}(v,H)=v(\bar{S}^T_i)-\sum _{j\in {\widehat{S}}^T_i}v(\bar{S}^T_j), \end{aligned}$$

(1)

being player i’s contribution in worth to the connected coalitions of his immediate successors and their successors in the tree.

The average tree value (AT value) for graph games, introduced in Herings et al. (2008, 2010) and generalized for hypergraph games in Kang et al. (2021), assigns to every $(v,H)\in \mathcal {G}_N^\mathcal{H}$ a payoff vector AT(v, H) with the payoff to player $i\in N$ given by

$$\begin{aligned} AT_i(v,H)=\frac{1}{|\mathcal {T}^{H}(K)|} \sum _{T\in \mathcal {T}^{H}(K)}m^{T}_i(v,H),\qquad K\in N/\Gamma ,\ K\ni i, \end{aligned}$$

(2)

being player i’s average marginal contribution corresponding to all admissible rooted spanning trees on the component the player belongs to. In particular, to a graph game $(v,\Gamma )\in \mathcal{G}_N^{\varGamma }$, the AT value assigns the payoff vector $AT(v,\Gamma )$ given by

$$\begin{aligned} AT_i(v,\Gamma )=\frac{1}{|\mathcal {T}^{\Gamma }(K)|} \sum _{T\in \mathcal {T}^{\Gamma }(K)}m_i^{T}(v,\Gamma ),\qquad K\in N/\Gamma ,\ K\ni i. \end{aligned}$$

(3)

3 The two-step average tree value

3.1 Motivation and definition

We introduce a two-step average tree value for hypergraph games, and in particular for graph games, which similar to the average tree value for graph and hypergraph games is based on the idea that the communication within a component of the underlying hypergraph can be represented by means of any of the admissible rooted spanning trees of the subhypergraph induced by the component and that the payoff to a player is determined by an averaging of the player’s marginal contributions with respect to all admissible rooted spanning trees on the component the player belongs to. An admissible rooted spanning tree on a component of a hypergraph corresponds to a partial ordering, not necessarily a linear ordering as for the Shapley value for TU games, on the set of players in the component and is such that each player with at least one successor in the tree has precisely one immediate successor in every component of his set of successors in the tree. In an admissible rooted spanning tree on a component only the player who is the root of the tree is able to transmit by communication information through a unique sequence of adjacent players in the tree to every other player in the component. In Kang et al. (2021) a procedure to generate all admissible rooted spanning trees of a hypergraph is described and it is shown that every player is the root of at least one admissible rooted spanning tree.

In general, for distinct players the numbers of admissible rooted spanning trees having these players as their roots are different. Therefore, the simultaneous averaging in the definition of the average tree value over all admissible rooted spanning trees unwittingly implies that the players who are able to transmit information to every other player participate in the solution with weights determined by the numbers of admissible rooted spanning trees having these players as their roots. The latter conflicts with the idea that every player in a (hyper)graph game is equally important for cooperation. To eliminate this drawback we consider in the definition of the two-step average tree value a two-step averaging procedure, in which for every component in the first step for each of its players the average of all its players’ marginal contributions corresponding to all admissible rooted spanning trees having this player as the root is calculated, and in the second step the average over all players of the payoffs obtained in the first step is computed. As we will see from the comparative analysis of both average tree solution concepts in the next sections, the procedure underlying the two-step average tree value provides it with properties valid on the same or wider subclasses of hypergraph games than the average tree value.

The two-step average tree value (TAT value) for hypergraph games assigns to every $(v,H)\in \mathcal {G}_N^\mathcal{H}$ a payoff vector TAT(v, H) with the payoff to player $i\in N$ given by

$$\begin{aligned} TAT_i(v,H)=\frac{1}{|K|}\sum _{r\in K}\frac{1}{|\mathcal {T}_r^{H}(K)|}\sum _{T\in \mathcal {T}_r^{H}(K)}m^{T}_i(v,H), \qquad K\in N/\Gamma ,\ K\ni i. \end{aligned}$$

(4)

In particular, to a graph game $(v,\Gamma )\in \mathcal{G}_N^{\varGamma }$, the TAT value assigns the payoff vector $TAT(v,\Gamma )$ given by

$$\begin{aligned} TAT_i(v,\Gamma )=\frac{1}{|K|}\sum _{r\in K}\frac{1}{|\mathcal {T}_r^{\Gamma }(K)|}\sum _{T\in \mathcal {T}_r^{\Gamma }(K)}m^{T}_i(v,\Gamma ),\qquad K\in N/\Gamma ,\ K\ni i. \end{aligned}$$

(5)

3.2 The TAT value versus the AT value

The following example shows that the TAT value differs from the AT value.

Example 1

Consider the graph game $(v,\Gamma )\in \mathcal {G}_N^{\varGamma }$ on a set N of 4 players with $v=u_{\{1,2\}}$ and $\Gamma =\{\ell _1,\ell _2,\ell _3,\ell _4,\ell _5\}$, where $\ell _1=\{1,2\}$, $\ell _2=\{1,3\}$, $\ell _3=\{1,4\}$, $\ell _4=\{2,3\}$, $\ell _5=\{3,4\}$, as depicted in Fig. 1.

Fig. 1

Graph $\Gamma$ in Example 1

Graph $\Gamma$ has three admissible rooted spanning trees with player 1 as the root, four with player 2 as the root, three with player 3 as the root, and four with player 4 as the root, as depicted in Fig. 2.

Fig. 2

The admissible rooted spanning trees of $\Gamma$ in Example 1

From (1) we obtain the following fourteen marginal contribution vectors:

$$\begin{aligned}&m^{T^1_1}(v,\Gamma )=m^{T^2_1}(v,\Gamma )=m^{T^3_1}(v,\Gamma )=(1,0,0,0),\\&m^{T^1_2}(v,\Gamma )=m^{T^2_2}(v,\Gamma )=m^{T^3_2}(v,\Gamma )= m^{T^4_2}(v,\Gamma )=(0,1,0,0),\\&m^{T^1_3}(v,\Gamma )=m^{T^3_3}(v,\Gamma )=(1,0,0,0),~m^{T^2_3}(v,\Gamma )= (0,1,0,0), \\&m^{T^1_4}(v,\Gamma )=m^{T^2_4}(v,\Gamma )=m^{T^3_4}(v,\Gamma )= (1,0,0,0),~m^{T^4_4}(v,\Gamma )=(0,1,0,0). \end{aligned}$$

Wherefrom,

$$\begin{aligned} TAT(v,\Gamma ){\mathop {=}\limits ^{(5)}}\frac{1}{4}\big ((1,0,0,0)+ (0,1,0,0)+(\frac{2}{3},\frac{1}{3},0,0)+(\frac{3}{4},\frac{1}{4},0,0)\big )= (\frac{29}{48},\frac{19}{48},0,0) \end{aligned}$$

and

$$\begin{aligned} AT(v,\Gamma ){\mathop {=}\limits ^{(3)}} \frac{1}{14}\big (8(1,0,0,0)+6(0,1,0,0)\big )=(\frac{4}{7},\frac{3}{7},0,0). \end{aligned}$$

Similar to the average tree value, but not to the Myerson value, the two-step average tree value may differ for different hypergraph games that have the same set of connected coalitions. For both two-step average tree and average tree values this is because different hypergraphs with the same set of connected coalitions may have different sets of admissible rooted spanning trees¹ and, therefore, they may have different marginal contributions of the players.

From (2) and (4) it immediately follows that the TAT and AT values for a hypergraph game coincide if for each component of the underlying hypergraph every player in this component is the same number of times the root of an admissible rooted spanning tree on this component.

Theorem 1

The two-step average tree value and the average tree value for a hypergraph game $(v,H)\in \mathcal {G}_N^\mathcal{H}$ coincide if, for every $K\in N/H$, the subhypergraph $H|_K$ is cycle-free, a linear cactus with cycles, or a complete graph.

Proof

Without loss of generality assume that H is connected. Let H be a linear cactus with or without cycles. Note that H is cycle-free if and only if H is a linear cactus without cycles. We first prove by induction on the number of cycles in H that $|\mathcal {T}^H_r(N)|=2^c$ for all $r\in N$, where c is the number of cycles in H. If $c=0$, then H is cycle-free and from Lemma 1 in Kang et al. (2021) it follows that $|\mathcal {T}^H_r(N)|=1$ and therefore $|\mathcal {T}^H_r(N)|=2^0$ for all $r\in N$.

Assume that the assertion holds true for every linear cactus with less than c cycles for some given $c>0$. We show that the assertion holds true if H is a linear cactus with c cycles. Take any $r\in N$ and $T\in \mathcal{T}_r^H(N)$. Since T is a rooted tree on N, there exists a unique $i\in N$ such that $\bar{S}^T_i$ is minimal among $\bar{S}^T_j$, $j\in N$, whose induced subgraphs contain all c cycles in H. For every $j\in N\setminus S^T_i$, in particular for $j=i$, it holds that $\bar{S}^{T'}_j=\bar{S}^T_j$ for all $T'\in \mathcal{T}_r^H(N)$. Therefore, $|\mathcal {T}^H_r(N)|=|{{\mathcal {T}}}_i^H({{\bar{S}}}^{T}_i)|$. To prove that $|\mathcal{T}_i^H({{\bar{S}}}^T_i)|=2^c$, let the components of $S^T_i$ in H be denoted by $K_1,\ldots , K_s,K_{s+1},\ldots ,K_t$, where $K_j$, $j\in \{1,\ldots ,s\}$, is such that one of the cycles in $H|_{K_j\cup \{i\}}$ contains i, and where $K_j$, $j\in \{s+1,\ldots ,t\}$, is such that no cycle in $H|_{K_j\cup \{i\}}$, if any, contains i. For $j=1,\ldots ,t,$ let $c_j$ denote the number of cycles in $H|_{K_j}$, then $\sum _{j=1}^s (c_j + 1) + \sum _{j=s+1}^t c_j = c$ and $0\le c_j <c$ for all $j\in \{1,\ldots ,t\}$. Note that $t\ge 2$ when $s=0$, because $\bar{S}^T_i$ is the minimal successor set in T whose induced subgraph contains all cycles in H.

Let $F^T_i=\{j\in S^T_i\mid i,j \in e,~ e\in H|_{{\bar{S}}_i^T}\}$ be the set of successors of i in T that are adjacent to i in $H|_{{\bar{S}}_i^T}$. Note that $F^{T'}_i=F^{T}_i$ for all $T'\in \mathcal{T}_r^H(N)$ and therefore denote this set by $F_i$. Since H is a linear cactus, it holds that $|K_j\cap F_i|=2$ for $j=1,\ldots ,s$ and $|K_j\cap F_i|=1$ for $j=s+1,\ldots ,t$. For $j\in \{1,\ldots ,s\}$ and with $K_j\cap F_i=\{h,k\}$, it follows from the induction argument and the fact that $H|_{K_j}$ is itself a linear cactus with $c_j<c$ cycles that $|\mathcal{T}_h^H(K_j)| =2^{c_j}$ and $|\mathcal{T}_k^H(K_j)| =2^{c_j}$, and therefore $|\mathcal{T}_i^H(K_j\cup \{i\})|=2^{c_j+1}$. For $j\in \{s+1,\ldots ,t\}$ and with $K_j\cap F_i=\{h\}$, it follows from the induction argument and the fact that $H|_{K_j}$ is itself a linear cactus with $c_j<c$ cycles that $|\mathcal{T}_h^H(K_j)|=2^{c_j}$, and therefore $|\mathcal{T}_i^H(K_j\cup \{i\})|=2^{c_j}$. Since the rooted trees in ${\mathcal T}_i^H(K_j\cup \{i\})$, $j=1,\ldots ,t$, can be chosen in any combination to be the rooted subtrees with root i of admissible rooted spanning trees in ${{\mathcal {T}}}_i^H({{\bar{S}}}^T_i)$, it holds that

$$\begin{aligned} |{{\mathcal {T}}}_i^H({{\bar{S}}}^T_i)|=\prod _{j=1}^t |{{\mathcal {T}}}_i^H(K_j\cup \{i\})|=2^c. \end{aligned}$$

This shows that $|\mathcal{T}^H_r(N)|=2^c$ for all $r\in N$ and therefore $|\mathcal {T}^H(N)|=\sum _{r\in N}|\mathcal {T}^H_r(N)|=2^c n$. Hence, for a hypergraph game $(v,H)\in \mathcal {G}_N^{\mathcal{H}}$ with H being a linear cactus with c cycles, it holds that

$$\begin{aligned} TAT(v,H)= & {} \frac{1}{ n}\sum _{r\in N}\frac{1}{2^c}\sum _{T\in \mathcal {T}_r^H(N)}m^T(v,H)\\= & {} \frac{1}{2^c n}\sum _{T\in \mathcal {T}^H(N)}m^T(v,H)\\= & {} AT(v,H). \end{aligned}$$

Finally, for a graph game $(v,\Gamma ^N)\in \mathcal {G}_N^{{\varGamma }}$ with complete graph it holds that $|\mathcal {T}^{\Gamma ^N}_r(N)|=(n-1)!$ for all $r\in N$ and $|\mathcal {T}^{\Gamma ^N}(N)|=n!$ and therefore

$$\begin{aligned} TAT(v,\Gamma ^N)= & {} \frac{1}{n}\sum _{r\in N}\frac{1}{(n-1)!}\sum _{T\in \mathcal {T}_r^{\Gamma ^N}(N)}m^T(v,\Gamma ^N)\\= & {} \frac{1}{n!}\sum _{T\in \mathcal {T}^{\Gamma ^N}(N)}m^T(v,\Gamma ^N)\\= & {} AT(v,\Gamma ^N). \end{aligned}$$

$\square$

If the underlying communication structure is the complete graph, the TAT and AT values for a graph game $(v,\Gamma ^N)\in \mathcal {G}_N^{{\varGamma }}$ coincide with the Shapley value for the TU game v.

4 Properties of the two-step average tree value

In this section we discuss several properties of the two-step average tree value for hypergraph games and make a comparative analysis with the properties of the average tree value. We show that on the entire class of hypergraph games the TAT value satisfies component efficiency, the total cooperation equal treatment property, and component fairness. The latter two are extensions of properties that hold for the AT value only on specific subclasses of hypergraph games. We further introduce the property of equal surplus of interactive players and show that on the entire class of hypergraph games both the TAT and AT values satisfy this property.

Similar to the AT value and most other values, the TAT value for hypergraph games on any subclass of hypergraph games satisfies the standard property of component efficiency.

• A value $\xi$ on $\mathcal {G}\subseteq \mathcal {G}_N^{\mathcal{H}}$ satisfies component efficiency (CE), if for every $(v,H)\in \mathcal {G}$ it holds that

  $$\begin{aligned} \sum _{i\in K}\xi _i(v,H)=v(K),\quad \text { for all }K\in N/H. \end{aligned}$$

CE requires that in every component of a hypergraph game its worth is fully distributed as payoff amongst its members.

Theorem 2

The two-step average tree value on any $\mathcal {G}\subseteq \mathcal {G}_N^\mathcal{H}$ satisfies component efficiency.

Proof

Take any $(v,H)\in \mathcal {G}$ and $K\in N/H$. From (1) it follows that $\sum _{i\in K}m_i^{T}(v,H)=v(K)$ for all $T\in \mathcal {T}^H(K)$. Hence,

$$\begin{aligned} \sum _{i\in K}TAT_i(v,H)= & {} \sum _{i\in K}\frac{1}{|K|}\sum _{r\in K}\frac{1}{| \mathcal {T}_r^H(K)|}\sum _{T\in \mathcal {T}_r^H(K)}m_i^{T}(v,H)\\= & {} \frac{1}{|K|}\sum _{r\in K}\frac{1}{| \mathcal {T}_r^H(K)|}\sum _{T\in \mathcal {T}_r^H(K)}\sum _{i\in K}m_i^{T}(v,H)\\= & {} \frac{1}{|K|}\sum _{r\in K}\frac{1}{| \mathcal {T}_r^H(K)|}\sum _{T\in \mathcal {T}_r^H(K)}v(K) \, =\, v(K). \end{aligned}$$

$\square$

The TAT value for hypergraph games on the entire class of hypergraph games satisfies also the total cooperation equal treatment property, introduced in Kang et al. (2021) for the class of hypertree games as a property of the AT value on that class.

• A value $\xi$ on $\mathcal {G}\subseteq \mathcal {G}_N^{\mathcal{H}}$ satisfies the total cooperation equal treatment property (TCETP), if for every $(v,H)\in \mathcal {G}$ and $K\in N/H$ satisfying $v(S)=0$ for all $S\in C^H(K)$, $S\ne K$, it holds that $\xi _i(v,H)=\xi _j(v,H)$ for all $i,j\in K$.

TCETP requires that if every connected proper subcoalition of a component in the hypergraph has worth zero, then all players in the component get the same payoff. This is a quite natural property of fair division, which reflects the situation when cooperation within a component is rewarding only if all players that belong to the component are present, i.e., the presence of each player within the component is needed to obtain some worth, and, therefore, all players of the component are rewarded by the same payoff.

Theorem 3

The two-step average tree value on any $\mathcal {G}\subseteq \mathcal {G}_N^\mathcal{H}$ satisfies the total cooperation equal treatment property.

Proof

Take any $(v,H)\in \mathcal {G}$ and $K\in N/H$ satisfying $v(S)=0$ for all $S\in C^H(K)$, $S\ne K$. By (1), for every $T\in \mathcal{T}^H(K)$ it holds that

$$\begin{aligned} m_i^{T}(v,H)=\left\{ \begin{array}{ll} v(K), &{} i=r(T), \\ 0, &{} i \in K\setminus \{r(T)\}. \end{array} \right. \end{aligned}$$

From (4), we obtain

$$\begin{aligned} TAT_i(v,H)=\frac{v(K)}{|K|},\quad \text { for all }i\in K. \end{aligned}$$

$\square$

The next example shows that the AT value does not meet TCETP.

Example 2

Consider a graph game $(v,\Gamma )\in \mathcal {G}_N^{\varGamma }$ on a set N of 4 players with $v=u_N$ and $\Gamma$ as in Example 1. For every $T\in \mathcal {T}^\Gamma (N)$ it holds that

$$\begin{aligned} m_i^{T}(v,\Gamma )=\left\{ \begin{array}{ll} 1, &{} i=r(T), \\ 0, &{} i \ne r(T). \end{array} \right. \end{aligned}$$

Then $TAT(v,\Gamma ){\mathop {=}\limits ^{(5)}}(\frac{1}{4},\frac{1}{4},\frac{1}{4},\frac{1}{4})$ and $AT(v,\Gamma ){\mathop {=}\limits ^{(3)}}(\frac{3}{14},\frac{2}{7},\frac{3}{14},\frac{2}{7})$.

Further, the TAT value for hypergraph games on the entire class of hypergraph games meets component fairness, introduced in Herings et al. (2008) for the class of cycle-free graph games as a property of the AT solution on that subclass and generalized in Kang et al. (2021) for the class of cycle-free hypergraph games as a property of the AT value on that subclass. To adapt component fairness for the entire class of hypergraph games we use the following axiom.

• A value $\xi$ on $\mathcal {G}\subseteq \mathcal {G}_N^{\mathcal{H}}$ satisfies component fairness (CF), if for every $(v,H)\in \mathcal {G}$ and bridge $e\in H$ it holds that

  $$\begin{aligned} \frac{1}{|K|}\sum _{i\in K} \big (\xi _i(v,H)-\xi _i(v,H\backslash \{e\})\big )= \frac{1}{|K'|}\sum _{i\in K'} \big (\xi _i(v,H)-\xi _i(v,H\backslash \{e\})\big ), \end{aligned}$$

  for all distinct $K, K'\in N/(H\backslash \{e\})$ satisfying $K\cap e\ne \emptyset$ and $K'\cap e\ne \emptyset$.

Component fairness requires that when deleting a bridge in the hypergraph underlying a hypergraph game, the average payoff difference is the same for each resulting component. When a bridge in a hypergraph is deleted, the component that contains the bridge splits into two or more components. It is a well-known property in graph theory that a graph is cycle-free if and only if all its links are bridges. For hypergraphs it holds true also that all hyperlinks of a cycle-free hypergraph are bridges, but the reverse is not correct, for example, as the next Lemma 1 shows, every hyperlink of a quasi-cycle-free hypergraph is a bridge.

A hypergraph $H\in \mathcal{H}_N$ is quasi-cycle-free if there exists a cycle-free hypergraph $H' \in \mathcal{H}_{N'}$ for some $N'$ satisfying the following conditions:

(i):

$N'\subseteq N$ and $|H'|=|H|$;

(ii):

$e'\in H'$ if and only if $e'=e\cap N'$ for some $e\in H$;

(iii):

For every $j\in N\setminus N'$ it holds that $|H_j|\ge 2$ and $j\in e_1\cap e_2$ for some $e_1,e_2\in H$, $e_1\ne e_2$, implies $e'_1\cap e'_2\ne \emptyset$, where $e'_1=e_1\cap N'$ and $e'_2=e_2\cap N'$.

From the definition it follows immediately that a cycle-free hypergraph is quasi-cycle-free. A quasi-cycle-free hypergraph is derived from a cycle-free hypergraph by adding players, if any, to the intersection of hyperlinks. The added players do not change the hyperlink structure of the original cycle-free hypergraph. In general a quasi-cycle-free hypergraph may contain cycles, but on the subclass of graphs every quasi-cycle-free graph is cycle-free.

Figure 3 depicts in (b) a quasi-cycle-free hypergraph H that is not cycle-free and is induced by the cycle-free hypergraph $H'$ depicted in (a). In $e_1\cap e_2$ one player and in $e_1\cap e_3$ two players from $N\setminus N'$ are added to the single player from $N'$ in $e'_1\cap e'_2\cap e'_3$. Since $|e_1\cap e_2|=2$ and $|e_1\cap e_3|=3$, H is not linear, and therefore, has cycles.

Fig. 3

Cycle-free $H'$ and quasi-cycle-free H induced by $H'$

The class of quasi-cycle-free hypergraph games on player set N is denoted by $\mathcal {G}_N^{\mathcal{H}^{qcf}}$. For quasi-cycle-free hypergraphs we have the following property.

Lemma 1

Every hyperlink of a quasi-cycle-free hypergraph is a bridge.

Proof

Suppose there exist a quasi-cycle-free hypergraph $H\in \mathcal{H}_N$ and a hyperlink $e\in H$ that is not a bridge in H, i.e., $|N/H|=|N/(H\setminus \{e\})|$. Let $K\in N/H$ be such that $e\in H|_K$. Then $|N/H|=|N/(H\setminus \{e\})|$ implies that $K\in N/(H\setminus \{e\})$, and therefore, K is connected in $H\setminus \{e\}$. Let $H'$ on $N'$ be a cycle-free hypergraph inducing H. Let $e'=e\cap N'$, then $e'\in H'$ and therefore $|e'|\ge 2$. Take any distinct $i,j\in e'$. Since K is connected in $H\setminus \{e\}$, there exists a chain $(i_1,e_1,i_2,\ldots ,i_{k-1},e_{k-1},i_k)$ in $H\setminus \{e\}$ between i and j satisfying $i_1=i$, $i_k=j$, and $e_t\ne e$ for all $t\in \{1,\ldots ,k-1\}$. Let $i'_1=i$, $i'_k=j$, $e'_t=e_t\cap N'$ for all $t\in \{1,\ldots ,k-1\}$, and $i'_t\in e'_t\cap e'_{t-1}$ for all $t\in \{2,\ldots ,k-1\}$. Because $H'$ is an inducing cycle-free hypergraph for H and $e_1,\ldots ,e_{k-1}$ are distinct hyperlinks in $H\setminus \{e\}$, $e'_1,\ldots ,e'_{k-1}$ are distinct hyperlinks in $H'\setminus \{e'\}$ and $e'_t\ne e'$ for all $t\in \{1,\ldots ,k-1\}$. If all $i'_1,\ldots ,i'_k$ are distinct, the sequence $(i'_1,e'_1,i'_2\ldots ,i'_{k-1},e'_{k-1},i'_k,e',i'_1)$ is a cycle in $H'$, which contradicts that $H'$ is cycle-free. If not all $i'_1,\ldots ,i'_k$ are distinct, we obtain a chain in $H'\setminus \{e'\}$ between i and j by replacing in the sequence any subsequence between two identical players by this player. By adding $e'$ to this chain we obtain a cycle in $H'$, which again contradicts that $H'$ is cycle-free. $\square$

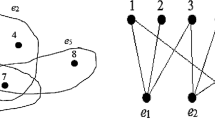
Remark that the set of hypergraphs with every hyperlink being a bridge is not exhausted by the subclass of quasi-cycle-free hypergraphs. In every hypergraph each hyperlink of which contains at least one player that belongs only to this hyperlink all hyperlinks are bridges. An example of such a not quasi-cycle-free hypergraph is $H=\{e_1,e_2,e_3\}$ on a set N of 6 players, where $e_1=\{1,2,4\}$, $e_2=\{2,3,5\}$, and $e_3=\{3,1,6\}$, as depicted in Fig. 4.

Fig. 4

A not quasi-cycle-free hypergraph with every hyperlink being a bridge

The next theorem states that the TAT value for hypergraph games satisfies CF.

Theorem 4

The two-step average tree value on any $\mathcal {G}\subseteq \mathcal {G}_N^\mathcal{H}$ satisfies component fairness.

Proof

Take any $(v,H)\in \mathcal {G}$ and bridge $e\in H$. Let $K\in N/H$ be such that $e\in H|_K$. Since e is a bridge in $H|_K$, K consists of at least two components in $H\setminus \{e\}$, denoted by $K_1,\ldots ,K_m$ for some $m\ge 2$. From (1) it follows that for every $T\in \mathcal {T}^H_r(K)$, $r\in K$, and $j\in \{1,\ldots ,m\}$, it holds that

$$\begin{aligned} \sum _{i\in K_j}m_i^{T}(v,H)=v(K)-\sum _{h\ne j}v(K_h), \,\text { if } r\in K_j, \end{aligned}$$

and

$$\begin{aligned} \sum _{i\in K_j}m_i^{T}(v,H)=v(K_j),\, \text { if } r\in K\setminus K_j. \end{aligned}$$

Therefore, for every $j\in \{1,\ldots ,m\}$,

$$\begin{aligned} \sum _{r\in K_j}\frac{1}{|\mathcal {T}_r^{H}(K)|}\sum _{T\in \mathcal {T}_r^{H}(K)}\sum _{i\in K_j}m^{T}_i(v,H)=|K_j|\big (v(K)-\sum _{h\ne j}v(K_h)\big ) \end{aligned}$$

and

$$\begin{aligned} \sum _{r\in K\setminus K_j}\frac{1}{|\mathcal {T}_r^{H}(K)|}\sum _{T\in \mathcal {T}_r^{H}(K)}\sum _{i\in K_j}m^{T}_i(v,H)=|K\setminus K_j|v(K_j). \end{aligned}$$

From (4) it follows that for every $j\in \{1,\ldots ,m\}$,

$$\begin{aligned} \sum _{i\in K_j}TAT_i(v,H)=\frac{|K_j|\big (v(K)-\sum _{h\ne j}v(K_h)\big )+|K\setminus K_j|v(K_j)}{|K|}, \end{aligned}$$

and therefore,

$$\begin{aligned} \frac{1}{|K_j|}\big (\sum _{i\in K_j}TAT_i(v,H)-v(K_j)\big )=\frac{v(K)-\sum _{h=1}^m v(K_h)}{|K|}. \end{aligned}$$

From CE of the TAT value it follows that

$$\begin{aligned} v(K_j)=\sum _{i\in K_j}TAT_i(v,H\setminus \{e\}), \end{aligned}$$

which together with the previous equality implies

$$\begin{aligned} \frac{1}{|K_j|}\sum _{i\in K_j}\big (TAT_i(v,H)-TAT_i(v,H\setminus \{e\})\big )=\frac{v(K)-\sum _{h=1}^m v(K_h)}{|K|}. \end{aligned}$$

Since the right side is independent of j, this completes the proof. $\square$

The next example shows that the AT value on $\mathcal {G}_N^{\mathcal{H}^{qcf}}$ does not meet CF.

Fig. 5

Quasi-cycle-free hypergraph H in Example 3

Example 3

Consider a quasi-cycle-free hypergraph game (v, H) on a set N of 4 players with $H=\{e_1,e_2\}$, where $e_1=\{1,2,3\}$ and $e_2=\{2,3,4\}$, as depicted in Fig. 5.

H is induced by the cycle-free graph $H'=\{\{1,2\},\{2,4\}\}$ (or $\{\{1,3\},\{3,4\}\}$). H contains six admissible rooted spanning trees, as depicted in Fig. 6, $T^1_1$ and $T^2_1$ having player 1 as the root and at which player 1 receives marginal contribution $v(N)-v(N\setminus \{1\})$, $T_2$ having player 2 and $T_3$ having player 3 as the root and at both of which player 1 receives marginal contribution $v(\{1\})$, and $T^1_4$ and $T^2_4$ having player 4 as the root and at which player 1 receives also marginal contribution $v(\{1\})$.

Fig. 6

The admissible rooted spanning trees of H in Example 3

For player 1 we have

$$\begin{aligned} AT_1(v,H)= \frac{1}{3}\big (v(N)-v(N\setminus \{1\})+2\,v(\{1\})\big ) \end{aligned}$$

and

$$\begin{aligned} TAT_1(v,H)= \frac{1}{4}\big (v(N)-v(N\setminus \{1\})+3\,v(\{1\})\big ). \end{aligned}$$

Deleting $e_1$ from H splits N into the components $\{1\}$ and $N\setminus \{1\}$. If a value $\xi$ satisfies CF and CE on $\mathcal {G}_N^{\mathcal{H}^{qcf}}$, then

$$\begin{aligned} \xi _1(v,H)-v(\{1\})= & {} \frac{1}{|N\setminus \{1\}|}\sum _{i\in N\setminus \{1\}} \big (\xi _i(v,H)-\xi _i(v,H\backslash \{e_1\})\big )\\= & {} \frac{1}{3}\big (v(N)-\xi _1(v,H)-v(N\setminus \{1\})\big ), \end{aligned}$$

because CE implies that $\xi _1(v,H\backslash \{e_1\})=v(\{1\})$, $\sum \limits _{i\in N\setminus \{1\}}\xi _i(v,H)=v(N)-\xi _1(v,H)$, and $\sum \limits _{i\in N\setminus \{1\}}\xi _i(v,H\backslash \{e_1\})=v(N\setminus \{1\})$. Hence,

$$\begin{aligned} \xi _1(v,H)=\frac{1}{4}\big (v(N)-v(N\setminus \{1\})+3\,v(\{1\})\big ), \end{aligned}$$

which is equal to $TAT_1(v,H)$, but not equal to $AT_1(v,H)$.

Next, we introduce the concept of equal surplus of interactive players and show that both the AT value and the TAT value for hypergraph games satisfy this property on the entire $\mathcal{G}_N^H$.

• A value $\xi$ on $\mathcal {G}\subseteq \mathcal {G}_N^{H}$ satisfies equal surplus of interactive players (ESIP) if for every $(v,H)\in \mathcal {G}$ and interactive players i, j in H it holds that

  $$\begin{aligned} \xi _i(v,H)-v(\{i\})=\xi _j(v,H)-v(\{j\}). \end{aligned}$$

ESIP states that interactive players receive the same amount of payoff in addition to their own worth. This is a quite reasonable property of fair division because interactive players, being players that belong to the same set of hyperlinks, either can cooperate only in a coalition they all belong to, or all of them stay alone within their own singleton coalitions, and therefore they cannot be distinguished in their marginal contributions to any connected non-singleton coalition they belong to. In the next section ESIP is used together with CE and CF to characterize the TAT value on a specific subclass of quasi-cycle-free hypergraph games, of which the underlying hypergraphs still may contain cycles.

Before stating the next result, we introduce some additional notation. For a hypergraph $H\in \mathcal {H}_N$, component $K\in N/H$, $r \in K$, and pair $i,j \in K$, let

$$\begin{aligned} \mathcal {T}^H_{r,(i,j)}(K)=\{T\in \mathcal {T}_r^H(K)\mid j \in S^T_i\} \end{aligned}$$

be the subset of trees in $\mathcal {T}_r^H(K)$ in which j is a successor of i and let

$$\begin{aligned} \mathcal {T}^H_{r,\{i,j\}}(K)=\{T\in \mathcal {T}_r^H(K)\mid \bar{S}^T_j\cap \bar{S}^T_i=\emptyset \} \end{aligned}$$

be the subset of trees in $\mathcal {T}_r^H(K)$ in which neither i is a successor of j nor j is a successor of i. Note that $\mathcal {T}^H_{i,(j,i)}(K)=\mathcal {T}^H_{i,\{i,j\}}(K)=\emptyset$ and $\mathcal {T}^H_{i,(i,j)}(K)=\mathcal {T}_i^H(K)$, and that $\{\mathcal {T}^H_{r,(i,j)}(K),\mathcal {T}^H_{r,(j,i)}(K),\mathcal {T}^H_{r,\{i,j\}} (K)\}$ is a partition of $\mathcal {T}_r^H(K)$ for all $r\in K\setminus \{i,j\}$.

Lemma 2

For any $H\in \mathcal {H}_N$ and interactive in H players $i,j\in K$, $K\in N/H$, it holds that $|\mathcal {T}^H_{i}(K)|= |\mathcal {T}^H_{j}(K)|$ and $|\mathcal {T}^H_{r,(i,j)}(K)|=|\mathcal {T}^H_{r,(j,i)}(K)|$ for all $r\in K\setminus \{i,j\}$.

Proof

We first show that to every $T\in \mathcal {T}^H_{r,(i,j)}(K)$, $r\in K\setminus \{j\}$, there corresponds some $T'\in \mathcal {T}_j^H(K)$ if $r=i$ and $T'\in \mathcal {T}^H_{r,(j,i)}(K)$ if $r\in K\setminus \{i,j\}$. Recall that $\mathcal {T}^H_{i,(i,j)}(K)=\mathcal {T}_i^H(K)$. Since T is an admissible rooted spanning tree of $H|_K$, $H_i=H_j$, and $j\in S^T_i$, it holds that $(i,j)\in T$ and $\bar{S}^T_j=\{j\}$. Let the rooted tree $T'$ on K be given by

$$\begin{aligned} \bar{S}^{T'}_h=\left\{ \begin{array}{ll} \bar{S}^T_i, &{} \text { if } h=j,\\ \{i\}, &{} \text { if } h=i,\\ \bar{S}^T_h, &{} \text { if } h\in K\setminus \{i,j\}. \end{array} \right. \end{aligned}$$

(6)

Since $H_i=H_j$, we have that $(j,i)\in T'$ and therefore $T'\in \mathcal {T}_j^H(K)$ if $r=i$ and $T'\in \mathcal {T}^H_{r,(j,i)}(K)$ if $r\in K\setminus \{i,j\}$. Hence, $|\mathcal {T}^H_{i}(K)|\le |\mathcal {T}^H_{j}(K)|$ and $|\mathcal {T}^H_{r,(i,j)}(K)|\le |\mathcal {T}^H_{r,(j,i)}(K)|$ for all $r\in K\setminus \{i,j\}$. Because of symmetry between i and j the inequalities are equalities. $\square$

The lemma shows that for any pair of interactive players i and j in some component K in a hypergraph H, there are always pairwise two admissible rooted spanning trees T and $T'$ in $\mathcal {T}^H(K)$ for which only the sets of successors of i and j differ from each other. Therefore, the number of admissible rooted spanning trees for which i has j as successor equals the number of admissible rooted spanning trees for which j has i as successor.

Theorem 5

The two-step average tree value and the average tree value on any $\mathcal {G}\subseteq \mathcal {G}_N^\mathcal{H}$ satisfy equal surplus of interactive players.

Proof

Take any $(v,H)\in {{\mathcal {G}}}$ and pair of interactive players i, j in H. We will show that

$$\begin{aligned} TAT_i(v,H)-TAT_j(v,H)=v(\{i\})-v(\{j\}) \end{aligned}$$

and

$$\begin{aligned} AT_i(v,H)-AT_j(v,H)=v(\{i\})-v(\{j\}). \end{aligned}$$

Let $K\in N/H$ be such that $i,j\in K$, and let $B=\{h\in K\mid H_h=H_i\}$ be the set of interactive players in H that contains i and j.

First, take any $T\in \mathcal {T}^H_i(K)$. Since $\mathcal {T}_i^H(K)=\mathcal {T}^H_{i,(i,j)}(K)$, it holds that $T\in \mathcal {T}^H_{i,(i,j)}(K)$. Let $T'\in \mathcal {T}^H_{j,(j,i)}(K)$ be defined as in (6). Then, ${\bar{S}}^T_i={\bar{S}}^{T'}_j=K$, $\{h\}\in S^T_i/H$ for all $h\in B\setminus \{i\}$, and $\{h\}\in S^{T'}_j/H$ for all $h\in B\setminus \{j\}$. From (1) it follows that

$$\begin{aligned} m^T_i(v,H)=v(K)-\sum _{h\in B\setminus \{i\}}v(\{h\})-\sum _{S\in (K\setminus B)/H}v(S) \end{aligned}$$

and

$$\begin{aligned} m^{T'}_j(v,H)=v(K)-\sum _{h\in B\setminus \{j\}}v(\{h\})-\sum _{S\in (K\setminus B)/H}v(S), \end{aligned}$$

with difference $v(\{i\})-v(\{j\})$. Moreover, $m_i^{T'}(v,h)=v(\{i\})$ and $m_j^T(v,H)=v(\{j\})$, also with difference $v(\{i\})-v(\{j\})$. Since, by Lemma 2, $|\mathcal {T}^H_{i}(K)|= |\mathcal {T}^H_{j}(K)|$, we obtain

$$\begin{aligned} \frac{1}{|\mathcal {T}_i^{H}(K)|}\sum _{T\in \mathcal {T}_i^{H}(K)}m^{T}_i(v,H)-\frac{1}{|\mathcal {T}_j^{H}(K)|}\sum _{T\in \mathcal {T}_j^{H}(K)}m^{T}_j(v,H)=v(\{i\})-v(\{j\}) \end{aligned}$$

and

$$\begin{aligned} \frac{1}{|\mathcal {T}_j^{H}(K)|}\sum _{T\in \mathcal {T}_j^{H}(K)}m^{T}_i(v,H)-\frac{1}{|\mathcal {T}_i^{H}(K)|}\sum _{T\in \mathcal {T}_i^{H}(K)}m^{T}_j(v,H)=v(\{i\})-v(\{j\}). \end{aligned}$$

Next, take any $r\in K\setminus \{i,j\}$ and $T\in \mathcal {T}^H_{r,(i,j)}(K)$, and let $T'\in \mathcal {T}^H_{r,(j,i)}(K)$ be as defined in (6). Then, ${\bar{S}}^T_i={\bar{S}}^{T'}_j$, $\{h\}\in S^T_i/H$ for all $h\in B\setminus \{i\}$, and $\{h\}\in S^{T'}_j/H$ for all $h\in B\setminus \{j\}$. From (1) it follows that

$$\begin{aligned} m^T_i(v,H)=v({{\bar{S}}}^T_i)-\sum _{h\in B\setminus \{i\}}v(\{h\})-\sum _{S\in ({{\bar{S}}}^T_i\setminus B)/H}v(S) \end{aligned}$$

and

$$\begin{aligned} m^{T'}_j(v,H)=v({{\bar{S}}}^{T'}_j)-\sum _{h\in B\setminus \{j\}}v(\{h\})-\sum _{S\in ({{\bar{S}}}^{T'}_j\setminus B)/H}v(S), \end{aligned}$$

with difference $v(\{i\})-v(\{j\})$. Moreover, $m_i^{T'}(v,H)=v(\{i\})$ and $m_j^T(v,H)=v(\{j\})$, also with difference $v(\{i\})-v(\{j\})$. And, if we take any $T\in \mathcal {T}^H_{r,\{i,j\}}(K)$, then there exists $h\in K\setminus \{i,j\}$ satisfying $\{i\},\{j\}\in S^T_h/H$ and therefore $m_i^{T}(v,H)=v(\{i\})$ and $m_j^T(v,H)=v(\{j\})$, again with difference $v(\{i\})-v(\{j\})$. Since for every $r\in K\setminus \{i,j\}$ it holds that $\{\mathcal {T}^H_{r,(i,j)}(K),\mathcal {T}^H_{r,(j,i)}(K),\mathcal {T}^H_{r,\{i,j\}}(K)\}$ is a partition of $\mathcal {T}_r^H(K)$ and, by Lemma 2, $|\mathcal {T}^H_{r,(i,j)}(K)|=|\mathcal {T}^H_{r,(j,i)}(K)|$, we obtain

$$\begin{aligned} \frac{1}{|\mathcal {T}_r^{H}(K)|}\sum _{T\in \mathcal {T}_r^{H}(K)}m^{T}_i(v,H)-\frac{1}{|\mathcal {T}_r^{H}(K)|}\sum _{T\in \mathcal {T}_r^{H}(K)}m^{T}_j(v,H)=v(\{i\})-v(\{j\}) \end{aligned}$$

for all $r\in K\setminus \{i,j\}$.

Taking the average of the |K| differences derived above, we obtain $TAT_i(v,H)-TAT_j(v,H)=v(\{i\})-v(\{j\})$.

In a similar way, we obtain

$$\begin{aligned} \frac{1}{|\mathcal {T}^{H}(K)|}\sum _{T\in \mathcal {T}^{H}(K)}m^{T}_i(v,H)-\frac{1}{|\mathcal {T}^{H}(K)|}\sum _{T\in \mathcal {T}^{H}(K)}m^{T}_j(v,H)=v(\{i\})-v(\{j\}), \end{aligned}$$

which, by (2), implies that $AT_i(v,H)-AT_j(v,H)=v(\{i\})-v(\{j\})$. $\square$

5 An axiomatization

Since according to Theorem 1 the TAT and AT values coincide on the class of cycle-free (hyper)graph games, the axiomatic characterizations of the AT value for cycle-free (hyper)graph games known in the literature, e.g., see Kang et al. (2021), are also valid for the TAT value.

Below, we obtain an axiomatization of the TAT value on the class of semi-cycle-free hypergraph games, the underlying hypergraphs of which may contain cycles.

A hypergraph $H\in \mathcal{H}_N$ is semi-cycle-free if there exists a cycle-free hypergraph $H' \in \mathcal{H}_{N'}$ for some $N'$ satisfying the following conditions:

(i):

$N'\subseteq N$ and $|H'|=|H|$;

(ii):

$e'\in H'$ if and only if $e'=e\cap N'$ for some $e\in H$;

(iii):

For every $j\in N\setminus N'$ it holds that $|H_j|\ge 2$ and $H_j=H_i$ for some $i\in N'$.

Obviously, a cycle-free hypergraph is semi-cycle-free and a semi-cycle-free hypergraph is quasi-cycle-free. A semi-cycle-free hypergraph H is derived from a cycle-free hypergraph $H'$ by adding players, if any, which become interactive with a connective player in $N'$. The added players do not change the hyperlink structure of the original cycle-free hypergraph.

Figure 7 depicts in (b) a semi-cycle-free hypergraph H with cycles induced by the cycle-free hypergraph $H'$ depicted in (a). In $e_1\cap e_2$ one player from $N\setminus N'$ is added to be interactive with the single player from $N'$ in $e'_1\cap e'_2$, and in $e_1\cap e_3$ two players from $N\setminus N'$ are added to be interactive with the single player from $N'$ in $e'_1\cap e'_3$.

Fig. 7

Cycle-free $H'$ and semi-cycle-free H induced by $H'$

The additional players in a semi-cycle-free hypergraph H belong to the same hyperlinks as the players they join in the inducing cycle-free hypergraph $H'$, while this property does not necessarily hold for the additional players in a quasi-cycle-free hypergraph, as is illustrated by Fig. 8.

Fig. 8

Three types of hypergraphs

The class of semi-cycle-free hypergraph games on player set N is denoted by $\mathcal {G}_N^{\mathcal{H}^{scf}}$. The next theorem shows that the TAT value for semi-cycle-free hypergraph games is characterized by CE, CF, and ESIP.

Theorem 6

The two-step average tree value is the unique value on $\mathcal {G}_N^{\mathcal{H}^{scf}}$ that satisfies component efficiency, component fairness, and equal surplus of interactive players.

Proof

From Theorems 2, 4, and 5 it follows that on $\mathcal {G}_N^{\mathcal{H}^{scf}}$ the TAT value satisfies CE, CF, and ESIP, respectively.

To prove the reverse, let $\xi$ be a value on $\mathcal {G}_N^{\mathcal{H}^{scf}}$ that satisfies CE, CF, and ESIP. We show that for any $(v,H)\in \mathcal {G}_N^{\mathcal{H}^{scf}}$ these three properties induce for every $K\in N/H$ a system of |K| linearly independent equations in |K| unknowns, which uniquely determines $(\xi _i(v,H))_{i\in K}$.

Take any $K\in N/H$. If $|K|=1$, let $K=\{i\}$, then CE implies $\xi _i(v,H)=v(\{i\})$. Assume $|K|\ge 2$, then $H|_K\ne \emptyset$. Let $H'\in \mathcal {H}_{N'}$ be a cycle-free hypergraph by which H is induced and let $K'=K\cap N'$, so $K'\in N'/H'$. For $h\in K'$, define $B_h=\{h\}$ if $|H_h|=1$ and $B_h=\{i\in K\mid H_i=H_h\}$ if $|H_h|\ge 2$. Note that

$$\begin{aligned} |K|=|K'|+\sum _{h\in K'}(|B_h|-1). \end{aligned}$$

For $e\in H|_K$, define $p_e=|K/(H\backslash \{e\})|$ and let $e'=e\cap N'$. Since H is semi-cycle-free and induced by $H'$, it holds that $e'\in H'$ and $p_e= |K'/(H'\backslash \{e'\})|$. Cycle-freeness of $H'$ implies that $|K'/(H'\backslash \{e'\})|=|e'|$, and therefore $p_e=|e'|$. Moreover, since $H'$ is cycle-free, from Proposition 4 on page 392 in Berge (1973) it follows that

$$\begin{aligned} \sum _{e'\in H'|_{K'}}(|e'|-1)=|K'|-1, \end{aligned}$$

and therefore

$$\begin{aligned} \sum _{e\in H|_K}(p_e-1)=|K'|-1. \end{aligned}$$

From CE and CF of $\xi$ we first derive a system of $1+\sum _{e\in H|_K}(p_e-1)=|K'|$ linearly independent equations, which uniquely determines $\sum _{i\in B_h} \xi _i(v,H)$ for all $h\in K'$. CE of $\xi$ implies that

$$\begin{aligned} \sum _{i\in K} \xi _i(v,H)=v(K) \end{aligned}$$

(7)

and for every $e\in H|_K$,

$$\begin{aligned} \sum _{i\in {\widehat{K}}}\xi _i(v,H\setminus \{e\})=v({\widehat{K}}), \,\text {for all }{\widehat{K}}\in K/(H\backslash \{e\}). \end{aligned}$$

(8)

CF of $\xi$ together with (8) implies that for each $e\in H|_K$,

$$\begin{aligned} \frac{1}{|K_1|}\big (\sum _{i\in K_1}\xi _i(v,H)-v(K_1)\big )=\frac{1}{|K_2|}\big (\sum _{i\in K_2}\xi _i(v,H)-v(K_2)\big ), \end{aligned}$$

for every $K_1, K_2 \in K/(H\setminus \{e\}).$ Note that $\widehat{K}\cap e\ne \emptyset$ for all ${\widehat{K}} \in K/(H\backslash \{e\})$. Hence, for each $e\in H|_K$,

$$\begin{aligned} \sum _{i\in {\widehat{K}}}\xi _i(v,H)=|{\widehat{K}}|\alpha _e+v(\widehat{K}),\,\text {for all }{\widehat{K}}\in K/(H\backslash \{e\}), \end{aligned}$$

(9)

where

$$\begin{aligned} \alpha _e=\frac{1}{|K|}\big (v(K)-\sum _{S\in K/(H\setminus \{e\})}v(S)\big ). \end{aligned}$$

Note that if $H_i=H_j=\{e\}$ for some $i,j\in K$, then (9) implies

$$\begin{aligned} \xi _i(v,H)-v(\{i\})=\xi _j(v,H)-v(\{j\}), \end{aligned}$$

which also follows from ESIP of $\xi$.

Equation (7) together with any $p_e-1$ of the $p_e$ equations in (9) for every $e\in H|_K$ yields a system of $1+\sum _{e\in H|_K}(p_e-1)=|K'|$ linearly independent equations with |K| unknowns. Since for each $e\in H|_K$ and $h\in K'$ it holds that $B_h\subseteq {\widehat{K}}$ for some ${\widehat{K}} \in K/(H\backslash \{e\})$, this system uniquely determines for every $h\in K'$ the total payoff of the players in $B_h$, i.e.,

$$\begin{aligned} \sum _{i\in B_h}\xi _i(v,H)=c_h, \end{aligned}$$

(10)

for some constant $c_h$.

Next, we examine the payoffs of the players in $B_h$ for any $h\in K'$. When $|B_h|=1$, the payoff of the unique player in $B_h$ is determined by equation (10). When $|B_h|\ge 2$, ESIP of $\xi$ implies that for every pair $i,j\in B_h$

$$\begin{aligned} \xi _i(v,H)-v(\{i\})=\xi _j(v,H)-v(\{j\}), \end{aligned}$$

yielding a system of $|B_h|-1$ linearly independent equations in $|B_h|$ unknowns. Combined with equation (10), these equations uniquely determine the payoff of each player in $B_h$, which completes the proof. $\square$

Example 3 above shows in particular that the AT value does not satisfy CF on $\mathcal {G}_N^{\mathcal{H}^{scf}}$, because the hypergraph in Example 3 is not only quasi-cycle-free but also semi-cycle-free.

The logical independence of the axioms in the characterization of the TAT value in Theorem 6 is demonstrated by the next example.

Example 4

• (1) Let the value $\xi ^1$ on $\mathcal {G}_N^{\mathcal{H}^{scf}}$ be given by

  $$\begin{aligned} \xi ^1_i(v,H)=v(\{i\}),\quad \text { for all } i\in N. \end{aligned}$$

  This value satisfies CF and ESIP, but not CE.

• (2) Let the value $\xi ^2$ on $\mathcal {G}_N^{\mathcal{H}^{scf}}$ be the AT value. This value satisfies CE and ESIP, but not CF, see Example 3.

• (3) Let the value $\xi ^3$ on $\mathcal {G}_N^{\mathcal{H}^{scf}}$ be given by

  $$\begin{aligned} \xi ^3_i(v,H)=\left\{ \begin{array}{ll} TAT_i(v,H), &{} \text { if } i\in N\setminus B,\\ \displaystyle {\frac{1}{|B|}\,\sum \limits _{j\in B}TAT_j(v,H)},&{} \text { if } i\in B, \end{array}\right. \end{aligned}$$

  where B is one of the sets of connective interactive players in H, if any. This value satisfies CE and CF, but not ESIP.

6 Core stability

In this section we study the core stability of the TAT value. The core of a hypergraph game is the set of payoff vectors that are component efficient and at which every connected coalition gets at least its own worth. Formally, the core of a hypergraph game $(v,H)\in \mathcal{G}_N^\mathcal{H}$ is given by

$$ \begin{aligned} C(v,H)=\Bigl \{x\in \mathrm{I\!R}^n\mid \Bigl [\sum \limits _{i\in K}x_i=v(K), \,\forall K\in N/H\Bigr ]\ \& \ \Bigl [\sum \limits _{i\in S}x_i\ge v(S), \,\forall S\in C^H(N)\Bigr ]\Bigr \}. \end{aligned}$$

Note that since $S\in C^H(N)$ if and only if $S\in C^{H|_K}(K)$ for some $K\in N/H$, it holds that

$$\begin{aligned} C(v,H)=\Bigl \{x\in \mathrm{I\!R}^n\mid (x_i)_{i\in K}\in C(v|_K,H|_K),\,\forall K\in N/H\Bigr \}. \end{aligned}$$

In Kang et al. (2021) it is shown that the AT value is core stable on the subclass of superadditive cycle-free hypergraph games. Since the TAT and AT values coincide on the entire class of cycle-free hypergraph games, this implies that the TAT value also is core stable on the subclass of superadditive cycle-free hypergraph games. We prove below that furthermore both the AT and TAT values are core stable on the wider class of superadditive semi-cycle-free hypergraph games.

Theorem 7

For any superadditive hypergraph game $(v,H)\in \mathcal {G}_N^{\mathcal{H}^{scf}}$ it holds that AT(v, H), $TAT(v,H)\in C(v,H)$.

Proof

First we prove that for any $K\in N/H$ and $T\in \mathcal{T}^H(K)$ it holds that $(m_i^T(v,H))_{i\in K}\in C(v|_K,H|_K)$. From (1) it immediately follows that $\sum _{i\in K}m_i^T(v,H)=v(K)$. We show now that $\sum _{i\in S}m_i^T(v,H)\ge v(S)$ for any $S\in C^{H|_K}(K)$.

If $S=\{i\}$, then from (1) and superadditivity of (v, H) it follows that $m_i^T(v,H)\ge v(\{i\})$. Assume $|S|\ge 2$. Since S is connected in $H|_K$ and T is an admissible rooted spanning tree of $H|_K$, there exists a unique $\ell \in S$ satisfying $S\subseteq \bar{S}^T_\ell$. Let ${\widehat{S}}^T_S=\{j\in K\setminus S\mid (i,j)\in T,\, i\in S\}$ be the set of immediate successors of S in T not in S. To apply superadditivity of (v, H), we prove that $\bar{S}^T_\ell$ is partitioned into the connected coalitions S and $\bar{S}^T_j$, $j\in {\widehat{S}}^T_S$. Suppose that $\bar{S}^T_j\cap S\ne \emptyset$ for some $j\in {\widehat{S}}^T_S$. Since $j \notin S$, there exists $k\in \bar{S}^T_j\cap S$ such that the directed path in T from j to k contains no other players in S than k. Let $h\in S$ be the immediate predecessor of j in T. Note that $H_h\ne H_j$ because $h\in S$ and $j\notin S$. The directed path in T from h to k induces a chain $(i_1,e_1,i_2,e_2,\ldots ,i_{r-1},e_{r-1},i_r)$ for some $r\ge 3$ in $H\setminus H|_S$ between $i_1=h$ and $i_r=k$, both in S, satisfying $i_2=j$ and $i_s\notin S$ for all $s\in \{2,\ldots ,r-1\}$. Moreover, since S is connected in $H|_K$, there exists a chain $(i_r,e_{r},i_{r+1},e_{r+1},\ldots ,i_{t-1},e_{t-1},i_t)$ for some $t\ge r+1$ in $H|_S$ between $i_r=k$ and $i_t=h$. Since $t\ge 3$ and $i_s\notin S$ for all $s\in \{2,\ldots ,r-1\}$, the sequence $(i_1,e_1,i_2,e_2,\ldots ,i_{t-1},e_{t-1},i_t)$ is a cycle in H with $i_1=i_t=h$ and containing $j\notin S$.

Let $H'$ on $N'$ be a cycle-free hypergraph inducing H. Let $h'=h$ if $h\in N'$ and otherwise let $h'$ be the unique player in $N'$ interactive with h in H. Similarly, let $j'=j$ if $j\in N'$ and otherwise let $j'$ be the unique player in $N'$ interactive with j in H. Since $H_h\ne H_j$, it holds that $h'\ne j'$. Let $i'_1=i'_t=h'$, $e'_{s}=e_{s}\cap N'$ for all $s\in \{1,\ldots ,t-1\}$, and $i'_{s}\in e'_{s}\cap e'_{s-1}$ for all $s\in \{2,\ldots ,t-1\}$. Because $e_1,\ldots ,e_{t-1}$ are distinct hyperlinks in H, $e'_1,\ldots ,e'_{t-1}$ are distinct hyperlinks in $H'$. If all $i'_1,\ldots ,i'_{t-1}$ are distinct, the sequence $C=(i'_1,e'_1,i'_2,e'_2,\ldots ,i'_{t-1},e'_{t-1},i'_t)$ is a cycle in $H'$ containing at least $h'$ and $j'$ on its path, which contradicts that $H'$ is cycle-free. If not all $i'_1,\ldots ,i'_{t-1}$ are distinct, we obtain from C a cycle in $H'$ containing at least $h'$ and $j'$ on its path by replacing in the subsequence $(i'_1,e'_1,i'_2,e'_2,\ldots ,i'_{t-2},e'_{t-2},i'_{t-1})$ of C any subsequence between two identical players by this player, which again contradicts that $H'$ is cycle-free. Hence, $\bar{S}^T_j\cap S=\emptyset$ for all $j\in {\widehat{S}}^T_S$. Since T is an admissible rooted spanning tree of $H|_K$, this also implies that $\bar{S}^T_j\cap \bar{S}^T_{j'}=\emptyset$ for all distinct $j,j'\in {\widehat{S}}^T_S$.

Therefore, we have

$$\begin{aligned} \sum _{i\in S}m^T_i(v,H)= & {} \sum _{i\in S}\big (v(\bar{S}_i^T)-\sum _{j\in {\widehat{S}}^T_i}v(\bar{S}_j^T)\big )\\= & {} v(\bar{S}^T_\ell )-\sum _{j\in {\widehat{S}}^T_S} v(\bar{S}^T_{j})\\\ge & {} v(S), \end{aligned}$$

where the first equality follows from (1), the second equality follows because for every $i\in S\setminus \{\ell \}$ the term $v(\bar{S}_i^T)$ cancels, and the inequality follows from the superadditivity of (v, H) and the fact that the connected coalition $\bar{S}^T_\ell$ is partitioned into the connected coalitions S and $\bar{S}^T_j$, $j\in {\widehat{S}}^T_S$. Together with $\sum _{i\in K}m^T_i(v,H)=v(K)$, we obtain that $(m_i^T(v,H))_{i\in K}\in C(v|_K,H|_K)$.

Since, for every $K\in N/H$, $C(v|_K,H|_K)$ is a convex set and both $(TAT_i(v,H))_{i\in K}$ and $(AT_i(v,H))_{i\in K}$ are convex combinations of $(m^T_i(v,H))_{i\in K}$ over all $T\in \mathcal {T}^H(K)$, we obtain that both $(TAT_i(v,H))_{i\in K}$ and $(AT_i(v,H))_{i\in K}$ are elements of $C(v|_K,H|_K)$ for all $K\in N/H$, which completes the proof. $\square$