Abstract
We report a density functional theory study of ZnO cluster doped with Eu and Mg along with native point defects using the generalized gradient approximation including the Hubbard parameter. The Zn atomic positions are found to be energetically more favorable doping sites than O. The Eu has a lower formation energy than Zn and O vacancies, helps in lowering the formation energy of point defects and induces spin polarization. Mg is less favorable dopant energetically and is not inducing any magnetism in the cluster. Presence of Eu and point defects along with Mg can help in sustaining spin polarization, implying that transition metal and rare earth dopant is a favorable combination to invoke desirable properties in ZnO based materials. Eu–Eu doping pair prefers ferromagnetic orientation and a spin flip is induced by Eu in the Eu–Mg configuration. Further, Eu doping increases the value of static refractive index and optical absorption in the UV region compared to the undoped ZnO cluster.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Cluster science is an interesting area in materials research, as clusters are often envisaged as building blocks for nanoscale materials, starting “from the bottom up” wherein the properties can be tuned by varying the size and composition [1]. Clusters serve as ideal model systems with well-defined structures and selection rules, and in this size regime, quantum confinement effects come into play. Therefore, the interplay of structural, magnetic and electronic properties become prominent and can be tuned by the variation in size, composition and defects in the clusters [2, 3]. The occurrence of cluster geometries is widely reported for a range of materials that encompass dilute magnetic semiconductors as well. Among them, ZnO nanoparticles continue to attract significant attention from both academic and industrial researchers due to their unique properties, such as high exciton binding energy (60 meV), wide band gap, and cost-effective synthesis methods. These properties can be harnessed in a variety of applications such as environmental sensors, photodetectors and transistors based on ZnO quantum dots (QDs) [4,5,6]. Rare earth (RE) dopants have been known to affect the electronic structures of semiconductors in general [7,8,9,10,11,12,13,14,15]. In addition, formation of defect complexes involving RE elements has been shown to play a key role in the optoelectronic properties of ZnO [5]. Among the RE atoms, Eu is of special interest, as Eu-doped wide band gap semiconductors exhibit many potential optoelectronic applications because of the partially filled Eu 4f states that introduce remarkable optical characteristics [16,17,18]. Eu can be easily incorporated into the cation sites in ZnO nanoparticles [16, 19]. Eu-doped ZnO nanocrystals possessing high crystallinity that have been prepared by nano emulsion method exhibited changes in magnetic properties with concentration [20]. Moreover, Eu doping concentrations are shown to affect the size, crystal structure and optical properties of nano dimensional ZnO. Co-doping ZnO nanocrystals with RE elements and transition metals (TMs) has also been reported to enhance the optical activity. Specifically, Eu + Mg is a favorable dopant combination, as the presence of a greater number of defect species created by the Mg incorporation helps in stabilizing Eu ions in the ZnO nanosheet [21, 22]. In addition, Mg dopants is perfect to tune the band structure for deep UV applications as it widens the ZnO band gap. Irrespective of the experimental reports on RE and TM doped ZnO nanomaterials, the electronic and magnetic properties of Eu doped ZnO clusters in presence of another TM dopant and native point defects has not been investigated in detail. Nevertheless, it is very important to understand the interplay of dopants and point defects in ZnO cluster. Here we report the findings yielded by a density functional theory (DFT) study of Eu-doped Zn12O12 clusters with and without native point defects, such as Zn and O vacancies (VZn and VO). As part of this investigation, we also conducted co-doping in the cluster with Eu and Mg, in presence of native defects, to understand the changes in structural, magnetic, and electronic properties of the ZnO cluster.
Computational Methodology
The DFT calculations were carried out using the plane wave based VASP package [23, 24]. We utilized projected augmented wave method (PAW) based pseudo potentials [25] while the exchange and correlation were treated using the generalized gradient approximation (GGA) in the Perdew–Burke–Erzenhof formalism (PBE) [26]. It is a well-known fact that GGA cannot accurately describe the interactions of d and f electron systems, and to accurately describe the orbital interactions we included the Hubbard U parameter using the Dudarev’s method as implemented in VASP [27]. For the dopant transition metal atom, the onsite d–d Coulomb exchange interactions were described using U = 4.0 eV and J = 1.0 eV, while the parameters U = 7.0 eV and J = 0.75 eV were adopted for the Eu atom. The choice of Hubbard parameters are taken from standard literature where reliable results are produced with these values [12]. Further, For the Eu atom, we have tested different U and J combinations and used the values that could reproduce experimental values reliably. An energy cut-off of 400 eV was chosen to accurately describe the plane waves included in the basis set. A Gamma-centered k grid was used to carry out the Brillouin zone integration. When simulating the cluster, we adopted the supercell method, which required enclosing it in a cubic box of 15 Å dimensions to ensure negligible interaction between the repeated images. Finally, the ZnO cluster was subjected to optimization such that the Hellmann–Feynman forces converge within a tolerance of 0.01 eV/Å.
Results and Discussion
Stability and Energetics of the Cluster
Generally, the properties of ZnO based DMS materials are tuned by doping in bulk phase, and that suffers from low composition rates as well as local fluctuations. In comparison to bulk and thin films, clusters exhibit peculiar physical and chemical properties owing to the size effects and enhanced surface-to-volume ratio, which also helps in the doping of foreign atoms [28]. Hence, larger impurity concentrations can be achieved in clusters, compared to bulk, and by assembling these stable clusters, doped with impurity atoms can be used to synthesize new class of DMS materials. We have selected the Zn12O12 cluster for our investigations, since it is the most stable geometry, denoted as the magic size cluster owing to its stability due to the cage-like structure [7,8,9]. Hence, this cluster geometry is a good precursor for investigating doped ZnO clusters.
It is possible to successfully stabilize the defects and dopants in this cluster geometry [10], because the pristine ZnO nanoparticles are not suitable for practical applications due to uncontrollable defects [19]. The optimized cluster structure is shown in Fig. 1. In this cluster, the coordination number of each atom is 3, and the atomic rings consist of 4 and 6 atoms. The uniqueness of this cluster geometry stems from all the atoms being located on the surface, which is effectively equivalent to ZnO nanoparticle or QD structures synthesized experimentally [19]. The Zn–O bond length in the optimized cluster is 1.83 Å, whereas in bulk wurtzite ZnO, the Zn–O bond length is 1.99 Å. To understand the effect of point defects on stability, we introduce one VZn and VO in the cluster and subjected to further optimization. Our findings revealed that, when VO is introduced, the Zn–O bond length in the vicinity of the defect changes to 1.91 Å, whereas bond length near VZn changes to 1.82 Å. The formation energy (Ef) of defects is calculated using the expression (1) [29] and the results are reported in Table 1.
where \(E_{D}\) and \(E_{T}\) are the total energies of defective and pristine clusters, respectively. The terms \(n_{i}\) and \(\mu_{i}\), respectively, represent the number and chemical potential of the atoms added to/removed from the cluster, and which is dependent on the experimental growth conditions [30]. Hence chemical potentials can vary from a maximum Zn rich limit to a minimum limit. In the present calculations, we consider the Zn rich conditions. The chemical potentials for Zn, Eu, and Mg are calculated as the total energy of the corresponding bulk element in the most stable form. For O, the chemical potential is calculated from the total energy of molecular O. The effect of charge in formation energy is not estimated, as no charged defects were included in these calculations. Our findings indicate that VZn forms more easily relative to the VO, which is also indicated by the results obtained in previous studies pertaining to same-sized clusters [19].
Further, we introduce one Eu atom as well as an Mg atom in the cluster, replacing Zn and O atoms, one at a time. Our aim is to find, among Zn and O, which is the easily replaceable atom with Mg and Eu. It is to be noted that since the Zn12O12 is a magic size cluster such that the coordination of both O and Zn atoms is three, and therefore any atomic position can be considered to do the doping, owing to the inherent cluster symmetry. Since, in the cluster, all the Zn positions, as well as all the O positions, are equivalent in terms of spatial arrangement and coordination, the doping can be carried out to any Zn or O position as these sites are equivalent. The formation energies (Table 1) show that Zn is preferable dopant site for both Eu and Mg which may be attributed to the comparable atomic sizes of these elements. It is seen that, among Eu and Mg, Eu is more stable dopant in the cluster, based on the lowest formation energies obtained. We continued the investigation by removing an O and Zn atom in both Eu doped and Mg doped clusters. The formation energies show that, the VZn is more easily formed than VO in Eu doped clusters. The formation energies of vacancy formation in presence of Eu dopant is much lower than in pristine ZnO cluster with point defects. This is due to the easiness in breaking of bonds owing to the presence of much larger Eu atom in the cluster. Though VO is taking more energy to form, it is also more probable defect in Eu doped clusters than in otherwise undoped pristine cluster. Turning to the energetic trends in the Mg doping, formation energies are much larger, and which indicates that Mg is very difficult to get doped in the cluster. However, the presence of VZn when Mg is doped to the Zn site is facilitating the doping to a small extent than VO. From the above trends in formation energy, it can be concluded that Eu doped to the Zn site is a favorable dopant in ZnO cluster and Eu can also assist the formation of native point defects. The ease of formation of defect complexes involving Eu and Mg than single point defects has also been observed in ZnO nanosheets previously [21, 22]. For further analysis of magnetic, electronic and optical properties, we have only taken the lowest energy doping configurations into consideration.
Magnetic Properties
Given that no magnetic moment is obtained from the optimized pristine ZnO cluster, different defect scenarios were examined to ascertain whether doping in presence of native point defects (O and Zn vacancies) would produce magnetism, since O and Zn are the most relevant defects reported for ZnO [31]. In addition, Mg with and without native defects, as well as Eu with and without native defects were considered. We also introduce Eu and Mg together with and without including native defects to understand different defect scenarios.
Initially, the magnetic polarization was analyzed in the presence of VO and VZn and the findings indicated that VO does not introduce any ferromagnetism (FM), while VZn induces magnetic polarization in the system. Similar results were obtained in previous studies, confirming the role of native defects in stabilizing FM in ZnO [32, 33]. The total magnetic moment of the cluster in the presence of VZn is 1.69 µB, with the largest value of local magnetic moment of 0.44 µB/atom obtained for the O atom. On the other hand, when Mg is introduced in the pristine cluster, no FM is observed. The introduction of VO along with Mg also couldn’t invoke any FM in the cluster. However, the presence of Mg + VZn complex induces a total magnetic moment of 1.69 µB. Some of the O atoms also acquire magnetic moments as large as 0.3 µB in presence of Mg + VZn complex in the ZnO cluster. Next, an Eu atom is introduced, and the presence of Eu introduces magnetic moments, whereby a high magnetic moment of 5.02 µB/atom is obtained for a single Eu atom, which in turn induces magnetic polarization in the nearby atoms. The O atoms in presence of Eu in the cluster acquire strong magnetic moments (as large as 1.43 µB); however, as some of the atoms acquire negative magnetization, the net magnetic moment reduces to 5.76 µB. Secondly, two Eu atoms without any other defects or dopants was introduced to the cluster to examine the possibility of ferromagnetic exchange coupling between an Eu–Eu pair. Interestingly, the magnetic moments of the two Eu atoms are oriented in opposite directions, and the total magnetic moment of the system is 2.85 µB. This is indicative of the origin of favorable FM in the cluster with increase in concentration of Eu atoms.
We also investigate the magnetic properties of the cluster in presence of Eu along with Mg without any additional defect. In this case, the cluster exhibited a total magnetic moment of − 6.14 µB. The individual magnetic moments of Eu and Mg are − 6.95 µB and 0.003 µB respectively. This weak magnetization of Mg atoms shows that it is difficult to establish magnetic polarization in the clusters with Mg atom alone, unless there exist significant amount of Eu atoms to establish the exchange coupling. To check the possibility of point defect mediated exchange, we have introduced VZn and VO along with Eu and Mg dopants. The presence of VO induces magnetic moment to the Zn atoms up to maximum individual moments of 0.14 µB while Eu and Mg moments were − 6.93 µB and 0.042 µB respectively with a total magnetic moment of − 6.05 µB in the cluster. The induction of VZn is also found to be favorable for magnetism in presence of Eu and Mg, as the magnetic moment turns out to be positive with a magnitude of 6.44 µB, though Mg shows zero moment. Both Zn and O atoms get magnetized with negative magnetic polarization with magnitudes of 0.2 µB and 0.3 µB respectively.
To investigate the preference of magnetic configurations the dopants might take, we have calculated the difference in total energies between FM and antiferromagnetic (AFM) alignment of Eu–Eu, Mg–Mg and Eu–Mg atoms doped to the Zn sites and presented in Table 2, along with the magnetic moments. The difference between FM and AFM is calculated as, ΔE = EFM − EAFM. A positive value means that AFM is favored and vice versa. Interestingly, only for Eu–Eu dopant configuration, the FM is favored and for others, it is AFM. The Mg–Mg pair retained magnetic moments (0.590 µB, 0.255 µB) only for the FM configuration, while for AFM the magnetic moments canceled out. For the Eu–Eu pair the total and local magnetic moments (0.51 µB, 0.64 µB) are consistent for the FM and AFM configurations. For the Eu–Mg dopant atoms, even though the magnitudes are similar, the parallel orientation of spins turned out to be AFM after relaxation. This shows that the presence of Eu atom in the nearest neighbor position of Mg atom not only induces spin polarization, but also forces a spin flip. Hence from our investigation, it is evident that even though the TM atom Mg is not getting magnetized in the pristine ZnO cluster, the presence of point defects and RE dopant such as Eu can help in sustaining favorable magnetic interactions in the clusters, provided their concentration is enough to induce long range magnetic exchange.
Electronic and Optical Properties
We calculated the electronic density of states (DOS) of the clusters to gain further insight into the magnetic and electronic properties. The DOS for the pristine ZnO cluster, as well that including VO and VZn, are shown in Fig. 2. The pristine ZnO cluster is non-magnetic with a symmetric DOS in the up and down channels, as shown in Fig. 2a, and the material magnetism was not affected by introducing an VO, as indicated in Fig. 2b. However, when a VZn is introduced, as shown in Fig. 2c, additional states appear in the spin down channel near the Fermi level (EF), indicating the presence of spin polarization and FM. This explains the magnetic behavior of ZnO clusters in presence of VZn. The O-p states and the Zn-d states are the main contributors to the DOS at the EF, in line with the findings yielded by previous studies focusing on ZnO nanostructures, where VZn was shown to introduce magnetism in an otherwise un-doped ZnO system [12, 19].
Figure 3 shows the electronic structure of ZnO cluster doped with Mg in three different cases, such as (a) without any additional defects (b) in presence of VO and (c) with VZ. The non-magnetic behavior of Mg doped ZnO cluster is evident from the DOS as well, as there is no spin splitting observed (panel a). The presence of VO is also not changing the magnetic character significantly. Conversely, VZn introduces additional levels, resulting in asymmetric DOS at the EF, rendering the Zn11MgO12 clusters to be ferromagnetic materials. The Eu doped ZnO cluster with and without additional defects are shown in the Fig. 4. The presence of single Eu atom in the cluster produces spin-splitting, evident from the DOS (panel a). However, the induction of VO along with Eu (panel b) couldn’t induce spin splitting and the presence of Eu + VZn is favorable for magnetic interactions as shown by the increases spin splitting at the EF (panel c).
For co-doping with two Eu dopants and a single Mg dopant, the electronic structure is shown in Fig. 5, indicating that simultaneous presence of Eu and Mg induces ferromagnetic behavior even in the absence of intrinsic defects. This is obvious from the occurrence of non-zero DOS in the spin up and spin down states at the EF (panel a). There is possibility of hybridization of Zn–s states with Eu f or d states in the Eu + Mg doped ZnO cluster, signifying the possibility of s–d or s–f interactions. The presence of VO along with Eu and Mg is not supporting ferromagnetic exchange as shown by the DOS (panel b). On the other hand, the presence of Eu + Mg along with VZn, gives rise to magnetic spin splitting (panel c). The Zn-d states are also contributing to the DOS at the EF, indicating that VZn can strengthen the ferromagnetic interactions. Contrary to the results obtained for the one-Eu doped and one-Mg doped clusters, VO supports magnetic interactions in the Eu + Mg doped ZnO cluster, as evident from the spin polarized electronic structure. Our results show that even though the VO is detrimental for magnetism in the pristine ZnO and Eu or Mg doped clusters, the co-doping of Eu + Mg along with VO turns out to be a favorable combination for FM. This can explain the long-range FM observed in ZnO clusters incorporating both RE and TM elements which may also contain native point defects.
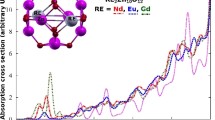
We calculate the refractive index of pristine and Eu doped ZnO cluster to understand the changes in optical absorption caused by the doping. Since our main concern is to understand the change in optical properties brought about by rare earth doping, we are focusing on the Eu doped cluster to calculate the optical properties. Also, among other dopants, defects considered, Eu doped cluster showed more stability. Furthermore, rare earth dopants are found to enhance the optical properties of semiconductor materials [34, 35]. Optical properties of materials are represented by the dielectric function [36] which consists of the real and imaginary parts represented as,
The real part implies the dispersion caused by the incident photon in the material. The imaginary part can be obtained by summing over all the transitions from occupied to unoccupied states whereas the real part can be obtained from imaginary part using the kramers–kronig relations. The absorption coefficient and refractive index can be calculated from the dielectric function. The calculated refractive index n(ω) and Absorption coefficient for pristine ZnO cluster and with Eu doping is shown in Figs. 6 and 7 respectively. The calculated static refractive index for the pristine and Eu doped clusters are 1.08 and 1.26 respectively. The absorption is increasing with Eu doping compared to the pristine cluster and mainly happens in the UV region, owing to the wide band gap nature of ZnO. Our results show that Eu doping is beneficial in enhancing optical absorption and gives a qualitative idea on the optical properties of the ZnO clusters. This is in accordance with previous experimental and theoretical studies which showed that presence of Eu dopant changes the optical properties of ZnO clusters [16,17,18].
Conclusions
We optimized the Zn12O12 cluster to find the most stable geometry, and all subsequent doping were carried out on this stabilized cluster. Our findings indicate that VZn is more stable compared to VO and is favorable for magnetic polarization in the cluster, even in the absence of other dopants. Eu dopants are also stable with negative formation energy and were shown to induce magnetic polarization and enhanced optical properties in the cluster. While the presence of Mg atom does not induce any magnetism in the cluster, dopant-vacancy complexes were shown to strengthen the magnetic properties. Our results on the formation energy of defect complexes, magnetism, and optical properties with dopants are in line with the trends observed in experiments for ZnO nanoclusters. In conclusion, our DFT study gives insights on how the presence of RE and transition metal dopant atoms affect the stability, magnetic, electronic and optical properties of ZnO clusters.
References
S. N. Khanna and A. W. Castleman (eds.) Quantum Phenomena in Clusters and Nanostructures (Springer, New York, 2003).
S. A. Aravindh (2014). Appl. Nano. Sci. 4, 593.
S. A. Aravindh (2014). Eur. Phys. J. D. 68, 120.
M. Bououdina, S. Azzaza, R. Ghomri, M. N. Shaikh, J. H. Dai, Y. Song, W. Cai, and M. Ghers (2017). RSC. Adv. 7, 32931.
S. Yang, D. L. Han, M. Gao, J. H. Yang, and Bayanhehsig (2014). Cryst. Eng. Comm. 16, 6896.
V. D. Mote, Y. Purushotham, and B. N. Dole (2016). Mater. Des. 96, 99.
J. M. Matxain, J. M. Mercero, J. E. Fowler, and J. M. Ugalde (2003). J. Am. Chem. Soc. 125, 9494.
A. C. Reber, S. N. Khanna, J. S. Hunjan, and M. R. Beltran (2006). Chem. Phys. Lett. 428, 376.
J. Carrasco, F. Illas, and S. T. Bromley (2007). Phys. Rev. Lett. 99, 235502.
M. K. Yadav, M. Gosh, R. Biswas, A. K. Ray Chauduri, A. Mukherjee, and S. Dutta (2007). Phys. Rev. B. 76, 195450.
M. S. Mahabali, M. D. Deshpande, S. Chakraborty, T. W. Kang, and R. Ahuja (2016). Eur. Phys. J. D. 70, 63.
N. Ganguli, I. Dasgupta, and B. Sanyal (2010). J. App. Phys. 108, 123911.
I. S. Roqan, K. P. O’Donnell, R. W. Martin, P. R. Edwards, S. F. Song, A. Vantomme, K. Lorenz, E. Alves, and M. Boćkowski (2010). Phys. Rev. B. 81, 085209.
S. A. Aravindh and I. S. Roqan (2015). IOP. Mater. Res. Exp. 2, 126104.
J. Luo, J. Lin, N. Zhang, X. Guo, L. Zhang, Y. Hu, Y. Lv, Y. Zhu, and L. Xingyuan (2018). Mater. Chem. C. 6, 5542.
S. Ji, L. Yin, G. Liu, L. Zhang, and C. Ye (2009). J. Phys. Chem. C. 113, 16439.
S. M. Ahmed, P. Szymanski, L. M. El-Nadi, and M. A. El-Sayed (2014). ACS. Appl. Mater. Inter. 6, 1765.
U. Vinoditha, K. M. Balakrishna, B. K. Sarojini, B. Narayana, and K. Kumara (2018). AIP. Conf. Proc. 1953, 030232.
S. Mitra, A. Aravindh, G. Das, Y. Pak, I. Ajia, K. Loganathan, E. N. Fabrizio, and I. S. Roqan (2018). Nano. Energy. 48, 551.
H. Yoon, J. H. Wu, J. H. Min, J. S. Lee, J. S. Ju, and Y. K. Kim (2012). J. App. Phys. 111, 07B523.
K. P. O’Donnell (2017). Sci. Rep. 7, 41982.
L. Yang, J. Dong, Y. She, Z. Jiang, L. Zhang, and H. Yu (2014). Appl. Phys. Lett. 104, 033109.
G. Kresse and J. Hafner (1993). Phys. Rev. B. 47, 558.
G. Kresse and J. Furthmüller (1996). Phys. Rev. B. 54, 11169.
P. E. Blöchl (1994). Phys. Rev. B. 50, 17953.
J. P. Perdew, K. Burke, and M. Ernzerhof (1996). Phys. Rev. Lett. 77, 3865.
S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys, and A. P. Sutton (1998). Phys. Rev. B. 57, 1505.
J. M. Matxain, J. E. Fowler, and J. M. Ugalde (2000). Phys. Rev. A. 62, 053201.
S. A. Aravindh, U. Schwingenschloegl, and I. S. Roqan (2014). J. App. Phys. 116, 233906.
Kingsley Onyebuchi Obodo, Cecil N. M. Ouma, Gebreyesus Grebremedh, Joshua T. Obodo, Stella O. Ezeonu, and Bachir Bouhafs (2019). Mater. Res. Exp. 6, 10.
A. F. Kohan, G. Ceder, D. Morgan, and C. G. Van de Walle (2000). Phys. Rev. B. 61, 15019.
S. A. Aravindh, U. Schwingenschloegl, and I. S. Roqan (2015). J. Chem. Phys. 143, 224703.
S. A. Aravindh and I. S. Roqan (2016). RSC. Adv. 6, 50818.
W. M. Mulwa, C. N. M. Ouma, M. O. Onani, and F. B. Dejene (2016). J. Sol. State Chem. 237, 129.
C. N. M. Ouma, S. Singh, K. O. Obodo, G. O. Amolo, and A. H. Romero (2017). Phys Chem Chem Phys. 19, 25555.
P. W. Tasker (1979). J. Phys. C. Sol. Stat. Phys. 12, 4977.
Acknowledgements
Open access funding provided by University of Oulu including Oulu University Hospital. S. Assa Aravindh gratefully acknowledges Academy of Finland Grant (# 311934).
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Aravindh, S.A., Roqan, I.S. & Alawadhi, H. Density Functional Theory Studies of Zn12O12 Clusters Doped with Mg/Eu and Defect Complexes. J Clust Sci 32, 55–62 (2021). https://doi.org/10.1007/s10876-020-01758-y
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10876-020-01758-y