Abstract
Resonance assignment of intrinsically disordered proteins is remarkably challenging due to scant chemical shift dispersion arising from conformational heterogeneity. The challenge is even greater if repeating segments are present in the amino acid sequence. To forward unambiguous resonance assignment of intrinsically disordered proteins, we present iHACANCO, HACACON and (HACA)CONCAHA, three Hα-detected 4D experiments with Cα as an additional dimension. In addition, we present (HACA)CON(CA)NH and (HACA)N(CA)CONH, new 4D Hα-start, HN-detect experiments which have two NH dimensions to enhance peak dispersion in a sequential walk through C′, NH and HN, and provide more accurate NH/HN chemical shifts than those that can be obtained from a crowded 1H, 15N-HSQC spectrum. Application of these 4D experiments is demonstrated using BilRI (165 aa), an outer-membrane intrinsically disordered protein from the opportunistic oral pathogen Aggregatibacter actinomycetemcomitans. BilRI amino acid sequence encompasses three very similar repeats with a 13-residue identical stretch in two of them.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Aggregatibacter actinomycetemcomitans is a Gram-negative opportunistic oral pathogen that is linked to periodontitis, infection of tissues supporting the teeth (for reviews, see Fine et al. 2006; Åberg et al. 2015; Fine et al. 2019). Although A. actinomycetemcomitans resides in subgingival multispecies biofilms, it is also able to migrate to underlying vessels and cause systemic diseases such as cardiovascular diseases (Kozarov et al. 2005; Hyvärinen et al. 2012). The host response to biofilms is mediated by inflammatory cytokines. In healthy junctional epithelium of tooth the balance of various cytokines and chemokines ensures that the host defence works appropriately. Some periodontal pathogens are able to impair the balance. Porphyromonas gingivalis can suppress the expression of chemokine interleukin(IL)-8 (Takeuchi et al. 2013) and A. actinomycetemcomitans biofilm is able to sequester and internalize IL-1β, IL-8 and IL-6, which leads to changes in biofilm composition and metabolic activity (Paino et al. 2011, 2012; Ahlstrand et al. 2017). It has been suggested that A. actinomycetemcomitans bacterial IL receptor I, BilRI is associated with this sequestering activity (Paino et al. 2013; Ahlstrand et al. 2017). BilRI is an outer membrane lipoprotein able to bind IL-1β, IL-8 and IL-10 and tumor necrosis factor (TNF)-α (Ahlstrand et al. 2017). Due to its rather low binding affinity it is assumed that BilRI acts by concentrating cytokines on cell membranes, which are then transferred to other components of the uptake system (Paino et al. 2013; Ahlstrand et al. 2017). We have engaged in the structural characterization of BilRI.
BilRI is an intrinsically disordered protein (IDP), as demonstrated by its 1H, 15N HSQC spectrum, which displays very limited signal dispersion (Ahlstrand et al. 2017). In the HN dimension their dispersion is only 0.63 ppm. This arises from a feature typical of IDPs, namely a biased amino acid composition with a pronounced number of polar or charged amino acids, low number of bulky hydrophobic amino acids and lack of aromatic amino acids (Dyson 2016). BilRI amino acid sequence is dominated by alanine (23%), lysine (14%) and aspartic acid (13%) residues. However, unlike the general trend (Dunker et al. 2001), BilRI sequence contains only one proline and one glycine. BilRI is positioned among IDPs in the mean net charge-hydropathy plot (Uversky et al. 2000) (Fig. 1a). The paucity in the variability of residue’s nearest neighbors narrows down the chemical shift range of a particular amino acid type, for example there are 12 Lys-Asp-Ala triplets in the sequence, which most likely results in close chemical shifts for the middle aspartic acid. Additionally, the BilRI sequence contains three very similar segments of about forty residues. The longest identical stretch is of 13 residues, present in two of these repeats, covering residues 71–82 and 111–122 (Fig. 1b).
a Mean net charge-hydropathy plot of BilRI. Data for the plot were created with the PONDR predictor (https://www.pondr.com/). b Amino acid sequence of A. actinomycetemcomitans BilRI. Amino acids are classified by type: yellow, small hydrophilic (A, G, N, P, Q, S, T); green, hydrophobic (I, M, V); red, negatively charged (D, E) and blue, positively charged (K) amino acids. BilRI sequence does not contain C, F, H, L, R, W or Y. The longest 13-residue repetitive segments are underlined in black, and the broken underline indicates a very similar segment. The second longest 11-residue repetitive segments are anderlined in blue, and the triplet K-D-A, which recurs twelwe times in the sequence is underlined in red. The first four residues are a cloning artefact
The 1H, 15N HSQC spectra of IDPs typically being very challenging to scrutinize, the resonance assignment most often relies on spectra other than the classical HN-detected experiments widely used for folded proteins (for reviews see e.g. Sattler et al. 1999; Permi and Annila 2004). Indeed, the conventional approach based on the HNCACB and HN(CO)CACB/CBCA(CO)NH experiments that link the intra- and sequential 13Cα and 13Cβ chemical shifts to 1HN and 15N frequencies, are very inefficient for many IDPs due to severe clustering of aliphatic carbon chemical shifts for each residue type. Instead, correlation of 15N and 13C′ frequencies provide much better results for IDPs (Yao et al. 1997; Mäntylahti et al. 2009; Bermel et al. 2012) Another obstacle arises from the increasing chemical exchange rate of amide protons with water at alkali pH and/or elevated measurement temperature (Mäntylahti et al. 2010). Yet another challenge for the assignment originates from the abundancy of proline residues in IDPs. As an N-substituted residue, proline lacks the amide proton, which results in gaps during the resonance assignment procedure. Although this can be a benefit in the case of globular proteins, it significantly hampers the resonance assignment of disordered systems (Hellman et al. 2014). Several different approaches have been proposed to overcome these obstacles imposed during the assignment procedure. These include increase of dimensionality from conventional 3D to 4–7D spectra (Fiorito et al. 2006; Motáčková et al. 2010; Nováček et al. 2011; Kazimierczuk et al. 2013; Brutscher et al. 2015) as well as detection of non-exchangeable spins 13C′ and 1Hα instead of 1HN (Bermel et al. 2006a, 2009; 2012; Mäntylahti et al. 2010, 2011; Permi and Hellman 2012). Our group has been resorting both to Hα-start, HN-detect pulse schemes (Mäntylahti et al. 2009; Hellman et al. 2014) or complete Hα-detection experiments (Mäntylahti et al. 2010, 2011; Permi and Hellman 2012) for the assignment of IDPs, which overcome hurdles associated with proline assignment and exchange broadening at alkali pH or elevated temperature. In addition to reduced susceptibility towards solvent exchange induced linebroadening, the Hα chemical shift is extremely valuable in structural analysis. The Cα, Hα and C′ shifts are particularly sensitive to the ϕ/ψ angles of the protein backbone and thus the most informative in the estimation of secondary structure content in an IDP (Borcherds and Daughdrill 2018).
Comprehensive assignments allow for detailed, residue-specific analysis of structure and dynamics (Konrat 2014). There are therefore grounds for an extra effort towards a more comprehensive backbone resonance assignment. IDPs are often comprised of repetitive amino acid sequences and hence higher dimensionality in combination with high resolution offer superior results. However, the increased dispersion of signals should not be obtained, if possible, at expense of sensitivity. Here we present the resonance assignment of BilRI, whose demanding amino acid sequence necessitated development of a suite of 4D pulse sequences that offer superior signal dispersion with respect to their well-established 3D counterparts without indirect sampling associated sensitivity loss.
Materials and methods
Protein expression and purification
The gene encoding BilRI (residues 21–181) was cloned to pET15b vector (Novagen) into the NdeI and XhoI sites. This leads to soluble recombinant BilRI protein with N-terminal His-Tag with a thrombin cleavage site.
Production of 13C, 15N labeled BilRI was carried out by transforming plasmids into the BL21(DE3) cells. Cells were grown in M9 minimal media, supplemented with 1 g/l of 15NH4Cl and 2 g/l 13C-d-glucose as the sole nitrogen or nitrogen and carbon source, respectively. Cell culture was incubated at 37 °C and temperature was decreased to 16 °C when OD of the cell culture reached 0.4 and protein production was induced with 1 mM IPTG when OD of the cell culture reached 0.6. Cells were further incubated at 16 °C for 16 h and collected by centrifugation. Cells were disrupted with sonication and resulting supernatant was clarified by centrifugation with 30,000×g.
Clarified supernatant of BilRI was applied to the 1-mL His GraviTrap column (GE Healthcare) and the His-Tag was removed by thrombin protease (GE Healthcare) digestion according to the manufacturer’s instructions. Protease digested mixture was applied to His GraviTrap column. BilRI, without His-Tag, eluted with flow-through. Flow-through was concentrated to volume of 1 ml with Vivaspin 2 concentrator. Concentrated BilRI sample was applied into the Superdex 75 16/60 gel filtration column (GE Healthcare). Buffer used in gel filtration contained 20 mM sodium phosphate (pH 6.5) and 50 mM NaCl (NMR buffer). Fractions with pure BilRI were pooled and concentrated for NMR studies. The gel filtration was performed by using the ÄKTA Purifier FLPC purification system (GE Healthcare).
NMR spectroscopy
BilRI NMR experiments were acquired using 0.5–1.0 mM 15N, 13C labeled protein samples in 5/95% D2O/H2O at pH 6.5. Chemical shifts were referenced to external 2,2,-dimethyl-2-silapentane-5-sulfonic acid (DSS). All data were acquired at 25 °C on a Bruker AVANCE III HD 800 MHz spectrometer, equipped with a TCI 1H/13C/15N cryoprobe. In addition to the new 4D experiments described here, the following experiments were used in the resonance assignment: 2D 1H, 15N-HSQC, constant time 1H, 13C-HSQC, 13C-detected 2D CON (Bermel et al. 2006b), 3D HN-detected HNCACB, CBCA(CO)NH, HNCO (reviewed in (Sattler et al. 1999; Permi and Annila 2004) and i(HACA)CO(CA)NH (Mäntylahti et al. 2009), 3D Hα-detected HA(CA)CON, iHA(CA)NCO and (HACA)CON(CA)HA (Mäntylahti et al. 2010, 2011). All 3D/4D experiments were collected using non-uniform sampling (Table 1). Sampling densities were 25% for the 3D experiments and 7–20% for the 4D experiments. NMR data were processed with TopSpin 3.5 (Bruker Inc) and analyzed with CcpNmr Analysis v. 2.4.2 (Vranken et al. 2005). BilRI chemical shifts have been deposited to the BMRB database (www.bmrb.wisc.edu) with accession code 27824.
Results and discussion
Peaks in the BilRI 2D 1H, 15N-HSQC spectrum display overwhelming overlap (Fig. 2a) and a very narrow distribution in the HN dimension. As it was later revealed, all but three of the 21 aspartic acid residues’ peaks are located in the middle region pile of peaks, 8.27–8.38, 121.2–121.9 ppm, together with 11 of the 13 methionine residues’ amide peaks. The Asp and Met α signals heavily overlap also in the 1H, 13C CT-HSQC (Suppl. Fig. S1). The CON spectrum, on the other hand, shows remarkably well dispersed signals (Fig. 2b) with peaks from all C′–NH pairs present. We thus first attempted the assignment with spectra having the CON spectrum as the root spectrum, namely Hα-detected experiments HA(CA)CON, iHA(CA)NCO and (HACA)CON(CA)HA (Mäntylahti et al. 2010, 2011). 3D HN-detected experiments HNCACB, CBCA(CO)NH, HNCO and i(HACA)CO(CA)NH (Mäntylahti et al. 2009) were acquired to collect HN, C′, Cα and Cβ chemical shifts. With this set of seven 3D spectra, we assigned the majority of backbone resonances. However, there were several ambiguous assignments, in particular within the aforementioned repeating segments. Moreover, while precise Hα and C′ shifts were obtained from the 3D Hα-detected experiments and the CON, due to heavy overlap, Cα/Cβ shifts were far more difficult to read from the HNCACB and CBCA(CO)NH spectra. Indeed, a precise Cα/Cβ chemical shift for 66% of the residues was obtained, while for Hα, resolved peaks for 87% of the residues were observed (Suppl. Fig. S2).
a 2D 1H, 15N-HSQC spectrum of BilRI. The peaks are labeled with residue numbers and one-letter amino acid codes. Crosses indicate peaks found at lower contour levels. Residue numbering corresponds to that of whole BilRI protein (1–181) although the construct used was shorter (21–181). b 2D CON spectrum of BilRI. The peaks are labeled with residue number and amino acid code of the amide nitrogen in the C′-NH pair. The peak of the only proline of the BilRI amino acid sequence, which resonates at 172.8 (26Ser C′), 138.1 (27Pro NH) ppm is not shown. Asterisks indicate impurities. Both 2D spectra were acquired at 800 MHz 1H frequency, 25 °C from a 1 mM BilRI sample at pH 6.5
To resolve these ambiguities and to extend the number of accurate chemical shifts, we resorted to 4D NMR spectroscopy. In order to bypass the Cα overlap problem in 3D HN-detected experiments and to establish direct connectivities between Hα and Cα, and to provide dispersion to solve ambiguities arising from occasional overlap of C′, Hα resonances encountered in the 3D Hα-detected experiments, we devised Hα-detected 4D experiments with Cα as an additional dimension. In addition, we developed and employed new 4D Hα-start, HN-detect experiments which can bridge stretches over single prolines similar to 3D experiments described in Hellman et al. (2014), but which have two NH dimensions to enhance peak dispersion in a sequential walk through C′, NH and HN, and to provide for more accurate NH/HN chemical shifts than those that could be obtained from the crowded regions of the 1H, 15N HSQC.
4D iHACANCO, HACACON and (HACA)CONCAHA experiments
The proposed 4D iHACANCO, HACACON and (HACA)CONCAHA experiments are extensions of their established 3D counterparts (Mäntylahti et al. 2010, 2011) with additional sampling on the fourth 13CA dimension (Fig. 3). The coherences flow through the 4D iHACANCO, HACACON and (HACA)CONCAHA experiments in Eqs. 1, 2, 3:
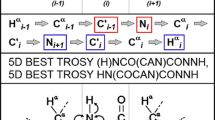
a–c Schematic presentation of magnetization transfer pathway during the 4D iHACANCO d, 4D HACACON e and 4D (HACA)CONCAHA f experiments. Red arrows indicate direct transfer pathway from 1Hα(i) to 15N(i) or 15N(i + 1) whereas green arrows indicate a nested CαC′ZNZ →NZCα transfer in d) known as the intraresidual filter (Permi 2002; Brutscher 2002) or highly selective CαC′ZNZ →Cα transfer in e). Arrows indicate out-and-back type magnetization transfer, whereas one-way arrows represent coherence transfer route which is unidirectional. One-letter codes above the arrows indicate time points in the pulse sequence. d Intraresidual iHACANCO experiment to correlate 1Hα(i), 13Cα(i), 13C′(i) and 15N(i) chemical shifts, e the HACACON experiment, which correlates chemical shifts of 1Hα(i), 13Cα(i), 13C′(i) and 15N(i + 1) resonances. f The (HACA)CONCAHA experiment for correlating 1Hα(i), 13Cα(i), 13C′(i) and 15N(i + 1) resonances. Narrow and wide filled bars on 1H and 15N channels correspond to rectangular 90° and 180° pulses, respectively, applied with phase x unless otherwise stated. All 13C pulses are band-selective shaped pulses, denoted by filled narrow bars (90°) and filled and unfilled half ellipsoids (180°). Unfilled bars are applied on-resonance. The 1H, 15N, 13C′, and 13Cα carrier positions are 4.7 (water), 118 (center of 15N spectral region), 174 ppm (center of 13C′ spectral region), and 56 ppm (center of 13Cα spectral region). The 13C carrier is set initially to the middle of 13C′ region (174 ppm), shifted to 13Cα region (56 ppm) prior to 90° 15N pulse ϕ1 in scheme d). In scheme e) and f), the carrier is initially at 56 ppm and shifted to 174 ppm prior to 90° 13C pulse ϕ2, and shifted back to 56 ppm before 90° 13C pulse ϕ4. The first band-selective 180° 13C pulse, refocusing 13Cα magnetization (56 ppm, denoted with an asterisk) had duration of 788 μs at 800 MHz. Other band-selective 90° and 180° pulses for 13Cα (56 ppm) and 13C′ (174 ppm) were applied with durations of 240.0 μs and 192.0 μs at 800 MHz, respectively. Band-selective 90° and 180° pulses for 13C′/13Cα have the shape of Q5 and Q3 (Emsley and Bodenhausen 1992) and duration of 240.0 μs and 192.0 μs at 800 MHz, respectively. The adiabatic 180° Chirp broadband inversion pulse for inverting 13Cα and 13C′ magnetization in the middle of t1 period had duration of 500 μs at 800 MHz (Böhlen and Bodenhausen 1993). The Waltz-65 sequence (Zhou et al. 2007) with strength of 4.17 kHz was employed to decouple 1H spins. The GARP (Shaka et al. 1985, 1987) with field strength of 4.55 kHz was used to decouple 13C during acquisition. Delay durations: τ = 1/(4JHC) ~ 1.7 ms; τ2 = 3.4 ms (optimized for non-glycine residues) or 2.2–2.6 ms (for observing both glycine and non-glycine residues); ε = duration of GH + field recovery ~ 0.4 ms; 2TC = 1/(2JCαC′) ~ 9.5 ms; TCA = 1/(6JCαC′) ~ 3.3 ms; TA = 1/(4JC′N) ~ 16.6 ms; TC′ = TC + TCC; TCC = 1/(JCαCβ)–1/(4JC′N)–1/(2JCαC′) ~ 0–2.5 ms; TNC ~ 14 ms; TCN ~ 14 ms; TN ~ 14 ms. Maximum t1, t2 and t3 are restrained in scheme d, t2,max < 2.0*TC′, t3,max < 2.0*TCN, in scheme e, t2,max < 4.0*TA, t3,max < 2.0*TCA, in scheme f, t1,max < 2.0*TA, t2,max < 2.0*TNC, t3,max < 2.0*TCN. Frequency discrimination in 15 N and 13C′ dimensions is obtained using the States-TPPI protocol (Marion et al. 1989) applied to ϕ1 and ϕ2, respectively, whereas the quadrature detection in 13Cα dimension is obtained using the sensitivity-enhanced gradient selection (Kay et al. 1992; Schleucher et al. 1994). The echo and antiecho signals in 13Cα dimension are collected separately by inverting the sign of the GC gradient pulse together with the inversion of ψ, respectively. Phase cycling: ϕ1 = x, − x; ϕ2 = 2(x), 2(− x); ϕ3 = 4(x), 4(− x); ϕ4 = x; ψ = x; rec. = x, 2(− x), x, − x, 2(x), − x. Selective 180° pulse for 13Cα in the middle of delay 2TA induces a Bloch-Siegert shift to 13C′ magnetization, a careful adjustment of phase (bsp) of the last 13C′ 90° (phase y) pulse is necessary in scheme d). Gradient strengths and durations: GC = 13 k G/cm (1.6 ms), GH = 13 k G/cm (0.4 ms). The pulse sequences code and parameter file for Bruker Avance system are available from authors upon request
respectively. All experiments start with the 1Hα(i)→ 13Cα(i) transfer, and the density operator immediately after the ϕ3 pulse is described as Hαz(i)Cαz(i) (time point a). Subsequently, the magnetization is transferred to the 13C′ spin followed by the labeling of 13C′ chemical shift in t1 or t2. The relevant density operator after the ϕ2 pulse in all experiments is described as Cαz(i)C′y(i) (time point b). Next, the desired coherence is transferred to the 15N spin of the sequential residue in HACACON and (HACA)CONCAHA experiments, described with the density operator Cαz(i)C′z(i)Ny(i + 1) (time point c). In the iHACANCO experiment, the magnetization is solely transferred to the 15N spin within the residue, described with the density operator Cαz(i)C′z(i)Ny(i) (time point c). After labeling the 15N chemical shifts in t1 (or t2), the magnetization is transferred to the 13Cα coherence after the ϕ4 pulse. The relevant density operators (time point d) are Cαy(i)Nz(i) for iHACANCO, Cαy(i)C′z(i) for HACACON and Cαy(i)Nz(i) for (HACA)CONCAHA schemes. The 13Cα chemical shift is labeled during the t3 period between time points d–e.
While the HACACON (Fig. 3b) is the conventional out-and-back experiment, the (HACA)CONCAHA and iHACANCO utilize the intraresidual filter for the selective 13Cα(i)→ 15N(i) transfer (Permi 2002; Mäntylahti et al. 2010, 2011). Especially in the iHACANCO experiment, the magnetization transfer is nested and further clarification is delivered in the following. After converting magnetization to the Hαz(i)Cαz(i) coherence (time point a), the 1JCαC′, 1JCαN, 2JCαN and 1JCαCβ couplings are active during the time interval (2TC + 2TA + 2TC′ + TCC) = 52–57 ms, which converts it to the Cαz(i)Ny(i) coherence (time point c). However, during the delay 2TCC, that can be selected to be 0–5 ms based on the relaxation properties of 13Cα spins, only 1JCαCβ is active. This is to maximize the transfer efficiency during the (2TC + 2TA + 2TC′ + TCC) delay. Of note, to avoid chemical shift evolution of 13Cα–13C′ multiple-quantum coherence during 2TA –t2, an additional but opposite frequency labeling period for 13Cα has been implemented in the 2TC′ period. Efficiently, only the chemical shift evolution of 13C′ will take place during t2, but the attainable resolution is limited by 2TC′ (= 2TC + TCC) i.e. t2,max is 19–22 ms, depending on the setting of 2TCC (0–5 ms).
Thus, the 4D iHACANCO, HACACON and (HACA)CONCAHA experiments yield correlations at ωHA(i), ωCA(i), ωC′(i), ωN(i); ωHA(i), ωCA(i), ωC′(i), ωN(i+1), and ωHA(i), ωCA(i), ωC′(i–1), ωN(i) frequencies, respectively. Given that frequency labeling of 13Cα chemical shifts is implemented in a constant-time manner, without lengthening the actual pulse sequence and incorporating sensitivity enhanced gradient echo in t3, there is no sensitivity loss involved in increasing the dimensionality of these Hα-detected experiments. Hence, the coherence transfer efficiencies provided with the corresponding 3D experiments by Mäntylahti et al. (2010, 2011) are directly comparable to 4D implementations shown in Fig. 3. Indeed, by taking into account typical values of one-bond couplings 1JCαC′ = 53 Hz, 1JC′N = 15 Hz, and 1JCαCβ = 35 Hz, and the average random coil values for one-bond (1JCαN = 10.6 Hz) and two-bond (2JCαN = 7.5 Hz) couplings between backbone 13Cα and 15N spins (Delaglio et al. 1991), as well as transverse relaxation times (T2) for 13Cα (= 100 ms), 13C′ (= 200 ms) and 15N (= 200 ms) spins, we can estimate coherence transfer efficiencies for these experiments in IDPs (Mäntylahti et al. 2010, 2011). The HACACON is superior in sensitivity (I ~ 0.28) in comparison to iHACANCO and (HACA)CONCAHA experiments, with coherence transfer efficiencies of 0.22 and 0.18, respectively. Particularly, for the assignment of prolines, sensitivities of iHACANCO and HACACON are superior to the (HACA)CONCAHA scheme, which yields coherence transfer of 0.026 for proline residues. The sensitivity loss is associated with the 15N(i)→ 13Cα(i) transfer, 2TNC, during which the 15N magnetization is further modulated by 1JNCδ coupling interaction in prolines.
Figure 4 compares 3D Hα-detected with the new 4D spectra: problems associated with multifold overlap and ambiguities in choosing the right sequential connection when using 3D spectra can be surpassed, and the assignment procedure expedited by extending frequency labeling to Cα.
Problematics in resonance assignment with 3D Hα-detected experiments can be resolved with 4D HACACON and 4D (HACA)CONCAHA experiments. The upper row of 2D planes from 3D HA(CA)CON and iHA(CA)NCO spectra shows that the sequential walk from 97Ala to 96Glu is ambiguous because the 97Ala Ha, C′ shift pair observed in the HA(CA)CON can be found in several planes of the iHA(CA)NCO and is overlapping with other peaks. While there is overlap in the 4D spectra also, the planes are far more easily interpreted and allow for unambiguous assignment of 98Ala-97Ala-96Glu. Grey labels mark peaks with maximum in adjacent 15N or 13C planes
With the help of these Hα-detected 4D experiments, 76% of the α correlations of were successfully assigned (Suppl. Fig S2). Considering that some N, C′ resonances are separated by less than 0.05 ppm in the CON spectrum, e.g. corresponding resonances within73/113KDAISE78/118 differ only by 0.03–0.04 ppm, all peaks were not expected to be resolved in spectra with spectral resolutions of 0.11 (15N) and 0.05 (13C) ppm. The Hα, Cα shifts were as ineffective in providing the needed dispersion, the smallest peak separations being comparable, e.g. the 76/116Ile alpha peaks differ by only 0.01 and 0.05 ppm in 1H and 13C, respectively, and those of 77/117Ser even less (Suppl. Fig. S1).
4D (HACA)CON(CA)NH and (HACA)N(CA)CONH experiments
Analogously to 4D Hα-detected experiments described above, the 4D HN-detected experiments (Fig. 5), with an isolated proline assignment enhancement, are based on their 3D counterparts (Hellman et al. 2014). Again, sampling of an additional 15N dimension can be implemented in without introducing sensitivity loss thanks to the gradient enhanced coherence order selective coherence transfer (COS-CT) (Kay et al. 1992; Schleucher et al. 1994). Magnetization transfer through (HACA)CON(CA)NH and (HACA)N(CA)CONH experiments are briefly described in Eqs. 4 and 5, respectively:
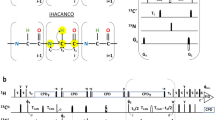
a and b schematic representation of the magnetization transfer pathways during the c 4D (HACA)CON(CA)NH and d 4D (HACA)N(CA)CONH experiments, respectively. Red arrows highlight direct transfer pathway from 1Hα(i) to 15N(i) or 15N(i + 1) whereas green arrows indicate a nested CαC′ZNZ →NZCα transfer in c or NZCα →CαC′NZ transfer in d, known as the intraresidual filter (Brutscher 2002; Permi 2002). Black arrows stand for the coherence order selective coherence transfer, COS-CT (Kay et al. 1992; Schleucher et al. 1994). Arrows with solid line denote the actual magnetization transfer pathway, whereas an arrow with a broken line displays coherence transfer that is suppressed by the intraresidual filter. The 4D (HACA)CON(CA)NH experiment establishes connectivities between 1HN(i–1) (t4), 15N(i–1) (t3), 15N(i) (t2), and 13C′(i–1) (t1) frequencies. The 4D (HACA)N(CA)CONH scheme correlates 1HN(i + 1) (t4), 15N(i + 1) (t3), 13C′(i) (t2) and 15N(i) (t1) frequencies. These two experiments allow also bridging the gap between XPX motifs, where X is any other residue except proline. Narrow and wide bars correspond to 90° and 180° pulses for 1H and 15N, respectively. Pulses are applied with phase x unless otherwise marked. All 13C pulses are band-selective shaped pulses, denoted by filled narrow bars (90°) and filled and unfilled half ellipsoids (180°). Unfilled half ellipsoids denote on-resonance 180° pulses. The 1H, 15N, 13C′, and 13Cα carrier positions are 4.7 (water), 118 (center of 15N spectral region), 174 ppm (center of 13C′ spectral region), and 56 ppm (center of 13Cα spectral region). The 13C carrier resides at 174 ppm throughout the experiments. Band-selective 90° and 180° pulses for 13C′/13Cα have the shape of Q5 and Q3 (Emsley and Bodenhausen 1992) and duration of 240.0 μs and 192.0 μs at 800 MHz, respectively. The Waltz-65 sequence (Zhou et al. 2007) with strength of 4.17 kHz was employed to decouple 1H spins. The GARP-4 (Shaka et al. 1985) with field strength of 1.14 kHz was used to decouple 15N during acquisition. Delay durations: τ = 1/(4JHC) ~ 1.7 ms; τ2 = 2.6 ms (for the scheme c) or 2.2 ms (for the scheme d); ∆ = 1/(4JHN) ~ 2.7 ms; ∆2 = 1/(2JHN) ~ 5.5 ms; ε = duration of GH + field recovery ~ 1.2 ms; 2TC = 1/(6JCαC′) ~ 6.2 ms or 28 ms; 2TC′ ~ 9.4 ms; 2TC′N ~ 33 ms; 2TNCA ~ 29 ms; The 13Cα15N transfer delay 2TCAN ~ 50–56 ms to suppress the auto-correlated pathway, or 2TCAN ~ 25 ms for observing both sequential and auto-correlated cross-peaks. Maximum t1 and t3 is restrained in scheme c, t1,max < 2.0*TC′N, t3,max < 2.0*TNCA, and t3 is restricted in scheme d, t3,max < 2.0*TNC. Frequency discrimination in 13C′ and 15N dimensions is obtained using the States-TPPI protocol (Marion et al. 1989) applied to ϕ1 and ϕ2. Frequency discrimination in the second, t3, 15N dimension is accomplished by the COS-CT implementation (Kay et al. 1992; Schleucher et al. 1994). The echo and antiecho signals in the 15N dimension are collected separately by inverting the sign of the GN gradient pulse together with the inversion of ψ, respectively. Phase cycling: ϕ1 = x, − x; ϕ2 = 2(x), 2(− x); ϕ3 = x; ϕ4 = 4(x), 4(− x); ψ = x; ϕrec. = x, 2(− x), x, − x, 2(x), − x. Gradient strengths and durations: GN = 13 k G/cm (1 ms), GH = 13 k G/cm (1 ms). The pulse sequence codes and parameter files for Bruker Avance system are available from authors upon request
Like in the Hα-detected experiments (vide supra), the magnetization is first transferred from 1Hα to 13Cα spin (time point a), and further to either 13C′(i–1) spin in (HACA)CON(CA)NH (density operator Cαz(i–1)C′y(i–1)) or selectively to 15N(i) spin in (HACA)N(CA)CONH (density operator Cαz(i)Ny(i)) at time point b. This is followed by the frequency labeling of 13C′(i–1) and 15N(i) chemical shifts during t1 in (HACA)CON(CA)NH and (HACA)N(CA)CONH experiments, respectively. Next, the desired magnetization is transferred to the sequential 15N spin or intraresidual 13C′ spin, described by the density operators Cαz(i–1)C′z(i–1)Ny(i) and Cαz(i)C′y(i)Nz(i + 1) in (HACA)CON(CA)NH and (HACA)N(CA)CONH, respectively (time point c). Frequency labeling of 15N(i) and 13C′(i) chemical shift takes place in t2. The suppression of sequential 15N pathway in (HACA)N(CA)CONH is accomplished using the intraresidual filtering between time points b and c, and in (HACA)CON(CA)NH between time points c and d. Finally, the chemical shift of 15N(i–1) and 15N(i + 1) chemical shifts are recorded for Cαz(i–1)Ny(i–1) and C′y(i)Nz(i + 1) coherences in (HACA)CON(CA)NH and (HACA)N(CA)CONH between time points d–e.
Hence, the 4D (HACA)CON(CA)NH and (HACA)N(CA)CONH spectra exhibit correlations at the intersection of ωHN(i–1), ωN(i–1), ωC′(i–1), ωN(i) and ωHN(i+1), ωN(i+1), ωC′(i), ωN(i) frequencies, respectively. As the magnetization transfer cascade originates from the Hα spin, and the transfer route includes sampling of 15N frequencies of prolines as well, the experiments facilitate assignment of isolated proline residues (XP or PX dipeptide stretches, where P is a proline and X stands for any non-proline residue) together with other residues in IDPs with high sensitivity. Analogously to Hα-detected experiments, under identical conditions (vide supra), the coherence transfer efficiency for both prolines and non-prolines in the 4D (HACA)CON(CA)NH experiment reaches 0.19, if 2TC is set to 28 ms (and 0.15 with 2TC = 6.2 ms) and in the (HACA)N(CA)CONH experiment I ~ 0.20. Hence, both of these experiments are optimal also for the proline assignment in XPX moieties.
In the 1H, 15N HSQC only 41% of the residues displayed resolved peaks, whereas from the two 4D spectra, accurate amide 1H, 15N shifts were obtained for 85% of BilRI residues. Still overlapping peaks were found for residues 73Lys-80Met, 113Lys-120Met and 153Lys-154Ala in the 71/111/151EVKDAI/VSEKM80/120/160 stretches as well as for residues 103Asp-105Ala, 143Asp-145Ala in the middle of the 99/139KDAKDAAADKM109/149 stretches. Despite the overlap, with the help of the high peak resolution in the CON, it was possible to walk sequentially the whole amino acid sequence with the exception of the first three residues, which are not part of the native BilRI sequence. These residues are missing also from the 1H, 15N HSQC, likely due to fast chemical exchange of their amide proton with the solvent protons. Examples of the resolving power of the additional 1H, 15N HSQC dimension are presented in Fig. 6 and Suppl. Figs. S3, S4. The sequential walk over a proline residue is depicted in Suppl. Fig. S5.
Resolving power of the i-1 amide nitrogen in the fourth dimension. Compared are 3D HNCO and 4D (HACA)N(CA)CONH planes from the 1H, 15N-HSQC region shown in the upper left corner. From 2D HN-C′ planes retrieved from the 3D HNCO at 15N frequencies marked with lines of different colors it is difficult to determine the number of peaks present and their chemical shifts in this overlapping peak area of the 1H, 15N-HSQC. Tentative peak positions are shown with broken lines. In contrast, in the 4D (HACA)N(CA)CONH spectrum four nicely resolved peaks are found. The fourth dimension, i.e. the second chemical shift marked in the 4D planes effectively spreads peaks overlapping in the 2D and 3D spectra
It is interesting to note that throughout the identical stretches 71/111EVKDAIVSEKMDAM83/123 and 99/139KDAKDAAADKM109/149 the corresponding peaks are resolved in the CON spectrum. Naturally, the chemical shift differences become small in the middle of the repeats, ~ 0.03–0.04 ppm for both C′ and NH, but the peaks remain, however, distinct. 76/116Ile Cα-Hα is resolved into separate peaks in a high-resolution CT 1H, 13C-HSQC spectrum (t1 acquisition time 51 ms) as well. To have a different chemical shift, the corresponding atoms in the stretches should experience a mutually different structural environment. Future studies will uncover whether this arises from nearest-neighbor effects being effective over five residues or from distinct long-range interactions within the protein.
During the past several years, several different NMR experiments and assignment schemes have been developed for studying IDPs. Based on the detected spin, these can be categorized to three different classes i.e. HN-, 13C′- and Hα-detection approaches (for review, see e.g., Brutscher et al. 2015). The HN-detected experiments offer the highest sensitivity under acidic conditions and can be combined with the BEST and TROSY implementations (Solyom et al. 2013; Brutscher et al. 2015). However, they show limited performance under alkali conditions and/or with IDPs having high proline content, which can be partially compensated using an Hα-start, HN-detected approach as shown here and also previously demonstrated (Mäntylahti et al. 2009; Hellman et al. 2014; Yoshimura et al. 2015). For instance, Yoshimura et al. (2015) proposed 13C′-13C′ TOCSY transfer in HNCOCONH -type experiments which show connectivities for i, i ± 1, i ± 2 residues i.e. enabling connection of i and i ± 2 residues over a single proline at i ± 1 position. The (HACA)CON(CA)NH and (HACA)N(CA)CONH experiments proposed here link the residues flanking a single proline through its 15N chemical shift.
Unlike HN-detected experiments, the 13C-detection is almost non-susceptible to amide proton exchange with water at high pH. The 13C-detection based experiments for the assignment of IDPs generally apply the ‘CON′ strategy for connecting the neighboring residues in low-complexity regions of IDPs, which is also suitable for the assignment of prolines (Pantoja-Uceda and Santoro 2014; Sahu et al. 2014; Brutscher et al. 2015; Chaves-Arquero et al. 2018). Theoretical coherence transfer efficiency in the 13C-detected experiment, hacaCONcaNCO (Pantoja-Uceda et al. 2014) attains 0.19, which is comparable to the sensitivity of the (HACA)CON(CA)NH experiment proposed here. However, given that γH/ γC equals 4 and the attainable sensitivity has γ3/2 dependence on the detected spin, the 13C-detection results in an inherent sensitivity loss by a factor of 8 with respect to the 1H-detection. This can partially be redeemed using a 13C-detection optimized probehead and 13C′-detection, which offers higher resolution in the direct detection dimension due to absence of homonuclear couplings. If such a probehead with an inner coil for 13C is not available, this sets limit to the feasible sample concentration (> 0.3–0.5 mM) which might become an issue with some IDPs. On the other hand, homonuclear couling between HN and Hα can be removed in 1H-detected experiments using the homonuclear BASH decoupling scheme (Ying et al. 2014).
Finally, the Hα-detected experiments offer higher sensitivity with respect to the 13C-detection, enable assignment of consecutive prolines and are not prone to linebroadening due to chemical exchange with the solvent (Mäntylahti et al. 2010, 2011). However, given that Hα resonances may partially be underneath the water signal unless sample is prepared in 99.99% D2O, all experiments proposed here employ the sensitivity-enhanced, echo/antiecho gradient selection in conjunction with the water flip back approach. This enabled us to carry out all the measurements in 95% H2O and accomplish a nearly complete assignment of Hα resonances of the 165-residue BilRI. When working with more dilute samples (< 0.25 mM), dissolving protein into D2O might be advantageous.
In all, with the proposed suite of 4D experiments, a complete assignment of backbone HN, NH, C′ chemical shifts was obtained for all but the three N-terminal residues, which are not part of the BilRI native sequence. Hα, Cα and Cβ chemical shifts were obtained for 87, 76, and 66% of the residues, respectively. These experiments offer alternative approach for the assignment of IDPs. Hence, they should not be considered superior per se to the existing methods, but as demonstrated here, they have features that may facilitate accomplishing the assignment of challenging IDPs such as BilRI.
Conclusions
In this paper, we have presented a suite of Hα-detected and Hα-start, HN-detected 4D experiments that by exploiting chemical shift dispersion brought by an additional Cα or N dimension, facilitate the unambiguous backbone resonance assignment of IDPs in comparison to their established 3D counterparts. The Hα-detected experiments provide versatile strategy for the assignment of proline-rich amino acid sequences and/or proteins at alkali pH, prone to fast chemical exchange with the solvent. The proposed 4D Hα-detected experiments provide information with the most vital chemical shifts i.e. Hα, 13Cα, and 13C′ for conformational restraining in IDPs. The Hα-start, HN-detected (HACA)CON(CA)NH and (HACA)N(CA)CONH experiments offer an alternative assignment protocol for IDPs, by providing connectivities over three sequential residues with the HN-detection that allows for connecting single proline-containing segments of the amino acid sequence. The feasibility of the proposed experiments was experimentally verified on with BilRI, a 165-residue protein, containing three highly similar 40-residue repeats and 12 K-D-A triplet sequences, which represents an extremely challenging case of resonance assignment of IDPs.
References
Åberg CH, Kelk P, Johansson A (2015) Aggregatibacter actinomycetemcomitans: virulence of its leukotoxin and association with aggressive periodontitis. Virulence 6:188–195. https://doi.org/10.4161/21505594.2014.982428
Ahlstrand T, Tuominen H, Beklen A, Torittu A, Oscarsson J, Sormunen R, Pöllänen MT, Permi P, Ihalin R (2017) A novel intrinsically disordered outer membrane lipoprotein of Aggregatibacter actinomycetemcomitans binds various cytokines and plays a role in biofilm response to interleukin-1β and interleukin-8. Virulence 8:115–134. https://doi.org/10.1080/21505594.2016.1216294
Bermel W, Bertini I, Felli IC, Piccioli M, Pierattelli R (2006a) 13C-detected protonless NMR spectroscopy of proteins in solution. Prog Nucl Magn Reson Spectrosc 48:25–45. https://doi.org/10.1016/j.pnmrs.2005.09.002
Bermel W, Bertini I, Felli IC, Kümmerle R, Pierrattelli R (2006b) Novel 13C direct detection experiments, including extension to the third dimension, to perform the complete assignment of proteins. J Magn Reson 178:56–64. https://doi.org/10.1016/j.jmr.2005.08.011
Bermel W, Bertini I, Felli IC, Pierattelli R (2009) Speeding up (13)C direct detection biomolecular NMR spectroscopy. J Am Chem Soc 131:15339–15345. https://doi.org/10.1021/ja9058525
Bermel W, Bertini I, Felli IC, Gonnelli L, Koźmiński W, Piai A, Pierattelli R, Stanek J (2012) Speeding up sequence specific assignment of IDPs. J Biomol NMR 53:293–301. https://doi.org/10.1007/s10858-012-9639-0
Böhlen J-M, Bodenhausen G (1993) Experimental aspects of chirp NMR spectroscopy. J Magn Reson Ser A 102:293–301. https://doi.org/10.1006/jmra.1993.1107
Borcherds WM, Daughdrill GW (2018) Using NMR chemical shifts to determine residue-specific secondary structure populations for intrinsically disordered proteins. Meth Enzymol 611:101–136. https://doi.org/10.1016/bs.mie.2018.09.011
Brutscher B (2002) Intraresidue HNCA and COHNCA experiments for protein backbone resonance assignment. J Magn Reson 156:155–159. https://doi.org/10.1006/jmre.2002.2546
Brutscher B, Felli IC, Gil-Caballero S, Hosek T, Kummerle R, Piai A, Pietarelli R, Solyom Z (2015) NMR methods for the study of intrinsically disordered proteins structure, dynamics, and interactions: general overview and practical guidelines. Adv Exp Med Biol 870:49–122. https://doi.org/10.1007/978-3-319-20164-1_3
Chaves-Arquero B, Pantoja-Uceda D, Roque A, Ponte J, Suau P, Jimenez MA (2018) A CON-based NMR assignment strategy for pro-rich intrinsically disordered proteins with low signal dispersion: the C-terminal domain of histone H1.0 as a case study. J Biomol NMR 72:139–148. https://doi.org/10.1007/s10858-018-0213-2
Delaglio F, Torchia DA, Bax A (1991) Measurement of 15N–13C J couplings in staphylococcal nuclease. J Biomol NMR 1:439–446. https://doi.org/10.1007/bf02192865
Dunker AK, Lawson JD, Brown CJ, Williams RM, Romero P, Oh JS, Oldfield CJ, Campen AM, Ratliff CM, Hipps KW, Ausio J, Nissen MS, Reeves R, Kang C, Kissinger CR, Bailey RW, Griswold MD, Chiu W, Garner EC, Obradovic Z (2001) Intrinsically disordered protein. J Mol Graph Model 19:26–59. https://doi.org/10.1016/S1093-3263(00)00138-8
Dyson HJ (2016) Making sense of intrinsically disordered proteins. Biophys J 110:1013–1016. https://doi.org/10.1016/j.bpj.2016.01.030
Emsley L, Bodenhausen G (1992) Optimization of shaped selective pulses for NMR using a quaternion description of their overall propagators. J Magn Reson 97:135–148. https://doi.org/10.1016/0022-2364(92)90242-Y
Fine DH, Kaplan JB, Kachlany SC, Schreiner HC (2006) How we got attached to Actinobacillus actinomycetemcomitans: A model for infectious diseases. Periodontol 42:114–157. https://doi.org/10.1111/j.1600-0757.2006.00189.x
Fine DH, Patil AG, Velusamy SK (2019) Aggregatibacter actinomycetemcomitans (Aa) under the radar: myths and misunderstandings of aa and its role in aggressive periodontitis. Front Immunol 10:728. https://doi.org/10.3389/fimmu.2019.00728
Fiorito F, Hiller S, Wider G, Wüthrich K (2006) Automated resonance assignment of proteins: 6D APSY-NMR. J Biomol NMR 35:27–37. https://doi.org/10.1007/s10858-006-0030-x
Hellman M, Piirainen H, Jaakola V, Permi P (2014) Bridge over troubled proline: assignment of intrinsically disordered proteins using (HCA)CON(CAN)H and (HCA)N(CA)CO(N)H experiments concomitantly with HNCO and i(HCA)CO(CA)NH. J Biomol NMR 58:49–60. https://doi.org/10.1007/s10858-013-9804-0
Hyvärinen K, Mäntylä P, Buhlin K, Paju S, Nieminen MS, Sinisalo J, Pussinen PJ (2012) A common periodontal pathogen has an adverse association with both acute and stable coronary artery disease. Atherosclerosis 223:478–484. https://doi.org/10.1016/j.atherosclerosis.2012.05.021
Kay LE, Keifer P, Saarinen T (1992) Pure absorption gradient enhanced heteronuclear single quantum correlation spectroscopy with improved sensitivity. J Am Chem Soc 114:10663–10665
Kazimierczuk K, Stanek J, Zawadzka-Kazimierczuk A, Koźmiński W (2013) High-dimensional NMR spectra for structural studies of biomolecules. ChemPhysChem 14:3015–3025. https://doi.org/10.1002/cphc.201300277
Konrat R (2014) NMR contributions to structural dynamics studies of intrinsically disordered proteins. J Magn Reson 241:74–85. https://doi.org/10.1016/j.jmr.2013.11.011
Kozarov EV, Dorn BR, Shelburne CE, Dunn WA Jr, Progulske-Fox A (2005) Human atherosclerotic plaque contains viable invasive Actinobacillus actinomycetemcomitans and Porphyromonas gingivalis. Arterioscler Thromb Vasc Biol 25:e17–e18. https://doi.org/10.1161/01.ATV.0000155018.67835.1a
Mäntylahti S, Tossavainen H, Hellman M, Permi P (2009) An intraresidual i(HCA)CO(CA)NH experiment for the assignment of main-chain resonances in 15N, 13C labeled proteins. J Biomol NMR 45:301–310. https://doi.org/10.1007/s10858-009-9373-4
Mäntylahti S, Aitio O, Hellman M, Permi P (2010) HA-detected experiments for the backbone assignment of intrinsically disordered proteins. J Biomol NMR 47:171–181. https://doi.org/10.1007/s10858-010-9421-0
Mäntylahti S, Hellman M, Permi P (2011) Extension of the HA-detection based approach: (HCA)CON(CA)H and (HCA)NCO(CA)H experiments for the main-chain assignment of intrinsically disordered proteins. J Biomol NMR 49:99–109. https://doi.org/10.1007/s10858-011-9470-z
Marion D, Ikura M, Tschudin R, Bax A (1989) Rapid recording of 2D NMR-spectra without phase cycling – application to the study of hydrogen-exchange in proteins. J Magn Reson 85:393–399. https://doi.org/10.1016/0022-2364(89)90152-2
Motáčková V, Nováček J, Zawadzka-Kazimierczuk A, Kazimierczuk K, Zídek L, Sanderová H, Krásný L, Koźmiński W, Sklenář V (2010) Strategy for complete NMR assignment of disordered proteins with highly repetitive sequences based on resolution-enhanced 5D experiments. J Biomol NMR 48:169–177. https://doi.org/10.1007/s10858-010-9447-3
Nováček J, Zawadzka-Kazimierczuk A, Papoušková V, Zídek L, Sanderová H, Krásný L, Koźmiński W, Sklenář V (2011) 5D 13C-detected experiments for backbone assignment of unstructured proteins with a very low signal dispersion. J Biomol NMR 50:1–11. https://doi.org/10.1007/s10858-011-9496-2
Paino A, Tuominen H, Jääskeläinen M, Alanko J, Nuutila J, Asikainen SE, Pelliniemi LJ, Pöllänen MT, Chen C, Ihalin R (2011) Trimeric form of intracellular ATP synthase subunit β of Aggregatibacter actinomycetemcomitans binds human interleukin-1β. PLoS ONE 6:e18929. https://doi.org/10.1371/journal.pone.0018929
Paino A, Lohermaa E, Sormunen R, Tuominen H, Korhonen J, Pöllänen MT, Ihalin R (2012) Interleukin-1β is internalised by viable Aggregatibacter actinomycetemcomitans biofilm and locates to the outer edges of nucleoids. Cytokine 60:565–574. https://doi.org/10.1016/j.cyto.2012.07.024
Paino A, Ahlstrand T, Nuutila J, Navickaite I, Lahti M, Tuominen H, Välimaa H, Lamminmäki U, Pöllänen MT, Ihalin R (2013) Identification of a novel bacterial outer membrane interleukin-1Β-binding protein from Aggregatibacter actinomycetemcomitans. PLoS ONE 8:e70509. https://doi.org/10.1371/journal.pone.0070509
Pantoja-Uceda D, Santoro J (2014) New 13C-detected experiments for the assignment of intrinsically disordered proteins. J Biomol NMR 59:43–50. https://doi.org/10.1007/s10858-014-9827-1
Permi P (2002) Intraresidual HNCA: An experiment for correlating only intraresidual backbone resonances. J Biomol NMR 23:201–209. https://doi.org/10.1023/A:1019819514298
Permi P, Annila A (2004) Coherence transfer in proteins. Prog Nucl Magn Reson Spectrosc 44:97–137. https://doi.org/10.1016/j.pnmrs.2003.12.001
Permi P, Hellman M (2012) Alpha proton detection based backbone assignment of intrinsically disordered proteins. Methods Mol Biol 895:211–226. https://doi.org/10.1007/978-1-61779-927-3_15
Sahu D, Bastidas M, Showalter S (2014) Generating NMR chemical shift assignments of intrinsically disordered proteins using carbon-detect NMR methods. Anal Biochem 449:17–25. https://doi.org/10.1016/j.ab.2013.12.005
Sattler M, Schleucher J, Griesinger C (1999) Heteronuclear multidimensional NMR experiments for the structure determination of proteins in solution employing pulsed field gradients. Prog Nucl Magn Reson Spectrosc 34:93–202. https://doi.org/10.1016/S0079-6565(98)00025-9
Schleucher J, Schwendinger M, Sattler M, Schmidt P, Schedletzky O, Glaser SJ, Sørensen OW, Griesinger C (1994) A general enhancement scheme in heteronuclear multidimensional NMR employing pulsed field gradients. J Biomol NMR 4:301–306. https://doi.org/10.1007/BF00175254
Shaka AJ, Keeler J (1987) Broadband spin decoupling in isotropic liquids. Prog Nucl Magn Reson Spectrosc 19:47–129. https://doi.org/10.1016/0079-6565(87)80008-0
Shaka AJ, Barker PB, Freeman R (1985) Computer-optimized decoupling scheme for wideband applications and low-level operation. J Magn Reson 64:547–552. https://doi.org/10.1016/0022-2364(85)90122-2
Solyom Z, Schwarten M, Geist L, Konrat R, Willbold D, Brutscher B (2013) BEST-TROSY experiments for time-efficient sequential resonance assignment of large disordered proteins. J Biomol NMR 55:311–321. https://doi.org/10.1007/s10858-013-9715-0
Takeuchi H, Hirano T, Whitmore SE, Morisaki I, Amano A, Lamont RJ (2013) The serine phosphatase SerB of Porphyromonas gingivalis suppresses IL-8 production by dephosphorylation of NF-κB RelA/p65. PLoS Pathog 9:e1003326. https://doi.org/10.1371/journal.ppat.1003326
Uversky VN, Gillespie JR, Fink AL (2000) Why are "natively unfolded" proteins unstructured under physiologic conditions? Proteins 41:415–427. https://doi.org/10.1002/1097-0134(20001115)41:3%3c415:AID-PROT130%3e3.3.CO;2-Z
Vranken WF, Boucher W, Stevens TJ, Fogh RH, Pajon A, Llinas M, Ulrich EL, Markley JL, Ionides J, Laue ED (2005) The CCPN data model for NMR spectroscopy: development of a software pipeline. Proteins 59:687–696. https://doi.org/10.1002/prot.20449
Yao J, Dyson HJ, Wright PE (1997) Chemical shift dispersion and secondary structure prediction in unfolded and partly folded proteins. FEBS Lett 419:285–289. https://doi.org/10.1016/s0014-5793(97)01474-9
Ying J, Roche J, Bax A (2014) Homonuclear decoupling for enhancing resolution and sensitivity in NOE and RDC measurements of peptides and proteins. J Magn Reson 241:97–102. https://doi.org/10.1016/j.jmr.2013.11.006
Yoshimura Y, Kulminskaya N, Mulder FAA (2015) Easy and unambigous sequential assignments of intrinsically disordered proteins by correlating the backbone 15N and 13C′ chemical shifts of multiple contiguous residues in highly resolved 3D spectra. J Biomol NMR 61:109–121. https://doi.org/10.1007/s10858-014-9890-7
Zhou Z, Kümmerle R, Qiu X, Redwine D, Cong R, Taha A, Baugh D, Winniford B (2007) A new decoupling method for accurate quantification of polyethylene copolymer composition and triad sequence distribution with 13C NMR. J Magn Reson 187:225–233. https://doi.org/10.1016/j.jmr.2007.05.005
Acknowledgements
Open access funding provided by University of Jyväskylä (JYU). This work is supported by the grants from the Academy of Finland (Number 288235 to PP, 265609, 272960 and 303781 to RI).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tossavainen, H., Salovaara, S., Hellman, M. et al. Dispersion from Cα or NH: 4D experiments for backbone resonance assignment of intrinsically disordered proteins. J Biomol NMR 74, 147–159 (2020). https://doi.org/10.1007/s10858-020-00299-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10858-020-00299-w