Abstract
Peak overlap in crowded regions of two-dimensional spectra prevents characterization of dynamics for many sites of interest in globular and intrinsically disordered proteins. We present new three-dimensional pulse sequences for measurement of Carr-Purcell-Meiboom-Gill relaxation dispersions at backbone nitrogen and carbonyl positions. To alleviate increase in the measurement time associated with the additional spectral dimension, we use non-uniform sampling in combination with two distinct methods of spectrum reconstruction: compressed sensing and co-processing with multi-dimensional decomposition. The new methodology was validated using disordered protein CD79A from B-cell receptor and an SH3 domain from Abp1p in exchange between its free form and bound to a peptide from the protein Ark1p. We show that, while providing much better resolution, the 3D NUS experiments give the similar accuracy and precision of the dynamic parameters to ones obtained using traditional 2D experiments. Furthermore, we show that jackknife resampling of the spectra yields robust estimates of peak intensities errors, eliminating the need for recording duplicate data points.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Millisecond protein dynamics is essential for most protein processes including folding, ligand binding, enzymatic catalysis, and allosteric regulation. Nuclear magnetic resonance (NMR) spectroscopy is especially well suited for characterization of protein dynamics since a unique signal is obtained for each nucleus, enabling studies at atomic resolution at nearly native conditions. The parameters that can be determined for a molecule exchanging between two states are the exchange rate (kex), the population of the excited state (pB) and the difference in chemical shifts between the exchanging states (Δϖ). These parameters report on kinetics, thermodynamics and structure of the excited state. A number of distinct NMR techniques have been developed for studies of millisecond dynamics and, if the exchange rate is on the order of hundreds of inverse seconds and the population of the excited state is at least 0.5%, Carr-Purcell-Meiboom-Gill (CPMG) relaxation dispersion (RD) is the method of choice (Orekhov et al. 1994; Loria et al. 1999; Sekhar and Kay 2013).
Severe signal overlap often precludes analysis of important peaks in two-dimensional NMR spectra, such as in the 1H–15N correlation maps typically used in relaxation experiments. The overlap particularly complicates the dynamic studies of large and disordered protein systems. Increase of spectral dimensionality in combination with non-uniform sampling (NUS) has been widely used during the last decade for dramatic improvement of resolution in the spectra. However, applications of NUS for quantitative analysis such as studies of molecular dynamics is only emerging (Matsuki et al. 2011; Mayzel et al. 2014a, b; Long et al. 2015; Oyen et al. 2015; Linnet and Teilum 2016; Stetz and Wand 2016). The method requires caution to avoid biases in the results due to the inherent non-linearity (Schmieder et al. 1997; Hyberts et al. 2014) of many techniques developed for NUS spectra reconstruction.
In this work, we introduce three-dimensional NUS HNCO-based versions of the 13CO and 15N RD experiments and validate the method of co-processing for unbiased spectra reconstruction. We also present jackknife resampling, a rigorous statistical procedure for determining confidence regions of the extracted parameters without using repeated measurements. Finally, we demonstrate incremental data accumulation with concurrent spectra processing as a tool for monitoring progress of achieving targets on precision of the peak intensities. The new experiments and analysis are illustrated using two protein systems with well understood dynamics on the millisecond time scale: the SH3 domain from the yeast protein Abp1p partially bound to a peptide from the protein Ark1p and the disordered cytosolic domain of the CD79A chain from the B-cell receptor.
Methods
Processing of NUS spectra
The RD technique requires accurate measurements of peak intensities in an array of NMR spectra recorded as a function of frequency (ν) of the refocusing pulses in the CPMG sequence. Traditionally, processing and measuring of peak intensities are performed independently for each spectrum. For processing of individual NUS RD spectra we used one of the modern algorithms Iteratively Reweighted Least Squares with Virtual-Echo (IRLS-VE) (Mayzel et al. 2014; Kazimierczuk and Orekhov 2011).
An alternative approach used in this work exploits the fact that positions and line shapes of peaks are invariant to the CPMG frequency. The most general models for signals in the two- and three-dimensional RD experiments are (Korzhnev et al. 2001; Gutmanas et al. 2004):
where the model of the ν-th spectrum on the left is presented as a sum over components enumerated by index i. Each component consists of a peak intensity coefficient α i and two (three) normalized vectors V H, V N, and V CO, which describe positions and line shapes of a peak for 1H, 15N, and 13CO spectral dimensions, respectively; the symbol ⊗ denotes the tensor product operation, which generates a two (three) dimensional peak object from the vectors. The model in Eq. 1 contains a relatively small number of unknowns because vectors V are shared between spectra with different CPMG frequencies. The parameters in the model can be obtained with high fidelity from a few NUS measurements by co-processing of spectra obtained for all ν values simultaneously using multi-dimensional decomposition algorithm (co-MDD) (Mayzel et al. 2014a; Hiller et al. 2009; Orekhov and Jaravine 2011). The number of the model parameters, and consequently the minimal amount of the experimental data needed, can be further reduced by additional assumptions about the functional form for the vectors (Long et al. 2015; Jaravine et al. 2006).
Error estimations with resampling
The most common practice for estimating errors in relaxation dispersion experiments is based on repeating measurements for some of the CPMG frequencies, from which either the global peak intensity error, if number of repeated measurements is small, or per residue intensity error is estimated. Here, we propose jackknife resampling that eliminates the necessity of the duplicate measurements and provides reliable error estimates for individual residues. Hence, the new method allows sampling of the RD at more CPMG frequencies during the same total experimental time, which in turn is beneficial for subsequent relaxation analysis.
Statistical resampling-based analysis is a natural and preferable alternative to the repeated measurements approach when NUS is utilized for spectra acquisition (Isaksson et al. 2013). In the delete-d jackknife procedure presented below, a set of realizations is produced from the recorded data by randomly omitting a small fraction of measurements. According to the theory, d—the amount of the omitted data should be equal or exceed the square root of N—the total number of NUS data points. In our particular case, since the omission must not significantly reduce sensitivity of the spectra and the chances for accurate peak reconstruction, we omitted \(~\sqrt N\) points. Strictly speaking, for the delete-d jackknife resampling, all possible subsamples \(\left( {\frac{N}{d}} \right)=\frac{{N!}}{{d!\left( {N - d} \right)!}}\) have to be computed. This number quickly becomes very sizable and as an approximation, one can take a small random subset from all possible subsamples. The standard errors of the peak intensities that are calculated over the resampling trials must be up-scaled with the so-called inflation factor \(~F=~\sqrt {N/d}\). The inflation factor is needed because intensities in the spectra, obtained by deleting d out of N observations are highly correlated and the regular standard deviation over resampling trials gives underestimated values (Efron 1993).
In the current study, we consistently used 20 different resampling trials by randomly omitting 15–20% of the acquired data points both for 2D and 3D datasets. As a result of the resampling procedure, for each peak at every CPMG field strength a set of 20 intensities were obtained. The standard deviation of the set, up-scaled with an inflation factor, gives an estimate for the peak intensity error. It should be emphasized that, in contrast to the global error usually obtained from the duplicate measurements, the errors estimated by delete-d jackknife resampling are individual for every peak and every CPMG frequency. Another way to utilize the power of resampling techniques is to obtain parameters of the exchange for every resampling trial and then perform statistical analysis of these values to estimate the uncertainties. The possible drawback of the later method is two-fold: first down-sampled spectra have slightly lower signal-to-noise ratio and thus the intensity error is higher, second in order to calculate the relaxation parameters for each resampling trial one still needs estimates of the peak intensity errors. For the relaxation analysis we have not observed any significant difference between these two methods (data not shown), though in some complex tasks, for example backbone assignment, (Isaksson et al. 2013) the latter method is the only possible method to access the uncertainty.
Error estimations with targeted acquisition
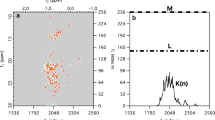
An additional advantage of using NUS concerns optimal planning of the RD experiment and addresses the following practical questions: which sparse level and correspondingly how much measurement time is needed for achieving required precision of the measured relaxation rates? Is it feasible to obtain good RD data for a defined set of residues in a particular protein sample? In the traditional approach, the decision about the total measurement time is taken before the experiment starts. Thus, miscalculations are common where either the experiment is too short and RDs of insufficient quality are obtained or the measurement time is too long and spectrometer time is wasted. A solution is found in the concepts of incremental NUS and targeted acquisition (TA) (Jaravine and Orekhov 2006), where the signal processing and statistical analysis are performed in steps concurrently with the experiment (Fig. 1). With such approach, the variation of peak intensities calculated over consecutive steps can be used as a crude estimate of the peak precision at a given time of the experiment.
Schematic presentation of the TA procedure for the real-time estimate of the peak intensity precision. The spectra are processed in steps as more and more NUS points are acquired. The precision of individual peak intensities is estimated as the difference between the intensities obtained at two successive steps
Spectra analysis and calculation of dynamic parameters
Recorded spectra were processed with mddnmr software using either IRLS algorithm (Kazimierczuk and Orekhov 2011) with Virtual-Echo modification (Mayzel et al. 2014b) or co-processed with co-MDD. For co-MDD the number of iterations and regularization parameter lambda were set to 2000 and 10−4, respectively; number of iterations for the IRLS was set to 30. Peak intensities, estimated using the seriesTab script included in the nmrPipe software (Delaglio et al. 1995), were converted into effective transverse relaxation rates \({R_{2,eff}}({\nu _{cpmg}})=\ln \left( {{I_0}/I} \right)/T,\) where \(~I\) and I 0 are the intensities with and without the constant time relaxation delay of duration \(T\) and \({\nu _{cpmg}}\) is the repetition rate in the CPMG pulse train. Residues with significant chemical exchange (p < 0.01) in individual fits were fitted to a global two-state model using the software CATIA (Hansen et al. 2008).
Protein expression and purification
Uniformly 13C/15N labeled cytoplasmic domain of human CD79A was produced using an in-house developed cell-free expression system as previously described (Isaksson et al. 2013). Purified and lyophilized CD79A was dissolved to a final concentration of ca. 200 µM in aqueous buffer containing 20 mM NaPi pH 6.8, 1 mM EDTA, Complete EDTA-free protease inhibitor cocktail (Roche), 2 mM DTT, and 10% D2O.
Uniformly 13C/15N labeled SH3 domain from Abp1p was produced and purified as previously described (Vallurupalli et al. 2007). The added peptide was a 17-residue fragment (KKTKPTPPPKPSHLKPK) from the protein Ark1p (Haynes et al. 2007), purchased from EZBiolab. The purified NMR sample was 0.8 mM protein, 50 mM NaPi pH 7.0, 100 mM NaCl, 1 mM EDTA, 1 mM NaN3 and 10% D2O.
NMR spectroscopy
All NMR data were acquired at Varian INOVA spectrometers equipped with the room-temperature probe heads at the static magnetic fields of 18.8 T. The sample temperature was 25 °C in all cases. 15N- and 13CO-CPMG dispersions were acquired by the standard pulse sequences (Lundstrom et al. 2008; Vallurupalli and Kay 2006) as well as using sparse sampling in the three-dimensional HNCO type experiments described above. Experimental details are summarized in Table 1. Sampling schedules, generated using the program nussampler, which is part of the mddnmr software (Orekhov and Jaravine 2011), had flat random distribution in the relaxation pseudo dimension and exponential matched to 100 ms acquisition in the indirect spectral dimensions. Both classes of experiments were recorded in an interleaved fashion.
Results and discussion
Pulse sequences for measurements of 15N and 13CO relaxation dispersions at high resolution
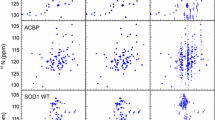
A common problem, even for many small well-folded proteins, is severe spectral overlap that precludes reliable determination of peak volumes, which in turn complicates accurate characterization of protein dynamics for all residues. This problem is of course even more serious for larger or intrinsically disordered proteins. An obvious way of mitigating or reducing this problem is to extend the data to a third dimension. Unfortunately, this increases the measurement time so that a relaxation data set that requires 12 h to record in the normal way would require approximately 1 week recorded in three dimensions, which is prohibitively long. However, if sparse rather than uniform sampling is employed, the data can be recorded in a fraction, perhaps one-tenth, of that time, which would mean that the time requirements would be similar as for the two-dimensional case. With this in mind, we designed three-dimensional pulse sequences for the measurements of 15N and 13CO CPMG relaxation dispersion. In both these experiments, the flow of magnetization is 1H → 15N → 13CO (t1) → 15N (t2) → 1H (t3) and they can thus be thought of as HNCO experiments with constant time relaxation delays inserted at appropriate places.
Figure 2 shows the pulse sequence used for measurements of 15N and 13CO dispersions. While the 13CO version of the pulse sequence is a straightforward extension of the one already published (Lundstrom et al. 2008), a remark can be made regarding the 15N version. At the start of the relaxation delay, the density matrix is equal to 2NxHz and it will evolve between anti-phase and in-phase operators in a manner that depends on the number of applied refocusing pulses. Since the different operators have different relaxation rates this introduces artifacts to the dispersion profiles if not addressed. We chose the approach of Palmer and coworkers (Loria et al. 1999) where the time spent as in-phase and anti-phase are equalized, regardless of the number of applied refocusing pulses, by splitting the relaxation delay in half and exchanging in-phase and anti-phase operators in between.
Pulse sequences for measurement of a 13CO and b 15N CPMG relaxation dispersions. Narrow and wide rectangles represent rectangular 90° and 180° pulses, respectively. All pulses are centered at 4.77, 176 and 119 ppm for 1H, 13C and 15N, respectively. The phase of all pulses is x if not specified. The shaped pulse on proton is used to selectively excite the water resonance. A 1.5 ms rectangular pulse was used here. All rectangular 90° pulses on 13C are applied at a field strength that yields null at 58 ppm. The 180° pulse represented by an open rectangle is shifted 118 ppm upfield and applied with a field strength that gives a null at 176 ppm. Shaped pulses of duration 450 μs on 13C are used to selectively invert or refocus 13CO. These are similar to the RE-BURP variety of selective pulses (Geen and Freeman 1991) but have improved inversion profiles (Lundstrom et al. 2008). The simultaneous pulses (applied as a complete train in each scan) during 15N→13CO transfer have phases ϕ2(i) = 2(x,y,x,y,y,x,y,x,−x,−y,−x,−y,−y,−x,−y,−x) so that both the x and the y components of transverse magnetization are refocused properly in the presence of off-resonance effects and pulse imperfections (Gulltan et al. 1990). The phase cycling is ϕ1 = y,−y; ϕ3 = y,y,−y,−y; ϕ4 = y,−y; ϕ5 = x; ϕ6 = x; ϕ7 = 4(x),4(−x); ϕ8 = x, ϕ9 = x,x,−x,−x, receiver = x,−x,−x,x. Quadrature detection in t1 is achieved by incrementing the phase ϕ5 (or ϕ9) by π/2 and in t2 by incrementing the phase ϕ6 by π and inverting the gradient g6. For every increment in t1 and t2 the phases of ϕ5 (or ϕ9) and ϕ8 are incremented by π, respectively. Proton decoupling is achieved by WALTZ-16 at a field of 6 kHz and 13Cα decoupling is achieved by SEDUCE-1 that is cosine modulated at 118 ppm (McCoy and Mueller 1992). Decoupling during acquisition employs WALTZ-16 at a field-strength of 1.2 kHz for 15N (Shaka et al. 1983) and WURST-2 (bandwidth of 12 ppm, centered at 176 ppm, maximum (rms) B1 field of 0.6 (0.4) kHz) for 13CO (Kupce and Freeman 1995). The delays are τa = 2.3 ms, τb = 1.36 ms, τeq = 3 ms, T = 10 ms, TN = 14 ms, Δ = 0.5 ms ξ1 = max (0, TN - t1/2), ξ2 = max (0, t1/2 - TN). In this scheme, data is recorded in constant-time mode for t1 < 2TN, whereas magnetization decays for t1 > 2TN. The gradient-strengths in G/cm (durations in ms) are g1 = 4.0(0.5), g2 = 10.0(1.0), g3 = 7.0(1.0), g4 = −6.0(0.6), g5 = 3.3(0.6), g6 = −30.0(1.25), g7 = 4.0(0.3), g8 = 2.0(0.4), g9 = 29.6(0.125)
When comparing the sensitivity of the new three-dimensional pulse sequences with the standard two-dimensional ones, there is a difference between pulse sequences designed to measure 13CO and 15N millisecond dynamics. For 13CO, the sensitivity in a single scan is only slightly worse (due to evolution at 13CO), implying that the overall sensitivity per measurement time will be about \(\sqrt 2\) lower for the three-dimensional version. In two-dimensional experiments that measure 15N relaxation dispersions, there is obviously no need to transfer magnetization from 15N to 13CO and back, implying that the sensitivity losses for the three-dimensional experiment is larger because of relaxation losses during the transfer periods.
The benefits of increased resolution with an extra dimension in the NUS-CPMG are different for different proteins. This was expected and is summarized in Table 2. Proteins, for which the 15N-HSQC is highly resolved, such as Abp1p SH3 domain (Drubin et al. 1990), benefit less than proteins with poorly dispersed spectra, such as the intrinsically disordered cytoplasmic domain from CD79A (Isaksson et al. 2013). When peak overlap is not too severe, the 3D pulse sequences can be run in 2D mode, which may allow resolving signals overlapped in either 15N or 13CO dimensions. However, we did not try this in our work.
Accurate relaxation parameters from 2D NUS RD experiments
First we validated our quantitative NUS spectra reconstruction approach for the traditional 2D versions of the RD experiments obtained for SH3 domain from the yeast protein Abp1p, partially bound to a peptide from the protein Ark1p. Binding of a ligand with K d = 4.4 μM (Haynes et al. 2007) and k ex = k on [L] + k off manifests as CPMG dispersions for various nuclei for a subset of protein residues (Lundstrom et al. 2008, 2009a, b; Hansen et al. 2008a). Furthermore, the difference in chemical shifts between the free and bound states can be measured directly from peak positions in spectra of free and saturated SH3 domain. For a partially bound sample, this allows to not only compare determined values for k ex and p B for different pulse sequences but also how accurately chemical shifts of the excited state are determined. Figure 3 and Table 3 demonstrate comparison of the dynamic parameters p B , k ex and Δϖ obtained from two-dimensional 13CO and 15N RD experiments recorded in full and with NUS. The NUS spectra were obtained by randomly sub-sampling the fully sampled reference spectra at different sparse levels. Figure 3 shows that in our two-dimensional RD experiments, reliable parameters of the millisecond dynamics can be obtained using down to 25% sparse sampling. This result is in line with recent applications of co-processing to 2D relaxation data (Linnet and Teilum 2016). The observed increase in the error of the dynamic parameters as NUS gets sparser is within the limits expected for the square-root dependence of the spectral signal-to-noise ratio on the measurement time experiments. Thus, the use of NUS and co-MDD processing does not introduce noticeable bias or additional noise into the analysis.
Analysis of the 2D 15N and 13CO RD experiments on Abp1p SH3 domain partially bound to the Ark1p peptide. Global parameters kex (a, b) and pB (c, d) obtained from the RD as well as RMSD (e, f) between the Δϖ measured directly and derived from RD are shown versus the spectrum sparse level. Shown is a typical result obtained for a NUS scheme (random seed, flat random distribution) using different estimates of errors for the R 2 values: (black) from the duplicate measurement and (red) from 20 jackknife resampling trials, respectively. Circles and error bars give fitted values and uncertainties of kex and pB of the parameters. The areas indicated by gray color and restricted by the red lines show an anticipated error obtained as an extrapolation of the uncertainty in the reference spectrum to shorter measurement times as ~1⁄√t
Accurate relaxation parameters from 3D NUS RD experiments
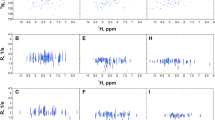
In order to validate the new 3D NUS RD experiments, they were tested for two different proteins and the derived dynamic parameters were compared with the results from the standard 2D experiments. For the disordered cytosolic domain of CD79A chain from the B-Cell receptor, the RD profiles in 2D and 3D experiments were flat. When comparing fits of the RD data to the models with and without conformational exchange, we did not find millisecond dynamics at a significance level of p < 0.01 for any individual amino acid residues, and hence, proceeded with comparing the pairwise root-mean-square-deviation (RMSD) between the experimental data and the best fit to a constant function for the 3D NUS and the standard 2D experiments. The average over all NH group RMSD values for the three- and two-dimensional 15N RD experiments were 0.35 ± 0.19 s−1, and 0.19 ± 0.09 s−1, respectively. Figure S1 shows 15N relaxation dispersions for the residues with the smallest, the median and the largest RMSD for the 3D NUS 15N RD experiment and the same residues in the standard 2D experiment. Even the highest value of 1.1 s−1 for residue A15 is tolerable and the conclusion is that NUS in the three-dimensional pulse sequences does not introduce artefacts into CPMG RD profiles. Clearly, the new experiments can provide just as good precision as the well-established 2D experiments while greatly improving the peak resolution.
The analysis of the relaxation dispersions of the Abp1p SH3 domain with partly bound Ark1p peptide demonstrated that the new 3D NUS RD experiments are well suited for studies of millisecond dynamics. Table 4 summarizes and compares the results of all experiments when fitted to a global two-state model and Fig. 4 shows that 15N as well as 13CO experimental data are described well by this model. The global parameters, p B , and k ex , are identical within error regardless of either 2D or 3D experiment was used to probe the dynamics. Small difference between the results obtained from 15N and 13CO may be explained by apparent coupling between p B , and k ex , parameters.
15N (top row) and 13CO (bottom row) relaxation dispersion profiles from the 3D NUS experiments for serval residues of Abp1p SH3 domain partially bound to a peptide from Ark1p. The residues with the smallest (N16/E7), median (S52/W37) and largest (V32) |Δϖ| are shown. Filled circles represent experimental data collected using the three-dimensional pulse sequence with sparse sampling at 18.8 T. The line represents the best fit to a global two-state model
We have previously noted that the 13CO dispersion profiles for Asp/Asn residues may deviate from the expected appearance and shown that this is due to an unrefocused coupling with the side-chain 13CO during the relaxation delay (Lundstrom et al. 2008). When an increasing number of refocusing pulses is applied, the coupling regime changes from weak towards strong, implying that R 2,eff is modulated by νCPMG even in the absence of chemical exchange. Since the coupling constant is dependent on the χ1 dihedral angle, the effect is not equally serious for all residues of these types. We have included an option to refocus the coupling at the expense of slightly lowered sensitivity (Lundstrom et al. 2008) but chose to not use this refocusing element here. Plots for all residues showing the relaxation dispersions are found in Supplementary Figure S2.
Lastly, we compared |Δϖ| extracted from the fits of 3D RDs and those measured from the difference in the peak positions in the spectra of free SH3 domain and SH3 domain saturated with Ark1p peptide. Figure 5, demonstrates excellent correlations for both 15N and 13CO |Δϖ|. For 13CO, the pairwise RMSD between the values are equally good for the three-dimensional and two-dimensional experiments. For 15N, the values determined from the 2D experiment agree somewhat better with the RMSDs of 0.12 and 0.19 ppm, respectively.
Correlation between the magnitude of difference in chemical shift obtained from the 3D RD experiments (a 3D 15N-NUS-CPMG and b 13CO-NUS-CPMG) and calculated from free Abp1p SH3 domain and SH3 domain saturated with Ark1p peptide. All residues with significant chemical exchange are shown. Pairwise RMSD between |ΔωCPMG| and |ΔωDirect| are shown in the bottom-right corners of the panels. The straight line represents |ΔωCPMG|=|ΔωDirect| to guide the eye
Comparison of RD’s obtained with co-MDD and IRLS-compressed sensing algorithms
For the processing of sparsely sampled three-dimensional RD experiments we compared Multi-Dimensional Decomposition co-processing (co-MDD) using Eq. 1, and a representative compressed sensing algorithm—Iteratively Reweighted Least Squares with Virtual-Echo enhancement (IRLS-VE) (Mayzel et al. 2014; Kazimierczuk and Orekhov 2011). Results are summarized in Table 4. For the 13CO relaxation dispersion experiment both co-MDD and IRLS-VE showed comparable and correct within experimental error results, although the exchange rate error and |Δϖ| correlations for the IRLS reconstruction were notably higher. For the 15N relaxation dispersion experiment, IRLS-VE and co-MDD correspond to each other, although IRLS-VE again gives slightly elevated errors compare to co-MDD processing. Furthermore, comparison with the reference relaxation parameters, derived from fully sampled two-dimensional pulse sequences, shows that IRLS-VE leads to a slightly augmented value of the exchange rate and understated value of the excited state population.
It was important to check how robust the 3D NUS experiments are in respect to the amount of NUS points and if it was possible to further reduce the measurement time. Table 5 depicts the results of the 15N RD analysis obtained using co-MDD and IRLS-VE at different NUS levels. Co-MDD produces correct results down to 4.1% NUS level with only a small increase of the errors. IRLS-VE also works although the errors are notably higher and rapidly increase as the NUS level decreases.
From this study and from reports of other groups (Long et al. 2015; Linnet and Teilum 2016), we conclude that co-MDD and related methods that simultaneously process spectra corresponding to all CPMG frequencies perform better than the compressed sensing algorithms, which are the most successful when processing single spectra.
Estimation of R2 errors with jackknife approach
Correct estimation of the precision of the relaxation rates in the RD experiments is crucial for accurate calculation of dynamic parameters and their uncertainties. The commonly used approach is to perform duplicate measurements of the relaxation rates for several CPMG frequencies and to derive the error estimates from the variance of the obtained R2 values. In this work, we present an alternative approach based on the jackknife resampling. By randomly omitting a fraction (10–20%) of the NUS data, we produce multiple sufficiently independent spectra realizations, from which intensity errors can be obtained for each peak. Figure 3 and Table 4, show that accuracy and precision of the fitted dynamic parameters k ex , p B , and Δϖ obtained from the traditional duplicate measurements and by the jackknife procedure are very similar. This validates the jackknife approach and renders the repeated measurements in NUS spectra unnecessary. Omitting the repeated measurements allows to further reduce time of the RD experiment or to sample of more CPMG frequencies for improving reliability of the analysis.
Targeted acquisition approach to real-time R2 error evaluation
One of the advantages of sparse data acquisition is that the spectra can be processed at any time during acquisition. As a consequence, it is possible to estimate spectrum quality in real-time during the experiment. Depending on the task, various parameters like desired number of peaks, peak intensity or R2 error, as in the current study, can be set as an experiment ‘target’ in the procedure that we call Targeted Acquisition (TA) (Isaksson et al. 2013; Jaravine and Orekhov 2006; Jaravine et al. 2008). Errors in intensity and R2 for a peak can be estimated as the variation between the values at consecutive moments of data collection, e.g. between 4 and 5% NUS. The TA approach can be thought as a proxy of the resampling method with only a single resampling event. In order to improve the statistics, we calculate an average intensity error over multiple spectral peaks. This should be distinguished from the true jackknife resampling, where intensity errors of individual peaks are obtained from the statistical analysis over multiple resampling trials. Figure 6 demonstrates and compares various approaches for TA error estimation, where black lines correspond to the traditional error estimation from duplicate measurements, red dashed lines correspond to variation of R2 values between consecutive TA steps, and red solid line corresponds to the jackknife approach for R2 error estimation. As can be seen from the black curves the R2 error shoots up at 4.15% NUS. This is the NUS level, where there is simply not enough data for good spectra reconstruction by co-MDD. As both TA and jackknife approaches relies on subsampling, their R2 errors estimates depend on the spectrum quality at 10–20% lower NUS levels. This explains why the R2 errors obtained from TA and jackknifes shoot up at 5% NUS and have somewhat higher, i.e. by less than 30%, values relative to the errors obtained from the duplicate measurements. R2 errors obtained by all three methods are comparable, which allows use of the more practically convenient jackknife as well as validates the TA approach for quantitative monitoring of the spectrum quality improvement in real time during the experiment.
R2 error estimation with Targeted Acquisition. TA calculations were performed post hoc by subsampling the 8.3% NUS three-dimensional 15N relaxation dispersion experiment on Abp1p SH3 domain partially bound to a peptide from Ark1p. Spectra were processed and analyzed in steps starting from 3.3% NUS, at each step 1% NUS points was added to the final 8.3% NUS. 15 random TA realizations were made to average the effect of various random seeds. Black dotted lines and black dot at 8.3% NUS correspond to R2 error estimated as a global error from duplicate measurements, black dashed line corresponds to global error from duplicate measurements at 8.3% NUS scaled according to the measurement time. The red dot at 8.3% NUS correspond to R2 error estimated from jackknife resampling. Red dotted lines correspond to R2 error calculated as a variation of R2 values on consecutive TA steps. Red solid line corresponds to R2 error calculated via jackknife resampling on every TA step
Conclusions
In this work, we introduce a new approach for acquisition and processing of the relaxation dispersion experiments for the protein backbone 15N and 13CO atoms. The main advantage of the new method is the much-improved spectral resolution, which allows characterization of protein dynamics of those peaks, that overlap in the traditional spectra. We present two new 3D pulse sequences for 15N and 13CO RD experiments. In order to keep the measurement time of the high resolution 2D and 3D experiments short and comparable to the duration of the traditional 2D experiments, we use NUS. We show that the best accuracy and precision of the derived parameters of the conformational exchange are obtained when the NUS spectra corresponding to the individual CPMG frequencies are co-processed using multi-dimensional decomposition. Quantitative analysis of the spectra processed individually with the compressed sensing is also possible, although the results are noticeably worse. In order to further reduce the measurement time, we introduce a new method for estimation of errors in the relaxation rates. Namely, we suggest to replace the time consuming repeated measurements with the jackknife resampling of the NUS data. In practice, it may be difficult to predict required experimental time and NUS level needed to achieve acceptable precision of the relaxation rates for a signal of interest. We show that estimates of the precision may be obtained during the experiment in real time, thus allowing to “target” the RD experiment for a predefined precision. The error estimates obtained from the jackknife resampling and targeted procedure are similar to the errors derived from the traditional approach with the duplicate measurements.
References
Delaglio F et al (1995) NMRPipe: a multidimensional spectral processing system based on UNIX pipes. J Biomol NMR 6, 277–293
Drubin DG, Mulholland J, Zhu ZM, Botstein D (1990) Homology of a yeast actin-binding protein to signal transduction proteins and myosin-I. Nature 343:288–290
Efron BT (1993) R: An introduction to the bootstrap. Chapman & Hall, New York
Geen H, Freeman R (1991) Band-selective radiofrequency pulses. J Magn Reson 93:93–141
Gullion T, Baker DB, Conradi MS (1990) New, compensated carr-purcell sequences. J Magn Reson 89:479–484
Gutmanas A, Luan T, Orekhov VY, Billeter M (2004) Accurate relaxation parameters for large proteins. J Magn Reson 167:107–113
Hansen DF, Vallurupalli P, Kay LE (2008a) An improved 15 N relaxation dispersion experiment for the measurement of millisecond time-scale dynamics in proteins. J Phys Chem B 112:5898–5904
Hansen DF, Vallurupalli P, Lundstrom P, Neudecker P, Kay LE (2008b) Probing chemical shifts of invisible states of proteins with relaxation dispersion NMR spectroscopy: how well can we do? J Am Chem Soc 130:2667–2675
Haynes J et al (2007) The biologically relevant targets and binding affinity requirements for the function of the yeast actin-binding protein 1 Src-homology 3 domain vary with genetic context. Genetics 176:193–208
Hiller S, Ibraghimov I, Wagner G, Orekhov VY (2009) Coupled decomposition of four-dimensional NOESY spectra. J Am Chem Soc 131:12970–12978
Hyberts SG, Arthanari H, Robson SA, Wagner G (2014) Perspectives in magnetic resonance: NMR in the post-FFT era. J Magn Reson 241:60–73
Isaksson L et al (2013) Highly efficient NMR assignment of intrinsically disordered proteins: application to B- and T cell receptor domains. PLoS ONE 8:e62947
Jaravine VA, Orekhov VY (2006) Targeted acquisition for real-time NMR spectroscopy. J Am Chem Soc 128:13421–13426
Jaravine V, Ibraghimov I, Orekhov VY (2006) Removal of time barrier for high-resolution multidimensional NMR spectroscopy. Nat Methods 3:605–607
Jaravine VA, Zhuravleva AV, Permi P, Ibraghimov I, Orekhov VY (2008) Hyperdimensional NMR spectroscopy with nonlinear sampling. J Am Chem Soc 130:3927–3936
Kazimierczuk K, Orekhov VY (2011) Accelerated NMR spectroscopy by using compressed sensing. Angewandte Chem 50:5556–5559
Korzhnev DM, Ibraghimov IV, Billeter M, Orekhov VY (2001) MUNIN: application of three-way decomposition to the analysis of heteronuclear NMR relaxation data. J Biomol NMR 21:263–268
Kupce E, Freeman R (1995) Adiabatic pulses for wide-band inversion and broad-band decoupling. J Magn Reson Ser A 115:273–276
Linnet TE, Teilum K (2016) Non-uniform sampling of NMR relaxation data. J Biomol NMR 64:165–173
Long D, Delaglio F, Sekhar A, Kay LE (2015) Probing invisible, excited protein states by non-uniformly sampled pseudo-4D CEST spectroscopy. Angewandte Chem 54:10507–10511
Loria JP, Rance M, Palmer AG (1999) A relaxation-compensated Carr-Purcell-Meiboom-Gill sequence for characterizing chemical exchange by NMR spectroscopy. J Am Chem Soc 121:2331–2332
Lundstrom P, Hansen DF, Kay LE (2008) Measurement of carbonyl chemical shifts of excited protein states by relaxation dispersion NMR spectroscopy: comparison between uniformly and selectively (13)C labeled samples. J Biomol NMR 42:35–47
Lundstrom P, Lin H, Kay LE (2009a) Measuring 13Cbeta chemical shifts of invisible excited states in proteins by relaxation dispersion NMR spectroscopy. J Biomol NMR 44:139–155
Lundstrom P, Hansen DF, Vallurupalli P, Kay LE (2009b) Accurate measurement of alpha proton chemical shifts of excited protein states by relaxation dispersion NMR spectroscopy. J Am Chem Soc 131:1915–1926
Matsuki Y, Konuma T, Fujiwara T, Sugase K (2011) Boosting protein dynamics studies using quantitative nonuniform sampling NMR spectroscopy. J Phys Chem B 115:13740–13745
Mayzel M, Rosenlöw J, Isaksson L, Orekhov VY (2014a) Time-resolved multidimensional NMR with non-uniform sampling. J Biomol NMR 58:129–139
Mayzel M, Kazimierczuk K, Orekhov VY (2014b) The causality principle in the reconstruction of sparse NMR spectra. Chem Commun 50:8947–8950
McCoy MA, Mueller L (1992) Selective shaped pulse decoupling in NMR - homonuclear C-13 carbonyl decoupling. J Am Chem Soc 114:2108–2112
Orekhov VY, Jaravine VA (2011) Analysis of non-uniformly sampled spectra with multi-dimensional decomposition. Prog Nucl Magn Reson Spectrosc 59:271–292
Orekhov VY, Pervushin KV, Arseniev AS (1994) Backbone dynamics of (1-71)bacterioopsin studied by two-dimensional 1H-15N NMR spectroscopy. Eur J Biochem 219:887–896
Oyen D, Fenwick RB, Stanfield RL, Dyson HJ, Wright PE (2015) Cofactor-mediated conformational dynamics promote product release from Escherichia coli dihydrofolate reductase via an allosteric pathway. J Am Chem Soc 137:9459–9468
Schmieder P, Stern AS, Wagner G, Hoch JC (1997) Quantification of maximum-entropy spectrum reconstructions. J Magn Reson 125:332–339
Sekhar A, Kay LE (2013) NMR paves the way for atomic level descriptions of sparsely populated, transiently formed biomolecular conformers. Proc Nat Acad Sci USA 110:12867–12874
Shaka AJ, Keeler J, Frenkiel T, Freeman R (1983) An improved sequence for broad-band decoupling - Waltz-16. J Magn Reson 52:335–338
Stetz MA, Wand AJ (2016) Accurate determination of rates from non-uniformly sampled relaxation data. J Biomol NMR 65:157–170
Vallurupalli P, Kay LE (2006) Complementarity of ensemble and single-molecule measures of protein motion: a relaxation dispersion NMR study of an enzyme complex. Proc Natl Acad Sci USA 103:11910–11915
Vallurupalli P, Hansen DF, Stollar E, Meirovitch E, Kay LE (2007) Measurement of bond vector orientations in invisible excited states of proteins. Proc Natl Acad Sci USA 104:18473–18477
Acknowledgements
The work was supported by the Swedish Research Council (Research Grant 2015-04614); Swedish National Infrastructure for Computing (Grant SNIC 2016/5-61). The Swedish NMR Centre is acknowledged for spectrometer time. We a grateful to Linnea Isaksson for preparing the CD79A sample.
Author information
Authors and Affiliations
Corresponding author
Additional information
Maxim Mayzel and Alexandra Ahlner have contributed equally to this work.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Mayzel, M., Ahlner, A., Lundström, P. et al. Measurement of protein backbone 13CO and 15N relaxation dispersion at high resolution. J Biomol NMR 69, 1–12 (2017). https://doi.org/10.1007/s10858-017-0127-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10858-017-0127-4