Abstract
A problem identified in the literature around task design is the persistence of a gap between teacher intention and student activity. We show how principles designed around the making of distinctions and having an explicit language of mathematical thinking can eliminate the “gap” by guiding teacher planning, teacher actions in the classroom and student activity in the classroom. We show how our task design principles have developed during the time of our collaboration, over a period of 20 years, across several research projects. We argue for the importance, in task design, of an explicit theory of change and an explicit image of mathematical thinking, where the theory of change is applicable to researchers, teachers and students.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In this article, we articulate principles for task design that, through a focus on the making of distinctions, allow for a convergence of teacher intentions and student mathematical activity. We draw on insights from our collected research and exemplify our approach through an analysis of three research projects (from 1998, 2000 and 2007) where task design featured as an important element. A contribution of this article to the field is to further develop the notion of what it means to engage in developing ways of working in a classroom that lead to “transforming action” (Watson and Mason 2007, p. 210). An implication we draw out is the importance, in task design, of having an explicit image of mathematical thinking and an explicit theory of change that is applicable to researchers, teachers and students.
Our design principles have evolved alongside our epistemological commitment to enactivism (Varela et al. 1991) and the continuing pedagogical influence of the work of Gattegno (1987). Following this introduction, we review relevant literature about task design and flag up the persistence of a problem around a gap between teacher intentions and student activity. We then offer a historical account of the development of our design principles and in doing so elaborate the theoretical framework and methodology that informs our research as well as our view of mathematics. Finally, we present evidence from three tasks in order to demonstrate how task design based on the making of distinctions can lead to the transforming actions that mean the “gap” between teacher intention and student activity does not arise as an issue.
The particular community that is the focus of this article centred around one school (School S) in the Bristol area of the UK that was in “partnership” with the University of Bristol, meaning that the mathematics department took prospective teachers from the 1-year postgraduate course (PGCE) for secondary prospective teachers, on an annual basis. Alf Coles joined this department in 1996, having already begun research collaborations with Laurinda Brown. Alf became a school-based mentor for the PGCE course and, in 2001, head of the mathematics department. Between 1996 and 2003, Laurinda made this school her main research site and visited, where possible, weekly. During these visits (often for a day), she would work in Alf’s classroom, observing, sometimes co-teaching and always reflecting on events afterwards. This collaboration led to publications (e.g. Brown and Coles 1997, 2010) and research projects (which we report on later).
Task design and ways of working
We take, as our definition, that a task is “anything that a teacher uses to demonstrate mathematics, to pursue interactively with students, or to ask students to do something. Task can also be anything that students decide to do for themselves in a particular situation” (Watson and Ohtani 2012, p. 4). In any task, as well as learning some mathematics, students are learning about what learning mathematics is like in this classroom; for us, the choice to use any task cannot be dissociated from a choice about ways of working. Looking into the history of research in task design, a Special Issue of Educational Studies in Mathematics (ESM) in 1993 (containing work by four authors) was framed around the notion that task design is concerned with “the nature of the mathematical activity, the conceptual content, and the nature of learning” (Bell 1993, p. 6). We find this three-part categorisation (the nature of mathematical activity, conceptual content and the nature of learning) a helpful one and use this to think about more recent research in the area.
Task design was the focus of a Study Group of the International Commission on Mathematical Instruction (ICMI) in 2013, where scholars from around the world were invited in order to express something about the “state of the art” in mathematics education. Two contributions explicitly linked task design to the nature of mathematical activity intended: Geiger and Redmond (2013) considered tasks that promoted mathematical modelling with technology, in this case the patterns of thinking are laid down by the modelling cycle into which students are inducted; Lithner et al. (2013) discussed how tasks can be used to promote creative reasoning, the pattern of thinking here is in the creativity and the reasoning that cuts across specific mathematical content. More typically, the task design focus was on particular conceptual content, for example proof and proving (Lin and Tsai 2013; Komatsu and Tsujiyama 2013), or specific topics such as rational numbers (Van Dooren et al. 2013) or rich number tasks (Goos et al. 2013). A small number of contributions drew on implications from the nature of learning, for example by making a link to a particular theoretical perspective such as the anthropological theory of didactics (Garcia and Ruiz-Higueras 2013). None of these studies considered all three aspects mentioned in the ESM Special Issue.
Looking further back in the literature and focusing on some of the major international programmes involving task design, it is clear that different emphasis is placed on mathematical activity, content and learning. Davydov’s curriculum for the early development of algebraic and number awareness encompasses all three components (Schmittau 2005), as does Gattegno’s (1988) curriculum. Cuoco et al. (1996) discuss a suggestion for a new curriculum that would be based around developing in students particular “habits of mind” (that could remain constant while the particular items of mathematical content adapted to the needs of the time) and they provide an extensive list of what such habits should look like (e.g. “students should be conjecturers”). Their focus is therefore primarily on the kinds of mathematical activity that tasks should engender. In contrast, the tradition of design research (DBRC 2003) aims to provide teachers with high-quality tools (generally designed by researchers) to solve particular educational problems (generally identified by researchers). Design research can operate on problems from the scale of a single task in a lesson to an entire curriculum. Part of the aim is to articulate theories and connections (Swan 2014). In a sense, design research is a theory of learning for the researcher, but the same theory is not applied to students (i.e. in general in design research, students do not engage in design research about mathematics). The focus of specific instances of design research is often on the conceptual content of tasks.
The French Didactical Engineering programme (Artigue and Perrin-Glorian 1991) incorporates principles both to guide the researcher in developing classroom tasks designed for specific purposes and to guide the solution of problems thrown up by the education system itself. Similar to design research, there is a cycle of preparation (a priori analysis of possible mathematical tasks), experimentation in the classroom and then a posteriori analysis. In relation to the classroom, there is a commitment to a particular way of working on mathematics (that students should be guided to their own discoveries) and a theory of how researchers should work to create such contexts. The conceptual content of tasks is of high importance within Didactical Engineering (Artigue 2014). As with Design Engineering, the theories applied to students (e.g. about the importance of discovery) are distinct from those applied to teachers/researchers (e.g. about the importance of a priori analysis). Another programme that encompasses both a view on mathematical activity and on learning is the Dutch Realistic Mathematics Education (RME) programme. RME aimed to support student meaning-making through having an explicit model of learning (involving specified levels) and a specific model of what is important in the doing of mathematics (or mathematising) (Van Den Heuvel-Panhuizen 2003). Students would go through a process of progressively refining (or mathematising) models that allow them to bridge the gap between their intuitive understanding of real (or imaginable) situations on the one side and their understanding of more formal mathematical systems on the other side (ibid, p. 13). Within RME, there is an explicit theory of learning and change for students, but there is not an equivalent for teachers and researchers, i.e. there is no equivalent of the progression of models or of horizontal and vertical mathematising, that is applied to learning about teaching.
What we take from this brief review is that developing ways of working in a classroom is supported by having an explicit image of mathematical thinking and having a theory of learning or change. Different programmes use theories of learning as applicable to designers of tasks or to students using the tasks. None use the same theory of change for both teachers and students, and we believe this is one reason why there continues to be a significant problem, identified in the literature, around the student experience of tasks, compared to the intentions of the designer or teacher. Mason et al. (2005, p. 131) raise the issue of how an expert’s awarenesses get translated into instructions for the learner that do not lead to those same awarenesses. Mason et al. (2005) connect this issue to Chevallard’s (1988) didactic transposition, the problem of moving from the knowledge used in a sphere, such as mathematics, to the knowledge to be taught. The contexts in which mathematical knowledge is used can never be faithfully replicated in a classroom. We see a similar issue being highlighted by Tahta (1980) when he distinguishes “outer” and “inner” aspects of tasks. The outer task is what is made explicit by the teacher, and the inner task is the relationship or awareness the teacher hopes students will gain. The problem for teachers is that the more the desired behaviours in students are specified, the less these behaviours are likely to emanate from students’ own awareness. We see essentially the same issue being described by Watson and Mason (2007):
Engaging learners in activity is important, but in order to learn from that activity they need to experience some kind of shift or transformation in what they are sensitised to notice and attend to mathematically. (p. 209)
And no matter what we do as teachers, we cannot make that shift or transformation happen for learners. We also agree with Watson and Mason’s (2007) emphasis on:
the importance of developing ways of working, a classroom rubric in which the learners are drawn into patterns of thinking, in which some transforming action takes place. (p. 210)
In other words, one solution to the problem of how to connect teacher intentions and student activity is to focus on developing particular ways of working, or patterns of thinking with students that lead to “transforming action”. What is not made explicit is how, as teachers or researchers, we go about doing this. What we aim to show in this article is that if, as teachers, we can occasion patterns of thinking that support “transforming action”, then the dilemma around teacher intention and student activity fades away. What we demonstrate is the significance of the role of making distinctions in occasioning transforming action and we suggest one reason for this significance is that a theory of change based on the importance of making distinctions can be used to guide the actions of researchers, teachers and students.
Task design in three research projects
In this section, we have looked back over the 20 years of our collaboration and chosen three projects across this time to give a sense of how our task design developed. Within that historical constraint, we have chosen the projects that involved School S and where task design was prominent in either the aims or outcomes. We have selected from the project documentation only those sections that mention task design. Through describing each study, we articulate the enactivist principles that underpin our work and also articulate the influence of the pedagogy of Caleb Gattegno.
Project 1:
Teacher Training Agency (TTA) Teacher-Research Grant (1998)
Close to the start of our collaboration, we were successful in securing a small grant for Alf to work with Laurinda on a piece of teacher-research. The research aim was:
To investigate whether a secondary mathematics classroom culture can be established in which students develop a need for algebra, using it themselves without prompting, having gained a sense of its power, and, if so, what factors led to this’. (Coles 2000, p. 1)
The research focused on Alf’s year 7 class of 27 students (age 11–12) and took place over a 3-month period. The outcome of the project was that the answer to the research question was a “yes”, we were successful in establishing a classroom culture in which students develop a need for algebra, and the factors we identified as being significant were:
-
developing a wider classroom culture to do with “becoming a mathematician”;
-
the teacher commenting on and highlighting the mathematical behaviour of students whenever it was observed;
-
the choice of activities and teaching strategies used within those activities, e.g. the use of common boards;
-
an emphasis on students writing both in the act of doing mathematics and in reflection on what they have learnt. (Coles 2000, p. 1).
At this stage in our research, the precise principles underlying the choice of activities (the third bullet point) were left unspecified. By “common board” what we were referring to was a strategy where students would write up results of their own work, or pin up pages of their work, in a space that was visible to all. This strategy will make more sense when we have described a task later in the article. However, what is significant to point out is that our focus in 1998 was on establishing a classroom culture, a way of working (in this case to do with the need for algebra) and we were viewing tasks as subsidiary to that goal. The significance of an image of mathematical behaviour is present (in point 2), and the teacher comments were designed to support more students engaging in particular patterns of mathematical activity.
Project 2:
Economic and Social Research Council (ESRC) grant: ‘developing algebraic activity in a ‘Community of Inquirers’’ (2000–2001)
As part of the TTA project, we set up a Steering Group of teachers and academics to help validate the findings. Laurinda was then successful in a larger bid to the ESRC to continue the focus on the development of a classroom culture in which students had a need for algebra. The ESRC project involved four teachers from the TTA Steering Group (one of whom was Alf, who also acted as a researcher on the project), and it had the following aims:
-
1.
to create year 7 mathematics classroom cultures which provoke a need for algebra;
-
2.
to investigate the similarities and differences between the mathematical classroom cultures developed in each of the teacher’s classrooms;
-
3.
to investigate the nature and extent of support needed from the collaborative group for teachers to plan their classroom activities starting from the students’ powers of discrimination;
-
4.
to develop theories and methodologies to describe the complex process of teaching and learning.
The “powers of discrimination” mentioned in point three links to the enactivist methodology behind the ESRC project (a stance that is behind all of our work). Before describing the outcomes of the ESRC project, we set out briefly our methodological thinking as it colours our view of task design.
Enactivism has roots in phenomenology (Merleau-Ponty 1962), systems thinking (Bateson 1979) and a radical view of biology (Maturana 1988; Maturana and Varela 1987). Within enactivism, cognition is viewed as “embodied action” (Reid and Mgombelo 2015, p. 171); in other words, there is a commitment to the inseparability of thought and action (Varela et al. 1991) and a rejection of the view that we operate in the world via making use of inner representations of objects, with thoughts about these representations leading to actions (Varela 1999). Instead, all the world can do is “trigger”—how we respond is determined by our structure, that is, by the particular relations and physical components that make up ourselves (“structure determinism” Reid and Mgombelo 2015, p. 172). Through a recursive process of acting in the world and the world acting back, we learn to coordinate our actions with others. Hence, enactivism rejects any sharp “inner-outer” division in relation to mind; the social and environmental context within which any action occurs cannot be dissociated from that acting/knowing. The approach has been labelled “double embodiment” (Reid and Mgombelo 2015, p. 178), to capture the idea that enactivism “breaks down the traditional split between individual and world. In enactivism, both are defined by the body, which is at the same time part of both” (ibid). Another way of saying this (Davis et al. 1996) is that context is not viewed as a site or container for cognition, we are part of our own context and our context is part of us: “enactivist theorists begin and end their analyses with an acknowledgment of the fundamental inextricability of all things” (Davis et al. 1996, p. 156).
From an enactivist standpoint, propositional knowledge arises from awareness of actions. Maturana and Varela (1987), key enactivist writers, state “cognition is effective action, an action that will enable a living being to continue its existence in a definite environment” (1987, p. 29). So an action is effective if it allows a living being to continue operating in a specific context. Knowledge, which requires cognition, is therefore also equated with effective action. Again, knowing cannot be separated from the knower nor the context in which the knower acts, hence, “[a]ll doing is knowing and all knowing is doing” (Maturana and Varela 1987, p. 27).
Enactivism also carries implications for how learning can occur, where learning and change are seen as synonymous. In a classroom, the most significant features of the “environment” for any individual are the other individuals in the room. Any interaction between teacher and student or between student and student must, in the process, alter the structure of both. Enactivism is a profoundly social theory, we are quite literally changed through interaction with others, or, more precisely, we change ourselves through interaction with others who likewise change themselves. We cannot not change, however minimally, in every encounter. Equally, we cannot specify any change we want to provoke in others. It is in this sense that we understand Stewart (2010), in a book on enactivism, when he writes, “instruction, in the strict sense of the word, is radically impossible” (p. 9). All we can do, as teachers, is provoke, stimulate, trigger; how students respond will be a function of their own structures and histories and cannot be determined by us.
So, how do we as teachers know how to provoke, stimulate, trigger? As living beings our most basic mental function is that of noticing difference and patterning: “pattern recognition is the basic mental process and, as such, is the ground for all that we call learning” (St. Julien 1997, p. 275). The implication for the classroom is therefore to move away from presenting knowledge as fixed, to be memorised. Instead, the challenge for us as teachers is to see whether we can present more than one example of a concept so that students can react by noticing a distinction. It is the idea of the fundamental role of difference for cognition that was behind the ESRC aim to make use of students’ powers of discrimination.
The outcomes of the ESRC project that relate to task design are detailed below. The text is taken from a final report (Brown et al. 2001)—the quotations (unless referenced) are from the four teachers, taken from their final discussion about what they felt had been significant for them on the project.
Objective 1:
To create year 7 mathematics classroom cultures which provoke a need for algebra.
The four factors from the initial study were recognised by all the teachers as being important in achieving this objective. The first two factors were seen as linked and essential to developing the mathematical classroom culture. The teachers had criteria for their choice of activities (with students aged 11–12):
The activities, which were complex, and needed students to use a variety of skills to work on them (‘multi-skill’ tasks).
Using complex problems which are capable of being offered to any person with any level of mathematics. The sense of doing activities that are GCSE standard or something you might do with year 13.
and a language for description and action of teaching strategies:
Strategies for (the teacher) ‘avoiding answering the question’. They have got a lot better about being willing to give their idea, not waiting until they know they have got the right answer. There are no wrong answers, just the willingness to share an idea. They are so familiar with sitting listening to each other, checking with each other and checking each other’s work.
The extended use of the common boards in the classroom.
Continuing with students writing about ‘what have I learnt?.
(Brown et al. 2001, p. 10)
Objective 4:
To develop theories and methodologies to describe the complex process of teaching and learning.
Encouraging the making of distinctions through the use of same/different has shown the importance of narrowing the gap between action and communication in the continuing professional development of teachers. The important awareness for teacher educators is of not letting abstraction upon abstraction build in communication:
… rather than adding layers of continued abstraction, we should go back where we started, to the concreteness and particularity of our own experience—even in the endeavour of reflection. The fundamental insight of the enactive approach … is to be able to see our activities as reflections of a structure without losing sight of the directness of our own experience (Varela et al. 1991, p. 12).
(Brown et al. 2001, p. 11)
The ESRC outcomes, related to Objective 1, include more detail about “choice of activity”, compared to the TTA findings, and there is also more detail about associated teaching strategies for working with these tasks (e.g. “multi-skill tasks”). The importance of the role of the distinctions is also apparent in the report on Objective 4, and new compared to the TTA project. The strategy labelled “same/different” is mentioned, i.e. offering contrasting examples and asking students: What is the same? What is different? There is an evolution therefore in the task design and more explicit implications drawn from the theory of learning and change (based on making distinctions) that underpinned the whole research project.
Project 3:
National Centre for Excellence in the Teaching of Mathematics (NCETM) grant: “enquiring schools project—the economy of teaching mathematics” (2007–2009).
The third project that we describe was inspired by one of Laurinda’s prospective teachers on the PGCE course expressing an interest in continuing to explore the work of Caleb Gattegno. The research aims in this case were:
establishing a collaborative cross-school research group of teachers responding to […] student teachers’ interest in the work of Gattegno, to investigate the effective use of current resources to support the learning of mathematics and to develop new ideas. We aim to support these new teachers to the profession in continuing their reflective and research practices (https://www.ncetm.org.uk/enquiry/5207, accessed 8 Feb 2011).
We take some space to describe the thinking of Gattegno since, as with enactivism, this has been a major influence on our thinking about task design. Gattegno saw mathematics as the awareness of relationships (1965). Awareness was a technical term for Gattegno, whose purpose is, “to illuminate our fields of action” (1987, p. 25). He turned “awareness” into a countable noun—we can enumerate awarenesses. There is a link to mathematics. For Gattegno, we are being algebraic whenever we step back from a procedure, or a dynamic (in any sphere) to become aware of it. Writing something as simple as x + y entails a stepping back from the process of addition, to represent that dynamic. In fact, for Gattegno, all mathematics was algebraic, since awareness of relationships and awareness of dynamics are intimately linked, “all is algebra in mathematics, because to say ‘algebra’ is to say the awareness of the mind at work on whatever content” (Gattegno 1965, p. 22). Gattegno privileged the visible and the tangible in the learning of mathematics. Dick Tahta, in commenting on Gattegno’s pedagogy, wrote:
There is very little in Gattegno’s work … about meaning or conceptual understanding. But there are plenty of things to try out which give students something to do and something to talk about (Unpublished memorial lecture, n.d., p. 1)
Gattegno worked with imagery and another quotation of his that we have both lived with is that mathematics “is shot through with infinity” (1984, p. 20). The connection we make here is that once we become aware of a relationship (i.e. once we are mathematising, or thinking mathematically), then it becomes possible to imagine that relationship iterated and hence explore implications to infinity. Gattegno also distinguished “powers of the mind” (1971) that he believed all humans possess, which means all humans are able to think mathematically. These powers (also referred to in Brown and Coles 2011, p. 866) are:
1) extraction, finding ‘what is common among so large a range of variations’; 2) making transformations, based on the early use of language ‘This is my pen’ to ‘That is your pen’; 3) handling abstractions, evidenced by learning the meanings attached to words; and 4) stressing and ignoring, without which ‘we can not see anything’ (paraphrased from Gattegno 1971, pp. 9–11).
Making distinctions play a role in (1) and (4), linking to our enactivist stance. In other words, Gattegno’s view of the nature of cognition, as with enactivism, reserves a central role for the making of distinctions. The outcomes of the NCETM project were discussed in Brown and Coles (2011). They will not be re-stated here except to say that the outcomes were all linked to the teacher participants developing their own task design principles linked to ways of working. In other words, the way of working on the research project was about supporting teachers to become explicit about the ways of working they wanted to promote in their own classrooms. It was partly this experience, of supporting others in developing ways of working they were committed to, that helped us articulate design principles that can support such diversity.
Principles of task design
Arising from the projects described above, we have synthesised our design principles and exemplified them with specific reference to the way of working at School S. The first three principles are, we suggest, significant in terms of closing the gap between teacher intention and student activity. The last four (italicised) are specific to the particular way of working at School S and the image of mathematical behaviour that we were trying to promote. The principles are:
-
(1)
considering at least two contrasting examples (where possible, images) and collecting responses;
-
(2)
asking students to comment on what is the same or different about contrasting examples and/or to pose questions;
-
(3)
introducing language and notation arising from student distinctions;
-
(4)
starting with a closed activity (which may involve teaching a new skill);
-
(5)
having a challenge prepared in case no questions are forthcoming;
-
(6)
opportunities for the teacher to teach further new skills and for students to practise skills in different contexts;
-
(7)
opportunities for students to spot patterns, make conjectures and work on proving them, hence involving generalising and algebra (Kieran 1996).
Principles 1–3 connect to the enactive view of knowing and learning, with their emphasis on the making of distinctions (seen within enactivism as our basic mental function). By working with at least two examples (principle 1) and asking for comments on similarities and differences (principle 2), we support students in sharing distinctions and, through this sharing, the making of new distinctions, which is tantamount to learning from the enactive perspective. Language and notation are introduced to label distinctions students make (principle 3), supporting new ways of seeing. By “examples” (principle 1), we mean to capture a wide range of possibilities, including images, animations and procedures.
Principles 4–7 link to the work of Gattegno. The closed activity will, where possible, involve something visible or tangible and will give all students something to do and therefore talk about (principle 4). Having a challenge (principle 5) and opportunity to teach skills in different contexts (principle 6) are linked to the power humans have of extraction. When we do something for different purposes and in different contexts, we hone skills and can potentially retain them without the need for memorisation. As Tall (2011) reminds us, the crystalline structure of mathematical concepts implies the students will make the necessary connections, if they are making distinctions in a mathematical context. Principle 7 comes from the view of mathematics as being essentially about relationships, which inevitably lead to pattern and the possibility of conjecturing, no matter what content is being covered.
In the next section, we exemplify these principles, first with a write up of a task and then with two tasks that arose in lessons. We attend to how the design principles operate to establish a way of working in the classroom and, in our analysis, we will demonstrate how the principles help to connect teacher intentions (which are exemplified in principle 7) with student activity. We have chosen data, as with the research projects, that span the time of our collaboration and also across three contexts of task design: planning (the first is a task as written up for teachers in School S), an unexpected classroom sequence (the second is a task that arose spontaneously in response to student ideas) and a carefully designed classroom sequence (the third is a task designed to provoke distinctions). The data are offered in the spirit of “paradigmatic examples” (Freudenthal 1981, p. 135) from across our research, of how task design based on making distinctions can foster ways of working that occasion transforming action. We have reported on these examples at a conference (Coles and Brown 2013).
Principles exemplified
Task 1: equable shapes
One exemplification of these design principles is a task (we call it “Equable Shapes”) that begins with the shapes in Fig. 1 drawn on the board. The origins of this task are obscure. The version of the task presented below was developed at School S, from an idea Laurinda had used in her teaching. Often, in School S, tasks would be borrowed from elsewhere but worked on by Laurinda and Alf in the earlier years of our collaboration and as a department when Alf became head of mathematics. There was a scheme of work in the school which specified certain “common tasks” (such as “Equable Shapes”) had to be done in a certain time slot with a certain year group. Discussion amongst teachers often led to changes in task beginnings, which were written up for the following year. What follows is the write up of the task, written for teachers, from the scheme of work. The convention in these write ups was that italicised text gave an example of the kind of thing the teacher might say to the class. Normal text is instruction for the teachers. We analyse the write up against the seven design principles above.
-
Draw these two rectangles on the board.
-
Question: What is the same or different about these 2 shapes? Figure 1
-
Someone will comment on the rectangles being different sizes. They may mention area and perimeter. If not, introduce these terms as ways that mathematicians determine the sizes of shapes.
-
Add, underneath each rectangle: A =
-
P =
-
For the first rectangle, A = 25 and P = 25; for the second one A = 21, P = 20
-
Invite students to comment on what is the same or different between these values. Someone will notice that the first rectangle has the same value for area and perimeter and the second one does not.
-
Mathematicians call shapes which have the same value for area and perimeter, EQUABLE shapes. So our first rectangle is equable and the second one is not.
-
Ask students what they could ask whether they were “thinking mathematically” about what we have just done.
-
Examples:
-
Are there any other equable rectangles?
-
Is there an equable square?
-
What other equable shapes are there?
-
-
Initially, the focus should be on strategies for finding other equable rectangles, rather than answers, e.g. trial and error, or students may try and use or adapt the ratio of lengths in the first rectangle—if one length is a quarter will it always be equable? If I double the lengths will it still be equable?
-
A useful skill for trial and error is to “be organised”—perhaps by fixing a height and then finding the width (if one exists) that makes the rectangle equable.
-
A common board may be used to help with being organised:
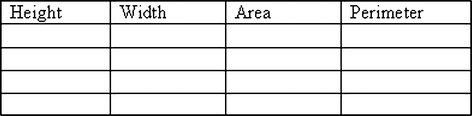
-
Where this can go
-
At some point, it is likely someone will suggest (or you can) using algebra. Using letters for both sides leads to solving: ab = 2a + 2b.
-
This is not particularly helpful. More useful is to choose a fixed length (e.g. 6) and call the other side n. Then equating area and perimeter leads to the equation: 12 + 2n = 6n, which now is accessible.
-
It is interesting to create a table of height and widths of equable rectangles. If answers are kept as fractions, there are some intriguing patterns that can be generalised and even proved (School S, Scheme of Work).
The shapes in Fig. 1 are “two contrasting examples” (principle 1). With this image on the board, the teacher asks students, “what is the same and what is different” (principle 2). Generally, in the UK, students will at some point begin to comment about the different sizes of the rectangles. Students may or may not need support in remembering that mathematicians use the ideas of “area” and “perimeter” to judge the size of rectangles. This awareness leads the teacher to invite the students to find the area and perimeter of both shapes (a closed task, principle 4). The results are:
-
10 by 2.5 cm rectangle: Area = 25 cm2, Perimeter = 25 cm
-
7 by 3 cm rectangle: Area = 21 cm2, Perimeter = 20 cm
Again, the offer from the teacher is for students to comment on anything they notice that is the same or different. A student will usually notice that, for the first rectangle, the value of the area and perimeter is the same. At this point, the teacher introduces the label “equable” (principle 3) as a name for the 10 by 2.5 rectangle. The teacher can then ask students what questions they could pose (principle 2) and gather ideas on the board. The teacher-prepared challenge is: What other equable rectangles can we find? Are there equable shapes that are not rectangles? (principle 5). The work on rectangles offers opportunities for pattern spotting, generalising, algebra and conjecture (principle 7). In working on generalising what they notice, students are using skills of distinguishing area and perimeter and, depending on the direction in which the activity goes, skills may need to be taught to support students in solving linear equations, using Pythagoras’ theorem, say, or using trigonometry, while focused on the idea of finding equable shapes (principle 6). The write up from the scheme of work continues and offers thoughts on “Further extensions” that include discussion of some of these wider possibilities.
The Equable Shapes task was typical of the kind of activity (a “common task”) that would be used six times a year with classes in School S. The write up gives some sense of the expected student responses and some typical teacher adaptations to those responses. Each common task might last for 4 weeks of lessons (12 h, or sometimes more), and they were designed largely to cover the content specified in the curriculum in each year. Sometimes tasks would be repeated from 1 year to the next, with students going more deeply into the task as they got older. The rest of the curriculum time would be planned by teachers to work on any issues needing further work arising from the common tasks, or to work on topics that may not have been covered. In terms of developing ways of working, our analysis demonstrates how the first three principles allow a focus on area/perimeter and on students making the new distinction “equable”. This distinction is not an important one within the UK curriculum, but it was one chosen because of the challenge it then led to (finding other equable shapes) which allowed both for conjecturing and provoked the need for the development of new skills (e.g. as mentioned, Pythagoras’ theorem, to investigate equable triangles, or trigonometry to investigate equable regular polygons). In the write up, there is reference to what “mathematicians” do. In School S, with year 7 groups, we were explicit that the overall purpose for the year was for students to get involved in: “becoming a mathematician”. There is also mention of an opportunity to get students thinking about what to do next, if they were to be “thinking mathematically”—another phrase that was promoted in the school. The teacher intentions, in using this task, are about engaging students in working within a mathematical structure (which is a specific example of the more general problem of finding shapes whose areas and perimeters are in the same ratio) and responding to student responses. Within this structure, it is inevitable that the distinctions students make will be mathematical ones, and because the teacher intention is not tied to specific desired responses (beyond the “closed task” phase and the identification of “equable” as a label), there is no sense of a “gap” between teacher intention and student activity.
Having offered some of the context of School S and seen how the principles influenced the design of tasks, we now focus on the classroom. The classroom examples below have been chosen for analysis because they illustrate two further dimensions: how the principles were enacted by teachers not in the context of work on a “common task”, and how the principles were enacted by students. The classroom examples arose more or less spontaneously in the practice of two teachers. These examples allow us to address the question empirically, of how the task design principles operated to influence the way of working in the classroom.
Task 2 (transcript 1): fractions of quantities
The transcript below is from a video recording of a lesson, taken as part of the ESRC project. The transcript shows the emergence of a task spontaneously within a lesson of Teacher A, who worked in School S. The original problem for students had been to find rectangles with area 12. Three examples were on the board when Student 2 was given the pen. The students (aged 11–12) were in year 7, and the examples on the board were a 3 by 4 rectangle, a 2 by 6 and a 12 by 1 (Teacher A refers to these examples in line 42).
[Student 2 takes the board pen and board ruler and draws a half square by 24 square rectangle, giving it the label 1/2 by 24] | |
39 | Students: half a square? |
40 | Student 2: half a square |
41 | Student 8: half of 44, half of 48, sorry |
42 | Teacher A: excellent. Oh, lovely. Well done. [Students applaud] So, 3 times 4 is 12, 2 times 6 is 12, 1 times 12 is 12 and a half times 24 is also 12 |
43 | Student: and do we do that as well |
44 | Teacher A: pardon |
45 | Student 8: and a quarter times 48 is 12 |
46 | Teacher A: and a quarter times 48… |
47 | Student 8: and an eighth times… |
48 | Student: three quarters |
49 | Teacher A: and an eighth times… |
50 | Student: i’m not saying |
51 | Student: you can actually go on |
Following this exchange, the teacher then wrote 1/4 × 48 and got two students to confirm the answer. Teacher A then wrote on the board (see boxes) as the conversation developed.
57 | Teacher A: What about a third? |
|
58 | Student: What? | |
59 | Student 9: 36 | |
60 | Student: No, you can’t really draw a third | |
61 | Teacher A: Why, how do you work it out for those that are struggling a bit. [Directed at Student 9.] How do you know? He’s right, it is 36. How do you know it’s 36? |
|
Two students responded to this question, and then Student 10 said, “3 twelves are 36”. Teacher A picked up this idea and asked what 4 twelves are, pointing to the 1/4 × 48 written on the board. Teacher A asked (line 69), what 1/6th would be, a student responded “72”. Another student asked (line 72), “What about 100? How could you draw it though?” and three turns later, a student asked (line 76), “Sir, what would just a straight line be?”
In this short episode, that was not planned, we see the design principles in action. The questions the class were initially working on are closed (principle 4), for example, line 49, “And an eighth times”. The teacher wrote up 1/4 × 48 and 1/3 × 36, so there were two examples for students to see (principle 1). Students were patently the ones posing the questions and sometimes answering them, for example in lines 45, 47, 72 and 76 (principle 2). The teacher contributed to posing challenges in lines 57, 61, 69 (principle 5). It is the students who first introduced the language of fractions, Teacher A provided the notation (e.g. 1/4 × 48) to describe the rectangles they were considering (principle 3). There is clearly scope for spotting patterns in this task, as many students did; generalising came with the awareness that you could take any unit fraction as the height and still make a rectangle of area 12, taken to its limit by a student in line 76, “what would just a straight line be?” (principle 7). Part of what students were doing, in this short episode, was practising a relatively mundane skill of finding fractions of quantities, but they were doing it in a novel context and with their attention on the area of the resulting rectangle (principle 6). We recognise here an example of mathematics “shot through with infinity” (Gattegno 1984, p. 20).
There is a section of the transcript (lines 45–51) where, if names were removed, it would be impossible to tell whether students or teacher were speaking. This exchange was prompted by a student drawing a shape with a fractional side length. One connection that is made by a student (Student 10) is that to answer, 1/3 × ? = 12, you can work out 3 × 12. We interpret this statement from Student 10 as an example of the kind of shift in attention (transforming action) that Watson and Mason (2007, p. 209) describe as being central to learning mathematics. Student 10 articulated an awareness of a relationship that then supported other students in extending the implied pattern (1/6 × ? = 12, means 6 × 12 = ?, etc.), awareness of relationship is an example of mathematical thinking.
What is significant for us, in this lesson, is the way the design principles of the department appear to have influenced how Teacher A adapts in an episode that arose spontaneously from an unplanned student response to an activity. Teacher A was creating the task as the lesson unfolded. Perhaps even more striking is the way the students played a role in creating the task, with Teacher A allowing discussion of student ideas to run and focusing the whole class on certain questions (e.g. lines 49 and 57). We know, from interviews carried out as part of the ESRC project, that “going with” student ideas in the way we see in this transcript was something Teacher A was, at that time, just beginning to experiment with. The design principles support a classroom environment in which students articulate distinctions to which the teacher can respond, in pushing them to develop new awarenesses (in this case linked to fractions as operators). In the context of a task that arose spontaneously in a lesson there are opportunities for students to notice patterns and make predictions, i.e. what it means to “think mathematically” in the context of School S. The design principles and the way of working on mathematics in this classroom are closely intertwined and again, we do not see any evidence of a “gap” between teacher intention and student activity. The teacher, in making distinctions in relation to the distinctions of the students, is occasioning deeper mathematical thinking.
Task 3 (transcript 2): both ways
The transcript below is from a video taken in 2008 (as part of an ESRC Studentship, see Coles 2013, p. 95) of a teacher (W) who had been in the department for several years and who had worked with this group of (aged 12–13) students for a year and a half. The task we called “Both Ways”. Teacher W had drawn the image in Fig. 2 and invited students to suggest a number to go in the top left circle.
A student had suggested 74 as the starting number, which the class then worked through, getting answers of 740 in both circles in the bottom right. Teacher W looked at these answers on the board as she said the first line of the transcript.
Transcript notation: (.) indicates a small pause, (2) a 2 s pause, ( ) undecipherable speech | |
1 | Teacher W: oh right (.) okay |
2 | Student: yeah but why (.) why does it come to that |
3 | Student: is that meant to happen miss |
4 | Student: yeah it is |
5 | Student: no |
6 | Student: oh yeah miss |
7 | Student: because if you do 74 times ( ) |
8 | Teacher W: um (4) any comments (.) any comments (.) yeah |
9 | Student: cos it can’t be seven hundred and forty which is the bottom one (.) because seventy four times five is three hundred and seventy and then (1) no (1) no ignore me |
10 | Student: it (.) the two answers in the little circles no matter what you start up there will always be the same (.) because if you start there no matter what (.) if it’s times five times two it’s like times ten |
A little later in the lesson, Teacher W drew a second “Both Ways” image, it was the same as Fig. 2 except the “×5” arrows were replaced by “+2”.
33 | Teacher W: okay I’ve changed the number machine (.) you may not have noticed (.) okay can we have any thoughts at the moment (1) about what’s going to happen in these two circles (1) any thoughts (.) Student 1 yeah go on |
34 | Student 1: might be (.) still going to be the same |
35 | Teacher W: same (1) anything else (1) any other comments |
36 | Student: I think they’re going to be different because they’re different order um (4) what’s it called when |
37 | Teacher W: order of operations |
38 | Student: ( ) |
39 | Teacher W: so you think it’s different (.) timesing by two and adding two is different to adding two and timesing by two (1) |
40 | Student: yeah |
41 | Teacher W: okay so because they’re different operations |
42 | Student: I think it’s going to be the same as well (.) because both numbers are times five and added by two (.) so it’s kind of the same thing you’re doing |
43 | Student: I reckon they’re going to be different (.) because if you start with one again (.) if you times by five and plus two it’s going to be seven (.) and if you add two first it’ll be three and then you times five which is fifteen (.) so plus-ing on two first will make it a bigger number |
44 | Teacher W: okay everybody can you draw that in the back of your book (.) don’t worry if it’s a mess (.) just draw circles squares and two more circles (.) put those in and I want you to choose your own starting number |
This activity meets the design principles presented earlier, the task is initially closed (principle 4) and the teacher offers two examples (principle 1) and invites comments and predictions (line 33, principle 2). There are opportunities for pattern spotting and conjecturing (principle 7), evident in what the students do. In lines 2 and 3, we see students asking questions having made the, perhaps surprising, distinction that there is no distinction to be made between the final circles of Fig. 2. In lines 7, 9 and 10, all the student comments include the word “because”, and in line 10, a statement of proof is offered as to why the answers at the end are the same. When Teacher W sets up the second problem and asks students what they think will happen, all the responses that follow use the language of similarity and difference, commenting about reasons the answers at the end might be the same or different. As in transcript 1, we see evidence here that students in this department responded to tasks by making distinctions that lead to them asking questions, noticing pattern and generalising. In the classroom of Teacher W, some students’ generalisations have taken the form of mathematical proof. The opportunities for teaching new skills (principle 6) and for new notation (principle 3) arise when the desire for proof takes the form of algebraic argumentation.
We see evidence in this small lesson excerpt that students have taken on a particular pattern of thinking, linked to making distinctions about mathematical patterns, and that this is supporting them in the transforming actions mathematical reasoning. In the “closed” phase of the task, the teacher quite deliberately focuses on specific distinctions (these ones are the same, these ones are different) to raise questions. Students will then go on to explore their own “both ways” problems with a range of different operations. As with the previous examples, it is inevitable, working within the mathematical structure of this problem, that students will make distinctions that will allow the teacher to develop or name new mathematical ideas and skills (for example, the use of brackets). Teacher intention once more is in a place where the notion of a “gap” with student activity does not make sense—the teacher intention is to set up a context in which she is able to respond to students’ mathematical distinctions.
Discussion
We have demonstrated how our design principles are linked to both enactivism and Gattegno’s ideas about learning mathematics. Both perspectives see the making of distinctions as one of the basic mental functions and a key to learning. The more general design principles (1) starting with contrasting examples, (2) students comparing/contrasting and (3) naming the distinctions that students make are all linked directly to the making of distinctions and hence to learning. We see the principles operating in (at least) three ways to support ways of working in the classroom. Firstly, the principles inform teacher planning, for example in the activity “Equable Shapes”. In this task, the starting point of the two rectangles inevitably focuses students on the distinction between perimeter and area, from which questions and challenges can be generated that provoke further work with that distinction. Secondly, transcript 1 provides evidence that, over time, these principles can also inform teacher actions in the classroom, in adapting tasks in the light of student responses. We see evidence that the principles have become part of Teacher A’s practice of teaching. Thirdly, there is evidence in transcripts 1 and 2 that the principles can inform (implicitly) student actions in the mathematics classroom. What becomes apparent across the transcripts is that once a way of working has been established in which students see their role as the making of distinctions about mathematical patterns, the specific details of any task become less significant. Students notice patterns and make predictions in ways that allow the teacher to highlight new mathematical ideas.
In Teacher A’s lesson (transcript 1), we see a snapshot of a way of working in which the design principles of School S have become part of what students see themselves as doing in mathematics lessons. Student 2 offers 1/2 × 24, and another student immediately offers 1/4 × 48. In this context, the activities that Teacher A chooses to offer students become less important, as students can make distinctions and generate questions without prompting. We interpret the students in this short excerpt as exhibiting “inquiry as a form of engagement” (Watson and Mason 2007, p. 213) rather than inquiry being structured into the task. In transcript 2, there is evidence of students posing questions spontaneously, although we see a difference compared to the spontaneity of transcript 1. It was clear from subsequent discussion with Teacher A that the task students ended up engaging with in transcript 1 was not planned. In contrast, Teacher W had crafted her two starting examples on the “Both Ways” task and there was no surprise (for Teacher W) in how the students responded and that the distinctions they made led to a motivation to explore different starting numbers and then, later, different operations on the “arms”.
Conclusion
In this article, we have argued that with a focus on distinctions, there is a potential route out of the problems highlighted by Mason et al. (2005) around the divergence of teacher intention and student activity. Instead, there can be a deliberate setting up of a pattern of thinking, a way of working on mathematics, in which students are the ones who make distinctions to which the teacher can respond, leading to transforming actions. In the examples we have presented there was a particular way of working, with associated language (within School S), that was valued. We suggest one reason the design principles are able to operate on three levels (to influence teacher planning, teacher actions in the classrooms and student activity) is that they are based on a theory of learning. The design principles embody how, as a department, School S viewed mathematical thinking; the stated aim, as a department, was to develop students’ mathematical thinking. Teacher intentions were to support mathematical thinking and teach skills within a context that was meaningful to students and which would allow the immediate application of those new skills. The problem does not arise of a gap between intentions for students and what students did in classrooms. The students made distinctions about mathematical objects, which was an inevitable part of tasks in this department, and the teachers made distinctions about the students’ distinctions in order to develop, share and deepen the mathematical awarenesses embedded within those student distinctions. We also see it as significant that our principles have been derived over time. Developing ways of working in a classroom takes time, and developing ways of working in a department takes longer. And, as a beginning teacher, for example, it also takes time to become aware of what ways of working in a classroom we even desire in the first place. While this article has exemplified our own theories and principles, we want to point towards the importance of becoming aware of the theories and principles embodied in our actions in order to open them up, over time, to question and change.
References
Artigue, M. (2014). Didactic engineering in mathematics education. In S. Lerman (Ed.), Encyclopedia of mathematics education (pp. 159–162). New York: Springer.
Artigue, M., & Perrin-Glorian, M.-J. (1991). Didactic engineering, research and development tool: Some theoretical problems linked to this duality. For the Learning of Mathematics, 11(1), 3–17.
Bateson, G. (1979). Mind and nature: A necessary unity (p. 2002). Cresskill, New Jersey: Hampton Press Inc.
Bell, A. (1993). Principles for the design of teaching. Educational Studies in Mathematics, 24(1), 5–34.
Brown, L., & Coles, A. (1997). The story of Sarah: Seeing the general in the particular? In E. Pehkonen (Ed.), Twenty first annual conference of the international group for the psychology of mathematics education (Vol. 2, pp. 113–120). Lahti: PME.
Brown, L., & Coles, A. (2010). Mathematics teacher and mathematics teacher educator change. Journal of Mathematics Teacher Education, 13(5), 375–382.
Brown, L., & Coles, A. (2011). Developing expertise: How enactivism re-frames mathematics teacher development. ZDM, The International Journal on Mathematics Education, 43(6–7), 861–873.
Brown, L., Sutherland, R., Winter, J., & Coles, A. (2001). Final report: ‘Developing algebraic activity in a ‘community of inquirers’. Economic and Social Research Council. Document Number R000223044.
Chevallard, Y. (1988). On didactic transposition theory: some introductory notes. Paper presented at the International Symposium on Research and Development in Mathematics Education, Bratislava, Czechoslovakia. Available online at http://yves.chevallard.free.fr/spip/spip/rubrique.php3?id_rubrique=6. Accessed 20th Aug 2012.
Coles, A. (2000). Developing a need for algebra. In The Teacher Research Grant Scheme, Summaries of findings 1998–1999. London: Teacher Training Agency.
Coles, A. (2013). Being alongside: For the teaching and learning of mathematics. Rotterdam: Sense Publishers.
Coles, A., & Brown, L. (2013). Making distinctions in task design and student activity. In C. Margolinas (Ed.), Task design in mathematics education: Proceedings of ICMI Study 22 (pp. 183–192). Oxford: ICMI.
Cuoco, A., Goldenburg, E., & Mark, J. (1996). Habits of mind: An organizing principle for mathematics curriculum. Journal of Mathematical Behavior, 15(4), 375–402.
Davis, B., Sumara, D., & Kieren, T. (1996). Cognition, co-emergence, curriculum. Journal of Curriculum Studies, 28(2), 151–169.
DBRC. (2003). Design-based research: an emerging paradigm for educational inquiry. Educational Researcher, 32(1), 5–8.
Freudenthal, H. (1981). Major problems of mathematics education. Educational Studies in Mathematics, 12, 133–150.
Garcia, F. J. G., & Ruiz-Higueras, L. (2013). Task design within the Anthropological Theory of the Didactics: Study and research courses for pre-school. In C. Margolinas (Ed.), Task design in mathematics education: Proceedings of ICMI Study 22 (pp. 421–430). Oxford: ICMI.
Gattegno, C. (1965). Mathematics and imagery. Mathematics Teaching, 33(4), 22–24.
Gattegno, C. (1971). What we owe children: The subordination of teaching to learning. London: Routledge Kegan Paul.
Gattegno, C. (1984). Infinity. Mathematics Teaching, 107, 18–22.
Gattegno, C. (1987). The science of education. Part 1: Theoretical considerations. New York: Educational Solutions Worldwide Inc.
Gattegno, C. (1988). The science of education. Part 2B: The awareness of mathematization. New York: Educational Solutions Worldwide Inc.
Geiger, V., & Redmond, T. (2013). Designing mathematical modelling tasks in a technology rich secondary school context. In C. Margolinas (Ed.), Task design in mathematics education: Proceedings of ICMI Study 22 (pp. 119–128). Oxford: ICMI.
Goos, M., Geiger, V., & Dole, S. (2013). Designing rich numeracy tasks. In C. Margolinas (Ed.), Task design in mathematics education: Proceedings of ICMI Study 22 (pp. 589–598). Oxford: ICMI.
Kieran, C. (1996). The changing face of school algebra. Invited lecture presented at the 8th International Congress on Mathematics Education, Seville, Spain. Available online at http://www.math.uqam.ca/_kieran/art/algebra.html. Accessed 17th Sep 2001.
Komatsu, K., & Tsujiyama, Y. (2013). Principles of task design to foster proofs and refutations in mathematical learning: Proof problem with diagram. In C. Margolinas (Ed.), Task design in mathematics education: Proceedings of ICMI Study 22 (pp. 471–480). Oxford: ICMI.
Lin, P.-J., & Tsai, W.-H. (2013). A task design for conjecturing in primary classroom contexts. In C. Margolinas (Ed.), Task design in mathematics education: Proceedings of ICMI Study 22 (pp. 249–258). Oxford: ICMI.
Lithner, J., Jonsson, B., Granberg, C., Liljekvist, Y., Norqvist, M., & Olsson, J. (2013). Designing tasks that enhance mathematics learning through creative reasoning. In C. Margolinas (Ed.), Task design in mathematics education: Proceedings of ICMI Study 22 (pp. 221–230). Oxford: ICMI.
Mason, J., Graham, A., & Johnston-Wilder, S. (2005). Developing thinking in algebra. London: Paul Chapman Publishing.
Maturana, H. (1988). Reality: The search for objectivity or the quest for a compelling argument. The Irish Journal of Psychology, 9(1), 25–82.
Maturana, H., & Varela, F. (1987). The tree of knowledge: the biological roots of human understanding. Boston: Shambala.
Merleau-Ponty, M. (1962). Phenomenology of perception (C. Smith, Trans.). London: Routledge & Kegan Paul (original work published 1945).
Reid, D., & Mgombelo, J. (2015). Roots and key concepts in enactivist theory and methodology. ZDM, The International Journal on Mathematics Education, 47(2), 171–183.
Schmittau, J. (2005). The development of algebraic thinking. ZDM, The International Journal of Mathematics Education, 37(1), 16–22.
St. Julien, J. (1997). Explaining learning: the research trajectory of situated cognition and the implications of connectionism. In D. Kirshner & J. Whitson (Eds.), Situated cognition: Social, semiotic and psychological perspectives (pp. 261–279). New Jersey: Lawrence Erlbaum Associates.
Stewart, J. (2010). Foundational issues in enaction as a paradigm for cognitive science: From the origin of life to consciousness and writing. In J. Stewart, O. Gapenne & E. D. Paolo (Eds.), Toward a new paradigm for cognitive science (pp. 1–32). Cambridge, Massachusetts: The MIT Press.
Swan, M. (2014). Design research in mathematics education. In S. Lerman (Ed.), Encyclopedia of mathematics education (pp. 148–151). New York: Springer.
Tahta, D. (1980). About geometry. For the Learning of Mathematics, 1(1), 2–9.
Tahta, D. (n.d.). Caleb Gattegno memorial lecture. Unpublished paper from Dick Tahta’s personal archive, currently held by Alf Coles and Laurinda Brown.
Tall, D. (2011). Crystalline concepts in long-term mathematical invention and discovery. For the Learning of Mathematics, 31(1), 3–8.
Van den Heuvel-Panhuizen, M. (2003). The didactical use of models in realistic mathematics education: An example from a longitudinal trajectory on percentage. Educational Studies in Mathematics, 54(1), 9–35.
Van Dooren, W., Vamvakoussi, X., & Verschaffel, L. (2013). Mind the gap—task design principles to achieve conceptual change in rational number understanding. In C. Margolinas (Ed.), Task design in mathematics education: Proceedings of ICMI Study 22 (pp. 519–528). Oxford: ICMI.
Varela, F. (1999). Ethical know-how: Action, wisdom and cognition. Stanford, California: SUP.
Varela, F., Thompson, E., & Rosch, E. (1991). The embodied mind: Cognitive science and human experience. Massachusetts: The MIT Press.
Watson, A., & Mason, J. (2007). Taken-as-shared: A review of common assumptions about mathematical tasks in teacher education. Journal of Mathematics Teacher Education, 10(4), 205–215.
Watson, A. & Ohtani, M. (2012). Task design in mathematics education discussion document. ICMI Study 22 Announcement and Call for Papers. Available online at http://ncm.gu.se/media/ncm/dokument/ICMI_Study_22_announcement_and_call_for_papers.pdf. Accessed 28th Oct 2014.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Coles, A., Brown, L. Task design for ways of working: making distinctions in teaching and learning mathematics. J Math Teacher Educ 19, 149–168 (2016). https://doi.org/10.1007/s10857-015-9337-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10857-015-9337-4