1 Introduction

Since a thin film is grown between a semiconductor and metal as an interfacial layer, metal/semiconductor (MS) structures convert to metal/interlayer/semiconductor (MIS) type structures, and the existence of such interlayer gives them capacitor properties, which capable storage more and more electronic charges and so supply an additional/excess capacitance (Cex.) and conductance (Gex.) to the real-values of them [1,2,3,4,5,6,7]. While the C and G values at higher frequencies are independent of the frequency in ideal conditions and rise with applied biases increment, this case is considerably different at lower frequencies, and so the C and G values become quite dependent on the ability of Nss to follow alternating signal [4, 6, 8]. In addition, when these devices have an interlayer, series resistance (Rs), Nss, and dislocations, they considerably influence the electrical, optical, and dielectric features of the devices. The basic sources of the Rs are the back-ohmic and rectifier front-contacts, the probe wires usage for electrical measurements, the bulk-semiconductor resistivity, the existence of an interlayer as native or deposited interlayer, the doping atoms inhomogeneities, and the inhomogeneity of barrier height (BH) at M/S interface [1,2,3, 9, 10].

The stability of the surface of the semiconductor has an important role in the fabrication of semiconductor devices like an MS-type structure with/without an interlayer. In other words, all semiconductor devices are more useful for studying surfaces of semiconductors because their reliability and stability are highly related to preparing surface conditions and fabrication processes [11,12,13]. During the elaboration of these MS and MIS, more and more Nss and dislocations may be produced, and their energies may be located at the junction in the semiconductor bandgap. These surface states act as recombination centers that can capture or release some electrons. They usually originate from non-saturated dangling bounds depending on the chemical composition of the interlayer and crystal lattice disorders [1,2,3, 14, 15]. The effect of these traps can be minimized either by good surface preparation and fabrication processes in very clean environments or by sufficiently high frequency utilizing voltage-dependent capacitance and conductance measurements (C/G-V). The charges at traps cannot contribute to the measurements C and G values at higher frequencies (f ≥ 0.5 MHz) because the relaxation time (τ) of them is long enough to permit the charges to move in or out of the trap in response to alternating signal [16,17,18,19,20,21]. But, Rs effects can be decreased by (i) making impedance measurements at enough low frequencies and (ii) applying an adjustment to the experimentally obtained C and G values for higher frequencies [2, 3].

In general, these traps are classified into five groups: (i) interface-trapped charges between interlayer and semiconductor, (ii) fixed oxide charges located near the interface; (iii) oxide trapped charges created by radiation, (iv) mobile ionic charges, (v) shallow-traps located near the conduction band (donor-type) or valance band (acceptor-type). Although there are many methods in the literature to determine and characterize the interface traps/states (Dit or Nss), the most sensitive and accurate is the conductance method developed by Nicollian and Goetzberger which is more susceptible to Nss values ∼109/(eV.cm2) [1, 2]. On the other hand, the one disadvantage of this method is quite laborious and time-consuming when compared to the low-high frequency capacitance (CLF-CHF) model developed by Castagne [22] and Hill and Coleman methods [16]. The conductance model is based on experimentally measured Cm and Gm values of the device as a function of voltage and frequency.

In our previous study [21], both the Au/(ZnCdS:GO(1:1)-PVP)/n-Si (MPS1) and Au/(ZnCdS:GO(1:0.5)-PVP)/n-Si (MPS2) SDs were fabricated onto the same n-Si wafer in same condition to determine the effect of doping rate of (ZnCdS:GO) on the electrical characteristics by using from the I–V and C/G-V (at 3 kHz and 3 MHz) measurements. For this aim, the basic electrical parameters (n, BH, and Rs) of them were also extracted from both the TE theory and Cheung functions to see their voltage dependence. Experimental results show that the MPS2 type SD is the best performance with respect to higher RR, Rsh, and BH values, and low value of n, low leakage current, low Nss, low Rs, and high rectification ratio (RR = Iforward/Ireverse at ±5 V), high BH when compared MPS1 type SD. Therefore, in this study, we aimed to achieve a better understanding of the effects of Nss, their lifetimes (τ), and Rs effects on the main electrical parameters, conduction mechanisms, and nature of barrier height (BH) formed at the M/S interface by using the used both conductance and (CLF-CHF) methods. For this aim, the impedance measurements were performed by utilizing a controllable HP 4192 A LF impedance analyzer between 1 kHz and 1 MHz, and all of them were performed via a microcomputer through an IEEE − 488 AC–DC converter card. Experimental results show that all basic physical parameters depend considerably on frequency and voltage.

2 Experimental procedures

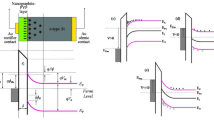
In the present study, Au/n-Si structures with (ZnCdS:GO) with (1:0.5) interlayer were fabricated onto an n-Si wafer which is a P-doped single crystal with 2” diameter, 100 orientation, 1 Ωcm resistivity, and ∼300 μm thickness. Firstly, the wafer was cleaned by utilizing the standard RCA technique and dried with N2 gas. Secondly, high-pure Al (99.999%) with 150 nm was thermally grown onto the back side Si substrate at 1µ Torr pressure and then sintered at 500 °C in nitrogen-ambient to get good ohmic contact. Thirdly, the prepared (ZnCdS:GO:PVP) solution was also thermally coated onto the front of the Si substrate with a 3000-rpm spin coater. Finally, the 99.999% pure Au Schottky contacts with 1 mm diameter were thermally grown onto the (ZnCds-GO:PVP) interlayer. A schematic diagram of the fabricated Au/(ZnCdS-GO:PVP)/n-Si (MPS) type structures and measured C-V-f and G-V-f systems were also represented in Fig. 1a, b respectively.

Fig. 1
figure 1

a A schematic presentation of the fabricated Au/(ZnCdS-GO:PVP)/n-Si (MPS) structures and b the measured C-V-f and G-V-f system

Full size image

The fabricated samples were fixed on a copper-holder via conductive silver paste to perform electrical measurements and connected to the sample by thin silver-coated Cu wires. The impedance measuring was realized by utilizing an impedance analyzer named HP-4192 A LF between 3 kHz and 3 MHz at RT in VPF-475 cryostat to obstacle any external effect at about 1 mTorr, and all measurements were controlled by a microcomputer via an AC–DC converter card of IEEE/488.

3 Experimental results and discussions

The values of C and G/ω versus voltage for various frequencies and versus frequency for various voltages are presented in Fig. 2a, b and Fig. 3a, b, respectively, accumulation, depletion, and inversion zones are clearly seen in Fig. 2a and 3a, which correspond to high, intermediate, and low bias voltages such as an MIS or MOS-type diode and capacitor. Obviously, the augmentation of C and G with decreasing biases was observed, particularly in the depletion zone. This increase or discrepancies in the C and G/ω versus V curves result from a special density distribution of Nss and their τ. On the other, the observed broad peak behaviors in the forward bias C-V curves are the results of the series resistance of the structures. As can be observed by regions, while the Nss ​​are effectual, especially in depletion and weak inversion at lower frequencies, Rs is effectual only at accumulation at higher frequencies, respectively [1, 3, 7, 9]. Because interface traps can readily track an ac signal and so on, they make an additional contribution to both the actual C and G/ω values at lower and moderate frequencies [23,24,25,26,27]. Under an external electric field, the electronic charges at the surface states can be restructured and rearranged, especially at low frequencies, leading to a shift in the C/G-V plots.

Fig. 2
figure 2

a The C - V curves at distinct frequencies and b C - lnf curves at the distinct biases

Full size image
Fig. 3
figure 3

a The G/ω - V curves at distinct frequencies and b G/ω - lnf curves at distinct biases

Full size image

Both the space charge (Qsc) and depletion-layer capacitance (C) per unit area of the structure are given as follows [3]:

$$Q_{sc} = \sqrt {{2q\varepsilon _s \varepsilon _0 N_D \left( {V_D - V - \frac{{kT}}{q}} \right)}}$$
(1)
$$C = \frac{{\left| {\partial Q_{SC} } \right|}}{{\partial V}} = \sqrt {{\frac{{q\varepsilon _s \varepsilon _0 N_D }}{{2\left( {V_D - V - \frac{{kT}}{q}} \right)}}}}$$
(2)

Equation 2 can be rearranged as follows:

$$1/C^2 = \frac{{2(V_D - V - \frac{{kT}}{q})}}{{(q\varepsilon _s \varepsilon _0 A^2 N_D )}}$$
(3)

Here, VD (= V0 + kT/q) is the diffusion potential, and V0 is the point where the 1/C2 - V plot intersects the y-axis at zero. The density of donor atoms (ND) can be extracted from the 1/C2 - V plot’s slope as follow (Fig. 4):

$${N}_{D}=\frac{2}{q{\epsilon }_{s}{\epsilon }_{0}{A}^{2}\left(\frac{d{C}^{-2}}{dV}\right)}$$
(4)
Fig. 4
figure 4

The 1/C2 - V plots for distinct frequencies

Full size image

The Fermi energy (EF), depletion-layer thickness (WD), maximum electric field (Em) at junction, and ΦB(C-V) values were calculated by using intercept voltage (V0) and slope of the 1/C2 - V plot (Fig. 4) by using following relations for each frequency, respectively [2, 28]:

$$E_F = \left( {\frac{{kT}}{q}} \right)\ln \left( {\frac{{N_c }}{{N_D }}} \right), W_D = \sqrt {{\frac{{2\varepsilon _s \varepsilon _0 V_D }}{{qN_D }}}} ,\, E_m = \sqrt {{\frac{{2qN_D V_0 }}{{\varepsilon _s \varepsilon _0 }}}} \, and\,\Phi _{B\left( {C - V} \right)} = V_0 + \frac{{kT}}{q} + E_F$$
(5)

Thus, the calculated electrical parameters of the structure between 10 kHz and 3 MHz are presented in Table 1.

Table 1 Some basic electrical parameters of the Au/(ZnCdS-GO:PVP)/n-Si structure
Full size table

As can be clearly seen from Table 1; Fig. 5a, while the value of ND decreases with increasing frequency, Em increases almost exponentially. Besides, both the WD and ΦB (C-V) rise with frequency increment almost linearly, as presented in Fig. 5b. Because the decrease of capacitance leads to an increase in the 1/C2 and so on, this plot gives a large intercept voltage. As shown in Fig. 5b, the barrier height is changed with lnf as ΦΒ (C-V) = (3.9 × 10-3x + 0.5694) eV. It is clear that the frequency-dependent coefficient of BH (3.9 × 10-3) eV/Hz.

Fig. 5
figure 5

a The change in Em andNDvalues with frequency. b The change in WDand FB values with frequency

Full size image

The Rs of the structure is also strongly influential on the C-V and G/ω-V plots, especially at the accumulation region for high frequencies. As seen in Fig. 3a and 4a, while C starts to decrease slightly at the accumulation region, G/ω increases sharply due to the decrement in series resistance with frequency increment (G = 1/R). Such behavior at accumulation or positive bias region is called “inductive behavior” and is usually attributed to Rs and interfacial layer [2, 3]. Therefore, the voltage-dependent profile of resistance (Ri) was extracted from the Nicollian and Brews [2] technique for each frequency by using Eq. 6 and is given in Fig. 6. As shown in Fig. 6a, the values of Ri usually decrease with increasing voltage for each frequency up to -0.5 V and then give a peak between ±0.5 V due to a special distribution of Nss in the bandgap of semiconductor. However, as shown in Fig. 6b, the value of Ri becomes voltage independent at high frequencies at accumulation region, which corresponds to the real value of Rs at higher frequencies. In other words, Rs decreases almost exponentially with frequency for all voltage levels due to the inability of the AC signal to follow Nss at higher frequencies.

Fig. 6
figure 6

a The Rs - V plot for distinct frequencies. b The Rs- lnf plot for distinct frequencies

Full size image
$$R_i \left( {V_i } \right) = \frac{{G_{mi} }}{{G_{mi}^2 + \left( {\omega C_{mi} } \right)^2 }}$$
(6)

As explained above, Ri is the resistance of the sample for any applied bias voltage, but the real value of Rs is corresponding to the strong accumulation region (at about 1.5 V) at enough high frequencies. Therefore, Eq. 6 can be rewritten as following.

$${R}_{s}\left({V}_{a}\right)=\frac{{G}_{ma}}{{G}_{ma}^{2}+{\left({\omega C}_{ma}\right)}^{2}}$$
(7)

In other words, in Eq. 7; Cma and Gma are the measured capacitance and conductance values at strong accumulation region (Va≅1.5 V).

In order to see the Rs effects on the C and G/ω data for higher frequencies, the related plots for 1 MHz were adjusted to eliminate the Rs effect by utilizing Eq. 8. which was proposed by Nicollian and Brews [2]: If the Rs effect is not eliminated, especially at high frequency and forward bias, it can lead to incorrect calculations and interpretations of the electrical and dielectric properties of the structure.

$$C_c = \frac{{\left[ {G_m^2 + \left( {\omega C_m } \right)^2 } \right]C_m }}{{\left( {\omega C_m } \right)^2 + a^2 }},\ G_c = \frac{{\left[ {G_m^2 + \left( {\omega C_m } \right)^2 } \right]a}}{{\left( {\omega C_m } \right)^2 + a^2 }}\ where\ a = G_m - \left[ {G_m^2 + \left( {\omega C_m } \right)^2 } \right]R_s ,$$
(8)

Thus, corrected Cc and Gc/ω values were obtained from Eq. 8 and are presented in Fig. 7a and b, respectively, and there is a noticeable increase in Cc compared to Cm, but the Gc/ω curve displays a distinctive peak at about 1 V. These results are indicated that Rs is quite effectual both on the C and G/ω data for higher frequencies and so Rs should be considered in the electric and dielectric parameters calculation or conduction mechanism of these devices [29,30,31,32,33,34]. On the other hand, the Rs effect can be ignored at lower frequencies in the inversion and depletion regions.

Fig. 7
figure 7

a The measured and corrected capacitance at 1 MHz. b The measured and corrected conductance at 1MHz

Full size image

It is well known that in MS contacts with/without a thin interlayer, many surface states or traps may occur between the interlayer and the semiconductor, which have energy levels in the forbidden bandgap of the semiconductor. They can arise from various sources, such as the cleaning of wafer and/or fabrication processes, disorders in the periodic lattice, and non-saturated dangling bonds at the interlayer/semiconductor interface. Thus, they act like recombination centers that can capture or release positive/negative electronic charges and so leads to an addition/excess capacitance and conductance [1,2,3,4,5,6,7]. There are many techniques to calculate surface states, such as the forward bias I-V technique proposed by Card and Rhoderick [35], the high-low frequency capacitance technique, and the conductance or statistical model proposed by Nicollian-Goetzberger [1]. This method is based on measuring the capacitance (Cm) and conductance (Gm/ω) of the structure as a function of voltage and frequency, and subsequently calculating the parallel conductance (Gp/ω) by solving a small signal equivalent circuit. Parallel conductance represents the loss mechanism occurring when the Nss capture or emit charges, and is used to extract the Nss and their lifetimes. In addition, the most accurate/reliable one is the conductance technique [36] which is the frequency of applied bias voltage for a certain dc voltage in the depletion region is expressed as follows:

$$\frac{{{G_p}}}{\omega }=\frac{{\omega {G_m}{C_i}}}{{G_{m}^{2}+{\omega ^2}{{\left( {{C_i} - {C_m}} \right)}^2}}}=\frac{{qA{N_{ss}}}}{{2\omega \tau }}\ln (1+{(\omega \tau )^2})$$
(9)

In Eq. 9, τ is the lifetime of the charges at traps, which shows the characteristic time required to fill and empty these traps [37, 38]. As presented in Fig. 8, Gp/ω - lnf curve gives a peak for each bias and so Nss and τ can be obtained from the peak value of parallel conductance by the following expressions [1, 2]:

$$N_{ss} = {\text{ }}(G_p /w)_{\max } /\left( {0.402qA} \right)~~~~~wt = {\text{ }}1.98~~ort = {\text{ }}1.98/w$$
(10)
Fig. 8
figure 8

The Gp/w - lnf plots for distinct voltages

Full size image

The conductance analysis of the structure was performed, and the voltage-dependent of the Nss and their τ between 0.40 and 1.30 V were determined. The voltage-dependent of Nss and τ values were presented as Nss- V and τ - V plots by utilizing Eq. 10 and represented in Fig. 9. As shown in Fig. 9, Nss were changed between 2.78 × 1012 at 0.40 V and 2.61 × 1012 eV−1cm−2 at 1.3 V and also the Nss-V curve has a two distinctive peaks which corresponds to the 0.5 V (2.87 × 1012 eV−1cm−2) and 1.2 V (2.68 × 1012 eV−1cm−2), respectively. On the other hand, theτ values were changed between 105 µs (at 0.4 V) and 15.3 µs (at 1.3 V) and also decreased with increasing voltage as almost exponentially [39]. It can be noted that the distribution of Nss densities with an average value of 1012 eV−1cm−2 is quite acceptable for MIS-type devices, and these low values are stemmed from the passivation effect of the interfacial layer used (ZnCdS-GO:PVP) [40, 41].

Fig. 9
figure 9

The acquired voltage-dependent of Nss and t by conductance method

Full size image

There is another way to acquire the voltage-dependent profile of Nss, which can be performed by measuring the measured capacitance (Cm) at enough high frequency (≥ 1 MHz) and at enough low frequency (≤ 1 kHz), which is known as the (CHF-CLF) capacitance method. This technique is easier and faster when compared with the conductance method, and moreover, it gives accurate results close to it. According to the technique, at low frequency, Nss can respond easily to the ac signal and so yield an excess C to the real value of them, but at higher frequency, tracking ac signal is not simple and so didn’t contribute to the measured capacitance [1, 3, 42, 43]. Therefore, the Nss values can be calculated from the difference between the CLF and CHF capacitance as given follow:

$$qA{N}_{ss}=\left[{\left(\frac{1}{{C}_{\text{L}\text{F}}}-\frac{1}{{C}_{i}}\right)}^{-1}-{\left(\frac{1}{{C}_{\text{H}\text{F}}}-\frac{1}{{C}_{i}}\right)}^{-1}\right]$$
(11)

Here, Ci is the interfacial layer capacitance, CLF is the measured C at low frequency (3 kHz), CHF is the measured C at high frequency (3 MHz), and A is the contact area of the rectifier. Thus, the voltage-dependent profile of Nss was also extracted from Eq. 11. The Nss-V plot gives a distinguishing peak nearly at 0.3 V due to a specific dispersion of Nss in the forbidden bandgap of the semiconductor, as presented in Fig. 10.

Fig. 10
figure 10

The voltage-dependent curve of Nss obtained from the low-high frequency capacitance technique

Full size image

Similar results on the interfacial pure and metal or metal-oxide doped organic/polymer interfacial layer, Nss and Rs effects both on the basic electrical parameters, conduction mechanism, and the nature of barrier height (BH) formed at Au/n-Si interface in wide range of frequency, temperature, and voltage have been reported in the literature in the last years [13, 42,43,44,45,46,47,48]. According to they, Rs is usually rooted from the ohmic/rectifier contacts, the used probe wires, bulk-resistance of the semiconductor, surface states/traps at interlayer/semiconductor surface, some impurities at surface of semiconductor, and non-uniform doped acceptor/donor atoms into semiconductor. On the other hand, interface states are usual rooted from the unsaturated dangling bonds, oxygen vacancies, doping energy level of donor/acceptor atoms, the defect in the crystal lattices, and some other impurities formed during fabrication processes. On the other hand, when the electrical measurements are taken only in a single or narrow frequency and voltage range, they cannot provide sufficiently reliable and accurate results on the electrical parameters, the nature of barrier height between metal and semiconductor, and conduction mechanisms. Therefore, admittance (Y = 1/Z) or impedance measurements, which include a set of C-V-f and G-V-f curves over a wide range of voltages (-4/1.5 V by 50 mV steps) and frequencies (from 3 kHz to 1 MHz) by using an HP 4192 A LF impedance meter for 19 different frequencies to get more accuracy and reliable results on the basic electrical parameters as a function of frequency and voltage, nature of barrier height at Au/n-Si interface, and conduction mechanism of the fabricated Au/(ZnCds-GO:PVP)/n-Si (MPS) type structures instead of congenital metal/insulator/semiconductor (MIS) type structures.

4 Conclusion

In this study, we prepared Au/(ZnCdS-GO:PVP)/n-Si (MPS) type structures instead of MOS-type structures. Both their frequency and voltage-dependent basic electrical parameters were acquired by the measured impedance spectroscopy method in the 3 kHz − 3 MHz interval and in the − 4.00 V to 1.50 V range, respectively. These values were found as 1.69 × 1016cm−3, 0.444 eV, 0.193 eV, 0.606 eV, 1.31 × 10−5 cm, 7.66 × 104 V/cm for 10 kHz, and 1.42 × 1016cm−3, 0.461 eV, 0.198 eV, 0.628 eV, 1.46 × 10−5 cm, 7.80 × 104 V/cm for 3 MHz, respectively. All of them were raised with rising frequency except for ND. The voltage-dependent profile of the density of Nss and their τ were extracted from the conductance techniques, and while the values of Nss were changed between 2.78 × 1012 at 0.40 V and 2.61 × 1012 eV−1cm−2 at 1.3 V and the Nss-V plot shows two distinctive peaks which are corresponding to 0.5 V (2.87 × 1012eV−1cm−2) and 1.2 V (2.68 × 1012 eV−1cm−2), respectively. Besides, τ decreases with voltage increment and varies between 105µs (at 0.4 V) and 15.3 µs (at 1.3 V). The voltage-dependent profile of Nss was also extracted from the (CLF-CHF) capacitance method as a second way. The calculated lower values of Nss are indicated that (ZnCdS-GO:PVP) polymer interlayer leads to the passivation effect of the surface states.