1 Introduction

Chalcogenide glassy materials are advantageous over crystalline ones because of their smooth tuning property, low cost, and significant efficiency in optoelectronic applications [1,2,3,4,5,6]. Lead sulfide (PbS) is an important narrow direct band gap semiconductor with several excellent physical and chemical properties [7, 8]. It has numerous applications, such as tunable near-infrared detectors [9, 10], biological markers [11, 12], thermoelectric materials [13], photocatalysts [14], quantum dot solar cells [15], and new-generation solar cells [16,17,18,19]. PbS belongs to the IV–VI group of semiconductor compounds with face-centered cubic (fcc) crystal structures [20]. In addition, PbS is a P-type semiconductor with high light absorbing capacity in the visible and NIR ranges due to its tunable band gap within this spectral range [21,22,23], recommending it as an excellent P-type absorber for solar cells [24].

The films of PbS have been grown in many forms for current applications using a variety of techniques, including chemical bath deposition (CBD), vacuum evaporation, spray pyrolysis, electrochemical deposition, etc. [25,26,27,28].

The study and characterization of linear optical absorption, dielectric, and dispersion, in addition to the calculation of related parameters like the extinction coefficient, refractive index, and energy gap, are crucial for the optical material properties and performance of optoelectronic devices.

When a material is exposed to a strong light beam, the polarisation becomes non-linear proportional to the electric field, and non-linear effects appear to dominate. This suggests that linear and non-linear susceptibilities can participate in the susceptibility contribution to polarizability (P).

The non-linear refractive index n(2) and the third order of non-linear susceptibility χ(3) are important parameters utilised to achieve optically limiting behaviour and are used in a variety of applications. Values of n2 and χ(3) are strongly enhanced by different factors, such as the polarizable bond density and their orientations with respect to the induced electric field, the material compactness, the bond length of polarizable species, the density of localised states, the density of cloud electrons in the outer shell and their distance from the nucleus, etc. [29]. It is believed that PbS could be promising as non-linear optical (NLO) candidates because of their large refractive nonlinearity and high 3rd-order non-linear optical susceptibility [30]. That is because of the great density of electrons in Pb82 placed far apart from the nucleus, large Pb–S bond length of 0.29696 nm [31, 32] in addition to the easy formation of polarizable atoms and ions in chalcogenide glasses induced by high electric fields.

The dopant nature and concentration can play important roles in tuning the physical properties and efficiencies of Pbs-based devices. The incorporation of zinc atoms as a doping element into the PbS crystal structure leads to defect formation, increasing the density of polarizable species that can respond to intensive fields [31, 33]. Zn2+ with a radius of 0.74 Å occupies the sites of Pb2+ with a radius of 1.19 Å [34] as a substitutional element and results in a shrinkage of the lattice [35], a matter that leads to a material compactness increase and, in turn, a refractive index increase.

In this work, the optical linear and non-linear properties of (PbS)1−x (Zn)x thin films prepared by thermal deposition have been investigated. The effects of Zn-doping, film thickness, and annealing temperature have been examined. The results were discussed and compared with the corresponding reported ones..

2 Experimental

Both un-doped and Zn-doped PbS thin films with different thicknesses from 50 to 250 nm were deposited on glass substrates using the thermal evaporation method by the Edwards E306A coating system. During the preparation of our films, the deposition rate changed from 1.2 to 3.5 Å/s. The chamber was evacuated to 4 × 10−4 mbar at the start of the deposition process and 3.63 × 10−5 mbar at the end. High purity of 99.99% PbS and Zn powders provided by the Aldrich Association were used for the present samples. The powder mixture of (PbS)1−x (Zn)x (x = 0, 0.01, 0.03, 0.05 wt%) was prepared from the high purity stoichiometric amounts of (Zn and PbS). Then, the mixture was cold pressed in tablet form. In order to obtain homogeneous compounds, the mixtures of samples are heated for 2 h at 300 °C, 3 h at 350 °C and 2 h at 400 °C. The samples were milled again for 2 h and the resultant powders were pressed into tablets. These tablets have been sintered at 600 °C for 3 h to ensure the homogeneity of the forming compounds, that were used as sources of our thin films. These tablets were placed in a molybdenum boat (melting point around ≈ 2620 °C).

The compressed tablets of un-doped and Zn-doped PbS were deposited on clean glass substrates, washed by acetone, and cleaned in heated distilled water using an ultrasonic cleaner (VGT-1613 QTD) with a digital timer of 2000 mL capacity. A digital film thickness monitor, model INFICON, was used to measure the film thickness and the rate of deposition (SQM-160).

The crystallographic structure of the as-deposited films on glass was investigated by X-ray diffraction pattern (Bruker D8 Advance—Germany) with Cu as a target and Ni as a filter (Cu kα1; λ = 1.5406 Å) at 30 kV and 30 mA with scanning speed equal to 2.5°/min.

The surface morphology and compositional contents of the present (PbS)1−x Znx films were examined using field emission scanning electron microscopy (FE-SEM) JSM-6100 (JEOL, Japan) microscope with a 30 kV acceleration voltage. Using the FE-energy SEM's dispersive analysis of X-ray (EDAX) instrument, the chemical compositions of the films were also examined using (EDS unit, HNU5000, USA). A very thin film of gold, about 10 nm thick, was applied to the samples prior to the examination.

The optical characteristics (absorption A (λ), transmittance T (λ) and reflection R (λ)) of the films were investigated at room temperature with a computer-programmable Jasco V570 (Japan) double-beam spectrophotometer, at normal incidence in the wavelength range of 200 to 2500 nm, with a scan speed of 400 nm/min.

3 Results and discussion

3.1 XRD analysis

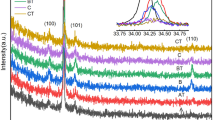
Figure 1 demonstrates the XRD patterns of (PbS)1−x (Zn)x where x = 0, 0.01, 0.03, 0.05 w.t%. As shown for the film of x = 0, all peaks correspond to PbS compounds, confirming the good purity of this film. Besides, no phases corresponding to the Zn element could be depicted for Zn-doped films, indicating that zinc was incorporated into the PbS lattice. With increasing levels of Zn-doping, both the intensity and the number of crystalline peaks decrease, indicating an increase in microstructure disorder. For pure PbS, some peaks corresponding to (111), (200), (202), (311), (222), (400), (313), (402), (422), and (511) are observed at 2θ = 25.97, 30.084, 43.064, 50.984, 53.426, 62.535, 68.889, 70.944, 78.947 and 84.797 respectively, which are consistent with JCPDS COD 9008694 standard data.

Fig. 1
figure 1

XRD diffraction patterns of undoped and Zn-doped PbS thin films (thickness d = 200 nm)

Full size image

The favorable orientation of crystallisation in F.C.C cubic structure has occurred along the most intensive peak (200). The effect of doping leads to intensity reduction and peak broadening, which is indicated by the decrease in -values with doping. as shown in Fig. 1 and Table 1.

Table 1 XRD parameters of the (PbS)1−x Znx films calculated using the preferred (2 0 0) orientation
Full size table

The crystallite size (D), the lattice strain (ɛ), the dislocation density (δ), the lattice constant (a), d-spacing, X-ray density dXRD and bulk density dbulk are calculated using the following equations, respectively:

$$D = \frac{0.94\lambda }{{\beta \cos \theta }}$$
(1)
$$\varepsilon = \frac{\beta \cos \theta }{4}\sim D^{ - 1}$$
(2)
$$\delta = \frac{1}{{D^{2} }}$$
(3)
$$a = d \sqrt {h^{2} + k^{2} + l^{2} }$$
(4)
$$d = \frac{\lambda }{2\sin \theta }$$
(5)
$$d_{{{\text{XRD}}}} = \frac{{8M_{{\text{w}}} }}{{N_{{\text{A}}} a^{3} }}$$
(6)
$$d_{{{\text{bulk}}}} = \frac{m}{{\pi r^{2} h }}$$
(7)

where \(\theta\) is Bragg's angle, is the X-ray wavelength, is the full width of the half maximum of the corresponding XRD peak, Mw is the molecular weight of (PbS)1−x Znx and NA is Avogadro's number.

As shown in Table 1, the crystallite size D decreases with Zn doping, which is characteristic of substitutional doping [34,35,36]? Since it is easy for doped Zn having a smaller (0.74 Å) ionic radius than that (1.19 Å) of Pb2+ to occupy substitutional sites in PbS lattice, leading to a reduction in the crystalline size, a matter that can be confirmed by the observed peak shift to lower \(\theta\) values leading to a cos \(\theta\) increase (Eq. 1). The increase in both ε and δ with a doping level increase, which can be attributed to the defect formation in the lattice structure, could be predicted regarding Eqs. 1–3, where ε and δ are proportional to D−1 and D−2 as clear by Eqs. 2 and 3, respectively.

The microstructural parameters of grown films listed in Table 1, show that the crystallite size decreases from 24.84 to 13.40 nm when the Zn dopant concentration increases to 0.05. Besides, a rising trend in lattice defects such as micro-strain and dislocation density with increasing Zn concentration can be depicted. Such a type of change could result due to the crystalline degradation nature [37]. Furthermore, the decreases in dXRD and dbulk with Zn-doping could be attributed to the depicted decrease in unit cell volume [38, 39], as shown in Table 1.

The observed increases in both d-spacing and lattice constant and the cell volume \(V = a^{3}\) may be understood regarding Eqs. 4 and 5 as the (200) peak shifting to smaller 2θ-values.

3.2 Morphological properties

Figure 2 shows SEM micro-images of (PbS)1−x Znx (x = 0, 0.01, 0.03, 0.05 wt%) thin films deposited on glass substrates. It is revealed that the grains are homogenously distributed on the film surface and densely agglomerated with a tendency towards spherical shapes. The grains are different in size depending on the Zn-doping level. The average particle sizes calculated by the J-programme were found to range from 70 to 275 nm.

Fig. 2
figure 2

SEM images of (PbS)1−x Znx thin films

Full size image

3.3 Elemental composition analysis (EDX)

Figure 3 shows the elemental composition analysis of the films determined by the energy-dispersive X-ray. The weight and atomic percentages of compound elements were determined. As shown, only Pb, S, and Zn elements are identified, confirming that the films are free from impurities. However, the depicted ratios of sulphur in both pure and Zn-doped PbS are smaller than their values corresponding to stoichiometric compounds. This may be attributed to the release of sulphur during the film's thermal deposition.

Fig. 3
figure 3

EDX for (PbS)1−x Znx films at x = 0 (a), x = 0.01 (b), x = 0.03 (c) and x = 0.05 (d)

Full size image

3.4 Linear optical characterization

Figure 4 shows the spectral variations of optical absorption A (λ), transmission T (λ) and reflection R (λ) of (PbS)1−x (Zn)x thin films, where (x = 0, 0.01, 0.03, 0.05 w.t%). All films reveal nearly similar spectral behaviour. They manifest relatively high absorption in the visible (∼ 350–800 nm) range compared with their value in the NIR region, which takes almost low constant values in the NIR (λ ≥ 1500 nm) range, indicating the NIR-transparent nature of the present films. Besides, with increasing the level of Zn-doping, the absorption grows less, and the fundamental edge shifts towards lower λ values, indicating an increase in the band gap energy.

Fig. 4
figure 4

a Optical absorption, b transmission, and c Reflection spectra of (PbS)1−x Znx thin films where d = 200 nm

Full size image

Figure 4b shows that the transmission increases with λ reaching a value of 70%, confirming the good transparency of the present films in the NIR-spectral range.

As shown in Fig. 4c the present films manifest low and more intensive reflection in the VIS and NIR regions, respectively. The simultaneous decrease and increase of T and R with λ, respectively, in the NIR (∼ 1200–2000 nm) region for all considered films suggests the occurrence of relatively high free carrier concentrations. This effect is governed by the plasma oscillation of free carriers and is associated with a shift to a shorter wavelength [39,40,41].

Moreover, the energy tail width of the localised states that existed in the forbidden band can be described by the following exponential Urbach relation [42] in the low range of the absorption coefficient values:

$$\alpha = \alpha_{o} \exp \left( {\frac{h\nu }{{E_{{\text{u}}} }}} \right),$$
(8)
$$\alpha = 1/d\ln \left[ {\frac{{(1 - R)^{2} }}{T}} \right]$$
(9)

where \({\mathrm{\alpha }}_{o}\) is a constant, Eu is the Urbach energy that measures the tail width of the localized states and d is the film thickness. The values of Eu are estimated from the slopes of ln \((\alpha )\) Vs hv plots as shown in Fig. 5 and recorded in Table 3. As shown Eu non-sequentially varies with Zn-doping possessing the highest value for x = 0.03 wt% (Table 2).

Fig. 5
figure 5

Plots of (ln α − hυ) for (PbS)1−x Znx thin films

Full size image
Table 2 Values of absorption coefficient measured at a solar maximum wavelength (λ = 500 nm), as well as, values of, the energy band gap Eg, and Urbach energy Eu for (PbS)1−x Znx compounds
Full size table
Table 3 Values of dielectric and dispersion parameters for (PbS)1−x Znx compounds
Full size table

In order to determine the energy gap (Eg) values of the present films, the following Tauc's equation [43, 44] can be utilized;

$$\alpha h\nu = \beta \left( {h\nu - E_{{\text{g}}} } \right)^{r} \;{\text{and}}$$
(10)

where β is an energy–independent constant and the exponent r characterises the electronic transition type. Good fitting to straight-line portions of (αhv)2 vs \(h\nu\) plots was achieved when r = 1/2 indicating allowed direct transitions. The value of the intercept of the linear portion with the ordinate at (αhv)2 = 0 gives the value of Eg as shown in Fig. 6. The determined values of Eg are recorded in Table 3. It is clear that Eg increases from 1.25 to 1.64 with increasing Zn-doping level which is consistent with other reported results [45].

Fig. 6
figure 6

Plots of (αhv)2 vs. hv for (PbS)1−x Znx thin films

Full size image

The surface SELF and volume VELF energy losses functions utilised to certify the electromagnetic radiation dealing with the material surface and bulk and the interaction with the material electrons are given by the following relations [46, 47], respectively.

$${\text{SELF}} = \frac{{\varepsilon_{im} }}{{\left( {\varepsilon_{r}^{2} + 1} \right)^{2} + \varepsilon_{im}^{2} }}$$
(11)
$${\text{VELF}} = \frac{{\varepsilon_{im} }}{{\varepsilon_{r}^{2} + \varepsilon_{im}^{2} }}$$
(12)

where εr and εim are the real and imaginary dielectric constant components, respectively. As shown in Fig. 7, the energy dependence of SELF and VELF functions for films of x = 0.03 at d = 150 nm and 200 nm have almost the same behaviour, where each of them manifests two essential lower and higher peak intensities. However, the intensities of the VELF peaks are more intense than their corresponding SELF peaks by 4.95, 8.28 and 2.125, 4.9 times for the I and II peaks of the films of 150 and 200 nm, respectively. This may be attributed to the relatively larger penetration depth of electromagnetic radiation and interactions with more involved electrons.

Fig. 7
figure 7

Energy dependences of volume (VELF) and surface (SELF) of (PbS)0.97 Zn0.03 thin films 150 nm (a) and 200 nm (b) thick

Full size image

The studies of optical dielectric and dispersion and the determination of their parameters are important due to their roles in optical communication development and optical device performance [48]. As shown in Fig. 8, the plots of the real dielectric constant versus λ2 are linear in the λ (2300–2470 nm) range, realising the following Spitzer-Fan equation [49,50,51],

$$\varepsilon^{\prime} = \varepsilon_{{\text{L}}} - \left( {\frac{{e^{2} }}{{\pi c^{2} }}} \right)\frac{N}{{m^{*} }}\lambda^{2}$$
(13)
$$= \varepsilon_{{\text{L}}} + 4\pi x_{{\text{c}}}$$
(14)
$$= \varepsilon_{{\text{L}}} - \left( {\frac{\lambda }{{\lambda_{p} }}} \right)^{2}$$
(15)

where \({\varepsilon }_{L}\) is the high-frequency dielectric constant of the lattice, N/m* is the free carrier concentration to the effective mass, χc is the free carrier's contribution in the real part of the dielectric constant and \({\lambda }_{p}\) is plasma wavelength. These parameters were determined using the plot's slopes and intercepts and recorded in Table 3.

Fig. 8
figure 8

Plots of (ε − λ2) for (PbS)1−x Znx thin films

Full size image

In the same λ—range of normal dispersion ∼ 2300–2470 nm \({{(n}^{2}-1)}^{-1}\) vs \(\left(h\upsilon \right)2\) plots are linearly verifying the Wemple–Didomenico single oscillator model [35], expressed by the following relation;

$$(n^{2} - 1)^{ - 1} = \frac{{E_{{\text{o}}}^{2} - \left( {h\upsilon } \right)^{2} }}{{E_{{\text{o}}} E_{{\text{d}}} }}$$
(16)

where Eo and Ed are the oscillator and the dispersion parameters, respectively. E0 and Ed can be calculated with the help of the slopes and intercepts of the plots in Fig. 9 and recorded in Table 3.

Fig. 9
figure 9

(n2 − 1)−1 vs. (hv) 2 plots for (PbS)1−x Znx thin films

Full size image

3.5 Non-linear optical characterization

The optical linear and non-linear effects are subjected to the induced optical power level and the material optical response. At low optical power, the bound electron of an atom is affected by a harmonic electrical restoring force that leads to small symmetrical harmonic displacements of the electron around its original position. The values of these displacements are linearly dependent on the electric force, and optical properties like polarisation depend linearly on the electric fields. Such optical linear effects take place only at power levels lower than the binding electric field intensity of the bound electrons. However, the optical non-linearity is due to the anharmonic response of the medium induced by intensive electric fields, such as the very powerful laser field. This leads to asymmetric polarisation that is no longer linearly proportional to the electric field [52].

Thus, the polarisation (P) in a medium could be resulted from linear and non-linear susceptibility contributions, depending on the applied light power intensity, i.e.

$$P = \chi^{1} E + P_{{{\text{NL}}}} ;\;P_{{{\text{NL}}}} = \chi^{(2)} E^{(2)} + \chi^{(3)} E^{(3)}$$
(17)

where χ1 is the linear susceptibility, PNL is the non-linear optical polarizability, and χ(2) and χ(3) are the 2nd and 3rd order of the non-linear optical susceptibilities, respectively.

The linear susceptibility can be determined using the following equation[53]

$$\chi^{(1)} = \frac{{n_{0}^{2} - 1 }}{4\pi }$$
(18)

where n0 = \(\sqrt{\frac{{E}_{d}}{{E}_{0}}+1}\) is the static refractive index given by the value of n when hv = 0 in Eq. (16)

Miller’s generalized rule [54] has correlated χ(3) to χ(1) through the following expression,

$$\chi^{\left( 3 \right)} = A\left( {\chi^{(1)} } \right)^{4} = \frac{A}{{\left( {4\pi } \right)^{4} }}(n_{0}^{2} - 1)^{4}$$
(19)

where A = 1.7 × 10–10 esu which is valid almost for all materials [55].

The non-linear refractive index n2 is related to χ(3), according to Tichy and Ticha [53], as follows;

$$n_{2} = \frac{{12\pi \chi^{\left( 3 \right)} }}{{n_{0} }}$$
(20)

Both the non-linear refractive index n2 and third-order optical polarizability χ(3) are crucial parameters for numerous optical non-linear applications [56,57,58,59]. χ(3) describes third harmonic generation, two-photon absorption, and intensity-dependent refractive index, and plays an important role in the specification of material validity for non-linear optical systems. Besides, n2 is an essential parameter for the performance of nonlinear optical devices [60]. Furthermore, the energy dispersion of the nonlinear absorption coefficient is described by the so-called F-function [61, 62]; where

$$F = {{\left[ {\left( {\frac{2hv }{{E_{{\text{g}}} }}} \right) - 1} \right]^{3/2} } \mathord{\left/ {\vphantom {{\left[ {\left( {\frac{2hv }{{E_{{\text{g}}} }}} \right) - 1} \right]^{3/2} } {\left( {\frac{2hv }{{E_{{\text{g}}} }}} \right)^{5} }}} \right. \kern-0pt} {\left( {\frac{2hv }{{E_{{\text{g}}} }}} \right)^{5} }}$$
(21)

This F-function, which depends on the energy band structure, is important to specify the energy states that are coupled. Variations of the energy dependences of n2, χ(3) and F-function influenced by Zn-doping, film thickness, and annealing temperature are given in Figs. 10, 11, and 12, respectively. The maximum values of these non-linear parameters were estimated and recorded in Table 4.

Fig. 10
figure 10

Spectral variations of n2, χ(3)and F- function for (PbS)1−x Znx films. (x = 0, 0.01, 0.03 and 0.05 Wt.%) d = 200 nm

Full size image
Fig. 11
figure 11

n2 (a), χ(3) (b) of (PbS)1−x Znx x = 0.03 W.t% thin films at different thicknesses

Full size image
Fig. 12
figure 12

Effect of annealing on χ(3) (x = 0.03, d = 50 nm)

Full size image
Table 4 Effect of film composition on Non-linear parameters for (PbS)1−x Znx films, d = 200 nm
Full size table

As shown in Fig. 10a, b, n2 and χ(3) have the same spectral variation. Depending on the film band gap energy, they start to increase with increasing the photon energy to a maximum value, then decrease with further energy increases and start tending to a constant value. Besides n2 and χ(3) maxima of the same films lie approximately at the same energy value, which is generally shifted towards the higher values as Zn-doping levels increase. As shown in Fig. 10b and Table 4, the moderate (2.65 × 10–11 esu) value of χmax(3) of pure PbS may be partially attributed to one or more of the different contributing factors. Chalcogenides containing, in general, highly polarizable atoms and/or ions in the material matrix are expected to have large non-linear properties. Lead Pb82 has a relatively large number of cloud electrons in the outer shell, which are placed far apart from the nucleus. This simplifies the polarisation process. Besides, the relatively long length of 0.29696 nm of the Pb–S bond [31, 32] strongly contributes to the polarisation in the optical medium. Finally, the relatively higher value of grain size (Table 1) of pure PbS film means higher values of material compactness, and consequently, the refractive index increases, indicating a high number of polarizable Pb–S bonds (Fig. 13).

Fig. 13
figure 13

Effect of annealing on χ(3) values for (PbS)0.97 Zn0.03 (d = 150 nm)

Full size image

Besides, the observed decrease of χ(3) with inserting Zn-dopant with x = 0.01 wt% may be due to the formation of Zn–S bonds with a lower bond length (0.27805 nm) on the expense of Pb–S with a larger bond length (0.29696 nm) [31, 32]. With increasing Zn-doping up to x = 0.03 the value of χ(3) remarkably increases to be 1.63 × 10–10 esu, which may be attributed to the increase in defect formation in the material structure [31, 33] in addition to the energy activated of both Pb–S and Zn–S bonds. The rapid decline of χ(3) with a further increase of Zn-doping level up to x = 0.05 wt% could be interpreted by the extra formation of weak polarizable (Zn–S bonds) instead of the relatively stronger (Pb–S) ones, and/or the decrease of the densities of both Pb–S and Zn–S bonds as a result of the depicted relatively higher deficiency of sulphur content in this film.

Figure 10c depicts the spectral variations of F-function for pure and Zn-doped films. F-function begins increasing at energy values of 0.57, 0.61, 0.73, and 0.78 > Eg/2 eV for films with x = 0, 0.01, 0.03, and 0.05 Wt.%, attaining its maximum values at 0.80, 0.86, 1.03 and 1.12 eV then it decreases with further hv-increase inclining to a constant value at 1.04, 1.11,1.33 and 1.46 eV < Eg This behaviour of F − hv satisfies the two-photon absorption condition Eg/2 < hv < Eg. Besides, the ratio of Eg/FEmax of the energy gap and the energy position of FEmax were found 1.56, 1.66, 1.50 and 1.45 for x = 0, 0.01, 0.03 and 0.05 Wt.% of the present (PbS)1−x Znx thin films. These ratio values are close to the reported values of 1.4 for different chalcogenide materials [63,64,65,66], realising the condition of two-photon absorption.

In a trial to enhance the best values 16.8 × 10–10 and 1.63 × 10–10 esu attained for n2, χ(3), respectively, by the film of x = 0.03 at d = 200 nm, the effects of both film thickness and annealing temperature were examined. To avoid repetition, the optical parameters affected by either the film thickness or annealing temperature and required for NLO-calculations were determined by the same method employed here.

As shown in Figs. 11, 12 and Table 4, both n2, χ(3) values are generally decreased with film thickness increase. This may be mainly attributed to the increase of the weak polarizable Zn–S bonds on the expense of the strong Pb–S ones.

Besides, the decrease in material density and consequently the decrease of the refractive index, the thermally eliminated localized states as well as the density decrease of both Zn–S and Pb–S polarizable bonds as a result of sulfur release may be responsible for the relatively low values of both n2, χ(3) with annealing. Nevertheless the enhancing and inhibiting factors of non-linear properties which were previously discussed could be comprmized leading to attain the enhanced 2.78 × 10–10, 2.93 × 10–10 esu result of n2 and χ(3) for annealed (at 200 °C) films of 150 nm thick. As shown in Tables 4 and 5 these results are comparable with the reported ones of some oxides, chalcogenide and organic materials.

Table 5 Effect of film thickness and annealing temperature on Non-linear parameters, x = 0.03 Wt.%
Full size table

4 Summary and conclusions

The (PbS)1−x (Zn)x thin films with light Zn-doping were deposited using the thermal deposition technique, analysed by XRD, SEM and EDS and characterised by UV–VIS–NIR spectroscopy. PbS films crystallise in F.C.C structure with a preferable (200) orientation. The grains on the film surfaces are homogeneously distributed, with an average particle size 34–64 nm depending on the Zn-dopant ratio. With the increase in Zn-doping concentration, the grain size decreases while the microstructure disorder, microstrain, and dislocation density increase.

The lower sulphur ratios revealed for either Zn-doped or undoped films than their corresponding stoichiometric values are dependent on the thermal deposition conditions.

The films show an allowed direct transition with an energy gap value that increases with Zn-doping and annealing temperature, but decreases with increasing film thickness.

Absorption, dielectric, and dispersion parameters varied depending on Zn-doping, film thickness, and annealing temperature, which strongly affect the optical NLO properties.

Finally, the satisfactorily enhanced 2.78 × 10–10 and 2.93 × 10–10 esu values of n2 and χ(3), respectively, obtained for (PbS)0.97 (Zn)0.03 films of 150 nm thick and annealed at 200 °C may recommend such films be applied in highly intensive optical radiation systems.