1 Introduction

After discovering the high-temperature superconductors (HTS), critical current density and electrical conductivity of HTS has remained interesting and challenging topics. High temperature cuprite superconductor YBa2Cu3O7−d (denoted as YBCO or Y-123) is one of the most interesting materials in the world of superconductors. Y-123 is the first disclosed HTS which has critical superconducting transition temperature, \({T}_{co}\), that even exceeds the boiling temperature of liquid nitrogen [1]. The cost of cooling Y-123 by liquid nitrogen is very less as compared to liquid helium. These findings made great progress in the technology applications used for the transportation of higher currents. Furthermore, Y-123 has many applications typically in energy storage devices, medicine, electronics and transportation [2,3,4,5]. Many investigations have been conducted in the last ten years to enhance the superconducting properties of HTS materials. The introduction of efficient pinning centers, which will inhibit the vortices motion, within HTS matrix is the most convenient way to achieve this aim. The inclusion of nanoparticles in the HTS matrix causes defects generation, thus the production of proficient artificial pinning centers [6,7,8,9]. Semiconductors nanoparticles have been used in different applications field due to their interesting properties, and were studied as the most effective nanoparticles in enhancing the transport properties in the superconducting materials [10,11,12,13,14,15,16,17,18,19]. Among the semiconductor materials; cadmium sulfide nanoparticles have been extensively studied [20]. In addition to hexagonal wurtzite, CdS also has cubic zinc blends and high-pressure rock salt crystal structures. The excellent properties of CdS and its extensive applications make it an excellent candidate for improving the properties of superconductors [20].

In our previous work, we have prepared CdS nanoparticles using hydrothermal method [20]. The prepared nanoparticles had hexagonal phase with average size of 12 nm and the electrical properties of bismuth-based compound (Bi,Pb)2Sr2Ca2Cu3Oy with additional CdS (12 nm) nanoparticles were studied in details [17].

In the present work, we have prepared cubic CdS nanoparticles using the low-temperature soft aqueous route, with an average size of 6 nm, The purpose of which is to conduct a comparative study of the effect of CdS (6 nm) and CdS (12 nm) nanoparticles addition on the electrical properties of Y-123 compound. A solid-state reaction was used for the synthesis of pure and added YBCO with an 0.1 wt% additional amount of CdS nanoparticles with sizes 6 nm and 12 nm. The Y-123 system's superconducting characteristics and flux pinning mechanisms are the main focus of this work.

2 Materials and methods

2.1 Synthesis of CdS nanoparticles

Cadmium chloride hydrates CdCl2.H2O and sodium sulfide nonahydrate Na2S.9H2O was used to synthesize semiconductor CdS nanoparticles via an aqueous approach as precursors and using polyvinylpyrrolidone PVP as capping agent. A three-neck round-bottomed flask was used, 5 ml of CdCl2.H2O and 20 ml of PVP (0.1 M) were used to make a solution. NaOH (2 M) was used to adjust the pH to 11.5. Next, the solution was dropped under vigorous stirring and degassing by using argon gas for half hour. Then, 4.5 ml of Na2S.9H2O (0.1 M) degassed were added to the mixture. The solution was stirred at 95 °C under argon reflux for four hours. After cooling down the solution to room temperature, the orange precipitate was collected through centrifugation and washed with ethanol for several times. The samples were then dried for further characterizations.

2.2 Incorporation of CdS nanoparticles in YBa2Cu3Oy superconductor

The solid-state reaction method was used for the synthesis of pure and CdS nanoparticles added YBCO samples. A mixter of highly pure oxides CuO (99.9%), Y2O3 (99.9%) and Ba2CO3 (99.9%) was used to prepare a single phase YBCO with the chemical formula Y:Ba:Cu = 1:2:3, by considering two thermal cycles. The obtained powder was annealed at 950 °C for 12 h in air. The synthesized CdS (6 nm) and (12 nm) nanoparticles were added to Y-123 during the second cycle in excess of x = 0.1 weight percent of the sample’s total mass. The samples were subsequently made into pallet shapes and sintered for 8 h at 950 °C in the air.

2.3 Characterization techniques

The structure and purity of the nanoparticles were investigated using an advanced X-ray diffractometer Bruker D8 which has CuK radiations with the value of \(\lambda\)=1.5418 Å. A FEI Tecnai G2 transmission electron microscope was used to analyze the morphology of the produced nanoparticles. Optical absorption properties of the prepared samples were carried out using a T60 UV–Visible spectrophotometer. A Micrometrics Tristar II 3020 surface area and porosity analyzer was used to determine the specific surface areas of the sample based on Nitrogen absorption desorption.

The temperature dependence of the electrical resistivity of one's own and with the presence of applied magnetic fields which ranges from 0 to 100 mT was examined using alternating current technique with lower frequency. It was based on a clamp amplifier which has resolution of 2 nV. According to a 5 V cm−1 criterion, as a function of ground temperature and applied magnetic field, the critical transport current density was estimated. The temperature was taken with a Platinum sensor with a resolution of more than 2 mK. The excitation current was injected along the sample’s length when a magnetic field was provided along its short axis.

3 Results and discussion

3.1 Characterization of CdS nanoparticles

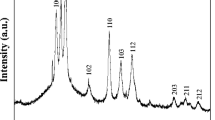
The X-ray diffraction patterns of CdS nanoparticles synthesized using the hydrothermal and aqueous methods are displayed in Fig. 1a and b, respectively. The diffraction peaks of CdS nanoparticles prepared by hydrothermal process shows the presence of hexagonal CdS with space group P63mc (Fig. 1a). The diffraction peaks of CdS nanoparticles prepared by aqueous method clearly show that those nanoparticles present a cubic structure with a space group F \(\overline{4 }3\) m (Fig. 1b).

Fig. 1
figure 1

X-Ray diffraction pattern of a CdS (6 nm), b CdS (12 nm) nanoparticles, variation of \(\beta \mathrm{cos}\theta\) versus \(4 \mathrm{sin}\theta\) of c CdS (6 nm), d CdS (12 nm) nanoparticles

Full size image

The Scherer formula can be used to estimate the average crystallite size (D).

$$D\, = \,\frac{k\,\lambda }{{\beta_{D} \,\cos \theta }}$$
(1)

where shape factor is denoted by \(k=\) 0.89, wavelength of X-ray radiation is represented by \(\lambda\) and the full width at half maximum of the peak is denoted by \({\beta }_{D}\) at diffraction angle \(\theta\).

The Scherer equation states that the peak widening of the diffraction spectrum is solely caused by the crystallite size. However, it is also recognized that additional elements, such as lattice strain ((\(\varsigma\)), may significantly influence peak broadening [21].

$$\varsigma \, = \,\frac{{\beta_{S} }}{{4\,{\text{tan}}\theta }}$$
(2)

where \({\beta }_{S}\), denotes the widening brought on by lattice strain.

Williamson-Hall defines the linear relationship between the size of crystals (Eq. 1) and crystal defects/distortion (lattice strain) as the peak broadening for uniform strained crystals (Eq. (2)) [21],

$$\beta \,{\text{cos}}\theta \, = \,\frac{k\,\lambda }{D}\, + \,4\,\varsigma \,{\text{sin}}\theta$$
(3)

The variations of \(\beta \mathrm{cos}\theta\) versus \(4 \mathrm{sin}\theta\) for CdS (6 nm) and CdS (12 nm) nanoparticles are depicted in Fig. 1c and d, respectively. The line shows the theoretical development, and the dots indicate the investigational data. One may determine the size of the crystallites by looking at the y-axis intercept of refined line, and its slope can be used to determine the strain. The calculated crystallite size and lattice strain values for CdS nanoparticles synthesized by aqueous method and hydrothermal method are \(D=3\) nm, \(\varsigma =-10.8\) \(\times\) 10–3 and \(D=\) 11 nm, \(\varsigma =\) 0.9 \(\times\) 10–3, respectively.

Transmission electron microscopy images of CdS nanoparticles synthesized by using the aqueous and hydrothermal methods are shown in Fig. 2a and b, respectively. As shown, all nanocrystals are very uniformly spherical or oval. The CdS nanoparticles with cubic structure (synthesized by aqueous method) and CdS nanoparticles with hexagonal structure (synthesized by hydrothermal method) has an average diameter of 6 nm and 12 nm, respectively, based on statistical assessments of a variety of particles at various locations (Fig. 2c and d). These results are fairly consistent with those obtained by the Williamson-Hall approach.

Fig. 2
figure 2

TEM image of a CdS (6 nm) and b CdS (12 nm) nanoparticles, the corresponding size distribution of c CdS (6 nm) and d CdS (12 nm) nanoparticles

Full size image

Nitrogen adsorption/desorption isotherms of the CdS nanoparticles are presented in Fig. 3. According to BDDT classification, the hysteresis loop of the CdS nanoparticles is classified as type IV isotherms with type H3 hysteresis. The obtained values of the specific surface area are 74.2 m2/g and 60.9 m2/g for the CdS (6 nm) and CdS (12 nm), respectively. The larger surface area of CdS (6 nm) allows a greater surface contact with the grains of the host matrix YBCO.

Fig. 3
figure 3

N2 adsorption–desorption isotherms of CdS (6 nm) and CdS (12 nm) nanoparticles

Full size image

The optical absorption spectrum of CdS (6 nm) nanoparticles can be seen in Fig. 4a and showing an absorbance band at around 450 nm. In order to calculate the energy bandgap Eg, the following relationship can be used:

$$\left| {\alpha h\nu } \right|^{1/n} \, = A\left( {h\nu \, - \,E_{g} } \right)$$
(4)

where; \(\alpha\): the Kulbelka Munk function, \(h\nu\) is the incident photon’s energy, \(A\): constant and \({E}_{g}\) is the optical band gap, and n constant relates to the nature of electronic transitions in the semiconductor and is equal to 1/2 for a direct bandgap semiconductor. CdS (6 nm) nanoparticles had an energy bandgap of 2.34 eV as determined by Tauc's plot (Fig. 4b).

Fig. 4
figure 4

a Absorbance spectra, and b Tauc’s plot of CdS (6 nm) nanoparticles

Full size image

3.2 Analysis of superconducting properties

Measurements of the pure and implanted Y-123 with CdS samples resistivity dependence on temperature \(\rho (T)\) can be observed in Fig. 5. It is observed that the different samples exhibits the same behavior, which is metallic in the steady state and superconducting in the superconducting transition to zero resistance. Porosity and grain boundary diffusion are important factors in normal state resistivity. In comparison to the pure sample, all the CdS-supplemented samples have decreased normal-state resistivities. A linear equation, such as below can be used to represent the resistivity curves in metallic behavior:

$$\rho_{n} \left( T \right)\, = \,\rho_{o} \, + \,\alpha T$$
(5)

where \(\alpha\) is thought as a parameter that varies with intrinsic electrical relations, and \({\rho }_{o}\) is the residual resistivity. Table 1 provides the calculated values for the onset transition temperature \({T}_{c}^{onset}\), the zero-resistivity temperature \({T}_{co}\), and the residual resistivity \({\rho }_{o}\) for added and pure samples. The data demonstrates that the sample with added CdS nanoparticles (6 nm) exhibits the lower residual resistivity \({\rho }_{o}\). This suggests that the sample's disorganization, porosity, and impurity scattering in the CuO2-plane are at their lowest levels. Additionally, Table 1 clearly demonstrates that \({T}_{co}\) was partially maintained in Y-123 with the addition of both CdS nanoparticles. Moreover, we discovered that added CdS (12 nm) had an almost constant value of \({T}_{c}^{onset}\) as compare to the pure sample. On the other hand, for the CdS (6 nm), \({T}_{c}^{onset}\) is increased; which indicate that the size reduction of nanoparticles affects the intra-granular properties of YBCO (Inset of Fig. 5). As shown by Fig. 6, CdS (6 nm) nanoparticles connect to YBCO grains and fill the voids between the grains. Metal bridges will be created among superconducting grains, improving the connectivity between them. There may be a composition change in the connection region as a result of the interaction between YBCO grains and CdS nanoparticles. Electrical transport in polycrystalline samples depends on the contribution of conductive planes alternated by insulating layers, inhomogeneity, and defects present and weak bond grain boundaries. Moreover, the variation of the composition at the grain boundaries is considered as fundamental parameter which controls the behavior of the weak links. TEM image (Fig. 6) shows the connection of CdS nanoparticles (6 nm) to YBCO grain. As can be seen from this image, by incorporating CdS nanoparticles, it will be possible to fill the gaps between the matrix grains and, as a result, improve grain boundary connections, therefore the improvement of electric transport. These nanoparticles can, on the other hand, anchor vortices and increase critical current density. Nano-metal particles, such as TiO2, SiO2, Y2O3, BaZrO3, and Nd2O3 [6,7,8], were successfully incorporated into the host YBCUO and improved superconducting volume fraction and inter-grain coupling.

Fig. 5
figure 5

Electrical resistance temperature dependency for samples containing varying concentrations of CdS nanoparticles. Inset: Curves of electrical resistivity vs temperature in the transition area

Full size image
Table 1 \({\mathrm{T}}_{\mathrm{c}}^{\mathrm{onset}}\),\({\mathrm{T}}_{\mathrm{co}}\), \(\Delta \mathrm{T}\) and \({\uprho }_{0}\) values obtained for pure and CdS added Y-123
Full size table
Fig. 6
figure 6

TEM image showing CdS (6 nm) connected to YBCUO grain

Full size image

We evaluated the magneto-resistivity of pure and implanted HTS samples under various magnetic fields \(\rho \left(T,H\right)\). As shown in Fig. 7 with an increasing magnetic field, the wide region's temperature decreases because it is magnetic field sensitive.

Fig. 7
figure 7

Changes of the electrical resistivity with temperature at different applied magnetic fields of a pure, with b CdS (6 nm) and c CdS (12 nm) samples

Full size image

Figure 8 depicts the dependency of the resistive transition width \(\Delta {T}_{co}={T}_{co}\left(H=0\right)-{T}_{co}(H)\), as a function of the applied magnetic field for pure and implanted YBCO with CdS. The power law scaling relation provides a good fit for the transition width data,

$$\Delta T_{co} \, = \,a(\mu_{o} H)^{n}$$
(6)
Fig. 8
figure 8

The shift of the zero-resistivity temperature \(\Delta {T}_{co}\) as a function of applied magnetic field for pure and CdS-added samples

Full size image

Table 2 includes a list of the parameter n and the factor a. In our case, \(n\) is found to be similar in pure and CdS added samples. However, the values of the factor, \(a\), are lower for sample sintered with CdS (6 nm) and higher for sample sintered with CdS (12 nm), compared to the pure one. This result confirms the beneficial effect of CdS (6 nm) addition on the improvement of the electrical conduction in the material.

Table 2 n and a value obtained for pure and CdS added Y-123
Full size table

Vortex-glass and vortex-fluid are two dissipative states inherent to the mixed resistivity state. Many models have been proposed, including flux creep (TAFC) which is thermally activated [22], Ambegaokar, Halperin (AH) [23], thermally activated flux flow (TAFF), etc.…, can explain the resistivity broadening under the magnetic field. The magneto-resistivity \(\rho (T,H)\) curves have been shown to follow the Arrhenius relation as follows [25, 26]. Some research [24] have demonstrated that the TAFF model could be applicable in the tail region around the \({T}_{g}\) (\({T}_{g}\) is the glass transition temperature), according to the Arrhenius relation, the magneto-resistivity \(\rho (T,H)\) curves follow the following rules.

$$\rho \left( {T,H} \right)\, = \,\rho_{0} \,{\text{exp}}\,\left( { - \,\frac{U}{{k_{B} T}}} \right)$$
(7)

where kB denotes the Boltzmann constant and U denotes the flux pinning energy that changes with temperature as well as magnetic field. The linear data at the tail of the slope of the \(\mathrm{ln}\frac{\rho }{{\rho }_{0}}\) versus \(\frac{1}{T}\) plot can be used to directly calculate the U value (Fig. 9). The changes of the flux pinning energy U for pure and samples with CdS nanoparticles addition are shown in Fig. 10. With an increase in magnetic field strength, U decreases for all samples. The flux pinning energy U in the sample sintered with CdS (6 nm) is higher than that reported for the pure sample, however the sample with CdS (12 nm) added shows the lowest flux pinning energy. This result demonstrates again that adding nanoparticles of smaller size enhances the vortex pinning capability.

Fig. 9
figure 9

\(\mathrm{ln}\frac{\rho }{{\rho }_{0}}\) versus \(\frac{1}{T}\) at different magnetic fields of a pure, b CdS (6 nm) and c CdS (12 nm) added samples

Full size image
Fig. 10
figure 10

the variations of the flux pinning energy \(U\) with applied magnetic field of pure and with CdS samples

Full size image

Temperature dependences of the critical current density \({J}_{c}(T)\) were examined under self and applied magnetic fields for the samples sintered with and without the addition of CdS nanoparticles, and the results are shown in Fig. 11. The critical current density for each sample increases monotonically with decreasing temperature from near to \({T}_{co}\) down to T = 25 K. The pure sample has the maximum current density, as seen in the \({J}_{c}(T)\) variation at self-magnetic field (Fig. 11a). The critical current density values for both sintered CdS added samples are basically the same and are lower than those for the pure sample. This finding demonstrates that adding CdS nanoparticles causes the material's quality to decline; in fact, this may be because adding CdS causes a denser grain boundaries higher crystalline defects. We examined the critical current density dependency on temperature under applied magnetic field \({\mu }_{0}H=100 \mathrm{mT}\), \({J}_{c}(T,H)\), for pure and CdS added Y-123 samples to investigate the related effect of CdS addition in critical current density and vortex pinning (Fig. 11b). As can be seen, when compared to the pure sample, the sample with CdS (12 nm) added has the lowest current density. The sample treated with CdS (6 nm) has the maximum current density throughout the whole temperature range, and at T = 25 K, it has a value that is approximately twice that of the pure sample. These results show that the flux-pinning capabilities were increased by the addition of CdS (6 nm) nanoparticles.

Fig. 11
figure 11

the dependence of temperature on transport critical current density at self and applied magnetic fields for sintered materials containing CdS (6 nm) and CdS (12 nm) nanoparticles

Full size image

The critical current density dependences on temperature under applied magnetic field \({\mu }_{0}H=100\mathrm{ mT}\), were studied using the theories of thermally induced flux motion and collective flux-pinning [27] to provide additional evidence and informations about the pinning mechanism for pure and CdS-added samples. These models give the following expression for \({J}_{c}(T)\) temperature dependence:

$$J_{c} \left( T \right)\, \approx \,J_{c} \left( 0 \right)\left( {1\, - \,t^{2} } \right)^{\alpha } \left( {1\, + \,t^{2} } \right)^{\beta }$$
(8)

where \({J}_{c}\left(0\right)\) is the critical current density at 0 K,\(t=\frac{T}{{T}_{co}}\) is the decreased temperature. The exponents \(\alpha\) and \(\beta\) are related to the pinning process,

For the \(\delta \varepsilon\) pinning mechanism for the stress/strain field [28],

$$J_{c} \left( T \right)\, = \,J_{c} \left( 0 \right)\left( {1\, - \,t^{2} } \right)^{\frac{7}{6}} \left( {1\, + \,t^{2} } \right)^{{ - \frac{11}{6}}}$$
(9)

for the \(\delta {T}_{c}\) pinning mechanism, which results from spatial changes in the transition temperature \({T}_{c}\) that are spread at random [29],

$$J_{c} \left( T \right)\, = \,J_{c} \left( 0 \right)\left( {1\, - \,t^{2} } \right)^{\frac{7}{6}} \left( {1\, + \,t^{2} } \right)^{\frac{5}{6}}$$
(10)

For the \(\delta l\) pinning mechanism linked to the spatial fluctuation of the charge-carrier mean free path caused by crystal lattice defects [27],

$$J_{c} \left( T \right)\, = \,J_{c} \left( 0 \right)\left( {1\, - \,t^{2} } \right)^{\frac{5}{2}} \left( {1\, + \,t^{2} } \right)^{{ - \frac{1}{2}}}$$
(11)

Figure 12 shows the results of fitting of the experimental data \({J}_{c}\left(T\right)\) for pure and CdS added samples under the applied manetic field using the three models discussed above \({\mu }_{0}H=100\mathrm{ mT}\). Figure 12 displays the theoretical curves from Eqs. (2), (3), and (4) as solid lines. It is observed that the experimental \({J}_{c}\left(T\right)\) values for the pure and CdS (12 nm) added samples are well fitted by the pinning over the major temperature range. However, the experimental data for the YBCO implanted with CdS (6 nm) throughout the entire curve region \({J}_{c}\left(T\right)\), cannot be explained by a single model. In fact, the pinning mechanism \(\delta l\) is mainly responsible at low temperatures, decreases when the temperature increases, then transforms into \(\delta \varepsilon\) at temperatures close to \({T}_{co}\). This result confirms that the implantation of CdS nanoparticles with size 6 nm in the superconducting matrix causes the fluctuations in the mean free path which are responsible for the \(\delta l\) pinning at low temperatures.

Fig. 12
figure 12

Under applied magnetic field, the fitting results of the experimental data \({J}_{c}\left(T\right)\) for a pure, b CdS (6 nm), and c CdS (12 nm) added samples \({\mu }_{0}H=100\mathrm{ mT}\)

Full size image

4 Conclusion

The impact of the implantation of CdS nanoparticles of sizes 6 nm and 12 nm, synthesized by the aqueous route and hydrothermal technique on the transport properties of the superconducting compound YBa2Cu3Oy, has been thoroughly studied. Samples were created utilizing the solid state reaction method with additional amounts of CdS, x is 0 and x is 0.1 wt%, to the mass of the sample. According to the ρ (T) measurements, the CdS-added samples have decreased residual and normal-state resistivities in comparison to pure samples. Moreover, it was demonstrated that adding CdS (6 nm) causes a rise in \({T}_{c}^{onset}\) and almost maintained \({T}_{co}\) values. The \({J}_{c}(T,H)\) measurement shows that the sample implanted with CdS (6 nm) exhibits a narrower resistive transition width \({T}_{co}\) and higher values of pinning energy under applied magnetic fields, demonstrating the valuable role of CdS nanoparticles of size 6 nm on the upgradation of the electrical conduction of YBCO, as well as demonstrating that the size reduction of added nanoparticles improves the vortex pinning capacity. Furthermore, with a magnetic field applied, the temperature dependence of the critical current density \({J}_{c}(T)\) was examined. It was demonstrated that the sample with CdS (6 nm) added shows higher \({J}_{c}\) value than the pure and CdS (12 nm) added samples.