Ag–(In–Bi) solid-state bonding

Abstract

Solid-state diffusion bonding is a metallurgical technique to bond interfaces. We identify Ag–(In–Bi) as a material system that can be bonded at 65 °C. This work aims to demonstrate low-temperature bonding and to determine if Bi precipitates form through a solid-state diffusion mechanism. Bonds were formed at 65 °C utilizing a 78.5-at% In–Bi eutectic foil and a 95-at% In–Bi foil, with bonding times 1, 2, 4, and 8 days. These foils were sandwiched between two pieces of Ag, forming an Ag/In–Bi foil/Ag bonding stack. Thanks to bridging of AgIn₂, a temperature stability of ~166 °C is possible. Using a bonding material with higher In content (in our case 95 at% In) than the eutectic did not reduce the growth rate of AgIn₂. The BiIn₂ left over from the reaction was surrounded by the growth of AgIn₂. The solid-state bonding results presented in this paper indicate that dissolution is a necessary condition for the unique Bi precipitates previously seen in the Ag–(In–Bi) solid–liquid system.

1 Introduction

In solid-state bonding also commonly called diffusion bonding, atomic interdiffusion between metals joins the surfaces. Solid-state bonding will resist temperatures higher than the bonding temperature and is attractive for applications where elevated temperature stability is required. Common solid-state bonding techniques are Au–Au [1, 2] and Cu–Cu thermocompression [3, 4] and Ag sintering [5]. If dissimilar metals are used intermetallic compounds (IMCs) may form. Intermetallic bonds are mechanically strong, electrically conductive, hermetic, and compatible with die-level and wafer-level manufacturing. Additionally, IMCs often have elevated melting points, higher than that of the pure elements forming the IMC.

Bonding at low (T_m < 200 °C) temperatures is required for bonding temperature-sensitive materials, such as poled piezoelectric materials, ferromagnets, or polymers [6]. We initially explored Ag–(In–Bi) solid–liquid interdiffusion (SLID) system as a metallurgical bonding technique to join temperature-sensitive electronics at 150 °C [7]. To our knowledge, no low-temperature solid-state bonding has been conducted on the Ag–In–Bi system. Additionally, no stable ternary Ag–In–Bi phases have been discovered [8, 9]. The lack of a ternary phase, and the immiscibility of Ag and Bi (illustrated by the Ag–Bi phase diagram [9]), simplify the thermodynamics of the system. From our previous work with the SLID Ag–(In–Bi) system, only Ag reacts with In, reducing the In content in the In–Bi layer (originally eutectic) during bonding. Additionally, we saw that when bonding at 150 °C the first Ag–In IMCs (see Fig. S1) would be AgIn₂, then Ag₉In₄, and ζ phase was never detected. Since diffusion is significantly slower in solid-state bonding, we do not expect to see the ζ phase during solid-state bonding either. Therefore, the quasi-static thermodynamic stable layering expected is Ag/Ag₉In₄/Bi/Ag₉In₄/Ag.

The present work aims to demonstrate low-temperature solid-state bonding of Ag–(In–Bi) at 65 °C. This temperature provides a ~7- °C buffer to the T_m of the eutectic In–Bi, but it retains an elevated temperature to sustain higher diffusion. In addition, we also want to determine if Bi precipitates form through a solid-state diffusion mechanism, and we provide an analysis of the resulting bondline characteristics and phase evolution.

2 Methods

2.1 Bonding

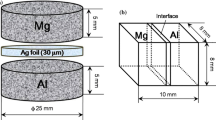
Ag foil (99.9-at% Ag) with a thickness of 0.28 mm was diced into squares with dimensions of 0.4 cm × 0.4 cm (Top) and 0.7 cm × 0.7 cm (Bottom). The larger cuts were pressed between two polished aluminum chucks utilizing a hydraulic press with 2 × 10⁷ Pa, while the smaller with 1 × 10⁷ Pa in order to flatten the surface and edges, improving the mating. The Ag cuts were then polished with 1-μm diamond solution, resulting in a roughness average (R_a) of (250 ± 40) nm. This roughness was measured using an interferometer Wyko NT9100. Prior to bonding, the Ag cuts were cleaned utilizing water and dried with N₂. Ag has a good oxidation resistance (the room temperature oxide layer thickness is less than 20 Å [10]), but bonding should be done after polishing as Ag does react with sulfur-containing gases in the air. An In–Bi foil was placed between the cuts. Two different foil compositions were used: eutectic In–Bi (78.5-at% In, T_m = 72.7 °C), and 95-at% In (solidus ~110 °C, liquidus ~140 °C) both at 99.99% purity. Both were prepared by Testbourne Ltd. The eutectic composition was chosen as the same composition used in our previous SLID experiments, facilitating comparisons. The 95-at% In foil was chosen to examine the effects of reduced Bi content on bonding, while retaining a depressed solidus as compared to using pure indium.

As seen in Fig. 1 the eutectic contains “tad-pole” and lamellar structures of the (In) phase. Since the sample was not quenched the epsilon phase which would have formed at 65 °C, transformed to the (In) phase during the sample cooling. The (In) phase was found by EDX to have between 93-at% In and 94 at%, in close agreement with the phase diagram. This (In) phase is mechanically soft. Pure indium has a Brinell hardness of 8.83 MPa. When alloyed with Bi, the Brinell hardness can be calculated using the equations presented in [11], where 93-at% In composition gives Brinell hardness of 11.2 MPa. This is in contrast to Ag which has twice as high Brinell hardness: 24.5 MPa [11]. The calculated Brinell hardness for BiIn₂ and Bi₃In₅ are nearly the same as the 93 at% (In) phase: 13.2 MPa and 13.3 MPa, respectively. The contrast in hardness between the Ag and the other phases is known to cause difficulties during cross-sectioning by grinding and polishing. This leads to pullout of the softer material, generating voids in the cross-section [12].

Fig. 1

Backscattered electron micrograph of cross-sectioned In-Bi 78.5-at% In eutectic foil after 2 days at 65 °C

The In–Bi foil thicknesses ranged from 110 to 10 µm. A tungsten carbide spacer 290 μm thick was placed on the top of the stack to distribute the pressure applied by the lever arm fixture. The bonding pressure was 12.6 MPa. Bonding was done under a flow of N₂ ~3 l/min in a Thermal Chamber Lenton WHT6/30. The temperature was monitored and set by the built-in temperature controller. The oven was kept at 65 °C. The bonding time was varied from 1, 2, 4, and 8 days. The micrographs in section III.A.I are only for the 1-day bonding time. While images in section III.A.II are for the bonding times of 2, 4, and 8 days.

2.2 Characterization

Samples were cross-sectioned and the bondline surface was prepared by grinding and polishing. Cross-sections are imaged by scanning electron microscopy (SEM) and energy-dispersive X-ray spectroscopy (EDX). ImageJ software was used to measure the cross-sectional area of features in the micrographs utilizing tracing and contrast tools [13]. This area was divided over the length of the analyzed section to attain the average thickness of the IMC.

3 Results

3.1 Eutectic preform bonding

3.1.1 Bonding at 65 °C for 24 h

The bondline shows variation in the progress of the bonding process, which is dependent on the position where the micrograph is taken. Figure 2 shows the approximate locations of the micrographs, as well as deflection of the dies. The deflection of the dies is suspected to be from the sample polishing which erodes the corners more than the middle. Deflection from the applied pressure is not expected to be significant due to the tungsten carbide spacers. Tilt angle of the top die was not significant, meaning both dies were effectively parallel to each other.

Fig. 2

Shows the approximate micrograph locations for Fig. 3 Ag–(In–Bi) solid-state bonds, bonded at 65 °C for 24 h, at different locations along the cross-section. 3 a) (III), Fig. b) (II), and Fig. 3 d) (I)

Fig. 3a through d show the micrographs resultant from bonding at 65 °C for 24 hrs. Near the edge of the bond, unreacted In is present, whereas the middle of the bondline has significant content of Bi3In5, showing that also the BiIn2 phase is depleted of In while more AgIn₂ is formed. Fig. 3 Ag–(In–Bi) solid-state bonds, bonded at 65 °C for 24 hours, at different locations along the cross-section.3 a shows the cross-section nearest the edge of a successful solid-state bond, using eutectic preform, bonded for 24 hrs at 65 °C. Indium from the preform has reacted with the Ag forming AgIn₂. The eutectic preform is depleted of all the (In) phase, leaving behind BiIn₂. AgIn₂ penetrates into the foil, showing significant Ag–In interdiffusion. The contact points of the (In) phase with the Ag most likely act as nucleation points along the bondline for the initial growth of the AgIn2 phase, resulting in a varying AgIn2 thickness along the bondline. The expected Tm of this bondline would be 89.5 °C (the Tm of BiIn2), thus exceeding the Tm of eutectic In–Bi by 17 °C Indium Ag–(In–Bi) solid-state bonds, bonded at 65 °C for 24 h, at different locations along the cross-section. Fig. 3a shows the cross-section nearest the edge of a successful solid-state bond, using eutectic preform, bonded for 24 h at 65 °C. Indium from the preform has reacted with the Ag forming AgIn₂. The eutectic preform is depleted of all the (In) phases, leaving behind BiIn₂. AgIn₂ penetrates into the foil, showing significant Ag–In interdiffusion. The contact points of the (In) phase with the Ag most likely act as nucleation points along the bondline for the initial growth of the AgIn₂ phase, resulting in a varying AgIn₂ thickness along the bondline. The expected T_m of this bondline would be 89.5 °C (the T_m of BiIn₂), thus exceeding the T_m of eutectic In–Bi by 17 °C.

A fracture filled with polishing residue is shown at the top of the image, this is also seen in Fig. 3b and Fig. 3d. It is unknown if this is from the bonding or from the sample preparation. AgIn₂ particles are seen inside the BiIn₂. A layer of Ag₉In₄ seems to exist based on the contrast in the micrograph, but is too thin to be measurable. Figure 3b (Location II) shows a cross-section closer to the middle of the bonding die than Fig. 3a. Bi₃In₅ particles are observed through Backscattered Electron contrast, verified by EDX. These particles of Bi₃In₅ are often but not always at the middle of the bondline. The growth shape of the Bi₃In₅ particles is in the form of a large agglomerate or aggregate of spheres. Near the middle of the bond in Fig. 3d (Location I) Bi₃In₅ bridges the bondline at many sections. As seen in Fig. 3d, Bi₃In₅ is seen at some places directly adjacent to the AgIn₂ phase, in contrast to Fig. 3b.

Fig. 3

Ag–(In–Bi) solid-state bonds, bonded at 65 °C for 24 h, at different locations along the cross- section. 3 a) shows the cross-section nearest the edge of a successful solid-state bond, using eutectic preform, bonded for 24 h at 65 °C. Indium from the preform has reacted with the Ag forming AgIn₂. The eutectic preform is depleted of all the (In) phases, leaving behind BiIn₂. AgIn₂ penetrates into the foil, showing significant Ag–In interdiffusion. The contact points of the (In) phase with the Ag most likely act as nucleation points along the bondline for the initial growth of the AgIn₂ phase, resulting in a varying AgIn₂ thickness along the bondline. The expected T_m of this bondline would be 89.5 °C (the T_m of BiIn₂), thus exceeding the T_m of eutectic In–Bi by 17 °C

3.1.2 Bonding at 65 °C for 2, 4, and 8 days

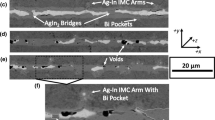
Near the middle of the bond after 2 days of bonding, almost complete conversion to Bi₃In₅ has occurred as seen in Fig. 4 Ag–(In–Bi) solid-state bonds bonded at 65 °C for different bonding times. 4a. A large fracture through the AgIn₂ is at the bottom. In contrast to the figures presented in Fig. 3 this crack was not filled with polishing residue and therefore appears more significant. Additionally, the fracture occurs inside the AgIn₂ phase, meaning the Ag–In interdiffusion occurred before fracturing; hence, this fracture happened after bonding at 65 °C. The presence of the fracture does therefore not hinder the analysis of the bonding process. A small amount of BiIn₂ remains. After 4 days of bonding, Fig. 4b shows all the BiIn₂ has been consumed and complete conversion to Bi₃In₅ has occurred. Still the Ag₉In₄ has not grown considerably. Figure 4c is a cross-section near the middle of the bond after 8 days of bonding. The AgIn₂ IMC is seen to bridge the gap through the Bi₃In₅. Displaced AgIn₂ particles can be seen within the Bi₃In₅ layer, as shown in Fig. 4d. As seen in Fig. 4c and d, the Ag₉In₄ still has not grown to a measurable thickness, even after 8 days of bonding.

Fig. 4

Ag–(In–Bi) solid-state bonds bonded at 65 °C for different bonding times. a) Cross-section near middle of bond where almost complete conversion to Bi₃In₅ has occurred (Bonding 2 days). b) Cross-section showing fracture transitioning from AgIn₂ interface voids, to AgIn₂/Bi₃In₅ layer interface (Bonding 4 days). c) Cross-section showing AgIn₂ bridging. Fracturing is no longer clearly seen, indicating a reduction on the interface voiding. Pullout of either Bi₃In₅ or BiIn is an artifact of the cross-section preparation (Bonding 8 days). d) Cross-section showing rapid edge diffusion and AgIn₂ particles near the bond interface and in the middle of the foil (Bonding 8 days)

3.2 95-at% In preform bonding 65 °C for 8 days

A foil with 95-at% In was bonded for 8 days, at the conditions as the previous samples. Figure 5a shows this sample. Two notable differences are the presence of (In) phase and the BiIn₂ phase and the large width of the bondline. Ag₉In₄ is again unmeasurable but can be seen at the interface between AgIn₂ and Ag by contrast. Figure 5b shows that BiIn₂ often forms at the surface between AgIn₂ and (In). The AgIn₂ seems to grow around these pockets of BiIn₂ and at some points can be seen to almost completely envelop them. The average thickness of the AgIn₂ for the top and bottom for the cross-section shown in Fig. 5b was 7.9 µm. At the middle of the same bond (different images) the average was 10 µm. This was larger than the thickness measured for the eutectic foil at the same conditions of 7.1 µm. When comparing Fig. 5a and b, it can be seen that there is an increased distribution density of BiIn₂ particles in Fig. 5a, which is located at the edge of the bond.

Fig. 5

a) Cross-section of solid-state bond using 95-at% In, near the edge of the top die. Plastic deformation and formation of BiIn₂ is seen. Figure 5 b) Cross-section near the middle of the bond showing the growth of BiIn₂ and how the AgIn₂ grows around the particles

3.3 Voiding and fractures

Figures 6 and 4b taken after 4 days of bonding show fracturing within the AgIn₂ phase. In Fig. 6 the initial contact between the foil and Ag substrate is frequently seen with a plane of voids. Longer bonding times for the 78.5-at% In foil seem to reduce the degree to which this voiding occurs, as seen through Fig. 4a–c.

Fig. 6

Edge of bond showing where the 78.5-at% In foil contacts the substrate and the interface voiding (After 4 days at 65 °C)

4 Discussion

4.1 Evolution of phases and layer structure with bonding time

Figure 7a and b show growth sequences for Ag–(In–Bi) solid-state bonding at 65 °C, using eutectic In–Bi and 95-at% In, respectively. The growth model assumes homogeneous diffusion of elements in the vertical direction, no horizontal diffusion of elements, and no squeeze out of the bonding material. The growth model assumes the formation of AgIn₂ as the final phase, treating the layering Ag/AgIn₂/Bi₃In₅/AgIn₂/Ag as the final structuring. The thickness of Ag₉In₄ is below 1 µm in our bonding results, so this is ignored for simplification.

Fig. 7

a) Growth sequence of Ag–(In78.5 at%) bonding at 65 °C for an approximate time of 8 days. Stage I, II, III, and IV all can be obtained within 1 day of bonding. Stage IV and V can both be obtained after 2 days of bonding. Figure 7 b) Growth sequence of Ag–(In 95 at%) bonding at 65 °C

When the eutectic In–Bi is heated to the bonding temperature, In and Ag interdiffuse, forming AgIn₂ below and above the original bondline contact. Indium is most readily depleted from the (In) phase, eventually disappearing and leaving behind only BiIn₂. Further diffusion transitions the BiIn₂ into Bi₃In₅. This phase is illustrated in the middle of the bondline; however, Fig. 3b and d show different locations of this phase. Eventually the bondline is converted to Ag/AgIn₂/Bi₃In₅ layering. BiIn phase was never observed, indicating that the reaction between the Bi₃In₅ and AgIn₂ is significantly slow.

The proposed growth sequence has a simplified planar growth, while the observed results sees a complex topography of layering, whereby bridging of AgIn₂ across the bond gap can occur if the bondline is thin enough, as seen in 4c). The bridging of AgIn₂ means that this bondline will be solid up to the T_m of AgIn₂ ~166 °C, since the AgIn₂ should provide a solid connection between the two bonding interfaces until it melts. This temperature stability is approximate, since mechanical failure due to creep can occur before the melting point of AgIn₂. For bondlines thinner than 12 µm measured between original interfaces in Fig. 4c we predict more frequent bridging of AgIn₂, improving the mechanical strength at elevated temperatures. If bridging does not occur, the melting point of the bondline would be the liquidus of Bi₃In₅, ~95 °C. Although, partial melting will begin at the solidus ~88 °C, resulting in a conversion to the BiIn phase and liquid phase before melting completely. Figure 7b shows the growth sequence for bonding with 95 at% In. BiIn₂ grows adjacent to the AgIn₂, but as seen in Fig. 5b this growth is not uniformly layered, but coalesces and grows as particles at discrete locations along the AgIn₂ layer.

Due to the mechanically soft nature of the In–Bi compounds the foil is plastically deformed by the applied bonding pressure. Evidence for this is that the thickness of the foil is always larger outside the chip as seen in Fig. 4d. We believe that as a consequence of the squeeze out, some of the AgIn₂ scallop particles are broken off from the substrates (likely at the already weak fracture line caused by the interface voiding) and displaced through plastic flow. This all implies that the plastic flow persists during the formation of AgIn₂. Since both the rate of formation of AgIn₂ and the length of time the plastic flow persists are unknown, we cannot conclude decisively that the plastic flow is causing the AgIn₂ to migrate to the middle of the bondline. Some of the particles are explained by the limitations of cross-sectioning where the complete 3-D growth of the AgIn₂ cannot be seen, giving the illusion of particles.

4.2 Bondline thicknesses analysis

The volume ratios between AgIn₂ and the two IMCs (BiIn₂ and Bi₃In₅) for a complete reaction (assuming an infinite supply of Ag) can be extracted from reaction (1) and (2) by dividing the summated product terms by each other, in the following manner:

$${8}.{\text{5Ag}}_{{\left( {\text{s}} \right)}} \, + \,{2}0({\text{95at}}\% {\text{In}},{\text{5at}}\% {\text{Bi}})_{{({\text{s}})}} \, \to \,{8}.{\text{5AgIn}}_{{{2}\left( {\text{s}} \right)}} \, + \,{\text{BiIn}}_{{{2}\left( {\text{s}} \right)}}$$

(1)

$${2}.{\text{98Ag}}_{{({\text{s}})}} \, + \,{13}.{95}({78}.{\text{5at}}\% {\text{In}},{21}.{\text{5at}}\% {\text{Bi}})_{{\left( {\text{s}} \right)}} \, \to \,{2}.{\text{98AgIn}}_{{{2}\left( {\text{s}} \right)}} \, + \,{\text{Bi}}_{{3}} {\text{In}}_{{{5}({\text{s}})}}$$

(2)

$$\frac{{v}_{Bi{In}_{2}}{V}_{Bi{In}_{2}}^{m}\left(Product\right)}{{v}_{Ag{In}_{2}}{V}_{Ag{In}_{2}}^{m}\left(Product\right)}=1.5$$

(3)

$$\frac{{v}_{{Bi}_{3}{In}_{5}}{V}_{{Bi}_{3} {In}_{5}}^{m}\left(Product\right)}{{v}_{Ag{In}_{2}}{V}_{Ag{In}_{2}}^{m}\left(Product\right)}=1.1$$

(4)

For BiIn₂:AgIn₂ the ratio is 1.5, and for Bi₃In₅:AgIn₂ the ratio is 1.1. This is equivalent to the bonding stages depicted in Fig. 7a, where stage III is a fully converted bond to BiIn₂ and AgIn₂ and stage V is a fully converted bond to Bi₃In₅ and AgIn₂. As seen in Fig. 8 the ratios of Bi₃In₅:AgIn₂ achieves the calculated value of 1.1 after 4 days of bonding. The sample’s ratio for 1 day bonding in Fig. 8 is 1.6, near the theoretical value for BiIn₂:AgIn₂ (1.5).

Fig. 8

Taken from images near the center of the bonds (Not the images shown in results section, these sections can be found through Fig. S3 to Fig. S6). The thickness ratios of Bi₃In₅:AgIn₂ are shown above the bars. All measured values are within a ± 0.15 µm measurement uncertainty

Average thickness of AgIn₂ plotted against average thickness of the In–Bi compounds (Includes voids). Values are for only one bond layer either the top or the bottom.

As seen in Fig. 8, the thickness of the AgIn₂ layer is correlated with the thickness of In–Bi compounds. This means that the growth of AgIn₂ at these scale lengths is limited by the amount of available In. Since In depletes so readily from the foil, a thicker foil provides more accessible In for further growth of AgIn₂. It is thus of interest to determine the (In) depletion zone defined as the approximate distance between AgIn₂ and the eutectic. Figure 9 was taken where no top chip exists, where there exists excess In–Bi eutectic, the zone thickness was measured to approximately ~18 µm.

Fig. 9

Illustrates the measurement of the (In) depletion zone, after bonding with In–Bi 78.5-at% In for 8 days at 65 °C

This represents the (In) depletion zone of one interface between Ag and In–Bi eutectic. Our bonded samples have two such interfaces (top and bottom die), therefore the depletion zone is ~36 µm, which is comparable to the thicknesses of the In–Bi compounds measured in Fig. 8. This supports the observation found in Fig. 8 that for foils under ~36 µm, the growth of AgIn₂ will be hindered by the supply of In.

Therefore, to properly measure the growth rate of AgIn₂, sections with excess In available must be examined to remove the influence of foil thickness on the diffusion rate. At the edge of the bond, where no top die exists, there is excess eutectic such that complete depletion of the (In) phase did not occur (such as Fig. 9).

4.3 Ag–In interdiffusion modeling

Diffusion-controlled grain boundary growth fits a linear regression when the cubed thickness is plotted vs time [14]. On the contrary, diffusion-controlled lattice growth fits a linear regression when the squared thickness is plotted vs time [15]. Grain boundary diffusion growth can be modeled by the diffusion law (Eq. 5), where $(k)$ is the growth constant and $(n)$ is the power factor, where for a purely grain diffusion-controlled growth ($n$=1/3).

$$\Delta x={(\frac{1}{n}kt)}^{n}$$

(5)

$\Delta x$ is the growth during bonding and $t$ is the bonding time, $\mathrm{k}$ is the growth constant and is a function of temperature described by the Arrhenius relation [15].

The linear regression is forced through the origin, neglecting IMC growth during heating and cooling. The uncertainties given are extreme values, representing the largest and smallest AgIn₂ thickness, properly transferred to error bars for squared thickness (2*relative error for thickness) and cubed thickness (3*relative error for thickness). Figure 10b shows a poorer fit to the data points, when a squared thickness is utilized. Although the regression line fits within the error bars, it is clear that the data points in Fig. 10b call for a curved fit rather than a linear. The plot of cubed thickness vs. bonding time (Fig. 10a), shows a better fit to a linear regression, indicating that the growth is more grain boundary dependent in contrast to lattice.

Fig. 10

Measurements of AgIn₂ thickness taken at sections which had excess available (In). These sections can be seen in the supplementary material through Fig. S7 to Fig.S10. a) Plotting the bonding time against the ${x}^{3}$ AgIn₂ thickness. b) Plotting the bonding time against the x² AgIn₂ thickness

4.4 Comparision with Ag–(In–Bi) SLID bonding

In our previous work on Ag–(In–Bi) SLID [7], first a layer of AgIn₂ is formed and then a layer of Ag₉In₄. The left-over Bi was mostly contained as In–Bi IMCs, in the middle of the bondline, as seen in Fig. 11. This is also the most diffused sample in our previous work, containing bridged sections of both Ag₉In₄ and AgIn₂. At some places, the degree of conversion of the AgIn₂ to Ag₉In₄ resulted in sections where contact is made between the Ag₉In₄ and the In–Bi IMCs. In the solid-state diffusion bonding, Ag₉In₄ never grew to a measurable thickness and the Ag–In IMC bridging is limited.

Fig. 11

Cross-section of Ag–(In–Bi) SLID bond bonded at 150 °C with no holding time. Similar bonding conditions as [7]

The Bi precipitates as seen in Fig. 11 (appearing at positions far behind the original bonding interfaces) clearly contribute or are associated with a degree of bondline variability. In general bondline variability is not desirable and so a better understanding of the mechanism by which the precipitates form can improve bondline control. At the time the exact mechanism by which these precipitates formed was uncertain, but by conducting solid-state bonding, the mechanism can be better understood.

Two theories were proposed, one involving solid-state diffusion of In and Bi into the Ag; another involving uneven dissolution of Ag and filling the etched pockets with liquid Ag–In–Bi. In the present work, we bond below the T_m of the interlayer, thus determining if solid-state diffusion is the cause of these Bi precipitates. The E3 eutectic point in the ternary system of Ag–In–Bi has the minimum T_m possible for the system of 71.46 °C [11]. In the present work, we bond below this E3 eutectic point, preventing dissolution of Ag. The liquid atomic composition at this point is 0.1-at% Ag, 21.98-at% Bi, and 77.92-at% In, and the solid state is a three-phase equilibrium of AgIn₂, BiIn₂, and ɛ (84.74-at% In). According to the binary phase diagram, Bi does not form any phase with silver under ~170 °C [16, 17].

In all experiments conducted at 65 °C, no Bi precipitates and protruding Ag–In IMCs are seen at the Ag/IMC interface. This is in contrast to the Ag–(In–Bi) SLID bonding [7], where Bi precipitates are seen throughout the bondline (Fig. 11). It is therefore evident that these features arise from the presence of a liquid phase, effectively etching Ag at random positions.

This is in contrast to the systematic study by H.F. Zou et al. on the Cu–(Sn–Bi) system [18] which showed that Bi precipitates did occur within the Cu₁₁In₉ phase by solid-state diffusion after 17 days at 120 °C (below liquification for Sn–Bi). Note, both Cu IMCs have non-stoichiometric phases, while AgIn₂ is completely stoichiometric. This indicates the lattice of the Cu–Sn IMCs are imperfect, these IMCs contain significant anti-site defects and vacancies which correspond with their diffusional findings [19]. It is postulated here that the tetragonal lattice of AgIn₂ does not accept Bi atoms as readily as Cu–Sn IMCs and prevents lattice solid-state diffusion of Bi.

4.5 95-at% In preform bonding 65 °C for 8 days

Since no bridging is observed, the expected T_m of this bondline would be ~140 °C (liquidus of the 95-at% In phase). Partial melting will begin at ~110 °C (solidus). Given a smaller foil thickness we expect significant AgIn₂ bridging, with the ejected Bi being contained in BiIn₂ pockets surrounded by the growth of the AgIn₂.

If a temperature stability of ~166 °C is acceptable for the final bondline, then it is recommended that a foil containing more In than the eutectic be used for solid-state bonding, since the left-over BiIn₂ is mostly contained by the growth of AgIn₂. The small Bismuth content still acts as a significant depressant, lowering the partial melting temperature, which is suspected to facilitate more rapid diffusion. However, the growth of AgIn₂ appeared to increase with an alloy containing more (In). The 95-at% In foil showed 10 µm of AgIn₂ at the middle of the bond shown in Fig. 5b after 8 days, compared to 8.6 µm with the eutectic foil measured from Fig. 9 where excess eutectic is present so growth was not limited by the depletion zone. This is effectively comparing stage II in Fig. 7a to stage II in Fig. 7b. Theoretically this increase in growth rate would result in sooner bridging of the bond, however it is uncertain how the phases for a thinner bondline of 95-at% In would evolve. More work is needed to determine if there is a diminishing return when Bismuth content is decreased with regards to the growth rate of AgIn₂.

4.6 Voiding and fractures

The location of the interface voids seen Fig. 6 suggests these to be Kirkendall or impurity type voiding. Kirkendall voids are voids resulting from unequal atomic fluxes, being compensated by vacancy creation, then migration, and eventual saturation into voids. A degree of grain boundary impingement at the void accumulation spots, through trace impurities or inherent, has been argued to be necessary for their formation [20].

These interface voids are weak points in the bond, and in Fig. 4b fracturing transverses these weak points. However as indicated in Fig. 4b, a fracture transition occurs when the voiding is too minimal to act as the weakest path, instead propagating at the interface between the AgIn₂ and Bi₃In₅. The voiding seen in Fig. 4c is not located at the interface and is believed to be from the pullout of the Bi₃In₅ due to polishing. Other sources of voiding include contaminations, oxidation, lack of intimate contact, and finally moisture or entrapped gases, such as air.

5 Conclusion

We demonstrated solid-state bonding of Ag–(In–Bi) at as low temperature as 65 °C, both using an In–Bi 78.5-at% In eutectic foil and a 95-at% In foil, with bonding times 1, 2, 4, and 8 days. The thickness of the foil was seen to have a major impact on the obtained layer thickness of AgIn₂, with the amount of the (In) phase being the limiting factor.

AgIn₂ bridges the bondline in our 8-day bonds. This gives a theoretical temperature stability ~166 °C (if bridging was over the complete bondline), despite the bond not fully depleting the In from the Bi₃In₅. A thinner foil would increase bridging at shorter bonding times; however, this will also limit the total amount of AgIn₂ formed.

Bi is contained in the middle of the bond during solid-state bonding in the form of either (In), BiIn₂, or Bi₃In₅. This gives evidence that dissolution is a necessary condition for the Bi precipitates which occur in the Ag–(In–Bi) SLID system, but not in the solid-state system.