1 Introduction

Transparent conducting oxides (TCOs) have received a lot of attention in recent years due to their high transmittance in the visible range and outstanding electrical conductivity [1]. TCOs have been used in a variety of applications for these reasons, including photovoltaics, energy-efficient windows [2], electroluminescent devices [3], gas sensors [4], electrocatalysis [5], photocatalysis, laser diodes, and light-emitting diodes (LEDs) [6]. Many materials, such as ZnO, In2O3-based films, and SnO2-based films, are transparent conducting oxides. [7]. Tin oxide and related compounds, in particular, have attracted a lot of attention because they have natural n-type conductivity with a large band gap of nearly 3.5–4.6 eV, a stable structure, and the ability to alter electrical properties based on doping concentration [8, 9].

They also have strong electrical conductivity (10−4S cm), optical transmittance (> 85), and electrochemical stability [10, 11]. However, because of its limited stability and surface area, SnO2 has some disadvantages. Due to its high exciton binding energy (130 meV) [12] compared to ZnO (60 meV) [6], SnO2 nanocrystal is a promising material for short-wavelength optoelectronic systems and is a feasible candidate for UV luminescence devices. The observed efficient excitonic photoluminescence emissions at room temperature are due to this high exciton energy. Due to its exceptional optical, electrical, electrochemical, and photocatalytic capabilities, SnO2 (Tin oxide), an n-type wide band gap transparent oxide semiconducting material, has piqued interest in a variety of applications. Because of its excellent gas detecting performance and low cost, it is used in gas sensing. Photocatalytic applications, solar cells, lithium-ion batteries, optical data storage, gas–discharge displays, flat panel displays, transparent conducting electrodes, and other applications are all good candidates for SnO2 [13,14,15].

However, because of its limited stability and surface area, SnO2 has some disadvantages. However, because they are highly reactive and have a large surface area, synthesizing stable nanostructured materials with the desired properties is difficult. This results in the formation of secondary phases. As a result, choosing the right synthesis process is crucial for achieving the specified restrictions, such as homogeneity, shape, crystallite size, and so on. To obtain stable SnO2nanomaterials, Molybdenum trioxide (MoO3) was chosen. Photochromic [16], thermochromic [17], gasochromic [18], and electrochromic [19] materials and/or devices, various solar cells as hole transport layer or back contact with high work function pseudocapacitive as electrode, photocatalytic system, and organic light-emitting diodes are just a few of the applications. In addition, to enhance the optical properties of materials, rare earth neodymium oxide was used. Rare earth oxides having one-dimensional structures, such as La2O3, Sm2O3, Gd2O3, and Nd2O3, have been widely used in many functional devices due to their unique electrical, optical, magnetic, catalytic, and chemical features [20]. Nd2O3 has sparked a surge of interest in recent years, opening up a slew of new possibilities in a variety of fields. It is one of the most fascinating oxides in the industrial world because it has been widely used in a variety of applications such as ceramic capacitors, ultraviolet absorbents, color television tubes, coloring glass, catalyst, and carbon-arc-light electrodes [21]. Due to its significant luminance properties, it is used in Nd-layer applications and Nd3+ ions of particular interest for silicon-based solar cells. The main objective of this study is to synthesize transparent conductive materials to modulate their physical properties to be used in spintronics and optoelectronic applications. The nanosized tin:molybdenum oxide films were mainly successfully prepared via lower cost and temperature sol–gel technique [22, 23]. Thin films obtained by a sol–gel technique which has been effectively adapted for production because of its high throughput, controllable thickness, as well as high uniformity, high purity, lower time preparation, and higher dopant concentrations. The study includes synthesis of a series corresponding to this formula oxide (Sn0.7−xMo0.3NdxO2+δ) (0.0 ≤ x ≤ 0.3) by sol–gel method, to enhance its electrical and optical properties of materials. Another important objective is to use a simple and low cost method for achieving this target.

2 Experimental work

The nanosized tin:molybdenum oxide (Sn0.7−xMo0.3:NdxO2+δ) (0.0 ≤ x ≤ 0.3) thin films were prepared by sol–gel/spin coating technique using tin nitrate (Sn N4O12, Merck), ammonium dimolybdate ((NH4)2MoO4, Aldrich, 99.89%), and neodymium nitrate (Nd(NO3)3·6H2O, Merck, 99.9%) as precursors, Ethylene glycol (Aldrich, 99.8%) and diethylamine (Merck, 99.5%) as solvents. For this study, SnN4O12 and (NH4)2MoO4 were dissolving in ethylene glycol and distilled water (3:1), and the resultant solution was mixed with 7 ml of diethylamine under magnetic stirring for 1 h. The resultant solution was mixed at 50 °C for 1 h until a homogeneous Sn:Mo sol was achieved. The obtained Sn:Mo sol was kept for 1 night at 30 °C. Then a required amount of Nd(NO3)3.6H2O with content (0.1 ≤ x ≤ 0.3) was dissolved in ethylene glycol and distilled water then added to the Sn:Mo sol at a constant atomic ratio of Mo:Sn. The obtained solutions for the doped samples were then mixed at 50 °C and aged 1 night at 30 °C. Finally, clean glass substrates were used to deposit the prepared Sn0.7Mo0.3 O2+δ and doped with different Nd ions sols. Then, the prepared sols were deposited on the substrate through the spin coating method at 2000 rpm and 20 s for each layer until reaching the required thickness. The coated substrates were dried at 150 °C for 1 h to evaporate the residual solvents. Finally, the resulted films were calcined at 470 °C for 1 h. The sol–gel technique is a time-effective technique, where the films take 48 h for deposited, dried, and thermally treated providing the combusted films [24].

XRD data of the thin films were collected at ambient conditions on an Empyrean diffractometer by Panalytical (Almelo, The Netherlands), and filtered CuKα radiation, tube operated at 30 mA and 45 kV, and using a Ni filter to eliminate Kβ. The crystal structure of the prepared samples was investigated based on XRD patterns, the scanning range was 20 to 80 (2θ), step scan mode with step size of 0.026 (2θ), and counting time of 20 s/step. Instrumental broadening was corrected using quartz standard sample. FTIR studies were carried out with JASCO 460 PLUS, FTIR spectrometer range from 400 to 2000 cm−1. Morphological properties were studied by using Scanning electron microscope. Transmittance and reflectance were measured in the wavelength range 300–1800 nm by using a double-beam spectrophotometer; JASCO V-570 model. Photoluminescence properties were measured using JASCO Spectrometer/data system, at the excitation wavelength 230 nm. The vibrating sample magnetometer was used to determine the magnetic characteristics.

3 Results and discussion

3.1 XRD analysis

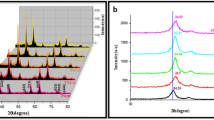
The purity of the prepared films admitted out in PXRD investigation. Figure 1a demonstrates the PXRD diffraction pattern of Sn0.7−xMo0.3NdxO2+δ, (0.0 ≤ x ≤ 0.3) respectively; the films are polycrystalline in nature, as is observed in the diagram. The peaks pointed out at 2θ = 26.59, 33.38, 37.96, 38.99, 51.79, 54.77, 57.84, 61.90, 64.76, 65.98, 71.30, and 78.73 are indexed with corresponding planar orientations, (110), (011), (020), (111), (121), (220), (002), (130), (112), (031), (022), and (231), respectively. These assimilated into the Cassiterite, tetragonal SnO2 rutile structure. All existed diffraction peaks perfectly matched with ICSD card no. 98-3-9175. The absence of any other phase such as MoO3 or Nd2O3 or impurity peaks revealed that Mo and Nd dopants properly incorporated into pure SnO2 lattice sites through the sol–gel synthesis. The incorporation of Nd into the SnO2 matrix could be confirmed by the shift in the 110 peak positions. Moreover, with increased Nd doping, the intensity of the diffraction peaks diminishes, which may be due to impurities that counteract the growth of SnO2 as shown in Fig. 1b. The same behavior for the decrease in the intensity of the diffracted peaks with the increase of dopant level was obtained before by Lekshmy et al. [25] during their studies on the effect of Mn-doped SnO2 thin films prepared by the Sol–Gel Coating.

Fig. 1
figure 1

a XRD pattern of (Sn0.7−xMo0.3: NdxO2+δ) (0.0 ≤ x ≤ 0.3). b (110) peak shift due to Nd doping

Full size image

The crystallite size was determined using the Scherrer equation from the most intense peak plane 110 using the following equation:

$$D \, = \, k\lambda /\beta_{hkl} \cos \theta_{hkl},$$
(1)

where k is the shape factor, λ is the wavelength of X-Ray, θhkl is the Bragg angle, and βhkl is the corrected full width at half maximum (FWHM) after subtracting the instrumental broadening. Table 1 shows the average crystallite size estimated for several samples. The calculated crystal size for pure and doped samples is 59 to 41 nm. This means that the presence of Nd3+ ions in SnO2 prevented crystal grains from growing. The presence of Nd3+ ions in the crystallographic structure increases the formation of oxygen vacancies as required by the charge balance. This effect is in conjunction with the larger ionic radius of Nd+3 ion = 1.123 Å in comparison to Sn4+ ion = 0.83 Å at six coordinations. This can disturb the long range crystallographic ordering, and hence, reducing the crystallite size. On the other hand, the lattice strain (ε) grew with doping, from 0.46% for pure without Nd doping to 0.523% for 0.3 Nd-doped samples. Such findings can be explained by the fact that the incorporation of Nd3+ is accompanied with the generation of lattice defects in SnO2. The defects increase the lattice strain, and consequently, slow down the growth of crystallites in the case of doped sample. The defects increase the lattice strain, and consequently, slow down the growth of crystallites in the case of doped sample and hence, reducing the crystallite size. The dislocation densities of thin films are given by the Williamson and smallman’s relation [26, 27]:

$$d = \, n/D^{2},$$
(2)
Table 1 Crystallite size, microstrain%, and dislocation density of Sn0.7-xMo0.3:NdxO2+δ(0.0 ≤ x ≤ 0.3)
Full size table

where D is dislocation density, n is a factor which equals unity, giving minimum dislocation density, and D is the crystallite size. It is clear that the dislocation density decreases with the increase in Nd doping.

3.2 FTIR study

FTIR is a technique for obtaining information about a material's chemical bonds and functional groups. FTIR spectra of nanosized Sn0.7Mo0.3O2+δ film doped with various contents of Nd ions in the range 1700–400 cm−1 are given in Fig. 2. The given spectra exhibited some weak and robust absorption peaks, identified to stretching and bending vibrations in nanosized pure and doped (Sn0.7−xMo0.3 NdxO2+δ) (0.0 ≤ x ≤ 0.3) films [28, 29]. The two bands at 470 and 603 cm−1 are corresponding to bending and stretching vibrations of Sn–O–Mo and Sn–O– and the change in their intensities confirms the introduction of Nd in Sn:Mo structure and can be denote the reconstructed of Sn–O–Mo structure. The bands are located in the range 912 to 600 cm−1 are corresponded to asymmetric stretching modes of Sn–O–, Mo–O–, O–Mo–O, and O–Sn–O vibrations in Sn:Mo structure [28, 30]. When Nd3, Mo3 ions replaced into SnO2 lattice, the absorption peaks moved to lower wavenumber side. This shifting is most likely due to changes in bond length that occur when Sn4+ ions in the crystal lattice are replaced with lighter Nd3+ ions. The same behavior in the shift of the peak position due to doping was obtained by Inderan et al. [31] during their studies of Ni-doped SnO2 prepared by the hydrothermal method. All thin films presented a dominant band at 1401 cm−1 which corresponds to the interaction of Sn with hydrogen lined Mo–O, as a weak acid [32, 33]. The band at 1613 cm−1 appeared in both nanosized Sn:Mo and doped with Nd films; the intensity and the shape of the band suggest that it may correspond to the deformation mode of –OH stretching vibration, as humidity in the films [34]. From the FTIR spectra it can be obvious that these peaks 1650–800 cm−1 become stronger with the increase of Nd ratio in the Sn:Mo structure, which denotes the absorbing ability of films to –OH decreases. This might be due to the substitution of Sn with Nd ions in the Sn:Mo lattice, which supports the formation of Sn–O– Nd and eliminates –OH groups.

Fig. 2
figure 2

FTIR spectra of a Sn0.7Mo0.3, b Sn0.6Nd0.1Mo0.3O2, c Sn0.5Nd0.2Mo0.3O2, and d Sn0.4Nd0.3Mo0.3O2 films

Full size image

3.3 Morphological properties

Figure 3a, b shows the typical morphology of pure Sn0.7 Mo0.3O2+δ and Sn0.4Mo0.3Nd0.3 O2+δ. The SEM image of both showing microstructure and aggregates of smaller individual nanoparticles, foam-like structure can be observed. This could be due to strong interactions between nanoparticles during calcinations, which are caused by their high surface energy. The grain distribution estimated from the SEM (Fig. 3c, d) images for films showed that the grain size changes from 50 to 500 nm, where the image region was heavily aggregate as is observed in Fig. 3a, b.

Fig. 3
figure 3

a SEM image for Sn0.7Mo0.3O2+δ, b SEM of Sn0.4Mo0.3Nd0.3 O2+δ, c, d The grain distribution of Sn0.7Mo0.3O2+δ and Sn0.4Mo0.3Nd0.3 O2+δ

Full size image

3.4 Optical properties

The optical properties of all samples were studied in the wavelength range of 300–1800 nm. Figure 4 shows the optical transmission (T) spectrum of Sn0.7−xMo0.3NdxO2+δ films (0 ≤ x ≤ 0.3). The decrement in transmittance of the films with higher Nd doping content can be explained by the rise in scattering of photons, due to the larger surface roughness of the prepared films [35]. The optical absorption coefficient (α) of Sn0.7−xMo0.3NdxO2+δ films with different Nd concentrations are depicted in Fig. 5. Absorption coefficient is estimated by the following Beer–Lambert’s law [36]:

$$\alpha \, = \, \ln \, \left( {1/T} \right) \, \left( {1/d} \right),$$
(3)
Fig. 4
figure 4

Relation between transmission and wavelength (nm)

Full size image
Fig. 5
figure 5

Absorption coefficient vs. wavelength (nm)

Full size image

where d is the films thickness and T is the transmittance. The thickness of the film without Nd equals 500 nm and the thickness of the films doped with different Nd contents is 530 nm. It is observed that (α) increases with increasing Nd content and decreases with increasing wavelength (λ). The direct allowed energy band gap (Eg) of Sn0.7−x Mo0.3NdxO2+δ samples have been calculated from the correlation between the incident photon energy (hυ) and the absorption coefficient (α) as is given below [37]:

$$\alpha \, h\nu \, = A\left( {h\nu \, - E_{g} } \right)^{n}.$$
(4)

The band gap energy has been evaluated by extrapolating the straight line portion of the plot to the (hυ) axis to get the value of optical band gap (Eg) as is shown in Fig. 6a–d. The results show that when Nd doping levels rise, the optical band gap widens, which is consistent with the changes in crystallite size. In addition to when the degree of doping rises, the Burstein–Moss effect on band gap broadening, a well-known quantum confinement phenomena, causes the band gap to widen by shrinking the crystallite size [38, 39]. Also, structural disorder in the lattice may cause changes in the intermediate energy level distribution inside the band gap, resulting in variations in Eg values. The band gap is also affected by the strain caused by the Nd dopant as ensured by XRD data. The increase in Eg indicates that Sn0.70-xMo0.3NdxO2+δ films could be used in optoelectronic devices.

Fig. 6
figure 6

a–d (αhυ)2 versus hυ

Full size image

The extinction coefficient (k) is a ratio that describes how rapidly the intensity of light diminishes when it travels through a substance. A detailed examination of the relationship between k and wavelength reveals that k rose as both the wavelength and the Nd content increased as shown in Fig. 7. The refractive index (n) is an important optical constant that explains the function of the incident photon in beginning particle polarization, as (n) is unmistakably influenced by the material's packing density and polarization [40, 41]. Also the refractive index (n) is an important parameter for optical material and their applications; they consider it as the main parameter for device design. The refractive index can be calculated by using these relations [42]:

Fig. 7
figure 7

Extinction coefficient against wavelength

Full size image
$$R=\frac{{(n-1)}^{2}+{k}^{2}}{{(n+1)}^{2}+{k}^{2}},$$
(5)
$$n=\frac{(1+R)}{(1-R)}+\sqrt{\frac{4R}{{(1-R)}^{2}}}-{k}^{2}.$$
(6)

The dependence of the reflectance on the wavelength is shown in Fig. 8. The relation between the refractive index and the wavelength is shown in Fig. 9. It is obvious that raising the Nd content leads to an increase in n.

Fig. 8
figure 8

Dependence of reflectance on wavelength

Full size image
Fig. 9
figure 9

Relation between refractive index and wavelength

Full size image

3.5 Photoluminescence

The photoluminescence spectra of (a) nanosized 0.7Sn:0.3Mo film doped with various molar ratios of Nd to Sn (b) 0.2 and (c) 0.3 are illustrated in Fig. 10. The spectra of 0.7Sn:0.3Mo display major two emission peaks located at wavelengths of 425 and 466 nm. Besides, there are two less intense emission bands located at 562 and 622 nm. These emission peaks are decreased with the introduction of the Nd element without any shift in the position of the peaks. By the increase of Nd ions, the distance between Nd ions decreases. Owing to this decrease in distances between Nd ions, the phonons are forced by Nd ions to exchange energy to the electrons which are close to Nd ions resulting in the decrease in emission intensity. This phenomenon is known as concentration quenching. However, the fundamental edge, located at wavelengths less than 400 nm, is found to show a slight shift towards higher wavelengths with the introduction of Nd dopant.

Fig. 10
figure 10

The photoluminescence spectra of a nanosized 0.7Sn:0.3Mo film doped with various molar ratios of Nd to Sn, b 0.2, and c 0.3

Full size image

3.6 Magnetic measurements

To probe the magnetic properties of Sn0.7−xNdxMo0.3O2+δ, (0.0 ≤ x ≤ 0.3) nanoparticles, room temperature magnetization measurements were performed on the samples and are shown in Fig. 11a–c. The magnetization (M) of Sn0.7Mo0.3O2+δ sample shows a negative response to the driving magnetic field (H) as shown in Fig. 11b. This behavior is known as a diamagnetic behavior and is released from the absence of unpaired electrons in 4d10 in the electronic configuration. The magnetic behavior of the samples is completely changed by introducing Nd ions into the structure of the samples, Fig. 11a, c. The behavior is released from the presence of unpaired electrons in 4f in the electronic structure of Nd. Figures 11a and c show that the sample with a low concentration of Nd, Sn0.6Nd0.1Mo0.3O2+δ has a paramagnetic behavior, while samples containing a high concentration of Nd, (Sn0.5Nd0.2Mo0.3O2+δ, Sn0.4Nd0.3Mo0.3O2+δ) show a ferromagnetic behavior. It was an expected behavior due to increasing magnetic ions content in the materials leads to increase the magnetic order in these materials; this behavior is appeared in increasing the saturation magnetization in Fig. 11a. The saturation magnetization (Ms) is increased from 0.723 to 1.0238 (emu/g) with increasing Nd ions concentration from 0.2 to 0.3. The obtained magnetic parameters are listed in Table 2.

Fig. 11
figure 11

Magnetic hysteresis loop

Full size image
Table 2 Magnetic parameters, saturation magnetization (Ms), coercivity (Hc), remanent magnetization (Mr)
Full size table

4 Conclusion

The series of (Sn0.7−xMo0.3:NdxO2+δ) (0.0 ≤ x ≤ 0.3) Nd3+ thin films were prepared by sol–gel/spin coating technique at 470 °C for 1 h. Thin films were examined by XRD, to insure its phase formation. XRD analysis revealed the formation of all thin films in the form of Cassiterite, tetragonal SnO2 rutile structure, the crystallite size, and microstrain and dislocation densities were also determined from the XRD patterns. It was found that the crystallite size decreases with the increase in Nd doping and it was in the nanometer range, moreover both the microstrain and dislocation density grow with increasing Nd doping. The FTIR analysis defined the bands of the thin films. The morphology of the thin film studied by scanning electron microscope shows aggregates of smaller individual nanoparticles, foam-like structure. The energy band gaps (Eg) are estimated by using the optical data. It was found that Eg increases with the increase in the Nd content. Moreover, the calculated extinction coefficient (k) was increased as both the wavelength and the Nd content increased. The refractive index (n) was found to increase with increasing the Nd content. The photoluminescence spectra of Sn0.7 Mo0.3 display major two emission peaks located at wavelengths of 425 and 466 nm. Besides, there are two less intense emission bands located at 562 and 622 nm. These emission peaks are decreased with the introduction of the Nd element without any shift in the position of the peaks. By the increase of Nd ions, the distance between Nd ions decreases. Magnetic measurements with a Vibrating Sample Magnetometer (VSM) unit reveal hysteresis loops in samples with high Nd content (Sn0.5Nd0.2Mo0.3O2+δ, Sn0.4Nd0.3Mo0.3O2+δ) that lead to ferromagnetic behavior. From examining the obtained optical results it is obvious that the increase in the energy band gap with Nd addition enables us to use it in the optoelectronic applications.