1 Introduction

Amorphous semiconductors, and chalcogenides in particular, are interesting materials that display a broad range of physical phenomena resulting in wide-ranging studies of their fundamental properties and their application [1, 2]. Amorphous germanium telluride (a-GeTe) is of particular interest as it forms the basis of Ge–Sb–Te alloy systems that have been exploited in phase-change memory (PCM) applications [3, 4]. a-GeTe has a crystallisation temperature > 150 °C and can be reversibly switched between the amorphous and crystalline state at high speed [5]. Despite the significant research attention this and other applications have attracted, a full understanding the electronic and thermoelectric properties of these materials remains a challenge due to their non-crystalline structure. Recently the role of oxidation in a-GeTe has been studied, demonstrating its role in the detrimental modification of the crystallization dynamics and chemistry of thin films [6,7,8,9,10].

Electronic and optical studies [11, 12], including photoconductivity [13], have resulted in a continuously evolving understanding of the electronic structure of a-GeTe thin films. Evidence supports the presence of a bandgap (at 300 K) of ~ 0.75 eV [14] to 0.85 eV [15], a donor state at ~ 0.25 eV above the valance band, and one or more acceptor states at ~ 0.35 eV below the conduction band. Modelling of a-GeTe using density functional theory (DFT) approaches has also led to the prediction of mid-gap states upon melt quenching, though with a narrower bandgap (~ 0.4 eV) [16]. It was further suggested that the mid-gap state is directly associated with the presence of homopolar Ge–Ge bonding, itself linked to tetrahedral Ge bonding. Thermoelectric power studies of bulk GeTe have yielded a Seebeck coefficient (S) value of ~ 35 to 80 μV K−1 at 300 K [17,18,19,20,21]. In contrast, reports for measurement of S in a-GeTe thin films by Bahl [22] (200 nm), Dutsyak [23] (< 1 μm thick) and Hughes [24] (100 nm) yielded much higher values of ~ 800 μV K−1, with measurement of crystalline GeTe yielding values similar to those reported for bulk sample [17]. However, the study of 500 nm annealed polycrystalline (rhombohedral) GeTe films yielded a value of S ~ 80 μV K−1 [25] similar to the bulk. Interestingly, the study of hot-pressed GeTe rods formed from < 200 μm diameter particles yielded a values of S ~ 170 μV K−1 at 300 K. In all of the above it is likely that some of the variation in reported properties between studies may be due to the effects of oxidation.

The measurement of the Seebeck coefficient, under dark conditions (Sdark), can be used to experimentally determine the majority carrier type of a semiconductor, including amorphous systems for which the Hall effect can provide anomalous results [26,27,28]. As indicated above the positive values of S reported lead to the conclusion that a-GeTe is a p-type semiconductor in common with the majority of chalcogenides. A general understanding of p-type conductivity in amorphous chalcogenides is given by considering the presence of lone pair electrons leading to the formation of defects and valence alternation pairs (VAPs) that ultimately result in an excess of holes in the valance band [29].

Though it is generally the case that S is measured under dark conditions, S can also be strongly affected by additional factors including by the absorption of light [30,31,32,33,34]. Although Mondal et al. [35] reported an increase in the magnitude of S upon light exposure (Slight) in Pb2CrO5, in general it is found that illumination of a sample with light reduces the magnitude of S such that |Sdark| >|Slight|. This reduction can in some cases be large enough that the sign of Sdark and Slight may differ and the majority carrier type is reversed [31].

Here we report the measurement of Sdark and Slight of ~ 100 nm oxidised a-GeTe films as a function of optical excitation wavelength across the visible and near-IR spectral region. It is found that the variation between Sdark and Slight reveals a dependency of photon energy that also includes a sub-electronic bandgap (Eg) behaviour.

2 Experimental procedure

a-GeTe thin films of 100 nm nominal thickness were sputtered from a target of composition Ge50Te50 (purchased from Testbourne) onto high resistivity (> 1012 cm\(\Omega\)−1) 1 mm thick fused silica substrates using a Kurt J. Lesker Nano 38 Sputter thin film deposition system. The substrate was inserted at room temperature with less than a 10 °C increase observed during deposition. High purity argon was used as the sputtering gas and the distance between the target and the substrate was 150 mm. The films were deposited using a deposition power 60 W, a DC bias of 214 V, and whilst maintaining a base pressure of ~ 3.4 × 10−3 mbar with an argon gas flow of 20 SCCM. The film thickness was measured on a KLS Tencor P16 Stylus Profiler and determined to be 100 ± 5 nm.

To enable electrical measurements Cr (100 nm)/Mo (50 nm) top electrodes were defined by sputtering through a shadow mask with 2 mm diameter circle apertures. Cr was sputtered (1000 W) for 15 min followed by Mo at the same power for 5 min. The ohmic nature of the contacts was confirmed in subsequent electrical measurement (in the dark), displaying linear current–voltage (I–V) characteristics (Fig. 1), yielding a measured conductivity of 5.6425 × 10−10 ± 1.74 × 10−11 S cm−1. It is immediately noted that this value is six orders of magnitude smaller than that typically reported for a-GeTe [9] and three orders smaller than that reported for similar film by Hughes et al. [24]. As such it is clearly evident that modification of the deposited film had taken place during or following its deposition, noting that the films were transferred and stored under dark but ambient atmosphere conditions hence oxidation was likely to have occurred.

Fig. 1
figure 1

I–V scan of a-GeTe film obtained using adjacent Cr (100 nm)/Mo (50 nm) electrodes. The distance between the measured electrodes was ~ 1.8 cm. Inset is an image of the a-GeTe sample

Full size image

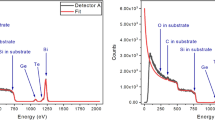
Compositional analysis Rutherford backscattering spectrometry (RBS) measurements were performed by the EPSRC National Ion Beam Centre that confirmed the presence of oxygen throughout the films, yielding a film composition of composed of Ge = 34.4% ± 0.3 and Te = 33.8% ± 0.2 and O = 31.8% (Fig. 2 and Table 1). A ~ 2 mm diameter 2 meV 4He ion beam was used with a charge collection of 10 µC. Backscattered He ions were simultaneously collected at Cornell (detector A) and IBM (detector B) geometries for scattering angles of 173.2° and 148.6°, respectively.

Fig. 2
figure 2

RBS spectra of 100 nm GeTe film on SiO2. The left (detector A) spectrum is acquired using the Cornell geometry and the right spectrum (detector B) collected in the IBM geometry

Full size image
Table 1 Elemental composition of a-GeTe film
Full size table

Spectra were analysed using SIMNRA assuming Rutherford cross sections throughout with the best fits being determined by eye [36]. No pile up correction was applied. The spectra were calibrated for energy by measuring a Au/NiCu/SiO2/Si standard sample and the solid angle charge product was internally calibrated for each spectrum by fitting to the Si in the SiO2 substrate. The substrate model used in the SIMNRA fit was kept simple by assuming a single layer of GexTeyOz on a SiO2 substrate; where the fitted peak representing the O in the GexTeyOz film was lower than the measured data, the O concentration was scaled by the ratio of the measured to fitted peak areas. For the Cornell geometry, the O in the film was separated from the O edge of the O in the substrate and a simple background subtraction based on the Si signal could be applied. For the IBM geometry, the two O signals overlapped and so a more complex background was subtracted from the peak representing the O in the GexTeyOz film after fitting a polynomial to the O edge below and Si signal above the peak. It is usual to determine a single best sample composition to give the best fits to the spectra at both geometries simultaneously. In this case, independent fits (Table 1) were made so that their comparisons could give an indication of the absolute uncertainty in the O concentration. Errors quoted in the table are from counting statistics (1/√(counts)) alone. The differences between the calculated values is larger than these errors demonstrating that there are systematic errors (for example, accuracy of stopping powers or accuracy of fit) that are hard to estimate from first principles. Interestingly the RBS analysis was also able to detect trace amounts of residual Cl on the surface of the fused silica substrate. Analysis of the spectra collected above and in-plane yielded the film composition given in Table 1.

XPS analysis was used to determine the value of Ef and the top of the valence band energy level for the films and presented in Fig. 3 [37]. The samples were mounted on a metal plate, using silver epoxy to provide electrical contact between the plate and the a-GeTe film. The sample was then biased to − 10 V to ensure that the secondary electron tail could be observed. The sample was Ar+3000 sputtered to remove any carbonatious surface material and oxide layer prior to measurement. It is noted that the O 1s peak remained following sputtering confirming, in agreement with the RBS analysis, the presence of oxygen within the film. A Fermi edge scan on the metal contact pad (which was grounded to the sample plate) was undertaken and used to calibrate the energy scale.

Fig. 3
figure 3

XPS spectra of 100 nm a-GeTe film on SiO2. a C 1s region, showing the near-complete removal of carbon contamination from the surface of the GeTe film after Ar+3000 sputtering, b O 1s spectra showing that oxygen remains even after extensive sputtering, indicating its presence throughout the a-GeTe film. c Valence band region of the metal contact pad, showing the Fermi edge fitted with a Fermi–Dirac function. d Valence band region of the a-GeTe film, showing the valence band onset fitted using the linear intercepts method

Full size image

The a-GeTe Fermi level was determined to be Ef = − 4.05 eV by taking the difference of the excitation energy (1486.6 eV) and the secondary electron tail (~ 1482.55 ± 0.1 eV) which is presented in Fig. 4. The a-GeTe valence band maximum (VBM) with respect to the Fermi energy was found to be 0.16 ± 0.1 eV yielding a valence band energy of Ev = − 4.21 eV.

Fig. 4
figure 4

Secondary electron tails detected from the a-GeTe film using XPS

Full size image

Seebeck measurements were undertaken within a bespoke vacuum chamber with a base pressure of ~ 2 × 10–6 mbar. The chamber also acted as a faraday cage with electrical (triax and type-K thermocouple), optical fibre and sealed liquid/gas feedthroughs enabling electrical measurement, optical excitation, and cooling of the sample under test. A schematic of the system and control hierarchy is provided in Fig. 5.

Fig. 5
figure 5

a Schematic of the system and control hierarchy. b Schematic of the Seebeck system and measurement of the transmitted light intensity. c Intensity of incident, transmitted and absorbed light

Full size image

The optical fibre vacuum feedthrough enabled variable wavelength optical excitation of the sample, ensuring no light exposure of the metal contacts. A stable temperature gradient was established across the sample by passing a controlled flow of cooled N2 gas through a cooling block and Peltier heating of a second separated block across which the sample was placed, ensuring that the temperature did not exceed 100 °C. This is well below the crystallisation temperature of oxidized a-GeTe films of ~ 180 °C [6]. The sample temperature was measured before and following each electrical measurement by lowering two (small) type-K thermocouples probes onto the sample at the opposing points of electrical measurement. Studies were undertaken at four different values of ∆T = 15, 27, 41 and 58 °C. The electrical measurements were performed using a Keysight B1500A equipped with a high-resolution source measure unit (HRSMU). Illumination of the sample was enabled by coupling the monochromated (via Bentham TMc300 monochromator) output of a tungsten halogen source (Osram 64623 HLX) into a one-metre multimode optical fibre (Thorlabs M37L01), through a vacuum optical feed-through (Thorlabs V2H6S) and the internal fibre (MV12L05) directed to provide close illumination of the sample under test. High-quality long pass filters were used to ensure the rejection of second order reflections, and neutral density filters used to control light intensity. By adjustment of the fibre tip-to-sample separation the diameter of the incident light spot on the sample was controlled to maximise the exposure area whilst minimising the risk of direct or scattered light being incident on the electrical probes. This was undertaken to prevent any photovoltaic effect occurring during optical measurements (e.g. in the case of Schottky contacts being present). All measurements of Slight were undertaken starting from the lowest energy (longest wavelength), with continuous monitoring of the electrical signal to ensure that electrical equilibrium had been reached following each change of wavelength, prior to measurements to determine Slight. Conductivity and photoconductivity measurements utilised the above described setup and a two-probe measurement technique. This allows direct comparison of the results obtained in each case. In this method, the measured value of conductance was normalised by the distance between the two electrical contacts (1.8 ± 0.1 cm) through which the current flows. In the case of some amorphous semiconductors, a high current may lead to a phase change effect due to Joule heating, causing a transition of the film from an amorphous to crystalline structure. To limit this risk conductivity measurements were obtained by sweeping a small voltage range from − 3 to 3 V; in all cases no behaviour indicative of a phase change was observed.

3 Results

The Seebeck coefficient in p-type semiconductor in the dark is described by [38]:

$$S_{{{\text{dark}}}} = \frac{\Delta V}{{\Delta T}} = + \frac{{k_{{\text{B}}} }}{q}\left[ {\frac{{E_{{\text{f}}} - E_{{\text{v}}} }}{{k_{{\text{B}}} T}} + r + \frac{5}{2}} \right],$$
(1)

where kB is the Boltzmann constant, q is the electron charge, Ef is the Fermi level, Ev is position of the valence band, and T is temperature. The parameter r is a scattering parameter equal to 3/2 for impurity scattering and − 3/2 for lattice scattering of carriers. Under light illumination, the Seebeck coefficient may be modified by the excitation of charge carriers across the bandgap, or to and from trapped states. In such circumstances both electrons and holes may contribute to the measured value of Slight. Assuming that carrier excitation due to light absorption occurs throughout the thin film, true for the 100 nm films used, the modified conductivity, σlight, is given as:

$$\sigma_{{{\text{light}}}} = \sigma_{{\text{e}}} + \sigma_{{\text{h}}},$$
(2)

where σe(h) is the electron (hole) conductivity. As a result of the modified conductivity the Seebeck coefficient is now obtained as:

$$S_{{{\text{light}}}} = \frac{{\sigma_{{\text{e}}} S_{{\text{e}}} + \sigma_{{\text{h}}} S_{{\text{h}}} }}{{\sigma_{{\text{e}}} + \sigma_{{\text{h}}} }}.$$
(3)

The measured value of Sdark was obtained to be 0.434 ± 0.011 mV K−1, confirming the p-type nature of the film, Fig. 6.

Fig. 6
figure 6

Seebeck coefficient of a-GeTe film determined using the measured Seebeck voltage as a function of the applied temperature gradient

Full size image

The value obtained is of the same order of magnitude to that reported for a-GeTe films which were deposited in a similar way [18,19,20] though reduced by approximately a factor of 2. This indicates that the oxidised a-GeTe films remain amorphous, whereas polycrystalline films display a value of Sdark that is at least an order of magnitude lower. Using Eq. 1 with the measured values of Ef and Ev from XPS studies (assuming lattice scattering dominates [21]) yields an expected value of Sdark,calc = 0.6 mV K−1 at 300 K, again of the same order of magnitude as the measured value. Conversely, use of the measured value of Sdark to calculate the expected Fermi level results in an underestimate of ~ 60 meV in comparison to that measured using XPS.

Upon illumination with monochromatic light to measure Slight a wavelength dependent reduction in the Seebeck coefficient compared to Sdark is observed, Fig. 7. This reduction in the Seebeck coefficient upon light illumination infers that the Fermi level within the a-GeTe film is increased as a result of exposure, i.e. the film becomes less p-type. It was confirmed that upon returning the film to dark conditions that Sdark was recovered. However, this process is not immediate but required many hours to complete implying long-lived (deep) charge carrier trap states may be involved in the observed behaviour. It is noted that the wavelength dependence, Slight(λ), extends across the entire spectral region accessible (400 nm to 1800 nm) and surprisingly shows the greatest reduction from Sdark at the lowest photon energies.

Fig. 7
figure 7

Seebeck coefficienct of a-GeTe obtained as a function of monochromatic light excitation at wavelengths between 400 and 1800 nm. The potential optical bandgap is indicated with a green arrow (Color figure online)

Full size image

Inspection of the variation of Slight(λ) in Fig. 7 reveals distinctive regions of similar behaviour. Upon initial exposure to light at 1800 nm (0.68 eV), Slight(1800 nm) is ~ 0.025 mV/K lower than Sdark corresponding to a ~ 6% decrease. Slight(λ) is seen to increase approximately linearly with reducing wavelength to ~ 1410 nm (0.88 eV). As the wavelength is reduced further, Slight(λ) continues to increase linearly but at a greater rate up until ~ 970 nm (1.28 eV). The change in gradient of Slight(λ) at 0.88 eV is slightly above the reported optical bandgap of a-GeTe of ~ 0.75 eV [8] to 0.85 eV [11]. This is in line with a widening of the bandgap upon oxidation, which is well-known to occur when chalcogenide glasses are oxygen doped.

At energies below the optical bandgap the magnitude of Slight(λ) must be governed by the interaction of photons with charge carriers within, or excited to, sub-bandgap charge states (e.g. trap-to-band and band-to-trap transitions). Previous studies of photoconductivity have also revealed a sub-bandgap response (down to photon energies of 0.2 eV) at room temperature which reduces with temperature in line with the observed behaviour [13]. Similarly, Longeaud et al. found evidence of acceptor states at energies of 0.37 eV and 0.41 eV above the VB and a donor state at 0.26 eV below the CB [14]. These, combined with the presence of VB and CB tail states with Urbach energies of 32 meV and 59 meV, respectively, provide a clear rationale to expect a sub-bandgap photo-Seebeck response.

The increase in the sensitivity of Slight(λ) to light exposure at energies above 0.88 eV is in alignment with the increase in the density of states (DOS) at the valance band edge, and the ability to optically excite valence electrons across the bandgap, Eg. A value of Eg is therefore tentatively assigned as Eg = 0.88 eV on the basis of these photo-Seebeck measurements alone. Attempts to directly measure the optical band edge of the a-GeTe films via both absorption and photothermal deflection spectroscopy proved unsuccessful due to the thinness of the films.

As the excitation wavelength is reduced further from ~ 970 to 400 nm Slight(λ) displays three further regions of behaviour, all of which show a reduced gradient to that observed in lower energy (higher wavelength) excitation regions. The initial reduction of the energy dependence of Slight(λ) at ~ 970 nm (1.27 eV) coincides with the reported onset of saturation of optical absorption in 800 nm a-GeTe films [14]. There then follows an increase in this dependence over the region from 620 nm (2.0 eV) to 450 nm (2.75 eV) which coincides with the reported peaks in binding energy obtained from valance band XPS studies [39, 40]. Finally, at the highest energies available (below 2.75 eV) the dependence of Slight(λ) on wavelength appears to disappear, and the reduction from Sdark is at its smallest.

To provide further information on the photogenerated processes that result in the observed behaviour of Slight(λ) in Fig. 7 the photo-Seebeck voltage, Vlight(λ), can be studied. Figure 8 presents Vlight(λ) as a function of excitation wavelength for ΔT = 15, 27, 41 and 58 °C.

Fig. 8
figure 8

Measured Seebeck voltage normalised by the number of absorbed photons. a Under excitation at wavelengths between 400 and 1100 nm and b between 1100 and 1800 nm. The narrow peak at ~ 1380 nm is an experimental artefact

Full size image

To correct for the variation in light intensity with wavelength Vlight(λ) is normalized by the number of photons absorbed at each wavelength (Fig. 5c). The prominent peak appearing at ~ 1380 nm is an artefact of the normalization originating from the strong optical fibre attenuation around this band (due to hydroxyl groups, Fig. 5c). From Fig. 8 it is clearly observed that the variation of Vlight(λ) either side of Eg (~ 1410 nm, 0.88 eV) is different. Below Eg there is evidence, in the form of ‘shoulders’, of optically induced transitions centred at ~ 1600 nm (0.78 eV) and ~ 1700 nm (0.73 eV), corresponding to a transition energy of ~ 0.1 eV and ~ 0.15 eV below Eg. Previous modulated photocurrent (MPC) and PDS studies have indicated that both the valance and conduction band display extended tails with characteristic energies of 0.33 eV and 0.6 eV, respectively [14]. Furthermore, to accurately reproduce the DOS obtained via MPC measurements, an additional donor state was required with an energy of 0.26 eV above the valence band. An additional pair of acceptor states with energies of 0.37 eV and 0.41 eV above the valence band were also included to obtain fits to PDS studies and pin the dark Fermi level at the experimental value (0.31 eV). The energy difference between the reported donor and two acceptor states is 0.11 eV and 0.15 eV matching that of the transition energy of the observed peaks in Vlight(λ). As such the increase in Vlight(λ) below Eg provides a direct experimental observation that would support the presence of these states.

Turning attention to the behaviour of Vlight(λ) at energies above Eg it is seen that whilst there is an increase in Vlight(λ) with ΔT, no evidence of any wavelength dependence is observed as the excitation wavelength is decreased from ~ 1410 to 1100 nm (1.13 eV) (Fig. 8). Excitation in the 1100 nm to 470 nm region does then result in the re-emergence of the dependence of Vlight(λ) on wavelength. Inspection of Vlight(λ) in the region of ~ 1100 nm to ~ 700 nm shows the presence of a broad peak with its maximum at ~ 800 nm, with an accompanying small (reproducible) feature at ~ 950 nm. This broad peak in Vlight(λ) coincides with the change in the dependence of Slight(λ) at ~ 950 nm (highlighted in orange, Fig. 7). Reducing the excitation wavelength further from ~ 700 to 600 nm reveals the presence of a further peak in Vlight(λ) at ~ 675 nm, which again corresponds to the change in the dependence of Slight(λ) seen at this wavelength (highlighted yellow, Fig. 7). At excitation wavelengths below 600 nm Vlight(λ) then begins to rapidly increase with a evidence of a further feature centred at ~ 440 nm, leading to the final change in dependence of Slight(λ) on wavelength (highlighted green, Fig. 7).

As discussed above, any modification of the Seebeck coefficient under illumination is related to the generation of excited carriers yielding an excited hole (electron) population of magnitude ∆p (= ∆n). ∆p should be proportional to the incident light intensity, I0 (λ), for low excitation powers and thus as I0 (λ) is reduced Slight(λ) should approach Sdark. Figure 9 shows Slight(λ) as a function of incident light power, obtained individually for selected values of λ, and it is observed that as I0 (λ) is reduced Sdark is approached.

Fig. 9
figure 9

Seebeck coefficient measured under selected monochromatic wavelengths as a function of illumination intensity

Full size image

The value of 100% in Fig. 9 corresponds to no attenuation of the monochromatic light, as was used in undertaking the measurements Slight(λ) at 100% light intensity. We note that the values of Slight(λ) in Fig. 9 are lower than those presented in Fig. 7 as a result of prior light exposure. Likewise, direct comparison of values of Slight(λ) at each exposure power in Fig. 9 cannot be undertaken (unlike Fig. 7) due to the experimental method. At the lowest light intensity, the Seebeck coefficient increases towards the dark value. It is of interest to note that the change in Slight(λ) with increasing I0(λ) is seen to saturate for intensities greater than ~ 0.1% of that used to obtain the data shown in Figs. 7 and 8.

Finally, the photoconductivity of a-GeTe with respect to the intensity of light is presented in Fig. 10 obtained in the presence of the temperature gradient given ∆T. Upon illumination with light a photocurrent is observed which quickly saturates at ~ 16% of the maximum value of I0(λ) for ∆T = 15, 27 and 41 °C. Prior to saturation of the photocurrent, its magnitude increases with reducing wavelength in line with the increase in absorption coefficient. The behaviour of the photocurrent measured for ∆T = 58 °C displays a different behaviour, which is found to be reproducible, at values of I0(λ) above that which saturation is observed at lower values of ∆T. As I0(λ) is increased above this point (~ 16%) the photocurrent is found to decrease, with the effect being more prominent for wavelengths with a higher absorption coefficient. This behaviour is reversed again as the highest value of I0 (λ) (100%) is reached.

Fig. 10
figure 10

Photoconductivity measurement of a-GeTe as function of light intensity and wavelength

Full size image

4 Discussion

In the above description of the experimental behaviour of Slight(λ) we turned to the detailed studies of a-GeTe and its proposed DOS to provide an initial interpretation of the observed spectrum. However, it is clear that the presence of oxygen within the film has modified the electrical properties. Firstly, we observe an increase in Eg from that reported for a-GeTe (~ 0.75 eV) [14] to ~ 0.88 eV in these a-GeTe-O systems. This is in agreement with ab initio molecular dynamics simulations [8] that show substitution of Te by O results in an increase in the bandgap of ~ 0.06 eV, whilst the formation of ‘dumbbell-like’ O-VTe-Ge defects lead to an increase of ~ 0.08 eV. We note that such simulations typically underestimate the bandgap compared to experimental measurements hence a larger increase as observed within would not be unexpected. Additionally, the simulations are based on the incorporation of low O concentrations by the replacement of Te with O within the supercell, whereas in the material studied within a high O concentration was found during RBS analysis (~ 31%) with a similar Ge and Te concentration (~ 34% each). Previous studies of GeTe-O systems have suggested that at high (> 10%) O concentration the formation of GeO2 and TeO2 crystals occurred [7]. We note that both of these materials are wide bandgap (> 3 eV) and therefore a thin film (100 nm) would be transparent whereas the film studied in our case remained dark brown/grey (Fig. 1).

It is also apparent that the presence of oxygen in these a-GeTe films reduces the value of Ef − Ev from 0.31 eV in a-GeTe [14] to 0.16 eV in the studied a-GeTe-O system. This change is also reflected in the ab initio simulations [8] in the case of introducing O-VTe-Ge defects where Ef − Ev is significantly reduced. As such this then rules out the presence of a donor state centred at 0.25 eV above the valence band as found in a-GeTe. Nonetheless, the study of Vlight(λ) at energies within the bandgap (Fig. 8) does reveal evidence of optically active states with excitation energies of ~ 0.1 eV and ~ 0.15 eV below Eg. The presence of O-VTe-Ge defects, and also interstitial O, has been predicted to result in the formation of gap states which may be a source of such states.

The absorption of higher energy photons, for example 1.24 eV to 3 eV (400 nm to 1100 nm) has a significantly weaker effect (evidenced by a reduced gradient) than that at lower energies in the reduction of the Seebeck coefficient. This implies that excitation at very high energies with respect to the bandgap probably produces either more trapped electrons (which cannot diffuse or recombine with free holes) or electrons which quickly relax again into their original (ground) state before any diffusion or recombination can occur.

Upon further decrease in the energy of the photons towards the bandgap, the Seebeck voltages show some changes from 1 to 0.95 eV that may be due to the recombination of the excited electrons with the trapped holes. Considering the fact that the bottom of the conduction band is mostly formed from positively charged unoccupied p states [40], excitation into this state results in trapped electrons too. This follows the spectrum in Fig. 7 for the band to band excitation as the Seebeck coefficient shows more p-type behaviour. As the energy of incident photons is increased to be well above Eg (to ~ 1.24 eV) the dependency of ∆S(λ) again changes with three regions of varying behaviour being identified (Fig. 7).

5 Conclusion

The measurement of the photo-Seebeck coefficient of an amorphous semiconductor based on the direct measurement of the Seebeck voltage has been investigated. The Seebeck coefficients obtained under varying monochromatic light excitation showed that not only trap states are detectable using this technique, but there is also a potential of additional information such as the optical bandgap energy and an indication of the modification of carrier concentration and bonding arrangements of semiconductors due to light exposure. For example, the value of the bandgap for a-GeTe was determined using the photo-Seebeck spectrum of this sample. It is also noticed that this value is highly depended on the oxidation state of the device under test. The power dependence of the photo-Seebeck coefficient can be linked to variation in the carrier concentration of holes and electrons upon absorption of light, and which was directly observed in the measurement of a-GeTe. Incident photons with lower energies than the optical bandgap interacts with the carriers within the sub-bandgap (either trap to band or band to trap) which directly affect the variation of the Seebeck coefficient. It is proposed that at higher excitation energies incident light produces more trapped electrons and/or electrons quickly relax to their original state. The changes in the photo-Seebeck spectra at higher energies are directly related to the bonding energies of the compounds. The variation of the Seebeck coefficient under influence of light is also depended on the structure of the amorphous chalcogenides which propose positively charged states that can interact with the excited or trapped electrons.