Abstract
In order to meet the increasing requirements for materials in the electrical and electronic industry, in this paper, Si-B oxides were designed and synthesized via the organic monomers of Si and B, and the Si-B/epoxy nanocomposites were prepared by ultrasonic dispersion and thermal curing. The Si-B oxides were dispersed uniformly in epoxy resin with great compatibility and the average size of the particles was about 6 nm. Results showed that with the increase of doping content, the dielectric constant and dielectric loss of the Si-B/epoxy nanocomposites decreased, but the effect on the conductivity was not obvious. The dielectric strength and corona resistance life of the Si-B/epoxy nanocomposites increased at first and then decreased. When the doping content was 6 wt%, the corona resistance life of the Si-B/epoxy nanocomposites reached up to 17.6 h, which was 8.38 times of that of pure EP. It was proved that the dielectric properties and corona resistance of epoxy could be effectively improved by doping the Si-B oxides.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Epoxy resin (EP) is widely used due to its excellent electrical properties, such as motor, power electronic devices, integrated circuit packaging, etc. [1,2,3]. For dielectric materials used in the circumstance of high electric field, they should have good dielectric properties and corona resistance. Many insulating materials have little difference in dielectric strength, but their corona resistance is quite different. For applications under high electric field, corona resistance is particularly important. Therefore, it is of theoretical and practical significance to improve the corona resistance of dielectric materials.
Inorganic/organic nano-composite polymer materials have attracted wide attention due to their excellent properties, which combine the advantages of organic polymers and inorganic materials [4,5,6,7]. It is reasonable to believe that they have potential to be developed into new materials with special properties [8,9,10]. In the research of EP composites, there are many studies on their dielectric properties, and the commonly used nanoparticles are SiC [11], SiO2 [12, 13], ZnO [14], Al2O3 [15], TiO2 [16, 17]. The addition of nanoparticles improves the thermal stability, mechanical properties and electrical properties of EP composites for varying degrees. However, there are few reports on corona resistance of EP materials [18,19,20].
At present, it is difficult for single polymer or single filler filled polymer composites to meet the requirements of multifunctional properties. The pool compatibility between inorganic nano fillers and organic matrix leads to the agglomeration of traditional nano-fillers [21,22,23]. Besides, the surface functionalization of nanoparticles usually make the preparation process more complex. In this paper, nanometer Si-B oxides were synthesized by Si and B organic monomers, and Si-B/EP nanocomposites were prepared by blending method. The morphology of Si-B/EP nanocomposites were characterized. The effect of Si-B oxides content on dielectric properties of materials were analyzed, and the factors affecting corona resistance were discussed emphatically.
2 Materials and methods
2.1 Materials
The following materials were obtained from the respective companies: phenyl triethoxy silane(PTES), from Hubei Ju Sheng Technology Co., Ltd, China; tributyl borate, from Tianjin Guangfu Fine Chemical Research Institute, China; distilled water, self-made; ethanol absolute, from Tianjin Tianli Chemical Reagent Co., Ltd, China; Epoxy resin used was bisphenol A diglycidyl ether (BPADE), which was prepared through the molecular distillation technology by Suzhou Jufeng Electrical Insulation System Co., Ltd, China, its polymerization degree was 0, and the epoxide equivalent was 170 g/equiv; reactive diluent: glycidyl neodecanoate(product model: E10P), from hexion specialty chemicals, Holand; curing agent: latent curing agent 594(594), from Wuxi Qianguang chemical materials Co., Ltd, China; imidazole, from Tianjin kemi’ou Chemical Reagent Co. Ltd.
2.2 Preparation of Si-B oxides
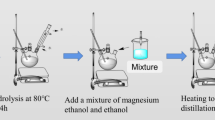
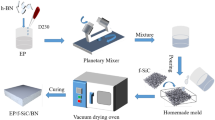
43.2 g of PTES and 4.6 g of tributyl borate (mole ratio 9:1) were taken in three mouth bottles. In the case of high-speed stirring, 50% ethanol solution was dropwise added to the bottle until the quality of the water reached 10.08 g. Under the condition of reflux, reactants were heated to make PTES and tributyl borate hydrolyze for 4 h at 80 °C. Then the reflux was changed to distillation and the temperature gradually increased to 120 °C. When the temperature reached 120 °C, the residual ethanol and water in the Si-B oxides were removed under vacuum distillation, and then the reaction was complete.
2.3 Preparation of Si-B/EP resin and Si-B/EP composite specimens
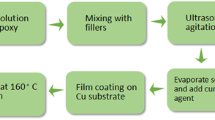
Pre-weighed 594 and the obtained Si-B oxides were added into three mouth bottles. The mixture was stirred until it was uniform and transparent. And then, pre-weighed BPADE were added and continued stirring until the mixture was transparent and uniform. Finally, ultrasonic treatment was performed for 30 min after diluent and imidazole were added. Colorless transparent Si-B/EP nanocomposite resin was prepared. Before used, the resin should be filtered by 1000 mesh strainer and then the bubbles in the resin would be removed in the vacuum oven.
Preparation of Si-B/EP nanocomposite disc specimens: the disc mold of stainless steel was coated with mold release agent and heated in a 150 °C oven. A certain amount of Si-B/EP nanocomposite resin was poured into the heated mold. It was found that the EP resin could crosslink by heating as follows: 150 °C for 1 h, 170 °C for 12 h. Finally, the Si-B/EP composite specimens were obtained. All of the as-prepared composite specimens had a carefully controlled thickness of 1 ± 0.1 mm. Preparation of thin film specimens for corona resistance testing was as follows: A coating of the prepared mixture was brushed onto a clean aluminum foil paper which was attached to clean glass panels. The same heating program was executed as the disc specimen. The thickness of the film wad controlled at 25 ± 1 μm. Samples of Si-B/EP nanocomposites with 0 wt%, 4 wt%, 5 wt%, 6 wt% and 7 wt% doping content were prepared.
2.4 Characterization
The morphology of the Si-B oxide nanoparticles was observed using a transmission electron microscopy (TEM, JEM-2100). The relative permittivity of the Si-B/EP nanocomposite was measured using a Novocontrol Dielectric Spectrometer (GmbH Germany), CONCEPT 40 in a frequency range from 100 to 106 Hz. Prior to dielectric measurements, aluminum electrodes were deposited onto both surfaces of the specimens by sputtering. The diameter of aluminum electrodes was about 30 mm. The thickness of all specimens was about 1 mm. Conduction current characteristics were tested from 10 to 80 kV/mm. HT-100 breakdown voltage tester (Guilin Institute of Electrical Appliances) was used for testing breakdown field strength of composite materials. The frequency of the applied voltage was 50 Hz. Dielectric strength was calculated as the electrical voltage divided by the sample thickness at the breakdown point. Since the short-term breakdown properties of solid dielectric shows a very strong dependence on the electrode distance. The thickness of specimens with diameter of 100 mm was controlled around 1 mm. Corona resistant test electrode system was made in accordance with IEC60343 [24] standard. Tests were carried out at room temperature, power–frequency and 80 kV/mm field strength.
2.5 Nano-composite interface model
The diagram of the interface model is shown in Fig. 1. Potential Barrier Model [25] proposed that the interaction zone (interfacial zone) is an independent region with the following characteristics:
First, interaction zone consists of bonded region and transition region; Second, the stronger the interaction strength between nanoparticles and polymer matrix, the thicker the interaction zone; Third, fermi level of interaction zone is different from that of nanoparticle and polymeric matrix; Fourth, the interaction zone is a low density region as well as a less stoichiometric region, leading to the increase of free volume and the formation of traps; Fifth, the interaction zone is a conductive region compared with the polymeric matrix.
3 Results and discussion
3.1 Characterization of Si-B nanoparticles
In order to observe the morphology of Si-B oxide particles, a TEM sample of Si-B oxide particles is prepared by ultrasonic dispersion in ethanol medium. The morphology of the particles is shown in Fig. 2a. The size of Si-B oxide particles has a certain degree of dispersion. Particle size of most nanoparticles is about 200 nm.
The TEM image of composites with 6 wt% Si-B oxide particles is shown in Fig. 2b. After dispersed in EP matrix, the Si-B oxide particles became far smaller, with the size of 6 nm, and the organic/inorganic interface is not clear. It indicates that the compatibility between Si-B oxide particles and EP is extremely well. The reason is that some organic structures remain on the surface of Si-B oxides synthesized by Si and B organic monomers, which increases the compatibility with organic matrix. Because of the small particle size and invisible agglomeration, single nanoparticle can only be observed in the very thin section of TEM sample. Figure 3 shows the dispersion of nanoparticles in a wide range, the nano-dispersed phase cannot be observed from a larger angle of view. Figure 4 shows the surface distribution of Si and B elements. It is obvious that the distribution of Si and B elements is uniform, indicating the uniformly dispersion of Si-B nanoparticles in EP matrix.
Figure 5a, b illustrate infrared spectra of phenyltriethoxysilane and tributyl borate, respectively. Figure 6 is the infrared spectrum of Si-B oxides. In Fig. 6, the residual weak C-H vibration peaks can be observed, such as C-H asymmetric stretching vibration peaks at 2975 cm−1, C-H stretching vibration peaks at 2928 and 2888 cm−1, methyl stretching vibration peaks at 1444 cm−1 and methylene stretching vibration peaks at 1482 cm−1. The results indicate that the reaction of ethoxy group on organosilicon monomer and butoxy group on organoborane monomer had been greatly consumed with few remnant. Thanks to the high hydrolysis activity of tributyl borate, the weak C-H vibration peaks are caused by the incomplete hydrolysis of phenyltriethoxysilane and a small amount of ethoxy residue. The hydrolysis degree of Si and B organic monomers meets the preset requirements. In addition, there is no obvious O–H stretching vibration absorption peak in the range of 3700–3200 cm−1 in Fig. 6, which indicates that the vast majority of O–H resulted from hydrolysis of Si and B organic monomers is eliminated by condensation reaction and Si-B oxides are finally formed.
3.2 Dielectric properties and the Cole–Cole plot
The relative permittivity is a parameter that characterizes the polarization of the medium. Figure 7 shows the relative permittivity of nanocomposites with different doping contents in the frequency range of 100–106 Hz. In Fig. 7, the relative permittivity of all the samples decreases with the increase of measurement frequency, which is consistent with the general law of dielectric physics [26]. In the low frequency region, polarization is easy to establish. In the high frequency region, the dipole polarization cannot keep up with the change of frequency gradually. The relative permittivity of Si-B/EP nanocomposites is lower than that of pure EP in the whole frequency range, and the relative permittivity of Si-B/EP nanocomposites decrease with the increase of doping content. The orientation polarization and interfacial polarization are the main factors affecting the relative permittivity. According to the Potential Barrier Model, the decrease of relative permittivity is related to the restriction of dipole movement in the interaction zone.
Figure 8 shows the electronic conductivity spectrum of Si-B/EP nanocomposites at room temperature. The electronic conductivity of the composites increases with the increase of frequency, which conforms to the general electronic conductivity law of polar polymers. It shows the conductivity caused by Ohmic conductivity and dipolar polarization. The polarization conductance increases with the increase of frequency. Interestingly, the conductivity does not change significantly with the variation of doping content. According to the mechanism of Potential Barrier Mode, the explanation can be given as follows: Although the transition zone formed by filling nanostructures is easier to form conductive channels [27], the polarization of space charge will be limited near the transition region, which reduces the current of interface polarization. The effective dipole moment and the dipole polarization current decrease due to the interaction between dipoles on nanoparticles and dipoles on macromolecule matrix. These comprehensive effects result in an inconspicuous change of the conductivity with the change of doping amount.
Figure 9 shows the loss tangent of Si-B/EP nanocomposites at room temperature. The dielectric loss of composites consists of conductivity loss and polarization loss [28]. From Fig. 8, it can be seen that the electronic conductivity of composites increases linearly with the increase of frequency. In Fig. 9, the loss tangent of composites changes little at low frequency because of the weak interfacial polarization. With the increase of frequency, the loss tangent of composites increases slowly, which is because that, the interface polarization can’t keep up with the change of electric field frequency in high frequency [29]. The increase of loss tangent is caused by the increase of polarization loss of dipole turning, which enlarges the difference of loss tangent with the increase of frequency.
In the full frequency range, the dielectric loss of nano-doped composites is lower or equal to that of pure EP materials, but in the high frequency region, the difference of dielectric loss between samples with different doping amounts becomes larger. The reason is that number of the interface increases due to the finite doping amount. However, the interaction between dipole on nanoparticles and dipole on macromolecular matrix will increase to a certain extent. In the low frequency region, the increase of interfacial polarization and the corresponding dielectric loss between composites with different doping amounts are limited. Moreover, the polarization of space charge nearby will be restricted by the transition region, which reduces the interface polarization, resulting in the loss reducing caused by interface polarization [26]. In high frequency range, the inhibiting effect of transition zone on dipole polarization becomes more and more obvious with the increase of frequency, which indicates that the difference of dielectric loss become large between composite samples with different doping content.
The relaxation behavior is an important property of polymers. In order to reduce the influence of space charge injected into electrodes and conductors on the analysis results, the electrical modulus (M*) is introduced. The electrical modulus is defined as the inverse complex dielectric permittivity (ɛ*). Electrical modulus is a physical quantity that characterizes the resistance of dielectric polarization to external electric field changes. In composites, the relaxation phenomenon in the low frequency region is attributed to the heterogeneity of the system. The advantage of using the electric modulus to identify bulk relaxation properties is that variations in the large values of permittivity and conductivity at low frequencies are minimized [30, 31]. The expression of the electric modulus is presented by the following equation:
Figure 10a shows the real part of the electric modulus (M′) and Fig. 10b shows the imaginary part of the electric modulus (M″) versus the frequency of the nanocomposites with different levels of particle loading. M′ increases with the increase of doping amount of nanoparticles. The increase of M′ indicates that the resistance of dielectric polarization to the change of external electric field becomes strong. It shows that the permittivity of the material changes slightly in the same change of external electric field. Combining with Fig. 7, the higher the loading of Si-B nanoparticles, the slower the permittivity decreases with the increase of frequency, which means that the slope of permittivity spectrum decreases. The result is consistent with the result of M′.
In order to further analyze the relaxation behavior of Si-B/EP nanocomposites, we introduce the following discussion. The Cole–Cole plot is used to denote a single Debye relaxation, while in practice the relaxation observed in the polymer usually shows extensive dispersion curves. These can be understood as a superposition of multiple individual Debye relaxations. Davidson and Cole recommend using the improved semicircle equation to represent electrolyte relaxation [32], this equation is expressed as:
where ɛ0 and ε∞ represent the static and the high frequency values of the permittivity, and β is a parameter that represents the unevenly dispersed relaxation times in the polymer. When β = 1, Eq. 2 represents a pure Debye process. In terms of the formalism of the electrical modulus, the Cole–Davidson model can be transformed as following [32]:
where β is a parameter, \( 0 < \beta \le 1 \)
Figure 11a–c are the Cole–Davidson arcs of Si-B/EP composites doped with 0 wt%, 4 wt% and 6 wt% Si-B oxides, respectively. The best fitting results of Cole-Davidson method are β0 wt% = 0.408, β4 wt% = 0.391 and β6 wt% = 0.374. The arc in the Davidson-Cole diagram corresponds to the relaxation process in the polymer. The decrease of parameter β with the increase of doping amount indicates that the polydispersity of the relaxation time is greater. As adding nanoparticles into EP matrix, more heterogeneous composite structures are formed. In addition, the inhibition of dipolar polarization relaxation induced by Si-B oxide particles will lead to an increase in the upper limit of relaxation time dispersion. Therefore, the β value decreases.
3.3 The space charge limited current
In terms of the theory of space charge limiting current, in low electric field, the electric current in the polymer follows Ohm’s law. When the electric field exceeds a certain field strength, the number of carriers will increase because of de-trapping of the trapped space charges, and the current increase. The volt-ampere curve shows a turning point, and the voltage of turning point is the aging threshold. When the voltage exceeds the aging threshold, the current goes into the space charge limited current area. In the space charge limited current area, the trap structure of the polymers plays an important role to the current. The slope of the curve in the space charge limited current region mainly reflects the de-trapping velocity of carrier. The larger the slope is, the faster the space charge de-trapping rate is [33].
As shown in Fig. 12, the aging threshold of the composites decreases with the increase of nanoparticles content, but it is higher than that of pure EP materials. The slope of space charge limited current region decreases with the increase of doping content. With the increase of doping amount, the number of traps in composites increases and the distribution is relatively homogeneous at low content, which leads to the increase of the number of trapped carriers. Therefore, the initial electric field intensity required for de-trapping and the aging threshold increase. As the doping content of nanoparticles increases, the trap density in the composites increases [34] and the average distance between traps decreases, with some of the traps overlapping. The result is to make the interaction between trap structures become larger and reduce the energy required for de-trapping and the aging threshold.
The Si-B oxide nanoparticles are dispersed in EP and form a large number of carrier traps in the organic/inorganic interface. The organic/inorganic interface increase with the increase of nanoparticle content. The greater the probability of interaction between the dispersed phases of nanoparticles, the greater the probability of producing deep traps [34]. When the carrier is trapped by a deep trap, it is difficult to jump out the trap and easy to form the space charge electric field. The more the doping amount, the stronger the space charge electric field. Besides, the space charge electric field will be more continuous with the more uniform dispersion. The space charge electric field will limit the migration of carriers and reduce the current slope in the space charge limited current region. In addition, the effective value of the external electric field will be more weakened as the increase of doping amount, which makes the de-trapping rate of carriers slow down.
3.4 The breakdown strength and Corona resistance
Figure 13 shows the two-parameter Weibull distribution of dielectric strength data of Si-B/EP composites at room temperature. With the increase of doping content of Si-B oxide, the breakdown field strength of Si-B/EP composites increases at first and then decreases, and reaches up to a maximum of 32.36 kV/mm when the doping content is 5 wt%. Compared with Si-B/EP composites, the breakdown field strength of pure EP materials was 31.23 kV/mm. Due to the uniform dispersion of the nanoparticles, the trap structures are uniformly distributed in the materials, which reduces the accumulation of space charges and makes the space charges electric field uniformly distributed. The upper result helps to reduce the electric tree caused by the uneven electric field and improve the breakdown field strength [33]. When the content of nanoparticles further increases, the probability of interaction between the dispersed phases of nanoparticles will increase. Therefore, the trap structures inside the material increase sharply and the average distance between traps is shortened, which make the initiation of electrical tree become easier [35]. Therefore, the breakdown field strength decreases.
Figure 14 shows the relationship between corona resistant life and doping content of Si-B/EP composites at room temperature and power–frequency. The corona resistant life increases at first and then decreases with the incremental addition of nanoparticles. When nanoparticle content is 6 wt%, the corona resistant life of Si-B/EP composites reaches to 17.6 h, while that of pure EP is only 2.1 h.
There are considerable carrier traps in the interface between Si-B nano-oxide particles and EP. They capture carriers and form space charge electric field which will hindere the migration of charged particles produced by air ionization [36]. Therefore, the particles not only have excellent corona resistance, but also have shielding effect to protect EP matrix due to the formation of space charge electric field, which make the corona corrosion rate of EP matrix slow down. In addition, even when nano-oxide particles are exposed on the surface of polymer, oxides protective layer will be formed, which can prevent charged particles from bombarding the polymer matrix. The air ionization around electrodes under corona action will produce ozone and other gases, which will cause the oxidative degradation of polymer matrix. Because of the barrier effect of nano-oxide protective layer, the oxidative degradation will be prevented. Moreover, the nanoparticles dispersed in the polymer can also prolong the path of carrier migration in the composites, that is to say, reduce the carrier mobility. All these are the reasons for the improvement of corona resistant life of Si-B/EP composites.
Figure 13 shows that the breakdown field strength of Si-B/EP composites begins to decrease when the doping content of Si-B exceeds 5 wt%. When the doping content reaches 7 wt%, the breakdown field strength of Si-B/EP composites decreases to 28.77 kV/mm. That is to say, in this experiment, the breakdown field strength of composites has a significant impact on the corona resistant life. With the decrease of breakdown field strength, the corona resistance life of composites is shortened.
Figure 15a, b show that corona breakdown occurs at the location of electric field content at the edge of the electrode. The corona resistance life of pure EP material is 2.1 h, and the corona breakdown point has a wide range of corona erosion. In addition, a large number of polymer residues adsorbed on the surface of EP around the corona breakdown point, due to the decomposition splash caused by corona erosion. The corona resistance life of Si-B/EP nanocomposites doped with 6 wt% is 17.6 h. The corona breakdown point has a relatively small corona erosion range. The amount of polymer residues adsorbed on the surface of composite materials is also relatively less. This indicates that their corona corrosion processes are different. For pure EP, because there’s no nanoparticles doped, corona erosion will act directly on EP matrix and bombards continuously until breakdown. Because of the high decomposition temperature of nanoparticles, it can absorb and scatter the energy of corona bombardment. Not only the inorganic phase itself has better corona resistance, but also the shielding effect of space charge electric field formed by trapped carriers in the organic/inorganic interface can protect the surrounding organic matrix. Therefore, the corona resistance of the composite material is enhanced.
4 Conclusions
In this paper, Si-B oxides were designed and synthesized. The Si-B/epoxy nano-composites have been investigated. The dielectric constant and dielectric loss of Si-B/epoxy nano-composites decrease gradually with the increase of Si-B nanoparticles content. It is interesting that the conductance does not change significantly with the increase of doping amount. The dielectric relaxation behavior of composites was studied by analyzing the Cole Davidson arc. The asymmetric distribution of relaxation time becomes wider with the increase of filler loading. As the dipole interaction in the interface region widened the relaxation time distribution. The results indicate that the interaction zone around Si-B nano-particles plays an important role in the dielectric constant, dielectric loss and conductance. With the increase of filler loading, the trap density in the composite increases and the interaction between traps becomes larger which reduces the de-trapping energy and the electric aging threshold. Meanwhile, the concentration of deep traps increases. The repulsion effect of space charge electric field becomes stronger, and the protective effect of nanoparticles on EP matrix becomes better. However, due to the decrease of dielectric strength, the corona resistance would not been further improved. When the doping content was 6 wt%, the maximum value was 17.6 h, which was 8.38 times that of pure EP material.
References
A. Bouzidi, K. Omri, W. Jilani, H. Guermazi, I.S. Yahia, J. Mater. Sci. 29, 5908 (2018)
B. Zhang, W. Gao, P. Chu, Z. Zhang, G. Zhang, J. Mater. Sci. 29, 1964 (2017)
H. Gu, C. Ma, J. Gu, J. Guo, X. Yan, J. Huang, Q. Zhang, Z. Guo, J. Mater. Chem. C. 4, 5890 (2016)
K. Prabakaran, S. Mohanty, S.K. Nayak, J. Mater. Sci. 25, 4590 (2014)
Y. Xiong, X. Lü, J. Polym. Res. 17, 273 (2009)
C. Wang, M. Zhao, J. Li, J. Yu, S. Sun, S. Ge, X. Guo, F. Xie, B. Jiang, E.K. Wujcik, Y. Huang, N. Wang, Z. Guo, Polymer 131, 263 (2017)
H.-P. Cong, X.-C. Ren, P. Wang, S.-H. Yu, Energy Environ. Sci. 6, 1185 (2013)
Z. He, W. Dai, J. Yu, L. Pan, X. Xiao, S. Lu, N. Jiang, J. Polym. Res. 21, 595 (2014)
X. Zhang, Y. Shen, B. Xu, Q. Zhang, L. Gu, J. Jiang, J. Ma, Y. Lin, C.W. Nan, Adv. Mater. 28, 2055 (2016)
Z. Hong, L. Zhe, F. Wang, J. Mater. Sci. 52, 5048 (2017)
R. Pal, M.J. Akhtar, K.K. Kar, JOM 70, 1295 (2018)
Z. Wang, Y. Cheng, M. Yang, J. Huang, D. Cao, S. Chen, Q. Xie, W. Lou, H. Wu, Composite B 140, 83 (2018)
M. Kurimoto, Y. Yamashita, T. Yoshida, T. Kato, T. Funabashi, Y. Suzuoki, IEEE Trans. Dielectr. Electr. Insul. 25, 1022 (2018)
X. Wang, Q. Chen, H. Yang, K. Zhou, X. Ning, J. Mater. Sci. 29, 12765 (2018)
H. Yong, G. Du, C. Nan, Compos. Sci. Technol. 124, 36 (2016)
A. Bouzidi, K. Omri, W. Jilani, H. Guermazi, I.S. Yahia, J. Inorg. Organomet. Polym Mater. 28, 1114 (2017)
K. Kumar, P.K. Ghosh, A. Kumar, Composite B 97, 353 (2016)
G. Iyer, R.S. Gorur, A. Krivda, IEEE Trans. Dielectr. Electr. Insul. 19, 310 (2012)
M. Gao, P. Zhang, F. Wang, L. Lin, Z. Li, in Annu. Rep.—Conf. Electr. Insul. Dielectr. Phenomena, CEIDP (2013), pp. 234–237
B.M.A. Desai, P. Mishra, N.J. Vasa, R. Sarathi, T. Imai, Micro Nano Lett. 13, 1280 (2018)
L. Chen, X. Pan, D. Zheng, Y. Gao, X. Jiang, M. Xu, H. Chen, Nanotechnology 21, 345201 (2010)
T.T.X. Hang, N.T. Dung, T.A. Truc, N.T. Duong, B.V. Truoc, P.G. Vu, T. Hoang, D.T.M. Thanh, M.G. Olivier, Prog. Org. Coat. 79, 68 (2015)
M. Salami-Kalajahi, V. Haddadi-Asl, S. Rahimi-Razin, F. Behboodi-Sadabad, H. Roghani-Mamaqani, M. Najafi, Int. J. Polym. Mater. Polym. Biomat. 62, 336 (2013)
IEC 60343-1991, Recommended Test Methods for Determining the Relative Resistance of Insulating Materials to Breakdown by Surface Discharges (1991)
S.T. Li, G.L. Yin, S.N. Bai, J.Y. Li, IEEE Trans. Dielectr. Electr. Insul. 18, 1535 (2011)
Z. Wu, S. Gao, L. Chen, D. Jiang, Q. Shao, B. Zhang, Z. Zhai, C. Wang, M. Zhao, Y. Ma, X. Zhang, L. Weng, M. Zhang, Z. Guo, Macromol. Chem. Phys. 218, 1700357 (2017)
M. Khan, A.A. Khurram, T. Li, T. Zhao, T. Subhani, I.H. Gul, Z. Ali, V. Patel, J. Mater. Sci. Technol. 34, 2424 (2018)
X. Huang, C. Zhi, P. Jiang, D. Golberg, Y. Bando, T. Tanaka, Adv. Funct. Mater. 23, 1824 (2013)
Z. Wang, Y. Cheng, M. Yang, J. Huang, D. Cao, S. Chen, Q. Xie, W. Lou, H. Wu, Composite B 140, 83 (2018)
A.A. Bakr, A.M. North, G. Kossmehl, Eur. Polym. J. 13, 799 (1977)
G.M. Tsangaris, G.C. Psarras, N. Kouloumbi, J. Mater. Sci. 33, 2027 (1998)
J.W. Zha, Z.M. Dang, T. Zhou, H.T. Song, G. Chen, Synth. Met. 160, 2670 (2010)
X. Wang, Y. Fan, H. Chen, R. Yang, W. Zhao, J. Mater. Sci. 28, 12795 (2017)
D.-L. Yuan, D.-M. Min, Y. Huang, D.-R. Xie, H.-Y. Wang, F. Yang, Z.-H. Zhu, X. Fei, S.-T. Li, Acta Phys. Sin. 66, 097701 (2017)
P. Preetha, M.J. Thomas, IEEE Trans. Dielectr. Electr. Insul. 18, 1526 (2011)
H. Shi, L.Z. Liu, L. Weng, W.W. Cui, X.S. Zhu, Polym. Compos. 37, 763 (2016)
Acknowledgements
This work was financially supported by the Fundamental Research Fundation for Universities of Heilongjiang Province (LGYC2018JC033), the National Natural Science Foundation of China (No. 51277044).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhao, W., Fan, Y. & Chen, H. Dielectric properties and corona resistance of Si-B/epoxy nano-composites. J Mater Sci: Mater Electron 30, 16298–16307 (2019). https://doi.org/10.1007/s10854-019-02000-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10854-019-02000-w