Introduction

The topic of severe plastic deformation (SPD) processes is attracting many researchers because of the exceptional enhancement of the properties of metals and alloys that can be achieved by simply applying very large plastic strains. The most significant change in properties is the strength, which may be increased tenfold by FALEP. Such high strength results from the extreme level of grain fragmentation inherent to ultrafine-grained (UFG) or even nano-structured metals induced by large strains. The emergence of modern research on SPD can be traced to 1946, when Bridgman received the Nobel prize for his high-pressure experiments, among which the high-pressure torsion (HPT) method of SPD was introduced by applying extremely large strains on metals under high pressure [1]. The topic of SPD research gained new interest when Segal proposed the equal channel angular pressing (ECAP) process [2]. Since then, SPD research has been a stimulating topic of materials science; see a recent review of the history of the development of SPD research in Ref. [3].

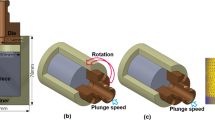
The different effects of SPD on the metallurgical state of alloys have been examined in detail. However, the continuum solid mechanics descriptions of SPD are less developed. The present work examines the mechanics of three ECAP-like angular extrusion processes: the ECAP, NECAP (non-equal channel angular extrusion), and the FALEP processes (friction-assisted lateral extrusion process), with particular attention to FALEP. Only the case of perpendicular entrance and exit channels is examined. Schematics of these processes are presented in Fig. 1, and their main characteristics are discussed below.

Figure 1
figure 1

Schematic presentation of the ECAP, NECAP, and FALEP processes.

Full size image

ECAP In ECAP, the entry and exit channels have equal cross sections. A single pressing force is applied along the axis of the entry channel in the simplest configuration [4], while a second resisting force along the extrusion axis of the exit channel is sometimes applied to provide back-pressure in more advanced ECAP equipment [5, 6]. The back-pressure adds a compressive stress component across the plane of maximum shear at the channel intersection and throughout the material as it moves through the exit channel. The sample fills the entry channel completely ahead of the punch, increasing the hydrostatic pressure, especially when back-pressure is applied, making it easier to deform difficult-to-work materials. The friction forces between the sample and the channel hinder the process and lead to gradients in the strain fields [7]. Friction can be reduced by die-walls that are moving with the sample [8,9,10,11]. It is possible to deform bar samples without length limitation in the ECAP-Conform process [12, 13]. The possibility of upscaling ECAP without significant change in the properties has been shown by Mathaudhu et al. [14] and Frint et al. [8].

NECAP In non-equal channel angular pressing, the entry and exit channels have different cross sections, with the exit channel being smaller. The strain imposed in a single pass is larger compared to ECAP; however, higher pressures are required. One advantage of NECAP compared to ECAP is that there is no need for back-pressure, because the hydrostatic stress is higher in the plastic deformation zone due to the reduced diameter of the outgoing channel. NECAP experiments were presented in 2009 by Tóth et al. [15], followed by an analysis of the strain state in Hasani et al. [16].

FALEP The friction-assisted lateral extrusion process was proposed in 1992 [17, 18]. Since then, FALEP has been further applied in studies by Kobune and Itoh [19], Vu et al. [20] and by Pariyar et al. [21]. In the FALEP process two punches are used, one to apply compressive force in the entry channel–like in ECAP–while a second punch translates a sliding anvil, applying a shear force by friction at the bottom of the sample as it moves in the exit channel. There is no sliding between the side anvil and the sample, as illustrated in Fig. 1. The combination of compression and shear within the sample enables plastic flow, with each stress component being lower than the flow stress of the material.

Previous analytical approaches addressed ECAP and NECAP, and they are briefly reviewed here.

The simplest plastic deformation approach for ECAP was proposed by Segal [4] which considers that simple shear localises in a narrow band around the intersection plane of the two channels. This approach simpliflies calculations and was adopted in many studies (examples: Beyerlein et al. [22], Furukawa et al. [23], Estrin and Vinogradov [24]). However, because of the thin layer, the strain rate should be very large, which is physically questionable. Indeed, observations on scribed flow lines showed that the deformation can extend into a large region at the intersection area of the channels [5, 25,26,27].

Tóth et al. [28] introduced a flow line function for 90° ECAP, from which the velocity gradient field could be obtained analytically. They applied the flow line approach for texture predictions, with good agreement with experiments. Such modeling was also applied for a 120° ECAP die [29], for NECAP [15, 16], and also for T-ECAP [30]. Hasani and Toth [25], as well as Wagner et al. [31], proposed an extension of the original 90° approach of Tóth et al. [28] for arbitrary ECAP die angles.

Beyerlein and Tomé [32] introduced a fan-type plastic deformation zone (PDZ) in ECAP, with circular flow lines within the PDZ, and determined the velocity gradient field and the shape changes of an initial spherical material element. The application of this model showed a gradual rotation of the crystallographic texture as a function of the angle of the fan with respect to the ideal shear model.

Paydar et al. [33] examined 90° ECAP using an upper-bound analysis by minimizing the total energy that contained the plastic and the friction energies. They applied this only on a fan-shaped area for the plastic zone, assuming a circular velocity field. They concluded that the size of the fan depends on the friction only, for zero friction, the zone is only the ideal shear plane, while for significant friction, it can extend to the whole corner region of the die. The experimental verification was done on commercially pure aluminum, using a very short sample, and without back-pressure.

Hasani and Tóth [34] also developed a fan-type PDZ approach for 90° ECAP by solving the flow line function. They found that the flow lines must be elliptical within the PDZ, not circular. In their approach, the flow lines continued without discontinuity at the boundaries of the PDZ, contrary to the modeling of Beyerlein and Tomé [32] and Paydar et al. [33], where there is a discontinuity in the velocity gradient. Therefore, it is possible that the flow lines are rounded, the shear zone is large, while the simple shear state is valid within the deformation zone (see Eq. (12) in Hasani and Tóth [34]. This particular result will be exploited in the present calculations as well.

There is only one analysis for FALEP, carried out by Nakamura et al. [17], which is an upper-bond calculation. In that work, it was assumed that there is no pressure gradient in the inlet channel and that the shear stress applied by the shear-anvil is equal to the shear flow stress of the material. Apart from these two very simplistic assumptions, they analyzed the geometry defined by the relation: \(\frac{h}{a} + 0.5 \cdot \frac{a}{b} = 1\), where a and b are the diameters of the incoming and outgoing channels, respectively, and h is the sample height. Unfortunately, this restriction implies that h becomes negative for \(\frac{a}{b} > 2,\) so the analysis is invalid for larger a/b ratios.

In the present work, continuum mechanical descriptions of the FALEP process are developed for the elastic and plastic stress and strain states. The effect of friction on the necessary loading forces is also incorporated and compared for ECAP, NECAP, and FALEP. It is shown that FALEP has very significant advantages with respect to classical rolling and other SPD processes, so it shall be the prefered candidate for new processes in modern sheet production.

Plasticity analysis for FALEP

In the following, we first analyze the strain and stress states in the plastic zone. An elastic analysis is also carried out above the plastic zone to properly account for the effect of friction. Two reference systems are used: one fixed to the die (x, y, z) and another defined on the theoretical shear plane (xʹ, yʹ, zʹ), as defined in Fig. 2.

Figure 2
figure 2

a The definitions of the two reference systems used here for angular extrusion with perpendicular channels. The dashed area is the assumed plastic deformation zone. b Schema for the angles in the shear strain formula.

Full size image

Plastic strain state

There is a remarkable similarity between the strain states that develop during ECAP, FALEP, and NECAP. For each, we adopt the hypothesis that simple shear takes place in a band along the plane of intersection between the two channels, as indicated in Fig. 2a. The thickness of the band is not a parameter in the equations that follow. This approximation of the deformation zone is borrowed from the flow-line model of Hasani and Tóth [34] described above for ECAP, where a homogeneous simple shear was described analytically by elliptical flow lines. It is assumed that similar plastic deformation mode can take place also in NECAP and FALEP.

Angular extrusion is a large strain process, so we first define the plastic deformation gradient tensor \({\underline{{\underline{F}}}}^{\prime }\), which describes the deformation of an incompressible, infinitesimally small material element as simple shear by \(\gamma\), in the xʹ-yʹ-zʹ reference system (note that \(\gamma\) is negative):

$${\underline{{\underline{F}}}}^{\prime } = \left( {\begin{array}{*{20}c} 1 & \gamma & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right).$$
(1)

Then \({\underline{{\underline{F}}}}^{\prime }\) is expressed in the x-y-z testing reference system with the help of the rotation matrix \({\underline{{\underline{R}}}}\),

$${\underline{{\underline{R}}}}_{{{x}^{\prime } \to {x}}} = \left( {\begin{array}{*{20}l} {{\text{cos}}\beta } \hfill & { - {\text{sin}}\beta } \hfill & 0 \hfill \\ {{\text{sin}}\beta } \hfill & {{\text{cos}}\beta } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right)$$
(2)

using the transformation operation \({\underline{{\underline{F}}}} = {\underline{{\underline{R}}}} \cdot {\underline{{\underline{F}}}}^{\prime } \cdot {\underline{{\underline{R}}}}^{t }\):

$${\underline{{\underline{F}}}} = \left( {\begin{array}{*{20}l} {1 - \gamma {\text{sin}}\beta \,{\text{cos}}\beta } \hfill & {\gamma {\text{cos}}^{2} \beta } \hfill & 0 \hfill \\ { - \gamma {\text{sin}}^{2} \beta } \hfill & {1 + \gamma {\text{sin}}\beta \,{\text{cos}}\beta } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right).$$
(3)

The use of \({\underline{{\underline{F}}}}\) is to get the deformed length \({\text{d}}{\user2{q}}\) of a small material vector from its \({\text{d}}{\user2{Q}}\) undeformed state by the transformation: \({\text{d}}{\user2{q}} = {\underline{{\underline{F}}}} \cdot {\text{d}}{\user2{Q}}\). The deformation gradient tensor is very useful for calculating changes in the shape of a material element after it passes through the die (see later below). The shear strain value can be readily expressed in terms of the incoming and outgoing angles of a material flow line that crosses the shear plane [35] (see Fig. 2b):

$$\left| \gamma \right| = {\text{ctg}}\alpha + {\text{ctg}}\beta .$$
(4)

For 90° dies, this formula reduces to [16]:

$$\left| \gamma \right| = \frac{a}{b} + \frac{b}{a}.$$
(5)

The plastic deformation gradient Eq. (3) can be rewritten using only the geometrical parameters of the two channels:

$${\underline{{\underline{F}}}} = \left( {\begin{array}{*{20}l} 2 \hfill & { - a/b} \hfill & 0 \hfill \\ {b/a} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right).$$
(6)

The inverse of \({\underline{{\underline{F}}}}\) is:

$${\underline{{\underline{F}}}}^{ - 1} = \left( {\begin{array}{*{20}l} 0 \hfill & {a/b} \hfill & 0 \hfill \\ { - b/a} \hfill & 2 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right).$$
(7)

Once \({\underline{{\underline{F}}}}\) and \({\underline{{\underline{F}}}}^{ - 1}\) are known, the Eulerian finite deformation tensor can be readily constructed by its definition:

$${{\underline{{\underline{E}}}}}_{E} = \frac{1}{2}\left( {{{\underline{{\underline{I}}}}} - {{\underline{{\underline{F}}}}}^{{ - 1^{t} }} {{\underline{{\underline{F}}}}}^{ - 1} } \right) = \frac{1}{2}\left( {\begin{array}{*{20}l} {1 - \left( {b/a} \right)^{2} } \hfill & {2b/a} \hfill & 0 \hfill \\ {2b/a} \hfill & { - \left( {a/b} \right)^{2} - 3} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right) .$$
(8)

For the special cases when \(a/b\) = 1 (ECAP):

$${{\underline{{\underline{E}}}}}_{E} = \left( {\begin{array}{*{20}c} 0 & 1 & 0 \\ 1 & { - \,2} & 0 \\ 0 & 0 & 0 \\ \end{array} } \right),$$
(9a)

and when \(a/b \gg 1 \left( {\text{extreme FALEP}} \right) {\text{with }} \gamma \cong - \frac{a}{b}\):

$${{\underline{{\underline{E}}}}}_{E} \cong \frac{1}{2}\left( {\begin{array}{*{20}l} 1 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & { - \left( {a/b} \right)^{2} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right)\quad \left( {a/b \gg 1} \right).$$
(9b,c)

Note that for extreme FALEP, when \(a/b \gg 1\), the deformation mode slightly differs from simple shear. For simple shear, the Eulerian strain tensor is:

$${{\underline{{\underline{E}}}}}_{E} \left( {\text{simple shear}} \right) = \frac{1}{2}\left( {\begin{array}{*{20}l} 0 \hfill & \gamma \hfill & 0 \hfill \\ \gamma \hfill & { - \gamma^{2} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right).$$

Shape change due to plastic strain in FALEP/ECAP/NECAP

An important aspect of a large strain experiment is the shape change produced by the deformation. Frequently, the initial grain shape is elongated already in the x or y direction, so in the following, we consider this general case. The equation of such an initial ellipse in the X–Y plane of testing is the following:

$$\left( {\frac{X}{{A_{0} }}} \right)^{2} + \left( {\frac{Y}{{B_{0} }}} \right)^{2} = 1,$$
(10)

where \(A_{0}\) and \(B_{0}\) are the long and short half-axes of the ellipsoid. During shearing within an angular die, this initial ellipsoid is transformed into another shape. The equation of the new ellipse can be calculated using the deformation gradient tensor. F transfers an initial vector dQ(X,Y,Z) into its deformed state dq(x,y,z). For a vector (X,Y,Z) in the reference configuration, the deformed vector coordinates (x,y,z) after extrusion can be determined by:

$$\left( {\begin{array}{*{20}c} x \\ y \\ z \\ \end{array} } \right) = \left( {\begin{array}{*{20}l} 2 \hfill & { - a/b} \hfill & 0 \hfill \\ {b/a} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right)\left( {\begin{array}{*{20}c} X \\ Y \\ Z \\ \end{array} } \right).$$
(11)

Using Eq. (10), this is rewritten as:

$$\left( {\begin{array}{*{20}c} x \\ y \\ z \\ \end{array} } \right) = \left( {\begin{array}{*{20}l} 2 \hfill & { - a/b} \hfill & 0 \hfill \\ {b/a} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right)\,\left( {\begin{array}{*{20}l} X \hfill \\ {B_{0} \sqrt {1 - \left( {\frac{X}{{A_{0} }}} \right)^{2} } } \hfill \\ 0 \hfill \\ \end{array} } \right).$$
(12)

This relation provides two equations:

$$x = 2X - \frac{a}{b}B_{0} \sqrt {1 - \left( {\frac{X}{{A_{0} }}} \right)^{2} } ,\quad y = \frac{b}{a}X.$$
(13a,b)

By eliminating X, we get the equation of the deformed ellipse:

$$x = 2gy - gB_{0} \sqrt {1 - \left( {g\frac{y}{{A_{0} }}} \right)^{2} } , {\text{where }} g = \frac{a}{b}.$$
(14)

The function \(y\left( x \right)\) can be expressed from this equation:

$$y\left( x \right) = \frac{{ \pm 2A_{0}^{2} x + g B_{0} A_{0} \cdot \sqrt {B_{0}^{2} g^{2} + 4A_{0}^{2} - x^{2} } }}{{\left( {B_{0}^{2} g^{2} + 4A_{0}^{2} } \right)g}}.$$
(15)

The values of the new large half axes and the orientation \(\varphi\) of the deformed ellipse are derived in Appendix 1:

$$A = \frac{{A_{0} B_{0} }}{\sqrt 2 }\sqrt {H + \sqrt {H^{2} - \frac{4}{{A_{0}^{2} B_{0}^{2} }}} } ,\,\,\,B = \frac{{A_{0} \cdot B_{0} }}{A}, {\text{where }} H = \frac{b}{{a^{2} B_{0}^{2} }} + \frac{4}{{B_{0}^{2} }} + \frac{{a^{2} }}{{b^{2} A_{0}^{2} }}.$$
(16a,b)
$$\varphi = - \frac{1}{2}{\text{arc}}\sin \left( {\frac{{4bA_{0}^{2} }}{{a\left( {B^{2} - A^{2} } \right)}}} \right).$$
(17)

Strain rate state in FALEP

The strain rate state for NECAP was examined by Hasani et al. [16]. Here, we recall the velocity gradient (\({\underline{{\underline{L}}}}\)) and the Eulerian strain rate tensor (\({\dot{\underline{\underline{\boldsymbol{\varepsilon}} }}} \)), expressed in the reference system (x, y, z) of Fig. 2a:

$${\underline{{\underline{L}}}} = \dot{\gamma }\left( {\begin{array}{*{20}l} {\sin \beta \cdot \cos \beta } \hfill & { - \cos ^{2} \beta } \hfill & 0 \hfill \\ {\sin ^{2} \beta } \hfill & { - \sin \beta \cdot \cos \beta } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right),~~~{\dot {{\underline{{\underline{\boldsymbol{\varepsilon}}}} }}} = \frac{{\dot{\gamma }}}{2}\left( {\begin{array}{*{20}l} {\sin 2\beta } \hfill & { - \cos 2\beta } \hfill & 0 \hfill \\ { - \cos 2\beta } \hfill & { - \sin 2\beta } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right).$$
(18a,b)

Here \(\dot{\gamma }\) is the shear strain rate on the intersection plane (note that it is negative), which is oriented at an angle β with respect to the horizontal channel. The components of these tensors can be rewritten using the channel dimensions a and b:

$${\underline{{\underline{L}}}} = \frac{{\dot{\gamma }}}{{a^{2} + b^{2} }}\left( {\begin{array}{*{20}l} {a \cdot b} \hfill & { - b^{2} } \hfill & 0 \hfill \\ {a^{2} } \hfill & { - a \cdot b} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right), {\dot {{\underline{{\underline{\boldsymbol {\varepsilon}}}} }}} = \left( {\begin{array}{*{20}l} {\dot{\varepsilon }_{{{\text{xx}}}} } \hfill & {\dot{\varepsilon }_{{{\text{xy}}}} } \hfill & 0 \hfill \\ {\dot{\varepsilon }_{{{\text{yx}}}} } \hfill & {\dot{\varepsilon }_{{{\text{yy}}}} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right),$$
(19a,b)
$${\text{where }} \dot{\varepsilon }_{{{\text{xx}}}} = - \dot{\varepsilon }_{{{\text{yy}}}} = - \dot{\gamma }\frac{a \cdot b}{{a^{2} + b^{2} }},{\text{ }} \dot{\varepsilon }_{{{\text{xy}}}} = \dot{\varepsilon }_{{{\text{yx}}}} = \dot{\gamma }\frac{{a^{2} - b^{2} }}{{2\left( {a^{2} + b^{2} } \right)}}.$$
(20a,b)

The ratio of the two primary strain rate components is:

$$\frac{{\dot{\varepsilon }_{{{\text{xy}}}} }}{{\dot{\varepsilon }_{{{\text{yy}}}} }} = \frac{1}{2}\left( {\frac{a}{b} - \frac{b}{a}} \right).$$
(21)

There is a particularity in Eq. (20b) above for the case of ECAP, where the shear components are zero. The reason is that the strain rate state is expressed in the x–y reference system where the simple shear state is represented by equal compression and tension Eq. (20a). At the same time, the same shear components of the velocity gradient are nonzero; they are equal and opposite, describing a pure rigid body rotation. These particularities of the ECAP deformation mode were examined already in Tóth et al. [28].

The stress state in FALEP

Here, we examine the Cauchy stress tensor for the case of FALEP, which is energy conjugate to the Eulerian finite strain tensor Eq. (8) [36]. For NECAP, the calculation process is similar and is detailed in Appendix 2.

As the die is open for the outgoing material flow, the \(\sigma_{{{\text{xx}}}}\) normal stress component can be taken zero in the plastic zone, so the stress tensor has the form:

$${\underline{{\underline{\sigma}}}} = \left( {\begin{array}{*{20}l} 0 \hfill & \tau \hfill & 0 \hfill \\ \tau \hfill & {\sigma _{{{\text{yy}}}} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\sigma _{{{\text{zz}}}} } \hfill \\ \end{array} } \right).$$
(22)

The deviatoric stress state is:

$$\underline{{\underline {S} }} = \underline{\underline{\sigma }} - \underline{\underline{\sigma }}_{h} , {\text{ where}}\,\,\underline{{\underline {\sigma} }}_{h} = \underline{\underline{I }} \cdot \frac{{\sigma_{{{\text{ii}}}} }}{3} = \underline{{\underline {I} }} \cdot \frac{{\sigma_{{{\text{yy}}}} + \sigma_{{{\text{zz}}}} }}{3}.$$
(23)
$$\underline{{\underline {S} }} = \frac{1}{3} \cdot \left( {\begin{array}{*{20}l} { - \sigma _{{{\text{yy}}}} - \sigma _{{{\text{zz}}}} } \hfill & {3\tau } \hfill & 0 \hfill \\ {3\tau } \hfill & { - \sigma _{{{\text{zz}}}} + 2\sigma _{{{\text{yy}}}} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & { - \sigma _{{{\text{yy}}}} + 2\sigma _{{{\text{zz}}}} } \hfill \\ \end{array} } \right).$$
(24)

Relation between stress and strain

We assume von Mises (isotropic) material behavior, for which the yield function is:

$$f\left( {\underline{{\underline {S} }} } \right) = \frac{1}{2}S_{{{\text{ij}}}} \cdot S_{{{\text{ij}}}} - \tau_{0}^{2} { = 0},\,\, \to f\left( {\underline{{\underline {S} }} } \right) = \frac{1}{2}\left( {S_{{{\text{xx}}}}^{2} + S_{{{\text{yy}}}}^{2} + S_{{{\text{zz}}}}^{2} + S_{{{\text{xy}}}}^{2} + S_{{{\text{yx}}}}^{2} } \right) - \tau_{0}^{2} { = 0,}$$
(25)

where \(\tau_{0}\) is the flow stress in simple shear. Using the associated flow rule for the strain rate component \(\dot{\varepsilon }_{{{\text{zz}}}}\), a relation is obtained between \(\sigma_{{{\text{yy}}}}\) and \(\sigma_{{{\text{zz}}}}\):

$$\dot{\varepsilon }_{{{\mathrm{zz}}}} = \dot{\lambda }\frac{\partial f}{{\partial S_{{{\mathrm{zz}}}} }} = \dot{\lambda }\frac{{ - \sigma_{{{\mathrm{yy}}}} + 2\sigma_{{{\mathrm{zz}}}} }}{9} = 0 \to \sigma_{{{\mathrm{zz}}}} = \frac{{\sigma_{{{\mathrm{yy}}}} }}{2}.$$
(26)

Therefore, the deviatoric and hydrostatic stress states are:

$$\underline{{\underline {S} }} = \left( {\begin{array}{*{20}l} { - \frac{1}{2}\sigma _{{{\text{yy}}}} } \hfill & \tau \hfill & 0 \hfill \\ \tau \hfill & {\frac{1}{2}\sigma _{{{\text{yy}}}} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right),\,\,\,\,\underline{{\underline {\sigma} }}_{h} = \left( {\begin{array}{*{20}l} {\frac{{\sigma _{{{\text{yy}}}} }}{2}} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {\frac{{\sigma _{{{\text{yy}}}} }}{2}} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\frac{{\sigma _{{{\text{yy}}}} }}{2}} \hfill \\ \end{array} } \right).$$
(27)

Substituting the deviatoric stress components Eq. (24) into the yield function Eq. (25), we obtain:

$$\sigma_{{{\text{yy}}}}^{2} + 4\tau^{2} { = 4}\tau_{0}^{2} .$$
(28)

A further relation can be found between the \(\sigma_{{{\text{yy}}}}\) and \(\tau\) stress quantities by using the associated flow rule for the \(\dot{\varepsilon }_{{{\text{yy}}}}\) and \(\dot{\varepsilon }_{{{\text{xy}}}}\) strain rate components:

$$\dot{\varepsilon }_{{{\text{yy}}}} = \dot{\lambda }\frac{\partial f}{{\partial S_{{{\text{yy}}}} }} = \dot{\lambda }\frac{{\sigma_{{{\text{yy}}}} }}{2},\,\,\,\,\dot{\varepsilon }_{{{\text{xy}}}} = \frac{{\dot{\gamma }}}{2} = \dot{\lambda }\frac{\partial f}{{\partial S_{{{\text{xy}}}} }} = \dot{\lambda } \cdot \tau .$$
(29)

The ratio of these two strain rates is:

$$\frac{{\dot{\varepsilon }_{{{\text{xy}}}} }}{{\dot{\varepsilon }_{{{\text{yy}}}} }} = \frac{2 \cdot \tau }{{\sigma_{{{\text{yy}}}} }}.$$
(30)

Now using Eq. (21), we obtain:

$$\frac{\tau }{{\sigma_{{{\text{yy}}}} }} = \frac{1}{4}\left( {\frac{a}{b} - \frac{b}{a}} \right).$$
(31)

Using Eqs. (28), (31), both Cauchy stress components can be expressed by the geometrical parameters a and b, and the simple shear yield stress, \(\tau_{0}\):

$$\sigma_{{{\text{yy}}}} = \frac{2}{{\sqrt {1 + \frac{1}{4} \cdot \left( {\frac{a}{b} - \frac{b}{a}} \right)^{2} } }} \cdot \tau_{0} ,\,\,\,\,\tau = \frac{{\tau_{0} }}{{\sqrt {1 + \frac{4}{{\left( {\frac{a}{b} {-} \frac{b}{a}} \right)^{2} }}} }}.$$
(32a,b)

It is interesting to notice that Eq. (32b) shows zero shear stress for the case of ECAP (when a = b). The reason of this result is that the corresponding shear strain component is zero in ECAP, so isotropic plasticity leads to zero shear stress. At the same time, some ECAP tooling possesses a bottom part that slides to reduce the effect of friction on the sample (for example; [8]), that is, the shear stress is zero. Increasing the shear stress artificially is not possible because the bottom punch must be in displacement control to account for volume constancy of the specimen, so the shear stress accommodates to the required value. In ECAP, the required value is actually zero. In FALEP, it is not: the shear stress can be calculated from the force applied on the punch and theoretically should be the value given by Eq. (32b).

Elastic analysis

In the upper part of the sample, the deformation is only elastic, so an elastic analysis is appropriate. The Cauchy stress and infinitesimal strain tensors for the case of a rigid die are:

$${\underline{{\underline{\sigma}}}} = \left( {\begin{array}{*{20}l} {\sigma _{1} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {\sigma _{2} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\sigma _{3} } \hfill \\ \end{array} } \right),~~~~~~{\underline{{\underline{\varepsilon}}}} = \left( {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {\varepsilon _{2} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right)~.$$
(33)

For elastic behavior, the stress and strain tensors are related by the elastic formula:

$$\sigma_{{{\text{ij}}}} = C_{{{\text{ijkl}}}} \cdot \varepsilon_{{{\text{kl}}}} ,$$
(34)

where \(C_{{{\text{ijkl}}}}\) is the elasticity tensor. Assuming isotropic elasticity, one can obtain from Eq. (34):

$$\sigma_{{{\text{xx}}}} = \sigma_{{{\text{zz}}}} = \left( {K - \frac{2}{3}G} \right) \cdot \varepsilon_{{{\text{yy}}}} ,\,\,\,\sigma_{yy} = \left( {K + \frac{4}{3}G} \right) \cdot \varepsilon_{{{\text{yy}}}} .$$
(35)

Here G is the shear modulus and K is the compressibility modulus. The latter can be expressed as a function of the Poisson number ν, and the Young modulus E:

$$K = \frac{E}{{3\left( {1 - 2v} \right)}}.$$
(36)

The two equations in (35) provide a relation between \(\sigma_{zz}\) and \(\sigma_{yy}\):

$$\sigma_{{{\text{zz}}}} = \frac{{K - \frac{2}{3}G}}{{K + \frac{4}{3}G}} \cdot \sigma_{{{\text{yy}}}} .$$
(37)

This relation shows that \(\sigma_{{{\text{zz}}}} < \sigma_{{{\text{yy}}}}\). For example, the ratio of \(\frac{{\sigma_{{{\text{zz}}}} }}{{\sigma_{{{\text{yy}}}} }}\) for aluminum is 0.516, not far from the perfectly plastic case, where it is 0.5 Eq. (26).

The effect of friction on the extrusion force

Equation (32a) shows the stress level of the compression needed for the plastic deformation in the plastic zone. However, the external compressive force for pushing the sample through the die is somewhat larger because of the friction of the sample with the die walls. Friction is expected at the lateral surfaces of the vertical part of the die (Fig. 2a), on four surfaces: two on the walls with normal vectors parallel to the x axis, and two walls that are oriented with their normal vectors parallel to the z axis.

The friction force operates on the sample in the direction of the y axis. It causes a progressive increase in the value of the necessary force to extrude the material. The stress state can be considered hydrostatic-elastic in the sample above the plastic zone because that part of the sample is completely constrained by four walls, by the compression punch, and by the sample itself. In the plastic part, however, there are only two walls that produce friction forces on the sample because there is no stress along the x axis. Within this part, the stress tensor is considered to be constant. The corresponding friction force, \(T_{{{\text{fr}}.}}^{a}\), applied on the sample in the plastic zone, is:

$$T_{{{\text{fr}}.}}^{a} = - 2\mu \cdot a \cdot b \cdot \sigma_{{{\text{zz}}}} \left( b \right) \to T_{{{\text{fr}}.}}^{a} = - \mu \cdot a \cdot b \cdot \sigma_{{{\text{yy}}}} \left( b \right).$$
(38)

\(\mu\) is the friction coefficient between the sample and the lateral surfaces of the die. Note that \(T_{{{\text{fr}}.}}^{a}\) is positive because \(\sigma_{{{\text{yy}}}}\) is negative. The equilibrium condition of the forces in the y direction on a horizontal material slice of thickness dy, in the upper part of the sample, leads to the following equation:

$$\sigma_{{{\text{yy}}}} \left( {y + {\text{d}}y} \right) \cdot a^{2} - \sigma_{{{\text{yy}}}} \left( y \right) \cdot a^{2} - 2\mu \cdot \sigma_{{{\text{yy}}}} \left( y \right) \cdot a \cdot {\text{d}}y - 2\mu \cdot \sigma_{{{\text{zz}}}} \left( y \right) \cdot a \cdot {\text{d}}y = 0.$$
(39)

Using Eq. (37):

$$\sigma_{{{\text{yy}}}} \left( {y + {\text{d}}y} \right) \cdot a^{2} - \sigma_{{{\text{yy}}}} \left( y \right) \cdot a^{2} - \sigma_{{{\text{yy}}}} \left( y \right) \cdot 4\mu \cdot \frac{{K + \frac{1}{3}G}}{{K + \frac{4}{3}G}} \cdot a \cdot {\text{d}}y = 0.$$
(40)

In differential form, Eq. (40) reads:

$$\sigma_{{{\text{yy}}}} \left( y \right) = \frac{p}{4\mu} \cdot \frac{{K + \frac{4}{3}G}}{{K + \frac{1}{3}G}} \cdot \frac{{{\text{d}}\sigma_{{{\text{yy}}}} \left( y \right)}}{{{\text{d}}y}}.$$
(41)

The integration of this equation leads to:

$$\sigma_{{{\text{yy}}}} \left( h \right) = \sigma_{{{\text{yy}}}} \left( b \right) \cdot e^{{\frac{4\mu }{a} \cdot \frac{{K + \frac{1}{3}G}}{{K + \frac{4}{3}G}} \cdot \left( {h - b} \right)}} .$$
(42)

Using Eq. (32a), we obtain the stress variation as a function of h:

$$\sigma_{{{\text{yy}}}} \left( h \right) = \frac{{2 \cdot \tau_{0} }}{{\sqrt {1 + \frac{1}{4} \cdot \left( {\frac{a}{b} - \frac{b}{a}} \right)^{2} } }} \cdot e^{{\frac{4\mu }{a} \cdot \frac{{K + \frac{1}{3}G}}{{K + \frac{4}{3}G}} \cdot \left( {h - b} \right)}} .$$
(43)

One can then obtain the compression force necessary for the extrusion:

$$T_{{{\text{comp}}.}} = \sigma_{{{\text{yy}}}} \left( h \right) \cdot a^{2} + \sigma_{{{\text{yy}}}} \left( b \right) \cdot \mu \cdot a \cdot b,$$
(44)

where the friction force acting on the bottom plastic zone is added from Eq. (38).

The force on the shear-punch can also be calculated from the shear stress by adding the friction force between the punch and the die:

$$T_{{{\text{shear}}}} = \tau \cdot a^{2} + \mu^{*} \cdot a^{2} \cdot \sigma_{2} \left( c \right).$$
(45)

Here \(\tau\) is from Eq. (32b), and \(\mu^{*}\) is the friction coefficient between the punch and the die at the bottom of the shear-punch (not with the sample).

During extrusion, a steady-state condition develops after an initial transition stage, during which the extruded material increases its yield stress by strain hardening as the material passes through the plastic zone. Therefore, for the \(\tau_{0}\) value one must take the shear yield stress belonging to the final hardened state after extrusion.

Discussion

The calculations presented above were developed for obtaining analytical formulas for the stress and strain rate states, the effect of friction, and the shape changes of an initial elliptic grain in the ECAP/NECAP/FALEP processes. Here, we first examine the main characteristics of the results with the help of suitable figures.

Important elements in metal forming are the amount of strain and the shape change that a material element is experiencing during its passage in the die. Figure 3 shows the shear strain, the large and small half axes of the ellipse, the aspect ratio, and the orientation of the axis of the ellipse with respect to the outgoing exit channel direction (the x axis) for an initially spherical grain with 60 µm diameter, as a function of the a/b ratio. The shear strain is limited to the value of 2 in ECAP for a 90° die. In NECAP, large a/b ratios cannot be reached; experiments for a/b = 2 are reported in Tóth et al. [15], Hasani et al. [16], Asgari et al. [37], Fereshteh-Saniee et al. [38], Hasani et al. [39]. However, FALEP can result in extremely large strains compared to ECAP or NECAP. As can be seen in Fig. 3, the shear strain is higher than 20 in one step, which is equal to 10 passes (!) in ECAP. To demonstrate that this is not only theoretical, Fig. 4 shows a half-extruded aluminium AA1050 sample produced at room temperature by FALEP in the LEM3 laboratory (Metz, France).

Figure 3
figure 3

Shear strain, dimensions, and orientation of an initially spherical grain as a function of the geometry of the ECAP/FALEP/NECAP process. The initial diameter of the grain is 60 µm.

Full size image
Figure 4
figure 4

Example of a FALEP half-extruded AA1050 sample, deformed to a shear of 20 in one step.

Full size image

One can see from Fig. 3 the changes in the initially spherical grains. The change in grain shape is tremendous in FALEP: the initial 60 µm diameter grain is elongated into an ellipse of 1200 µm × 3 µm for a/b = 20. Such a grain shape change promotes the grain fragmentation process. Indeed, the final fragmented grain size was about 0.6 µm and equiaxed in the Al sample shown in Fig. 4. This size is about the same order as the average thickness of the ellipse, which varies from 0 to 3 µm along the elongated ellipse. It is also demonstrated in Fig. 3 that the deformed ellipse aligns with the direction of the outgoing channel very close; at an a/b = 5, the ellipse large axis is within 1° oriented with the channel. Note that at this value of the die geometry, the orientation of the shear plane is actually larger; it is 11.3°.

It is also very important to compare the extrusion forces necessary to carry out FALEP vs NECAP. Equations (44) and (45) were developed to calculate the pressing and shear forces in FALEP. These relations were applied for the AA1050 alloy in Fig. 5a for the following selected case: \(\tau_{0} = 100{\text{ MPa}}, a = 20 {\text{ mm}}, b = { }2{\text{ mm}}, E = 70 {\text{ GPa}}, G = 25 {\text{ GPa}}, \nu= 0.33\). The sample length was left as a variable: \(h = 2 {\text{ mm}} - 50{\text{ mm}}\), for different friction coefficient values. As can be seen, the normal extrusion force gradually decreases as the sample slides through the die. This effect is due to the reduced surface area of the sample that has frictional contact with the die. Our experiments confirmed this effect. It is also natural that the extrusion force rapidly increases when friction is higher. It is interesting that the shear force remains nearly independent of both the friction and the die geometry (represented by a/b in Fig. 5a). The situation is completely different for NECAP, presented in Fig. 5b, for the same material parameters as for FALEP. In NECAP there is only a single compression force for which the formula is developed in Appendix 2, in Eq. (63). As can be seen in Fig. 5b, the extrusion forces are very high in NECAP with respect to FALEP; about five times higher! Therefore, by adding a relatively small shear force, there is a tremendous gain in FALEP in the normal extrusion force. This can be understood by analyzing the relation between the compression and shear stresses in the plastic zone; we obtain from Eq. (31) for a/b >  > 1:

$$\sigma_{{{\text{yy}}}} \cong 4\frac{b}{a}\tau .$$
Figure 5
figure 5

The compression and shear extrusion forces as a function of the sample length in the vertical channel for a FALEP and b NECAP of AA1050, including the effect of friction, for a channel section of 20 mm × 20 mm, and a/b = 10 (outgoing channel’s diameter is 2 mm).

Full size image

This relation shows that the compression stress depends strongly on the geometry, the b/a ratio. For example, for b/a = 1/10, the compression stress is 2.5 times smaller than the shear force, so it is mostly the shear stress that controls the deformation process. Indeed, we obtain for this case from the flow criterion of Eq. (28): \(\tau = 0.98 \cdot \tau_{0}\). Nevertheless, \(\sigma_{{{\text{yy}}}}\) cannot be too small because it is the compression force that produces the necessary friction force for achieving the non-sliding condition between the shear anvil and the sample. Indeed, using the Coulomb friction law, the non-sliding condition requires that \(\sigma \ge \tau\). Therefore, according to Eq. (28), the minimum compression stress in the deformation zone is: \(\sigma_{{{\text{yy}}}} \left( {{\text{min}}.} \right) = \sqrt{\frac{4}{5}} \tau_{0} = 0.894 \cdot \tau_{0}\). The normal extrusion stress on the punch is, of course, larger than that because of the friction of the sample with the die, expressed by Eq. (43).

Another way to show the efficiency of the FALEP process is to examine the extrusion forces as a function of the geometry of the die, the a/b ratio. This is displayed in Fig. 6, for different friction coefficient values. As can be seen, the extrusion force decreases very much by increasing the a/b ratio (Fig. 6a), while it increases constantly without the assistance of the shear force, which is the case for NECAP (Fig. 6b).

Figure 6
figure 6

The compression and shear extrusion forces as a function of the sample length in the vertical channel for a FALEP and b NECAP of AA1050, including the effect of friction, for a channel section of 20 mm × 20 mm, and for variable a/b ratio (sample length is h = 50 mm).

Full size image

The efficiency of the FALEP process can also be seen by the much higher plastic strain achieved in the workpiece compared to conventional forming processes, yet producing the same final shape. To demonstrate this, we compare FALEP to rolling. Starting with an initial thickness \(h_{0}\) of the workpiece and arriving at a thickness h of the rolled sheet, the equivalent strain in rolling is: \(e = \left( {2/\sqrt 3 } \right) \cdot {\text{ln}}\left( {h_{0} /h} \right)\), while in FALEP it is: \(e = \frac{{\left( {h_{0} /h + h/h_{0} } \right)}}{\sqrt 3 }\). Figure 7 shows the comparison of these two strains as a function of the ratio of the initial thickness to the final one (\(h_{0} /h\)). It can be seen, especially for high \(h_{0} /h\) ratios, that FALEP imposes a much higher strain in the material. To reach the UFG/nano steady state of a metal in SPD, a minimum equivalent strain of about 6 is required, which can be readily achieved in FALEP in a single step at \(h_{0} /h = 10\), while in rolling it cannot be reached, even for a thickness reduction of 30, as seen in Fig. 7. To achieve such a large strain by rolling, a reduction of \(h_{0} /h = 181\) would be required, which is difficult to reach, and requires multiple passes with inter-pass heat treatments.

Figure 7
figure 7

The equivalent strain in FALEP versus rolling as a function of the thickness reduction ratio.

Full size image

Finally, we compare the presented extrusion force predictions with some experimental results. We have conducted FALEP experiments at room temperature on commercially pure aluminum, OFHC copper, and a Nb-53%Ti alloy. The testing parameters, elasticity constants, and measured and predicted extrusion forces are presented in Table 1. As can be seen, the predicted extrusion forces agree well with the normal forces, while the shear forces are predicted to be about 20% lower level for the OFHC copper and the Nb-53Ti alloy. Note that the friction coefficients were not measured; they are estimated values. The lower predicted shear force is probably due to the extra friction taking place in the outgoing channel, which was made larger only beyond 5 mm distance from the exit point. Nevertheless, the overall agreements between measured and predicted extrusion forces are good, verifying that the equations developed here can be used to estimate the extrusion forces in the FALEP process.

Table 1 FALEP experimental testing parameters and measured as well as predicted extrusion forces for different materials (the latter in bold letters)
Full size table

Finally, concerning the assumed simple shear deformation mode in the present analysis, it is possible to verify it experimentally in an indirect manner: by measuring the crystallographic texture of the extruded sample. In all our texture measurement so far, we observed simple shear textures that were oriented parallel to the assumed shear plane (see, for example, in Abhishek Pariyar et al. [21] and Vu et al. [20]), demonstrating that the simple shear approximation is a reasonable one in the theoretical modeling.

Conclusions

FALEP is an SPD process that can be the preferred candidate for introduction in industry for forming strip and sheet. In order to help engineers in planning such installations, the basic mechanics of FALEP must be established, as has been done in the present work. The main conclusions of the analysis can be summarized as follows:

  1. 1.

    The mechanics of FALEP has been developed and expressed in terms of simple geometric parameters and the flow stress of the material.

  2. 2.

    Analyses of the shape and orientation of elliptical grain shapes resulting from FALEP have been developed.

  3. 3.

    Friction is a major factor that affects the extrusion forces; its role is expressed in analytical formulas for FALEP/NECAP/ECAP.

  4. 4.

    FALEP has been compared to ECAP and NECAP. It has been shown that FALEP requires about five times smaller extrusion force by adding only a small shear component.

  5. 5.

    The extrusion force in FALEP can be decreased by reducing the exit channel dimension (the a/b ratio).

  6. 6.

    The amount of equivalent deformation in a single step in FALEP is far greater than can be achieved by rolling, where multiple passes are required to obtain the same final sheet dimensions.