Introduction

Semiconducting materials showing photocatalytic activity by forming excitons in the visible electromagnetic spectrum are highly demanded nowadays [1,2,3,4,5]. In this regard mullite [6,7,8] and mullite-type materials of either O8 EMBO4 [9,10,11,12,13,14] and Schafarzikite [15,16,17,18], O9 [19,20,21] or O10 [22,23,24] type, especially the multiferroic O9 phase Bi2Fe4O9 [25,26,27,28], are widely used [29,30,31,32,33,34,35,36,37,38]. The respective pseudo-binary phase diagram Bi2O3–Fe2O3 has been repeatedly investigated [39,40,41,42,43,44,45], providing descriptions of some thermodynamically stable phases such as perovskite-type BiFeO3 [32, 43], mullite-type Bi2Fe4O9 [25, 28, 29, 31, 32, 34,35,36,37,38, 46,47,48] and sillenite-type Bi25FeO40 [40]. Additionally, the metastable perovskite-type (Bi1-xFex)FeO3 phases were reported [49, 50]. All these phases comprise of stereochemically active lone-electron pairs (LEP) of Bi3+ cation—a prerequisite for the stabilization of the mullite-type O9 phases [51,52,53,54,55,56,57]. These Bi-containing phases show band-gap energies between 2.1 and 2.8 eV either from direct or indirect transitions [58]. The mullite-type Bi2Fe4O9 exhibits an additional transition around 1.8 eV that lies with its energy as a middle band (EM) between the valence band energy (EV) and the conduction band energy (EC) [34]. Whereas the conduction band consists of OFe eg and TFe t2g orbitals of octahedral (superscript O) and tetrahedral (superscript T) coordinated Fe atoms, respectively, the middle band is formed by TFe eg and OFe t2g orbitals of the split Fe 3d band, aided by the electrons from the photo activated oxygen 2p orbitals. Additionally, the middle band could act as a recombination center annihilating the redox potential of the exitons [34]. Using the DASF method [59], the existence of this middle band has been demonstrated [58]. To avoid an increased recombination due to the middle-band d-d-transitions of the Fe-atoms, isostructural Bi2Al4O9 [19, 60,61,62,63] and Bi2Ga4O9 [19, 47, 64,65,66,67,68,69] compounds are also known to be photo-catalytically active [70,71,72]. Both these phases show band gap energies around 2.4–2.8 eV with a slightly higher energy for the gallium-containing phase [72, 73]. Of notes, the band-gap narrowing was found to be strongly correlated to the conduction band lowering [30] in the Bi2(Fe1-xAlx)4O9 solid solution. As this is most probably the case for both aluminum and gallium-containing phases, the latter one is of less applicational interest due to much higher costs of gallium. Instead, aluminum-containing mullite-type O9 phases would be interesting tuning their band gaps as a function of average crystallite-sizes.

A variety of methods can be used to synthesize the named compounds, e.g. hydrothermal process [74], chemical coprecipitation [31] or EDTA route [75, 76], sol–gel [36, 77, 78], combustion [79] or solid state reaction methods [41] and melt processes for single crystals [61, 80, 81]. All these methods usually lead to thermodynamically stable materials providing an average crystallite size (ACS) in the micro-crystalline (MC, bigger than ~ 100 nm) or bigger nano-crystalline (NC, between ~ 4 and ~ 100 nm) range, but rarely in the smaller nano-crystalline or even quantum-crystalline (QC, smaller than ~ 4 nm) range [82]. Using the polyol method [83, 84], it has been shown that the formation of NC’s with controlled sizes is possible [30, 58]. However, in most cases, the formation of a given NC is accompanied by secondary phases such as binary oxides, perovskites or sillenites [49, 50, 58]. This is, on the one hand, advantageous as the simultaneous formation of different phases enables a well distributed appearance of heterojunctions [30] that supports the photo-catalytic performance. On the other hand, such concomitant multi-phase formation should be avoided to systematically follow the performance intrinsically associated with crystal-chemico-physical parameters of a given phase. As such, a systematic study of the reaction precursors formed at an early stage of the phase formation and their transformation to the final product is investigated for mullite-type Bi2Al4O9, leading to phase-pure samples with ACS smaller than 25 nm.

Experimental

Synthesis

For the synthesis of the precursor phases Bi(NO3)5·5H2O and Al(NO3)3·9H2O or Fe(NO3)3·9H2O were used 20 g of the stoichiometric mixtures were finely ground in an agate mortar and, after transferring to a 200 mL beaker, 40 drops (~ 2.0 g) of glycerin (1,2,3-propantriol) were added. The beakers with the mixtures were placed in a fume hood in a hot oil bath at 390 K (Al, Al/Fe) or 380 K (Fe) under magnetic stirring. Within a few minutes, the mixtures first liquify due to the solubility of the metal nitrates in glycerin and the release of crystal water, then releasing NOx, before they solidify again in foam type bubbles. Solidification of the aluminum-containing endmember took a few minutes after NOx releases, whereas the iron-containing sample solidified immediately during NOx outgassing. Mixed samples (Al/Fe) of the solid solution between both endmembers were synthesized accordingly. The dry foams were further heated at 470 K for 2 h (Al, Al/Fe) or 420 K (Fe), before they were ground into fine powders. This fine powder is designated as nano-crystalline bismuth metalate precursor (BMO-ncP). Parts of these samples were heated in a Pt-crucible with a heating rate of 10 K/min to 870 K and then immediately cooled down by taking the crucible out of the furnace (1) kept at 870 K for ½ h (2) or heated up to 970 K and kept there for ½ h (3). The resulting products are further called (1) quantum-crystalline bismuth metalate precursor (BMO-qcP), (2) quantum-crystalline bismuth metalate mullite-type (BMO-qcM) and (3) nano-crystalline bismuth metalate mullite-type (BMO-ncM), where the M in BMO will be replaced by an A for the aluminum endmember, F for the iron endmember and AFx for Bi2(Al1-xFex)4O9 composition with a respective x showing the iron content 0.x. An overview over the synthesized samples is given in Table 1

Table 1 Synthesized samples and their abbreviations
Full size table

Room-temperature X-ray diffraction

The measurements of freshly prepared samples were carried out at ambient condition in a range between 5 and 85° 2θ with a step size of 0.0149° and a data collection time of 4 s/step. X-ray powder diffraction (XRPD) data were collected on a Bruker D8 Discover diffractometer in Bragg–Brentano geometry equipped with Cu radiation and a LynxEye X-ET detector discriminating all other radiation contributions than CuKα1,2 and minor parts of CuKβ. The fundamental parameter approach, where the fundamental parameters were fitted against a LaB6 standard material, was applied for the Rietveld refinements using “DiffracPlus Topas” software version 4.2 or 6 (Bruker AXS GmbH, Karlsruhe, Germany). For the determination of the micro-strain versus average crystallite size behavior of Bi2Fe4O9, respective parameters were Rietveld refined from data obtained and provided by Kirsch et al. [58].

To obtain diffraction data suitable for the calculation of the respective atomic pair-distribution-functions (PDF), samples were placed in a borosilicate glass capillary of 0.3 mm outer diameter and 0.01 mm wall thickness. They were mounted on a Stoe Stadi-MP diffractometer (Stoe & Cie. GmbH, Darmstadt, Germany) in Debye–Scherrer geometry. Homogeneous irradiation of the powders was achieved through a sample spinner. Ge(111) monochromatized MoKα1 radiation was used for the measurement with a Mythen-1 K detector between 3 and 95° 2θ using a step size of 0.005°, and 11,484 s measurement time per data point, resulting in a total measurement time of 60 h for each pattern of the samples and the empty capillary, used to determine the background and capillary signals. From these measured data, the total scattering function S(Q) and the reduced pair distribution function G(r) were calculated using the program PDFgetX3 [85].

High-temperature X-ray diffraction

Temperature-dependent (TD) data measurements between 300 and 1000 K were carried out using a HTK-1200 N high-temperature chamber (Anton Paar GmbH, Graz, Austria) on a X’Pert Pro diffractometer (PANalytical B.V., Almelo; Netherlands) equipped with a divergence slit (0.25°), an anti-scatter slit (0.5°), a soller slit (0.04 rad) and a mask (10 mm) in the primary beam and with a soller slit (0.04 rad), a Ni-filter, as well as a X'Celerator detector system in the secondary beam. CuKα1,2 XRPD data were collected in a range of 5–60° 2θ with a step width of 0.0167°/step. Both TD measuring series were collected in 10 K steps, step time one minute, with 5 min equilibration time before the data collection starts. All Rietveld refinements were carried out using the “DiffracPlus Topas” software (Bruker AXS GmbH, Karlsruhe, Germany) using the implemented fundamental parameter approach for the description of the diffractometer profiles, determined using a LaB6 standard reference material and additionally validating the results against a Si standard reference material.

Thermal analysis

Simultaneous thermogravimetric analysis and differential scanning calorimetry (TGA/DSC) measurements were performed on a simultaneous TGA/DSC 3 + STAR e system (Mettler Toledo, Schwerzenbach, Switzerland). Approximately 10 mg of each polycrystalline sample was measured with a heating rate of 10 K/min from 298 to 1273 K against 10.0(1) mg Al2O3 (Corundum) as reference. Blank data were collected beforehand using 10 mg Al2O3 in both the reference and the sample crucible. Synthetic air (80 vol.% N2 and 20 vol.% O2) with a flow rate of 20 mL/min throughout the heating range was used. Data were normalized to the respective initial mass, and a drift correction was applied based on the reference measurement.

Band-gap determination and room-temperature UV/Vis spectroscopy

The UV/Vis diffuse reflectance measurements were obtained on a Shimadzu UV/Vis spectrophotometer UV-2600 equipped with an ISR-2600 plus two-detector integrating sphere. For background measurements, barium sulfate was used. The diffuse reflection spectrum measurement wavelength range was 190–850 nm, and data were collected in 1 nm steps. 80 repetitions were accumulated to obtain a highly noise reduced spectrum.

From UV/Vis reflectance spectroscopic data, the calculation of electronic band gap of a given semiconductor can be expressed as:

$$F\left( R \right) = B\left( {h\nu - E_{{\text{g}}} } \right)^{{\text{n}}}$$
(1)

where F(R) is the Kubelka–Munk absorption [86] calculated from the reflectivity R as F(R) = (1 − R)2/(2R), B is the absorption parameter, h is the Planck’s constant, ν is the frequency of light, and Eg is the bandgap energy [eV]. For plotting an expression as \(\left( {h\nu } \right)^{{\text{n}}}\) versus E, n is the nature of transition with n = 1/2, 2/3, 2 or 3 for direct allowed, direct forbidden, indirect allowed and indirect forbidden transition, respectively. Using the Tauc method [87,88,89] to determine these transition energies, it is nevertheless necessary to know the nature of transition to calculate the electronic band gap by this relationship. Note that the simple Tauc approximation is only valid for single band transitions. To overcome the difficulty of knowing the transition nature, Souri et al. [59] came up with the idea for thin layer materials to get rid of the constant transition exponent n by calculating the derivative of the absorption spectrum. Following this procedure, Kirsch et al. [58] demonstrated that the type of band gap can be estimated also for powder samples. As such, we use the derivation of absorption spectra fitting method (DASF) [82]

$$A\left( \lambda \right) = D\lambda \left( {\frac{1}{\lambda } - \frac{1}{{\lambda_{{\text{g}}} }}} \right)^{{\text{n}}}$$
(2)

where D = B(hc)n−1z/2.303), z is thickness of the reflecting layer or penetration depth of the powder, A is the layer absorbance, λ is the wavelength of light, λg is the wavelength for corresponding bandgap. Equation (2) can be also expressed as:

$$\frac{{d\left[ {{\text{ln}}\left( {A\left( \lambda \right)/\lambda } \right)} \right]}}{{d\left( {1/\lambda } \right)}} = \frac{{\text{n}}}{{\left( {\frac{1}{\lambda } - \frac{1}{{\lambda_{{\text{g}}} }}} \right)}}$$
(3)

Which further leads to determine the absolute band-gap value Eg = hc/λg = 1239.81/λg [eV]. This band-gap value could be obtained from the zero crossing of the DASF spectrum, which again needs a tangential approximation of the respective transition peak. To overcome this procedure, the band-gap energy is determined from the transition peak energy (Ev) and its respective full-width at half maximum (Fv) using Eg = Ev − σFv. σ is the standard deviation of a normal distribution function and σ = 1 is used for the band-gap determination. Therefore, all reflectance spectra were Kubelka-Monk transferred to absorption spectra and the Tauc-types of the bandgap (direct or indirect) were compared with those of absolute bandgap values determined by the DASF method. This RATD (Reflection–Absorption-Tauc-DASF) analysis is the actually only tool to determine both the absolute value of the band gap and the type of band-gap transition directly from UV/Vis data.

High-temperature UV/Vis spectroscopy

Temperature-dependent UV/Vis data have been collected using a heating Pike Technologies UV/Vis DiffuseIR heating chamber (Pike Technologies, USA) with a quartz-glass window. Spectra were collected from 295 to 973 K with a constant heating rate of 2 K/min. Data were collected in the medium resolution mode with continuous scans lasting 108 s each. For the calculation of the DASF data, 11 measurements (± 5 + center) were center-average resulting in a temperature range of ± 9.9 K ≡ 10(1) K. From each average data set, the respective DASF spectra were calculated.

Infrared and Raman spectroscopy

ATR-FTIR measurements were carried out on a Thermo-Fischer Nicolet iS10. For the measurement, a few fine grains of the respective sample have been placed over the spectrometer crystal and pressed down by a stamp. For each sample 16 scans in the range of 650–4000 cm−1 were performed. Background scans of the same quantity at ambient atmosphere conditions were acquired prior to sample measurements. The spectrometer software OMNIC 9.6 was used for spectra recording. The obtained transmittance data (T [%]) were transformed to absorption (A [A.U.]) using A = log10(100/T) and in this way further used for data analysis.

Raman spectra were recorded on a LabRam ARAMIS (Horiba Jobin–Yvon) Micro-Raman spectrometer. A laser of 785 nm providing power of less than 20 mW was focused on the sample through a 50X objective (Olympus) with a numerical aperture of 0.75. The focus spot was estimated to be about 2 μm in diameter when closing the confocal hole to 200 μm, leading to an energy of less than 6.34 W/mm2. Each spectrum was recorded between 90 and 2000 cm−1 with a spectral resolution of approx. 1.2 cm−1 using a grating of 1800 grooves/mm and a thermoelectrically cooled CCD detector (Synapse, 1024 × 256 pixels). For the BMO-ncP (M = Al, Fe) samples, a strong fluorescence was observed in this configuration. Therefore, measurements were repeated using a laser of 633 nm wavelength providing power of less than 20 mW. The respective spectra were recorded between 90 and 2000 cm−1 with a spectral resolution of approx. 1.2 cm−1.

Theoretical calculations

The vacuum geometries of glycerin (endo and exo forms) and di-nitro-glycerin were optimized at the B3LYP [90,91,92] /6-31G* [93] level of theory as implemented in the Q-Chem 5.4.2 program package [94]. The lack of imaginary frequencies confirmed that the obtained stationary points were indeed true minima on the potential energy surface. Calculated vibrational frequencies were scaled with 0.9614, the usual factor for the B3LYP/6-31G* level of theory.

Results and discussion

A new precursor has been synthesized and identified enabling the formation of small nano-crystalline mullite-type O9 phases without any secondary co-crystallizations suitable for photo-catalytic applications in the visible-light range. The best crystallized precursor regarding its average crystallite size could be obtained using the first steps of the glycerin method for the formation of Bi2M4O9 (BMO) [95]. Taking the usual drying conditions for this method using 470 K could lead to the beginning transformation of the precursor phases, especially in the case of iron used as metal cation. Therefore, these conditions should be carefully selected and set depending on the metal cation (Table 1).

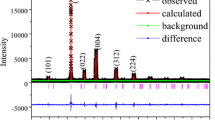
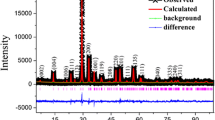
The diffraction pattern of BAO-ncP could be indexed using the hexagonal setting of a rhombohedral unit cell in space group R3 with lattice parameters a = 1.1342(2) nm, c = 2.746(1) nm, and V = 3.059(2) nm3. The respective Rietveld plot of the Pawley fit is given in Fig. 1. The room-temperature unit-cell volume of nano-crystalline Bi2Al4O9 mullite-type [61] (BAO-ncM) is found to be V = 0.3571(1) nm3. For a unit-cell containing 4 bismuth atoms, this results in a reduced volume per bismuth atom, \(V_{{\text{r}}}^{{{\text{ncM}}}}\) = 89.3(1) 106pm3. A comparable reduced volume for BAO-ncP, \(V_{{\text{r}}}^{{{\text{ncP}}}}\) = 95.3(2) 106pm3 could be calculated for 32 bismuth atoms per BAO-ncP unit cell. This corresponds to 6.7(1) % volume increase. The obtained unit-cell value of BAO-ncP lies close to those of perovskite-type α-BiAlO3 [96,97,98] described in space group R3c with lattice parameters a = 0.53755(1) nm, c = 1.33933(1) nm, and V = 0.3352(1) nm3 [96] with a corresponding reduced volume of \(V_{{\text{r}}}^{{{\text{Pero}}}}\) = 83.8(1) 10−6pm3. Doubling each perovskite lattice parameter (2a = 1.0751(1) nm, 2c = 2.6787(1) nm and 8 V = 2.6813(1) nm3) clearly points to increased lattice parameters for BAO-ncP. Comparing between the ordered α-BiFeO3 [99] and the disorder (Bi1-xFex)FeO3 [50] for any given x-value the lattice parameters are smaller for the disordered than those of the ordered compounds. Taking this analogy for the formation of disordered perovskite (Bi2Al)3Al3O9 is unlikely as the lattice parameters merely meet the expected values. Additionally, this did not give any reason for a doubling of the lattice parameters. Based on the spectroscopic data (see later), instead, formation of an organic–inorganic hybrid perovskite like (Bi2C2)Al4(O9Y3) ≡ Bi2Al4O9·C2Y3 seems to be more probable. Here C2 represents either two smaller or one bigger organic molecule. At this stage, the crystal-chemical composition of ABX3 perovskite-type is assumed to be comprised of bismuth and C2 at the A-site, aluminum at the B-site and oxygen and Y at the X-site. We further extend our assumption that Y could be either oxygen from the organic component or from water molecules, and both C2 and Y may refer to voids.

Figure 1
figure 1

Rietveld plot of BAO-ncP. The observed data (red), the calculated data (black interrupted), the difference curve (green) and the possible reflection positions (blue) for a hexagonal unit cell in R3 with a = 1.1342(2) nm and c = 2.7460(11) nm are given

Full size image

Isotypic phases are also obtained for the iron-containing precursor BFO-ncP. Also, two test samples (Bi2(Al0.7Fe0.3)4O9 (BAF3O-ncP) and Bi2(Al0.3Fe0.7)4O9 (BAF7O-ncP) of the aluminum–iron solid solution were successfully produced. The obtained lattice parameters, ACS calculated as LVol(IB) and the micro-strain (ε0), obtained from Pawley-Fits of the room-temperature X-ray data are given in Table 2. The a-lattice parameters and the unit-cell volumes increase with increasing iron content. Of notes, the c-lattice parameters lie close to each other within the standard deviations, pointing to a spatial influence of a large species (organic molecules) toward the c-direction. Additionally, there seems to be a correlation between ACS and ε0 in a way that an increasing micro-strain leads to a reduced crystallite size, or vice versa.

Table 2 Lattice parameters, average crystallite size LVol(IB) and micro-strain ε0 of the BMO-ncP phases, taken from Pawley fits in space group R3 (hexagonal setting)
Full size table

The ACS and ε0 can be compared to those of mullite-type Bi2Fe4O9, where Kirsch et al. [49, 58, 100] conducted intensive studies on the ACS-dependent physical properties. Indeed, if ε0 is plotted against ACS, as given in Fig. 2, the regions of different crystallite size states could be demonstrated. The quantum-crystalline (QC) state represents crystallites showing comparable bond length as usually obtained for surface atoms and consist of a few thousands of atoms in total. QCs show an equivalent isotropic sphere diameter (LVol(IB)) up to 4–5 nm, comparable to a closed-packed atomic arrangement of 7–9 shells, sometimes also called “surface crystals” [101]. Due to purely surface character these crystallites experience no true 3D micro-strain. The properties are size independent but might still depend on the morphology. On the other hand, a bulk type of bond-length distribution, correlated with bulk properties, could be obtained. These “bulk crystals” correspond to the micro-crystalline (MC) state. They have an intrinsic micro-strain of around 0.02%, mainly originating from intrinsic (necessary) defects. Depending on the crystallite size, these micro-crystals are usually called a crystalline powder up to single crystals (SC) if one individuum could be separated and taken. Also, here the properties are independent from the (average) crystallite size. A combination of both is the nano-crystalline (NC) state, which could be expressed as NC = QC1-sMCs (0 < s < 1), with s as the relative size parameter. As the properties of QC and MC are different, the (more or less) average properties of NC change with ACS. Therefore, for NC materials it is always necessary to define their ACS (or s). Borders for these states of different materials must be determined individually, as given in Fig. 2. Nevertheless, the usually used definition of 100 nm for the NC-MC border can be assumed to be close to real systems.

Figure 2
figure 2

Micro-strain versus average crystallite size (LVol(IB)) in Bi2Fe4O9 refined from data collected by Kirsch et al. [58]. The grey lines indicate the borders between the quantum- (QC), nano- (NC) and micro-crystalline (MC) state, the red line the value of the intrinsic bulk strain in Bi2Fe4O9. Single crystals (SC) are regarded as bigger individual MC’s

Full size image

From the 3D plots of the measured X-ray diffraction pattern, as given in Fig. 3, three regions could be categorized for better description of the temperature-dependent structural behavior of BAO-ncP. The first part is dominated by a temperature-independent behavior (within the standard deviations) of the a- and c-lattice parameters up to 420(10) K. This is followed by a decrease of the a- and an increase of the c-lattice parameter up to 540(10) K, resulting in a decrease of the unit-cell volume and the corresponding reduced unit-cell volume per bismuth cation (Fig. 3). At the same time the average crystallite size decreases. Above 540(10) K distinct Bragg reflections could not further be seen. However, the diffuse scattering was modeled with reflections constrained to the average crystallite size and refined to LVol(IB) = 1.4(1) nm. This second region is followed by the crystallization of pure mullite-type Bi2Al4O9 starting at 815(5) K. From 850(10) K on a linear growth of the average crystallite size is clear without significant change of the reduced volume (Fig. 3). Nevertheless, it is somehow interesting that the crystallite growth (Ostwald ripening) supersedes the lattice thermal expansion of this phase in the given temperature range.

Figure 3
figure 3

Temperature-dependent X-ray diffraction pattern of BAO-ncP (top) and BFO-ncP (bottom) given as 3D plot (left) and the evaluated lattice parameters and average crystallite sizes of the obtained precursor and mullite-type phases (right)

Full size image

Alike BAO-ncP, three temperature-dependent regions could also be seen for the BFO-ncP (Fig. 3). That is, first the Bragg reflections of BFO-ncP are observed, the a- and c-lattice parameter, the volume and reduced volume slightly increase up to 440(10) K. During the next ~ 20 K the volume increase is accompanied by a decrease of the ACS. Again, the disappearance of the Bragg reflections (formation of quantum-crystalline BFO-qcP, as will be confirmed in the PDF part) leads to a temperature range where the diffuse scattering represents an ACS of 1.4(2) nm. At 780(10) K the crystallization of mullite-type Bi2Fe4O9 starts with an ACS of 19(2) nm. From 850(10) K on the crystallite size increases with a growth rate of 0.20(3) nm/K, calculated from the simulation (Fig. 3) using a Boltzmann-sigmoid function:

$$V_{r}^{{{\text{Bi}}}} = V_{\min } + \frac{{\left( {V_{\max } - V_{\min } } \right)}}{{1 + e^{{\left( {\frac{{T_{50} - T}}{s}} \right)}} }}$$
(4)

where Vr refers to the reduced volume, Vmin and Vmax to the minimum and maximum obtained unit-cell volumes of the phases, respectively, and T50 to the temperature for 50% changes and s the slope. Replacing V by ACS enables the same for the average crystallite size. In this case a linear function for the increase of the ACS for the O9 phases was added. The slope of this linear function gives the average crystallite growth rate. Comparing the behavior of the aluminum- and iron-containing samples, some salient features can be pointed out:

  1. (I)

    The ACS of BFO-ncP is significant smaller than those of BAO-ncP and the phase decomposes at lower temperatures.

  2. (II)

    \(V_{{\text{r}}}^{{{\text{ncP}}}}\) of BAO decreases in the final state leading to a smaller \(V_{{\text{r}}}^{{{\text{ncM}}}}\) for the mullite-type phase, whereas for BFO an opposite behavior is obtained

  3. (III)

    The crystallite growth rate of the mullite-type BFO is with 0.20(2) nm/K more than 5-times higher than for BAO with 0.036(3) nm/K.

  4. (IV)

    BAO-ncM could be obtained as pure phase whereas for BFO-ncM secondary phases are obtained.

The growth behavior of the mullite-type phase (III) could be well understood in terms of the steepness of the liquidus curves which is much steeper for the aluminum than for the iron sample [80, 81] leading to the reduced growth rate. The change of the reduced volume of BAO-ncP (\(V_{{\text{r}}}^{{{\text{ncP}}}}\)) toward the thermodynamically stable reduced volume of mullite-type phase (\(V_{{\text{r}}}^{{{\text{ncM}}}}\)) through a sigmoidal behavior seems to the prima facie observation for the mullite-type phases. A detailed analysis of the BAO-qcP state is necessary to get more insights of the phase.

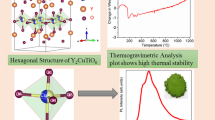
To get more information about the stability and to follow the observation from the high-temperature X-ray diffraction experiment, thermoanalytic investigations were carried out. Additionally, this sheds light into the composition of the organic–inorganic hybrid precursor. For BAO-ncP the mullite-type phase formation consists of several steps. First, ~ 5 wt% are lost up to ~ 465 K, followed by a combined double step of ~ 14.5 wt% and ~ 14 wt% up to ~ 570 K and ~ 610 K, respectively, as given in Fig. 4. This is followed by a loss of ~ 2.5 wt% up to ~ 845 K. The respective heat-flow curve shows that all these steps are of endothermic nature. The final mass loss of ~ 0.5 wt% is accompanied by an exothermic heat flow signal, resulting in a remaining mass of 63.4(1) wt% at 1050(1) K.

Figure 4
figure 4

Temperature-dependent mass change (blue) and heat-flow (red) and their first derivative (light blue and red, respectively) for BAO-ncP and BFO-ncP

Full size image

As visible in the combined plot of the DTA and HT-XRPD data given in Fig. 5, the remaining relative sample weight (rsw) of 63.5(1) wt% belongs to BAO-ncM, the nano-crystalline mullite-type Bi2Al4O9. This phase is formed in an exothermic reaction from the quantum-crystalline precursor (BAO-qcP). In a detailed view one can see a two-step event: first, the exothermal removal of remaining (assumed) organic content (burn away to nothing) directly followed by the release of crystallization energy. The endothermic signal below ~ 465 K can most probably be correlated to the loss of water (5.0(1) wt%). For other samples of the same composition, this first mass loss varies slightly which hints that this mass loss could at least partially originated from surface water. The bigger mass loss in the combined two step behavior between 465 and 610 K could be correlated with the loss of most of the organic content in the precursor. This is accompanied by a change of the lattice parameters of BAO-ncP in the first part and the formation of BAO-qcP in the second.

Figure 5
figure 5

Comparison of the DTA with the HT-XRD data of BAO-ncP and BFO-ncP

Full size image

If we consider the molar mass of Bi2Al4O9 of m = 669.88(2) g/mol equivalent to the remaining rsw = 63.5(1) wt%, the loss of the first 5.0(1) wt% corresponds to 1.8(1) H2O molecules. The loss of 14.5(1) wt% and 14.0(1) wt% then corresponds to 92.9(2) g/mol and 89.7(2) g/mol, respectively, in total 182.8(4) g/mol for the organic component. This is followed by an additional loss of 20.5(2) g/mol to the final BAO-ncM formation (see remaining organic component (RCO) in Table 1). It could be assumed that the latter is remaining organic carbon fixed in the quantum-crystalline sample burned off in an exothermic step. The organic content of the second step should correlate to 1 mol of 182.8(4) g/mol or 2 mol of 91.4(4) g/mol. Therefore, the organic molecules at this stage are assumed to be either 2 mol glycerin (Propane-1,2,3-triol, C3H8O3) with a molar mass of 92.09(1) g/mol, which is used in the synthesis, or Propane-1,3-diyldinitrate-2-ol (C3H5N2O7, Di-nitro-glycerin, Fig. 6) with a molar mass of 181.08(1) g/mol, which would be the di-ester formed from glycerin and the nitrate groups of the metal salts. Based on this analysis, two different chemical formulae for the BAO-ncP perovskite-type including possible vacancies given as □ are proposed to be possible:

  1. (I)

    [Bi2(C3H8O3)2]Al4[O9(□1-x(H2O)x)3]

  2. (II)

    [Bi2(C3H5N2O7)]Al4[O9(□1-x(H2O)x)3]

Figure 6
figure 6

3D view of glycerin (C3H8O3) and di-nitro-glycerin (C3H5N2O7) molecules. Carbon atoms are given in black, oxygen in red, nitrogen in blue and hydrogen in white. The directions a, b, and c correspond to the shortest, medium, and longest molecule length, respectively

Full size image

Comparison of the BAO-ncP infrared spectrum, as shown in Fig. 7, with those of glycerin and nitro-glycerin hint towards the composition (II). Density Functional Theory (DFT) calculations have been performed to obtain possible peak positions and intensities of both organic components in the gas phase. It turns out that for glycerin the endo- as well as the exo-configuration (Fig. 6) show comparable stabilities and both should be considered.

Figure 7
figure 7

ATR-IR spectra of the precursor phases BAO-ncP, the calculated mode positions with intensities shown as vertical sticks and a comparison of the obtained BAO IR spectra (top), including the isotypic precursor (top inset). The respective Raman spectra of the BAO species are as well compared (bottom) as the different precursor spectra (bottom inset)

Full size image

Both the calculated and the experimental IR spectra (Fig. 7) show three strong peaks at 802(3) cm−1, 1297(3) cm−1 and 1688(3) cm−1 which can be assigned with the presence of di-nitro-glycerin. Especially the peak at 1688(3) cm−1 does not belong to any glycerin configuration. Comparing the IR spectra between BAO-ncP and BAO-qcP, the quantum-crystalline precursor obtained after the endothermic decomposition, the vanishing of the peak confirms that the 1688(3) cm−1 mode is not originated from the inorganic solid. It is therefore reasonable to state that all obtained BMO-ncP phases contain the di-nitro-glycerin species (Fig. 7, inset). The IR spectrum of BAO-qcP shows low-intense absorptions between 1200 and 1700 cm−1, pointing to remaining NOx/(CHO)x attached to the quantum-crystalline phases. While transforming BAO-qcP to BAO-qcM this spectral intensity disappears. However, the leftover minor mode contribution at around 910(10) cm−1 can be assigned to the Al–O–Al modes (Q2) of the mullite-type double-tetrahedra [95, 102, 103], supporting the formation of quantum-crystalline mullite-type phase. This mode becomes well visible for the nano-crystalline Bi2Al4O9 (BAO-ncM) and more intense (Fig. 7) for the micro-crystalline sample BAO-mcM.

As the available spectral range of the infrared measurements could not provide further information about the metal–oxygen modes, Raman spectra were recorded. During the measurement using a laser of 633 nm wavelength it turned out that all BMO-ncP samples show strong fluorescence. Therefore, these samples had to be investigated using a laser of 785 nm wavelength. For all other samples measurements with the shorter wavelength were possible. This fluorescence is most probably originated in a high concentration of defects or “dangling bonds” of which electrons could be activated with an energy between 1.58 eV (785 nm) and 1.96 eV (633 nm). Two distinct Raman modes for BAO-ncP at low wavenumbers are visible at 114(1) cm−1 and 187(1) cm−1. These modes are obtained for all BMO-ncP phases (inset Fig. 7). For BiFeO3 perovskites these modes are assigned to the Raman active E(TO1) and A1(TO1) modes [104], explaining the corresponding modes of BFO-ncP and therefore of all BMO-ncP phases. From this the perovskite-type structure of the precursor is confirmed. This perovskite-type structure is lost during the transformation from BAO-ncP to BAO-qcP. Also, the accompanied loss of intensity of the di-nitro-glycerin modes, especially those at 1688(1) cm−1 supports the findings of the infrared investigations concerning a hybrid perovskite structure. The transformation from BAO-qcP to BAO-qcM is visible in the spectral range between 300 and 600 cm−1 on the shift of the broad mode which gets slightly structured with a low intense mode at 310(3) cm−1. This mode increases together with all other mullite-type modes in intensity during the formation of BAO-ncM and its crystallite growth to BAO-mcM.

From the DFT calculations, the spatial dimensions for the proposed three molecules within a perovskite-type structure have been additionally calculated, and the three different orthogonal length dimensions are given in Table 3. Whereas all three molecules differ only minor in the two shorter directions (a and b), a significant difference could be seen in the length (direction c) of the molecules.

Table 3 Length of the three orthogonal directions a, b, and c corresponding to the shortest, medium, and longest molecule length, respectively, calculated for exo- and endo-glycerin, and di-nitro-glycerin
Full size table

Considering these molecular length dimensions and comparing the available space within BiAlO3 [98], the di-nitro-glycerin fits well into the structure by replacing three bismuth atoms in a row, as sketched in Fig. 8. This could geometrically only happen in each second directional position, which is the reason for the doubling of the lattice parameters of the original BAO hybrid perovskite. Additionally, the space needed for the other two dimensions (Table 3) explains the further expansion of the lattice parameters. As the BiAlO3 structure is quite stable and well compensates defect and void distortions [98] the partial loss of the organic components before its decomposition to BAO-qcP might be explainable. Unfortunately, due to lack of data quality originated in the distorted nano-crystalline appearance of the phase, an ab-initio structure solution of the average long-range structure based on the Bragg reflections using the Rietveld method is not possible and DFT calculations fail due to the large number of atoms. Probably, electron diffraction and/or neutron pair-distribution function (PDF) analyses could better resolve such structural complexities.

Figure 8
figure 8

Crystal structure of BiAlO3 perovskite [98] with half of the bismuth atoms replaced by an organic molecule space holder (black rows) with the available length in an undistorted structure

Full size image

For the iron-containing precursor phase the same structure is assumed, as the diffraction patterns are comparable. Nevertheless, their thermal behavior is different. Opposite to BAO-ncP, an exothermic process is observed for BFO-ncP (Fig. 4) for both conversion steps. First one water molecule per formula unit (corresponding to 18.1(2) g/mol) is set free from the BFO-ncP structure containing sample. The exothermic transformation from BFO-ncP to BFO-qcP occurs during the loss of one di-nitro-glycerin (DNG, corresponding to 181.1(2) g/mol) accompanied by the destruction of the precursor structure at the same time (Fig. 5). Having an exothermic step here could mean, that the formation of BFO-qcP needs less energy than the oxidation of the DNG provides, opposite to what has been observed for the aluminum-containing phases. During the exothermic transformation of BFO-qcP to BFO-ncM (plus additional phases) a final loss of material (corresponding to 11.8(2) g/mol) is observed. Again, the remaining NOx/(CHO)x are assumed to be attached to the quantum-crystalline sample content. As additional phases α-Fe2O3 and β-Bi2O3 are observed; the latter one is exothermally transformed to α-Bi2O3 at 990(5) K.

Considering the phase stability and transformation, the aluminum-containing precursor BAO-ncP as starting material has been treated at different conditions. To obtain a quantum-crystalline precursor (BAO-qcP) the sample was heated with a heating rate of 10 K/min up to 870 K and removed from the furnace to room-temperature quenching. Taking the same parameters but leaving the sample for 30 min at 870 K led to the formation of mullite-type phase in a quantum-crystalline state (BAO-qcM). In contrast, heating for 30 min at 970 K results in nano-crystalline mullite-type sample (BAO-ncM). Micro-crystalline mullite-type Bi2Al4O9 (BAO-mcM) is synthesized at 1170 K for 48 h. The respective powder X-ray diffraction patterns are shown in Fig. 9. All these samples are phase pure and complementary to the infrared and Raman spectroscopy results.

Figure 9
figure 9

Stack diagram of the diffraction patterns of the different BAO states scaled to the highest intensity of BAO-mcM. For BAO-ncM and BAO-mcM no other reflections than those of the mullite-type phase are observed

Full size image

For the comparison of the local structure of different BAO states atomic pair distribution function (PDF) data were calculated from the respective X-ray diffraction measurements using Mo-radiation. The calculated PDF patterns of three BAO states and the comparison of the BAO and BFO precursor are given in Fig. 10. The bond-length distribution for BAO-ncP and BAO-ncM are comparable, showing similar distortions of the octahedrally coordinated aluminum atoms. Additional bond-length features associated with the tetrahedrally coordinated aluminum atoms are visible for BAO-ncM. Both phases show discrete bond-pairs, supporting the characteristic nano-crystalline phases. For BAO-qcP only a modulation of bond distances is visible, giving hints for a distorted local structure where the amplitude steeply decreases with increasing distances. Below 1.3(2) nm Fourier ripples are visible only (Fig. 10, top). This ACS correlates quite well with those determined directly from the X-ray diffraction pattern using an ACS-constrained peak fitting. As no longer distances are obtained from the modulated amplitudes, longer amorphous chains of primary building units can be excluded. As such, the quantum-crystalline state of the phase can be confirmed. Of notes, the resolution of Mo-PDF data is not good enough to determine the crystal structure of a complex organic–inorganic hybrid phase as the scattering cross-sections of the light atoms is not sufficiently different to get distinct information. Nevertheless, changes of the interatomic distances between BAO-ncP and BFO-ncP can be seen with marginal global shifts (Fig. 10) but no distinct differences in the crystal structures.

Figure 10
figure 10

Atomic pair distribution function (PDF) data of the different BAO states (top) and a comparison of the aluminum- and iron-containing precursors (bottom)

Full size image

The band-gap energy can be determined from the diffuse reflectance UV/Vis spectral data followed by the Reflection–Absorption-Tauc-DASF (RATD) method [15]. First, the diffuse reflectance data are converted to absorption using the Kubelka–Munk relation [86]. Afterward, energy requires for the indirect (Ei) and the direct (Ed) band-gap transition could be evaluated using the Tauc-method [87,88,89]. Additionally, the DASF method [58, 59] could be used to determine the band-gap energy (Eg) and with comparing this to Ei and Ed the type of transition. The respective RATD plot for BAO-ncP is shown in Fig. 11. As the DASF spectrum represents a first derivative of the obtained absorption spectrum, transition energies could be obtained from the zero-cross point of the curve. To determine these values, the obtained transition peaks in the DASF spectrum are fitted with Gaussian distribution functions. From the energy maximum Ev of these peaks, the full-width at half maximum (Fv) is subtracted to obtain the band-gap energy (Eg). This procedure is also valid for multiple transition for which the extrapolation of the tangential to zero absorption leads to wrong values for both, the DASF and the Tauc method. The determined band-gap energy for BAO-ncP was found to be Eg = 3.50(3) eV with an indirect transition. Using the half-width of the DASF Ev peak, expressed as Fv = 0.26(4) eV one might also assume the flatness of the transition bands to each other. A sharp maximum in the valence band combined with a sharp minimum in the conduction band would result in strong change of the absorption at the band edge, leading to a narrow Fv. Opposite, flat bands on both sides would generate a reduced slope of the absorption edge, leading to larger Fv values. Within the instrumental resolution Fv = 0.26(4) eV hints to a medium sharp transition. The respective fit-values of the different BAO states are summarized in Table 4. As already shown for Bi2Fe4O9 [58], the inter-band transitions can also be determined using the DASF method. In the RATD plot of BAO-ncP (Fig. 11) at least one additional peak at lower energy than the band-gap transition is clear. This peak is assigned to an intermediate band originating from anionic defects (Ed−) in the structure accompanied by Urbach tailing [105] to further lower energies. At the high-energy side of the band-gap peak, additional transitions of BAO-ncP could probably be explained in terms of cationic defects (Ed+). More obvious are these high-energy additions in the case of BAO-qcP and BAO-qcM (Fig. 12, right).

Figure 11
figure 11

RATD plot of the Bi2Al4O9 precursor (BAO-ncP). In the top row the UV/Vis reflectance (R) and the Kubelka–Munk transformed absorption (A) spectra are given. Ei is the indirect, Ed the direct transition energy determined from the Tauc (T) plot and Eg (= Ev–Fv) is the band gap energy using the DASF (D) method. Therein Ev is the transition peak maximum and Fv the band-gap flatness parameter determined from the half-width of the Ev peak

Full size image
Table 4 Band-gap energy (Eg), transition type, transition peak energy (Ev), band-gap flatness parameter (Fv), and inter-band energies for the assumed strongest anionic (Ed−) and cationic (Ed+) defects
Full size table
Figure 12
figure 12

Temperature-dependent DASF (D) data collected for BAO-ncP (left) and room-temperature data DASF plots of the different states

Full size image

The DASF curve can also be used to follow the temperature-dependent change of the band-gap energy. While a continuous decrease of band-gap energy with increasing temperature is expected [106, 107] a discontinuous change hints to structural phase transitions or transformations [108]. The temperature dependency of BAO-ncP up to 520(20) K, as shown in Fig. 12, follows in band-gap narrowing. Afterward, the decomposition of the perovskite-type precursor under loss of di-nitro-glycerin is as well visible along with a strong shift to lower transition energies. The gradual lowering of the band gaps at high temperatures can be explained due to formation of the QC mullite-type compound.

Summary and conclusion

The new organic–inorganic hybrid perovskite [Bi2(C3H5N2O7)]Al4[O9(□1-x(H2O)x)3] has been synthesized as nano-crystalline precursor. It enables the formation of small nano-crystalline mullite-type Bi2Al4O9 phases suitable for photo-catalytic applications in the range of visible-light. The crystal structure was not refined from the in-house X-ray Bragg and total scattering data due lack of sufficient data quality of the partially distorted phase. Nevertheless, the appearance of the phase could well be described based on spectroscopy, thermoanalytic and temperature-dependent diffraction data. Di-nitro-glycerin, as an organic component, is incorporated in the BiAlO3 rhombohedral perovskite parent structure replacing three bismuth atoms in a row. The ordered incorporation of di-nitro-glycerin leads to a doubling of the lattice parameters, accompanied by a slight expansion due to the molecular dimensions. The aluminum-containing precursor could easily be transformed to a quantum-crystalline precursor phase by controlling temperature and time, which, however, still contains some organic fragments produced during the transformation process. The band-gap energy change from 3.50(3) to 2.59(4) eV for the transformation of the nano-crystalline precursor to the nano-crystalline mullite-type phase, respectively. The respective band-flatness parameters are larger (double) for the quantum-crystalline than for the nano-crystalline precursor. The isotypic precursors for purely iron-containing phase and selective aluminum–iron solid solutions were also produced. Thermal transformation of the iron-containing precursor to the respective mullite-type phase is accompanied by the (intermediate) formation of iron oxides and bismuth oxides. It would be of future interest to test this experimental study for relevant tri-valent cations such as gallium. The temperature-dependent DASF data analysis enables a direct observation of the phase transformations via change of band-gap energy.