Chemical expansion of CeO_2−δ and Ce_0.8Zr_0.2O_2−δ thin films determined by laser Doppler vibrometry at high temperatures and different oxygen partial pressures

Abstract

The chemical expansion of ceria (CeO_2−δ) and ceria-zirconia (Ce_0.8Zr_0.2O_2−δ, CZO80) thin films is investigated by high-temperature laser Doppler vibrometry (LDV) at temperatures from 600 to 950 °C. The films are deposited on single-crystalline 8 mol-% yttria-stabilized zirconia substrates, which act as pumping cells to adjust oxygen non-stoichiometry in the thin films. Oxygen deficiency causes film expansion, leading to mechanical strain that bends the sample. The total displacement, i.e., the sum of bending and film-thickness change, is determined contact-less by LDV. A differential laser Doppler vibrometer (D-LDV) is realized to enable measurements on a very long time scale, which is necessary due to the long equilibrium times of the ceramic films. These displacements are compared to those acquired with a commercial single-point laser Doppler vibrometer (SP-LDV) for motions above 1 Hz. Here, both devices yield similar results. CZO80 films are found to bend a substrate much more than ceria films under similar experimental conditions. A model describing the displacement of the sample is derived from the Stoney model and applied to calculate deflections using literature data. The displacements at the center of the CZO80 sample measured with the SP-LDV increase from 0.18 nm at 10 Hz and 600 °C to 32.7 nm at 0.1 Hz and 800 °C. For ceria, the displacements range from 1.6 nm (10 Hz, 800 °C) to 79.4 nm (0.1 Hz, 900 °C). The D-LDV enables the detection of quasi-static displacements at very low frequencies. The ceria sample exhibits 218 nm at 0.001 Hz and 800 °C.

Introduction and motivation

At first, the motivation for the choice of investigated materials, sample design, and the experimental approach is outlined briefly.

Ceria and its solid solutions with zirconia are industrially used as active materials in, e.g., fuel cells, electrolyzers, catalysts, sensors, and batteries due to their ability to store and release oxygen from and into the surrounding atmosphere and/or their high ionic conductivity [1,2,3]. Especially in automotive exhaust catalysts, ceria-zirconia is a standard oxygen buffer material [3]. The insertion and release of oxygen leads to a change in stoichiometry, which can be associated with a change in volume [1, 4,5,6,7,8,9,10,11] called chemical expansion. Since a thin film adhering firmly to a negligibly expanding substrate cannot expand freely like the respective bulk material, the chemical expansion leads to the build-up of lateral mechanical stress in the film. As the active material in the aforementioned applications is often realized in the form of a thin film, the chemical expansion behavior of ceria-zirconia thin films with different ceria/zirconia ratios must be understood to tailor mechanical stress for given applications. The focus of this paper is on nominally undoped ceria and ceria-zirconia with 20% zirconia.

Mechanical stress due to chemical expansion can lead to cracking, delamination and even disintegration of the films, which are some of the main reasons for the failure of the components mentioned above [2] and must therefore be mitigated in order to extend their service life. For those components, chemical expansion should be minimized or compensated. On the other hand, the effect of chemical expansion can be maximized. Materials with high and reproducible chemical expansion coefficients could be used in a new class of high-temperature actuators. There is a demand for devices that can operate at temperatures beyond the Curie temperatures of common piezoelectric materials (e.g., up to 365 °C for lead zirconate titanate (PZT) ceramics [12]). These new actuators could be used in combustion engines, chemical reactors and other applications to influence, e.g., the flow of reactants at high temperatures, or generally harsh conditions.

It has been demonstrated that the formation enthalpies for oxygen vacancies in, e.g., Pr-doped ceria, are significantly lowered in thin films compared to bulk materials [13,14,15]. Those studies were conducted on Pr_0.1Ce_0.9O_2−δ films with thicknesses of approx. 131 nm [14] and 256 nm [13], which is around a quarter of the thickness of the thinnest film studied in this work. The higher film thicknesses used in this study are more application relevant.

Increasing non-stoichiometry and related chemical expansion in the thin films is achieved by periodically pumping oxygen ions from the film into the substrate, which acts as a pumping cell. The electrochemical approach has the advantage over directly regulating the oxygen partial pressure of the surrounding atmosphere that the oxygen activity in the film can be adjusted to wider ranges with higher rates. The resulting periodic displacement of the sample has to be determined with the lowest possible influence on the sample. A particularly suited method is laser Doppler vibrometry (LDV), as it can be applied without mechanical contact at high temperatures if a specially adapted setup is used, as done here. Previous studies by the authors [9, 11] using praseodymia-ceria (PCO) solid solutions have shown the unique ability to detect chemical expansion and related effects in thin-film samples without influencing the sample. PCO is known to show large chemical expansion. Therefore, it is a well-suited model system. CeO₂ and CZO are probably of higher industrial relevance. Even without cracks, they show significantly lower expansion effects than PCO. So, the processes occurring in those films are much more difficult to measure and need to be addressed by more advanced techniques like the LDV presented in this work. LDV is based on a non-contact optical measurement principle allowing for high-temperature characterization up to 1000 °C. This exceeds the range of operation of mechanically based characterization techniques by far, e.g., nanoindenters or nanoscale electrochemomechanical spectroscopy (NECS) is often limited to temperatures up to about 650 °C [10].

The impact of cracks in the thin films on the bending of the samples is regarded, and they are of particular practical relevance. To the best of the authors’ knowledge, this is the first study to correlate the impact of cracks with the direct characterization of the chemical expansion in thin films. Prior studies focused mainly on perfect, i.e., dense and mostly defect-free films, whereas imperfect films have not been addressed systematically so far. These cracks can develop during annealing of the samples due to a mismatch in the thermal expansion coefficients of the thin film and substrate or due to the thin film contraction during crystallization. In the aforementioned industrial applications, films are often required to be dense and compact, i.e., free of pores and cracks. However, during use in industrial reactors, combustion engines, etc., the components are subject to an aging process which consists to some extent of the formation of such cracks [2] after several duty cycles of heating and subsequent cooling or changing oxygen partial pressure. For the hypothetical application in an actuator, the films would have to be compact as well, because cracks would have the effect that the expansion does not lead to a build-up of lateral stress which ultimately causes the substrate to bend, but to the closing of the cracks. To better understand the influence of such cracks on the deformation behavior of the sample, they are microscoped and the images analyzed. The width of and distance between cracks in the thin films is compared to values derived from the thermal coefficients of expansion (TCEs) of the thin film and substrate materials and the annealing temperature. It is expected that for these imperfect samples a significantly lower bending of the substrates is observed than for dense films. The reason for this is that the chemical expansion of the film first leads to a (partial) closing of the cracks until the film resembles a dense film. Only from this point on, the additional chemical expansion should result in mechanical stress on the substrate, resulting in substrate bending. Also, the present work proposes and discusses a model predicting theoretical displacements as well as the origin and influence of cracks in the thin films.

Since the cracks accommodate the film expansion partially (decreased thickness change with respect to crack-free films due to decreased lateral stress) even more sensitive measurements are required which is the differential laser Doppler vibrometry (D-LDV).

Current state of research

Non-stoichiometry and chemical expansion

As oxygen non-stoichiometry is a function of temperature and oxygen activity [5, 16,17,18], this property can be studied by varying the oxygen partial pressure to which a sample is exposed. Alternatively, the oxygen activity in the thin-film samples can be adjusted by pumping of oxygen using the electrochemical approach mentioned above. Related periodic deformations of samples are observed [9,10,11]. Oxygen activity and therefore deficiency strives toward equilibrium with the surrounding atmosphere. If the concentration of impurities is sufficiently low and can be disregarded, the equilibrium reaction in Kröger–Vink notation [19] for cerium oxide CeO_2−δ and small non-stoichiometries δ reads [18, 20]:

$$2{\text{Ce}}_{{{\text{Ce}}}}^{ \times } + {\text{O}}_{{\text{O}}}^{ \times } \leftrightarrow 2{\text{Ce}}_{{{\text{Ce}}}}^{{^{^{\prime}} }} + {\text{V}}_{{\text{O}}}^{ \bullet\bullet} + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}{\text{O}}_{2} \left( g \right)$$

(1)

The left side of the defect equilibrium shows cerium ${\text{Ce}}_{{{\text{Ce}}}}^{ \times } { }$ and oxygen ${\text{O}}_{{\text{O}}}^{ \times }$ that are neutral with respect to the lattice. ${\text{V}}_{{\text{O}}}^{ \bullet\bullet }$ is a two-fold positively charged vacancy occupying an oxygen site, and ${\text{Ce}}_{{{\text{Ce}}}}^{^{\prime}}$ a cerium ion with a single negative charge on a cerium lattice site. For small non-stoichiometries δ and negligible impurities, the concentrations of oxygen and unreduced metal ions can be assumed to be constant [1, 4, 6, 7]. The electrons are localized at cerium lattice sites, reducing cerium ions from the tetravalent state to the trivalent state. The equilibrium constant K of Eq. (1) can then be expressed as:

$$K = \left[ {{\text{Ce}}_{{{\text{Ce}}}}^{^{\prime}} } \right]^{2} \left[ {{\text{V}}_{{\text{O}}}^{ \bullet\bullet} } \right]{\text{p}}_{{{\text{O}}_{2} }}^{1/2}$$

(2)

Inserting the neutrality condition

$$\left[ {{\text{Ce}}_{{{\text{Ce}}}}^{^{\prime}} } \right] = 2\left[ {{\text{V}}_{{\text{O}}}^{ \bullet\bullet} } \right]{ }$$

(3)

into Eq. (2), the relationship between the oxygen vacancy concentration $\left[ {{\text{V}}_{{\text{O}}}^{ \bullet\bullet } } \right]$ and the oxygen partial pressure in the surrounding atmosphere ${\text{p}}_{{{\text{O}}_{2} }}^{{}}$ reads:

$$\left[ {{\text{V}}_{{\text{O}}}^{ \bullet\bullet} } \right] \propto {\text{ p}}_{{{\text{O}}_{2} }}^{{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 6}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$6$}}}}$$

(4)

The non-stoichiometry δ can be expressed in terms of the oxygen vacancy concentration:

$$\delta \propto [{\text{V}}_{{\text{O}}}^{ \bullet\bullet } ]$$

(5)

It has been shown that the partial substitution of ceria with zirconia affects the reducibility of the solid solution by lowering the formation enthalpy of oxygen vacancies [21], leading to a change in the vacancy concentration [22] and the ionic conductivity [23] under identical circumstances. Since Zr is not reduced itself in CZO80 at higher oxygen activities, but lowers the enthalpy of reduction of the system [21], Eqs. (1)–(5) apply for both CeO₂ and CZO80.

The non-stoichiometry δ in the thin film causes a chemical expansion $\varepsilon_{{\text{C}}}$ [1, 4,5,6,7] with the chemical expansion coefficient $\alpha_{{\text{C}}}$:

$$\varepsilon_{{\text{C}}} = \alpha_{{\text{C}}} \delta$$

(6)

The physical mechanisms linking changes in composition to local changes in lattice parameters and, finally, to chemical expansion are not fully understood. In [24], Schmitt et al. conclude that no single mechanism is responsible, but that there are many different contributions:

• (a) Growth in ionic radii of the metal ions upon reduction: The radius of the reduced ${\text{Ce}}^{3 + }$ ion is around 15% larger than that of the unreduced ${\text{Ce}}^{4 + }$ ion [25], which leads to a change in lattice parameter upon partial reduction [26].

• (b) Electrostatic repulsion between charged constituents of the lattice [27]: The nearest neighbors of the vacancy are cations (${\text{Ce}}^{3 + }$ or ${\text{Ce}}^{4 + }$), which are repelled by the net positive charge of the vacancy. Mechanisms a) and b) are often described as competing [4].

• (c) Defect interactions at high defect concentrations: At higher defect concentrations, defects can no longer be treated as isolated from each other, but their interactions must be considered. The association of [28, 29] results in lower electrostatic energy which diminishes the chemical expansion [28].

More details on these mechanisms due to the formation of oxygen vacancies are found in [24]. It should be noted that other mechanisms, such as piezoelectricity and phase transformations, may lead to a volume change as well. However, in terms of this study they can be largely neglected. Piezoelectricity is described in [30, 31]. There, an ordering of the defects in Gd-doped ${\text{CeO}}_{2}$ is achieved by application of an electric field, which breaks the cubic symmetry of the crystal. In [30], the electric field is on the order of $5 \cdot 10^{5} {\raise0.7ex\hbox{${\text{V}}$} \!\mathord{\left/ {\vphantom {{\text{V}} {{\text{cm}}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{cm}}}$}}$, and in [31] it is $5 \cdot 10^{4} { }{\raise0.7ex\hbox{${\text{V}}$} \!\mathord{\left/ {\vphantom {{\text{V}} {{\text{cm}}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{cm}}}$}}$. In this work, the voltage is largely applied to the substrate and not to the thin film of interest. Such piezoelectric deformations is therefore not taken into account here. A charge-transfer driven phase transition in ceria is reported in [32] for the temperature range between − 25 and + 75 °C. As this is well below the temperature range considered in this work, these findings are also not taken into account here.

Electrochemical pumping

The oxygen activity in the film of interest can be adjusted by the oxygen partial pressure in the surrounding atmosphere [1, 5, 6, 14, 22, 23, 33]. Here, the time constants are determined by the gas exchange in the furnace and ranges from several 10 min to hours, which is too long even for measurements with the laser Doppler vibrometer (LDV) planned here. Alternatively, an oxygen ion conducting substrate can be used as an electrochemical pumping cell by applying a voltage U, see Fig. 1. Here, the film of interest is deposited directly on the substrate.

Figure 1

Schematic of the electrochemical pumping of the sample with the substrate coated with a thin film of ceria or CZO80, the Pt_0.9Rh_0.1 front electrode, the Pt back electrode, the waveform generator, and the power amplifier which provides the pumping current

This approach has some distinct advantages over adjusting the atmosphere in the furnace. Apart from the comparative ease of conducting experiments in air or other gas atmospheres, one is able to control the effective oxygen partial pressure in the film in wide ranges with high rates, and therefore frequencies. In consequence, one is able to adjust the oxygen activity by pumping the sample cell with a periodic pumping potential, and to achieve reversible chemical expansion and substrate bending by applying an electrochemical bias to the sample, as shown in Fig. 1.

The oxygen partial pressure at the interface of film and substrate can be described by the Nernst equation [34]:

$${\text{p}}_{{{\text{O}}_{2} }}^{{{\text{eff}}}} = {\text{p}}_{{{\text{O}}_{2} }}^{{{\text{atm}}}} {\text{exp}}{\left(\frac{- 4U_{{{\text{eff}}}} e_{0} } {k_{B} T}\right)}$$

(7)

In Eq. (7), ${\text{p}}_{{{\text{O}}_{2} }}^{{{\text{eff}}}}$, ${\text{p}}_{{{\text{O}}_{2} }}^{{{\text{atm}}}}$, $e_{0} , \;k_{B}$, and T are the effective oxygen partial pressure at the film-substrate interface, the oxygen partial pressure of the surrounding atmosphere, the elementary charge, the Boltzmann constant, and the absolute temperature, respectively. The effective voltage U_eff depends on the conductivity of film and substrate, as described in Appendix “Enhanced vertical expansion in a constrained film”. After a sufficiently long time, the oxygen activity in the film approaches the equilibrium and corresponds to ${\text{p}}_{{{\text{O}}_{2} }}^{{{\text{eff}}}}$ [10, 22], see Sections “In-film stress and substrate bending” and “Discussion”.

Combining Eqs. (5) and (7), one obtains:

$$\left[ {{\text{V}}_{{\text{O}}}^{ \bullet\bullet } } \right] \propto {\text{p}}_{{{\text{O}}_{2} }}^{{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 6}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$6$}}}} \propto {\text{exp}}{\left({{\frac{2}{3}\frac{{e_{0} U_{{{\text{eff}}}} }}{{k_{B} T}}}}\right)}$$

(8)

Due to kinetic limitations, the oxygen vacancy concentration does not reach the equilibrium value given by Eq. (8) instantly. Because the diffusion and exchange of oxygen between the thin film and the substrate is a relatively slow process [10, 11, 22, 33], the equilibrium is only achieved asymptotically, and only after long equilibration times, which translate to very low pumping frequencies. At high pumping frequencies corresponding to short equilibration times, equilibrium is not reached, and the vacancy concentration is significantly lower than the one given by Eq. (8). This fact explains the dependence of the chemical expansion on pumping frequency as long as the pumping frequency is not sufficiently low to reach nearly equilibrium.

In-film stress and substrate bending

Non-stoichiometry δ and chemical expansion ε, i.e., isothermal relative change of the lattice parameter $a$ in the thin film, are correlated via the chemical expansion coefficient, α_C:

$$\varepsilon = \frac{{a\left( {T,\;{\text{p}}_{{{\text{O}}_{2} }} } \right) - a\left( {T,\;0.21\;{\text{bar}}} \right)}}{{a\left( {T,\;0.21\;{\text{bar}}} \right)}} = \alpha_{{\text{C}}} \delta \left( {T,\;{\text{p}}_{{{\text{O}}_{2} }} } \right) \propto {\text{exp}}{\left({{\frac{{2e_{0} U_{{{\text{eff}}}} }}{{3k_{B} T}}}}\right)}$$

(9)

Moreover, the expansion of a thin film deposited on a substrate is laterally constrained. It can freely expand vertically, but not in the xy-plane (defining the z axis as perpendicular to the film). This lateral constraint of the expansion leads to the build-up of stress, which in turn bends the substrate. If the radius r of the substrate is significantly larger than its thickness t_s and significantly smaller than the bending radius R, this bending can be described as spherical and calculated from the Stoney model [35, 36] using a small-angle approximation (see Appendix “Derivation of the biaxial modulus and biaxial strain”). As illustrated in Fig. 2, the displacement of the sample surface D consists of two contributions, the substrate bending $D_{0}$ and the vertical expansion of the thin film $\Delta t_{{\text{f}}}$:

$$D = D_{0} + \Delta t_{{\text{f}}}$$

(10)

Figure 2

Schematic of the samples and of the contributions to the displacement D. The 8YSZ crystal serves as substrate and pumping cell. On the front side, the oxide thin film (CZO80 or CeO₂) and a Pt_0.9Rh_0.1 cover electrode are deposited. The back side is covered by a Pt thick-film electrode

The displacement at the center of the sample with the vertical expansion Δt_f and deflection D₀ as derived in Appendices “Sample holders” and “Derivation of the biaxial modulus and biaxial strain” reads:

$$D = D_{0} + \Delta t_{{\text{f}}} = \varepsilon_{{\text{f}}} t_{{\text{f}}} \left( {3r^{2} \frac{{E_{{\text{f}}} \left( {1 - \nu_{{\text{s}}} } \right)}}{{E_{{\text{s}}} t_{{\text{s}}}^{2} \left( {1 - \nu_{{\text{f}}} } \right)}} + \frac{{1 + \nu_{{\text{f}}} }}{{1 - \nu_{{\text{f}}} }}} \right)$$

(11)

This enables the calculation of expected values for the displacement from literature data for the chemical expansion ε. Plots in the results section show, if not stated otherwise, maximum displacements taken at the center of the sample.

Another effect of partial substitution of ceria with zirconia is a shift in the chemical expansion coefficient $\alpha_{{\text{C}}}$ [7]. In the solid solution Ce_0.8Zr_0.2O_2−δ, the reducibility is greatly enhanced with respect to ceria [21, 22], the conductivity is enhanced [23], and the chemical expansion coefficient $\alpha_{{\text{C}}}$ is reduced [7]. In [5], it is found that the enhanced reducibility in CZO80 outweighs the diminished chemical expansion coefficient, resulting in a higher chemical expansion in CZO80 than in pure ceria under equal conditions. Note that in the range of temperatures, pumping voltages applied to the samples and the resulting oxygen partial pressures (${\text{p}}_{{{\text{O}}_{2} }} { } > { }10^{ - 18} \;{\text{bar}}$) in this work, the non-stoichiometry in CZO80 is always greater than in undoped ceria [21, 22].

Experimental details

Sample preparation

The substrates consist of commercially available, nominally 300-μm-thick (100)-oriented, 8 mol percent yttria-stabilized zirconia (8YSZ) substrates (MTI Corp., USA). To allow radial symmetry, they were milled to a circular shape with a radius of $r = \left( {5.0 \pm 0.1} \right)$ mm, accounting for spalling at the edge during the milling process. Subsequently, Pt (C3620 Pt Paste, Heraeus GmbH, Germany) back electrodes were deposited by screen-printing and sintered at 1000 °C for 1 h. Its diameter and thickness are 9.5 mm and about 5 µm, respectively. Ceria or CZO80 thin films were deposited on the front side by pulsed laser deposition (PLD) and annealed in air (see below). The film thickness ranges from about 1.1 µm to 3.3 µm (see Table 1). Finally, Pt_0.9Rh_0.1 (m&k GmbH, Germany, 99.996% purity) cover electrodes were deposited on the oxide thin film by PLD. At the front side, where LDV measurements are taken, the diameters of the oxide films of interest and of the highly reflective Pt_0.9Rh_0.1 electrode are 9.5 mm and 9.0 mm, respectively. The thickness of the PLD electrodes ranges from 200 to 300 nm.

Table 1 Parameters of the samples used for this work

The preparation of the ceria and CZO80 targets used for the PLD is described in [22]. To minimize the formation of droplets in the deposited oxide thin films [37], the targets were reannealed at 1000 °C for an hour and sanded before each deposition. Thin films were deposited using a COMPex 205 KrF Excimer Laser (Coherent Inc., USA). It was operated at a wavelength of 248 nm with 200 mJ pulses of 50 ns duration at a repetition frequency of 10 Hz and a base pressure of 10⁻⁵ mbar in the deposition chamber. The illuminated area was approximately 1 mm² and the laser fluence $2 \cdot 10^{5} \;{\raise0.7ex\hbox{${\text{J}}$} \!\mathord{\left/ {\vphantom {{\text{J}} {{\text{m}}^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{m}}^{2} }$}}$.The Pt_0.9Rh_0.1 cover electrode with thickness 300 nm was deposited with 350 mJ pulses of 50 ns length and 1 mm² illuminated area (laser fluence $3.5 \cdot 10^{5} \;{\raise0.7ex\hbox{${\text{J}}$} \!\mathord{\left/ {\vphantom {{\text{J}} {{\text{m}}^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{m}}^{2} }$}}$) at a frequency of 30 Hz. The depositions were performed at room temperature. Note that the cover electrodes were deposited after conducting X-ray diffraction (XRD).

After film deposition, the samples were annealed in ambient air for crystallization and equilibration of potential oxygen non-stoichiometry. The ceria sample was annealed at 1000 °C for 4 h before deposition of the PLD electrode. The first CZO80 sample (CZO80-1) was annealed at 800 °C for 10 h. The second CZO80 sample (CZO80-2) was originally annealed for 10 h at 700 °C. After the measurements at and below 700 °C (denoted CZO80-2-700), it was re-annealed at 750 °C for another 10 h before conducting measurements at and below 750 °C (denoted CZO80-2-750). After these measurements, it was kept at 800 °C for another 10 h before taking measurements at and below 800 °C (denoted CZO80-2-800).

All heating and cooling rates during annealing and during the experiments were set at $3{ }\;{\raise0.7ex\hbox{${\text{K}}$} \!\mathord{\left/ {\vphantom {{\text{K}} {{\text{min}}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{min}}}$}}$ at temperatures below $T < 600 \;^\circ {\text{C}}$, $2\;{\raise0.7ex\hbox{${\text{K}}$} \!\mathord{\left/ {\vphantom {{\text{K}} {{\text{min}}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{min}}}$}}$ at temperatures, $600 \;^\circ {\text{C}} < T < 800\;^\circ {\text{C}}$, and $1\;{\raise0.7ex\hbox{${\text{K}}$} \!\mathord{\left/ {\vphantom {{\text{K}} {{\text{min}}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{min}}}$}}$ at temperatures $T > 800 \;^\circ {\text{C}}.$ It should be noted that the formation of cracks in the CZO films of this study was not prevented even by applying small rates of 1 K/min.

Characterization of the samples

The thicknesses of the substrates were measured with an Extramess 2000 digital gauge (Mahr GmbH, Germany) at the center and four points at the edge of the substrate. Film thicknesses were measured at four points on the edge of the annealed film using an XP-2 stylus profilometer (Ambios Technology Inc, USA). The film thickness was taken as the mean height of the step detected. The thicknesses of the substrates and films in Table 1 are the mean values with standard deviations of the respective datasets.

XRD spectra were taken with an D5005 X-ray diffractometer (Siemens AG, Germany) operating in Bragg–Brentano geometry. Measurement range was 25° ≤ 2θ ≤ 100°, with an angular increment of Δ2θ = 0.015°. The radiation used is Cu-K_α with 40 kV acceleration voltage and 40 mA current.

Scanning electron microscope (SEM) images were made with a SmartSEM microscope (Carl Zeiss AG, Germany) with 5 kV acceleration voltage and 1.5 nA current, detecting secondary electrons with an in-lens detector.

Experimental setup: SP-LDV and D-LDV

Measurements with a single-point laser Doppler vibrometer (SP-LDV) were taken with a commercial device using a OFV 505 LDV sensor head with a wavelength of 633 nm and an OFV-5000 LDV controller with a DD-900 displacement decoder (both Polytec GmbH, Germany) in a setup designed specifically for high-temperature applications. This setup is shown schematically in Fig. 3a and described in more detail in [9, 11]. The sample contacted in an alumina sample holder and placed inside a HTSS 75-180/16 tube furnace (Carbolite Gero GmbH, Germany). The clamping of the sample is done around the edge of the sample, so that it does not influence the bending of the sample, and is symmetrical. Electrochemical pumping is achieved with a 33502B waveform generator (Keysight Technologies, USA) and a voltage-controlled power amplifier (I.E.D. GmbH, Germany and MST Scientific, Germany), which provides the electrochemical pumping current. The displacement voltage signal U_LDV from the LDV controller is detected with a PCI-5122 oscilloscope (NI Corporation, USA). The range of applicable pumping frequencies is limited by low-frequency noise from environmental influences like thermal turbulences in the furnace which cause refractive index fluctuations, building vibrations, and other natural and artificial noise sources. Another source of low-frequency noise is temperature control. With the sample being placed approx. 30 cm inside the furnace and supported by an alumina tube with a thermal coefficient of expansion (TCE) of around $5\cdot {10}^{-6} {\mathrm{K}}^{-1}$ [38], a temperature fluctuation of ± 1 K would result in an uncorrelated, slow displacement of up to 1.5 μm, yielding a large, low-frequency noise contribution and preventing detection of small deflections at low frequencies with the SP-LDV.

Figure 3

Schematic of the LDV setups. The sample is maintained at the desired temperature in air by the tube furnace, the position of the laser spot is adjusted with a tilt mirror. In the case of the SP-LDV (a), the reference beam is kept within the LDV probe head, while in the case of the D-LDV (b), the reference beam is placed on the sample holder or the edge of the sample

The high uncertainty of measurement at low frequencies deserves a measurement setup that eliminates or compensates disturbances. One possibility is differential laser Doppler vibrometry (D-LDV). Such measurements are taken on the ceria sample using a differential laser Doppler vibrometer conceived and realized by the authors [39, 40]. It employs a Koheras Basik X15 fiber laser (NKT Photonics, Denmark) with 1550 nm wavelength. This system is optimized for low frequencies, in a setup shown schematically in Fig. 3b. The decoder is an OFV-5000 LDV controller with a DD-500 displacement decoder (Polytec GmbH, Germany). In the case of differential measurement, the reference beam is placed on the sample holder or the edge of the sample, and the interference signal does not include the uncorrelated length fluctuations of the sample holder. The effect of atmospheric turbulences on the displacement signal is also greatly diminished. The lowest pumping frequency applied to samples in the D-LDV setup is 0.001 Hz. The displacement signal is detected with an NI PCI-5122 oscilloscope card identical to the one used with the SP-LDV.

The pumping voltages applied to all samples range from 0 to 0.25 V, 0.5 V, and 0.75 V, depending on the specific experiment. Pure ceria thin films are known to exhibit only small degrees of expansion at p_O2 ≥ 10⁻¹⁸ bar [6, 41]. At 800 °C, this corresponds to a pumping voltage of 0.75 V. To achieve higher non-stoichiometries and displacements, the ceria sample was additionally exposed to a voltage of up to 1.0 V. The pumping frequencies applied to the sample in the SP-LDV were 10 Hz, 5 Hz, 1 Hz, 0.5 Hz, and 0.1 Hz. The temperature ranges were 600–800 °C for CZO80 and 800–950 °C for ceria. All measurements were taken in ambient air.

Experimental results

Crystal phases

The XRD pattern of a CZO80 sample after annealing at 700 °C is shown in Fig. 4. Films with a preferred texturization are observed that corresponds to the [100] orientation of the YSZ single crystals. The spectrum exhibits only the CZO80 (200), (400), and (220) reflexes and lacks the dominant (111) reflex, which one would expect for a polycrystalline untextured film [1, 42]. The corresponding 8YSZ (200) and (400) reflexes [43] of the substrate are also visible.

Figure 4

XRD pattern of a CZO80 film on a 8YSZ substrate after annealing for 10 h at 700 °C, compared to data from Ce_0.75Zr_0.25O₂ [42] and 7.5YSZ [43]

Morphology of thin films

In Fig. 5a–d, SEM images of the CeO₂ (a), (b) and CZO80 (c), (d) samples are shown.

Figure 5

a, b SEM images of the CeO₂ sample after annealing at 1000 °C and conducting the LDV experiments and c, d of sample CZO80-2 after annealing at 700 °C. The surfaces show visible cracks and some droplets [37], but are otherwise compact, i.e., no delamination and no pores are visible even at the largest magnification (b, d). Blurring is attributed to electrostatic charge build-up on the sample surface because CeO₂ and CZO80 are electric insulators at room temperature

The images of both samples show cracks in the thin films. In Fig. 5a, it can be seen that the CeO₂ thin film is segmented into irregularly shaped segments. The mean distance of the cracks was taken as the mean value of the height and width of 23 such segments, 46 values in total, and was found to be $d_{{{\text{crack}}}}^{{{\text{CeO}}_{2} }} = \left( {8 \pm 2} \right)$ µm. In Fig. 5b, one crack and a segment of the thin film are shown in detail. The segment itself consists of irregularly shaped crystallites with sizes ranging from several tens to several hundred nm, and the crack has a mean width of $w_{{{\text{crack}}}}^{{{\text{CeO}}_{2} }} = \left( {53 \pm 12} \right)\;{\text{nm}}$, taken at 11 positions.

The cracks of a CZO80, shown in Fig. 5c, have a mean distance of $d_{{{\text{crack}}}}^{{{\text{CZO}}80 - 2}} { } = { }$(42 ± 18) µm, taken on two diagonal lines across the image with a total of fifteen cracks. The crack shown in Fig. 5d has a mean width of (61 ± 18) nm, taken at eight positions.

LDV measurements

The displacement can be described as spherical, as can be seen in Fig. 6. A SP-LDV scan of the sample surface consisting of nine points is shown here. A maximum displacement of 48.4 nm is found at the center of the sample. The other points show a high radial symmetry. Fitting a sphere to the data yielded a fitted displacement of $D_{{{\text{fit}}}} = 48.3\;{\text{nm}}$. This is in good agreement with the displacement at the center. A bending radius of $R_{{{\text{fit}}}} = \left( {234 \pm 5} \right)\;{\text{m}}$ and a coefficient of determination of ${\text{COD}}_{{{\text{fit}}}} { } = { }0.996$ are found. At the outer four points and at the four points at half-radius, data could not always be acquired, due to the fact that displacements here are smaller than at the center, and are therefore more prone to be superimposed with noise. This is especially the case for a combination of lower temperatures, lower excitation voltages and very high or very low frequencies. High frequencies correlate with low displacements because equilibrium is not reached, very low frequencies result in increased noise. All of these limiting effects result in a reduced signal-to-noise ratio. The data taken at these points are not evaluated except for fitting a sphere to confirm the spherical shape of the displacement and ensure the sample is still clamped symmetrically in the sample holder.

Figure 6

Typical distribution of the displacement across the sample. The eight points at half radius and at the edge of the PLD electrode were taken to ensure that the displacement was spherical, which was confirmed by fitting a sphere to the data. The displacement values taken at the outer points are not further evaluated here

The proneness of the outer points to be overlaid with noise partially explains the discrepancy between an exact calculation of R from D₀ according to Eq. (11) and the result of a spherical fit shown in Fig. 6, which serves only to demonstrate that the displacement can be described in good approximation as spherical. For further evaluation, only the maximum displacement at the sample center is taken.

LDV measurements on the CeO₂ sample

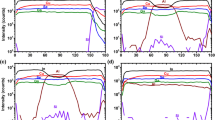
In Fig. 7a–d, the measured displacements of the CeO₂ sample at 800 °C, 850 °C, 900 °C, and 950 °C are shown. It can be seen that the displacements increase with increasing pumping voltage and temperature, and with decreasing pumping frequency. Measurements at lower temperatures were attempted with the SP-LDV, but yielded no clearly discernible peaks and are therefore not shown here.

Figure 7

The displacements at the center of the CeO₂ sample at temperatures ranging from 800 to 950 °C with pumping voltages ranging from 0.25 to 1.0 V_PP and excitation frequencies ranging from 0.1 to 10 Hz. At T = 800 °C, D-LDV measurements ranging down to 0.001 Hz are also shown. The bottom part of the figure shows the common legend

The curves of the displacement taken with the SP-LDV plotted over the frequency flatten toward low frequencies. A minor exception from this observation is the measurements obtained at 900 °C, where the displacements seem to start rising again below 0.5 Hz pumping frequency. The maximum displacements measured with the SP-LDV are 35.4 nm at 800 °C, 50.1 nm at 850 °C, 79.4 nm at 900 °C, and 49.2 nm at 950 °C. At 950 °C, the measured displacements obtained with a pumping voltage of 1.0 V are consistently lower than those obtained with 0.75 V. At 800 °C, additional D-LDV measurements are shown. They extend to lower frequencies than are accessible with the SP-LDV. After reaching a plateau between pumping frequencies of 0.5 Hz and 2 Hz, the displacements start to increase again and reach another plateau below 0.01 Hz, with a maximum displacement of 218 nm.

LDV measurements of the displacement of the Ce_0.8Zr_0.2O₂ samples

Except for the pumping voltage range, the SP-LDV measurements on the CZO80 samples were taken in the same way as on the CeO₂ sample. They are expected to exhibit measurable displacements at lower temperatures than the sample with a CeO₂ thin film due to the enhanced reducibility outweighing the diminished chemical expansion coefficient [1, 5, 21]. The temperature range was chosen lower than that for CeO₂.

In Fig. 8a–e, the displacements at five different temperatures ranging from 600 to 800 °C are shown. It is again apparent that the displacement increases with increasing temperature and pumping voltage, and decreases with increasing pumping frequency. The measured displacements reach a plateau at low pumping frequencies. The maximum displacements are 13.1 nm at 600 °C, 19.6 nm at 650 °C, 30.2 nm at 700 °C, 25.2 nm at 750 °C, and 32.7 nm at 800 °C.

Figure 8

a–e The measured displacements of the CZO80 samples, taken with the SP-LDV at the sample center at temperatures ranging from T = 600 °C to T = 800 °C, excitation frequencies ranging from f = 0.1 Hz to f = 10 Hz, and pumping voltages ranging from U_pump = 0.25 V_PP to U_pump = 0.75 V_PP

It can also be seen that the displacements of sample CZO80-2 diminish after exposure to temperatures higher than the pre-annealing temperature. In particular, the displacement of sample CZO80-2 is decreased after re-annealing. At 600 °C with U_pump = 0.75 V and f_pump = 1 Hz, the displacement taken after re-annealing at 750 °C is diminished by 18% compared to the displacement taken after annealing at 700 °C. At 650 °C, this discrepancy is 38%, and at 700 °C it is 42%. After re-annealing at 800 °C, the displacement taken at 700 °C is 32% lower than after re-annealing at 750 °C. Possible reasons for this finding will be discussed in Section “Thin-film morphology and origin of cracks”.

Not all data curves extend to the lowest frequency of 0.1 Hz, since it was not always possible to identify a peak due to low-frequency noise. Both samples were damaged either during application of a new PLD electrode (CZO80-1) or during measurement (CZO80-2); therefore, the D-LDV measurements could not be repeated.

Discussion

Crystallographic phases

By depositing the films on [100]-oriented single crystal substrates with a similar lattice constant, the largely amorphous as-deposited films are textured during the annealing process. This is illustrated by the fact that the XRD spectra exhibit only the (200), (400), and (220) reflexes, and lack the dominant (111) reflex [1, 1]. The 8YSZ reflexes of the substrate are also visible. The (220) reflex at 48° is weaker than the (200) and (400) reflexes in the present study, while from the literature it is expected to be stronger than the other two [42]. The composition of the spectrum of mainly the (200) and (400) reflexes indicates the film adopted the preferential (100) texture of the substrate during annealing and crystallization.

SP-LDV and D-LDV data

The detection limit of the measurement, taken as the root mean square of the 20 frequency bins above and 20 frequency bins below the excitation frequency in the Fourier transform of the time signal (i.e., the effective noise level around the excitation frequency), ranges from 0.07 nm at 10 Hz and 600 °C to 9.7 nm at 0.1 Hz at 950 °C for the SP-LDV and from 0.2 nm at 10 Hz to 9 nm at 0.001 Hz and 800 °C for the D-LDV, demonstrating the ability to detect small displacements at lower frequencies with the novel differential approach than previously possible.

The SP-LDV measurements on the CeO₂ sample shown in Figs. 7a and 9 show a deviation from the measurements taken with the D-LDV at frequencies below 1 Hz. The latter are considered to be correct. The deviation of the SP-LDV values is attributed to non-application compliant use of the device, as explained in Appendix “Discussion of the second plateau in D-LDV data”.

Figure 9

The normalized displacements taken at the centers of the two CZO80 samples and the CeO₂ sample T = 800 °C with pumping voltages of U_pump = 0.75 V and U_pump = 1 V and pumping frequencies ranging from f = 0.1 Hz to f = 10 Hz (SP-LDV) and f = 0.001 Hz to f = 10 Hz (D-LDV)

Comparison with calculated displacements and literature data

For some combinations of temperature and oxygen partial pressure, there are in-situ HT-XRD and dilatometry data available [1, 8] showing the isothermal chemical expansion upon partial reduction. From these data, the expected displacements were calculated for the different samples and are listed in Tables 2 and 3. Lacking the Young’s modulus and Poisson’s ratio of CZO80 and of CeO₂ at higher temperatures, those for undoped ceria at 600 °C were used instead [44]. Because the films studied here are much thicker than those in [13,14,15] and no analogous data were available for the materials used in this work, literature data from bulk samples are used here for comparison and calculation of expectation values.

Table 2 Expected displacements $D_{{{\text{CeO}}_{2} }}^{{{\text{calc}}}}$ of the CeO₂ sample calculated from literature data [6, 8, 44,45,46] and from the sample parameters with Eq. (11)

Table 3 Expected displacements D^calc of the CZO80 samples calculated from literature data [5, 6, 44, 46] and the sample parameters with Eq. (11)

CeO₂

The calculated values of the displacement for CeO₂ at T = 800 °C and T = 900 °C are obtained using Eq. (11), the parameters in Table 1, and the materials data from [6, 8, 44,45,46]. The uncertainty is calculated with Eq. (30). The results are listed in Table 2. The Poisson ratio of 0.33 and elastic constant Young’s modulus of 11 mol-per cent yttria-stabilized zirconia (11YSZ) were taken from [46], with the Young’s modulus approximated as C₁₁ and extrapolated to 800 °C and 900 °C. Values of $E_{{11{\text{YSZ}},{ }800\;^\circ {\text{C}}}}^{{}} { } = { }352\;{\text{GPa}}$ and of $E_{{11{\text{YSZ}},{ }900\;^\circ {\text{C}}}}^{{}} { } = { }345\;{\text{GPa}}$ were found, agreeing with the value of 330 GPa in 8YSZ at 800 °C derived from MD simulations [47] and used in [11].

For the Young’s modulus and Poisson ratio of ceria, the values at 600 °C from [44] were used, lacking data at higher temperatures and under partial reduction. The calculated displacements are not reached. However, it shall be noted that these calculations are valid for dense, crack-free and homogenous, i.e., virtually undisturbed films only. Real samples like used in industry and characterized in this work may exhibit grains, clusters or cracks as presented in Section “Morphology of thin films”. At T = 800 °C, the experimentally detected displacement of $D_{{{\text{CeO}}_{2} ,800\;^\circ {\text{C}}}}^{{{\text{exp}},{\text{ D - LDV}}}} { } = { }218{ }$ nm taken with the D-LDV falls short of the calculated value $D_{{{\text{CeO}}_{2} ,800\;^\circ {\text{C}}}}^{{{\text{calc}}}} { } = { }\left( {1388{ } \pm { }66} \right)$ nm by a factor of 6.4.

The general trend is as expected. There is a clear dependence of the displacement from temperature, pumping voltage, and pumping frequency. The measured displacements approach a plateau toward lower excitation frequencies and increase with increasing temperature and pumping voltage. However, the course of the measured displacements is reduced overall compared to the calculated values for undisturbed films. Physical effects potentially leading to this deviation are discussed below in Section “Thin-film morphology and origin of cracks”.

The measured displacement of D = 48.4 nm shown in Fig. 7 corresponds to an expansion of ε = 0.006% according to the model described above (Eq. 11). Under the conditions of the experiment (T = 900 °C, U_pump = 1.0 V, corresponding to an oxygen activity of $1.37 \cdot 10^{ - 18}$ bar), [8] reports an expansion of 0.78% in undoped ceria.

CZO80

Expected values for CZO80 of the displacements calculated from literature data [5, 6, 44,45,46] and the thicknesses of the substrates and films listed in Table 1 with Eq. (11) are listed in Table 3. As elastic parameters for partially reduced CZO80 at elevated temperatures are lacking, those for CeO₂ at 600 °C were used instead [44]. The Poisson’s ratio of 0.33 and the Young’s modulus were again taken from [46], with the value at 800 °C extrapolated from the data. The uncertainties are calculated as a total error differential using the uncertainties of the thicknesses of the substrates and thin films, and that of the sample radius according to Eq. (30). It can again be seen that the measured displacements do not reach the calculated values, which range from 309 nm at 700 °C to 341 nm at 800 °C. As the CZO80 samples were only investigated with the SP-LDV and are far from reaching equilibrium, the calculated and measured displacements will not be extensively discussed.

The measured displacements taken from sample CZO80-2 at 700 °C were found to be diminished by 18–42% after re-annealing at 750 °C. Possible reasons for this finding are discussed in 5.4 and 5.5, together with the discrepancies between the model and the experimental data.

Comparison of CeO₂ and CZO80

CZO80 builds up a greater oxygen non-stoichiometry δ than pure ceria in the range of temperatures and oxygen partial pressures considered in this work. At 800 °C, the non-stoichiometry in CZO80 exceeds that in ceria in the oxygen partial pressure range of ${\text{p}}_{{{\text{O}}_{2} }} { } > { }5 \cdot 10^{ - 22} \;{\text{bar}}$ [21], corresponding to $U_{{{\text{pump}}}} { } < { }1.1\;{\text{V}}$. In this range, CZO80 has a smaller chemical expansion coefficient α_c than undoped ceria [5, 7]. Only in the range of large non-stoichiometries of about $\delta \approx 0.2$ does α_c approach the value found in pure CeO₂ [5], which is not achieved within the conditions used in this work. The greater non-stoichiometry in CZO80 outweighs the smaller expansion coefficient [5], leading to the expectation that CZO80 exhibits larger chemical expansion ε than ceria under the conditions to which the CZO80 thin films are exposed in this work. This arises from the fact that the added zirconia promotes the reduction by lowering the formation enthalpy for oxygen vacancies due to energetically preferring sevenfold coordination over eightfold [21]. As a consequence, a higher oxygen non-stoichiometry compared to pure ceria occurs under the same conditions, which overcompensates the smaller chemical expansion coefficient [5].

The change in film thickness $\Delta t_{{\text{f}}}$ in the ceria sample with a pumping voltage of U_pump = 1 V corresponds to an oxygen activity of $1.7 \cdot 10^{ - 20}$ at T = 800 °C. It causes a chemical expansion in the bulk material of $\varepsilon = 0.00186$ [8]. This results in a change in film thickness of $\Delta t_{{\text{f}}} = 12.8\;{\text{nm}}$ (see Eq. (24) in Appendix “Derivation of the biaxial modulus and biaxial strain”), which is considerably lower than the detected displacement of 218 nm measured with the D-LDV under these conditions. It is apparent from this ratio that the dominant contribution to the displacement is the substrate bending. This corresponds to data from prior research on praseodymia ceria solid solution thin films that were acquired with the SP-LDV setup [11]. There, ratios between substrate bending and film thickness change of up to 60 are found, mainly depending on the ratio of film to substrate thickness.

Considering Eq. (11) and given that the substrate bending D₀ is large compared to the change in film thickness $\Delta t_{{\text{f}}}$, one can normalize the displacement with respect to substrate and film thicknesses for better comparability. The normalized displacements correspond to a sample with a film thickness of $t_{{\text{f}}}^{*} = 1$ µm and a substrate thickness of $t_{{\text{s}}}^{*} = 300$ µm:

$$D_{{{\text{norm}}}} = D \cdot \frac{{t_{{\text{f}}}^{*} }}{{t_{{\text{f}}} }} \cdot \left( {\frac{{t_{{\text{s}}} }}{{t_{{\text{s}}}^{*} }}} \right)^{2}$$

(12)

In Fig. 9, normalized displacements of undoped ceria are compared to those of CZO80 at 800 °C. It can be seen that the CZO80 samples exhibit much larger normalized displacements at U_pump = 0.75 V and high excitation frequencies of 1 Hz and above than the ceria sample does even at U_pump = 1 V (which is equivalent to a lower oxygen activity and hence higher non-stoichiometry in the thin film) at the same pumping frequencies. This is attributed to larger expansion due to greatly enhanced reducibility of the solid solution stemming from the addition of zirconia, as proposed by [21]. The trend of the displacement toward lower frequencies is the same for both materials in that the curve flattens and seems to become a plateau. The pumping frequency dependence of the displacement of the CZO80 sample is stronger compared to the CeO₂ sample, which exhibits a relatively flat curve of displacement over frequency in the high-frequency region above 1 Hz. This suggests that in CZO80 a higher ionic mobility is found and that it is easier for an oxygen vacancy to migrate through the material than in undoped ceria. This can be explained by the greater ionic conductivity in CZO80 compared to ceria [22, 23].

Thin-film morphology and origin of cracks

Cracks can partially accommodate the chemical expansion of the films, and thus their formation and temperature dependence of width must be discussed. Cracks are clearly visible in SEM images of the annealed oxide thin films. For comparison with the experimental values, the width of the cracks and distance between them are calculated from the distance, from the mismatch in thermal coefficients of coefficients (TCEs) of the substrate and film materials, and the temperature difference between room temperature and the respective annealing temperatures. It is found that the observed cracks in the CZO80 thin film agree roughly with the expected values, but leave room for other explanations, and the cracks in the CeO₂ thin film cannot stem purely from the mismatch in TCEs.

The TCEs of CeO₂ and 8YSZ used here are $\alpha_{T}^{{{\text{CeO}}_{2} }} { } = { }12.68{ } \cdot { }10^{ - 6} \;{\text{K}}^{ - 1}$ for CeO₂ [6] and ${\upalpha }_{{{\text{T}},8{\text{YSZ}}}} { } = { }10.2 \cdot 10^{ - 6} \;{\text{K}}^{ - 1}$ for 8YSZ [6], with a difference of $\Delta \alpha_{T} \approx 2.5 \cdot 10^{ - 6} \;{\text{K}}^{ - 1}$. The cracks in Fig. 5a have a mean distance of $d_{{{\text{crack}}}}^{{{\text{CeO}}_{2} }} { } = { }$(8 ± 2) µm, taken as the mean value of the width and length of 23 film segments. On a segment of the size $d_{{{\text{crack}}}}^{{{\text{CeO}}_{2} }}$, a temperature drop of ΔT = 1000 K would cause a mismatch in absolute thermal contraction between the thin film and the substrate of

$$\Delta L_{{{\text{YSZ - CeO}}_{2} }} = \Delta \alpha_{T} \cdot \Delta T \cdot d_{{{\text{crack}}}}^{{{\text{CeO}}_{{2}} }} = \left( {20 \pm 6} \right)\;{\text{nm}}$$

(13)

This does not agree with the cracks shown in Fig. 5b having a mean width of $w_{{{\text{crack}}}}^{{{\text{CeO}}_{2} }} { } = { }$(53 ± 12) nm, taken at 11 positions.

The TCE of CZO80 is $\alpha_{{T,\;{\text{CZO}}80}} = 11.96 \cdot 10^{ - 6} \;{\text{K}}^{ - 1}$ [5], with a mismatch of $\Delta \alpha_{T} \approx 1.8 \cdot 10^{ - 6} \;{\text{K}}^{ - 1}$ with respect to 8YSZ. The cracks in Fig. 5c have a mean distance of $d_{{{\text{crack}}}}^{{{\text{CZO}}80}}$$= { }$(42 ± 18) µm, taken on two diagonal lines across the image, with a total of fifteen cracks. On a segment of the size $d_{{{\text{crack}}}}^{{{\text{CZO}}80}} ,$ a temperature drop of ΔT = 700 °C would cause a mismatch in absolute thermal contraction between the thin film and the substrate of

$$\Delta L_{{{\text{YSZ - CZO}}80}} = \Delta \alpha_{T} \cdot \Delta T \cdot d_{{{\text{crack}}}}^{{{\text{CZO}}80}} = \left( {52 \pm 22} \right)\;{\text{nm}}$$

(14)

This agrees within the statistic error margin with the cracks shown in Fig. 5b having a mean width of $w_{{{\text{crack}}}} { } = { }$(61 ± 18) nm, taken at 8 positions.

Another mechanism leading to cracks in the thin films is the contraction of the film due to a phase transformation during annealing. The as-deposited films are largely amorphous [48, 49] and exhibit an oxygen deficiency [48] because oxygen is more volatile than cerium and zirconium and, therefore, pumped out of the deposition chamber with greater ease than the metal ions. During crystallization, the amorphous material of the film contracts [49, 50], due to the crystallization itself and due to the elimination of the oxygen deficit and the corresponding, negative chemical expansion. Ceria films grown on different substrates have been investigated regarding their lattice parameters [49, 51] showing contraction during the crystallization process. Ceria films deposited by spray pyrolysis were reported to contract by as much as 5% during annealing at 800 °C [49], which by far exceeds the ratio of crack width to crack distance. This ratio w:d for the samples investigated in this work is 0.0066% (CeO₂) and 0.0015% (CZO80).

Heating to higher temperatures than the annealing temperature might cause the cracks to close further and the edges of the film segments might ultimately be pressed against each other, creating lateral stress in the thin film. This stress would cause the sample to bend, which would then be the reference state from which the sample is bent by the stress caused by chemical expansion during electrochemical pumping, and the bending due to chemical expansion remains unaffected.

On the other hand, heating to temperatures above the annealing temperature could be considered equivalent to re-annealing at higher temperatures. This would cause the cracks to widen by two mechanisms: Firstly, re-annealing and subsequent cooling to lower temperatures might result in wider cracks caused by the mentioned mismatch in TCEs. Secondly, it might lead to further crystallization, i.e., growth of crystallites, leading to further contraction of the film, as reported in [49].

This would result in lower substrate bending and therefore displacement after re-annealing, which could explain the diminished displacements taken from sample CZO80-2 after re-annealing the sample at 750 °C and 800 °C.

In summary, the cracks are therefore assumed to close partially due to the difference in TCEs during heating to the temperatures at which the LDV experiments are performed, and close further due to chemical expansion in the thin film.

Comparison of the model and experimental data

The fact that the measured displacements do not reach the calculated values can be attributed to a variety of factors. Among them are the cracks in the thin films shown in Fig. 5 and their influence as discussed in Section “Thin-film morphology and origin of cracks”. Other, but potentially minor effects, include overpotentials during pumping at the electrode-film and substrate–electrode interfaces, oxygen leakage through the Pt_0.9Rh_0.1 PLD electrode covering the thin film, and the possibility that the defect chemical equilibrium is not reached even at the lowest pumping frequencies.

The possibility that the PLD electrodes are not gas-tight and oxygen was supplied by the surrounding air cannot be ruled out. This would lead to a reduced effective pumping voltage. This possibility is further discussed in Appendix “Oxygen leakage through the PtRh electrode”.

In the case that equilibrium is simply not reached even after 1000 s, corresponding to the lowest pumping frequency of 0.001 Hz, the displacement would not reach a steady plateau, as it clearly does in Figs. 9 and 7a) Significantly higher equilibration times reported previously for the conductivity of a CZO thin film prepared from the same target as in this work can be explained by the absence of a three-phase boundary as described in [52,53,54], which is then the factor limiting the exchange of oxygen through the gas/thin film interface.

Contribution of the substrate to the bending of the sample

Considering the findings of [10], the displacement from the YSZ substrate alone needs not be taken into account to a small overall contribution only. There, samples with different film thicknesses were prepared, and the displacement correlated with the film thickness. An extrapolation to $t_{{\text{f}}} = 0\;{\text{nm}}$ showed that the displacement contribution of the substrate was $\pm \;1\;{\text{nm}}$, and substrate bending due to an anisotropically expanding substrate was disregarded.

In [55], the ionic conductivity of 8YSZ is found to be independent of the oxygen partial pressure in a large range. This means that in the studied p_O2 range, the concentration of oxygen vacancies must also be virtually constant. Instead of taking up and storing additional oxygen, the highly conductive substrate acts releases surplus oxygen at the three-phase boundary consisting of the substrate, the screen-printed backside electrode, and the surrounding air. With a constant oxygen vacancy concentration, the lattice parameter can also be regarded as constant, meaning that the chemical expansion in the substrate is negligible.

Conclusions

The displacements of the samples, which are dominated by the deflection D₀, are determined and can be described as spherical in good approximation (Fig. 7), as was predicted by the model. Slight deviations from the spherical shape are assumed to be caused by the edge of the sample neither being covered by the thin film nor the electrode. It has been shown that the application of SP-LDV is an adequate tool to determine the displacement of the sample at high temperatures at a nanometer scale in the frequency range above 1 Hz. Due to the higher noise level in the low-frequency range of the SP-LDV, small vibrations in the nanometer range below 1 Hz cannot be detected. At lower frequencies, another experimental approach is required. As a consequence, the authors have developed a new differential LDV (D-LDV), allowing for measurements at very low frequencies by eliminating atmospheric perturbations and the influence of thermal expansion of the sample holder due to temperature instability. This novel system is demonstrated to be able to measure for the first time displacements at 1 mHz, where the excitation frequency is low enough for the displacement to become quasi-static.

The larger normalized displacements in the CZO80 samples than in the ceria sample can be explained by two main factors. Firstly, the fact that the higher non-stoichiometry in CZO80 [21, 22] overwhelms the lower chemical expansion coefficient in CZO80 with regard to ceria [5, 7]. Secondly, the lower ratio of crack width to crack distance in CZO80 leads to a smaller expansion being consumed by the closing of the cracks before the sample is bent by lateral stress in the thin film.

Furthermore, in the case of CZO80, the displacements did not reach the expected values by a factor of approx. 24–44 at 700 °C and 22–32 at 800 °C. In the case of ceria, this factor was even 92 at T = 800 °C and 159 at T = 900 °C with the SP-LDV and 6.4 at T = 800 °C with the D-LDV. The potential reasons for this behavior are partially discussed above and include cracks in the films, contact potentials leading to the build-up of space charges in the sample, and the lack of reliable data for modeling. These include mechanical properties of the used materials at high temperatures and under partial reduction.

It was found that the displacements exhibited by sample CZO80-2 were significantly smaller after re-annealing it at higher temperatures. The original annealing temperature was 700 °C, and displacements were diminished by around a factor of 2 after re-annealing it at 750 °C for another 10 h.

Thinking of potential applications, dense and compact films are required for ceria-based thin films as actuator materials. Undoped ceria will only be relevant for actuator purposes if the oxygen activity can be set below a_O2 approx. $10^{ - 20}$. To realize actuators with higher controllability and lower energy consumption, ceria zirconia or ceria praseodymia solid solutions are to be favored.

In applications using ceria and its solid solutions as, e.g., solid electrolytes, mechanical stress and/or displacements due to chemical expansion are undesirable. It could be shown that cracks prevent the film-substrate sandwich from displacement effectively. Consequently, a preparation route resulting in defined crack width and density could eliminate these application relevant problems. Here, the different TCEs between substrate and film have to be considered closely. If the film has an insulating function, additional challenges may arise, as top and bottom electrode might be short-circuited by these cracks.

Measurements on further CZO systems are in progress, with the aim of determining the displacement of samples with other Ce/Zr ratios. In addition, the influence of the substrate thickness will be investigated by conducting similar experiments on samples with identical, co-deposited films, but differently thick substrates.

Appendix

Evaluation of LDV data

The evaluation of LDV data requires several steps, depending on the time dependence of the displacement, e.g., the presence of plateaus or other anharmonic contributions.

An LDV time signal is shown in Fig. 10a. It is apparent that the displacement cannot be discerned from the time signal, making further data processing steps necessary. The according Fourier transform of the displacement signal shown in Fig. 10b exhibits a delta-shaped peak at the pumping frequency, with the height of the peak proportional to the mean value of the displacement over the duration of the measurement. The displacement D is calculated from the height of the peak U_LDV via the relation

$$D = \Gamma_{{{\text{LDV}}}} \cdot U_{{{\text{LDV}}}}$$

(15)

with $\Gamma_{{{\text{LDV}}}}$ being the decoder range of the LDV controller in m V^–1. In the case of the SP-LDV, it is $\Gamma_{{\text{SP - LDV}}} = 100\; {\raise0.7ex\hbox{${{\text{nm}}}$} \!\mathord{\left/ {\vphantom {{{\text{nm}}} {\text{V}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\text{V}}$}}$.

Figure 10

a Time signal and b spectrum after Fourier transformation of a LDV measurement at the center of the CeO₂ sample at T = 900 °C with U_pump = 1 V, f_pump = 1 Hz, and R_D = 50 nm/V

In Fig. 10b, a second peak at the double excitation frequency can be seen. This is due to the fact that the displacement signal is not perfectly sinusoidal. Due to its small size relative to the first peak at 1 Hz, anharmonic effects can be disregarded and the displacement is given by the first peak at the excitation frequency.

In the case of very low-frequency measurements with the D-LDV, additional steps are taken to filter the signal. The time signal is filtered with a sixth-order digital Butterworth bandpass filter [56] before the Fourier transform, and the height of the delta-shaped peak at the excitation frequency is extracted from the spectrum. The displacement is calculated from the height of the peak analogous to the SP-LDV, with the difference that the factor of proportionality between the height of the peak and the displacement is increased by the wavelength ratio of the two sensor heads λ_D-LDV/λ_SP-LDV to account for the different laser wavelengths: ${\Gamma }_{{\text{SP - LDV}}} { } = { }244\;{\raise0.7ex\hbox{${{\text{nm}}}$} \!\mathord{\left/ {\vphantom {{{\text{nm}}} {\text{V}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\text{V}}$}}$.

Sample holders

The samples were placed inside an ultrasound-milled alumina sample holder with a flat, circular depression to accommodate the sample with a tolerance of 100 µm. The samples were clamped around the outermost edge only, as laid out in [6]. To ensure that the back side of sample does not stick to the sample holder, no glues or bonds were used. This method ensures that the sample holder has negligible influence on the bending of the sample, and the sample can bend freely so that it is not constrained in its upward bending.

Derivation of the biaxial modulus and biaxial strain

Under the condition that the relevant properties (Young’s modulus E, Poisson’s ratio $\nu$, chemical expansion coefficient α_C, and thermal expansion coefficient α_T) of the film and substrate are isotropic, the lateral stress in the expanding film laterally constrained by a significantly thicker substrate will be uniform. This stress can be expressed as:

$$\begin{aligned} \sigma _{{{\text{f}},x}} & = \varepsilon _{{{\text{f}},x}} E_{{\text{f}}} + \nu _{{\text{f}}} \sigma _{{{\text{f}},y}} \\ \sigma _{{{\text{f}},y}} & = \varepsilon _{{{\text{f}},y}} E + \nu \sigma _{{{\text{f}},x}} \\ \sigma _{{{\text{f}},z}} & = 0 \\ \end{aligned}$$

(16)

Herein, the subscript f denotes the film, since only stress in the film is regarded. With $\sigma_{{{\text{f}},x}} = \sigma_{{{\text{f}},y}} = \sigma_{{\text{f}}}$ and $\varepsilon_{{{\text{f}},x}} = \varepsilon_{{{\text{f}},y}} = \varepsilon_{{\text{f}}}$ it follows:

$$\sigma_{{\text{f}}} = \varepsilon_{{\text{f}}} \frac{{E_{{\text{f}}} }}{{1 - \nu_{{\text{f}}} }}$$

(17)

${\raise0.7ex\hbox{${E_{{\text{f}}} }$} \!\mathord{\left/ {\vphantom {{E_{{\text{f}}} } {\left( {1 - \nu_{{\text{f}}} } \right)}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\left( {1 - \nu_{{\text{f}}} } \right)}$}}$ is also known as the biaxial modulus of the film [57].

Enhanced vertical expansion in a constrained film

Considering a cubicle of the size $t_{{\text{f}}}^{3}$ in the constrained film and applying chemical expansion, the expansion perpendicular to the film plane is enhanced by constraining the lateral expansion. This will be calculated in three steps for expansion in the three spatial directions z, x, and y (in this order).

• 1.

  Expansion in z direction:

  First, we consider the vertical expansion (in z-direction), which is not constrained. The expanded film thickness $t_{{\text{f}}}^{^{\prime}}$ after (unconstrained) expansion in z direction reads:

  $$t_{{\text{f}}}^{^{\prime}} = \left( {1 + \varepsilon_{{\text{f}}} } \right)t_{{\text{f}}}$$

  (18)
• 2.

  Constrained expansion in x direction:

  This expanded film thickness is now subjected to further expansion due to lateral strain as a consequence of the constrained lateral expansion. In a uniaxially constrained, expanding material, the proportionality factor between the strain and the expansion perpendicular to the constraint is the Poisson’s ratio $\nu$ of the respective material. As explained in 7.1, constraining the expansion of a film in x and y directions leads to an enhancement of lateral stress by a factor ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\left( {1 - \nu_{{\text{f}}} } \right)}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\left( {1 - \nu_{{\text{f}}} } \right)}$}}$ compared to a uniaxially constrained sample. Applying this factor to the vertical expansion due to lateral constraint in x direction the proportionality between the lateral stress and perpendicular expansion is ${\raise0.7ex\hbox{${\nu_{{\text{f}}} }$} \!\mathord{\left/ {\vphantom {{\nu_{{\text{f}}} } {\left( {1 - \nu_{{\text{f}}} } \right)}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\left( {1 - \nu_{{\text{f}}} } \right)}$}}$, and we obtain the expanded film thickness ${\text{t}}_{{\text{f}}}^{{^{\prime\prime}}}$ after expansion in z and x directions:

  $$t_{f}^{^{\prime\prime}} = \left( {1 + \frac{{\nu_{f} }}{{1 - \nu_{f} }}\varepsilon_{f} } \right)t_{f}^{^{\prime}}$$

  (19)
• 3.

  Constrained expansion in y direction:

  The vertical expansion due to lateral constraint in y direction is analogous to that in x-direction. The expanded film thickness $t_{{\text{f}}}^{{^{\prime \prime \prime } }}$ after expansion in all three directions reads:

  $$t_{{\text{f}}}^{{^{\prime \prime \prime } }} = \left( {1 + \frac{{\nu_{{\text{f}}} }}{{1 - \nu_{{\text{f}}} }}\varepsilon_{{\text{f}}} } \right)t_{{\text{f}}}^{{^{\prime \prime } }}$$

  (20)

  Inserting Eqs. (18)–(20) into one another, we obtain:

  $$\begin{aligned} t_{{\text{f}}}^{{^{\prime \prime \prime } }} & = \left( {\frac{{\nu_{{\text{f}}} }}{{1 - \nu_{v} }}\varepsilon_{{\text{f}}} + 1} \right)^{2} \left( {\varepsilon_{{\text{f}}} + 1} \right)t_{{\text{f}}} \\ \leftrightarrow t_{{\text{f}}}^{{^{\prime \prime \prime } }} - t_{{\text{f}}} & = \left( {\left( {\frac{{\nu_{{\text{f}}} }}{{1 - \nu_{{\text{f}}} }}\varepsilon_{{\text{f}}} + 1} \right)^{2} \left( {\varepsilon_{{\text{f}}} + 1} \right) - 1} \right)t_{{\text{f}}} \\ \end{aligned}$$

  (21)

  which, after eliminating all terms quadratic and cubic in $\varepsilon_{{\text{f}}}$ (since $\varepsilon_{{\text{f}}} \ll 1$), leads to the vertical expansion in a laterally constrained film:

  $$\Delta t_{{\text{f}}} = t_{{\text{f}}}^{{^{\prime \prime \prime } }} - t_{{\text{f}}} = \varepsilon_{{\text{f}}} t_{{\text{f}}} \left( {\frac{{1 + \nu_{{\text{f}}} }}{{1 - \nu_{{\text{f}}} }}} \right)$$

  (22)

Derivation of the deflection $D_{0}$

Here, the expected deflection D₀ will be calculated from the sample parameters and the bulk chemical expansion. As mentioned in 1.2, a small-angle approach is employed. For the sample and deflection depicted in Fig. 2, the deflection can be expressed as:

$$\begin{aligned} D_{0} & = R\left( {1 - \cos \varphi } \right) \\ & \approx R\left( {1 - \left( {1 - \frac{1}{2}\varphi ^{2} } \right)} \right)\quad ({\text{for small}}\;\varphi ) \\ v & = \frac{1}{2}R\varphi ^{2} \\ \end{aligned}$$

(23)

with R being the radius describing the spherical bending, and φ the bending angle. The sample radius r and the bending radius R are related via:

$$r = R \sin \varphi \approx R\varphi\,({\text{for small}}\;\varphi)$$

(24)

Inserting the two equations above into one another yields:

$$D_{0} = \frac{{r^{2} }}{2R}$$

(25)

The Stoney equation relates stress in thin films to the curvature of significantly thicker substrates [35, 36]:

$$\sigma_{{\text{f}}} t_{{\text{f}}} = \frac{{E_{{\text{s}}} t_{{\text{s}}}^{2} }}{{6\left( {1 - \nu_{{\text{s}}} } \right)R}},$$

(26)

wherein $\sigma_{{\text{f}}}$ denotes lateral stress in the film, $t_{{{\text{f}}/{\text{s}}}}$ the thicknesses of the film and substrate, $E_{{\text{s}}}$ the Young’s modulus of the substrate, and $\nu_{{\text{s}}}$ the Poisson’s ratio of the substrate. Solving the Stoney Equation for stress and equating it with the expression for the stress derived in 7.2 (Eq. 19), one obtains:

$$\varepsilon_{{\text{f}}} E_{{\text{f}}} \frac{1}{{1 - \nu_{{\text{f}}} }} = \frac{{E_{{\text{s}}} t_{{\text{s}}}^{2} }}{{6t_{{\text{f}}} \left( {1 - \nu_{{\text{s}}} } \right)R}}$$

(27)

$$\to R = \frac{1}{{6\varepsilon_{{\text{f}}} }}\frac{{E_{{\text{s}}} t_{{\text{s}}}^{2} (1 - \nu_{{{\text{f}})}} }}{{E_{{\text{f}}} t_{{\text{f}}} \left( {1 - \nu_{{\text{s}}} } \right)}}$$

(28)

Inserting this expression for the bending radius R into the sample bending (Eq. 27), one can now calculate the sample bending from the sample parameters and the expansion ε:

$$D_{0} = 3\varepsilon_{{\text{f}}} r^{2} \frac{{E_{{\text{f}}} t_{{\text{f}}} \left( {1 - \nu_{{\text{s}}} } \right)}}{{E_{{\text{s}}} t_{{\text{s}}}^{2} \left( {1 - \nu_{{\text{f}}} } \right)}}$$

(29)

Calculation of the uncertainty of the calculated displacement

The uncertainty of the calculated displacement follows from Gaussian error propagation using the uncertainties of the substrate and film thicknesses $\Delta \left( {t_{{\text{s}}} } \right)$ and $\Delta \left( {t_{{\text{f}}} } \right)$ listed in Table 1 and the uncertainty of the substrate radius $\Delta \left( r \right) = 0.1\;{\text{mm}}$:

$$\begin{aligned} \Delta \left( {D_{{{\text{calc}}}} } \right) & = \sqrt {\left( {\frac{{\partial D_{{{\text{calc}}}} }}{\partial r}\Delta \left( r \right)} \right)^{2} + \left( {\frac{{\partial D_{{{\text{calc}}}} }}{{\partial t_{{\text{f}}} }}\Delta \left( {t_{{\text{f}}} } \right)} \right)^{2} + \left( {\frac{{\partial D_{{{\text{calc}}}} }}{{\partial t_{{\text{s}}} }}\Delta \left( {t_{{\text{s}}} } \right) } \right)^{2} } \\ & = 3\varepsilon_{{\text{f}}} \sqrt {\left( {2t_{{\text{f}}} r\frac{{E_{{\text{f}}} }}{{E_{{\text{s}}} t_{{\text{s}}}^{2} }}\Delta \left( r \right) } \right)^{2} + \left( {\left( {r^{2} \frac{{E_{{\text{f}}} }}{{E_{{\text{s}}} t_{{\text{s}}}^{2} }} + \frac{{1 + \nu_{{\text{f}}} }}{{1 - \nu_{{\text{f}}} }}} \right)\Delta \left( {t_{{\text{f}}} } \right)} \right)^{2} + \left( {2t_{{\text{f}}} r^{2} \frac{{E_{{\text{f}}} }}{{E_{{\text{s}}} t_{{\text{s}}}^{3} }}\Delta \left( {t_{{\text{s}}} } \right)} \right)^{2} } \\ \end{aligned}$$

(30)

for a confidence level of 68,3%.

Calculation of the effective pumping voltage

With the deflections only barely reaching saturation (if at all), it is assumed that the majority of the substrate does not change its composition during voltage cycling, and with the back side of the substrate being exposed to air, the temperature-dependent total conductivity of single-crystal 8YSZ in air [58] is used. For the CeO₂ and CZO80 films, the temperature- and ${\text{p}}_{{{\text{O}}_{2} }}^{{}}$-dependent conductivities are taken from [19], where the same PLD targets and PLD setup were used as in this work, and interpolated to the ${\text{p}}_{{{\text{O}}_{2} }}^{{{\text{eff}}}}$ corresponding to the nominal voltage. A voltage divider with two ohmic resistances is modeled, and the corrected, effective pumping voltage $U_{{{\text{eff}}}}^{{}}$ defined as the electrochemical potential at the substrate–film interface reads:

$$U_{{{\text{eff}}}}^{{}} = U_{{{\text{pump}}}} \frac{{\frac{{t_{{\text{s}}} }}{{\sigma_{{\text{s}}} }}}}{{\frac{{t_{{\text{s}}} }}{{\sigma_{{\text{s}}} }} + \frac{{t_{{\text{f}}} }}{{\sigma_{{\text{f}}} }}}},$$

(31)

wherein $\sigma_{{\text{s}}}$ and $\sigma_{{\text{f}}}$ denote the conductivities of the substrate and film, and $t_{{\text{s}}}$ and $t_{{\text{f}}}$ the thicknesses of the substrate and film. The corrected effective oxygen partial pressure ${\text{p}}_{{{\text{O}}_{2} }}^{{{\text{eff}}}}$ is calculated from the temperature and effective pumping voltage by Eq. (7) (Fig. 11, Tables 4 and 5).

It is apparent that for high temperatures and pumping voltages, the difference between the nominal and corrected effective oxygen partial pressures is negligible compared to the errors from noise and inaccuracies of the applied voltages. As a consequence, only the nominal pumping voltage and temperature will be used to signify the experimental parameters.

Figure 11

The ${\text{p}}_{{{\text{O}}_{2} }}$-dependent conductivities of ceria and CZO80 at different temperatures, original data from [22]. These data were acquired from thin films which were prepared using the same PLD system and targets as for this work

Table 4 Correction of the applied voltages for the CeO₂ sample

Table 5 Correction of the applied voltages for the Ce_0.8Zr_0.2O₂ samples

Space-charge layers and overpotentials

The presence of different materials with different work functions in the sample leads to the build-up of space charge zones in the vicinity of the interfaces between the materials due to contact potentials. The work function of Pt is around 5.3 eV [59] to 5.65 eV [60], that of a (100) oriented ceria film around 4–4.4 eV [61]. This leads to the ceria film acquiring a positive potential relative to the Pt, which must be overcome. Based on these properties, the following hypothesis could explain the short plateau region of the displacement of the ceria sample seen in Figs. 7a and 9 in the frequency region between 2 and 0.5 Hz. It may be due to the applied pumping potential being countered by these space charges. Only after these space charges have been depleted by the pumping current, the displacement grows again. However, [53] reports that contact potentials do not affect the chemical capacitance and non-stoichiometry in praseodymia-ceria, and contact potentials are therefore disregarded.

Oxygen leakage through the PtRh electrode

Since the diffusion of oxygen through solids is temperature-activated and the diffusion coefficient has a finite value, this possibility must be considered. In the case of an oxygen supply from the ambient air through the PtRh electrode into the ceria/CZO80 thin film, the oxygen activity in the thin film would never reach the values calculated from Eqs. (7) and (11).

However, the diffusion coefficients of oxygen in ceria [62, 63] at 800 °C and 8YSZ [64] are significantly higher than in platinum [65] at 1450 °C, meaning oxygen transport from the PtRh–ceria/CZO80 interface through the thin film and into the substrate is faster than oxygen leak through the electrode. The rate of oxygen leakage through platinum reported in [65] at 1450 °C is 35 $\frac{{{\mu g}}}{{{\text{cm}}^{2} \cdot {\text{a}}}}$ through a Pt membrane of 25.4 µm thickness. Scaled to the dimensions of the PtRh electrode on the CeO₂ sample (9 mm diameter and 333 nm thickness), this equals to an oxygen flux of 54 ng per 1000 s, meaning that even at 1450 °C, only 0.04% of the total oxygen content in the ceria thin film can be re-supplied from the air through the electrode over the duration of one period at the lowest pumping frequency applied to the samples in this work. At the temperatures applied to the samples in this work, this already small portion is reduced further. Oxygen leakage through the PLD electrode can therefore be disregarded as a reason for the displacements not reaching the calculated values.

Discussion of the second plateau in D-LDV data

The displacements of the ceria sample shown in Figs. 7a and 9 show a deviation between the data acquired with the two LDVs. The displacements taken with the SP-LDV plateau below 1 Hz, while those taken with the D-LDV show a short plateau between 1 and 0.5 Hz, and then beg to rise again with decreasing excitation frequency. The deviation between the data from both LDVs is observed above the lowest excitation frequency applied in the SP-LDV setup, leading to the question which system detects the displacement correctly and why the other one is faulty in the frequency region where the deviation occurs.

The experiments were conducted on the same sample. They were repeated with both LDVs with the same sample holder without re-contacting the sample, and with the same waveform generator and power amplifier. Sampling the displacement from the SP-LDV with both PCI oscilloscope cards simultaneously and processing the acquired data on both computers yielded no difference in the detected displacement. Identical measurements with both LDV controllers and the SP-LDV yielded the same displacement as well, leaving the vibrometer sensor heads as the only possible reason for the discrepancy between the displacements detected with both LDVs. As the SP-LDV was built for high-frequency applications up to the MHz range and not intended to be used in the mHz range, the D-LDV, which was built specifically for low-frequency measurements, is considered more reliable at low frequencies below 1 Hz. The rise of the displacement at low frequencies toward a second plateau in the mHz range as detected with the D-LDV is therefore considered real.