Introduction

Fracture strengths and failure probabilities are highly important characteristics to evaluate the reliability of functional ceramic materials [1, 2]. Hence, an accurate determination of the materials’ fracture stresses and their statistical analysis is crucial. New challenges arise due to the application-driven ongoing trend toward thinner functional ceramic components. Well-established and widely used 3-point and 4-point bending tests as well as ring-on-ring (ROR) bending tests typically require rather thick specimens [3, 4], though. Furthermore, the 3-and 4-point bending tests exhibit drawbacks associated with the influence of edge defects, while the ring-on-ring testing geometry requires rather well prepared, flat and uniform discs [5, 6].

The ball-on-3-ball test (B3B) has been utilized in some studies, since it permits characterization of fracture stresses of thin specimens. Furthermore, the method is more tolerant regarding the uniformity of specimens [7]. The B3B test induces a well-defined stress field, where the highest stress exists in the center of the specimen. Hence, processing-induced damages at the specimen edges have no influence on the results [8]. However, an accurate measurement of the fracture load and a precise positioning of the test specimens are important to facilitate reliable results [7]. In fact, modern micro-indentation systems fulfill the necessary requirements regarding load control and positioning. Therefore, in the current work, as a novelty a B3B test has been implemented in a micro-indentation system.

Usually, fracture stresses are analyzed using Weibull statistics. This statistical approach yields the characteristic strength and the Weibull modulus and, thus, permits a derivation of failure probabilities for particular stress levels [2, 9, 10]. Weibull theory assumes that the probability of defects being present depends on the effective volume (for volume defects) or effective area (surface defects) [10, 11], which leads to differences in the reported results depending on the chosen reference. Predictions for components in different, especially application-relevant, dimensions therefore requires characterization of the characteristic strength, the Weibull modulus and the effective volume or surface area [12]. Consequently, verification and prediction becomes more accurate if characteristic strengths for different effective volumes and areas are available. However, such studies are limited [3], in particular for thin specimens with thicknesses of a few hundred micrometers and less. A recently published study revealed that B3B results are comparable to ROR values, however, the material thicknesses were > 1 mm [13]. Moreover, studies employing a small scale B3B tests and a subsequent fractographic investigation for specimens in the 100 µm range along with a comparison to another biaxial testing method for specimens in the mm range, which considers thus a significantly different effective volume and surface area, have not yet been reported.

In this work, fracture stresses of different ceramic materials, i.e., 92% and 99% pure Al2O3 and MgAl2O4 (Spinel), with different specimen thicknesses, are characterized by B3B and ROR tests. The individual data sets are analyzed using Weibull statistics. The analysis is extended toward considering effective volumes and surface areas with the goal to confirm the appropriateness of the test set-ups and methodologies and to present a foundation for the prediction of failure probabilities of application-relevant components.

Experimental

Two different commercially available Alumina materials (ALOTEC®99 and ALOTEC®92, CeramTec-ETec GmbH, Lohmar, Germany) as blocks with Al2O3 contents of 99.2 and 92%, respectively, were procured, in the following abbreviated as ALUMINA1 (ALOTEC®92) and ALUMINA2 (ALOTEC®99). Material properties are listed in [14].

Plates of average thicknesses of 120 and 250 µm were prepared using an Orbit 25 CNC grinding machine (BLOHM) with a diamond grinding disc of ~ 88 µm (D91) grain size and a C75 concentration. Afterward, the disc-shaped samples were extracted from the plates using a Typ22 STAE (Aciera) diamond hollow drill with an inside diameter of 3 mm, resulting in a total of 160 samples of different thicknesses with diameters of ~ 3 mm. Additional 45 specimens from ALUMINA1 as well as of ALUMINA2 blocks were prepared with an average thicknesses of 800 µm and a diameter of 12 mm for ROR testing. More details on the different test series are presented in Table 1.

Table 1 Different test series for ALUMINA1, ALUMINA2 and Spinel
Full size table

In addition, commercially available polycrystalline Spinel, MgAl2O4 (Perlucor®, CeramTec-ETec GmbH, Lohmar, Germany) samples were used for the B3B experiments. The samples were delivered by the manufacturer in a disc shape with a diameter of 3 mm and a thickness of 0.2 ± 0.01 µm. Material properties are given in [15, 16]. For this material, only B3B tests were carried out since in-house derived ROR data for specimens with thicknesses of 2 mm are already available in the literature [17].

The thickness of all samples was measured using a micrometer IP65 (Mitutoyo) associated with a measurement uncertainty of ~ 2 µm, yielding thicknesses that deviated slightly from the nominal values given in Table 1. In the results and discussion section, the fracture stress values and their distributions are discussed with respect to the real sample thicknesses.

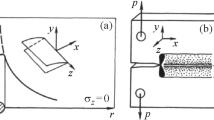
A B3B test set-up was designed with the objective to evaluate the strength of thin ceramic specimens in a thickness range between 60 and 300 µm. Due to this anticipated specimen thickness range, ball radii of 1 mm were chosen, based on the three main criteria for the B3B test outlined in the work of Börger et al. [7]. The stated ball radii should, therefore, lead to a support radius of ~ 1.155 mm following the equation given in [7]. Based on the boundary conditions and the estimated fracture loads in the mN to N range [18], the B3B set-up was designed for use in a micro-indentation system (CSM, Anton Paar), see also Fig. 1.

Figure 1
figure 1

a Schematic representation of the B3B test set-up, adapted for usage in a micro-indenter system (CSM, Anton Paar). The support balls are enclosed by a containment plate in order to prevent outward movement and rest on a glass plate to minimize friction. b Schematic of the ROR test set-up, see also [14, 16]

Full size image

The loading ball was produced from a sapphire rod with one end being rounded resulting in a hemispherical probe of 1 mm radius. Potential frictional effects can be neglected since the support balls are able to roll freely. In addition, to further reduce the friction, the support balls rest on a glass plate. The movement of the support balls was aided by a stainless steel containment plate surrounding them, while unnecessary movement of the support balls in-and outward was also prevented, following suggestions given in [19].

The tests were carried out with a loading rate of 5 N/min. The specimens’ central deflections, i.e., the displacement of the rod, and the loads were continuously recorded, as exemplified in Fig. 2. The rather nonlinear behavior at very low loads (< 1 N) can be attributed to initial settlement of the measurement system and is followed by a linear increase of the slope, indicating elastic deformation until fracture occurs. Note, some specimens still sustained load after initial crack growth, since the specimens were not fully fractured. However, the low compliance of the failed specimens led to large deflections with decreasing sustainable loads. The fracture initiations, visible in terms of load–displacement curves as deviations from linear elastic behavior, were used in the subsequent calculation of fracture stresses and Weibull analysis.

Figure 2
figure 2

Typical load–displacement curves recorded during the B3B testing of Al2O3 specimens. The apparent fracture loads are indicated by the square symbols. Nonlinear behavior at the beginning of the measurement (< 1 N) can be attributed to the settlement of the test system

Full size image

Based on the critical failure load F, the fracture stress σf for B3B tested specimens was calculated using the following relationship [19]:

$$\sigma_{{\text{f}}} = f\left( {\frac{{R_{{\text{a}}} }}{R},\frac{t}{R},v} \right) \cdot \frac{F}{{t^{2} }}$$
(1)

where t is the thickness of the specimen, v the Poisson ratio, Ra the support radius, and R the sample radius. The expression \(f\left( {\frac{{R_{{\text{a}}} }}{R},\frac{t}{R},v} \right)\) is a dimensionless function, which can be derived by an online tool based on finite element (FE) modeling made available by the University of Leoben [7, 20].

In contrast to the B3B tests, the ROR tests were performed using an electromechanical testing machine (INSTRON 1362), using similar procedures as outlined in [21,22,23]. The load was measured using a ± 1000 N load cell (Lebow Corporation) and the displacement by a linear variable differential transformer (Solartron Metrology) with the aid of a ceramic extension rod. In order to carry out the ROR tests, the samples were placed on a fixed Alumina support ring, and the load was applied with a loading rate of 1000 N per minute by an Alumina loading ring placed on the sample. The fracture stress σf was calculated using linear bending theory [24]:

$$\sigma_{{\text{f}}} = \frac{{3\left( {1 + v} \right)F}}{{2\pi t^{2} }}\left[ {\ln \left( {\frac{{D_{{\text{s}}} }}{{D_{{\text{l}}} }}} \right) + \left( {\frac{1 - v}{{1 + v}}} \right)\left( {\frac{{D_{s}^{2} - D_{{\text{l}}}^{2} }}{{2D^{2} }}} \right)} \right]$$
(2)

where F is the fracture load, v the Poisson’s ratio, t the thickness, D the diameter of the sample, Dl the diameter of the loading ring, and Ds the diameter of the support ring. The geometries were chosen based on the boundary conditions, as outlined in [25], which were satisfied by sample thicknesses of ~ 800 µm and ring diameters of Dl = 3.34 and Ds = 8.086 mm, respectively.

Based on the determined fracture stress values, Weibull statistical analyses’ were performed using [26]:

$$P_{{\text{f}}} = 1 - \exp \left[ { - \left( {\frac{{\sigma_{{\text{f}}} }}{{\sigma_{0} }}} \right)^{m} } \right]$$
(3)

where Pf is the failure probability. The characteristic strength σ0 is equivalent to the fracture stress for a failure probability of 63.2%, and m is the Weibull modulus, which describes the variability of the fracture stresses. A linear fitting procedure was implemented for the analysis. The obtained Weibull modulus as well as the 95% confidence interval were corrected to consider the number of tested specimens N following the relation:

$$m_{{{\text{corr}}}} = b \cdot m$$
(4)

where mcorr is then the corrected Weibull modulus, and b is a correction factor depending on N, which was derived from the corresponding standard [27]. In general, since the probability of a defect being present in a specimen depends on either the volume or surface area of the assessed materials (associated with the effect of either dominating volume defects or surface defects), the fracture strength of a material is affected by the size of the tested specimen as well as by potential stress gradients related to the testing method. Hence, the derived fracture strength has to be associated with an effective volume in the case of volume defects, Veff, while in case of surface defects the effective area, Seff, needs to be considered [10, 25]. The effective surface and effective volume are computed based on “principle of independent action” (PIA-criterion) [13, 28]. In case of the B3B test, the effective volume VB3B as well as the effective area SB3B can be calculated using a FE-model-based software tool that integrates the stresses over the finite elements [4, 20]. The value of Veff and Seff of the ROR test specimen can be calculated by expressions given in [29]. Using Veff or Seff, the material strength can be rescaled for different volumes or areas based on the Weibull theory [25]:

$$\sigma_{0,1} = \sigma_{0,2} \left( {\frac{{V_{{{\text{eff}},2}} }}{{V_{{{\text{eff}},1}} }}} \right)^{\frac{1}{m}}$$
(5)
$$\sigma_{0,1} = \sigma_{0,2} \left( {\frac{{S_{{{\text{eff}},2}} }}{{S_{{{\text{eff}},1}} }}} \right)^{\frac{1}{m}}$$
(6)

where σ0,1 and σ0,2 are the characteristic strength of the specimens for the considered testing geometry 1 and 2, corresponding in the current work to B3B and ROR, respectively. The associated effective volumes and effective areas are Veff,1, Veff,2 and Seff,1, Seff,2, respectively. In order to conclusively determine the dominant failure causing defect type, fractographic analysis are necessary. Therefore, SEM images of the fractured surfaces have been obtained using a Zeiss Merlin scanning electron microscopy instrument (Carl Zeiss Microscopy, Oberkochen, Germany). The critical flaw size α was estimated using the equation [30]:

$$\alpha = \frac{1}{\pi }\left( {\frac{{K_{{{\text{IC}}}} }}{\sigma }} \right)^{2}$$
(7)

where KIC is the fracture toughness given in the corresponding product data sheet and literature [14, 16].

Results and discussion

The results of the individual ALUMINA test series are summarized in Table 2. For ALUMINA1, Weibull moduli of all three test series (for B3B and ROR) are in good agreement, indicating that the fracture stress distributions are comparable. The same holds true for the individual test series results for ALUMINA2.

Table 2 ALUMINA1 and 2, average thickness t, characteristic strength σ0 and Weibull moduli mcorr with the upper and lower limits of the confidence intervals, average effective volume Veff and effective surface area Seff
Full size table

The characteristic strengths should decrease with increasing effective volume or surface area. A graphical representation of a double logarithmic plot of the characteristic strengths as a function of the effective volume or the effective surface area should reveal a linear dependency. The slope of this linear regression is equivalent to the Weibull modulus. The respective plots for the two ALUMINA materials are presented in Fig. 3. All results are well described by a linear trend line (red line) reflecting the validity of the data of each individual test series (Table 2). However, the Weibull moduli derived from the linear regression over all test series are slightly lower, compared to the values obtained for the individual test series. These lower values indicate that this might be a more conservative approach to predict the failure probability of larger components. Overall, the Weibull modulus of the individual test series is in good agreement with the one based on the effective volume approach (Fig. 3a, c). Therefore, volume defects appear to be the likely failure origin.

Figure 3
figure 3

Characteristic strengths of material ALUMINA1 as a function of the effective volume in (a) and effective surface areas in (b) Likewise for ALUMINA2, the characteristic strength as a function of the effective volume in (c) and the effective surface in (d). The used testing method B3B or ROR, respectively, is given in brackets. The red line represents a linear regression based on the respective 3 test series. The slope of this regression being equivalent to the Weibull modulus is presented at the bottom left corner

Full size image

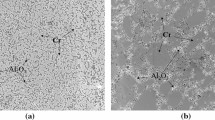
However, conclusions with respect to the dominant failure causing defect type should not be based only on statistical approaches. The failure origin was, therefore, further investigated by fractography. Representative SEM images of the fracture surface of the ALUMINA1 test series are show in Fig. 4, corresponding images of the ALUMINA2 samples are given in the supplementary material. In all alumina samples, the reason of failure seems to be pores near the sample surface. Based on Eq. (7), the critical flaw size αc is calculated for each test series, values are summarized in Table 3. The calculated critical flaw sizes are in good agreement with the actual observed fracture origin sizes.

Figure 4
figure 4

Representative SEM images of the fracture surfaces of ALUMINA1 specimens (tension side at the top). a Fracture surfaces after ROR testing (C1 test series), b at higher magnification, c B1 test series (after B3B test), d A1 test series (after B3B test). In all fracture surfaces, pores are the most likely failure origins

Full size image
Table 3 Summary of the calculated critical flaw sizes and observed fracture origin sizes of the selected ALUMINA test series specimens
Full size table

For both Alumina materials, the Weibull moduli are, within the limits of uncertainty, in reasonable agreement with the values given in the supplier’s data sheet [14]. However, the fracture strengths given in the data sheet are slightly higher compared to the ROR derived values (Table 2). Hence, the effective volume in their work might be slightly lower compared to our ROR samples.

For the spinel specimens, Table 4 summarizes the Weibull analysis results of the B3B along with the ROR-based results from [16]. The Weibull moduli agree reasonably well within the limits of uncertainty, however, as expected, the characteristic strength is significantly lower when derived from ROR tests compared to the B3B data.

Table 4 MgAl2O4, average thickness t, characteristic strength σ0 and Weibull moduli mcorr with the upper and lower limits of the confidence intervals, average effective volume Veff and effective surface area Seff. ROR from [16]
Full size table

The characteristic strengths of MgAl2O4 are presented in Fig. 5a, b as a function of the effective volume and effective surface area, respectively. For the spinel, only two test series are available. A linear regression based on only two datasets will always result in a perfect fit. According to the Weibull theory, the slope of the linear regression should be equivalent to the Weibull modulus. Indeed the slope derived values presented in Fig. 5 based on the effective volume is 7.6, and the value based on the effective surface is 6.1. Both of these values agree well within the limits of uncertainty with the individual test series results. Therefore, a linear dependency between the ROR and B3B results is confirmed. Overall, again the agreement of the effective volume approach with the Weibull moduli of the individual test series is better, indicating volume defects are more likely.

Figure 5
figure 5

Comparison of the ROR and B3B derived characteristic strength results as a function of the effective volume in (a) and effective area in (b). The red line represents the linear regression. Generally, a regression between only 2 data has limited meaning, but following the Weibull theory the slope of this regression is equivalent to the Weibull modulus. Hereby slope values agreeing well with the Weibull moduli of the individual test series confirm the linear dependency

Full size image

The statistical analysis based on different effective volumes, as presented here for volumes covering more than three orders of magnitude, can be used to give an accurate extrapolation of fracture stresses for particular failure probabilities of components with application relevant dimensions. Small scale pores within the MgAl2O4 have been reported as the reason of failure in the ROR tests [15]. SEM images of the MgAl2O4 specimens’ fractured surfaces after B3B testing have been made (Fig. 6). The main failure causing defect seems to be coarse-grained agglomerates and associated microcracks. Therefore, volume defects seem to be the main failure causing defect type for the MgAl2O4 specimens in the ROR as well as the B3B test.

Figure 6
figure 6

SEM images of the fractured MgAl2O4 surface after B3B testing. In (a), the red circle highlights an area with radial orientated microcracks, originating from coarse-grained agglomerates shown in (b)

Full size image

Conclusion

The fracture test methodology based on a combination of ball-on-3-ball and ring-on-ring tests using a custom-designed miniaturized ball-on-3-ball test setup was evaluated. The evaluation was based on the analysis of experimentally derived fracture stress data for different ceramic materials and an associated Weibull statistics. The analyses of the characteristic strengths as a function of the effective volume and effective area were in good agreement with the values derived from the analysis of the individual data sets for all materials. The agreement of the effective volume approach with the Weibull moduli of the individual test series was better, indicating volume defects are more likely, confirmed by the fractographic analysis. The illustrated considerations highlight the possibility to derive fracture stresses for application relevant ceramic components, from smaller or larger test bodies, even if different fracture test methods are used, as long as associated statistical analysis’ on basis of the effective volume or effective surface are applied. These findings are, therefore, a solid foundation for the prediction of failure probabilities of application relevant ceramic components. The combination of a micro-indentation system and the ball-on-3-ball test represents an easy, fast and reliable method to investigate the fracture behavior of small scale ceramic materials.