Mechanics of the small punch test: a review and qualification of additive manufacturing materials

Abstract

The small punch test (SPT) was developed for situations where source material is scarce, costly or otherwise difficult to acquire, and has been used for assessing components with variable, location-dependent material properties. Although lacking standardization, the SPT has been employed to assess material properties and verified using traditional testing. Several methods exist for equating SPT results with traditional stress–strain data. There are, however, areas of weakness, such as fracture and fatigue approaches. This document outlines the history and methodologies of SPT, reviewing the body of contemporary literature and presenting relevant findings and formulations for correlating SPT results with conventional tests. Analysis of literature is extended to evaluating the suitability of the SPT for use with additively manufactured (AM) materials. The suitability of this approach is shown through a parametric study using an approximation of the SPT via FEA, varying material properties as would be seen with varying AM process parameters. Equations describing the relationship between SPT results and conventional testing data are presented. Correlation constants dictating these relationships are determined using an accumulation of data from the literature reviewed here, along with novel experimental data. This includes AM materials to assess the fit of these and provide context for a wider view of the methodology and its interest to materials science and additive manufacturing. A case is made for the continued development of the small punch test, identifying strengths and knowledge gaps, showing need for standardization of this simple yet highly versatile method for expediting studies of material properties and optimization.

Introduction

Small punch testing (SPT) is a material characterization methodology which has been experiencing wider application in recent years due to the ability to use very small, thin samples to assess mechanical properties. The method was originally developed in the 1980s by Manahan and colleagues [1, 2]. The advantages of such a test make it an attractive option for material evaluation for numerous alloys in various industries, one such being the energy industry and its many different facets, from steam to nuclear. These methods are especially significant in nuclear power settings where many plants are reaching their end-of-life predicted ages and the long-term effects of neutron radiation are unknown [1, 3,4,5,6,7,8,9]. As the test employs very small samples, it is not only a good alternative where source material is scarce, but it is also useful in evaluating and tracking the evolution of material properties of a component that has been in service. As such, used components can be tested to gauge the effects of their working environments on the material properties, including the effects of radiation in nuclear power plants or the cyclic high-heat conditions to which a thin-walled turbine vane may be subjected. Small punch tests are thus considered non-destructive, as samples are designed to be incised from existing structures with minimal impact to the integrity of the mechanism and with much less material than traditional testing procedures allow, giving a clear picture as to the remaining lifetime of components [10, 11].

The small punch test is designed to subject a small test coupon to combined bending and stretching. The test configuration consists of an upper and lower die to hold a small, thin sample and a punch with a spherical head or ball to contact and deform the specimen, as shown in Fig. 1. The use of a ball in place of a machined punch allows for replacement of the ball after each test to prevent accumulation of damage to the punch affecting subsequent tests. The setup is adapted to a load frame which controls the punch displacement and measures the load, P, via a load cell, and a displacement gage is attached to accurately measure sample deformation due to deflection, δ, most commonly using a linear variable displacement transducer (LVDT) directly contacting the underside of the sample as shown here. Researchers have also employed an extensometer for displacement measurements, typically using a crack opening displacement (COD) type extensometer, which does not need to be placed directly beneath the sample in the confined space of the setup and thus facilitates easier setup but which may require a calibration function for proper use [12,13,14]. In this case, calculations would be carried out with respect to punch displacement rather than deflection of the bottom of the specimen.

Figure 1

Schematic of typical SPT apparatus components

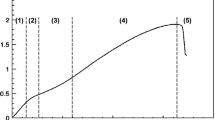
Small punch test responses are given as a force–displacement (P-δ) curve as shown in Fig. 2. This is divided into five sections of distinct behavior of (1) elastic bending, (2) plastic bending, (3) membrane stretching, and (4) plastic instability [15,16,17]. The fifth region is defined at the tail end of the fourth zone denoting the failure of the sample. However, as the exact point of failure can often be difficult to distinguish, its definition can vary from being taken as the entire region of the curve after the maximum load, or as the region only after a certain amount of load drop, or the occurrence of a sudden rupture [18, 19]. Transitions between zones of the P-δ curve are typically denoted by inflection points which are used in formulations for equating SPT results with traditional stress–strain results to acquire material properties, as will be detailed later in this review. Also denoted are the initial stiffness, k, the deflection at maximum load, δ_m, the specimen deflection at fracture δ*, and the strain energy, U, which may elsewhere appear denoted as E_SP, the small punch energy, which is also a measure of energy absorption up to the appearance of a fracture and often used for the determination of ductile-to-brittle transition temperature. The response shown in Fig. 2, however, is an idealized force–deflection curve and the divisions at which the regime changes and points of importance, such as P_y, the yield load, are not always as distinct as shown here.

Figure 2

Typical SPT load–displacement curve with important inflection and correlation points denoted, derived from [17]

Small punch tests are practical where source material is expensive and large quantities are hard to acquire. One such example is in the testing of precious metals, such as in testing gold alloys [20]. Cicero and co-authors utilized SPT to evaluate the tensile and fracture properties of 18 and 24 karat gold, with good agreement to results found through traditional tensile testing techniques. Small punch testing is also of interest, then, where producing samples solely for the purpose of destructive testing is costly not just in terms of material but also in manufacturing, as can be the case with samples produced via selective laser melting (SLM). The Air Force Research Lab estimated the cost of evaluating a new alloy for use with an additive manufacturing technique to be around $2 M, including materials, manufacturing, and a comprehensive battery if mechanical testing and analysis [21]. As such, utilizing miniaturized testing techniques such as SPT can cut down on costs in all aspects involved in new material evaluation, if evaluation methods equivalent to traditional testing techniques can be proven.

Traditional tensile test samples, as described by ASTM E8 [22], feature a gage section that is 50 mm long and 12.5 mm in diameter, for a volume of 6136 mm³, without including material outside of the gage, including the radius from the gage to the support and the support sections, which can double the total length. This also means a significant amount of material is lost in the manufacturing process while grinding down the gage section of the sample. In contrast, however, SPT samples can be fabricated as square plates or thin disks, the former of which being the larger of the two with sides of 10 mm and thickness of 0.5 mm for a volume of 50 mm³. As such, SPT samples require less than 1% of the volume of the gage section alone. Small punch test results have successfully been used with correlation from existing correlative models to develop material properties at varying temperatures, including yield and tensile strength, fracture toughness, and ductile-to-brittle transition temperature (DBTT), which is normally determined using extensive impact testing and consumes significant amounts of material, as well as the effects of degrading environments and varied conditions on these [23,24,25]. Although testing and specimen design are simplified with SPT, property acquisition is complicated by the complex stress states as compared to established conventional test practices, and furthermore by the differences arising from experimental design variations [26,27,28]. The primary objective of current SPT research, then, is to simplify the process of acquiring material properties from small punch tests.

Given that widespread standardization does not exist for SPT, however, these methods of acquiring material properties are not as well as understood or utilized as traditional testing techniques. International standards include emergent standards from Europe based on a workshop agreement, the CWA 15627, the Chinese standard, GB/T 29459, and similar work in Japan. Though no single standard is universally accepted, all have strong similarities, and the European code of practice is most often cited in the literature. Until 2013, the only active ASTM standard for small punch testing was ASTM F2977, used for small punch testing polymeric biomaterials used in surgical implants. A similar standard specific to ultra-high molecular weight polyethylene, F2183, was withdrawn in 2017 without replacement [29]. A work item was initiated in early 2018 for implementing a standard for testing metallic materials, WK61832. This was followed by the issuance of a formal standard in 2020, ASTM E3205 [30], which largely delivers the same guidance as that in the CWA 15627 and which is expected in the upcoming European standard, EN 10371.

Literature on the topic is limited when the subject matter is combined with additive manufacturing techniques such as SLM, due to the somewhat recent emergence of both topics. The ability of the SPT to predict the anisotropy of as-manufactured AM materials, specifically those made with SLM, has been shown in the literature, with fracture morphology being highly dependent on manufacturing orientation [31, 32]. Additionally, Dao et al. showed an orientation dependency for stainless steel 316 L manufactured via SLM when subjected to small punch creep tests [33]. Direct laser-deposited (DLD) C263 Ni-superalloy with varying heat treatments was tested at room and high temperature in SPT, and compared to cast material and tensile tests [34]. While the DLD material showed anisotropy and dependencies on heat treat and testing temperature, the significance of such was not as pronounced as in tensile tests, skewing correlations when compared to literature. In one study, SPT was utilized with stainless steel components manufactured via SLM, though to a very limited extent, exploring only the effects of layout and gas flow on the parts, and using SPT as a way to evaluate bond strength between particles [35]. Even then, however, the estimated mechanical properties calculated by the investigators show good correlation to values published elsewhere. Hurst et al. conducted a series of SP tests on samples made from layer additive manufactured IN718 typically employed in aerospace structure repair and on electron beam deposition manufactured Ti6Al4V [36, 37]. These experiments showed the SPT was responsive to the anisotropy typically present in AM layered materials, and results showed sensitivity to grain size, distribution, and orientation, and also differences between AM and conventional materials in terms of both material properties and fracture behavior. Similarly, a 12% Cr oxide dispersion strengthened steel, which displays highly directional properties due to the elongated grain structure, showed delamination fracture behavior similar to layered materials such as those produced via AM techniques when tested in SPT, and confirmed directional dependencies of material properties [38]. Additionally, IN718 samples taken from a direct laser deposition manufactured airfoil at several different heights of the build and tested with SPT showed responses varied based on location, highlighting changes in microstructure which caused differences in strength and ductility, this study, however, did not quantify material properties, but tracked changes in strength relative to each other and to a sample of equivalent wrought material [37]. Small punch testing has also been used to explore the variation in shear strength along a laser welded joint, a process which is arguably similar in theory to SLM, and in other studies to find the evolution of yield strength ultimate strength, elongation, fracture energy, and toughness along the different regions of the heat affected zone of a weld [39,40,41]. Given the process of adding layers to welds to create them, and that the SPT method was used successfully to track variations in the materials, which was validated in [41] by giving correlating hardness tests with matching trends, it stands to reason that a layered process with anisotropic properties such as SLM would benefit from the sensitivity of SPT. Small punch tests have also been used with pressed powder materials, which present complexities in their behavior similar to those of layer-wise construction methods, and achieved acceptable correlation with traditionally determined material property values such as yield and ultimate strength [42, 43]. Beyond those examples, the combined use of SPT and SLM or other additively manufactured materials is extremely limited. The current study will serve to summarize and distill the various techniques used in the literature in order to determine mechanical properties from small punch test results, with the aim of assembling a reliable set of procedures for full material characterization via SPT, as this method has yet to be standardized, so as to apply them to samples manufactured via SLM.

This document will outline many of the works related to small punch testing techniques and the relevant mathematical models, along with techniques for equating the results with conventional tests. Conventional testing methodologies related to SPT include tension, creep, fracture, shear, and fatigue, along with finite element models to approximate these. A sensitivity study using FEA will be outlined to show the adaptability of the SPT to materials which can vary greatly in mechanical properties. Finally, relationships will be given using a collection of published data for correlating mechanical properties with SPT data. Included in these will be several additively manufactured materials, and a case is made for the suitability of using SPT materials to assess them, in comparison with results for conventional materials given in the literature.

Basics of small punch testing

Although standardization of SPT is an ongoing effort, in 2004 the European Committee for Standardization (CEN) released a workshop agreement in order to develop a set of guidelines so as to direct the growing interest of the use of SPT in a uniform manner [44]. The resulting workshop agreement, CWA 15627, which was later updated in 2007, established guidelines for testing and translation of data into tensile, creep, and fracture properties, and is more widely utilized than the other standards. The CEN code of practice recommends round specimens of 8 mm in diameter with 0.5 mm thickness, using a lower die opening of 4 mm and a punch diameter of 2.4 mm [44, 45]. These parameters are typically used in the literature with some modifications sometimes being present, such as the variation of specimen width, with 10 mm round or square specimens also being common [39, 46,47,48]. Along with working parameters for the setup and testing of samples, the CWA 15627 also describes several relationships for relating SPT data to traditional test data. The guidance provided by the CSWA is what is most often found to be followed in the literature, and a European standard, EN 10371, is under development with much of the same guidance [49]. The recent ASTM standard E3205 also largely follows the same recommendations. The following sections will be dedicated to exploring these relationships, among others found to be relevant by consequent research efforts. Table 1 includes nomenclature for the various topics and relationships discussed herein.

Table 1 Nomenclature

Studies have shown that sample displacement, or more accurately the sample deflection, is most accurately measured directly from the sample by placing an LVDT opposite the indenter, rather than using cross-head displacement, in order to minimize compliance effects [50, 51]. Much like traditional tensile tests, most SP tests are displacement-controlled with a constant displacement rate, which is typically recommended to be in the range of 0.2–2 mm/min, though those equivalent to traditional creep tests are typically load controlled with a constant force [45, 52]. Measurement of displacement at a location other than directly below the sample, such as remotely from the cross-head, can cause compliance errors in the resulting load–displacement curves, as shown in Fig. 3. Although the general shape of the curve is preserved, both the load at the transition point from elastic to plastic and the total displacement are overestimated. This is due to small shifts in the load frame cross-head as it displaces, which in turn cause a shift in the resultant curve, due to the tight tolerances required for experimentation and relatively low load and displacement levels, as compared to conventional tests. Compliance effects have also been shown to be present when considering the stiffness of the loading system, frame, and geometry of the dies [45, 53, 54]. Use of COD type extensometers is also possible and is useful for assessing the displacement at the top of the sample where initial deformation can occur before the bottom of the sample is displaced, but requires correction for compliance of components such as the punch and crossbar [14]. Additionally, alignment issues due to variances in test setups can lead to undue friction between components of the setup, such as the punch and die, which can impact test responses [55]. These issues often dictate the necessity for compliance correction in the results, as will be presented in the following sections, if such is not accomplished through hardware modifications. Test responses can differ strongly depending on the type of material used, how it has been treated, testing conditions, and how it behaves according to these, whether brittle or ductile in nature. For example, sample preparation has been shown to produce a difference in correlations between SPT results and conventional tests, with polished specimens producing better correlations that rough specimens [56]. Load–displacement curves for brittle and ductile materials have been shown to differ greatly in size and definition [57]. Fracture initiation occurs at very different times, whereas for the ductile case the fracture initiation has been shown to be part of the stable plastic deformation regime and does not interrupt its progress, in the brittle case crack initiation occurs concurrent to peak loading and unstable growth leading to failure.

Figure 3

Compliance effects in load–displacement curves caused by measurement of displacement via load frame crossbar as compared to direct contact displacement transducer

Direct correlation with tensile properties

Determination of tensile properties from small punch tests is an issue which has been of debate since the miniaturized test method was first introduced. As such, several differing approaches and formulations have been suggested and tested over the years for evaluating various material types [58, 59]. Some guidelines for testing and translation of data into tensile, creep, and fracture properties have been established [44]. The agreement suggests several relationships for converting the load–displacement data directly into material properties typically established using stress–strain curves acquired from conventional testing. The correlations for determining material properties from small punch test data show dependencies on variables such as sample thickness, and use several inflection points of the curves, such as the yield load, P_y, and the max load, P_max, for determining material properties. These points coincide with changes between the P-δ regimes as outlined in Fig. 2. It has been shown [44], for example, that normalization of yielding load, P_y, by the square of the original specimen thickness, t, is a reliable method for estimating the 0.2% offset tensile yield strength via the use of a correlation constant, α, e.g.,

$$\sigma_{{{\text{ys}}}} = \alpha \left( {\frac{{P_{{\text{y}}} }}{{t^{2} }}} \right)$$

(1)

The determination of where P_y actually occurs, however, is of some debate, with several definitions having been proposed. The various methodologies which range from the use of tangents to offset displacements of 1% or 10% of the original thickness, t, with the original slope of the curve are shown in Fig. 4, and each method has support and contention [58, 60, 61]. Mao and Takahashi [62] originally defined the location of this value, P_y(Mao), by drawing a tangent of the initial stiffness and a tangent of the steady-state plastic stretching, previously defined as zone 3 in Fig. 2, and finding the point of intersection. This method has been shown to be sensitive to material and testing conditions [63,64,65]; [63] presented variations of the Mao and Takahasi expression for samples which had undergone plastic deformation prior to testing which depended on whether the material had experienced tensile or compressive stresses. It is also worth noting that because of the variability in the determination of P_y, however, Isselin and Shoji proposed a method of evaluating the small punch yield using the energy up to the beginning of plasticity, known as the elastic deformation energy [64]. Determination of the yield load has also been shown to be sensitive to experimental testing conditions, such as specimen thickness and support mechanisms [65]. Later, a new method related to that suggested by Mao and Takahashi was adapted in [44] by using a bilinear fit and minimized error to find the intersection point and projecting it vertically downwards onto the coinciding point, P_y(CEN), of the load–displacement curve. Taken at a literal sense, Lacalle and co-authors suggested the use of the first inflection point, P_y(I–II), of the curve where zone I changes to zone II as the location where the initial stiffness changes to define the yield point [20, 66]. Finally, the offset method has been suggested akin to that which is used to find the 0.2% offset yield strength, σ_ys, on stress–strain curves, by using a straight line parallel to the initial stiffness to find the point of intersection. Different offset amounts have been suggested for use with this method, including the use of 1/100^th, P_y(t/100) of the original thickness or using a larger offset of 1/10^th, P_y(t/10), of the original thickness [39, 67]. Each of these is shown in Fig. 4. Fixed amounts, such as a 0.3 mm offset, have also been suggested [68]. Although the two-tangent method and the modified version of it are highly cited in the literature [40, 63, 69], studies [60, 70, 71] show that the P_y(t/10) approach produces the strongest correlation with yield strength of those methods in Fig. 4, i.e.,

$$\sigma_{{{\text{ys}}}} = \alpha_{1} \left( {\frac{{P_{{{\text{y}}\left( {{\text{t}}/10} \right)}} }}{{t^{2} }}} \right) + \alpha_{2}$$

(2)

Figure 4

Various methods for determining the yield load, P_y, of the load–displacement curve of SPT, created using AW6016 T4 P − δ data from [63]

The constants in this relationship, like other correlation coefficients to be presented, are typically determined through a linear regression fit of the conventionally established mechanical properties of various materials plotted against the values of the equivalent SPT formulations, such as the yield strength plotted against P_y/t². For simplicity, this relationship is sometimes determined without the second constant, though use of the second constant can improve accuracy, depending on the material and test setup. Additionally, a series of studies by Chica et al. determined that these constants are influenced by the mechanical properties of the materials, namely the strain hardening behavior, and not accounting for it increases scatter in the correlation data. As such, they suggest that in order to optimize the fit of the t/10 method, the coefficients should be determined via a nonlinear complex regression, with the second constant multiplied by the minimum slope of zone III divided by the sample thickness [13, 72, 73].

Similarly, P_max, the maximum punch load indicated in a P-δ curve, has been shown to have a linear correlation with the ultimate tensile strength (UTS), σ_uts. Garcia et al. also showed that although the expression for ultimate tensile strength of

$$\sigma_{{{\text{uts}}}} = \beta_{1} \left( {\frac{{P_{{{\text{max}}}} }}{{t^{2} }}} \right) + \beta_{2}$$

(3)

and variations of it have been successfully used [20, 39, 51], the expression of

$$\sigma_{{{\text{uts}}}} = \beta_{1} \left( {\frac{{P_{\max } }}{{\delta_{{\text{m}}} t}}} \right) + \beta_{2}$$

(4)

where δ_m is the sample deflection measured as the displacement of the bottom of the sample at maximum load, provided more accurate results when compared to conventional test [11, 45, 58, 60]. This expression has produced effective calculations with a variety of metals, including several grades of high strength, stainless, and structural steels, aluminum alloys, and magnesium alloys, and is less dependent on the material tested than the previous formulation [60, 74]. An alternative method of determining UTS is based on evidence that P_max does not necessarily correspond with the initial appearance of a fracture as it does in conventional tensile tests, denoting onset of failure [75]; rather, necking occurs in Zone III of the force–displacement curve, and as such a more appropriate correlation point exists within this necking area which corresponds to the necking behavior in a tensile test. Additionally, the behavior of brittle materials in SPTs is more complex than those of ductile materials, and the load–displacement response is not as straightforward as the ideal case presented earlier [26]. As such, a relationship has been proposed which is a revision of that in Eq. (3) that utilizes a load, P_i, which occurs within Zone III, indicating the onset of necking or plastic instability within the SP sample and for which the correlation constant is independent of material properties and thus may be more universally appropriate for a range of materials [76]. The preceding equations for determining yield strength and ultimate tensile strength could then be used with the Ramberg–Osgood hardening law in order to determine the hardening exponent, n, and generate true stress–strain data [77].

Achieving consistent, uniform thickness for numerous samples can be difficult on such a small scale. Due to the impact of variations in thickness on resultant SPT curves and material property calculations, Lacalle and co-authors proposed a normalization process to reduce the effect of varying thickness on results from otherwise identical samples [48, 52]. While the expression describing the earlier part of the curve stems from plate plasticity theory [78], it was determined that the normalization equation needs to be split into two regions, as SPT curves generally deviate from plate theory behavior at the inflection point, P_II-III, where deformation transitions from plastic deformation, zone II, to membrane stretching, zone III. The expressions were proposed which can normalize test loads, P_test, to loads from a theoretical sample with a thickness of 0.5 mm, P_0.5, regardless of actual sample thickness, t, for more direct comparison between curves, and with increased accuracy in the latter part of the curve [48, 63, 79], e.g.,

$$P_{{0.5}} \left\{ {\begin{array}{*{20}l} {0.5^{2} \frac{{P_{{test}} }}{{t^{2} }}} \hfill & {P_{{test}} {\text{ < }}P_{{II - III}} } \hfill \\ {0.5\frac{{P_{{test}} }}{t} + \frac{{0.5P_{{II - III}} \left( {0.5 - t} \right)}}{{t^{2} }}} \hfill & {P_{{test}} {\text{ > }}P_{{II - III}} } \hfill \\ \end{array} } \right.$$

(5)

All further calculations conducted with these normalized curves would assume a sample thickness of 0.5 mm and have an ingrained adjustment on the determination of the σ_uts from P_max due to the expression for the latter part of the curve. Comparison through normalization of the curves in [48] also facilitated the deduction of the influence of sample or material orientation, which is especially relevant to anisotropic materials, and which was shown to be highly influential.

The theory of plates [80] has also been used to describe correlations very similar to those previously presented, along with a method of finding Young’s modulus, E, which involves a summation of the different stiffness values of the various components of the SPT rig and the sample itself [20]. This is in line with an expression presented by Giddings and co-authors, who used a straightforward methodology involving an FEA model to determine the correlation between the initial stiffness of the load–deflection curve and the Young’s modulus [81]. The small punch test technique was combined with various previously validated finite element models to evaluate the evolution of the Young’s modulus of polymethylmethacrylate, a commonly utilized bone cement, under varying conditions and temperatures. The equation directly relates k, the initial stiffness in the P-δ curve, to E, the Young’s modulus, via, λ, a proportionality constant related to Poison’s ratio and the frictional characteristics of the material in question. This relation was later normalized by dividing the initial stiffness, k, by t, the original specimen thickness, to mitigate differences to the resultant Young’s modulus stemming from variations in sample thickness and produce more accurate correlations [12, 18, 70], e.g.,

$$E = \lambda \left( \frac{k}{t} \right)$$

(6)

Although the proportionality constant, λ, has shown some material dependence, a proportionality constant suitable for a variety to of metals may be found by using a similar fitting methodology with the SPT responses and Young’s moduli of several materials together, as was done to determine constants in relationships described earlier. The tensile elongation of ductile materials has shown direct correlation with the displacement at maximum load, but has also shown high material dependence, and a universal correlation factor with a good fit was not found [39, 43, 60, 82]. To circumvent this issue, Chica et al. suggested introduction of an unloading/loading cycle to the SPT, and using the slope of this factor to determine the Young’s modulus, as the initial portion of the curve, k, can be affected by the plasticity properties of a material [83].

Case studies on a unique material processing method, powder metallurgy, which uses powdered metal product pressed into component shapes followed by a sintering process, have been conducted by utilizing some of the aforementioned relationships [42, 84]. The nature of this manufacturing process leads to variability in the mechanical properties within components due to the variation in porosity and cooling rates of the different regions of the component [85, 86]. The inherent porosity usually leads powdered metal products to be considered as brittle, in comparison with conventionally produced materials such as common structural steel [43]. In this case, the conventional material supported over three times the displacement and load before initiating fracture as compared to the powdered metal sample, and fracture patterns between the two samples corresponded to these results, with the conventional sample featuring significant plastic deformation and ductile fracture.

The analyses carried out in the canon of literature of SPT show that regressions comparing tensile and SPT results using the linear correlations presented earlier had an 80–90% R² correlation fit for the yield strength, ultimate strength, and elongation. A slight adjustment to the constants provided an even more accurate fit, inclusive of the data presented in that work and the present study. It is also worth noting that SPT samples extracted from several different positions of the powdered metal bars produced for the acquisition of both SPT and tensile test samples for the present study correlate to the variability in porosity of these mentioned earlier. As such, even in a porous material, an SPT sample serves as a valid representation of a component, or even a localized region, and the strength variations associated therein. This is of critical interest when considering functionally graded or directionally dependent materials such as those produced with additive manufacturing techniques [39, 40, 84]. Additional support for analyzing these types of materials was shown by testing IN713C cast samples with columnar grain structures which displayed directionally dependent material properties and fracture behaviors, akin to those in additive manufacturing materials [19].

Creep

A variety of studies have leveraged the SPT to procure creep deformation and rupture properties of materials [87,88,89,90,91]. Creep, which is a monotonic test, features a constant load application at elevated temperatures for prolonged periods. Milicka and Dobes established the existence of a linear correlation between the force of small punch creep tests and the stress from conventional creep tests which resulted in an identical time to rupture [52, 88, 89]. Factors such as differing coefficients of frictions from different ball or punch materials have been shown to affect rupture times, with higher coefficients of friction causing longer rupture times at a set load and temperature, thus supporting the need for standardization [55, 92,93,94]. Additionally, strong dependencies of the rupture time on testing conditions such as sample thickness, load level, ball diameter, temperature, and test environment have been shown; in the case of sample thickness, for example, achieving a similar time to rupture as a 0.3 mm thick sample with a 0.6 mm sample required over double the applied force [52, 90, 91, 95,96,97]. As such, it was established that the stress in a conventional creep test and the force in an SPT creep test can be related linearly with the use of a proportionality constant for a material at a certain temperature. A correlation has been developed between the small punch creep results and the conventional creep results as a ratio, Ψ, of the SPT force divided by conventional stress combined with the deflection at fracture, giving the relationship

$$\Psi = \frac{P}{\sigma } = \left[ {\frac{{A_{{\text{C}}} }}{{A_{{\text{S}}} }}} \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {n_{c} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${n_{c} }$}}}}$$

(7)

where the force P applied during the test is held constant, σ is the stress from the conventional test results, and where the constants A_c, A_s, and n_c are described by the following relations which are driven by the time to fracture, t_F, and combine the power law and the Arrhenius exponential law [88], i.e.,

$$A_{{\text{C}}} = \frac{{t_{{\text{F}}} }}{{\exp \left( {\frac{Q}{{{\text{RT}}}}} \right)\sigma^{{n_{{\text{c}}} }} }}$$

(8)

$$A_{{\text{s}}} = \frac{{t_{{\text{F}}} }}{{\exp \left( {\frac{Q}{{{\text{RT}}}}} \right)P^{{n_{{\text{c}}} }} }}$$

(9)

In these equations, Q, the activation energy in kJ/mol, and the stress exponent, n_c, preserve their value across conventional creep tests and SPT. The variable t_F represents the time to fracture, which needs to be identical for both tests for the validity of the formulation, R is the universal gas constant, and T is the absolute temperature. A modification to Eq. (7) was made substituting P with (P/δ*), where δ^* is the sample deflection at fracture, reduced results dispersal of the ratio ψ as it accounts for variability in ductility of the material and thus it was suggested that the force in the SPT divided by the deflection at fracture is proportional to stress in a conventional creep test [88]. Additional modifications were suggested for compensating for differences in temperature, which produced high overlap of the time to fracture between conventional and SPT creep tests. It has also been suggested that the ratio of force in the small punch test to creep in SPT is not quite constant, but instead decreases slightly as time to rupture increases [98]. This work also noted a relation between minimum creep rate in conventional creep tests and a minimum deflection rate for small punch creep tests, highlighting a much stronger dependence of the ratio on time to rupture and temperature.

The basis of much of the work on small punch creep tests fundamentally extends from the theories developed by Chakrabarty on membrane stretching over hemispherical punches [99]. A simple relationship has been established between central deflection and central creep strain of a non-creep sample and a creep sample based on membrane stretching, though it is dependent on specific punch and sample geometries [100]. The CEN workshop agreement [44] established guidelines for exploring creep properties using SPT based on the theories established by Chakrabarty on the stretching of materials over hemispherical punch heads [99, 101]. This equation, which correlates the force of the small punch test to stresses in conventional creep tests, which was previously defined as the ratio, Ψ, is given as

$$\frac{P}{\sigma } = 3.33k_{{{\text{sp}}}} r_{{{\text{die}}}}^{ - 0.2} r_{{{\text{punch}}}}^{1.2} t$$

(10)

where r_die is the radius of the opening of the lower die, r_punch is the radius of the punch, t is the thickness of the sample, and k_sp is a creep correlation factor. The constants were established through a regression fitting of several tests conducted via round robin. The correlation constant k_sp can be initially assumed to have the value of 1, though to get a more accurate result a comparison with conventional uniaxial testing must be done [10, 44, 101]. It is worth noting that often the calculation of k_sp yields values which do not deviate very much from unity, and as such use of the value of 1.0 can give reasonable estimates [102]. Utilization of this formulation aids in selection of the load, F, when designing SP creep tests with an equivalent time to rupture as a conventional creep test conducted at stress level, σ [10]. This method has also been shown to be reliable via verification using the Larson-Miller and Orr-Sherby-Dorn parameters to establish the same relationship [47].

The relationship established by CWA 15,627 has been used in several subsequent studies. Zhao et al. used SP creep tests at 650 °C with a constant load ranging from 225 to 350 N on four different zones in a P92 chromium steel welded joint to explore deviations in the weld area [41]. Comparisons between SPC results and conventional results as well as FEM results showed good agreement. Small punch creep results have been shown to be representatively equivalent to conventional creep results, with bending being the principal mode of deformation in the primary creep region, while the secondary and tertiary stages are mostly characterized by membrane stretching [90, 103].

The SPC test and the relationship between SP results and creep stress have been shown to be effective for unique materials as well. Adaptability and suitability of use with single crystal and anisotropic materials have been shown, though with some limitations; directionality and temperature have been shown to affect correlations [53, 102, 104]. A study by Bruchhausen et al. also utilized the k_sp relationship, but with directionally different materials and noted differences based on the testing direction in reference to the extrusion direction [102]. Due to the anisotropy of the material, the k_sp value was left at 1.0, as there was difficulty in evaluating the longitudinal material direction, due to the biaxiality of the stress field in SPT. The anisotropy is evident in the SPT creep results, and neither dataset matches directly with traditional tests. This study also showed that SPT results follow the Monkman–Grant relationship, while others have shown that the Larson-Miller law and Dorn equation for calculating load exponent and activation also work well [52, 89, 90, 102, 105]. Additionally, the Wilshire rupture model and logistic creep strain prediction equation have been used in conjunction to a high degree of accuracy [106].

Fracture properties

Several formulations have also been proposed to estimate the fracture properties of materials from SPT results. Primarily, the methodologies relevant to determination of fracture properties stem from the utilization of an equivalent fracture strain for membrane stretching of blanks over a rigid punch. The equivalent fracture strain, ε_qf, proposed by Chakrabarty [99] and confirmed by several researchers [4, 8, 62, 107, 108], is defined as

$$\varepsilon_{{{\text{qf}}}} = \ln \left( {\frac{t}{{t_{{\text{f}}} }}} \right)$$

(11)

where t is the initial sample thickness and t_f is the final sample thickness in the area in which fracture occurred. As with other properties, a linear relationship was established with the fracture toughness by testing of specific materials such as different grades of CrMo alloys and carbon steels [108,109,110,111,112] or with several different materials such as in [60] using the equation for equivalent fracture strain which utilizes direct measurement of sample thickness at the fracture, given as

$$J_{{{\text{Ic}}}} = A\varepsilon_{{{\text{qf}}}} + B$$

(12)

where J_Ic is the fracture toughness as evaluated using the J integral. The relationship, with constants A and B of 1695 and -1320, respectively, was considered valid for alloys with an SPT biaxial strain at fracture, ε_qf, of greater than 0.8, though it was not considered valid for brittle materials [60]. However, measuring sample thickness at fracture can be difficult to accomplish and lead to inaccurate results. As such, the equation for equivalent fracture strain was used by Mao et al. [62, 108, 113] to develop the expression

$$\varepsilon_{{{\text{qf}}}} = \ln \left( {\frac{t}{{t_{{\text{f}}} }}} \right) = \beta_{{{\text{qf}}}} \left( {\frac{{\delta^{*} }}{t}} \right)^{p}$$

(13)

where β_qf and p are constants determined to be 0.09 and 2.0, respectively, for a disk with a diameter of 3 mm and thickness of 0.25 mm, and δ^* is the deflection at fracture of the sample center, as shown in Fig. 2, sometimes correlating to the maximum load, and thus δ_m. These expressions can then be used to solve for fracture toughness, J_Ic, as established by Mao, which takes the form of Eq. 12 but with first and second constants valued at 345 and -113, respectively, and applying to a range of materials [62, 108]. It has been shown, however, that fracture toughness increases at a fairly linear rate with increasing sample thickness [114]. Kumar et al. [115] established quadratic equations for determining the value of constants β_qf and p in Eq. 13 dependent on the original sample thickness, t, to determine the equivalent fracture toughness, ε_qf, by testing various thickness samples using an FEA analysis and implementing an exponential fitment curve. Comparative fracture toughness results for 2.25Cr-1Mo between the original constants determined by Mao and those determined using the quadratics established by Kumar et al. showed a reduction in error of 8–20% over the Mao constants using the quadratic constants when the fracture toughness obtained was compared to that found using CT specimens.

An elastic–plastic fracture mechanics (EPFM) approach has also been utilized. Ha et al. [23] tested the methods of Joo et al. and Afzal Khan et al. [116, 117], the latter of which is an EPFM approach, involving the calculation of the energies of the different stages of deformation seen depicted in an SPT curve. The EPFM approach produced results consistent with those found using Charpy impact tests. The methods presented by Joo et al. were shown to work consistently for materials in cold conditions to estimate fracture toughness, specifically once the material has crossed below the ductile-to-brittle transition temperature, but not for ductile materials [23, 116]. A sharp-notched central pre-crack of length a was introduced into the design of the SPT specimen while applying this methodology, as seen in Fig. 5c and was successful in creating a stress concentration to replicate results congruent with those in other studies for the lower shelf energy region [118]. This method showed accuracy dependency on temperature and thickness and has the disadvantage of having to know the point of crack initiation, which can prove to be of some difficulty with SPT. Similarly, Tanaka et al. utilized CrMoV cast steel SPT specimens with fatigue pre-cracked center notches to evaluate fracture toughness at high temperature [119]. In this study, electrical potential drop was used to indicate the beginning of unstable crack growth to determine the load at crack initiation, though locating the inflection point of the electrical potential curve proved difficult. Additionally, this method utilized FEA to obtain fracture toughness from the SP test using master curves of creep damaged materials. This requires previous knowledge of the material from tensile testing to program the behavior into the FEM analysis to produce said master curves. It was also noted that this method may be dependent on the toughness of the material, as high fracture toughness correlated with high error.

Figure 5

Examples of specimen geometries utilized in SPT fracture studies including a standard round, b standard square, c central notched [118], d single-edge notched [122], e circumferentially notched [124], and f lateral cracked [125]

Concurrently, Lacalle et al. developed a method based on traditional fracture testing standards using SPT samples with a simple lateral notch along one edge, similar to a single-edge notch tension test (SENT), of varying lengths in order to obtain the J-R curves [120,121,122]. This method was later verified by [46]. A sketch of the samples used, which are of the common configuration of 10 × 10 × 0.5 mm, is shown in Fig. 5d. The initial notch length, a, is varied from 4 to 6 mm in length, and the radius, ρ, was around 75–100 microns, and was cut using a laser micro-cutting technique. Using this method, the areas under the various curves corresponding to the different length of cracks are measured to obtain a set of J-integral values defined as

$$J = \frac{{{\text{CU}}}}{{{\text{tb}}}}$$

(14)

where U is the strain energy under the curve of interest, t is the specimen thickness, b is the remaining width from the tip of the crack, and C is a coefficient of material flow stress and notch length with a built-in geometry dependent factor [20, 122], e.g.,

$$C = 0.12 + \frac{{58\left( {a - 3.0} \right)}}{{\sigma_{{\text{Y}}} }}$$

(15)

here σ_Y is the flow stress, given in MPa, and the expression (a − 3.0) is the effective notch length in mm calculated by subtracting the part of the specimen clamped by the dies from the total notch length. The flow stress is calculated as an average between the yield stress and ultimate tensile strength. Figure 6 shows a comparative response between two samples with varying initial notch lengths of a₁ and a₂, with strain energies of U₁ and U₂, respectively. Using the differential area between two subsequent curves, valued as strain energy, with different initial crack lengths gives the energy to extend the crack from one size to the next, taking the point of maximum loading to be the moment of fracture [46]. Calculating the strain energy to get from one notch to the next notch, that is, with two otherwise identical specimens with differing crack lengths to obtain the J-integral values, a composite fit curve can be fit to the plot of the J data points, which has been shown to correlated well with conventional results [46, 122]. This method has been used to find the fracture resistance of materials under plane stress to be verified, or analyzed for the first time for materials which are more difficult to procure enough of in quantities sufficient for traditional methods, such as gold and its alloys [20]. A study utilizing nanocomposite films used the area under the load–displacement curve up to the break point to estimate the fracture toughness, with acceptable results, though the samples in this study did not utilize the multi-specimen approach, which is key to accurately modeling the J-R curve to estimate fracture toughness [12]. In studies [46, 123] comparing the SENT method with two others, the SENT method proved the simplest and most reliable with the least amount of scatter in test data, though it presents the drawback of requiring multiple specimens with different crack sizes. The other two methods, though also providing reasonable results, had significantly greater drawbacks. The first, based on crack tip opening displacement formulations, required multiple interruptions of tests to find the exact instance of fracture initiation and SEM access to measure crack opening. The second is based on using complex numerical simulation methods employed for simulating traditional notched fracture samples to calculate the J-integral which requires large deformations and therefore extensive calculations.

Figure 6

Energy difference method for calculation of J integral, where a denotes the initial crack length and δ_m, the displacement at P_max, is taken as the point of fracture, derived from [46]

Several other notched specimen types have also been proposed to characterize fracture strength using SPT [79, 124, 125]. In order to overcome the limitation presented by the SENT method of representing only situations of plane stress, Turba et al. [124] presented a new style of circumferentially notched SPT specimen, the details of which can be seen in Fig. 5e. This design is purported to approximate a plane strain condition for materials which exhibited fully brittle fracture, rather than ductile or mixed-mode fracture. This sample was manufactured at a thickness of 1 mm with a notch depth of 0.5 mm so as to make its load bearing capacity approximately equal to that of an unnotched sample of the conventional 0.5 mm thickness. Fracture energy in this case was measured up to a displacement corresponding to a 20% drop from the maximum load, which was where the specimen was considered as fractured. The main limitations of the circumferentially notched specimen are the presence of mixed-mode loading as opposed to pure Mode I loading and the difficulty presented in introducing a fatigue pre-crack to improve said limitation. Cuesta and Alegre [125] conducted a study using a Charpy-like laterally pre-cracked specimen along with FE models to numerically simulate the pre-cracked specimen to obtain estimates of the fracture toughness, the geometry can be seen in Fig. 5f. Although complex, due to requiring varying depth cracks and extensive modeling, results were found which were within the valid variability range established by Charpy impact tests. A subsequent study from Cuesta et al. [79] using similar specimens showed the effects of crack shape and quality on the results. Although the methods did not have a direct effect, the overall shapes of the cracks and their uniformity affected the repeatability and quality of results, emphasizing the need for accurately machined pre-cracks with high-stress concentrations to increase reliability. A study by Álvarez et al. modeled the behavior of these types of notched specimens, along with comparisons to test results, to relate their behavior to that of conventional crack tip opening displacement results to establish a correlation between the two [126]. Further complications arise when considering the numerous notched samples proposed, as notch configuration and orientation, size, tip radius, and quality affect the fracture response, and furthermore the severity of the response is dependent on sample thickness [127,128,129]. A study by Martínez-Pañeda et al. studied the effects of notch configuration and quality, as imparted by the chosen machining method, while also introducing a cross-notched configuration derivate of that shown in Fig. 5f, where another crack is machined perpendicular and centered to the lateral crack shown [127]. The different configurations were also modeled to study the damage behavior for the use of determining Gurson–Tvergaard–Needleman model constants. The Gurson–Tvergaard–Needleman model has also been used to verify results of 4 mm centrally pre-cracked specimens with values in the literature by Shikalgar et al. as well as the use of other sample types by Van Erp et. al., including that of a notched dogbone and a 0.6 mm pre-holed specimen [130, 131].

A thorough literature review by Abendroth et al. also noted significant contributions by several other researchers to this area of SPT research [132,133,134]. Abendroth and Kuna provided significant contributions to damage modeling of the SPT using the Gurson model, particularly using neural networks trained via finite element simulations with incremental variations of hardening and damage parameters [17, 135, 136]. In each of these sequential works, the authors were able to systematically train a neural network for use in simulating both tensile and fracture properties of various materials, creating visualizations of damage within SPT samples, as well as verify the validity of predicted material properties via experimental testing. Misawa et al. determined a linear relationship for fracture toughness similar to those noted earlier in this article, in which the single constant relating J_Ic to the equivalent fracture strain is both material and geometry dependent, and has units of kJ/m² [132]. Other notable contributions include calculation of J_Ic and ductile-to-brittle transition temperature via the use of the calculated small punch energy by Bulloch, similar to the work cited earlier by Alegre et al. [134]. Abendroth et al. were then able to propose a parameter identification process with FEA and constitutive material models to describe both ductile and brittle behaviors, one of the few processes to claim as such [133]. Brittle materials were evaluated using a Weibull statistical failure analysis, which was shown to be effective with varying compositions of carbon bonded alumina ceramic.

A study by Altstadt et al. [38] on oxide dispersed strengthened steels using SPT showed the effects of anisotropy on fracture results, which is especially relevant so SLM materials. The anisotropic nature of the crystal growth leads the material to act like a layered structure, with different directions behaving differently under SPT loading. This study showed that when loading direction was parallel to each layer the layers would delaminate, while samples loaded perpendicular to layers tended to arrest growth of the crack each time in encountered a new layer. This translates to the load peaking, dropping suddenly, and then continuing to rise, often repeating this behavior multiple times. Results from this investigation arising from this behavior led to the determination of ductile-to-brittle transition temperatures to be inconsistent from traditional results with SP tests yielding much higher transition temperatures, with differences over 400 °C present. The effects of these behaviors on determination of other material properties are unclear.

Overall, SPT has been shown capable of characterizing the fracture behavior of various materials. Results show sensitivity to microstructural differences, and test results display response to differences in sample temperature and thickness. Samples with machined or fabricated fracture notches show some promising similarities to traditional notched sample testing, but dependence on material type and condition as well as sample geometry and preparation makes these approaches less reliable. Though a large body of literature exists, direct inferences on fracture behavior have been shown to be highly dependent on several factors, and as such various approaches have been studied, though no single method has strong confirmation, making direct correlations with conventional results difficult.

Ductile-to-brittle transition temperature

A number of the works mentioned in fracture section also deal with the determination of the ductile-to-brittle transition temperature (DBTT), serving to strengthen both correlations. However, it is prudent to discuss utilizing the SPT for determining the DBTT separately and methods associated with it, as it was one of the earlier influences for establishing the SPT method, especially as related to irradiated materials [4, 8, 25, 137, 138], as radiation has been shown to shift the DBTT to a higher temperature, creating a potential danger and unpredictability in calculating life estimates. The study of the evolution of irradiated materials, being of high interest for development of the SPT in general, was one of the main driving influences for studying the relationship between conventional Charpy and SPT tests and led to the development of the correlation still in use and recommended in the current and upcoming guiding documentation [30, 44, 49]. Today the study of irradiated materials via SPT still continues to be of high interest to researchers [139,140,141,142].

Small punch tests have been conducted at a range of temperatures in efforts to determine the DBTT of materials, and a clear correlation to conventional Charpy test results has been established [143,144,145]. A generally well-accepted relationship between T_SP, the transition temperature determined via SP, and T_CVN, the transition temperature as determined by energy absorption in Charpy impact tests, has been established as:

$$T_{{{\text{SP}}}} = \alpha_{{{\text{CVN}}}} T_{{{\text{CVN}}}}$$

(16)

The correlation factor, α_CVN, is material-dependent and can thus vary, but reflects the finding by several studies that T_SP is typically found to be lower than T_CVN. This is often attributed to the differences in the mechanics of the two test methods, as they subject the samples to vastly different strain rates and produce different stress states within the material, though the exact causes remain arguably unknown, as some attempts at varying strain rates during SP tests have produced only small differences in results [26, 67, 124, 146]. The transition temperature, T_SP, is determined by forming a transition curve using the calculation of the small punch energy, E_SP, at various temperatures, much like with a traditional Charpy test. The small punch energy is calculated using the integral of the area under the SP curve form zero up to the point of deflection at max force. For brittle materials, which may experience sudden drops in loading before continuing to rise, the small punch energy should be calculated up to the occurrence of the first significant drop, which corresponds to 10% of the maximum force, and indicates the appearance of a significant fracture [38, 45]. After fitting a curve to the energy versus temperature data, the small punch transition temperature can be determined as the mean of the highest and lowest energy values in the transition region, which correspond with the upper and lower shelf energies. This data should be compiled using a minimum number of tests as discussed in [4, 147]. Bruchhausen et al. also proposed a modified approach to this method that normalizes the fracture energies with the maximum force, to produce a clear, constant upper shelf energy and allow for curve fitting using a single function [146]. Sample preparation has been shown to influence results, as specimen surface texture can affect calculated energy levels [56, 148]. The use of SPT for determining DBTT, also often denoted as or associated with the fracture appearance transition temperature, FATT, has also been extended for determination of fracture toughness values and fracture behavior evolution in general for evaluation of in-service components in high-stress environments, such as in energy production [23, 149,150,151]. This is of high interest for both in-service and ex-service components in high pressure and temperature environments, such as those in energy applications, which may experience embrittlement due to service conditions, but which may not offer enough material to produce conventional fracture test samples. Some of the notched samples mentioned in the fracture section were developed or employed in an attempt to reconcile the differences between the two methods, yet it also seems unrelated to the presence of a notch, as findings between studies sometimes indicate a shift in DBTT and others do not [26, 45, 124]. Regardless of any differences, however, it is clear that the trends between the two methods do align, and as such this is a method which researchers show confidence and great interest in.

Several studies also give insights to the suitability of the use of the SPT for determining the DBTT of materials which are limited in quantity or variable in nature due to microstructural variations of otherwise. For example, Gai et al. applied the correlation of the SPT and Charpy V-notch to show applicability to the narrow fusion zone of weld beads produced by electron beam welding [152]. Sensitivity to location of sample extraction from the original body with respect to depth from the surface has also been shown [153]. The SPT has also been employed to test thin coatings, such as in [154, 155] and [156], which successfully determined the DBTTs of two bond coats utilized for thermal barrier coatings for the first time with the SPT. Additionally, the DBTT calculated via SP has been shown to be sensitive to evolutions in microstructure such as those seen when post-processing AM materials [24]. A dependency on sample orientation with respect to Charpy sample orientation has been noted [45]. Further, in [157] it was shown that while transition temperatures for ODS steels with variable grain structures could accurately be calculated regardless of the sample orientation when the material was hot-extruded, the same could not be said for hot-rolled materials. These various studies show sensitivity and accuracy for use with highly variable microstructures, such as those which may be present in AM structures. Of notable importance when considering applying such a technique with AM materials is the need to use an increased number of specimens for increased reliability due to their highly variable microstructures, as noted in [4].

Shear properties

A variant of the SPT is utilized for determination of shear properties which utilizes a flat punch rather than the typical rounded punch, known as shear punch testing (ShPT), and was derived from blanking operations used for metal forming [158, 159]. The shear punch test varies slightly from the small punch test, which is the primary focus of this paper, when considering formulations for determining material properties from ShPT test data, but has been shown analogous to uniaxial tension [159]. While the dimensions of most of the components are typically very similar, the rounded punch or ball is replaced with a flat punch of the same diameter with causes the primary deformation mode to be one of shearing in the sample along the edges of the punch. The shear stress, τ, can be calculated from the load–displacement data as

$$\tau = \frac{P}{{2\pi r_{{{\text{avg}}}} t}}$$

(17)

where P is the applied load, t is the initial specimen thickness, and

$$r_{{{\text{avg}}}} = \left( {r_{{{\text{punch}}}} + r_{{{\text{die}}}} } \right)/2$$

(18)

where the variable r_punch denotes the radius of the circular, flat-tipped punch, while r_die represents the radius of the opening of the lower die. This method of calculating shear stress from shear punch data is widely utilized in the literature as providing accurate results [3, 159, 160]. This is one of the more straightforward conversions of punch test data to traditional data that is reliably present in the literature. Conversion of load–displacement data to shear data via the use of this equation allows for more direct calculation of material properties in shear.

Linear relationships have been proposed for determination of tensile properties such as yield strength, ultimate strength, and strain hardening exponent from shear punch testing [161, 162]. It has been agreed upon that a linear relationship exists between the primary yield point of the shear-displacement curve and that of the tensile yield strength. However, such as is the case with the small punch test, the determination of where the yield point occurs is a topic of considerable debate, with a few methodologies having strong experimental support behind them. The relationship for determining the tensile yield strength, σ_ys, from the shear-displacement curve can be given as

$$\sigma_{{{\text{ys}}}} = \alpha_{\tau } \tau_{{{\text{ys}}}}$$

(19)

where τ_ys is the shear yield determined from the shear-displacement curves developed from the force–displacement results using Eq. (17). The primary method used for determining the point of shear yield was by using the point of first linear deviation from the shear-displacement graphs as the point where shear yield occurs [163, 164]. This method, however, is somewhat arbitrary and the point is not always well defined, making this method difficult to use. Consequently, after a redesign of typical SPT fixtures incorporating some compliance correction by adjusting the location of displacement measurement, a 1% offset shear strain method was suggested for defining the shear yield stress, where the shear strain, γ, can be calculated as

$$\gamma = {\raise0.7ex\hbox{$\delta $} \!\mathord{\left/ {\vphantom {\delta c}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$c$}}$$

(20)

where the clearance, c, is defined as the difference between the radii of the punch and die when using a flat-faced shear punch [162]. This method showed a marked improvement when compared to FEA simulation results relative to older methods [50, 162].

Guduru et. al tested various alloys and suggested a variation to the 1% offset shear strain method previously used [160]. In order to mitigate sample thickness effects associated with this method, they implemented a normalization factor when plotting the shear-displacement curves, normalizing the displacement by dividing it by the sample thickness and using a 1% offset to find the corresponding yield point. The correlation constant was then found by plotting the known 0.2% offset yield stress values of the various metals tested versus the shear yield values found with SPT. A correlation value of 1.77 was determined, so that the equation for correlating tensile yield stress and shear yield stress begins to approximate the von Mises yield criterion which utilizes a correlation factor with a value of 1.73 when the deformation mechanism is dominated by shear. Later, FEA models were similarly utilized to support this correlation against experimental results by using the von Mises yield criterion as a basis for comparison. FEA results indicated that much smaller offsets were necessary, with the difference between the correlation factor found and that given by the von Mises yield criterion being attributed mainly to compliance effects from the SPT test rig [165, 166]. Originally, experimenters incorrectly assumed the cross-head displacement correlated with the sample deflection. It was later shown that flex in the components of the load frame and of the small punch apparatus actually invalidate this assumption, and SPT force–displacement curves had to be offset in order to mitigate punch compliance effects [164]. As such, a measurement device was placed parallel to the punch in later studies, which helped to mitigate these effects, which were especially apparent in high strength materials [160, 162]. Additional support was given by SP testing electrodeposited copper samples, the properties of which were not included when determining the correlation factor or the subsequent FEA analysis, and comparing values determined using the correlation factor of 1.77 to miniaturized tensile testing results [165]. The correlation factors used for calculating tensile yield and ultimate strength produced values that were within 6% of the measured values from tensile tests [165]. It was later shown that compliance issues could be further eliminated by measuring the deflection, or displacement, of the sample itself, as it is represented in an FEA [163, 164]. As was the case for the small punch test, this was accomplished by locating a linear variable differential transformer (LVDT) directly below the sample, and was shown to be highly successful [50, 51]. In fact, in the case of the shear punch test, the offset using this correction with additional information gleaned from elastic loading tests reduced the necessary offset to 0.2%, matching earlier FEA simulations and changing the linear relationship definition to one which matches the von Mises shear yield criterion [50, 165, 166], such that the correlation constant relating yield stress to shear yield, α_τ, is determined to have a value of 1.73.

Similarly, a linear correlation has been established for calculating the ultimate tensile strength. A relationship was proposed stemming from the manufacturing process of blanking to which the shear punch test is akin, where the maximum shear load was related to the ultimate tensile strength by way of a factor dependent on the strain hardening exponent [167, 168]. However, this required previous knowledge of the strain hardening exponent in order to be utilized, typically requiring tensile tests to characterize, thus rendering the ShPT redundant. Subsequent studies eliminated the need for previously established constants and proposed a more direct relationship [50, 168, 169]. This relationship can be expressed as

$$\sigma_{{{\text{uts}}}} = \beta_{\uptau } \tau_{{{\text{uts}}}}$$

(21)

where τ_uts is the ultimate shear stress value, the maximum load determined from the shear-displacement graph and β_τ is the correlation factor. This equation is an adjustment from the original which included an additional offset parameter on the right side, to improve the overlap between shear punch and conventional uniaxial data and which varied with the class of alloy [163]. This offset parameter was subsequently eliminated by the aforementioned correction of compliance issues which made the datasets from SPT and conventional tests overlap more accurately [161, 162]. In [160], experimentation with a variety of materials led to a suggested universal correlation value of 1.8 for the constant β_τ. Subsequent support showed that this correlation also works well for a material not included in their primary study, electrodeposited Cu [165]. Other studies, however, while confirming the form of the relationship, found differing correlation constants for the UTS relationship based on the material, and the use of a single constant for all materials provided unreliable results [50, 170]. Rabenberg et al., for example, found correlation factors for the shear yield and ultimate shear strength of 1.5 and 1.4, respectively, in addition to utilizing a 2.2% offset to determine the shear yield point, all of which differ from several studies presented earlier, though it falls within a large range that they found present in the literature [170]. Their correlation factors were established through a series of tests with samples of aluminum, stainless steel, and Inconel of varying treatment conditions, and validated with irradiated 304SS. Works such as those by Wanjara et al. have shown the ability of the shear punch test to evaluate the properties of additive manufactured materials including the effects of treatments, microstructure-property relationships, the effects of treatments of such, and variations within the weld zone of electron beam welded stainless steel and aluminum [171, 172].

Fatigue

The small punch test (SPT) has yet to be leveraged for thorough evaluation of the fatigue behavior of materials. This is due to the difficulty of applying reversed loading in an SPT setup, or even zero-to-load setups, as a return to the origin displacement of zero could cause punch alignment issues upon subsequent load cycles, as a gap forms between the punch and the sample surface due to plastic deformation of the sample. With the constricted space used in SPT, forming an SPT setup which can apply more than the typical downward load of a typical SPT setup presents a challenge. Several reviews which cover miniaturized testing summarily stated that small samples gave high correlation with full size sample S–N curves and as such sample size was found to have little effect on results, though otherwise lacked insight on the matter [101, 173]. Hirose et al. used miniaturized cylindrical fatigue specimens to show that size did not have a significant effect on fatigue properties [174]. Li and Stubbins conducted fatigue crack growth tests using miniaturized three point bending samples well within the dimensions of SPT samples [175]. These samples, with the dimensions of 7.9 mm in length, 2 mm in width, and 0.8 mm in thickness, were pre-cracked with a 0.1 mm deep notch made by electro-discharge machining and cycled with a load ratio, R, of 0.1. The crack growth data corresponded very well with standard sized test specimens.

Prakash and Arunkumar presented a novel cyclic compression–compression small punch test routine which was inspired by monotonic and cyclic automated ball indentation for estimation of material properties, including fatigue life [18]. This method uses hysteresis energy of cyclic SPT as a parameter to quantify the fatigue life of materials. To quantify the fatigue damage, they defined a damage parameter as the difference between unity and the ratio of the plastic energy dissipated per cycle of damaged material to that of a virgin material. The determination of the damage parameter involves the summation of the plastic dissipation energy for damaged and virgin materials, in this case copper and stainless 304, by cycling materials at a frequency where the hysteresis is constant or stable. The load for cycling is a percentage of the maximum load determined by first conducting monotonic small punch tests. A significant effect was also found with variation of the frequency of cyclic loading, as thermal effects from excessively high frequency tend to alter material behavior and resultant hysteresis, emphasis was also placed on optimization of clamping torque, which varies based on the material being cycled [18]. The approach shows sensitivity to material condition and testing parameters with loads varying as little as 2 N showing differences in life. The damage parameters of copper at different fatigue life states calculated via cyclic loading were compared with damage estimated from monotonic SPT as well as tensile tests, and while the cyclic parameters were generally higher, they were within 7% difference of both monotonic SPT and tension tests.

A cyclic SPT study based on using the standards for testing ultra-high molecular weight polyethylene for surgical implants, ASTM F2183, showed that cyclic SPT gave repeatable and reliable results [176]. Test results showed the differences in life for varying loads and varying aging conditions, with distinctions showing for different aging times versus virgin material. Samples were cyclically loaded at 200 N/s with a triangular waveform, with loading between 2 N and a maximum of 60–94% of the maximum load of monotonic tests so as to result in failures below 10,000 cycles. A similar study by Jaekel et al. using polyetheretherketone polymeric biomaterials confirmed that cyclic testing with SPT was sensitive enough to detect differences in manufacturing conditions for the materials, even while restricting loading to the elastic range of the load–displacement curve [177]. These studies show the sensitivity of the SPT to material variations due to both testing and manufacturing conditions, which is important for additive manufacturing materials as processing parameter variations to the resultant microstructure and material properties.

While these studies mainly show that SPT can detect differences in fatigue life due to differences in processing or treatments, it is unclear whether the results directly translate to traditional fatigue life prediction data. The capabilities presented in the literature for fatigue testing with SPT are limited to zero-to-tension or tension-to-tension loading. Additionally, the stress states presented by small volume fatigue tests including the single punch cyclic SPT, the cyclic ball indentation test, and the hydraulic bulge test have been shown to differ significantly from those of uniaxial fatigue tests [178]. This makes correlation of data between reduced samples and conventional samples difficult. This type of loading also only gives a limited perspective on fatigue, as it provides no insight on reversed yielding or plasticity. A significant gap in SPT fatigue testing exists which needs a modified methodology capable of reversed loading in order to fill it, which presents a large challenge given the confined dimensions of the test system. Present works are directed at starting to fill these gaps, as shown in [31, 179], including test control variations for cyclic loading, as well as introduction of a dual-punch test setup to introduce fully reversed cyclic loading in an effort to replicate traditional fatigue testing damage. Concurrent work completed by Lancaster et al., utilized a similar dual punch setup to fatigue test variants of Ti-6Al-4 V manufactured by both electron beam melting and conventional forging [180]. Regardless of its scarcity, however, the literature on this topic shows the potential for fatigue testing with SPT, especially since sample size does not seem to have a significant effect.

Finite element analysis of the SPT

Finite element (FE) models and simulations of small punch tests have been extensively utilized to validate SP tests in order to evaluate material properties. Many of the studies reviewed have utilized FE models to varying degrees in order to acquire results and material correlations. Though some investigations utilize 3D models, such as when accounting for anisotropic material properties, 2D axisymmetric models have been shown to be sufficient for most studies [181, 182]. A study using Poly(methyl methacrylate) bone cement by Giddings et al. corroborated the findings of previous studies to evaluate the relationship between the initial stiffness of the SPT test and the Young’s modulus by varying the value of the modulus and the corresponding set of initial stiffness values [81]. The proportionality constant was found by utilizing an FEA model with an assumption of the Poisson’s ratio value and variation of the elastic moduli to note the initial stiffness then applying a least-squares fit. In this way a correlation factor between the two was determined for future predictions. This same method has been used with metals as well [183]. Kim et al. found correlation factors for determining the yield strength, Young’s modulus, and hardening coefficient [69]. A comprehensive study conducted by Garcia et al. on determination of correlation factors for SPT to mechanical property relationships utilized a FEA model to evaluate several points on the force–displacement curve to find the best fit for the correlations for calculation of yield and tensile strengths [60]. This study extended into determining a correlation coefficient for fracture toughness for ductile steels. A database method for studying ductile materials involving the extensive use of FEA models generating theoretical materials to investigate actual specimens has also been proposed, with limited results showing good agreement for yield and ultimate strengths [184]. Additionally, Guduru et al. and others have used correlation simulations to find correlation factors between the shear strength data produced using the shear punch test and tensile strength and yield strength [160, 165, 166, 168, 169].

Simulations have also been used for evaluating creep properties in SPT, with suitable correlation to traditional creep tests having been found. Simulations, like traditional tests, have primary, secondary, and tertiary stages, and showed failure in the expected areas [103, 185]. Using P92 steel welded joints, Zhao et al. simulated creep damage and determined correlations between the applied load and stress levels [41]. A strain model was then used to relate the creep strain of SPT to determine a relationship between strain rate and stress. Zhou et al. similarly found good correlation of FEA creep simulations and experimental results, along with the significant influence of specimen thickness, load level, ball size, temperature, and test atmosphere [91].

Fracture behavior has been studied using FE models with several different approaches. Kim et al. calculated critical fracture stresses for low alloy steels at very low temperatures by comparing maximum loads from SP curves to FE results [69]. Tanaka et al. utilized a FEM analysis from a notched 3D model in order to obtain fracture toughness from SP tests, in combination with the small punch energy value calculated from the force–displacement curve [119]. Master curves were created which relate the fracture toughness value estimated by small punch method, J_E, and the SP energy, E_SP, which require the use of a traditional tensile test to obtain a stress–strain curve. Simulation of a small punch test is conducted to obtain relationships between E_SP and the strain energy density W_SP at the crack tip of the SP specimen. Similarly, a simulation of a traditional CT fracture test serves to provide the relationship between J_E and the strain energy density at the crack tip of the CT specimen, W_CT. The relationship of W_SP = W_CT is then used to relate J_E to E_SP, thus allowing the use of these master curves as references for future test curves to estimate fracture toughness. This process is similar to one utilized previously by Foulds et al. [186]. The results of this method were dependent on certain limiting conditions. Similarly, Turba et al. used another novel fracture specimen previously described. In this case, FEA was used to optimize the notch size, calculate the stress intensity factor, and carry out an elastic–plastic analysis or said specimens. The stress intensity factor calculated using the FEA in combination with test results were then used to estimate a fracture toughness value [124]. Alvarez et al. utilized numerical models in combination with interrupted tests on notched specimens and SEM imaging to measure crack tip opening displacement and determine where cracks originated [126]. The Gurson-Tevergaard damage model has been used to simulate SPT results up to fracture with good agreement [187]. In this manner, material properties were determined by matching simulation to experimental results. The model was separated into six stages and parameters were determined one at a time using the inverse method. Dutta et al. suggested a method to improve the numerical prediction of fracture initiation and overall fracture energy curve calculation using the Gurson-Tevergaard-Needleman material model with split parameters [188], which was shown to improve prediction and determination of J-integral versus crack growth data [77]. Similarly, damage parameters for the Gurson-Tevergaard-Needleman model have been used to precisely simulate fracture of notched SPT specimens of varying configurations [127].

Simulations are often employed to determine material properties via the inverse method. The FEA for the solution of the inverse problem involves using the results of SPT to inversely solve for the stress–strain curve. A simulated SPT curve is assembled in a piecewise manner using assumed values for material model constants, adjusting them iteratively until the curve up to a particular point matches that of the experimental output. This is repeated until the output of the simulation matches that of the experiment, after which the acquired curve can be used to characterize an equivalent stress–strain response and thus establish material properties. Efforts have been made to speed the curve-fitting optimization process using a number of different algorithms to calculate the numerous iterations, including least squares, neural networks, and pattern searches, among others [17, 189,190,191,192]. This approach is often useful when not much is known about the material. Husain et al. used this iterative approach on the elastic portion of SPT curves to determine the elastic moduli and corresponding stress–strain relationships of three different steels, with promising results versus traditional tensile tests [193]. A comprehensive study using the inverse method was conducted by Campitelli et al. in order to assess the true stress–strain relationship [194]. The model which was developed showed the necessity for splitting the strain hardening into two stages for increased accuracy. The importance of the effects of compliance, friction, specimen thickness, and constitutive modeling were all verified. A model constructed by Egan et al. showed the importance of basing material property variance based on deformation shape [189]. The elastic–plastic behavior was found via three plasticity coefficients which were optimized using a pattern search curve fitting algorithm, cutting down on manual computation efforts. Similarly, Linse et al. combined the computing power of neural networks with an optimization routine using an axisymmetric model for the prediction of load–displacement curves by limited variation of material properties [190]. Results for identifying the hardening coefficients of reactor vessel steels with the optimization routine showed results correlated well.

Several studies have correlated experimental force–displacement curves with those produced by FEA models in order to determine compliance effects on experimental results. The FE simulation conducted by Egan et al. used experimental data to find the influences of maximum force depending on the material properties supplied and the sample geometry [189]. The effects of microdefects and microvoids were examined by Guan et al. [195]. Simulated curves with varied void sizes integrated in the models showed that although defects had little effect on the earlier parts of the curves, strength in the plastic region was affected and the defect produced large amounts of scatter. Hulka et al. analyzed the geometry presented in the CEN workshop agreement for sensitivity effects on results of inverse simulations which tested the influence of the mesh density, the modeling of the tools, the sample thickness, the material model used, and the effects of friction between the punch and sample and between the sample and the dies [196]. Similar studies have shown that sensitivity studies are useful for evaluating fracture properties as well, as [115, 197] showed model response and fracture location dependencies on sample thickness and friction, but an independence from mesh density. Sensitivity studies apply when modeling the shear punch test as well. Goyal et al., for example, explored the effects of several parameters on shear yield strength, such as effects of punch compliance, which was severe [198]. Less severe were offset effects and variations in lower die width and specimen thickness.

Simulations thus play an integral part in determination of material properties when utilizing small punch test, especially as the most accurate method of acquiring conventional data from SPT test data is by utilizing the inverse solution method. In an effort to reduce calculation time due to the numerous iterations necessary when curve fitting via the inverse method, correlation factors are often used to determine material properties. However, these have been shown, often through the use of FEA models, to have dependencies on material, geometry, and other test factors. As such, FEA is and will remain an integral part of material characterization with small punch testing.

FEA sensitivity study on the suitability of the SPT for AM materials

Due to the prevalence of use of FEA models to study the SPT, a parametric sensitivity study was carried out using an FEA model designed for the purposes of using the inverse solution on SPT results with a nickel superalloy [199]. The sensitivity study is used in order to gage the suitability of SPT for evaluating and optimizing material properties of AM materials, due to the high variability in material properties that may arise due to processing and post-processing parameter variations. A 2D axisymmetric model was utilized to carry out the simulations necessary, which was primarily verified against a model established by Campitelli et al. [194]. The upper and lower dies were modeled as rigid structures. The sample and punch were meshed with quadrilateral elements, with refinements on the edge of the punch and in the center of the sample where the deformation occurs. A friction factor of 0.1 was applied between the specimen and each die [60, 127, 182, 196]. Contact and friction of 0.05 was used between the punch and specimen. A displacement rate of 1 mm/min was employed, which is roughly equivalent to 0.02 mm/sec, as commonly employed in experimental setups following the CWA 15,627 guidelines with a recommended rate of 0.2–2 mm/min [45].

A full factorial experiment was designed to establish the effects of varying the Young’s Modulus, E, the strength coefficient, K, and the strain hardening exponent, n, on the mechanical properties as determined from simulation results. Five levels were tested for each of the three factors in a full factorial experimental array, which equates to 5³, or 125, necessary trials. These factors constitute the formulation of the Ramberg–Osgood relationship, which can describe the stress–strain response for a strain-hardening material:

$$\varepsilon = \frac{\sigma }{E} + K\left( {\frac{\sigma }{E}} \right)^{{\text{n}}}$$

(22)

Approximately average values of the mechanical properties of IN939 at room temperature were used as the median values for each factor, with two levels above and below the median values established as ± 10 and 20% to give a high range of influence [200,201,202,203]. The values of the levels for each factor are given in Table 2. The responses of varied cases from the study are shown in Fig. 7, which shows both the complete curves and a detailed view of the initial linear portions of such. The simulated responses vary widely from the linear portions to failure, regardless of the values of the factors used. The variation in the initial linear response shows its dependence on all three factors, even though the Young’s modulus has been shown to be the dominant factor. The combined effects of altering the factors of interest can easily be seen, beginning in the elastic range. As the factors are increased, there is a corresponding increase in the slope of the elastic region along with a continuous divergence of the curves as displacement increases. This small selection of curves shows how prominent the effect of changing these factors and their interactions are on material response. The influences of each factor and their interactions were thus evaluated using analysis of variance (ANOVA). A regression was executed on the results of the simulations, with which the influences of each factor on specific properties or portions of the force–displacement curve could be determined, as shown in Fig. 8. For this graph, the Pareto coefficients of each response were summed together and used to find the percentage contribution of each factor. Note that only the main factors are shown here, and so each set does not equal unity, but highlights the influence of each material property.

Table 2 Factor levels considered for full factorial parametric design study using IN939 as a basis, the average properties correspond with Level 3 [200,201,202,203]

Figure 7

Select varied representative responses from the parametric study, and the initial linear portions of such

Figure 8

Percent contribution of E, K, and n to each portion of the load–displacement curves

The normalized percentage values show that curve the strength coefficient, K, is the distinctly dominant factor for the majority of the force–displacement curve. The hardening exponent, n, is always second most influential to varying degrees, while the Young’s modulus, E, has little effect on most of the response. The exception to this, as expected, is in the elastic portion of the curve. However, although E affects the outcome the most in this region, the influences of K and n on the shape of the curve are nearly equal to that of E. Some of these behaviors are to be expected, as the power law in which K and n are used to describe material behavior pertains largely to the region of plastic deformation, while the elastic region is primarily described by Hooke’s law, in which only E is present. However, the high effects of K and n in the elastic portion indicate an early onset of plastic deformation, or a very small range of true elasticity. There is also a slight but notable effect from Young’s modulus in the plastification region, region II, and a nearly negligible contribution to the hardening region. A logical trend can be seen in the diminishing influence of E as displacement progresses and damage transitions from elastic to fully plastic, though a slight recovery of the displacement can be expected. Also noteworthy is that for all but the elastic and plastification zones, the interaction between K and n has a larger effect than E. As mentioned, this is not the case for the elastic zone since E is the dominating factor there and the interactions of E-K and E-n are much more relevant than K − n. However, for the plastification zone, although it has the second highest influence from E, the contribution from the interaction of K and n is nearly equal to that from E alone.

As the microstructures and material properties of AM materials have been shown to be highly sensitive to both processing parameters and post-processing conditions, the advantages of utilizing the small punch test to evaluate them become immediately evident [204, 205]. As the changes in SLM material microstructures can range from minor to major depending on the variations employed in processing, a high sensitivity evaluation method is vital. As SPT has been shown to be responsive to material property changes and anisotropy in small volumes caused by processing variations, this then becomes a highly attractive option for optimizing processing parameter settings and post-processing routines [31, 74, 104]. The Pareto plot and the resultant curves from the parametric study show that a model such as that utilized here, and consequently the small punch test, is sensitive enough to track incremental changes in material properties due to processing variations typical of AM materials. As such, the use of the SPT in combination with the inverse FEA method may be recommended as a way of expediting the otherwise cost and time prohibitive optimization process for AM and other materials.

Determination and use of correlation constants

As was reviewed previously, linear relationships exist between small punch test data and tensile data for the same material. Equivalent values for mechanical properties are determined by normalizing corresponding inflection points in the force–displacement data. These linear relationships involve the use of a correlation constant to equate them, which is determined by establishing the linear relationship by plotting tensile mechanical properties against their SPT counterparts. As shown previously, plotting various materials together yields correlation values which may be used to estimate material properties of a range of materials from their SPT results. The plots in Fig. 9, 10, and 11 account for an expanded array of materials from various sources, building on the relationships established in [60], and include partial experimental data from preliminary studies conducted for further works expanding on the topics explored here. This includes selective laser melted IN718 and IN625 compared to manufacturer specifications for the materials [206, 207], and direct metal laser sintered GP1 (a derivative of 17-4PH) compared to [208]. Direct laser-deposited C263 as reported by Davies et al. is also included as an additional AM material variant [34]. The effects of special materials with distinct behaviors, such as powdered metals, are also specifically considered. Several of the sources added are generalized via material class despite the inclusion of material variations including alloying differences or treatment variations, such as various grades of Eurofer (2), CrMoV (4), dual phase steels (4), boiler steels (4), and Al alloys (5). Additionally, there are several directional materials included as well, which are categorized under the general material name, rather than specifying the direction. The numerous versions of these materials each display unique material properties as a result of their alloying or processing variations. These present added variety in an effort to strengthen the validity of the correlations. These plots show the most popularly utilized correlations for σ_uts and σ_y as determined via tensile testing against the corresponding SPT values P_max/δ_mt and the P_y(t/10)/t², respectively. The 95% confidence interval and 95% prediction interval are also shown on each plot. The collection of data from the literature shown support a strong correlation of σ_uts with P_max/δ_mt. This is shown in Fig. 9. The linear regression is shown with a narrow CI bounding it, generated by a reliable sample size and low variability, supporting a good fit, and a relatively narrow prediction interval band. Although the combined data add scatter which reduce the R² values from those seen in [60], the data points generally fit well along the trend line, and the correlation values produced for the linear fit with a forced zero-value y-intercept, as is sometimes done for comparison [76], are similar to those proposed by Garcia et al. There is a significant change in both the correlation value and fit value when considering the y-intercept value, however, thus making this type of approximation with an included intercept value more optimal for a larger number of materials, as has been seen elsewhere [26, 56, 75]. The correlations both with a y-intercept, as shown in Fig. 9, and without a y-intercept value and which include various conventional and AM materials, are thus given as

$$\sigma_{{{\text{uts}}}} = 0.2282\frac{{P_{{{\text{max}}}} }}{{\delta_{{\text{m}}} t}} + 137.05 \left( {R^{2} = 0.824} \right)$$

(23)

$$\sigma_{{{\text{uts}}}} = 0.2751\frac{{P_{\max } }}{{\delta_{{\text{m}}} t}}\left( {R^{2} = 0.7858} \right)$$

(24)

Figure 9

Correlation of tensile and SPT tensile strength data, compiled from experimental data and various sources [16, 34, 38, 48, 51, 52, 54, 60, 63, 70, 77, 82, 187, 193,194,195, 208, 210,211,212,213,214,215]

Figure 10

Scatter of powdered metal alloys from [43] as compared to data points and trendlines established previously

Figure 11

Correlation of tensile and SPT yield data, compiled from experimental data and [38, 43, 48, 52, 54, 60, 63, 70, 77, 82, 187, 194, 195, 208, 210,211,212, 215]

The added data for the tested AM materials are on the higher end of the data range and present a wide spectrum of results depending on processing and treatment. Although these materials generally fall close to the fit line, there are obvious outliers in the plot which can negatively affect the overall fit. Due to their higher strength and lower ductility as compared to conventional counterparts, the AM materials present a larger effect of deviation. In Fig. 9, several points outside of the bounds of the majority mass of data belong to the AM class of materials including several, but not all, of the DLD C263, the direct metal laser sintering (DMLS) GP1, and the SLM 625. The deviation from the fit of these points may be attributed to the unique properties of AM materials and their high dependence on processing and post-processing parameters. However, other DLD C263 points and the SLM 718 fit well within the data. This suggests that a universal fit may serve to include this type of data along with that of conventional data, given uniformity in production and testing, but significant research is needed to strengthen this relationship. Excluding the AM data from the plot can increase the fit value of the data, but only marginally. The relationships, without the inclusion of the DLD C263, DMLS GP1, and SLM IN718 and IN625, thus become

$$\sigma_{{{\text{uts}}}} = 0.2323\frac{{P_{\max } }}{{\delta_{{\text{m}}} t}} + 127.03 \left( {R^{2} = 0.8387} \right)$$

(25)

$$\sigma_{{{\text{uts}}}} = 0.2771\frac{{P_{\max } }}{{\delta_{{\text{m}}} t}}\left( {R^{2} = 0.8046} \right)$$

(26)

This is a small change for the nonzero intercept equation, which bodes well overall for the inclusion of AM materials with a universal fit line relationship such as that given previously in Eq. 23, and thus the suitability of this method for evaluating AM materials in various states of manufacture.

Although not considered an additive manufacturing technology due to its manufacturing methodology, the powdered metallurgy (PM) alloys in [43] present a similar sensitivity and variance as AM materials. In the original work, this data fits well when using a normalization factor of P_max/t², but converting to normalization with respect to the displacement at maximum load as shown here and comparing it to a much more varied range of materials causes a very different fit. As shown in Fig. 10, the dark squares represent data from three different powdered metal alloy mixtures as well as heat treated versions of each, for a wide spectrum of characteristics. The result is that the data is scattered broadly with respect to the rest of the data, shown as light-colored circles. In this figure, the yellow points are given as reference data, and are comprised of the data shown in the original plot given in Fig. 9. Adding the PM alloy data to the plot to be considered with the overall fit changes the R² values to 0.762 and 0.7058 with and without y-intercept value, respectively, degrading the fit and increasing the difference between the two trendlines due to additional scatter. However, this is not simply an indicator of differences or scatter due to investigator testing methodology and setup possibly affecting data fits, as can be deduced to cause scatter across the various results in the literature, but instead raises considerations for limitations on material class for utilizing these correlations universally. Rather, due to the brittle nature and fracture morphology of the PM samples, this supports the alternatively proposed relationship for determining UTS which utilizes a specified displacement point in Zone III of the force–displacement curve which is not affected by material properties and may thus be more appropriate for a range of materials, whether ductile or brittle [43, 75, 76]. This data and its fit is also be affected by the locations of the samples with respect to the original donor component as a whole, as location within the original structure will affect the porosity and level of sintering which are artefacts of the PM manufacturing process, since samples nearer to the surface will undergo more direct pressure and sintering than those at the center, and thus have a less brittle nature [43]. Consequently, it may be necessary to consider both methodologies when evaluating the suitability of SPT for AM materials, as fracture morphology and response for AM samples can vary due to the degree of material anisotropy present depending on parameters such as orientation and post-processing treatments [31].

The yield strength correlation presents a higher level of scatter and thus lower fit values than the tensile strength correlation. Figure 11 shows the collection of various sources of SPT and tensile data compared using the t/10 offset yield strength method. Many of these were extracted from the plots given in the respective sources, as not all authors use the same yield strength correlation methodology. This presents a possibility of error, and also limits the data available for use, as the first portion of the plot which is needed to calculate the slope of the offset line is not always clearly visible due to small range of this portion of the curve. As such, there is significantly higher scatter in this data, and thus a poorer fit, than with the tensile strength data. Consequently, this plot features wider bands for both the 95% confidence and prediction intervals, indicating higher scatter in the collection of data. The correlation equations for the various materials, including several AM materials, are thus given as

$$\sigma_{{{\text{ys}}}} = 0.3214\frac{{P_{{{\text{y}}\left( {{\text{t}}/10} \right)}} }}{{t^{2} }} + 50.013 \left( {R^{2} = 0.7462} \right)$$

(27)

$$\sigma_{{{\text{ys}}}} = 0.3485\frac{{P_{{{\text{y}}\left( {{\text{t}}/10} \right)}} }}{{t^{2} }}\left( {R^{2} = 0.7402} \right)$$

(28)

Once again, using a nonzero σ_ys-intercept value for the yield strength correlation value increases the fit as described by the R² value but only by a minor amount. The zero-value σ_ys-intercept correlation value, however, is very similar to what is given by Garcia et al., though with a notably lower R² value. In addition to the minor effects of AM materials on the fit, some materials gathered from the literature present a special case in terms of behavior, such as 20MnMoNi55 in the yield plot. Excluding this point, for example, can increase the R² value of the best fit line to 0.77. Conversely, the powdered metal alloys fit well within the trendlines in this case. The poorer fit of this data indicates a need for refinement of this method for determining the appropriate yield point and normalization of data, given the variability in test and analysis methodologies between researchers. This is supported by the influence of strain hardening behavior as shown in the sensitivity study, and which has been suggested as needing to be accounted for in order to optimize this correlation [72, 73].

While the class of material matters, these plots and the resulting correlations are also sensitive to the variances between each researcher in their methodology, errors, the method, sensitivity, and accuracy of their displacement measurements, and the stiffness of their testing systems, as shown in [54, 209]. In fact, a collective study of various researchers has shown that scatter between different researchers’ setups is much more significant than the scatter for each researcher’s respective setup, especially for measurements associated with determining yield stress [209]. Note that no correlation plot is given here for the range of collected data for the Young’s modulus. This is due to both the general lack of data given in the literature to support this relationship, as well as the poor fit presented by the data found. Creating a correlation using only the limited data found in the literature, the fit line is characterized by an R² value of 0.431; adding the results of the various materials tested in the course of this study reduces this to 0.266. The poor fit is again an indication of the inadequacy of utilizing the k/t value to establish a correlation with the Young’s modulus, and that an alternative method should be pursued, such as that suggested in [83]. This region of the P-δ is particularly sensitive to errors in both data acquisition and due to differences in system stiffness between investigators. Additionally, the findings of the parametric study in "FEA sensitivity study on the suitability of the SPT for AM materials Section" show that both K and n influence the shape of the initial portion of the of the P-δ curve nearly as much as E does. This means that this region of the curve is not purely related to the Young’s modulus alone, but also the strength coefficient and the hardening exponent, due to plastic effects within this stage of deformation. As such, the relation of E to k/t is invalidated as it does not account for the strain hardening behavior of the material as the parametric study results suggest it should.

These relationships can then be used to produce material property estimates, which can be compared to conventional test results. The added scatter and diminished R² values are reflected in the values predicted using the nonzero y-intercept relationships, Eqs. 25 and 27, as well as in the high and varied errors as compared to published tensile material properties, as seen in Table 3. The yield strength errors in particular showcase a range of error indicating both under- and over-estimation. These can likely be linked to errors in the initial portion of the P-δ curve, which is utilized for determining P_y, thus cascading the errors. The accuracy of these values is also affected by the typically small range of this portion of the curve which makes graphical determination using only images from the articles more prone to error, as not all sources provided explicit data points. The error range for σ_uts estimation is smaller and consistently over-estimates versus the actual value. As such, though the fits of the correlation relationships indicate the ability to make reasonable estimates of material properties, the calculations indicate that these relationships are not wholly reliable for acquiring material properties. While the correlations produced here focus on using methods which are most prevailing in the literature, there are also emergent methods which warrant further investigation for their suitability for use with a large variety of data. Therefore, they may be used to assess trends in data due to processing changes in order to establish best practices in terms of processing and testing, but not yet recommended as a substitution to conventional testing for determining material properties. Rather, these methods should be implemented to expedite and economize the process of refining process settings for production of conventional or AM materials, and the correlations established used to give numerical trends, with full-sized test coupons produced to tensile test standards used for final determination of material properties. This extends to other material systems as well, of course, as the SPT may be utilized for refining processes and properties regardless of the manufacturing method or material system of interest and it is reliable enough to track relative changes due to variations in alloying contents as well.

Table 3 Error calculation for strength properties predicted using experimental results and correlation relationships established in this study

Summary

The small punch test, as a miniatured sample test technique, is proposed as able to alleviate the time and cost associated with optimizing material properties due to the simplified design of the sample and the experiment. As a consequence of this, however, the state of stress induced during experimentation is more complex than that of a conventional test such as a tensile test. This necessitates the use of more complicated techniques in analyzing data to determine material properties. Several procedures are outlined to equate SPT data with conventional stress–strain data, and though lacking formal standardization, many of these methods are well established in the literature. Relationships exist with conventional testing techniques including tension, creep, fracture, and fatigue, as well as a variation of the small punch test known as the shear punch test for acquiring shear properties. Although many of the methods outlined here have been explored widely in the literature, variations between studies show sensitivity to experimental and material conditions. Correlation factors have shown material dependency, though some constants have been proposed to be widely applicable to a range of materials. Though the data shown here shows general agreement, it is unclear whether these constants will serve suitable to analyzing all AM materials, due to the intrinsic differences to conventionally produced materials, or if correlation factors need to be established based on material type, orientation, condition, etc. Due to the process-dependent structures and behaviors of AM materials, it is also necessary to consider the use of other correlation methods than those focused on in Sect. 0, as emergent methods may present an opportunity for establishing correlation factors for materials with a wide range of fracture behavior. Due to this and the error and scatter shown in the correlation plots created from the collective data in the literature, correlation factors alone cannot be relied on to give accurate assessment of the material properties. The most reliable method of deducing material properties from SPT data is through extraction of a stress–strain curve via the implementation of the FEA inverse solution method.

Some areas of SPT as they correlate to conventional testing techniques have not been thoroughly established. Though strong equivalencies exist, there are numerous variations with establishing fracture properties, with no single approach being universally accepted, and dependencies on material type, condition, and orientation exist. Additionally, the use of the small punch creep test is prominent in the literature and the relationship for determining the equivalent stress level necessary to achieve the same time to rupture at a certain force with SPT is well-established. However, this relationship has been shown to be sensitive to material anisotropy, a trait which AM materials are well known to exhibit. Most prominent of the deficiencies in SPT research are those relating to fatigue. Research on cyclic loading in SPT is scarce and largely limited to zero-to-tension or tension-to-tension loading, with very few studies having explored reversed loading equivalent to tension-to-compression, necessary for estimating component life, especially as related to energy production applications. These deficiencies make it difficult to utilize the small punch test to thoroughly characterize materials to the extent achievable with conventional experimental techniques but present an opportunity for reducing the time and work necessary to optimize factors such as alloy composition, processing parameters, and post-processing routines. Though progress is actively being made and standards are being issued, the differences in test setups and approaches between investigators have and will continue to add scatter until these are under widespread use, producing correlations which do not provide accurate material property estimates. As such, for now the SPT continues to be seen as a supplemental method to conventional testing techniques rather than a replacement for it, able to track changes on a microstructural level and essential to assessing materials which are scarce or otherwise difficult to acquire, have regional differences in a component, or present other production challenges.