Introduction

The aim to decrease reliance on fossil fuels has led to research on energy harvesting, for example of thermal and solar energy. Thermoelectrics, the process in which thermal gradients can be transformed into an external voltage, is particularly useful when a long-lasting and maintenance-free power source is needed [1,2,3]. In addition to a high Seebeck coefficient and electrical conductivity, features such as chemical stability, non-toxicity and ease of manufacturing are of importance when choosing an appropriate thermoelectric material.

Transition metal nitrides are known for the above properties and have been studied extensively due to hardness, temperature resistance, mechanical and chemical stability [4]. Among the d-block nitrides, cubic chromium nitride (CrN) [5, 6] and cubic scandium nitride (ScN) exhibit interesting thermoelectric properties [7,8,9,10,11]. In addition to its chemical, thermal and mechanical stability, ScN has a relatively large Seebeck coefficient (reaching −180 μV/K at 800 K). When including its low electrical resistivity, large power-factors between 2.5 and 3.5 × 10–3 Wm−1 K−2 have been reported [12, 13]. Furthermore, ScN can also become p-type by Sc-site doping [14, 15]. However, ScN does have a relatively large thermal conductivity [16,17,18,19] of approximately 8–12 Wm−1 K−1 which will reduce the thermoelectric efficiency and make it an impractical thermoelectric material in pure form.

Previously, Alling [20] addressed this issue by proposing a ternary nitride mimicking the features of ScN. Scandium (which is a group-3 element) can be replaced with one group-2 and one group-4 element in a 50/50 proportion to obtain the same electron valence. The final compound should then have a MeAEN2 stoichiometry, with \(Me\) representing a transition metal from the group-4 elements and \(AE\) belonging to the group-2 (alkaline earth) elements, such as magnesium. The study focused on TiMgN2, and it was predicted to be stable using density functional theory (DFT). Band structure calculations predicted stoichiometric TiMgN2 to have a 1.11 eV band gap using the HSE06 [21] hybrid functional and 0.22 eV with the PBE GGA functional known to give band gaps that are smaller than the experimental values. The SQS model was also used to study (Tix, Mg1-x)N solid solutions where (Ti0.5, Mg0.5)N was shown to be a non-magnetic semiconductor with a predicted 1.33 eV band gap. These results were also supported by Irokawa and Usami [22]. An attempt to synthesize (Ti0.5, Mg0.5)N by magnetron sputtering was conducted by Wang and Gall [23, 24]. In their study, they found a negative temperature coefficient of resistivity and a vanishing density-of-states at the Fermi level measured by X-ray photoelectron spectroscopy, showing that (Ti0.5, Mg0.5)N is a semiconductor. In a separate study by the present authors, (Ti0.5, Mg0.5)N was determined to have a Seebeck coefficient value of -25 µV/K [25]. It was also shown that at approximately 800 °C, high-resolution scanning transmission electron microscopy (HR-STEM) shows that the rock-salt cubic random alloy of (Ti0.5, Mg0.5)N goes through a phase transformation at the grain boundaries, forming a quaternary (Ti0.5, Mg0.5)NxOy superstructure when oxygen is also present. Kim et al. [26] used hydrogen gas as a means to control the oxygen content in the grain boundaries of (Mg, Zr) oxynitride thin films, which in return can be used to tailor the optoelectronic properties of such films.

In a previous paper, we expanded the research on this group of compounds by studying the phase stability and band structure of ZrMgN2 and HfMgN2 [27]. It was shown that the stoichiometric compositions have an almost equal tendency to crystallize in both the NaCrS2 superstructure and the LiUN2 prototype monoclinic structures. ZrMgN2 shows a 0.89 eV indirect band gap when crystallizing into the NaCrS2 structure while as crystallization into the LiUN2 structure results in a 0.46 eV direct band gap. As for HfMgN2, the band gap increases as crystallization into NaCrS2 results in a 1.19 eV indirect band gap and crystallization into LiUN2 results in a 0.77 eV direct band gap. Predicted thermoelectric properties of the semiconducting compounds showed that in the range of a moderate change in the Fermi level, high room temperature Seebeck coefficient values can be achieved. Experimental synthesis of MgxZr2-xN2 by Bauers et al. [28] showed that Zr-rich samples are more metallic, while Mg-rich samples are more insulating, which shows a degree of tunability of the electrical properties.

In the present paper, we investigate the configurationally disordered solid solutions (Zr0.5, Mg0.5)N and (Hf0.5, Mg0.5)N using the special quasi-random structure (SQS) method in conjunction with DFT calculations. By comparing the formation energy of the disordered alloys of (Zr0.5, Mg0.5)N and (Hf0.5, Mg0.5)N in the rock-salt cubic structure with that of its LiUN2 ordered structure counterparts, the order/disorder transition temperature can be calculated within a mean-field approximation. The density-of-states of (Zr0.5, Mg0.5)N and (Hf0.5, Mg0.5)N are also studied, and these calculations are used to predict their energy band gap and thermoelectric properties.

Computational details

First-principles calculations were performed using DFT [29, 30] with the projector augmented wave method (PAW) [31] implemented in the Vienna ab initio simulation package (VASP) [32,33,34] version 5.2. Electronic exchange–correlation effects and the electronic band structure were modeled with the generalized gradient approximation (GGA) using the Perdew–Burke–Ernzerhof (PBE) functional [35]. It should be noted that the Kohn–Sham band gaps of standard GGA calculations are systematically smaller than experimental band gaps, but for the present work, this is not an issue since we are mostly concerned with screening candidate materials and dismissing metallic compounds. The plane wave energy cutoff was set at 600 eV. The required structure files for the crystal structures were obtained using the special quasi-random structures (SQS) method [36] for the DFT calculations. The SQS unit cell is presented by 128 atoms and all internal atomic positions were fully relaxed while the cell shape is kept at the rock-salt cubic structure. These SQS structures were previously used to model Zr1-xGdxN and Hf1-xGdxN [37]. The density-of-states (DoS) illustrations are prepared by the high-throughput toolkit (httk) [38] and the 3D rendering of the crystal structure by VESTA [39]. For the order/disorder phase transformation temperature, the formation energy per formula unit was calculated for each ternary compound and related to the competing LiUN2 ordered structure.

The present work uses the same correction of the N2 energy as used in the Materials Project, based on work by Wang et al. [40] as standard GGA exchange–correlation functionals in DFT which are known to, in general, have systematic errors in the prediction of energy differences between solid and gas phase systems [41]. Hence, to accurately reproduce the formation energy of a system relative to a gas endpoint, it is common to adjust the gas phase energy.

The calculations of SQS structures used a 4 × 4 × 4 k-point mesh for Brillouin zone sampling and were executed with the Monkhorst–Pack scheme [42]. For density-of-states (DoS) calculations, the tetrahedron method was used in order to obtain band gap values [43].

Finally, the Seebeck coefficient \(S\) and power-factor \({S}^{2}\sigma {\tau }^{-1}\) (τ being the charge carrier relaxation time) of the predicted semiconductors are calculated at room temperature and 600 K as functions of the chemical potential using Boltzmann transport theory with the constant relaxation time approximation. We use the software BoltzTraP [44] on DFT calculations with a 7 × 7 × 7 k-point mesh for Brillouin zone sampling.

Results and discussion

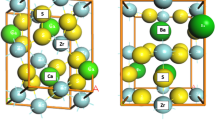
Figure 1 shows the three-dimensional rendering of the (Me0.5, AE0.5)N compound based on the SQS model, where Me is either zirconium or hafnium and AE is an alkaline earth element, in this case magnesium. In order to relax the unit cell, the lattice parameter of the cubic unit cell was calculated starting from an estimate from Vegard’s law. The calculated lattice parameter for ZrN, HfN and MgN is reported to be 4.618 Å, 4.538 Å [45] and 4.440 Å [41], respectively. Thus, (Zr, Mg)N and (Hf, Mg)N compounds with a 50/50 metal atom ratio would have a lattice parameter of 4.529 Å and 4.489 Å according to Vegard’s law. Cell relaxation was done by plotting the energy of the primitive cell versus the lattice parameter obtained from Vegard’s law in steps of ± 0.05 Å and ± 0.10 Å. A Gaussian fit of the resulting curve was then used to predict the lattice parameter leading to values of 4.556 Å and 4.508 Å. Both curves are shown in Fig. 2a and b.

Figure 1
figure 1

Unit cell of the (Me0.5, AE0.5)N compound based on the SQS model. The light orange colored spheres represent magnesium atoms, while the dark green colored spheres represent either zirconium or hafnium. The smaller grey colored spheres are nitrogen atoms

Full size image
Figure 2
figure 2

Gaussian fit of the energy vs lattice parameter for (Zr0.5, Mg0.5)N (top) and (Hf0.5, Mg0.5)N (bottom). Data points are based on Vegard’s law

Full size image

To calculate the order/disorder phase transition temperature, the formation energy of the (Me0.5, AE0.5)N random alloy, based on the calculated optimal lattice parameter, is compared to its ordered structure, the LiUN2 superstructure which was studied previously [27]. According to the thermodynamic stability criteria at constant pressure and temperature, the Gibbs free energies at the transition temperature, TC satisfy:

\(G^{{{\text{ord}}}} = G^{{{\text{dis}}}}\), where Gord and Gdis are the Gibbs free energy of the ordered and disordered structures, respectively. At zero pressure, using the approximation that the ordered phase is described by an ideally ordered structure, the above equation becomes:

$$E^{{{\text{ord}}}} = E^{{{\text{dis}}}} - T_{C}^{S}$$

and thus:

$$T_{C} = \frac{{E^{{{\text{dis}}}} - E^{{{\text{ord}}}} }}{S}$$

where TC is the transition temperature and S is the entropy of the disordered random alloy. For the approximation that the disordered phase can be described by an ideal random alloy, usually called the mean-field approximation, its configurational entropy per formula unit, that is per metal atom, is given as:

$$S = - k_{{\text{B}}} [x\ln x + (1 - x)\ln (1 - x)]$$

where x = 0.5 is the metal atom ratio in our case and kB is the Boltzmann constant. Table 1 provides the lattice parameters, formation energy of the disordered structure, LiUN2 ordered structure energy and calculated transition temperature. Note that the mean-field approximation is known to overestimate the real configurational transition. As an example, the mean-field transition temperature for ordering in (Ti0.5, Mg0.5)N was found to be 1272 K while a full scale cluster expansion followed by Monte Carlo simulations obtained 950 K or 75% of the mean-field value [20]. As the respective mean-field transition temperatures are predicted to be 740 K and 1005 K for (Zr, Mg)N and (Hf, Mg)N, respectively, any prospective as-deposited atoms for sample synthesis will more than likely “freeze” on impact and the samples resulting a random solid solution in the NaCl structure (possibly with some short-range-order). Thus, high temperature annealing would be required for allowing diffusion and structure ordering, keeping the annealing temperature below TC, a combination that ought to be challenging and motivates our further studies of the disordered structure below.

Table 1 Order/disorder transition temperature for (Zr0.5, Mg0.5)N and (Hf0.5, Mg0.5)N
Full size table

The density-of-states of both (Zr0.5, Mg0.5)N and (Hf0.5, Mg0.5)N are shown in Fig. 3. In both compounds, an energy gap can be seen at the Fermi level, with band gap values of 0.75 eV and 0.92 eV, respectively. These are somewhat larger than the value of 0.22 eV obtained with the PBE functional for the same 128-atom SQS in the (Ti0.5Mg0.5)N system [20]. As the Seebeck coefficient is related to the slope of the density-of-states near the Fermi level [46], calculating the thermoelectric properties becomes of interest. Figure 4 compares the Seebeck coefficient of (Zr0.5, Mg0.5)N and (Hf0.5, Mg0.5)N at 300 K and 600 K. The results show high Seebeck coefficient values exceeding ± 1000 \(\mathrm{\mu V}/\mathrm{K}\) at room temperature (comparable to that of an insulator). However, at these values, the electrical conductivity is close to zero. On the other hand, in the range of a moderate change in the Fermi level (i.e., moderate doping), a relatively high Seebeck coefficient value resulting in a notable power-factor becomes achievable. Figure 5 compares the power-factor of (Zr0.5, Mg0.5)N and (Hf0.5, Mg0.5)N at 300 K and 600 K. The predicted power-factor is, however, divided by the relaxation time. This value is obtained from experimental data and is thus difficult to calculate theoretically. However, as our compounds are modeled after cubic ScN, using experimental data from Burmistrova et al. [16] and the classical equation for conductivity (\(\upsigma =\mathrm{ n}{\mathrm{e}}^{2}\uptau {\mathrm{m}}^{-1}\)), the constant relaxation time for ScN is estimated to be equal to 6.5 × 10–14 \(\mathrm{s}\). An estimated power-factor at room temperature would then be between 2.5 and 3.5 \(\times\) 10–3 \({\mathrm{Wm}}^{-1}{\mathrm{K}}^{-2}\), similar to that of pure ScN, but possibly with a lower thermal conductivity value as it would be expected from a disordered alloy [47] between heavy elements such as zirconium or hafnium and a light element like magnesium. Please note that multivalent ternaries likely have different charge density distributions around the cations compared to binaries, and thus have different scattering physics. As a result, our assumption will only give a rough estimate until actual samples are characterized.

Figure 3
figure 3

Density-of-states for (Zr0.5, Mg0.5)N (left) and (Hf0.5, Mg0.5)N (right). Band gap values are calculated to be 0.75 eV and 0.92 eV, respectively

Full size image
Figure 4
figure 4

Seebeck coefficient value versus chemical potential of (Zr0.5, Mg0.5)N (top) and (Hf0.5, Mg0.5)N (bottom) at 300 K (black line) and 600 K (blue line). These calculations predict that the Seebeck coefficient value will decrease with the temperature

Full size image
Figure 5
figure 5

Power-factor/relaxation time value versus chemical potential of (Zr0.5, Mg0.5)N (top) and (Hf0.5, Mg0.5)N (bottom) at 300 K (black line) and 600 K (blue line). These calculations predict that the conductivity will increase with temperature, as expected for semiconducting material

Full size image

Thus, our results for (Zr, Mg)N and (Hf, Mg)N solid solutions motivate additional experimental research of these compounds and comparison with theory [48, 49]. In both ordered and disordered structures, the studied magnesium-based transition metal nitrides show semiconducting and thermoelectric properties. The predicted band gap, however, is underestimated compared to experimental data (as expected), and the calculated Seebeck coefficient is that of an insulator and requires doping levels similar to their measured carrier densities to be a semiconductor. In both cases, increasing the temperature predicts a decrease in the Seebeck coefficient. On the other hand, the electric conductivity (and consequently, the power-factor) is predicted to increase as expected in semiconductors, although ordered crystals show less resistivity compared to disordered structures. Synthesis of the ordered structures could potentially be done by low temperature magnetron sputtering thin film deposition, resulting in the disordered phase, followed by high-temperature annealing of the disordered phase in a nitrogen gas environment as a means for cation lattice ordering [50].

Conclusion

Rock-salt solid solutions of (Zr0.5, Mg0.5)N and (Hf0.5, Mg0.5)N alloys have been studied by DFT calculations using the SQS method. The mean-field simulation shows that the order–disorder phase transformation between the monoclinic LiUN2 prototype structure and the rock-salt cubic random alloy of the mentioned solid solutions occurs at 740 °C and 1005 °C, respectively. Together, with the low bulk diffusivities in nitrides, this highlights the importance of the disordered phases for (Zr0.5, Mg0.5)N and (Hf0.5, Mg0.5)N grown at normal PVD temperatures. The density-of-states for the two ternary nitride alloys are also calculated and predict semiconducting behavior with a PBE-GGA band gap of 0.75 eV and 0.92 eV. Seebeck coefficient and power-factors are also predicted, showing that in the range of a moderate change in the Fermi level, high room-temperature power-factor values can be achieved. Similar to previous theoretical studies on TiMgN2 which motivated research and synthesis of (Ti0.5, Mg0.5)N and showing that materials semiconducting and thermoelectric properties, the theoretical predictions regarding the properties of (Zr, Mg)N and (Hf, Mg)N solid solutions motivate additional experimental research and the actual synthesis of these nitride alloys.