Introduction

The absorption of H-atoms by fcc Cu has long been reported in experimental investigations [1,2,3,4]. The authors of those studies classify the binding sites as subsurface Cu-atoms, that is to say, bulk Cu, but not much is known on the mechanisms of hydrogen absorption in what concerns the preferred absorption sites. The solution enthalpy of H-atoms in Cu is large and positive relative to Cu(s) and H2(g), and it is not known that stable hydrides can form in this system [2, 5, 6]. However, the absorption energy of H-atoms at the bulk octahedral site of fcc Cu is negative relative to free atomic H, which implies that if atomic hydrogen is generated due to some external process, it is possible that Cu absorbs the H-atoms [2]. For other metals, the absorption of H is known to have detrimental effects in the corrosion resistance and mechanical properties [7]. To date, no clear evidence has been found that hydrogen can cause embrittlement of pure—oxygen free—copper at temperatures lower than 400 °C.

In a previous work on the absorption of H by Cu, the authors found that H-atoms bind preferably at the octahedral site, with an absorption energy 0.20 eV lower than that at the tetrahedral site [8, 9]. Additionally, absorption of H at a vacancy and a divacancy is more stable by 0.24 eV and 0.42 eV than that at the octahedral site, respectively [3, 8,9,10]. A similar situation occurs for Ni [11], and the authors suggest further that for Ni, the grain boundaries (GBs) are sites where the segregation of bulk absorbed H can occur. Some GBs are defects with excess volume which can create internal surfaces prone to binding H-atoms [12, 13]. For Cu, internal surfaces such as those present in vacancies and vacancy clusters lead to segregation of H from the bulk interstitial non-defective sites [3, 4, 8,9,10, 14, 15].

According to the hydrogen embrittlement models, the process of embrittlement requires a local accumulation of H-atoms [7]. Several embrittlement models mention the important role of GBs in the process, and this has been confirmed for other metals such as Ni [11]. Because H-atoms at interstitial positions in Cu are mobile at room temperature, they end up in traps such as defects, internal or external surfaces and eventually can escape the system and form H2 gas [16]. It is then important to understand if GBs or other defects in Cu can accumulate H-atoms in quantities that can be detrimental for the physical–chemical properties of the material. In this work, the H-atom absorption capacity of a series of lattice defects such as GBs and surfaces was investigated. Our data are compared with literature data for absorption of H-atoms at other lattice defects in copper.

Methods and models

Computational details

Density functional theory (DFT) calculations were performed using the Vienna Ab Initio Simulation Package (VASP 5.4.1) [17]. We employed the Perdew–Burke–Ernzerhof (Refs. [18, 19]) (PBE) exchange–correlation functional implemented in VASP, with ultrasoft pseudopotentials of the projector augmented wave [20, 21] (PAW) type. The PBE functional has shown good accuracy for describing the adsorption of H-atoms onto metal surfaces [22, 23], absorption of H at bulk Cu [8] and also for surface and bulk properties of metals [24, 25]. For the adsorption at the surfaces, in order to account for van der Waals interactions which are important for the correct description of hydrogen bonded structures and some adsorption phenomena, the zero damping D3 correction [26] was employed within the formalism of PBE-D3. However, the adsorption energies of H-atoms computed at the PBE level at the surfaces of Cu are orders of magnitude larger than the D3 correction to those energies. Additionally, the relative differences in the adsorption energies obtained with and without the D3 correction are negligible. Because of this and for allowing direct comparison with the absorption data from this work and the literature, the results for adsorption here presented and discussed have been computed at the PBE level.

The energies herein reported are electronic energies at 0 K which allow accurate direct comparisons between preferred binding sites in the solid with similar chemical environment [27,28,29].

Computed quantities

The computed quantities here described are defined as follows.

Absorption energy (ΔEabs) of H

$$ \Delta E_{\text{abs}} = E_{{(n{\text{H}}\_N{\text{Cu}})}} - \, \left( {nE_{\text{H}} + E_{{N{\text{Cu}}}} } \right) $$
(1)

where the electronic energies are EnH_NCu, the energy of a supercell of Cu—single crystal or with GBs—containing n H-atoms and a larger number N of Cu-atoms; EH, the energy of an H-atom in vacuum in the same supercell employed to model Cu; and ENCu, the energy of the supercell of pure fcc Cu containing N Cu-atoms. A more negative value for ΔEabs implies stronger absorption.

Segregation energy (ΔEseg) of H to site s

$$ \Delta E_{\text{seg}} = E_{{(n{\text{H}}\_{\text{sCu}})}} - nE_{{{\text{H}}\_{\text{bulkCu}}}} $$
(2)

where the electronic energies are E(nH_sCu), the energy of a supercell of Cu containing n H-atoms at the segregation site s; nEH_bulkCu, the energy of an H-atom in the most favorable absorption site in the bulk of a single crystal of Cu. A more negative value for ΔEseg implies stronger bonding at the segregation sites.

Adsorption energy (ΔEads) of H

$$ \Delta E_{\text{ads}} = E_{{(n{\text{H}}{-}{\text{Cu}}\_{\text{slab}})}} - \, \left( {nE_{\text{H}} + E_{{{\text{Cu}}\_{\text{slab}}}} } \right) $$
(3)

where the electronic energies are E(nH-Cu_slab), the energy of n H-atoms bound to a specific surface of Cu represented by a slab; EH, the energy of an H-atom in vacuum in the same supercell used for modeling the Cu slab; ECu_slab, the energy of the supercell containing the bare Cu slab. A more negative value for ΔEads implies stronger adsorption.

GB energy (γGB)

$$ \gamma_{\text{GB}} = \, \left( {E_{\text{GB}} {-}E_{\text{bulk}} } \right) /2A $$
(4)

where the electronic energies are EGB, the energy of the supercell that contains the GB; Ebulk, the total energy of a supercell of Cu single crystal that contains the same number of atoms as those present in the supercell used for modeling the GB; and A, area of the GB in the supercell. The quantity is divided by two in order to account for the fact that there are two identical GBs in the supercell. Lower values of γGB imply stronger cohesive bonding between the two grains.

It is known that when determined with pure DFT, the energy of an open-shell atom in vacuum—such as the H-atom—can be largely affected by the self-interaction error (SIE) [30]. In order to employ error cancelation in the improvement of the data, we have considered the same reference state for the H-atom for the determination of all the differential quantities described above: ΔEads, ΔEseg and ΔEabs. In this way, the SIE is canceled and the comparison between these quantities can be done with good accuracy.

Zero point energy (ZPE) corrections

For the calculation of the vibrational frequencies, only the H-atoms were allowed to be displaced, while the Cu-atoms were kept fixed at the positions resultant from the geometry optimizations. This approach is possible without significant loss of accuracy because of the decoupling between the vibrational frequencies of the H-atoms and those of the Cu-atoms and has been applied previously even for the study of the interactions between heavier atoms and Cu [31]. H-atoms and Cu-atoms have vibrational frequencies that differ by hundreds of wavenumbers, and this minimizes the errors introduced with such approach [32]. Vibrational frequencies were calculated by numerical differentiation of the forces using a second-order finite difference with a step size of 0.015 Å. The Hessian matrix was mass-weighted and diagonalized to yield the frequencies and normal modes of the system from which the ZPE corrections were obtained. We determined the ZPE for the cases with the largest and smallest energetic differences relative to the bulk and found that the ZPE contribution to the energy is in average 0.14 eV/H-atom, in agreement with previous finds [33]. The maximum ZPE difference obtained relative to the bulk was 0.06 eV/H-atom for the adsorption of 1 ML of H-atoms at the Cu(111) surface, and overall, the ZPE contribution to the relative energies is 0.02 eV/H-atom. Very small relative differences in ZPE were expected because the chemical bonds between H and Cu in the different structures studied are very similar. Because the ZPE contribution does not change the relative differences in energies for the cases studied here, we do not include those data in the discussion that follows.

Models

Copper single crystal

The lattice constant of face-centered cubic (fcc) Cu employed in this work, 3.632 Å, has been obtained with the PBE functional and differs only slightly from the experimental value, 3.603 Å [25]. A plane wave cutoff of 460 eV and a k-point mesh of (9 × 9 × 9) in the Monkhorst and Pack [34] sampling scheme were used, and Methfessel–Paxton smearing with a width of 0.05 eV was used. The self-consistent field (SCF) electronic energies were considered converged when their change between two cycles was smaller than 1 × 10−5 eV and the forces acting on each of the atoms were smaller than 0.002 eV Å−1. For the determination of the solution energies of H-atoms and their preferred binding sites in the Cu single crystal, a supercell with symmetry (3 × 3 × 3) containing 108 Cu-atoms was employed. Absorption of an H-atom was done at the tetrahedral and the octahedral lattice sites as previously reported [8]. All atoms of the supercell were unconstrained during the geometry optimizations.

GB

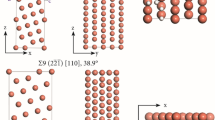
The GB models studied: Σ3(111)[110], 109.5°; Σ5(012)[100], 36.9°; and Σ11(1\( \bar{1} \)3)[110], 129.5° were constructed using the coincidence-site lattice (CSL) model and periodic supercells each containing two oppositely oriented tilt GBs. The CSL model is a robust tool for constructing GB models consisting of periodic structures of single crystals that have a high density of coincidence sites in the grain boundary plane [35, 36]. For the determination of the equilibrium structures, a pre-optimization of the GB supercell geometry was performed. In this pre-optimization, the supercells were allowed to relax along the direction perpendicular to the GB plane. Following that, an optimization of the internal coordinates of all atoms was performed. For the computation of absorption and segregation energies, the internal coordinates of all atoms of the supercell were optimized using the supercell sizes previously optimized for pure Cu. A plane wave cutoff of 460 eV and a k-point mesh of (7 × 9 × 3) in the Monkhorst–Pack sampling scheme were used, and first-order Methfessel–Paxton smearing with a width of 0.05 eV was used [37]. The self-consistent field (SCF) electronic energies were considered converged when the change was smaller than 1 × 10−5 eV between cycles and the force acting on each of the atoms was smaller than 0.002 eV Å−1.

Σ3(111) [110], 109.5° GB

This model of a coherent twin boundary consists of an orthorhombic supercell with 96 atoms containing two GB separated by 5 (111) planes of Cu-atoms. The GB plane has an area of 44.82 Å2. The relaxed structure is shown in Fig. 1a. The GB structure differs only slightly from the bulk with the enlarged distances between Cu-atoms only ≈ 0.3% larger than at the bulk. This is in agreement with the previous findings for Ni [11]. The obtained γGB is 56.179 mJ m−2 which agrees well with the literature data [10, 11, 38, 39]. The fact that the shift in the Cu–Cu distances is so small leads to a very low GB energy, making this GB the lowest energy symmetric tilt GB that occurs in copper [40]. This causes the Σ3 GB to be one of most frequently observed GBs in hot-rolled fcc Cu with a frequency of occurrence of 15%, considerably higher than the second most frequent, the sigma Σ13 with a frequency of occurrence of around 1% [41].

Figure 1
figure 1

Supercells delimited by black lines with the geometry optimized: a Σ3, b Σ5 and c Σ11 GB models, respectively. The dashed lines mark the GB atoms of the interface between the two planes

Full size image
Σ5(012)[100], 36.9° GB

This GB model consists of an orthorhombic supercell with 76 Cu-atoms containing two GBs separated by 5 layers of (012) planes of atoms of Cu. The GB plane has an area of 41.67 Å2. The size of this model has been shown to be sufficient to avoid spurious interactions between the two GBs [42]. The relaxed structure is shown in Fig. 1b. Upon geometry relaxation, the atomic rearrangement at the grain boundary is largely distorted from the bulk distances. The enlarged Cu–Cu bonds at the GB increase by ≈ 5% which together with the tilt causes the GB to have an open structure with considerable voids and an extra volume of ≈ 3% at the center of the GB plane. For Ni, open sites at a similar Σ5 GB function as segregation sites for H [11]. The value of γGB obtained was 877.121 mJ m−2, which is in excellent agreement with literature data [40, 43].

Σ11(1\( \bar{1} \)3)[110], 129.5° GB

This GB model consists of an orthorhombic supercell with 88 Cu-atoms containing two GBs separated by 6 layers of (1\( \bar{1} \)3) planes of atoms of Cu. The GB plane has an area of 41.89 Å2. The relaxed structure is shown in Fig. 1c. Upon geometry relaxation, the enlarged Cu–Cu bonds at the GB increase by ≈ 2% when compared to the bulk vales. This makes the GB have a more open and irregular structure than the Σ3, but more closed and bulk-like structure than the Σ5. The computed γGB is 494.773 mJ m−2, in agreement with the literature values [40].

Hydrogen segregation at the GB

For the study of segregation of H at the GBs, the octahedral sites were sequentially filled with H-atoms. After these sites were saturated, the neighboring tetrahedral sites started to be filled. Starting with 1 H-atom, the ΔEseg at different GB sites was obtained in order to understand the binding site preferences. The GBs were then sequentially filled with H-atoms with a step increase of one H-atom as follows: After the most stable segregation site for 1 H-atom was found, another H-atom was placed at the GB and the site preferences for the second H-atom were investigated; the addition of 3 H-atoms was done to the most stable configuration found for 2 H-atoms, and another scan for the preferred binding site of the third H-atom was done. This procedure was repeated until the GB was filled with H-atoms. This was done in order to determine the saturation limit of H at the GB and to understand the effect responsible for that limit. In all investigated geometries, all Cu and H-atoms of the supercells were allowed to relax during geometry optimization. The supercells employed are of sizes similar to those used in a similar work for Ni [11]. These model sizes are appropriate to model the reactions of H because they minimize the spurious interactions between the periodically repeating images of the GB and of the H-atoms at the lowest concentrations.

In order to report the concentration of H-atoms per unit area of GB, we had to consider a cutoff distance to the GB plane along the direction perpendicular to the GB plane. That distance is the point from which the segregation of H-atoms is not favorable anymore, 4.90 Å.

Hydrogen adsorption at the Cu(100), Cu(100) and Cu(111) surfaces

Adsorption of H-atoms at the Cu surfaces was done at the three low Miller index surfaces Cu(100), Cu(110) and Cu(111) that were represented by slabs with p(2 × 2) symmetry as shown in Fig. 2.

Figure 2
figure 2

Top views of the p(2 × 2) slab models of the Cu(100), Cu(110) and Cu(111) surfaces used to study the adsorption of H-atoms

Full size image

These (2 × 2) surface supercell models have been employed in previous works for the study of adsorption of H-atoms and are sufficient to reduce the spurious interactions between the periodically repeating H-atoms and also allow the study of high coverages [23]. The supercells with periodic boundary conditions (PBC) employed have a thickness of 5 Cu(100) and 5 Cu(110) atomic layers along the axis perpendicular to the surfaces and 4 atomic layers for Cu(111). Each supercell has a vacuum layer of 16 Å. Adsorption of H-atoms was investigated at one of the sides of the slabs. During optimization of the geometries, for Cu(100) and Cu(110), the three bottom layers of Cu-atoms were kept fixed, while the remaining top layers of Cu-atoms and all adsorbates were allowed to relax. For Cu(111), the two bottom layers of Cu-atoms were kept fixed, while the remaining top layers of Cu-atoms and all adsorbates were allowed to relax. For geometry optimizations, a plane wave cutoff of 460 eV and a k-point mesh of (2 × 2 × 1) in the Monkhorst–Pack sampling scheme were used, as well as Gaussian smearing with a width of 0.2 eV. The self-consistent field (SCF) electronic energies were considered as converged when the change was smaller than 1 × 10−5 eV between cycles and the force acting on each of the atoms smaller than 0.002 eV Å−1. The study of the adsorption of H-atoms started with a single H-atom per supercell in order to understand the adsorption site preferences, after which the coverage was increased sequentially until one monolayer (1 ML) coverage was reached. The definition here used of a monolayer is that recommended by IUPAC [44].

Results and discussion

Benchmarks

The obtained γGB for the GBs here investigated shows that our values agree with the literature data [40, 45]. Our data for γGB are consistently higher that the data obtained with molecular dynamics simulations [45], which tends to be systematically lower than both the experimental values and the values computed with DFT [46]. The grain boundary distribution [41] in fcc Cu shows that the frequency of occurrence is around 15% for Σ3, while Σ5 occurs less than 1% and that of Σ11 is around 1%. The frequencies of occurrence correlate [41] to some extent with the extent of distortion of the lattice geometry, local coordination and the difference in the Cu–Cu bond distances at the GB compared to the bulk [11, 40, 45]. According to some models, both smaller distortions and differences in the Cu–Cu bond distances when compared to the bulk will lead to a higher frequency of occurrence of the given GB [41]. Based on these facts, we followed certain criteria for the choice of the GB models in order to: include a GB that has a high frequency of occurrence in Cu, the Σ3; a case where the distortions at the GB are large when compared to the bulk, the Σ5; and an intermediate case between the Σ3 and the Σ5 in terms of geometrical distortions, the Σ11. These models allow us to attempt to rationalize the types of distortions present at the GB with their ability to bind H-atoms.

The obtained ΔEabs for absorption of a single H-atom at the bulk of Cu is − 1.60 eV for the tetrahedral site and − 1.84 eV for the octahedral site. The difference of − 0.24 eV obtained is in good agreement with literature data [8]. Based on this, the octahedral bulk site is considered as the reference state (EH_bulkCu in Eq. 2) for the computation of the segregation energies at the GBs.

In this work, we considered that energy differences smaller than or equal to ± 0.01 eV are beyond the limit of accuracy of the DFT methods employed and sites that lead to such energies are not considered as potential candidates for absorption, adsorption nor segregation of H-atoms.

Segregation of H-atoms at the Σ3, Σ5 and Σ11 GBs

We investigated the segregation of H-atoms at the three GBs by modeling the absorption of H-atoms at the available octahedral sites on the GB planes and at the sites in the vicinity of the GB planes. In the sites in the vicinity of the GBs, the distortions caused by the GBs are smaller than those at the GB plane, but are still significant in some cases, especially for the Σ5.

Starting with the Σ3 GB, we found that the largest value of ΔEseg at this GB is smaller than − 0.01 eV/H-atom and as such, we consider that the Σ3 GB does not contain potential segregation sites for H. The reason behind this is that the distortions of the geometry and the excess volume are small at Σ3. As mentioned in the section with the models details, the enlargement of the Cu–Cu bonds at this GB is only ≈ 0.3% when compared to the bulk. This is not sufficient to make this GB a segregation reservoir for H-atoms when compared to absorption of H-atoms at the bulk octahedral site. A similar result has been previously published for H in Ni [11]. Because of this, the Σ3 GB will not be included further in the discussion that follows.

The segregation of H-atoms was investigated at the Σ5 and Σ11 GBs as shown in Fig. 3.

Figure 3
figure 3

The Σ5 and Σ11 GB models with 6 and 14 H-atoms, respectively. The filling of the GB started at the GB plane, symmetric around the GB plane and proceeded toward the bulk as the number of H-atoms was increased. Cu (brown filled circle), H (gray filled circle)

Full size image

Because the sites at the GB plane or in its vicinity are those that lead to stronger bonding with H-atoms, the GBs were initially filled with H-atoms at the octahedral sites of the GB planes and the filling proceeded toward the bulk regions until the segregation of H-atoms was not favorable anymore. The resulting segregation energies are shown in Figs. 4, 5, 6 and 7.

Figure 4
figure 4

Segregation energies per H-atom (ΔEseg/H, eV) for the segregation of 1 to 3 H-atoms at the Σ5 GB

Full size image
Figure 5
figure 5

Summary of the segregation energies per H-atom (ΔEseg/H, eV) for the segregation of 1 to 6 H-atoms at the Σ5 GB

Full size image
Figure 6
figure 6

Segregation energies per H-atom (ΔEseg/H, eV) for the segregation of 1 to 3 H-atoms at the Σ11 GB

Full size image
Figure 7
figure 7

Summary of the segregation energies per H-atom (ΔEseg/H, eV) for the segregation of 1 to 14 H-atoms at the Σ11 GB

Full size image

It can be seen that the segregation of H-atoms is more favorable at Σ5 than at Σ11. This is due to the more open structure of the Σ5 GB and the excess volume, which provides a more favorable environment for bonding with H-atoms. A similar find has been previously reported for Ni for Σ5 and Σ3 GBs [11]. The volume expansion of the Cu lattice has a remarkable effect on the binding energies of H-atoms as it will be detailed in a subsequent section of this work. The plots in Figs. 5 and 7 show also that the segregation of H-atoms at an octahedral GB site is sensitive to the presence of other H-atoms at octahedral sites of the vicinity. This happens for both GBs and is reflected in smaller values of ΔEseg/H-atom for the segregation of 2 H-atoms when compared to the segregation of 1 H-atom at a time in the same segregation sites. The reduction of the magnitude of the ΔEseg as a function of the number of H-atoms is considerable and shows that in spite of having an open structure, even the Σ5 GB model used here is not capable of accommodating more than 3 H-atoms per unit area of GB. For 4 H-atoms, the tetrahedral sites become occupied and that does not lead to an energetic gain. Simultaneously, as the distance from the GB toward the bulk increases, the octahedral sites start to resemble those of the bulk single crystal Cu and these have the same binding energy as the reference, the octahedral site single crystal bulk Cu. Taking the absorption data as a function of the number of H-atoms for each GB—per area of GB plane—into account, we obtain the saturation limits for absorption of hydrogen. These are 1 H-atom per 13.93 Å2 for Σ5 and 1 H-atom per 13.96 Å2 for Σ11. However, for the Σ11 due to the much smaller ΔEseg for 3 H-atoms—which are in the limit of accuracy of the computational method—a more realistic number is obtained by taking the higher limit as 2 H-atoms which gives a saturation limit for the Σ11 of 1 H-atom per 20.29 Å2.

The obtained data show that for the segregation of H-atoms to occur at the GB, there has to be a minimum enlargement of the Cu–Cu bond distances at the GB that will change the coordination number of Cu-atoms. The Cu–Cu distances at the Σ5 GB are well above that enlargement threshold, while for Σ11, these are only slightly above and for Σ3 are below. From the geometrical parameters of the GBs studied, it is possible to state that an enlargement of 2% of the Cu–Cu bond distances seems to be close to the lower limit for which the segregation of H-atoms from the bulk is favorable. However, this case already leads to only a small amount of segregated H-atoms. Considering that the frequency of occurrence of Σ5 in the material is so small compared to the smaller angle Σ3, the data here obtained indicate that the absorption of H-atoms at perfect (non-defective) symmetric tilt GB does not amount to a significant concentration of H-atoms when considering the saturation limits for hydrogen shown above, weighted by the frequency of occurrence of each of the studied GBs in fcc copper.

Adsorption of hydrogen at the Cu(100), Cu(110) and Cu(111) surfaces

The adsorption of H-atoms was studied at the low Miller index surfaces of Cu: Cu(100), Cu(110) and Cu(111). This is done in order to understand what is the global minimum in terms of preferred binding sites for H-atoms, i.e., bulk versus GBs versus surfaces. While there is not much detailed data on the adsorption of H-atoms at all these surfaces of Cu, some data are available in the literature and allowed us to benchmark the method used. The study started by scanning through the possible adsorption sites for 1 H-atom, corresponding to a coverage of 0.25 ML, at the three surfaces shown in Fig. 2 in order to understand the binding site preferences. Following that, the coverage was increased to 1 ML. The resulting data are given in Table 1, and the geometries are shown in Fig. 8.

Table 1 Adsorption energies relative to the gas-phase H-atom (∆Eads) and segregation energies (∆Eseg) relative to octahedral bulk site for binding H-atoms at the three low Miller index surfaces of Cu
Full size table
Figure 8
figure 8

Preferred geometries for full surface coverage of H-atoms (1 ML) at Cu(100), Cu(110) and Cu(111). The preferred adsorption sites for 1 ML: shifted fourfold hollow for Cu(100); threefold hollow for Cu(110) and fcc hollow for Cu(111) are the same as for single H-atom adsorption (0.25 ML). Cu (brown filled circle), H (gray filled circle)

Full size image

The obtained adsorption energies for both the adsorption of single H-atoms [23, 47,48,49] and for the formation of 1 ML at Cu(100) [49] are in good agreement with literature data. For 1 ML at Cu(100), as previously reported by other authors [49], we also found that the shifted fourfold hollow geometry is more stable than the centered fourfold hollow. However, the difference between both structures is only 0.05 eV. For Cu(110), the geometry optimization of an H-atom placed at the fourfold hollow site leads to adsorption at the threefold hollow. The values in Table 1 show that the presence of neighboring H-atoms reduces the magnitude of the ∆Eads/H-atom. This is visible in the decrease in ∆Eads when the coverage is increased from 0.25 to 1 ML. This phenomenon is similar to what was found for the absorption—or segregation—of H-atoms at the GBs, where neighboring H-atoms reduce the values of ∆Eabs/H-atom. However, because the values of ∆Eads are so large, their reduction caused by the presence of neighboring H-atoms is comparatively small and the formation of a fully covered low Miller index surface of Cu from free H-atoms is still largely favorable.

Comparison between the different binding sites: Surface versus bulk versus GBs

The complete set of computed data for absorption at the bulk, at the GBs and adsorption at the surfaces is given in Tables 1, 2 and 3. Because all the data are absorption and adsorption data—that considers the same reference state (gas phase) for the H-atom as described in the computational details section—these are directly comparable.

Table 2 Absorption energies relative to gas-phase H-atom (∆Eabs) and segregation energies (∆Eseg) relative to the octahedral site for a single H-atom at the bulk of fcc Cu single crystal
Full size table
Table 3 Absorption energies (∆Eads) for absorption of H-atoms from gas phase to the Σ5 and Σ11 GBs and corresponding segregation energies (∆Eseg) from the bulk octahedral site
Full size table

The data from Tables 1, 2 and 3 show that the ∆Eabs/H-atom at the bulk of Cu is − 1.84 eV for the octahedral site, − 1.60 eV for the tetrahedral site, − 2.08 eV for a vacancy and − 2.26 for a divacancy. The most exoergic values of ∆Eabs/H-atom for absorption at the GBs are − 2.04 eV and − 1.76 eV for the Σ5 and Σ11, respectively. For the surfaces, the ∆Eabs/H-atom for the formation of 1 ML of H-atoms is − 2.40, − 2.42 and − 2.61 eV for Cu(100), Cu(110) and Cu(111), respectively. The absorption and adsorption data for atomic hydrogen show then that the overall energy minimum is for adsorption at the surfaces, with the Cu(111) the surface with the highest affinity for H-atoms. Adsorption at the Cu(111) surface is more stable by − 0.54 eV when compared to the most stable absorption site at the bulk, the Cu vacancy.

These results indicate that there is no strong driving force for the segregation of H-atoms at the GBs and that the thermodynamic minimum for the bonding of H-atoms with fcc Cu is adsorption at the surface. Overall, the results here presented that show the preference of H-atoms for binding at defects are in line with the fact that the solution enthalpy of 2H in Cu is positive with respect to H2(g) and that lattice defects and surfaces are necessary in order to stabilize the H-atoms in the material. This also agrees well with experimental observations that show that copper hydride is less stable than metallic Cu and H2(g) [5, 50].

The effect of lattice expansion in the binding energies of H-atoms with fcc Cu

In order to understand if the extra exoergicity of bonding of H-atoms with defects when compared to the perfect lattice can have its origins in the extra “available free volume” at the defect sites, we studied the binding energies of H-atoms at the octahedral and tetrahedral sites of fcc Cu as a function of the expansion of the perfect fcc Cu lattice. Taking the binding energy of the H-atom to the octahedral site of the non-expanded lattice as the reference, the lattice volume was increased in steps of 0.2% and 1% up to 20% expansion and the binding energies of the H-atoms for each expansion step were determined. The obtained data are shown in Fig. 9.

Figure 9
figure 9

Energy difference (∆Eexp) for binding an H-atom at the octahedral (blue filled diamond) and tetrahedral (brown filled circle) sites as a function of the expansion (%) of the fcc Cu unit cell. The binding energy of H at the octahedral site of the non-expanded lattice is taken as the reference for both sets of data

Full size image

It can be seen in Fig. 9 that the lattice expansion has a considerable effect in the binding energies of H-atoms both at the octahedral and tetrahedral sites. Because the coordination number of the H-atoms with Cu is the same for each set of data in Fig. 9, it is clear that the expansion alone can account for the extra gain in energy when H-atoms bind to defects because these sites have additional volumes when compared to non-defective lattice sites. The sites at the center of the Σ5 have an additional volume of ≈ 3% when compared to the perfect crystal. From the data in Fig. 9, it can be seen that 3% expansion of the perfect fcc lattice leads to an extra stabilization of − 0.22 eV/H-atom at the octahedral lattice site. Our data for segregation of H-atoms at the Σ5 GB show that the average segregation energy for H-atoms at the center of the GB is − 0.21 eV/H-atom. Similarly, the results for the other GBs studied in this work also match well the data in Fig. 9. The good match between the values for the expansion of the fcc lattice and for the segregation energies at the GBs suggests that the driving force behind the segregation of H-atoms at the GBs is the excess volume of the GBs.

Conclusions

The methodology employed allowed us to compare with good precision the absorption energies of H-atoms to single crystal Cu; different point defects at the bulk of single crystal Cu; to the Σ3, Σ5 and Σ11 symmetric tilt coherent grain boundaries (GB); and the adsorption to the low Miller index surfaces Cu(100), Cu(110) and Cu(111). The openness of some GB structures has long been suggested as a potential driving factor for the segregation of H-atoms. This is because binding H-atoms to vacancies in bulk Cu is favorable when compared to non-defective bulk sites. The three GBs studied provide a varied environment in terms of geometries and Cu–Cu distances at the GB planes. The Σ5 GB is more open, followed by the Σ11 and the Σ3 more resembling the bulk geometry. However, in spite of their openness, we found that the GB studied here that has the largest affinity for H-atoms, the Σ5, is not capable of storing a significant amount of H-atoms and has a limit of 1 H-atom per 13.89 Å2 of GB plane area. The affinity for H-atoms varies in the decreasing order: surfaces > vacancy > Σ5 GB > Σ11 GB > Σ3 GB ≈ bulk. The comparison between the data from this study and existing literature data shows that overall, the most favorable sites for bonding H-atoms with fcc Cu are the surfaces, with the Cu(111) the most favorable of the low Miller index surfaces.

The investigation of the effect of the lattice expansion on the binding energies of H-atoms shows that the volume expansion of the perfect lattice results in binding energies of H-atoms that match well the segregation energies at GBs with the same extra volume: the larger the available volume at a given interstitial site of a GB, the larger is the segregation energy of an H-atom at that GB site. This shows that the dominating effect that drives the segregation of H-atoms at GBs is the excess volume of the GBs.