Introduction

In the single crystal of a metal, direct interstitial diffusion is in general a much faster process than indirect interstitial diffusion, self-diffusion or substitutional solute diffusion because it does not require the formation of vacancies [1, 2]. Consequently, the vacancy formation energy does not contribute to the activation energy of this diffusion mechanism [1]. A solute such as hydrogen which occupies interstitial sites and is a small atom when compared to the solvent diffuses via the direct interstitial mechanism by hopping from an interstitial site to the nearest available interstitial site [2, 3]. Even if not strictly necessary for the diffusion to occur, the presence of defects such as vacancies, or discontinuities such as grains boundaries (GBs) or dislocations, is known to affect diffusion mechanisms [4,5,6] as these defects besides changing the tortuosity of the diffusion pathways act also as traps for hydrogen [7, 8]. In general, if a defect leads to an increase of the effective cross section of the diffusion path for a diffusing solute atom, that defect will enhance the diffusivity of the solute [4, 5, 9].

H-atoms diffuse in metals via the hopping mechanism and the knowledge of the activation energy or energy barrier (ΔEa) for the H-atom to escape an interstitial site is a necessary quantity for understanding and modeling its diffusion [1, 10]. Understanding diffusion mechanisms and how local structure affects diffusion requires the knowledge of the ΔEa for the different residence sites [11,12,13]. At the atomic scale, the determination of the geometrical and chemical factors responsible for the height of ΔEa is nontrivial due to the complex dependency of this quantity on the local atomic structure and composition [14]. The residence time t is a parameter often used to model both hydrogen distribution and concentration gradients at the continuum level in simple models that are conceptually free from the quantity ΔEa [5]. In these models, the value of t for a specific lattice site i (ti) depends on the absorption energy of the H-atom (ΔEabs_H) at that site. No distinction is made between ΔEabs_H and ΔEa because all sites—even the saddle points—are considered equivalent lattice sites in the computation of the overall t. ΔEabs_H and ΔEa differ only in magnitude and eventually in sign and because ΔEa is more positive than ΔEabs_H these models often disregard ΔEa. However, even in these models where conceptually t ∝ (ΔEabs_H)−1, the accurate determination of the overall t requires the knowledge of ΔEa. This is because the total t depends on the individual ti for all sites in the lattice and the values of ΔEa have also to be known to account for the kinetic effects in the distribution of hydrogen in the material.

Hydrogen has a relatively low ΔEa for diffusion in bulk fcc Cu single crystals with reported values that range from 0.29 eV to 0.49 eV. [15] Similarly as observed for other metals if the diffusion of H-atoms involves certain defects its ΔEa can be lower [16]. Results from a recent theoretical investigation suggest that the interaction between vacancies with H-atoms in Cu could make the diffusion of vacancies faster and the diffusion of H-atoms at these defects occur with ΔEa ≈ 0 [17]. H-atoms can stabilize vacancies at the Σ3 and Σ5 GBs of fcc Pd and increase their equilibrium concentration by orders of magnitude [18]. Similar phenomena are expected for other late transition metals such as Cu. The height of ΔEa for the diffusion of H-atoms at GBs is an important parameter in this and other mechanisms responsible for the diffusion of H and its accumulation, for example, in Cu [1, 5, 7, 19]. The knowledge of the interplay between the kinetic and thermodynamic driving forces for the formation of concentration gradients of H-atoms is necessary to understand hydrogen effects in the material [20]. At present, most of the mechanistic knowledge about diffusion is based on experimental data and little is known about how extended defects such as GBs affect diffusion mechanisms and the corresponding ΔEa at the atomic scale. Because hydrogen is lightweight, quantum or tunneling effects can contribute to the overall diffusion mechanism [21, 22]. However, the quantum mechanical contribution to the reaction coordinate—or path—dominates the overall diffusion mechanisms only as the temperature (T) approaches 0 K. For the diffusion of H in Cu at room temperature the quantum tunneling contribution to the overall diffusivity is rather small, and under these conditions, the classical hoping mechanisms dominate [23]. For the diffusion of H at Cu surfaces the so-called “quantum to classical” transition occurs at T = 60 K, and for bulk Cu a similar value of T is expected. As for most metals the diffusion coefficient (D) for H in bulk Cu changes with T according to the Arrhenius law up to a certain value of T [4]. But despite this it cannot be said that changes in T affect to the same extent the diffusivity at different lattice sites. In a defective crystal, an increase in temperature can change the relative contributions of different diffusion mechanisms to the overall diffusion by enhancing these mechanisms to different extents due to changes in the balance between ΔS and ΔH [14]. At low T these differences are small and for the purpose of understanding the diffusion mechanisms of interstitial solutes at different lattice sites it is safe to compare the ΔEa’s if this is done at constant temperature.

Computational methods

DFT calculations

DFT calculations of the GB structure, energy barriers for hydrogen diffusion and hydrogen segregation at the different sites of the two GBs were done with the Vienna ab initio simulation package (VASP 5.4.4) [24] with the Perdew–Burke–Ernzerhof [25, 26] (PBE) exchange–correlation functional with pseudopotentials of the projector augmented wave[27, 28] (PAW) type. The PBE functional has shown good accuracy for describing the structure of high angle low index symmetric tilt GBs of Cu and their interactions with impurities [7, 29, 30]. For all calculations, a plane wave cutoff of 460 eV was employed. Each supercell employed in this work contained two oppositely oriented tilt GBs whose tilt axes were parallel to the y-axis of the supercell and the z-axis was chosen to be perpendicular to the GB plane. The details of supercell geometry are given in Fig. 1 and Table 1. The k-point meshes in the Monkhorst–Pack sampling scheme were adjusted according to the symmetry of each supercell to produce minimal errors while keeping good computational efficiency: Σ5 = (6 × 8 × 3); Σ9 = (6 × 8 × 2), [31]. The energies herein reported are electronic energies at 0 K which allow accurate comparisons between bonds and binding energies at sites with similar chemical environment in the solid [32,33,34].

Figure 1
figure 1

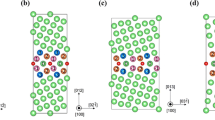
The fcc Cu GB models employed in this study. The hydrogen atoms placed at the different segregation sites are shown in gray. The gray lines define the supercells. Diffusion in the y- or x-directions in the GB planes is denominated along the GB and diffusion in the z-direction is denominated across the GB. Cu brown circles, H light gray circles.

Full size image
Table 1 Properties of the GB models employed: Σ5(310) [100], 36.9° and Σ9(2 \({\overline{2}}\,{\overline{1 }}\)) [110], 38.9°
Full size table

The absorption energy of a H-atom at a lattice site of the perfect fcc crystal is defined as

$$\Delta E_{{{\text{abs}}}} = E_{{{\text{H}}\_N{\text{Cu}}}} - \;(E_{{\text{H}}} + E_{{N{\text{Cu}}}} )$$
(1)

where EH_NCu it the energy of a supercell of single crystal fcc Cu containing the H-atom and a very large number N of Cu-atoms; EH, the energy of an H-atom in vacuum in the same supercell employed to model Cu; and ENCu, the energy of the supercell of pure fcc Cu containing N Cu-atoms. A more negative value for ΔEabs implies stronger absorption. The segregation energies of H-atoms at the GB sites (ΔEseg) were obtained from

$$\Delta E_{{{\text{seg}}}} = E_{{({\text{H}}\_{\text{sCu}})}} {-}E_{{{\text{H}}\_{\text{bulk}}}}$$
(2)

where E(H_sCu) is the energy of a supercell of Cu containing the H-atoms at the segregation sites of the GB and EH_bulk is the energy of an H-atom in the most favorable absorption site in the bulk of a single crystal of Cu. A more negative value for ΔEseg implies stronger bonding at the corresponding site. The GB energies (γGB) are here defined as

$$\gamma_{{{\text{GB}}}} = \, \left( {E_{{{\text{GB}}}} {-}E_{{{\text{bulk}}}} } \right)/{2}A$$
(3)

where EGB is the energy of the supercell that contains the GB, Ebulk is the total energy of a supercell of Cu single crystal that contains the same number of atoms as those present in the supercell used for modeling the GB and A is the area of the GB plane in the supercell. The quantity is divided by two to account for the fact that there are two identical GBs in the supercell. A lower γGB implies stronger cohesive bonding between the two grains. The models were constructed from the coincidence site lattice (CSL) method which is a robust method for the construction of high angle low index GBs that have a high density of coinciding sites at the GB planes [35, 36]. The equilibrium structures were obtained starting with a pre-optimization, where the supercells were allowed to relax along the direction perpendicular to the GB planes, from there the internal coordinates of the atoms were optimized and the procedure was iterated until convergence between both optimizations was reached.

The energy barriers for diffusion (ΔEa) were computed with the nudged elastic band (NEB) method as implemented in VASP [37, 38]. The electronic structure parameters for these computations were the same as for the geometry optimizations and 6–8 images were employed on the transition state (TS) search depending on the of symmetry of the diffusion path with lower symmetries requiring more images. The activation energies here reported have been determined as

$$\Delta E_{a} = E_{{{\text{TS}}}} {-}E_{{{\text{react}}}}$$
(4)

where ETS is the electronic energy of the saddle point that corresponds to the transition state, and Ereact is the electronic energy of the reactant structure which corresponds to the initial structure from which the diffusion takes place. A more positive value for ΔEa implies a larger energy barrier for diffusion. The reported differential electronic energies ΔE have been determined with respect to the reactant state. The diffusion distances here reported (đ) are the distances traveled by the atom corresponding to the length of the diffusion path and not the simple Euclidean or straight-line distances between the coordinates of the initial and final states.

Structural analysis: geometrical and symmetry features

As previously done for similar systems, in order to understand how the local geometry and symmetry of the lattice affect the segregation energies and diffusion barriers for H-atoms, we performed a detailed structural analysis. As previously described [29, 39] spatial tessellation methods are valuable tools for this type of analysis and in particular the method here employed, Voronoi tessellation, [40, 41] has good accuracy for structural analyses of this kind at GBs. [29, 41] The tessellations of the supercells were performed with the Laguerre–Voronoi method and the resulting polyhedra were used to determine lattice site-dependent quantities such as the volume expansion (Vx) and coordination number (Cn). The volume expansion (Vx, %) of an interstitial lattice site is here defined as relative to the bulk octahedral interstitial lattice site volume, as the latter is the preferred site for the absorption of H-atoms.

As previously implemented in a similar study, [42] based on the principles behind the Voronoi tessellation and of the Laguerre–Voronoi diagrams, the symmetry of the geometrical disposition of neighbors that surround a given lattice site occupied by an H-atom is directly related to the areas of the faces of the Voronoi or Laguerre–Voronoi polyhedron that encapsulates that lattice site. The details of this principle have been previously discussed [39]. Its main outcome for this kind of structural analysis is that it is possible to define a dimensionless symmetry quantifying parameter σ that accounts for the asphericity of the polyhedron that surrounds the lattice site occupied by a H-atom as follows

$${\sigma }_{A}=\frac{\sum_{i}\left({Av}_{i}\right)}{{A}_{WS}}$$
(5)

where Avi is the area of ith face that constitutes the Laguerre–Voronoi polyhedron that surrounds a given lattice site, and AWS is the area of the Wigner–Seitz sphere centered at the corresponding lattice site. Because of the equal volume of the Wigner–Seitz sphere and of the Wigner–Seitz cell for a given lattice site, [43] AWS can be computed from the volume of the Laguerre–Voronoi polyhedron which encapsulates that lattice site. Within this definition the smaller is σA for a lattice site, the higher is the symmetry of that site in terms of the geometrical disposition of nearest neighboring atoms. To quantify the differences in symmetry between lattice sites at the GBs and the preferred bulk site for H-atom absorption (the interstitial octahedral site), σ can be defined as a symmetry change relative to the interstitial octahedral site as

$$\sigma =\left({\left(\frac{\sum_{i}\left({Av}_{i}\right)}{{A}_{WS}} \right)}_{GB}-{\left(\frac{\sum_{i}\left({Av}_{i}\right)}{{A}_{WS}}\right)}_{bulk}\right)\times 100$$
(6)

where the left side term accounts for the symmetry of the interstitial GB site and the term to the right accounts for the symmetry of the interstitial octahedral site at the bulk. The larger is σ for a given lattice site, the lower is the symmetry of that site. A negative value of σ means that the corresponding site has higher symmetry than the bulk interstitial octahedral site of the fcc lattice. The values of σ are here expressed as % for convenience.

Nomenclature for diffusion paths

To simplify the discussion, the diffusion pathway from an initial site α to a final site μ will be denoted (αμ). Many of the diffusion pathways occur along directions where one or two Cartesian coordinates of the set (x, y, z) are constant. The coordinates that vary during diffusion are indicated as a subscript. For example, the diffusion pathway from α to its nearest symmetrically equivalent α along y-direction, with x and z coordinates kept constant, is indicated as (αα)y; the diffusion jump from α to μ following a path with varying x and z coordinates is represented as (αμ)x,z.

Σ5, Σ9 and Σ11 GB models

The GB models employed in this work are based on models that have been thoroughly benchmarked and tested in previous studies of segregation of hydrogen and substitutional impurities and will not be here discussed at length [7, 30, 42]. In previous studies of defects—such as vacancies—at these GBs, [39] we employed somewhat larger models of the GBs because the creation of vacancies implies structural relaxations that can be fairly extensive. Because the hydrogen atom is small and does not cause considerable displacements of the first neighbor lattice atoms upon diffusion, [4] its diffusion can be modelled safely with smaller supercells when compared with the case when the diffusing and solvent atoms have similar sizes [42]. In the latter case diffusion causes considerable displacements of the atoms that are first neighbors to the diffusion path and larger supercells are typically necessary to accurately account for lattice relaxations. The models here employed were sliced from the larger supercells previously employed [39] and reoptimized according to the procedure described in Sect. 2.1. The GB models here employed are shown in Fig. 1 and their properties are summarized in Table 1.

The resulting structures after optimization as described in the previous section have geometries and γGB which are in excellent agreement with literature data [7, 29, 30, 44,45,46]. The GBs here employed have the required symmetry to study the diffusion of the H-atom along and across the GBs and have the most important structural nuances of these two GBs.

Results and discussion

Segregation of H at Σ5 and Σ9 GBs

Before focusing on the study of the segregation of H-atoms at the GBs, it is important to understand how the absorption of H-atoms at the single crystal fcc lattice relates with the geometrical features of the absorption sites, namely coordination number (Cn), site volume (V), and σA (defined in Eq. 5). The resulting data are shown in Table 2.

Table 2 Absorption energies (ΔEabs) for a single H-atom the octahedral (oct) and tetrahedral (tet) interstitial sites of fcc Cu and their relationship with the symmetry parameters defined in Sect. 2.1.1
Full size table

The obtained energy difference between the oct and the tet sites is in very good agreement with our previously published data, [7, 8] and the coordination numbers obtained from the Laguerre–Voronoi tessellation are in agreement with the geometry of these sites. We have previously shown that the preference of H-atoms to oct or tet sites changes upon lattice expansion when the volume per site increases up to an inflection point [7]. In the cited study the analysis was direct without the need to employ symmetry quantifying tools because we have compared the ΔEabs for the same absorption sites of the single crystal—oct with tet—while the lattice was expanded isotropically. In the current case, the analysis of the symmetry effects in the preferences for absorption between two symmetrically inequivalent sites must include all the parameters shown in Table 2. There is a collective contribution to the preferred absorption at the oct site. Starting with a higher Cn and a larger V which favor the bonding between the Cu-atoms and the H-atom. The site symmetry contribution is also important, and the tessellation data show that the oct site has higher symmetry—by ≈ 20%—which is expressed by the smaller value of σA for this site.

The segregation of H-atoms to the different GB sites was studied to understand which pathways—from which and to which site—should be considered. The ΔEseg obtained for the sites shown in Fig. 1 are shown in Table 3.

Table 3 Values of ΔEseg for the different segregation sites of the Σ5 and Σ9 GBs shown in Fig. 1
Full size table

The values of ΔEseg at Σ5 are in excellent agreement with our previously published data employing larger GB models [7]. For Σ9 the ΔEseg for the H-atom is here reported for the first time, but the obtained trend agrees with the known effect that the local geometry has on the stabilization of H-atoms at the corresponding absorption sites [29]. The correlation between ΔEseg and the site distance from the GB planes is shown in Fig. 2.

Figure 2
figure 2

Correlation between the distance from the GB planes d (Å) and segregation energies for a single H-atom at the interstitial sites of the GBs relative to the bulk octahedral site (ΔEseg) (eV) as a function of (Vx) and of σ.

Full size image

As expected, the values of ΔEseg are more negative at and near the GB planes—with one exception for Σ9—and tend to zero as the distance from the GB planes increase. The Σ9 GB has sites with more negative ΔEseg at the GB plane, but the values tend faster to zero with d than for the Σ5 GB. The exception site for Σ9 is the site a. This site has a negligible Vx of ≈ 2%, a Cn of 9 and a large σ of 130%. The combination of asymmetry with very small volume expansion makes the segregation of H-atoms unfavorable. These observations show that to rationalize these data it is necessary to study the structure and symmetry of both GBs more in depth.

The correlations between the geometrical parameters Cn, Vx, and σ (defined in Eq. 6) are shown in Fig. 3.

Figure 3
figure 3

Correlations between coordination number (Cn) and volume expansion (Vx) for the different sites of each of the GBs, and segregation energies for a single H-atom at the interstitial sites of the GBs relative to the bulk octahedral site (ΔEseg) (eV) as a function of (Vx) and of σ. For the definition of these quantities, see Sect. 2.1.1.

Full size image

The correlation between Cn with Vx is closer to linear for the Σ5 GB than for the Σ9. This agrees with previous findings related to features of these two GBs in terms of their non-interstitial sites [39, 42]. Similarly to what has been previously observed for bulk single crystal, [7] for both GBs studied here an increase in Vx up to a certain value leads to stronger bonding with H-atoms—more negative ΔEseg. After a maximum Vx value has been reached the bonding with H-becomes weaker and this is more obvious for Σ5. For the single crystal, however, the correlation between Vx and the binding energy of the H-atom is close to linear for the tetrahedral and octahedral sites [7], while in the present case, the fact that the segregation sites have different Cn and σ causes the correlation between Vx and ΔEseg to deviate more from linearity. Σ9 has a structure which is more heterogeneous in terms of its relation between Cn with Vx which in turn is due to its larger asymmetry. The sites at Σ9 with more negative ΔEseg are b and c which have octahedral-like symmetry but have considerably larger volumes than the bulk. This leaves some room for the Cu-atoms that bind to H to slightly relax and maximize their interactions with the segregating H-atom. Site e has a distorted geometry, intermediate between octahedral and tetrahedral, and is elongated in a way that allows an efficient bonding between H and the surrounding Cu-atoms. These different features at the two GBs result in different correlations between Cn, Vx, σ and ΔEseg. Especially important is the type of distortions responsible for the increase in σ for each GB.

Diffusion of H in the single crystal and diffusion to and at the Σ5 and Σ9 GBs

Diffusion in fcc Cu single crystal

The diffusion path of an H-atom in the bulk of fcc Cu was studied for comparison and benchmarking purposes. The ΔEa was determined for diffusion from the most stable lattice site for the H-atom in fcc Cu: from the oct site to the nearest oct site. The resulting data is shown in Fig. 4.

Figure 4
figure 4

Energy (ΔE) as a function of the diffusion distance (đ) for an H-atom in bulk fcc Cu from an oct site to another oct site via an intermediate tet site. The tet site which corresponds to the transition state (Ts) is the local minimum halfway through the path. The NEB images used to describe the diffusion path of the H-atom are shown as smaller atoms. Cu brown circles, H light gray circles.

Full size image

Interstitial impurities that diffuse via the direct interstitial mechanism and that occupy the octahedral sites in fcc metals typically diffuse to the nearest oct site via the tet site [3, 4]. The obtained ΔEa = 0.42 eV is in excellent agreement with previously published experimental [47], and computational [8] data and the difference of 0.19 eV between the oct and tet sites is in excellent agreement with our ΔEabs values shown in Table 2 and our previously published value [7]. The data of Fig. 4 were computed with the NEB method and our ΔE between oct and tet sites was determined with high accuracy geometry optimizations followed by single point calculations. The excellent agreement between these data, as well as between the data of Fig. 4 and experimental data, shows that the NEB methodology employed here has high accuracy and can be safely used to study diffusion via paths with very low energy barriers at the GBs. Figure 4 also shows that the different geometries of the oct and tet sites have a considerable effect in the shape of the curve. The oct site with higher symmetry leads to a fairly constant until the H-atom reaches the saddle point and enters the geometrical domain of the tet site. There, the lower symmetry of the tet site makes vary with a more complex shape. When the H-atom is in the geometrical domain of the tet site leaving to the oct site, decreases in magnitude and there is an inflection point as the H-atom approaches the saddle point. The curve shows that the TS for diffusion from the oct to the tet site is of the early type, while the TS for diffusion from the tet to the oct site is of the late type, following the classification of Hammond’s postulate [48, 49]. For comparison it was also determined the energy barrier of a concerted diffusion mechanism where the H-atom diffuses directly from the oct site to the nearest oct site without going via the tet site. The resulting data are shown in Fig. 5.

Figure 5
figure 5

Energy (ΔE) as a function of the diffusion distance (đ) for an H-atom in bulk fcc Cu from an oct site directly to the nearest oct site through the transition state (Ts). The NEB images used to describe the diffusion path of the H-atom are shown as smaller atoms. Cu brown circles, H light gray circles.

Full size image

The diffusion via the concerted or direct oct–oct mechanism has a higher energy barrier, ΔEa = 0.79 eV. This is because this path implies both a side shift of the H-atom considering the initial direction of displacement and a slight shift of the equilibrium position of a Cu-atom at the saddle point and both these motions have an energetic cost associated. In this case there is a larger region in the vicinity of the saddle point where has smaller magnitude than for the case of the more favorable mechanism. This mechanism was initially proposed as the mechanism of diffusion for H in Cu but it is now known that H-atoms diffuse via the tet intermediate path shown in Fig. 2. The direct oct—oct mechanism is here considered for the purpose of understanding the origin of some high ΔEa values found at the GBs and the shape of the ΔE vs đ curves at the saddle points and their vicinity.

Diffusion at the GBs

For the study of the diffusion of H-atoms at the GBs we have considered different paths to and from the sites shown in Fig. 1 where all initial and final sites are preferred by the H-atoms when compared to the bulk single crystal oct site. This was done to explore the preferences for diffusion and to study the anisotropy of the diffusion near and at the GBs. In the determination of the different ΔEa’s three main types of diffusion pathways were considered: to the GBs—from neighboring sites more preferred than the bulk but less preferred than the sites at the GB plane such as from (ea)z at Σ5 and (db)x,z at Σ9 (Fig. 6); along the GBs planes—diffusion along the x- or y-directions where the initial and final sites are geometrically equivalent along y or x, with z constant or close to constant—such as (aa)x or (bb)x (Fig. 6); and across the GB along the z-direction such as from (ee)z or (dd)z (Fig. 6). Some diffusion pathways such as those often observed in the diffusion to the GBs or along the GB planes are more complex because the geometry and symmetry of the Cu-atoms along the diffusion path changes considerably with đ for some paths as it will be shown. The sets of data for diffusion at Σ5 and Σ9 GBs are shown in Figs. 7 and 8, respectively.

Figure 6
figure 6

Examples of diffusion pathways for H-atoms here studied. At the Σ5: to the GB plane (ea)z; at the GB plane along x (ba)x; at the GB plane along y (aa)y. At the Σ9: to the GB (db)x,z; at the GB plane along x (cb)x, at the GB plane along y (bb)y. For both GBs were also considered diffusion pathways across the GB, starting from a neighboring site to the GB plane and along the z-direction across the GB plane to the nearest symmetrically equivalent site, as for example from (ee)z for Σ5 and (dd)z for Σ9. Cu brown circles, H light gray circles.

Full size image
Figure 7
figure 7

ΔE as a function of the diffusion distances (đ) for an H-atom at the Σ5 GB. For the definition of the diffusion pathways see Sect. 2.1.1, Figs. 1 and 6.

Full size image
Figure 8
figure 8

ΔE as a function of the diffusion distances (đ) for an H-atom at the Σ9 GB. For the definition of the diffusion pathways see Sect. 2.1.1, Figs. 1 and 6.

Full size image

The data of Figs. 7 and 8 show the considerable anisotropy in the diffusion of an H-atom in the near and at the two GBs. The diffusion along the tilt axis of the GBs is not necessarily favored as it has been asserted previously for certain GBs in Ni, [50] and paths with other directions had to be here considered. It is often assumed for the sake of simplicity that the diffusion of an impurity at different GBs occurs with similar ΔEa’s. This would allow the extrapolation of diffusion coefficients obtained for a specific GB of a material to other or even all GBs of the same material [51]. Our data show that the ΔEa’s despite lower for both GBs than for the bulk, differ in magnitude and the diffusion tortuosity is very alike for many diffusion paths. From the two GBs the Σ9 has several paths with the lower ΔEa’s. Besides the difference in magnitude there are differences in the anisotropy of diffusion. At the Σ9 there are more paths with very low or close to zero ΔEa than at the Σ5. The reason for this is the more open character of the Σ9 which offers plenty of diffusion channels at and near the GB plane that contain a considerable excess volume [29] and allows for almost “friction-free” diffusion of H-atoms. This GB contains several diffusion channels with very low ΔEa along the y-direction where diffusion occurs without changes in the x-direction. These are diffusion channels with virtually no tortuosity which, together with the very low or virtually zero ΔEa’s, allow for very fast diffusion [52, 53]. The Σ5 GB also has channels with very low ΔEa’s but due to its more complex structure these diffusion pathways have higher tortuosity. The most striking example is the diffusion at Σ5 from the site a to another site a in the GB plane along the y -axis. This path has a very high ΔEa = 1.18 eV if the diffusion occurs on a straight line (aa)y, but the barrier is lower ΔEa = 0.30 eV if it occurs with a deviation of trajectory along the x-axis (aa)x,y. The diffusion across this GB along a straight line, (ee)z, has also a lower barrier ΔEa = 0.18 eV than for the bulk which shows that H-atoms have a much higher mobility at this GB than at the bulk, and not only at the GB plane but also on its vicinity. For the Σ9 GB the diffusion across the GB along a straight line, path (ee)z, has a higher ΔEa = 0.38 eV than for the Σ5. However, if the diffusion occurs along (ec)x,z, the ΔEa = 0.22 eV. Overall, the virtually non-existent ΔEa’s at the large channels of Σ9 will make these channels easy migration paths for the GB diffusion of H-atoms. This could explain observations that show preference for hydrogen evolution from certain GBs in experiments of permeability and degassing of hydrogen in Cu [39].

Global lowest energy diffusion pathways

From the complete sets of data for each GB it is possible to devise the most favorable diffusion path—minimum of energy—by combining the lowest diffusion pathways necessary to take the diffusing atom from an initial to a final position. Until it reaches the GB domains, the diffusion of H-atoms occurs in the bulk single crystal and has the ΔE vs đ shown in Fig. 4 which leads to an ΔEa = 0.42 eV. When diffusing toward the GBs planes, the so-called GB domains—sites where the GB geometry starts to influence both ΔEseg and ΔEa—start on site c for Σ5 and site e for Σ9. Until reaching these sites H-atoms diffuse with the ΔEa for the bulk. Here the GB geometry starts to affect the diffusion and from the ΔEseg data of Table 3, for both GBs the H-atoms will diffuse to the sites labeled b located at the center of the GB planes. At those sites the diffusion of H-atoms can proceed with very low energy barriers via intermediate sites (Figs. 7 and 8). The complete collection of data for each GB is shown in Figs. 9 and 10.

Figure 9
figure 9

ΔE as a function of the diffusion distances (đ) for an H-atom at the Σ5 GB. These are the two overall lowest energy diffusion pathways for this GB. For the definition of the diffusion pathways see Sect. 2.1.1, Figs. 1 and 6.

Full size image
Figure 10
figure 10

ΔE as a function of the diffusion distances (đ) for an H-atom at the Σ9 GB. These are the two overall lowest energy diffusion pathways for this GB. For the definition of the diffusion pathways see Sect. 2.1.1, Figs. 1 and 6.

Full size image

The data of Fig. 10 show the two lowest ΔEa diffusion pathways for the Σ9 GB. These paths involve sites c and b in the case of the path (bcb)x,y and involve only site c in the other case, (cc)y. Site b is lower in energy by − 0.06 eV than site c and the direct diffusion from b to b has a ΔEa = 1.20 eV as shown in Fig. 8, hence the diffusion from c to b had to be here considered. However, the diffusion from c to b has a ΔEa = 0.20 eV. It can also be seen that seen that ΔEa = 0.05 eV for diffusion from c to c along y, (cc)y, which is a considerably lower activation energy. The ΔEa for diffusion from (cc)y is then lower than both the ΔEa for diffusion along (bcb)x,y and the difference in ΔEseg between c and b. This shows that in the Σ9 GB the lowest energy diffusion path is along the GB in the y-direction and this diffusion occurs with a very low ΔEa = 0.05 eV. In this diffusion mechanism, the H-atom migrates parallel to the GB plane during diffusion along (cc)y, this path has low tortuosity, which together with the very low ΔEa allows for very fast diffusion. However, as mentioned above, at Σ9 the H-atom binds stronger to site b than to site c which will make the H-atom diffuse back from site c to site b after it has reached site c from the nearest site c. This leads to a rather complex diffusion mechanism as shown in Fig. 11, where the complete (lowest) ΔEa pathways for diffusion between the most favorable segregation sites at both GBs are illustrated.

Figure 11
figure 11

Diffusion pathways with the lowest activation energies (ΔEa) for diffusion of H-atoms between the preferred segregation sites, allowing these to cross the Σ5 and Σ9 GBs. The lowest-energy pathways for diffusion occur in the GB planes. Due to symmetry the pathways and potential energy diagrams for diffusion repeat infinitely making the pathways shown the preferred for migration of H-atoms at these GBs. Color code: Cu brown circles, initial and final sites for H—global minima—are shown as larger white circles, intermediate states and transition states are shown as smaller gray circles.

Full size image

Conclusions

The comparison between the diffusion of H-atoms at bulk fcc Cu and symmetric tilt GBs Σ9 and Σ5 shows that the diffusion pathways at these high angle low index GBs are complex when compared to the bulk. We determined the complete set of activation energies (ΔEa’s) for diffusion of H-atoms at these defects and found many favorable diffusion pathways with lower ΔEa than in the bulk. Some of these paths have ΔEa’s as low as 0.05 eV. In the large collection of possible diffusion pathways many have considerable tortuosity but there is a large number of paths with low tortuosity due to the existence of many interstitial sites at these GBs with more favorable symmetry for interstitial diffusion when compared to the bulk. From the complete set of ΔEa’s for both GBs we determined the lowest diffusion ΔEa’s for both grain boundaries that allow the H-atoms to cross the whole GB. At the Σ9 the H-atoms can cross the GB with a ΔEa of 0.05 eV and at Σ5 the value of ΔEa is 0.20 when compared to the bulk fcc crystal, ΔEa = 0.42 eV. Even if the diffusion of H-atoms is highly directional at these GBs it occurs with very low ΔEa and low tortuosity hence it will be fast. This is especially true for the Σ9 GB.

We performed a structural analysis of the diffusion pathways based on the Laguerre–Voronoi tessellation method that has shown that the volume expansions and the coordination numbers of the GB sites alone cannot account for the magnitude of the ΔEa’s. In order to improve these correlations, we developed a symmetry quantifying parameter that measures the deviation of symmetry of the GB sites from that of the bulk octahedral site. Only when this parameter is accounted for together with the volume expansions and the coordination numbers it is possible to correlate structural features of the sites with the ΔEa and to obtain descriptors of diffusion. The obtained set of data shows that the extrapolation of diffusion data for H-atoms between different types of GBs is nontrivial and should be done with care.