Abstract
The Leibniz–Reynolds transport theorem yields an omnimetric interface energy balance, i.e., one valid over all continuum length scales. The transport theorem, moreover, indicates that solid–liquid interfaces support capillary-mediated redistributions of energy capable of modulating an interface’s motion—a thermodynamic phenomenon not captured by Stefan balances that exclude capillarity. Capillary energy fields affect interfacial dynamics on scales from about 10 nm to several mm. These mesoscopic fields were studied using entropy density multiphase-field simulations. Energy rate distributions were exposed and measured by simulating equilibrated solid–liquid interfaces configured as stationary grain boundary grooves (GBGs). Negative rates of energy distributed over GBGs were measured as residuals, by subtracting the linear potential distribution contributed by applied thermal gradients constraining the GBGs from the nonlinear distributions actually developed along their solid–liquid interface. Rates of interfacial cooling revealed numerically confirm independent predictions based on sharp-interface thermodynamics, variational calculus, and field theory. This study helps answer a long-standing question: What creates patterns for diffusion-limited transformations in nature and in material microstructures?
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
“A very small cause that escapes our notice determines a considerable effect that we cannot fail to see, and then we say that the effect is due to chance.”—Henri Poincaré, Science et méthode, 1908.
Patterns encountered in nature, such as those exhibited by snow flakes and many crystallized mineral forms, and those found in the microstructures of cast alloys and fusion weldments, remain subjects of long-standing scientific interest and practical engineering importance [1, 2]. Alan Turing’s paper, “The Chemical Basis of Morphogenesis” [3], is credited as explaining that diffusion-limited processes can drive thermodynamically “open” systems to instability. Patterns then evolve spontaneously in response to Poincaré’s “very small cause(s).” But what, in fact, are the nature and function of such very small causes?
A century beyond Poincaré’s quoted remark, and six decades after Turing’s explanation of instability in chemically reacting systems, major issues remain unresolved concerning pattern formation dynamics in diffusion-limited systems. These issues entail the following questions: (1) How do specific patterns initiate during crystal growth, solidification, and other diffusion-limited phase transformations? (2) Is there an agent that provides a template, or guide, for pattern development, especially where neither prior structures nor preferred directionality is present in the metastable melt, solution, or vapor phase? This paper explores the origin of “very small causes,” or perturbations, that appear spontaneously in diffusion-limited systems and guide pattern formation.
Most fluid phases (gases and liquids) lack discernible internal structures, order, or directionality, excepting ephemeral correlations associated with their localized molecular configurations. For example, short-range order in supersaturated melts seldom extends beyond a few nanometers [4]. It is unlikely, therefore, that information residing at the atomic/molecular level guides patterns emerging at scales three to six orders-of-magnitude larger. Diffusion-limited patterns of interest falling within this category include well-organized cellular and dendritic forms, invaginated and highly ramified interfaces, including “seaweed” and other irregularly branched microstructures. Indeed, increasingly complex patterns might even be extensible to those found in biological systems.
In other words, to understand the origin of many natural patterns, and, ultimately, control microstructures derived from materials processes involving solidification, welding, and crystal growth, one must determine: (1) whether pattern-forming “signals” or “instructions” exist, and, if so, (2) do they fundamentally devolve from stochastic processes, or from higher-order deterministic sources.
This paper addresses both issues for crystal–melt interfaces in unary systems, by exploring the presence of interfacial energy fields that provide pattern-forming stimuli in 2D. The presence of such stimuli on solid–liquid interfaces described in earlier publications [5, 6] is finally revealed and measured here through novel measurements extracted from phase-field simulations. Capillary fields in the form of interfacial energy distributions are exposed and measured on simulated microstructures in the form of equilibrated solid–liquid grain boundary grooves (GBGs). Simulated interfacial data also allow quantifiable comparison with analytic predictions of interfacial energy fields derived from sharp-interface thermodynamics. Simulations and measurements reported in this study also confirm that equivalent pattern-forming fields arise within standard phase-field physics that manifest themselves as deterministic perturbations.
Numerical simulations are compared with predictions based on interface energy conservation and classic field theory. The comparison reveals the existence of persistent capillary-mediated energy fields that influence the dynamics of interfacial shape changes during phase transformation. Such fields stimulate complex pattern formation on unstable interfaces with, or without, benefit of noise.
Experimental observations: capillary-induced shape change
Prior microgravity studies
The idea that innate capillary phenomena, rather than “selectively amplified” noise [7,8,9,10], control pattern formation in diffusion-limited phase transformations was initially prompted by experimental observations of unusual solid–liquid interfacial shape changes. Needle-like crystallites progressively melted self-similarly under convection-free conditions in orbital microgravity, but suddenly, and surprisingly, spheroidized [11].
The first gravity-free studies yielding quantitative kinetic data on diffusion-limited crystal growth, melting, and pattern formation were the Isothermal Dendritic Growth Experiments (IDGE). Three IDGE experiments were flown by NASA during the mid-to-late 1990s on Space Shuttle Columbia using the US Microgravity Payload (USMP) platform. Video and precision thermal data, streamed directly from the IDGE-3/USMP-4 orbital experiments, indicated that capillary effects might be responsible for such unusual changes. These experiments recorded the evolving shapes of melting crystallites of ultra-purified pivalic anhydride (PVA) (2,2-dimethylpropionic anhydride) [11]. PVA is a transparent face-centered cubic crystal that melts at approximately 36 °C. Video (shape) data and precision thermal data for quasi-statically melting PVA crystallites were analyzed kinetically and reported through encouragement received from both NASA and the German Aerospace Center (DLR) at Köln-Porz, Germany [12,13,14].
IDGE melting data from USMP-4 showed that unexpected crystal shape changes occurred in microgravity during diffusion-limited melting. Slender, melting ellipsoidal crystallites initially experienced slowly increasing major-to-minor axial ratios. Then, at a further reduced size, these crystallites suddenly underwent dramatic decreases of more than an order-of-magnitude from their typical high axial ratios of 15–20, down to almost unity. The onset of large interfacial shape changes always occurred when the crystallites during slow melting entered a narrow range of sizes: viz., when their major axes were reduced to about 5 mm, and their minor axes simultaneously decreased to about 500 microns. These dramatic shape changes—viz., needles suddenly contracting into spheroids—were consistently recorded as diffusion-limited melting progressed toward extinction of PVA crystallites under quiescent microgravity conditions.
During terrestrial melting, by contrast, where gravity is present, buoyancy convection and rapid sedimentation totally obscure the onset of shape changes. Several aspects of these experimental observations in microgravity were later reproduced in a phase-field simulation of melting crystallites reported by Mullis [15]. Mullis’s numerical results provided the first inkling that conventional phase-field simulations, without modification, might also produce interface fields responsible for transformation-induced shape changes. Indeed, this paper advances that initial suggestion toward near certainty.
Our explanation of deterministic—versus stochastic—pattern dynamics is based on two independent insights: (1) heuristic observations in microgravity, as summarized above, of dynamic shape changes for crystallites melting under diffusion control, and, (2) to be described next in “Interface energy balances” section, the application of sharp-interface thermodynamics that imposes interfacial energy conservation over all relevant length scales. We will combine insights based on experimental observation involving quantitative shape and thermal analysis [13] with interface energy conservation, via Leibniz–Reynolds transport theory, which identifies the higher-order energy terms responsible for interfacial shape changes during melting and guides pattern formation during solidification [16].
Interface energy balances
Conservation principles applied in the form of the Leibniz–Reynolds transport theorem [17, 18] identify an overlooked higher-order energy term. We shall demonstrate that this term represents a thermodynamic field that exists ubiquitously on heterophase interfaces exhibiting capillarity and curvature gradients. Moreover, general formulas published recently for calculating energy redistribution on interfaces are also capable of predicting the initial geometric character of patterns evolved in both isotropic and anisotropic solid–liquid systems [5]. These same energy fields are, in a sense, nature’s pattern-forming “information,” which is provided autonomously by thermodynamics.
In this paper, we expose and measure the active presence of capillary-mediated energy fields on stationary interfaces, chosen as equilibrated grain boundary grooves simulated using a multiphase-field model. We then compare them to theoretical predictions from thermodynamics and field theory.
Stefan conditions
The Stefan condition conserves energy and/or species by balancing their release or intake at moving phase boundaries [2]. Indeed, Stefan conditions provide the accepted method, through control volume requirements, to connect the speed of a moving interface—related to its rate of phase transformation energy and species release—to the transport rates of these quantities. The rates of generation and transport must balance. Although usually credited to Josef Stefan’s lecture notes and journal publications from the late nineteenth century, for example, [19, 20], an energy balance similar to Stefan’s eponymous condition was introduced much earlier, appearing in 1831, by Lamé and Clapeyron [21]. So, interface energy and mass balances have been under discussion and use for nearly two centuries. Today, phase change kinetics, free-boundary problems, and most theories of diffusion-limited pattern dynamics invariably employ “Stefan balances” to impose conservation laws at moving heterophase interfaces.
The fundamental issue raised here regarding limitations in Stefan balances is to re-examine closely the length scales over which an interface must precisely balance its energy/mass budget. Our view, to be examined in detail, is that (1) energy and matter at interfaces, of course, are conserved, and (2) sources and fluxes of these quantities must remain balanced in control volumes of arbitrary spatial extent. In short, energy rates on, to, and from, an interface must balance “omnimetrically”, i.e., over all continuum length scales. As will be shown next in “Omnimetric energy balances” section, the Stefan condition, per se, does not satisfy these basic requirements if capillarity is present. As humorist Mark Twain once famously remarked, “. . . this [finding] will gratify some people, and surprise the rest.”
Omnimetric energy balances
Interface energy balances in the presence of capillarity were recently analyzed by applying the Leibniz–Reynolds transport theorem [17]. This theorem imposes Leibniz differentiation on both volume and surface integrals, taken in this case over a time-dependent 3D domain of pure solid and liquid undergoing freezing or melting. The sought-after omnimetric energy balance is captured by adding two steps to the Leibniz–Reynolds transport analysis. These include: (1) applying contraction mapping, to focus “bookkeeping” energy rates in a 3D domain to those exchanges occurring over the solid–liquid interface and (2) applying the 2D divergence theorem to a line integral tracking energy crossing the space curve formed by the intersection of that interface with the domain’s outer boundary [5, 22].
The Leibniz–Reynolds energy balance, when modified as indicated above, includes the energy terms found in Stefan’s balance, plus additional rates linked to capillarity, all of which have been recognized and discussed in theoretical surface thermodynamics [23]. Although these higher-order energy terms are identified, their functions in pattern dynamics in transforming systems are not. They include in particular capillary energy stored or released as an interface changes its area and crystallographic orientation to the melt, plus energy redistributed over the interface via divergence of capillary-mediated fluxes arising from interfacial gradients of the Gibbs–Thomson thermo-potential.
Moving interfaces
The Leibniz–Reynolds transport theorem specifically identifies six independent sources (excluding thermal radiation) that contribute to the interfacial energy balance for a moving anisotropic solid–liquid interface [5], whereas the Stefan balance, which excludes capillarity, includes only three. One such interfacial energy source, easily eliminated for our present purposes, is to consider isotropic solid–liquid interfaces, so that crystallographic orientation, per se, does not influence an interface’s energy density, i.e., \(\gamma _{s\ell }={\hbox {const}}.\ ({\hbox {J}}\,\hbox {m}^{-2})\).
Another capillary-mediated energy source identified by Leibniz–Reynolds analysis is the rate of interfacial deformation, or “stretching.” Area changes on evolving interfaces require some energy storage or release as a moving interface advances or retreats during phase transformation. The rate of area change for moving interfaces is proportional to the product of their local mean curvature and speed. Insofar as interfacial stretching and latent heat production both occur at rates proportional to an interface’s normal velocity, energetic effects from stretching or shrinkage can be combined with the local rate of latent heat production. This is accomplished by inserting a small correction to the volumetric latent heat, \({{\Delta }}{H}_f/\varOmega \, ({\hbox {J}}\,{\hbox {m}}^{-3})\), where \(\varOmega \,({\hbox {m}}^3\cdot\,{\hbox {mol}}^{-1})\) is the system’s molar volume, and \({{\Delta }}{H}_f\ ({\hbox {J}}\,{\hbox {mol}}^{-1})\) is the molar enthalpy change upon melting. Corrections to \({{\Delta }}{H}_f\) added to account for any stretching may be safely ignored provided that the average mean curvature of the microstructure, \({\mathcal {H}}\ll {\Delta }{H}_f/\gamma _{s\ell }\varOmega \approx 10\ ({\hbox {nm}}^{-1})\). Mean curvatures of mesoscopic solid–liquid microstructures would seldom exceed this level. This explains why Stefan’s balance, which excludes capillarity, predicts net (overall) transformation rates correctly, irrespective of the detailed intermediate solid–liquid microstructure, but fails to address properly energy exchanges occurring at smaller length scales.
Thus, the Leibniz–Reynolds transport theorem can be reduced to four independent rates that enter omnimetric energy conservation for isotropic interfaces [5]:
The first two terms in Eq. (1) are local rates of thermal conduction driven by macro-gradients within the bulk crystalline (c) and liquid (\(\ell \)) phases surrounding a moving interface, \({\mathbf {r}}(x,y,z,t)\). The third term represents the rate of latent heat produced (or absorbed) by normal motion of the interface during phase transformation, including—by adjustment of the volumetric enthalpy change—energy stored (or released) from interface “stretching.” All the energy rates described by the first three terms in Eq. (1) are associated with gradients or velocities directed along the unit normal, \({\mathbf {n}}\), to the interface. The subscript “LR” appended to the latent heat rate designates the local interface velocity consistent with the presence of the fourth energy rate term included in Eq. (1) that varies, point to point, over the interface. The average rate of latent heat released, when integrated over the solid–liquid interface, agrees with Stefan’s balance, as capillary modulations, which arise from a conservative vector field, tend to cancel over large scales on moving interfaces. (For proof, see Ref. [5], Section 5.2.2.)
The fourth energy rate, appearing in Eq. (1), is responsible for local capillary-based energetic addition and subtraction. It represents the interfacial energy rate associated with the surface divergence of the capillary-mediated tangential flux vector, \({{\phi }}_{\tau }({\mathbf {r}})\cdot {\varvec{\tau }}\). This flux, itself a conservative vector field, arises in response to gradients of the Gibbs–Thomson thermo-potential. Much more will be discussed later about the capillary flux, \(\phi _{\tau }\cdot {\varvec{\tau }}\), and its scalar divergence.
The Leibniz–Reynolds theorem tracks the fourth interfacial energy exchange rate as a line integral taken round the intersection of the solid–liquid interface with the exterior boundary of the 3D solid–liquid domain. This line integral sums any interfacial energy losses or gains that exit or enter this closed space curve. The line integral transforms to a standard area integral over the solid–liquid interface by applying the 2D divergence theorem [22], yielding the last term in Eq. (1). See again “Omnimetric energy balances” section.
Despite its technical origin, the fourth term appearing in the Leibniz–Reynolds interfacial energy budget—termed the “bias field”Footnote 1—is essential in achieving omnimetric balance. The Stefan condition, which excludes capillary, does not yield the desired multi-scale energy balance, particularly at smaller mesoscopic scales. For example, a positive flux divergence withdraws energy at points on an advancing freezing interface and slightly reduces the net energy rate released at those points. This reduction in energy rate would locally imbalance the nearly constant energy rate entering and required by the surrounding phases’ slowly changing macro-gradients. Long-range macroscopic thermal gradients act quasi-statically and change relatively slowly over time, compared to either latent heat or capillary-mediated energy sources that arise from fast-changing (microscopic) molecular scale events. The energy rate reduction resulting from an onset of positive flux divergence must, therefore, be “cancelled” by a prompt compensatory increase in local interface speed, from \({v}_{St}({\mathbf {r}})\rightarrow {v}_{LR}({\mathbf {r}})\), a modulation that boosts the local latent heat rate slightly and restores the local balance of interfacial energy. Conversely, a negative flux divergence that adds energy would raise the interface’s energy release rate by a small amount. A locally increased energy rate requires a compensatory decrease in interface speed that reduces the local latent heat rate and restores balance to that region’s energy budget. The capillary bias field, in this context, allows omnimetric energy balances down to the smallest mesoscopic scales affected by capillarity and pattern formation.
In general, we argue, capillary-mediated divergences occurring along an interface are automatically buffered by small countervailing speed adjustments (modulations) to the interface. These modulations insure “spectral” compliance of local energy conservation at every continuum spatial scale. Thus, it is multi-scale energy (and/or mass) conservation that is exposed here as fundamental dynamic mechanisms influencing pattern initiation on moving interfaces. Random noise might well be present during solidification and melting; however, it is the spectral, or omnimetric, balancing of the interface’s energy budget that thermodynamics demand. This intrinsic control mechanism, apparently, has not appeared in prior dynamic pattern analyses. As shown later, moreover, the multiscale balances just described are also captured by phase-field theories and their numerical models.
Now, applying similar notation to that used in Eq. (1), we write the Stefan condition as used in conventional interface balances describing solidification and crystal growth as [24, 25],
Note that the interface velocity appearing in Eq. (2), by contrast with \({\mathbf {v}}_{LR}({\mathbf {r}})\) in Eq. (1), now denotes the Stefan interface velocity, \({\mathbf {v}}_{\mathrm{St}}({\mathbf {r}})\), as the normal speed of the solid–liquid interface, without consideration of capillarity.
If one subtracts Stefan’s condition, Eq. (2), from the Leibniz–Reynolds energy balance, Eq. (1), and rearranges terms, an interesting expression appears that estimates the normal speed difference expected between moving interfaces with and without capillarity:
The right-hand side of Eq. (3) equals the interfacial speed difference, or “modulation” (\({\hbox {m}}\,{\hbox {s}}^{-1}\)), caused by capillary energy fields. Its left-hand side is the ratio of the scalar bias field \({\mathrm {(W\,{m}^{-2})}}\) to the system’s volumetric enthalpy density \({\mathrm {(J\,{m}^{-3})}}\). Also of interest in the case of moving interfaces are any discrete locations where this field reverses sign. Sign reversals occur at the roots (zeros) of the capillary bias field. Roots cause speed modulations that simultaneously increase and decrease over a small region surrounding the roots. The juxtaposition of opposing speed modulations causes inflections to form. Inflections, amplified by the transport fields surrounding the moving interface, can develop into bumps, branches, or “fingers” that protrude from the interface and enhance pattern complexity [5].
Connections between pattern formation, interfacial speed modulations, and the presence of fourth-order capillary fields were overlooked in early mathematical formulations of dendritic growth [26], in subsequent pattern-formation models for diffusion-limited systems [2], including a major monograph on pattern formation in solidification by Xu [27].
The authors also suggest, without formal proof at this time, that use of the Leibniz–Reynolds multi-scale energy balance, rather than the Stefan balance, might avoid mathematical singularities introduced by capillarity in sharp-interface models of pattern-forming dynamics. Another unintended consequence of relying on the Stefan condition to satisfy interfacial energy and/or mass conservation is that it limits use of the interface’s Gibbs–Thomson potential as a scalar boundary condition to match chemical potentials along curved heterophase interfaces. As shown later in “Thermodynamic properties of variational GBGs” section, applying the Gibbs–Thomson scalar potential, but ignoring its vector gradient and flux, overlooks a critical function of allowing omnimetric energy conservation to hold, especially at interfacial scales where patterns form.
Lastly, we demonstrate in “Phase-field model and results” section that thermodynamically consistent diffuse interface simulations, as used in this study, do not suffer these limitations, as their physics admit formation of equivalent interface energy fields.
Stationary isotropic interfaces
Stationary solid–liquid interfaces provide a simple, non-trivial setting on which to measure capillary-mediated potential gradients, fluxes, and their vector divergences. In particular, static solid–liquid interfaces neither generate nor absorb latent heat, nor do they change shape, undergo interface “stretching” or change orientation over time. Such interfaces, moreover, remain strain free, are neither subject to morphological instability nor stress relaxation, and, perhaps most importantly, may be probed with great precision to measure the distribution of their thermodynamic potentials and evaluate their active energy fields.
The Leibniz–Reynolds energy balance, Eq. (1), for a stationary interface in the form of a grain boundary groove constrained by an applied thermal gradient, \({\mathbf{G}}\), simplifies still further as,
where \({\mathcal {J}}({\mathbf{G}})\) is the jump that develops in the norm of the thermal gradient across the interface from the divergence of the tangential flux, namely \(|{\mathbf{G}}|_{\ell }-|{\mathbf{G}}|_{c}\). Equation (4) describes the effect of the interfacial bias field on a stationary solid–liquid interface. The interface’s shape, separating phases with identical thermal conductivities, \(k_{\mathrm{th}}\), is described by the position vector \({\mathbf {r}}(x,y,z)\). The presence of an interfacial energy field causes a “jump,” \({\mathcal {J}}({\mathbf{G}})\), to appear in the normal components of the thermal gradient across that interface. Note, that absent the presence of a bias field, for equal phase thermal conductivities surrounding a stationary solid–liquid interface, the thermal gradient would remain perfectly uniform and continuous, and would not change magnitude when crossing the interface.
Equation (4), moreover, also suggests a basis for detecting bias fields that manifest their presence as small nonlinear shifts in the interface’s thermo-potential. The change in thermo-potential along static solid–liquid interfaces is also proportional to the local energy rate of the bias field [the left-hand side of Eq. (4)], and proportional to the jump developed in the gradient across the interface [the right-hand side of Eq. (4)]. The basis for proportionality between shifts in interface thermo-potential and field energy rate is discussed in detail in “Detecting interfacial energy fields” section.
Grain boundary grooves
Background
Grain boundary grooves (GBGs) are commonly occurring features found along polycrystalline solid–liquid interfaces. GBGs have been studied in considerable detail because they influence solidification behavior by affecting interfacial stability. Specifically, grain boundaries intersecting solid–liquid interfaces initiate grooved “defects,” or cusps, which provide locations on moving interfaces that are prone to morphological instability. The linear theory for morphological instability was developed over 50 years ago [28,29,30]. Along this line, Wang et al. concluded from their experiments on GBGs on succinonitrile interfaces [31]:
“\(\dots \) the interface instability occurring first at the grain boundary groove probably becomes the origin of the entire planar interface instability.”
Wang et al.’s observation and conclusion, quoted above, indicates that GBGs provide the “trigger” mechanism for actually inducing morphological instabilities on polycrystalline solid–liquid interfaces.
Dynamic interactions of grain boundaries with stationary and moving solid–liquid interfaces were described in the 1960s by investigators using hot-stage optical and electron microscopy [32,33,34,35]. In situ studies of moving solid–liquid interfaces demonstrated that persistent defects, such as grain boundaries and screw dislocations, were often responsible for initiating morphological instabilities that led to increasingly complex patterns in solidifying dilute alloys [36,37,38]. Isolated GBGs on solid–liquid interfaces, moreover, provide well-studied examples of microstructures analyzed for both energy measurement and stability [39]. Dynamic effects induced by GBGs on solid–liquid interfaces were examined in greater detail by Yeh et al., who applied a phase-field model to simulate these instabilities and subsequent pattern formation [40].
Variational GBGs with different dihedral angles were selected in this study to provide a range of equilibrated microstructures that allow both theoretical calculation of their individual bias fields, as well as permitting quantitative comparison with independently measured interfacial energy fields using phase-field simulation. Stationary GBGs are used here as test microstructures to probe the presence of such fields.
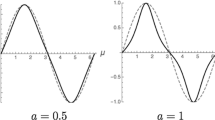
Variational groove profile, \(\mu (\eta ;{{\varPsi }})\), plotted in dimensionless Cartesian coordinates, \(\mu =x/2{{\varLambda }}, {\mathrm {and}}\ \eta =y/2{{\varLambda }}\), with dihedral angle \({{\varPsi }}=83.6^{\circ }\). The capillary metric, \({{\varLambda }}\), that scales all lengths, is set by the magnitude of the applied thermal gradient, \(G=\left| {\varvec{\nabla }}{T}\right| \). This gradient remains a constant vector field (for a variational GBG) always pointing in the \(+\eta \) direction. The presence of this thermal gradient constrains the size and shape of the variational GBG. The \(\mu \)-axis is coincident with the melting point isotherm, \(T=T_{\mathrm{m}}\). Light gray represents stable melt phase (\(\eta >0\)), whereas white areas (\(\eta <0)\) are stable crystals separated by a vertical grain boundary, GB. The melt within the cusp is increasingly supercooled with depth, suggested by gradient shading
Variational grooves
The mathematical term “variational” applied to analytically derived GBG profiles denotes interface forms obtained as solutions to the Euler–Lagrange differential equation, using methods of the calculus of variations [41]. Figure 1 is a variational profile derived for an isolated GBG, embedded, and held stationary, by a vertical thermal gradient. The configuration of solid and liquid represents a static thermodynamically “open” system, insofar as heat is uniformly conducted downward through the gradient from the hotter liquid through the cooler solid. Both phases have identical thermal conductivities, so that their steady-state heat-flow fields exhibit horizontal isotherms, vertical lines of heat flow, and a spatially uniform rate of entropy production in 2D.
The form of variational GBGs in a uniform thermal gradient was discovered by Bolling and Tiller [42]. Their mathematical solution yields solid–liquid profiles that in 2D minimize a GBG’s free energy functional.Footnote 2 The free energy of a variational solid–liquid GBG consists of capillary energy stored along its solid–liquid interface, which is increased by the “pull” of an intersecting grain boundary that curves and lengthens that interface. The grain boundary itself decreases its total area and energy as it contracts. Also included in a GBG’s variational energy functional is the volume-free energy within the slightly undercooled melt confined within the groove cusp, relative to its adjacent curved solid phase at the same temperature and pressure. The sequence of variational grooves plotted in Fig. 2 illustrates how crystal boundaries with different energy density, or surface tension, “pull” against a solid–liquid interface to form, under the same thermal gradient, unique variational profiles, each with its specified dihedral angle, \({{\varPsi }}\), and equilibrium groove depth, \(\eta ^{\star }({{\varPsi }})\).
Isometric variational GBG profiles, calculated from Eq. (5), with dihedral angles \({{\varPsi }}\in (0,<180^{\circ })\). A constant thermal gradient points left to right in each frame. The profile’s equilibrium arc length, cusp area (volume per unit thickness into the page), maximum melt supercooling, and reduction of grain boundary length, all diminish as \({{\varPsi }}\) increases
Importantly, variational GBGs do not accommodate any additional interfacial energy fields, including the bias field. Although variational GBGs are theoretical constructs, their mathematical profiles prove useful for our purposes, as they closely approximate real equilibrated GBGs. Specifically, the analytic shapes of variational GBGs may be used to calculate accurate estimates of capillary-mediated bias fields that, according to thermodynamics, should be present on real, or simulated, GBGs with the same geometric profile.
As suggested by Figs. 1 and 2, the dihedral angle, \({{\varPsi }}\), of a GBG is determined by force equilibrium among three interacting interfaces. Specifying the dihedral angle provides a natural boundary condition for the variational problem, equivalent to Young’s vector force balance at a GBG’s triple junction [12]. The flat, or outer, regions of a variational groove, far from its triple junction, become coincident with the system’s melting point isotherm, \(T=T_{\mathrm{m}}\), where the profile coordinates approach \(\eta =0\), and \(\mu \rightarrow \pm\, \infty \).

Micrograph adapted from Ref. [48]
Photomicrograph of a fully equilibrated symmetrical GBG, with a small dihedral angle, \({{\varPsi }}\approx 0\), in BCC succinonitrile [44, 45]. This material was purified to 7–9 \({\hbox {s}}+\) using distillation and multiple zone refining [46, 47]. Black area is melt phase, and gray areas are two crystallites separated by a vertical tilt boundary. The melting point of this ultra-pure material, \(T_{\mathrm{m}}\approx 58.082\pm 0.001\) °C, is the temperature realized along the flat regions of the profile [46]. A uniform thermal gradient of \(\approx \,4\,{\hbox {K}}\,{\hbox {m}}^{-1}\) points vertically upward, constraining the groove’s steady-state size and shape. The small thermal gradient maintains a relatively deep cusp of \(167\pm 15\,\upmu {\hbox {m}}\). Points marked along the solid–liquid interfaces refer to equivalent variational groove profile coordinates, \(x(y)_{{{\varPsi }}=0}\), calculated from Eq. (5).
Equilibrated GBGs
Stationary GBGs equilibrate in thermal gradients aligned with their grain boundaries. The photomicrograph of an equilibrated GBG, shown in Fig. 3, exhibits a stationary microstructure similar in shape with its variational profile, having the same dihedral angle and groove depth. (Cf. Fig. 2, \({{\varPsi }}=0\)). Note also how the variational profile coordinates plotted as points on the micrograph in Fig. 3 fit along the crystal–melt interface.
There is, as mentioned, a critical distinction between variational GBGs, with linear potential and curvature distributions, and what we term here as equilibrated GBGs, with nonlinear potential and curvature distributions and groove depths that are altered slightly by the presence of capillary-mediated energy fields. These differences, linear versus nonlinear potential and curvature distributions, allow us to evaluate the resident bias fields supported on equilibrated GBGs.
In the example offered in Fig. 3, the dihedral angle is small, \({{\varPsi }}\approx 0\), and the groove depth is large (\(\approx 170\ \upmu {\hbox {m}}\)). Equilibrated solid–liquid GBGs develop on spatial scales typically between a few tens of nanometers and several hundred microns, depending primarily on the magnitude of their thermal gradient. Similar GBGs have been equilibrated over a range of thermal gradients in experiments that yield values for the solid–liquid interface energy density of a number of transparent crystalline substances [48,49,50,51,52].
The steady-state size of an equilibrated GBG microstructure is inversely proportional to the square root of the magnitude of its thermal gradient. A typical value for the thermo-capillary length is \({{\varLambda }}\approx 3\times 10^{-4}\ {\hbox {m}}\), in many materials exposed to a relatively small thermal gradient of \(G\approx 1\ {\hbox {K}}\,{\hbox {m}}^{-1}\). Moreover, weak thermal gradients equilibrate slowly and produce relatively large groove cusps, whereas steep gradients, circa \(10^5\ {\hbox {K}}\,{\hbox {m}}^{-1}\), formed rapidly via laser or electron beam heating, reduce the cusp depth to a micron or less.

Data adapted from Ref. [48]
Experimental verification that the cusp depth of an equilibrated GBG in high-purity succinonitrile varies with the reciprocal square root of the magnitude of the thermal gradient, \(|{{\mathbf {\nabla }}}T|^{-1/2}\). Error bars of \(\pm \,5\%\) were added to the abscissa and ordinate values of these data points to suggest accuracy limitations established by the linear regression, positioned here with its slope equal to \(0.36\ {\mathrm {(m\,{K})}}^{1/2}\).
The plot in Fig. 4 correlates the norm, or magnitude, of applied thermal gradients, \(|{{\mathbf {\nabla }}}T|\), with experimentally observed steady-state sizes (cusp depths) of an equilibrated GBG in pure succinonitrile, similar to the one displayed in Fig. 3. The scaling relationship established with these data for equilibrated groove size and the applied thermal gradient agrees with that predicted from Eq. (6), expressing an inverse square-root relationship among thermal gradient, thermo-capillary length, \({{\varLambda }}\), and equilibrium groove depth.
Isotropic grain boundary grooves
Two categories of isotropicFootnote 3 variational GBGs have been analyzed in detail in earlier investigations: (1) isotropic grooves separating phases with equal thermal conductivity, the profiles, and linear thermo-potentials for which were solved by variational methods as used in this study [42]; and (2) the more general situation of isotropic grooves separating phases with unequal thermal conductivities. For unequal thermal conductivities, nonlinear potentials develop, which were analyzed theoretically, calculated, and then confirmed using an analog potentiometric device. The potentiometer consisted of alloy sheets, with dissimilar electrical conductivities, shaped and joined as a meter-sized variational “GBG.” As steady-state temperature and voltage distributions both obey Laplace’s equation, the nonlinear voltage distribution measured along this analog GBG profile for a large (7:1) conductivity ratio served to reflect the thermo-potential distribution of its equivalent GBG [53]. GBG profiles for other unequal liquid–solid thermal conductivities were computed by identical numerical methods, from which the theoretical profile for a 4:1 thermal conductivity profile was calculated, and later employed by Hardy [50], to determine the solid–liquid interface energy surrounding the rhombohedral c-axis of pure water ice.
Additional features attending strong anisotropy of the solid–liquid interfacial energy density on GBGs were analyzed by Voorhees et al. [54]. More recently, the influence of weak anisotropy on the dynamic stability of GBGs was studied experimentally by Wang et al. [39]. The capillary-mediated fields calculated later in “Capillary flux divergence” section, and then confirmed numerically using phase-field simulations in “Thermo-potentials on analytic profiles and phase-field isolines” section, also explain the observations of Wang et al. of how GBGs when set into motion affect interface stability.
The goals in the present study, however, remain: (1) to calculate capillary-mediated bias fields expected on equilibrated GBGs with variational profiles, and (2) establish the existence of interface energy fields independently as thermodynamic entities on simulated GBGs. Both tasks are accomplished more easily by studying isotropic GBGs: the first with variational profiles, and the second with simulated phase-field equilibrated GBGs.
Variational GBGs
Bolling and Tiller [42] solved the Euler–Lagrange equation [41] for the energy functional of a stationary GBG subject to flat (zero curvature) end-point conditions as \(\mu \rightarrow \pm\, \infty \), and \(\eta \rightarrow 0\). Details for constructing this functional may be found in [43].
The profile, \(\mu (\eta ;{{\varPsi }})\), for an isotropic GBG in \({\mathbb {R}}^2\), with arbitrary dihedral angle \({{\varPsi }}\in [ 0,\pi ]\) at its triple junction, \(\mu =0,\ \eta ^{\star }=\eta ({{\varPsi }})\), may be generalized as,
where the minus sign in Eq. (5) denotes the groove’s right-side profile, \(\mu \in [0,\infty )\), and the plus sign denotes its left-side profile, \(\mu \in (-\infty ,0]\). See again Fig. 1. Cartesian coordinates used in Eq. (5) are \(\mu =x/2{{\varLambda }}\) and \(\eta =y/2{{\varLambda }}\), where x and y are the groove’s physical coordinates, and \({{\varLambda }}\) is the thermo-capillary length that scales physical lengths into dimensionless numbers. The characteristic thermo-capillary length, \({{\varLambda }}\), of a variational GBG, which has a distribution of curvature, is defined from its Euler–Lagrange differential equation as
where the SI units for the quantities appearing in the thermo-capillary length, Eq. (6), are \(\gamma _{s\ell }\) (\({\hbox {J}}\,{\hbox {m}}^{-2}\)) ; \(\varOmega \) (\({\hbox {m}}^3\,{\hbox {mol}}^{-1}\)); T (K); G (\({\hbox {K}}\,{\hbox {m}}^{-1}\)); and \({\Delta {H}}_f\) (\({\hbox {J}}\,{\hbox {mol}}^{-1}\)).
The lower limit (dimensionless cusp depth) of a GBG’s vertical coordinate occurs at the groove’s triple junction, \(\eta ^{\star }({\varPsi })\), where maximum curvature and supercooling coexist,
In accord with Eq. (7), the maximum melt depth allowed for a variational GBG occurs when its dihedral angle \({\varPsi }\rightarrow 0\), and its cusp depth is \(\eta ^{\star }_{\mathrm{max}}=-\sqrt{2}/2.\) The cusp depth decreases as the groove’s dihedral angle increases, and becomes zero when \({\varPsi }\rightarrow \pi \). See again Fig. 2.
Thermodynamic properties of variational GBGs
Thermo-potential and interface curvature
A convenient thermo-potential, \(\vartheta (\eta (\mu );{\varPsi })\), may be defined along the curved solid–liquid interface of a GBG constrained by a uniform thermal gradient of magnitude G, pointing along the vertical \(\eta \)-axis. The location of the system’s melting point isotherm, \(T_{\mathrm{int}}=T_{\mathrm{m}}\), occurs as \(\eta \rightarrow 0\), where its local dimensionless thermo-potential is also set equal to zero, so \(\vartheta (\eta (\mu );{\varPsi })=0\) as \(\mu \rightarrow \pm \infty \).
In accord with its definition, the thermo-potential for the solid–liquid interfaces of GBGs [43] is
The thermo-potential represented by Eq. (8) is a scalar field easily extended throughout the rest of \({\mathbb {R}}^2\), i.e., beyond the \(\eta \)-range specified above for the location of the GBG’s solid–liquid interface. Replacing interfacial temperature, \(T_{\mathrm{int}}\), by the phase temperature, \(T_i(\mu ,\eta )\) (\(i=s,\ell \)), anywhere not occupied by the variational GBG, allows the extended thermo-potential to specify where stable melt (\(\ell \)) exists for a pure substance with melting point, \(T_{\mathrm{m}}\), namely where \(\vartheta (\eta )\ge 0\), and where stable solid (s) exists, namely \(\vartheta (\eta )\le 0\). See again Fig. 1.
Curvature of the solid–liquid interface, \(\kappa (y(x))\), at constant pressure, results in small shifts in the equilibrium thermo-potential. These shifts allow the thermodynamic activities of curved solid and its contacting liquid phase to match along a GBG’s curving solid–liquid interface. Specifically, convex interfaces (\(\kappa >0\)), where the outward normal vector points toward the liquid phase, have equilibrium temperatures slightly below the melting point of a flat interface (\(<\,T_{\mathrm{m}}\)), whereas concave interfaces (\(\kappa <0\)) have equilibrium temperatures elevated slightly (\(>\,T_{\mathrm{m}}\)).
The Gibbs–Thomson relationship [12] links the equilibrium thermo-potential, defined in Eq. (8), to a groove’s dimensionless curvature, defined here as \(\hat{\kappa }(\eta (\mu ))\equiv {2{\varLambda }\times \kappa (y(x))}\). One finds that this thermo-potential and the dimensionless interfacial curvature are related as
Curly brackets in Eq. (9) delineate the standard (dimensional) Gibbs–Thomson relationship in 2D [12]. The pre-factors \((\frac{2}{G{\varLambda }})\) (1/K) convert curvature-shifted equilibrium temperatures to non-dimensional thermo-potentials, appropriate for variational GBGs of size \({\varLambda }\), embedded in a thermal gradient G.
After rearranging terms on the right-hand side of Eq. (9), substituting the parametric definition given in Eq. (6) for \({\varLambda }^2\), and simplifying, one finds that the thermo-potential equals minus the interface’s dimensionless curvature,
The right-hand side of Eq. (10) can be evaluated by applying the standard Cartesian relationship for in-plane curvature, Eq. (11), middle expression.
Substituting the first and second derivatives derived for the profile of a variational GBG from Eq. (5), and simplifying the resulting expression, yields its interfacial curvature, which is linear with depth, Eq. (11), right-hand expression [43],
Equations (10) and (11) show that for any isotropic variational GBG, linear relationships hold among its thermo-potential, \(\vartheta (\eta (\mu );{\varPsi })\), dimensionless interface curvature, \(\hat{\kappa }(\eta (\mu ))\), and depth coordinate, \(\eta \), viz.,
Tangential interface gradients
A consequence of the scalar potential distribution, Eq. (12), along the solid–liquid interface of a variational GBG is the unavoidable appearance of a vector gradient field directed tangentially along its solid–liquid interface. The vector operator, \({\varvec{\nabla} }_{\tau }[\ \ ]\), for the tangential gradient in 2D is obtained by applying the chain rule to differentiate the GBG’s thermo-potential distribution, \(\vartheta (\eta (\mu ))\), with respect to its dimensionless arc length, \(\hat{s}\).Footnote 4 Dimensionless arc length is scaled similarly with the groove’s thermo-capillary length, \(2{\varLambda }\). The tangential, or arc-length, gradient may be found by applying the vector sequence,
The unit tangent vector, \({\varvec{\tau }}\), introduced into Eq. (13), points anticlockwise along both halves of the GBG profile, with solid on its left and liquid on its right. This interface vector defines the positive arc-length direction. The sign of the arc-length derivativesFootnote 5 that appear in definition (13) reflects the derivatives, \({\mathrm{d}}\eta /{\mathrm{d}}\hat{s}\), taken along the groove’s left and right profiles, per equations (5), which reverse sign when crossing the GBG’s triple junction,
The chain rule sequence for calculating tangential gradients of the Gibbs–Thomson thermo-potential along the left and right branches of a variational groove profile reduces to a pair of dimensionless quadratic expressions,
Capillary-mediated energy fluxes
Difficulties encountered specifying temperatures on surfaces and interfaces are briefly included in [55], and higher-order heat conduction phenomena near fast-moving solid–liquid phase boundaries are discussed by Serdyukov [56]. Superficial thermal gradients and heat fluxes on heterophase interfaces, as considered in this study, are, however, rarely addressed, as these gradients involve extremely small temperature differences mediated by capillarity, which vary spatially over mesoscopic distances along curved interfaces. So, when capillarity is present, irrespective of whether an interface is considered sharp—i.e., having zero thickness, or, more realistically, slightly diffuse—field theory shows that thermo-potential gradients develop as a necessary condition for the transport of thermal and mass fluxes from higher potential (flatter or concave areas) toward regions of lower potential (curved convex areas). The sufficient condition required for the appearance of capillary-mediated fluxes is that the interface have nonzero transport numbers for heat and mass flow.
Interfacial transport of capillary-mediated energy is analogous to another well-studied fourth-order phenomenon: viz., species diffusion along interfaces and free surfaces in response to superficial gradients of the chemical potential [57]. In fact, surface diffusivities and interfacial thermal conductances are always expected to be nonzero, especially at temperatures near \(T_{\mathrm{m}}\), appropriate to solid–liquid interfaces. Indeed, Mullis was able to compute interfacial fluxes near the tip region of 2D dendritic crystals with a noise-suppressed fourth-order accurate phase-field model [58]. Mullis’s flux data closely matched the capillary-mediated fluxes calculated for an appropriately scaled parabolic solid–liquid interface [5].
A phenomenon studied in reasonable depth and closely connected with capillary-mediated interfacial heat conduction is Bénard–Marangoni hydrodynamic flow. This thermo-mechanical phenomenon is associated with free fluid surfaces subject to tangential temperature gradients [59]. Bénard–Marangoni flows are usually driven by large thermal gradients that directly affect a fluid’s surface tension, inducing stress gradients and surface flow. Interface heat conduction via capillarity in solid–liquid systems, as explained in “Capillary flux divergence” section, arises instead through an indirect effect of small capillary-induced gradients of the Gibbs–Thomson potential.
Fourier’s law
Fourier’s law of heat conduction relates heat fluxes to their associated thermal gradients and conductivities, irrespective of dimensionality. Specifically, a thermal flux directed along a 2D interface by tangential thermal gradients, \({\varvec{\phi}}_{\tau }(x,y){\varvec{\tau }}\), bears units of (\({\hbox {W}}\,{\hbox {m}}^{-1}\)). Its corresponding thermal conductivity, \(k_{\mathrm{int}}\), has physical units of (\({\hbox {W}}\,{\hbox {K}}^{-1}\)). The energy flux along a solid–liquid GBG with a variational profile is found by applying Fourier’s law [55]. The superficial gradient responsible for this flux is the tangential gradient of the GBG’s Gibbs-Thomson thermo-potential, Eq. (14).
Fourier’s law when dimensionalized via a GBG’s applied thermal gradient, G / 4 (K/m), yields a superficial energy flux,
Tangential energy fluxes are directed opposite to their arc-length gradients, Eq. (14). The corresponding dimensionless vector flux, \(\hat{{\varvec{\Phi }}}_{\tau }(\eta (\mu ))\), Eq. (16), is recaptured by scaling Eq. (15) with the system’s thermo-capillary rate constant, \({k_{\mathrm{int}}}G/4\) (\({\hbox {W}}\,{\hbox {m}}^{-1}\)).
The dimensionless tangential flux is plotted in Fig. 5 for GBGs with several different dihedral angles.
It is important to note that tangential capillary fluxes travel along curved solid–liquid interfaces, but do not directly alter, or influence, the interface’s local energy budget. What occurs instead is that the left and right groove profiles support opposing, i.e., negatively and positively directed fluxes along each half of the GBG. These fluxes finally meet at the triple junction, where their \(\mu \)-components cancel and their \(\eta \)-components add. The combined flux components enter the grain boundary as a persistent current of thermal energy. As they travel along the solid–liquid interface, however, these fluxes merely “pass through,” remaining orthogonal to the interface’s normal vector. Consequently, tangential fluxes do not account for any direct influence on a microstructure’s local energy budget.
Plot of capillary-mediated interface flux [Eq. (16)] predicted along the left and right profiles of a variational GBG. Opposing fluxes from the left and right profiles move along the interface and approach each other, traveling from the flatter regions of the GBG toward their common triple junctions. Triple junctions are each located at the intersections of the dashed lines, where the left and right fluxes for grooves with various dihedral angles combine, and their \(\eta \)-components enter the grain boundary
Although it might seem unusual that a stationary solid–liquid microstructure can spontaneously “absorb” a continuous stream of thermal energy and insert it into the perturbing grain boundary, one should recall that an equilibrated GBG is a steady-state microstructure that remains open to the passage of copious amounts of thermal energy moving down the applied thermal gradient, from the melt, through the interface, to its cooler solid. The thermal gradient constraining the stationary GBG, in a sense, also supports the much weaker tangential Gibbs–Thomson thermal gradients responsible for capillary-induced interfacial heat fluxes.
As shown next, it is the more subtle influence of the capillary flux’s vector divergence—not the energy flux itself—that causes energy removal to occur along a stationary solid–liquid interface that actively alters the local energy budget. Although the effect of capillary flux divergence is concentrated primarily in the steeper parts of the GBG’s cusp, it will also be shown that a persistent distribution of cooling occurs over the entire GBG microstructure.
Capillary flux divergence
As discussed thus far, the persistent capillary-mediated energy flux along the solid–liquid interface of a stationary GBG does not result in changes to its energy budget. Only indirect effects result through that flux’s vector divergence. The deeper explanation for this distinction lies in a fundamental difference between steady-state thermal fields developed within the bulk solid and liquid phases, and the capillary-mediated fields on and along the GBG’s interface separating these phases. Specifically, steady-state heat flow obeys Laplace’s equation—the fluxes for which are harmonic and non-divergent—whereas that restriction applies neither to the tangential flux driven by capillary gradients along a sharp interface, nor to capillary fluxes passing between equilibrated bulk phases separated by a thicker diffuse interface. Both of these situations instead obey Poisson’s equation. The difference between non-divergent “Laplace fluxes” and divergent “Poisson fluxes” explains the fundamental origin of pattern-forming perturbations on moving interfaces, and shape-altering fields on stationary GBGs.
This distinction, moreover, accounts for the presence of autogenous Poisson sources—i.e., bias fields—the significance of which has not been addressed in theories of microstructure dynamics and pattern formation. Poisson sources enter as higher-order contributions to both interfacial energy and mass balances, especially at smaller length scales where patterns initiate. They represent, in fact are identical to, the higher-order capillary-mediated energy rate that appears in the Leibniz–Reynolds energy balance, Eq. (1).
Thus, heterophase interfaces support capillary thermo-potentials, the spatial distribution of which is governed by Poisson’s equation [60], namely
where \({\mathfrak {B}}(\eta (\mu );{\varPsi })\) is the bias-field rate, or Poisson source strength. The left-hand side of Eq. (17) shows that scalar bias fields in 2D are surface Laplacians of the Gibbs–Thomson thermo-potential, or, equivalently, (minus) the vector \({\varvec{\tau }}\)-divergence of the capillary-mediated tangential flux,
Bias fields on equilibrated GBGs
Stationary microstructures, such as GBGs interacting with their own interface fields, provide unique opportunities to generate and study persistent capillary fields. Upon equilibration with its applied thermal gradient, GBGs allow exposure and inspection of their equilibrated microstructure’s capillary fields and absent the complications that would normally accompany moving interfaces, such as time-dependent shape change, morphological instability, latent heat release, or species redistribution in the case of alloys.
The bias field in 2D may be determined analytically from its thermo-potential distribution by twice applying the chain rule for arc-length (\({\varvec{\tau}}\)) differentiation. The nested set of elementary operations represents the 2D (surface) Laplacian of the Gibbs–Thomson potential, \(\vartheta (\eta (\mu );{\varPsi })\), which defines (minus) the scalar bias field, \({\mathfrak {B}}(\eta (\mu );{\varPsi })\),
The operational sequence shown in Eq. (19), when applied to the equilibrium thermo-potential on a variational GBG, Eq. (12), yields a cubic expression for the field resident along its solid–liquid interface,
Such capillary-mediated energy sources—according to thermodynamics and field theory—should exist on real GBGs equilibrated in a fixed thermal gradient, or, as to be demonstrated next, on GBGs simulated in a thermodynamically consistent manner with a phase-field model.
An example of what has been observed experimentally using an equilibrated GBG is captured in the photomicrograph, Fig. 3. This microstructure developed by maintaining a GBG for several hours in a uniform thermal gradient in a high-precision, temporally stable thermostat. The supercooling developed at its triple junction is extremely small, less than 1 mK, which reflects the large radii of curvature even deep within the GBG’s cusp region—a result of its relatively small constraining thermal gradient of only \(4\ {\hbox {K}}/{\hbox {m}}\) [48].
Theoretical profile points added to Fig. 3 were calculated from Eq. (5), noting its near-zero dihedral angle, and calculating its characteristic thermo-capillary length, \({\varLambda }=1.18\times 10^{-4}\) (m). The thermo-capillary length, \({\varLambda }\), was determined from the GBG’s cusp depth, \(y^{\star }=1.67\times 10^{-4}\) (m), which corresponds to the dimensionless location of its triple junction at \(\eta ^{\star }=-\sqrt{2}/2\). At the scale and resolution of this micrograph, one is unable to detect discernible differences in the equilibrated interface shape from the one predicted using the variational profile formula.
Now, whether or not an active bias field is present on such a stationary solid–liquid interface after equilibration and whether or not higher-order GBG profile changes are induced by the bias field interacting with its own microstructure are the issues next addressed.
Bias-field distributions
The bias field, \({\mathfrak {B}}(\eta (\mu );{\varPsi })\), Eq. (20), predicts rates of capillary-mediated energy withdrawn at the interface at any cusp depth \(\eta \) for different dihedral angles, \({\varPsi }\). The associated energy rate distributions, \({\mathfrak {B}}(\mu (\eta );{\varPsi })\), are easily calculated from \({\mathfrak {B}}(\eta (\mu );{\varPsi })\) by cross-plotting Eq. (20) against the variational profile \(\mu (\eta ;{\varPsi })\), Eq. (5). The plots in Fig. 6 display energy removal rates over the right-hand half interface of GBG’s with various variational profiles.
Each such distribution indicates the presence along the solid–liquid interface of varying amounts of steady-state cooling, because the energy rates—which are negative over all interface points—represent positive flux divergences. This shows, counterintuitively, that GBGs, even at rest, withdraw persistent streams of thermal energy from the surrounding phases that slightly cool the entire interface. The cooling imposed by these bias fields is strongest along the solid–liquid interface itself, where energy is removed.
Theoretical energy extraction rates, \({\mathfrak {B}}(\mu (\eta ))\), along the right half of symmetric GBGs, calculated for various dihedral angles, \({\varPsi }\). Mirror-image curves exist for the left half, \(\mu \le 0\). All bias-field distributions show that \({\mathfrak {B}}(\mu )\le 0\), so that grooves are cooled by energy removal along their profiles. Where \(0\le {\varPsi }\le 83.6^{\circ }\), cooling curves exhibit smooth extrema that locate where maximum cooling rates occur at \(\mu \ge 0\). Where \({\varPsi }>83.6^{\circ }\), the point of maximum cooling rate is always located at \(\mu =0\) and occurs at cusped minima that steadily diminish in their peak intensity as \({\varPsi }\) increases to \(180^{\circ }\)
Cooling distributions are uniquely determined by a GBG’s dihedral angle, with the highest rates of energy adsorption occurring well within their cusps either near, or at, their triple junction. Curiously, GBGs exhibit capillary-mediated cooling without any heated regions. This behavior differs markedly from capillary-mediated energy distributions examined previously for other interfacial profiles, where both cooling and heating were found in all cases [14]. Specifically, previous studies of capillary energy fields included the following interfacial forms: (1) closed conic sections, such as the circle and ellipses; (2) protuberant “open profiles,” such as the parabola and hyperbolas [5]; and (3) several transcendental shapes, such as the cellular forms of Saffman–Taylor “fingers”. You et al. recently examined the stability and pattern-formation dynamics on phase-field simulated periodic Saffman–Taylor cells and found quantitative agreement confirming their dynamic simulations of cellular growth with a bias-field analysis for tip stability of the same shape [61, 62].
Phase-field simulations
Diffuse and sharp interfaces
Simulations of capillary-mediated energy fields were accomplished in the present study using a thermodynamically consistent multiphase-field model based on an entropy density functional [63]. In diffuse-interface simulations that employ the phase-field method, initial and boundary conditions are specified and the evolution of far-from-equilibrium microstructures are usually computed. In this study, grain boundaries with prescribed orientation and energy densities intersected initially with planar solid–liquid interfaces. These simulations evolved constrained states over many time steps, as the simulated GBGs relaxed within their thermal gradient field to yield their steady-state equilibrated microstructures.
Figure 7 portrays major aspects of the equilibration sequence leading to simulation of each equilibrated GBG microstructure studied. The starting configuration shows the grain boundary (dashed vertical line) separating crystals 1 and 2, intersecting with the GBG’s left and right solid–liquid interfaces, all of which are smooth, slightly diffuse borders separating crystals 1 and 2 and their melt. The ratio of the grain boundary energy to solid–liquid energy selected for this particular sequence produced at equilibrium a dihedral angle of \({\varPsi }=120^{\circ }\).
Images and isotherm sequences observed simulating an equilibrated diffuse-interface GBG. a Starting configuration. Three diffuse interfaces (crystal-1/melt, crystal-2/melt, crystal-1/crystal-2) begin relaxation. b Early equilibration of the thermal field displayed as gray-scale isotherms and (black) orthogonal lines of heat flow. c Late equilibration. Isotherm deflection in the melt spreads further from the triple junction located at \(1000{\Delta {X}}\), as evidence of interface cooling. d Diffuse GBG in its multiphase-field computational domain, \(2000{\Delta {X}}\) by \( 400{\Delta {Y}}\)
- (a):
-
Early in the equilibration process, the observed thermal field displays a grid of isotherms with orthogonal lines of heat flow that already suggest cooling of the melt within the groove cusp. Interface cooling causes upward deflection of the isotherms within the melt accompanied by bending, or “focusing,” of the lines of heat flow. The “jump,” or discontinuity, displayed by the thermal gradient is predicted by Eq. (4) and indicative of the presence of an active, persistent interface energy field.
- (b):
-
Several hundred thousand time steps later, isotherm deflection from interface cooling has spread further away from the triple junction, and inward bending of the heat flow lines is noticeable within the outermost five lines.
- (c):
-
Steady-state equilibration is eventually achieved after hundreds of thousands of numerical time steps, each one iteratively calculated by solving phase-field Eqs. (26) and (27).
- (d):
-
The phase image forms an equilibrated GBG consisting of a light gray region, the melt; a medium gray area, crystal 1, which forms a grain boundary with the dark gray area, crystal 2. All “interfaces” are, in fact, slightly diffuse: light gray/medium gray and light gray/dark gray borders represent smooth transition of the multiphase-field variables. Thermo-potentials are measured post-processing along the solid-to-liquid isolines given by an average value of the phase-field order parameters corresponding to phases that are in contact.
In accepting this procedure to confirm the existence of interfacial bias fields resident on simulated GBGs, one notes that phase-field models numerically solve coupled partial differential equations that characterize the dynamic behavior of diffuse heterophase interfaces with time-evolved continuous phase indicators. Phase-field models, moreover—and this is important—are not coded with any explicit physics that admit autogenous capillary fields. In fact, quite to the contrary, bias fields were originally discovered by combining analytic constructs based on sharp-interface thermodynamics, omnimetric energy conservation, and classic field theory [5]. Bias-field theory (for sharp interfaces) and phase-field numerics (for diffuse interfaces) develop their respective thermodynamic descriptions of interfacial energetics using independent mathematical and physical approaches that avoid tautologies or hidden circularity between them; they are each consistent descriptions, applicable to different physical limits that describe the nature of equilibrated solid–liquid interfaces.
Notable consistency will be shown between independent approaches predicting interfacial behavior for stationary microstructures that captures the essentials of our findings: viz., phase-field equilibrated GBGs harbor active capillary energy fields equivalent to bias fields, which were predicted previously with sharp-interface thermodynamics and field theory.
Detecting interfacial energy fields
Potential change and energy rate
Variational GBGs, as discussed in “Variational grooves” section, lack interfacial energy fields. If the interface of an equilibrated groove did not support an active interface energy field, then its thermo-potential distribution would remain linear with its depth coordinate, as already shown with Eq. (12) for variational GBGs. If, however, capillary-mediated energy fields do persist along equilibrated GBGs, then their presence should modify the distribution of their thermo-potentials. Detecting small nonlinear departures of nearly linear interface thermo-potential distributions remains the central challenge in making phase-field measurements capable of uncovering the existence of capillary fields on GBGs, and determining distributions of their energy rates.
Specifically, the steady distribution of cooling found along a GBG’s solid–liquid interface, predicted by Eq. (20) and displayed in Fig. 6, should add a small nonlinear component to the GBG’s otherwise linear thermo-potential distribution. Particularly useful is the fact that, at steady-state, the nonlinear additions to the thermo-potential are locally proportional to the rate of thermal energy added to, or removed from, the interface. That is, if the interface were cooled, its thermo-potential would be lowered in proportion to the cooling rate. If, instead, the interface were heated locally, then its potential at that location would rise by an amount proportionate to the heating rate. Lastly, if the interface were lacking a bias field, then its potential distribution would remain linear with depth.
This proportional linkage between the energy rate steadily added or removed on an interface, \(\delta \dot{Q}\), and the resulting steady-state change in local temperature, \(\delta {T}\), is based on a first-order variation between conjugate state variables: viz., between entropy, S, and temperature T, the product of which is energy. The resulting “calorimetric” relationship at steady state provides the proportionality expected at constant pressureFootnote 6 between small changes in temperature and the associated energy rate. Thus, in an open steady-state system at constant pressure, \(\delta \dot{Q}\propto \delta {T}\), indicating that capillary-mediated interface energy rates are precisely proportional to the changes they induce in the local interface temperature, or thermo-potential.
Finally, the steady-state relationship between interfacial energy rate and local interface thermo-potential, to be simulated in “Phase-field model and results” section, also possesses a mathematical foundation derived from scalar potential theory. The strengths of point sinks, or sources, of energy (or any other extensive quantity) released along boundaries may be represented mathematically as line integrals of their Green’s function distributions [18]. Some specific examples are discussed in [16] of this proportionate response for both instantaneous and continuous diffusion or conduction sources, where Green’s functions are distributed along planar and circular boundaries in different spatial settings. Those cited examples also demonstrate that steady-state source rates of extensive quantities induce, respectively, proportionate changes on a boundary’s conjugate intensive parameters.
Exposure and measurement of interface fields
Phase-field simulations were carried out to probe the solid–liquid interfaces of GBGs, which upon full equilibration in a steady thermal gradient should spontaneously develop active interface energy fields. The opportunity to equilibrate a stationary microstructure presents a novel opportunity for using phase field to verify interface behavior consistent with predictions for sharp interfaces. Capillary-mediated energy fields were exposed as thermo-potential “residuals” and measured in situ along the phase-field isoline of a simulated GBG’s solid–liquid interface. The method revealing these interfacial perturbations is explained next.
Phase-field model and results
Multiphase-field model
We employed the following entropy density functional for multiphase-field computations [63] applied to thermal grain boundary grooving,
This phase-field model ensures consistency with respect to classical irreversible thermodynamics. The bulk entropy density, \(s(e,\phi )\), depends on the internal energy density, e, where \(\phi =\left( \phi _{\alpha }\right) _{\alpha =1}^{N}\) is a vector of phase-field variables that lies in the \(N-1\) dimensional plane. N, in general, represents the total number of grains and phases. In the present simulations, we identified three phase fields to represent crystal-1 (\(\phi _1\)), crystal-2 (\(\phi _2\))—i.e., the two grains separated symmetrically by the grain boundary—and their common pure melt phase (\(\phi _3\)), all configured as the equilibrated GBG in Fig. 7d.
The functions \({a}\left( \phi ,\nabla \phi \right) \) and \({w}\left( \phi \right) \) represent the gradient energy density and multi-obstacle potential, respectively; \(\epsilon \) is a small length scale parameter related to the thickness of the simulated diffuse interface, and V represents the domain volume [63, 65]. The gradient energy density \(a\left( \phi ,\nabla \phi \right) \) is given by
where \(a_{\alpha \beta }\left( \phi ,\nabla \phi \right) \) defines the form of the surface energy anisotropy of the evolving phase boundary and \(\gamma _{\alpha \beta }\) is the surface free energy per unit area of the \(\alpha -\beta \) boundary which may additionally depend on the relative orientation of the interface. The vector quantity \({\mathbf {q}}_{\alpha \beta }=\phi _{\alpha }{\varvec{\nabla }}\phi _{\beta } -\phi _{\beta }{\varvec{\nabla }}\phi _{\alpha }\) is a generalized gradient vector normal to the \(\alpha -\beta \) interface. The surface energy of the \(\alpha -\beta \) phase boundary is chosen to be isotropic by assigning \(a_{\alpha \beta }=1.0\).
The multi-obstacle potential that accounts for multiple phase-field parameters is given by
where \(\displaystyle \sum = \left\{ \phi \;\vert \;\displaystyle \sum \nolimits _{\begin{array}{c} \alpha =1 \end{array}}^{N}\phi _{\alpha } = 1 \;{\mathrm {and}}\; \phi _{\alpha }\ge 0\right\} \). The higher-order term proportional to \(\phi _{\alpha }\phi _{\beta }\phi _{\delta }\) in function (23) is added to reduce the presence of unwanted third- or higher-order phases at binary interfaces. A methodology to calibrate the parameter \(\gamma _{\alpha \beta \delta }\) has previously been reported in the literature [63].
The pair of governing equations that account for energy conservation as a function of temperature, T, and the non-conserved phase-field variables, \(\phi _i\), is derived from the functional, Eq. (21), as
and
The quantities \({\delta {\mathcal {S}}}/{\delta {e}}\) and \({\delta {\mathcal {S}}}/{\delta {\phi }}\) are, respectively, variational derivatives of the entropy functional, \({\mathcal {S}}(\epsilon ,\phi )\), with respect to energy, e, and phase variable, \(\phi \). The parameter \({\mathcal {M}}\) denotes the mobility governing interface kinetics, whereas the mobility coefficient, \(L_{00}=kT^2\), is related to the system’s thermal conductivity, \(k\left( \phi \right) \), which is assumed to be equal for both phases. The choice of equal thermal conductivity for both phases, as explained in “Isotropic grain boundary grooves” section, is needed to compare phase-field measurements of an interfacial potential distribution with that for its variational GBG, the analytic profile for which, Eq. (5), depends on the assumption of equal thermal conductivities.
The internal energy density, e, is related to the molar latent heat, \({\Delta {H}}_f\), and constant specific heat \(c_{v}\), by the relationship \(e = -{\Delta {H}}_f\ h\left( \phi _{\alpha }\right) +c_{v}T\). The interpolation function \(h\left( \phi _{\alpha }\right) = \phi _{\alpha }^3\left( 6\phi _{\alpha }^2 -15\phi _{\alpha } +10\right) \) satisfies the constraints \(h(1) = 1\) and \(h(0) = 0\).
Evolution of the temperature field over the 2-D domain can be derived from Eq. (24), the energy equation, given that the variation of the phase energy, e, with respect to its entropy, \({\mathcal {S}}\), defines the thermodynamic temperature, T, of a pure material; thus, \({\delta {\mathcal {S}}}/{\delta {e}}=T^{-1}\). Substitution of the reciprocal temperature into Eq. (24) and then carrying out the gradient and divergence operations yield the temporal equation for the thermal field,
Here, \(\kappa _{\mathrm{th}} = k/c_{v}\) is the thermal diffusivity, and \({{\Delta {H}}_f}/{c_v}\) is the system’s characteristic adiabatic temperature. Equation (25) and the Legendre transform, \(e=f+Ts\), allow the kinetic equation for phase-field order parameters to be written as
where \(\lambda \) is a Lagrange parameter that maintains a unitary constraint on the sum of all local phase indicators, so that \(\sum _{\alpha =1}^N \phi _\alpha =1\), and the bulk free energy, \(f\left( T,\phi \right) \), is
The terms \({a,}_{\nabla \phi _{\alpha }}\); \({a,}_{\phi _{\alpha }}\); \({w,}_{\phi _{\alpha }}\); and \({f,}_{\phi _{\alpha }}\) each denote partial derivatives with respect to \({\nabla \phi _{\alpha }}\) and \({\phi _{\alpha }}\).
The phase-field model parameters described above were non-dimensionalized by selecting a capillary length scale, \(d_0 \equiv \gamma _{s\ell } T_{\mathrm{m}}c_v/{{\Delta {H}}_f}^2\) and a characteristic conduction time, \(t' \equiv {d_0}^2/k_{\mathrm{th}}\). In carrying out the numerical simulations, we chose dimensionless values for \(\kappa _{\mathrm{th}} = 0.1\) (again, assumed equal in both the crystals and their melt); \({{\Delta {H}}_f} = 1.0\); interfacial energy, \(\gamma _{s\ell } = 1.0\); interface mobility, \({\mathcal {M}} = 1.0\); and the melting temperature, \(T_{\mathrm{m}} = 0.99\).
Verification of three vertical scans of the thermo-potential distributions measured at three X-grid locations in the computational domain of an equilibrated GBG. (See again Fig. 7d.) All three scans of the thermo-potential appear to be linear in the Y-grid coordinate, but actually contain small nonlinear components of the thermo-potential, revealed as residuals by subtracting from the scanned measurements the value of the linear thermo-potential contributed by the applied thermal gradient, viz. \(|G|\times {{Y}}\)-grid. Residuals derived from these data are plotted in Fig. 9
The ratios of the grain boundary’s energy density to that of the crystal/melt boundary were selected to produce after steady-state equilibration a series of specific dihedral angles selected between \({\varPsi }=0\) and \(180^{\circ }\). Simulations started with either an initial configuration consisting of a flat crystal–melt interface intersected normally by a grain boundary, or, for greater computational efficiency, with a starting groove shape from a prior simulation run having a dihedral angle not too far from the new final value. Numerical iterations were extended well beyond the point where a desired equilibrium dihedral angle was initially achieved.
The following approach was adopted to assure that the evolved dihedral angle corresponds precisely to that predicted via Young’s force equilibrium and that each simulated groove profile was relaxed and fully equilibrated:
-
1.
We employed an explicit finite-difference scheme for iteratively solving Eqs. (26) and (27) in a 2D domain of grid size \(2000{\Delta {X}}\) by \(400{\Delta {Y}}\).
-
2.
We checked that the required steady 1-D thermal gradient, G, a linear temperature distribution, develops fully along the Y-grid, as shown for the three thermo-potential traces plotted in Fig. 8.
-
3.
We measured the dihedral angle at every time step [66]. After this angle converged to the expected \({\varPsi }\)-value, we continued equilibration for an additional \(10^4\) time steps, to rule out any chance of additional relaxation affecting the shape of the triple-junction region of the groove profile.
-
4.
We initialized the numerical domain with the equilibrated phase and thermo-potential fields corresponding to \({\varPsi } = 90^{\circ }\), \(120^{\circ }\), and \(180^{\circ }\), for subsequent simulations where the final angles were \({\varPsi } = 83.6^{\circ }\), \(150^{\circ }\), and \(165.5^{\circ }\), respectively. Adopting this strategy greatly reduced the time needed to attain full equilibration of the simulated GBG.
The number of grid points comprising the diffuse crystal–melt interface was far greater at highly curved regions in the cusp when compared to those where the crystal–melt boundary remained relatively flat. This disparity in the interface’s number of grid points reduced the accuracy of potential measurements over the flatter regions of the solid–liquid interface. To maintain sufficient accuracy everywhere along the interfacial isoline, \(\phi =0.5\), when extracting crystal–melt interfacial potentials, \(T_{\phi =0.5}\), we employed a numeric \(\phi \)-resolution range of \(\phi \in \left[ 0.499999,0.500001\right] \).
Recursion
The recursive task of extracting precise isoline thermo-potentials was achieved by scanning the groove’s computational domain and employing a numerical post-processing algorithm. An additional difficulty encountered with equilibrated isolated GBGs was that the radii of curvature of their solid–liquid isolines gradually approach extremely large values in the flattest regions close to the domain’s lateral edges. We found that for interface locations in the immediate vicinity of a groove’s triple point, the post-processing algorithm was capable of determining accurate isoline thermo-potentials that correspond to \(\phi = 0.5\). However, achieving precise potential measurements (\(T_{\phi =0.5}\)) proved more challenging along the flatter portions of the solid–liquid boundary, remote from the groove’s triple junction. This difficulty arose due to the narrowing of the diffuse interface when almost flat, a condition requiring far fewer boundary points to span the diffuse interface between the bulk phases. We then chose to perform a linear interpolation between \(T_{\phi _1}\) and \(T_{\phi _2}\) with \(T_{\phi _3}\) to estimate the thermal residuals more precisely, by requiring that the isoline \(\phi _{i}\ (i = 1,2)< {1/2} < {\phi _3}\).
Thermo-potentials on analytic profiles and phase-field isolines
Both the steady-state potential and curvature distributions along the analytic profile of a variational GBG, which has zero thickness, are perfectly linear in the variable \(\eta \). See again Eqs. (8) and (12). Therefore, if one were to subtract the value of the constraining (embedded) linear potential, \(4\times \eta \), from the interface thermo-potential of a variational GBG, \(\vartheta ({\eta }(\mu );{\varPsi })\), one would obtain a trivial null residual: \(\vartheta ({\eta }(\mu );{\varPsi })-4\eta =0\).
Now contrast what happens upon simulating a GBG subjected to phase-field equilibration, where superficial gradients of the Gibbs–Thomson interface potential appear and stimulate a divergent tangential flux. An interfacial energy sink, \({B(Y(X))}<0\), is created, by virtue of which the thermo-potential distribution along the microstructure’s isoline, \(\phi =0.5\), is slightly, and non-linearly, depressed from its linear “variational” form. Depression of the linear thermo-potential is linked to the fact that, as explained in “Potential change and energy rate” section, thermodynamics and heat conduction theory show that the expected change in temperature, or thermo-potential, caused by an interface sink of energy is proportional to its corresponding rate of energy withdrawal, B(Y(X)).
Consequently, the residuals, \({\mathfrak {R}}{(Y(X))} \equiv {T}_{\phi =0.5}-G{\times {Y(X)}}\), calculated along the interfacial isoline, \(\phi =0.5\), equal the interfacial energy rate, B(Y(X)) times a ratio, \({\xi }\), that proportions the shifts in thermo-potential (residuals) with their local capillary-mediated energy rates along the isoline. Thus, one obtains the relationship \({\mathfrak {R}}{(Y(X))}=T_{\phi =0.5}-G\times {{Y(X)}}= {B(Y(X))}\times \xi \).
Moreover, if the magnitude of the simulated 1-D gradient, G, was fixed, the value of the ratio \({\xi }\) also remained constant for other dihedral angles. Thus, the ratio, \(\xi \), found between the bias field cooling distributions and the residuals remained constant for all groove profiles tested, as shown in Fig. 9.
Comparison between phase-field residual measurements (data points, right ordinate) and analytical cooling rate distributions, \({\mathfrak {B}}(\mu (\eta );{\varPsi })\), (curves, left ordinate) for isotropic GBGs with different dihedral angles, \({\varPsi }\). All graphs were constructed using an ordinate ratio of \(2.0\times 10^4\) between residuals data and their corresponding field curves. An abscissa scale ratio of 400:1 is used to connect the phase field’s computational \({\Delta {X}}\)-grid (lower abscissa) with the non-dimensional \(\mu \)-scale (upper abscissa)
Also important, the energy distributions measured for each specified dihedral angle, \({B(X(Y);{\varPsi })}\), that develop along simulated phase-field isolines are congruent with the theoretical bias-field distributions, \({\mathfrak {B}}(\mu (\eta );{\varPsi })\), calculated from Eq. (20) and plotted in Fig. 6.
In fact, the implied equality itself, viz. \({\mathfrak {R}}{(Y(X))}= \xi \times {\mathfrak {B}}(\eta (\mu );{\varPsi })\), supported by these measurements is slightly imperfect, because it ignores higher-order differences existing between the analytic shapes of variational profiles, viz. Eq. (5), and the simulated phase-field isolines. The shapes of equilibrated GBGs are modified slightly by self-interaction with their capillary fields: (1) their local interface curvatures increase slightly from the additional interface cooling, and, consequently, (2) their cusp depths decrease slightly. The combination of increased curvature and decreased cusp depth allows the total rotation of a GBG’s normal angle between the triple junction and flat interfacial regions to remain constant at \({\varPsi /2}\), as required (in 2D) by topology.
Conclusions
-
1.
Application of the Leibniz–Reynolds transport theorem shows that Stefan balances at solid–liquid interfaces—which exclude capillarity—do not satisfy omnimetric energy balance. Stefan balances lack higher-order capillary-mediated terms needed to satisfy energy conservation on mesoscopic scales.
-
2.
Previous studies showed that capillary-mediated interface fields are capable of stimulating complex pattern formation on moving interfaces in low-noise environments [5]. The present study shows that stationary GBG microstructures support fields that cool their interfaces, allowing their measurement via multiphase-field simulations.
-
3.
Isotropic GBGs provide well-studied examples of stable microstructures that remain in thermodynamic equilibrium in the presence of steady thermal gradients. GBG profiles predicted from variational calculus are linear minimizers of the groove microstructure’s free energy and differ only slightly from simulated equilibrated GBGs that are nonlinear minimizers, because of self-interaction with their persistent interfacial energy fields.
-
4.
The distribution of interfacial energy rates on GBGs may be calculated from their variational profiles as surface Laplacians of their Gibbs–Thomson thermo-potential, or, equivalently, from (minus) the divergence of the tangential flux. Variational GBGs with isotropic solid–liquid energy density yield simple cubic expressions for their capillary energy fields.
-
5.
Multiphase-field simulations were performed on simulated GBGs with different dihedral angles to verify the existence of active capillary fields. Measurements of isoline thermo-potentials permit calculation of residuals by subtracting from the potentials the linear distribution imposed by the applied thermal gradient. Residuals are shown to be proportional to the time rate of the capillary energy field acting along the interface isoline.
-
6.
Phase-field residuals confirm, in every case tested, quantitative agreement with interfacial bias fields predicted from sharp-interface thermodynamics. Self-consistency and independence of simulated phase-field measurements and sharp-interface theory support the existence of bias fields on stationary crystal–melt interfaces in agreement with results found earlier for moving solid–liquid interfaces [5].
-
7.
The physical interface mechanism explored in this study shows that capillary-mediated fields provide perturbations capable of initiating diffusion-limited patterns. These include patterns in nature exhibited by snowflakes and crystallized mineral forms, as well as microstructures of cast alloys. Capillary-mediated interface fields might provide new approaches toward achieving improvements in solidification processing, welding, and crystal growth by control of microstructure at mesoscopic scales.
Notes
The term “bias field” is chosen for these thermodynamic fields, as they modulate, or bias, the local velocity on a moving interface to be slightly above or below the mean speed predicted by the Stefan condition.
Details of GBG functionals and the mathematics of “extremizing” their profiles via the Euler–Lagrange equation are available in Ref. [43].
Isotropy is approximated by some crystalline materials that exhibit weak variations (\(<1\%\)) of their crystal–melt interface energy, \(\gamma _{s\ell }\), around some particular crystallographic zone axis. For GBGs in BCC succinonitrile, an example of which is provided in Fig. 3, the fourfold anisotropic variation of the solid–liquid interfacial energy density is only \(\pm\, 0.5\)% around its three cubic [100] zone axes, with its mean value \({\gamma }_{s\ell }=(9.0\pm 1)\times 10^{-3} ({\hbox {J}}\,{\hbox {m}}^{-2}\)).
Arc length, \(\hat{s}\), increases as the unit tangent vector, \({\varvec{\tau }}\), advances anticlockwise along a GBG’s solid–liquid interface. The thermo-potential falls with increasing arc length along a GBG’s right profile, whereas this potential increases with increasing arc length along the left profile. Thus, the tangential gradient of a GBG’s thermo-potential switches from antiparallel to parallel with the local unit tangent vector and reverses sign when crossing its triple junction.
The derivatives \({\mathrm{d}}y/{\mathrm{d}}s={\mathrm{d}}\eta /{\mathrm{d}}\hat{s}\) are positive along the groove’s left profile and negative along its right profile. The depth coordinates, y or \(\eta \), become increasingly negative into the groove cusp. See Fig. 1.
See also Ref. [64], equation (4.42), and its discussion on pp. 52–55 that provide formal proportional relationships among heat content, enthalpy, and temperature changes in pure substances at constant pressure.
References
Thompson D (1948) On growth and form, 2nd edn. Cambridge University Press, Cambridge
Kassner K (1996) Pattern formation in diffusion-limited crystal growth. Directions in condensed matter physics. World Scientific Publ. Co., Ltd., Singapore
Turing A (1952) The chemical basis of morphogenesis. Philos Trans Roy Soc B 237:37–72
Warren B (1969) X-ray diffraction. Metallurgy and materials engineering. Addison-Wesley Pub. Co, Reading Reading Mass
Glicksman M (2016) Capillary-mediated interface perturbations: deterministic pattern formation. J Cryst Growth 450:119–139
Glicksman M (2012) Mechanism of dendritic branching. Metall Mater Trans A 43A:391–404
Langer J, Müller-Krumbhaar H (1978a) Theory of dendritic growth—I. elements of a stability analysis. Acta Metall 26:1681–1687
Langer J, Müller-Krumbhaar H (1978b) Theory of dendritic growth—II. Instabilities in the limit of vanishing surface tension. Acta Metall 26:1689–1695
Müller-Krumbhaar H, Langer J (1978) Theory of dendritic growth—III. Effects of surface tension. Acta Metall 26:1697–1708
Langer J (1980) Instabilities and pattern formation in crystal growth. Rev Mod Phys 52:1–28
Glicksman M, Lupulescu A, Koss M (2007) Capillary mediated melting of ellipsoidal needle crystals. In: Figueiredo I, Rodrigues J, Santos L (eds) Free boundary problems, international series in numerical mathematics, vol 154. Birkhäuser, Basel, pp 219–230
Glicksman ME (2011) Principles of solidification. Springer, New York
Glicksman M (2012) Capillary-mediated dendritic branching. IOP Conf Ser Mater Sci Eng 33:012097
Glicksman M (2015) Dendritic growth. In: Nishinaga T (ed) Handbook of crystal growth, 2nd edn. Elsevier, Boston, pp 669–722
Mullis A (2014) A phase-field model for the diffusive melting of isolated dendritic fragments. Metall Mater Trans A 45:3097–3102
Glicksman ME (2000) Diffusion in solids, field theory, solid-state principles, and applications. Interscience series. Wiley, New York
Leal L (1981) Advanced transport phenomena: fluid mechanics and convective transport processes. Cambridge University Press, New York
Kellogg O (1953) Foundations of potential theory. Dover Publications, New York, p 175
Stefan J (1889) Über einige probleme der theorie der wärmeleitung. Sitzer Wien Akad Math Naturw 98:473–484
Stefan J (1891) On the theory of formation of ice, in particular in the polar sea. Ann Physik Chemie 42:269–286
Lamé G, Clapeyron B (1831) Memoire sur la solidification par refroidissement d’un globe liquide. Ann Chim Phys 47:250–256
Schey H (1973) Div, grad, curl, and all that, an informal text on vector calculus. W.W.Norton & Co., New York
Gurtin M (1981) An introduction to continuum mechanics. Academic Press, New York
Alexiades V, Solomon A (1993) Mathematical modeling of melting and freezing processes. Ch.1. Hemisphere Publishing Corp., Washington, DC, p 21
Derby J, Yeckel A (2015) Heat transfer analysis and design for bulk crystal growth. In: Rudolph P (ed) Handbook of crystal growth, Ch. 20, 2nd edn. Elsevier, Amsterdam, p 808
Nash G, Glicksman M (1974) Capillarity-limited steady-state dendritic growth—II. Numerical results. Acta Metall 22:1291–1299
Xu JJ (2017) Interfacial wave theory of pattern formation in solidification. Springer series in synergetics (complexity), 2nd edn. Springer, Cham
Mullins W, Sekerka R (1963) Morphological stability of a particle growing by diffusion or heat flow. J Appl Phys 34:323
Mullins W, Sekerka R (1964) Stability of a planar interface during solidification of a dilute binary alloy. J Appl Phys 35:444
Voronkov V (1964) Conditions for formation of mosaic structure on a crystallization front. Sov Phys Solid State 6:2278
Wang L, Wang Z, Lin X, Wang M, Huang W (2012) The effect of interfacial energy anisotropy on planar interface instability in a succinonitrile alloy under a small temperature gradient. Chin Phys B 21:066801
Glicksman M, Vold C (1967) Observation of solidification and melting phenomena in metals using the electron microscope. Acta Metall 15:1409–1412
Glicksman M, Vold C (1969) Determination of absolute solid-liquid interfacial free energies in metals. Acta Metall 17:1–11
Glicksman M, Vold C (1972) Gradient hot-stage electron microscopy of binary metallic solid–liquid interfaces. J Cryst Growth 13–14:73–77
Vold C, Glicksman M (1972) Behavior of grain boundaries near the melting point. In: Hsu H (ed) The nature and behavior of grain boundaries. Plenum Press, New York, pp 171–183
Morris L, Winegard W (1969) The development of cells during the solidification of a dilute Pb–Sb alloy. J Cryst Growth 5:361–375
Schaefer R, Glicksman M (1970) Initiation of dendrites by crystal imperfections. Met Trans 1:1973–1978
Sharp R, Hellawell A (1970) Solute distributions at non-planar, solid–liquid growth fronts: II. Steady-state and transient conditions: no liquid stirring. J Cryst Growth 6:334–340
Wang L, Lin X, Wang Z, Huang W (2014) Orientation-dependent morphological stability of grain boundary groove. Chin Phys B 23:124702
Yeh S, Chen C, Lan C (2011) Phase field modeling of morphological instability near grain boundary during directional solidification of a binary alloy: the hump formation. J Cryst Growth 324:296–303
Weinstock R (1953) Calculus of variations. Dover books on advanced mathematics. Dover Publications, New York
Bolling G, Tiller W (1960) Growth from the melt. I. Influence of surface intersections in pure metals. J Appl Phys 31:1345
Glicksman M, Ankit K (2017) Detection of capillary-mediated energy fields on a grain boundary groove: solid–liquid interface perturbations. Metals 7:547
Huang SC, Glicksman M (1981a) Fundamentals of dendritic solidification: part I—steady-state tip growth. Acta Metall 29:701–716
Huang SC, Glicksman M (1981b) Fundamentals of dendritic solidification: part II—development of sidebranch structure. Acta Metall 29:717–734
Glicksman M, Voorhees P, Setzko R (1982) The triple-point equilibria of succinonitrile—its assessment as a temperature standard. In: Schooley JF (ed) Temperature, its measurement and control in science and industry, 5th edn. American Institute of Physics, New York, pp 321–326
Rubinstein E, Tirmizi S, Glicksman M (1990) Long-term purity assessment in succinonitrile. J Cryst Growth 106:89–96
Schaefer R, Glicksman M, Ayers J (1975) High-confidence measurement of solid/liquid surface energy in a pure material. Philos Mag 32:725–743
Jones D (1973) The measurement of solid–liquid interfacial energies from the shapes of grain-boundary grooves. Philos Mag 27:569
Hardy S (1977) A grain boundary groove measurement of the surface tension between ice and water. Philos Mag 35:471
Bayender B, Marasli N, Cadirli E, Sisman H, Gündüz M (1998) Solid–liquid surface energy of pivalic acid. J Cryst Growth 194:119–124
Bayender B, Marasli N, Cadirli E, Gündüz M (1999) Solid–liquid interfacial energy of camphene. Mater Sci Eng A 270:343–348
Nash G, Glicksman M (1971) A general method for determining solid–liquid interfacial free energies. Philos Mag 24:577
Voorhees P, Coriell S, McFadden G (1984) The effect of anisotropic crystal-melt surface tension on grain boundary groove morphology. J Cryst Growth 67:425–440
Carslaw H, Jaeger J (1959) Conduction of heat in solids, 2nd edn. Clarendon Press, Oxford, pp 17–19
Serdyukov S (2013) Higher order heat and mass transfer equations and their justification in extended irreversible thermodynamics. Theor Found Chem Eng 47:89–103
Antczak G, Ehrlich G (2007) Jump processes in surface diffusion. Surf Sci Rep 62:39–61
Mullis A (2015) Spontaneous deterministic side-branching behavior in phase-field simulations of equiaxed dendritic growth. J Appl Phys 117:114305
Basu A, Gianchandani Y (2008) Virtual microfluidic traps, filters, channels and pumps using Marangoni flows. J Micromech Microeng 18:115031
Jackson J (1999) Classical electrodynamics, 3rd edn. Wiley, New York
You J, Wang J, Li J, Wang J (2015) Tip-splitting instability in directional solidification based on bias field method. Chin Phys B 24:078107
Saffman P, Taylor G (1958) The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc R Soc Lond A 245:312–329
Nestler B, Garcke H, Stinner B (2005) Multicomponent alloy solidification: phase-field modeling and simulations. Phys Rev E 71:041609
DeHoff R (1953) Thermodynamics in materials science. Materials science and engineering series. McGraw-Hill Inc., New York
Stinner B, Nestler B, Garcke H (2004) A diffuse interface model for alloys with multiple components and phases. SIAM J Appl Math 64(3):775
Hötzer J, Tschukin O, Said M, Berghoff M, Jainta M, Barthelemy G, Smorchkov N, Schneider D, Selzer M, Nestler B (2016) Calibration of a multi-phase field model with quantitative angle measurement. J Mater Sci 51(4):1788–1797. https://doi.org/10.1007/s10853-015-9542-7
Acknowledgements
Authors acknowledge their preliminary discussions with Dr. Britta Nestler, Karlsruhe Institute of Technology, Institute of Applied Materials–Computational Materials Science, Germany. Author KA acknowledges support from the German Research Foundation (DFG) under Grant Number AN 1245/1-1.s and from the College of Engineering, Arizona State University. Author MEG gives special thanks for the Allen S. Henry endowed Chair of Engineering that provided financial support through the Florida Institute of Technology, Melbourne, Florida. Both authors thank the reviewer for several useful suggestions improving our manuscript and wish to express our heartfelt gratitude for the brave crew aboard shuttle Columbia, on flight STS-87, flown in November, 1997, one of whom, our IDGE Mission Specialist, Dr. Kalpana Chawla, perished when Columbia, upon reentering Earth’s atmosphere on February 1, 2003, was destroyed with the tragic loss of all its seven crew members.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflicts of interest. Sponsors had no role in the design of the study, or in the collection, analyses, or interpretation of data, or in the writing of the manuscript, and in the decision to publish the results.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Glicksman, M.E., Ankit, K. Measuring solid–liquid interfacial energy fields: diffusion-limited patterns. J Mater Sci 53, 10955–10978 (2018). https://doi.org/10.1007/s10853-018-2356-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10853-018-2356-7