A numerical study on anomalous behavior of piezoelectric response in functionally graded materials

Abstract

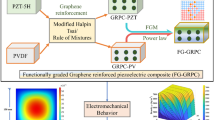
Finite element-based simulations have been performed on piezoelectric-based functionally graded materials (FGM). PZT (Lead zirconate titanate) and PVDF (Polyvinylidene fluoride) FGM composites have been investigated. Anomalous enhancement in output voltage has been observed at grading index n = 0.05 (Voltage = 210 V), which is 105 and 185% higher than the original material at n = 0 (PVDF) and n = ∞ (PZT), respectively. Further, role of Young’s modulus, dielectric constant, and piezoelectric constant was systematically investigated to understand this enhancement. It is found that performance of FGM not only relies on piezoelectric constants but also largely depends upon values of Young’s modulus and dielectric constant.

Appendix

To model the piezoelectric structure, finite element method has been used. For this study, script of finite element formulation has been written in MATLAB software. The 3D element has been chosen to discretize the piezoelectric cube. 3D element has three mechanical degrees of freedom (u, v, w) and one electrical degree of freedom (V).

In 3D solid element, any point coordinate (x, y, z) within the cube can be written as:

$$ \begin{aligned} x = \sum\limits_{i = 1}^{\text{nnel}} {N_{i} } x_{i} \hfill \\ y = \sum\limits_{i = 1}^{\text{nnel}} {N_{i} } y_{i} \hfill \\ z = \sum\limits_{i = 1}^{\text{nnel}} {N_{i} } z_{i} \hfill \\ \end{aligned} $$

(10)

where N _i is the shape function and nnel is number of node in element. x _i , y _i , and z _i are coordinates of the ith node of element.

Similarly, displacement and voltage field can be written as:

$$ \begin{aligned} u = \sum\limits_{i = 1}^{\text{nnel}} {N_{i} } u_{i} \hfill \\ v = \sum\limits_{i = 1}^{\text{nnel}} {N_{i} } v_{i} \hfill \\ w = \sum\limits_{i = 1}^{\text{nnel}} {N_{i} } w_{i} \hfill \\ V = \sum\limits_{i = 1}^{\text{nnel}} {N_{i} } V_{i} \hfill \\ \end{aligned} $$

(11)

u _i , v _i , and w _i are mechanical degrees of freedom and V is electrical degree of freedom in element at the node.

Strain and electrical field can be written as

$$ \begin{aligned} \left\{ \varepsilon \right\} = \left[ B \right]\left\{ q \right\} \hfill \\ \left\{ E \right\} = \left[ {B_{\phi } } \right]\left\{ \phi \right\} \hfill \\ \end{aligned} $$

(12)

$$ \begin{aligned} q = \left\{ {u_{1} \;v_{1} \;w_{1} \ldots u_{n} \;v_{n} \;w_{n} } \right\}^{T} \hfill \\ \phi = \left\{ {V_{1} \;V_{2} \; \ldots V_{n - 1} \;V_{n} } \right\}^{T} \hfill \\ \end{aligned} $$

$$ B = \left[ {\begin{array}{*{20}c} {\frac{{\partial N_{1} }}{\partial x}} & 0 & 0 & \cdots & {\frac{{\partial N_{n} }}{\partial x}} & 0 & 0 \\ 0 & {\frac{{\partial N_{1} }}{\partial y}} & 0 & \cdots & 0 & {\frac{{\partial N_{n} }}{\partial y}} & 0 \\ 0 & 0 & {\frac{{\partial N_{1} }}{\partial z}} & \cdots & 0 & 0 & {\frac{{\partial N_{n} }}{\partial z}} \\ 0 & {\frac{{\partial N_{1} }}{\partial z}} & {\frac{{\partial N_{1} }}{\partial y}} & \cdots & 0 & {\frac{{\partial N_{n} }}{\partial z}} & {\frac{{\partial N_{n} }}{\partial y}} \\ {\frac{{\partial N_{1} }}{\partial z}} & 0 & {\frac{{\partial N_{1} }}{\partial x}} & \cdots & {\frac{{\partial N_{n} }}{\partial z}} & 0 & {\frac{{\partial N_{n} }}{\partial x}} \\ {\frac{{\partial N_{1} }}{\partial y}} & {\frac{{\partial N_{1} }}{\partial x}} & 0 & \cdots & {\frac{{\partial N_{n} }}{\partial y}} & {\frac{{\partial N_{n} }}{\partial x}} & 0 \\ \end{array} } \right] $$

$$ B_{\phi } = \left[ {\begin{array}{*{20}c} {\frac{{\partial N_{1} }}{\partial x}} & {\frac{{\partial N_{2} }}{\partial x}} & \cdot & {\frac{{\partial N_{n} }}{\partial x}} \\ {\frac{{\partial N_{1} }}{\partial y}} & {\frac{{\partial N_{2} }}{\partial y}} & \cdot & {\frac{{\partial N_{n} }}{\partial y}} \\ {\frac{{\partial N_{1} }}{\partial z}} & {\frac{{\partial N_{2} }}{\partial z}} & \cdot & {\frac{{\partial N_{n} }}{\partial z}} \\ \end{array} } \right] $$

where n is total number of nodes.

Strain energy in element:

$$ S.E = \frac{1}{2}\int\limits_{\text{Volume}} {\varepsilon^{T} \sigma dV} $$

$$ S.E = \frac{1}{2}\int\limits_{V} {\left( {\left\{ q \right\}^{T} \left[ B \right]\left[ {C(z)} \right]\left[ B \right]\left\{ q \right\}} \right)dV} +\,\frac{1}{2}\int\limits_{V} {\left( {\left\{ q \right\}^{T} \left( {\left[ B \right]^{T} \left[ {e(z)} \right]^{T} \left[ {B_{\phi } } \right]} \right)\left\{ \phi \right\}} \right)dV} $$

$$ S.E = \frac{1}{2}\left[ {\left\{ q \right\}^{T} \left( {\left[ {K_{uu} } \right]} \right)\left\{ q \right\} + \left\{ q \right\}^{T} \left[ {K_{u\phi } } \right]\left\{ \phi \right\}} \right] $$

(13)

where

$$ K_{uu} = \int\limits_{V} {\left[ B \right]\left[ {C(z)} \right]\left[ B \right]dV} $$

$$ K_{u\phi } = \int\limits_{V} {\left[ B \right]^{T} \left[ {e(z)} \right]^{T} \left[ {B_{\phi } } \right]dV} $$

Electrical energy in element:

$$ E.E = \frac{1}{2}\int\limits_{V} {E^{T} DdV} $$

$$ E.E = \frac{1}{2}\int\limits_{V} {\left( {\phi \left\{ {B_{\phi } } \right\}^{T} \left[ {e(z)} \right]\left[ B \right]\left\{ q \right\} + \phi \left\{ {B_{\phi } } \right\}^{T} \left[ b \right]\left[ {B_{\phi } } \right]\phi } \right)dV} $$

$$ E.E = \frac{1}{2}\left\{ \phi \right\}^{T} \left[ {K_{\phi u} } \right]\left\{ q \right\} + \frac{1}{2}\left\{ \phi \right\}^{T} \left[ {K_{\phi \phi } } \right]\left\{ \phi \right\} $$

(14)

where

$$ \left[ {K_{\phi u} } \right] = \int\limits_{V} {\left\{ {B_{\phi } } \right\}^{T} \left[ {e(z)} \right]\left[ B \right]dV} $$

$$ \left[ {K_{\phi \phi } } \right] = \int\limits_{V} {\left\{ {B_{\phi } } \right\}^{T} \left[ {e(z)} \right]\left[ {B_{\phi } } \right]dV} $$

Kinetic energy in element:

$$ K.E = \frac{1}{2}\int\limits_{V} {\rho (z)\left\{ {\dot{q}} \right\}^{\rm T} \left\{ {\dot{q}} \right\}dV} $$

$$ K.E = \frac{1}{2}\left\{ {\dot{q}} \right\}^{T} \left[ M \right]\left\{ {\dot{q}} \right\} $$

(15)

where

$$ \left[ M \right] = \int\limits_{V} {\rho (z)\left[ N \right]^{T} \left[ N \right]} dV $$

N are the shape functions.

Total external work done on the element:

$$ W^{s} = \int\limits_{{S_{1} }} {\left\{ q \right\}^{T} \left\{ {f_{s} } \right\}ds + \left\{ q \right\}^{T} \left\{ {f_{p} } \right\} - \int\limits_{{S_{2} }} {\left\{ E \right\}^{T} \left\{ {f_{q} } \right\}ds} } $$

(16)

S ₁ = surface area on which external force is acting, S ₂ = surface area of piezoelectric layer where applied electric charge is acting, $\left\{ {f_{s} } \right\}$ = surface force intensity, $\left\{ {f_{p} } \right\}$ = point load, $\left\{ {f_{q} } \right\}$  = surface electrical charge density

$$ W^{s} = \left\{ q \right\}^{T} \left\{ {F_{m} } \right\} + \left\{ \phi \right\}^{T} \left\{ {F_{q} } \right\} $$

$$ \left\{ {F_{m} } \right\} = \int\limits_{S} {\left[ N \right]^{T} \left\{ {f_{S} } \right\}dS + \left[ N \right]^{T} \left\{ {f_{p} } \right\}} $$

$$ \left\{ Q \right\} = \int\limits_{{S_{2} }} {\left\{ {B_{\phi } } \right\}^{T} \left\{ {f_{q} } \right\}ds} $$

By using Hamilton’s principle as final equations can be written as

$$ \begin{aligned} \int\limits_{{t_{0} }}^{{t_{f} }} {\delta \left( {L + W^{s} } \right)dt = 0} \hfill \\ \begin{array}{*{20}c} {\text{where}} & {L = K.E - S.E + E.E} \\ \end{array} \hfill \\ \end{aligned} $$

Using Eqs. (13), (14), (15) and (16)

$$ \begin{aligned} \left[ M \right]\left\{ {\ddot{q}} \right\} + \left[ C \right]\left\{ {\dot{q}} \right\} + \left[ {K_{uu} } \right]\left\{ q \right\} + \left[ {K_{u\phi } } \right]\left\{ \phi \right\} = \left\{ {F_{m} } \right\} \hfill \\ \left[ {K_{\phi u} } \right]\left\{ q \right\} + \left[ {K_{\phi \phi } } \right]\left\{ \phi \right\} = \left\{ Q \right\} \hfill \\ \end{aligned} $$

In this study, static case has been considered which reduced the equation further by removing the dynamic force terms (inertia force and damping force)

$$ \begin{aligned} \left[ {K_{uu} } \right]\left\{ q \right\} + \left[ {K_{u\phi } } \right]\left\{ \phi \right\} = \left\{ {F_{m} } \right\} \hfill \\ \left[ {K_{\phi u} } \right]\left\{ q \right\} + \left[ {K_{\phi \phi } } \right]\left\{ \phi \right\} = \left\{ Q \right\} \hfill \\ \end{aligned} $$

As there is no external electrical force applied (Q = 0) final equation can be written as

$$ \begin{aligned} \left[ {K_{uu} } \right]\left\{ q \right\} + \left[ {K_{u\phi } } \right]\left\{ \phi \right\} = \left\{ {F_{m} } \right\} \hfill \\ \left[ {K_{\phi u} } \right]\left\{ q \right\} + \left[ {K_{\phi \phi } } \right]\left\{ \phi \right\} = 0 \hfill \\ \end{aligned} $$

Using these equations displacement and voltage can be calculated.