Abstract
Fe-doped Bi12MnO20–BiMn2O5 ceramics was sintered at 1130 K for 6 h in ambient air. Two centro-symmetric phases formed thermodynamically stable self-composite material that was deduced from X-ray pattern analysis. The lattice parameters were a = 10.147(8) Å—for the cubic I23 Bi12MnO20 phase; and a = 7.545(4) Å, b = 8.538(1) Å, c = 5.758(3) Å—for the orthorhombic Pbam BiMn2O5 phase. The 57Fe Mössbauer spectrum, recorded at room temperature, has shown pure electronic quadrupolar split. The major doublets reflected the occurrence of Fe3+ ions distributed in two sites, i.e., octahedral Fe4+O6 and square pyramidal Fe3+O5, with preferential occupation of the pyramidal sites, that was consistent with the Pbam phase symmetry. The third doublet resulted from the presence of iron Fe3+ in tetrahedral Fe3+O4 coordination and corresponded to a small admixture of the I23 phase. The DC resistivity ρ DC(T) dependence on temperature has shown thermally activated features, and the value of E a,DC varied in the range of 0.22–0.37 eV. The electric impedance was measured in the f = 20 Hz–1 MHz and 100–690 K range. Two electrical relaxations were determined using the electric modulus formalism M″(T). Low-temperature relaxation has shown the temperature-dependent activation energy E A,1 = 0.14–0.20 eV and characteristic time values of τ 01 = 10−10–10−12 s in 100–200 K range. It was attributed to the charge transfer between Mn4+/Mn3+ sites. The other relaxation occurred in the 170–220 K range, and it exhibited the following values: τ 02 = 10−11 s, and E A,2 = 0.27 eV. A disorder-related VRH polaron model was proposed for ρ DC(T) and for electric relaxation processes.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Introduction
In recent years, there has been an increasing interest in electromagnetic and electro-optic composite materials due to several promising potential applications in digital memory storage, spintronics, and a wide spectrum of sensor technologies [1]. A large family of oxides, which includes not only perovskites but also more complex structures, e.g., sillenites, has recently attracted interest due to their physical properties and technological applications [2, 3]. Sillenites exhibit various properties such as photorefractivity, photoconductivity, and enhanced velocity of ultrasound wave propagation, and such properties have potential applications. Sillenites, which contain tetrahedrally coordinated transition metal ions, e.g., Fe and Mn, offer tuning of electronic structure and photo-electronic features [4–6].
It is worth to notice that the phases with sillenites structure occur together with other binary phases in various, more complex systems. Manganites, which exhibit mixed Mn3+ and Mn4+ valence, attract attention due to their magnetic order, high electric permittivity, and possible magneto-electric coupling. The mixed valence can be obtained by deliberate doping with hetero-valence ions. The other opportunity originates from the structures, which contain non-equivalent crystallographic sites.
The synthesis of perovskite symmetry BiMnO3 samples demands high hydrostatic pressure at the sintering stage. When bismuth manganite ceramics is sintered at ambient air pressure, thermal decomposition occurs at ~900 K. The appearance of such meta-stable phases, which exhibit different crystallographic symmetries, has been related to structural defects and internal stresses. Therefore, polymorph forms, BiMnnOm, have been detected and discussed in literature [7, 8]. For instance, pure submicron BiMn2O5 particles have been obtained by means of hydrothermal method [9]. BiMn2O5 shows antiferromagnetic order below T Néel ~ 40 K [9–11].
When bismuth manganite ceramics is obtained by standard high-temperature sintering in ambient air pressure, the two-phase compound is crystallized. The analysis of X-ray powder diffraction data has shown that bismuth manganite ceramics exhibit, at room temperature, two centro-symmetric phases: the BiMn2O5 orthorhombic Pbam and sillenite Bi12MnO20 cubic I23 [12]. The BiMn2O5 phase remains in thermodynamic equilibrium with Bi12MnO20 phase [13–15]. BiMn2O5 has a structure, which contains octahedrally coordinated Mn4+ ions and Mn3+ ions located in square pyramids [16, 17], whereas Bi12MnO20 contains Mn4+O4 tetrahedrons.
Recently, the novel self-composite term was introduced to describe a material, whose elemental composition is not changed, whereas the local distribution of phases varies [18–20]. Therefore, the Bi12MnO20–BiMn2O5 compound, consisting of two stable phases, can be called a self-composite material.
Bi12MnO20 shows the energy gap of ~1.66 [6], which is wider than the BiMn2O5 energy gap: the calculated E gap = 1.03 eV and the indirect band gap of ~0.78 eV [21]. Impedance tests have shown marked dispersion of dielectric permittivity. The step-like anomaly in the low-temperature range corresponded to non-ferroelectric relaxation. The Bi12MnO20–BiMn2O5 compound shows small polaron mechanism of electric conductivity with activation energy value 0.4 eV [12, 22].
The mixed Mn3+ and Mn4+ valence in several bismuth manganite compounds was related not only to magnetic ordering but also to the small polaron mechanism of conductivity [9, 23]. Moreover, in case of increased structural disorder, the variable range hopping (VRH) of small polaron can manifest in low-temperature ranges [24–28].
Doping with Fe ions can serve as a probe for determination of the local crystal lattice symmetry or environment of the ions in the Fe/Mn sublattice. Such an approach is provided by the Mössbauer spectroscopy. In case of low level doping, <10 %, one can expect occurrence of increased disorder in the Fe-doped manganites, while the crystal lattice remains iso-structural with symmetry of the parent material [14, 29–33].
The aim of this work was to characterize structural and electrical features of Fe-doped Bi12MnO20–BiMn2O5 ceramics. We have chosen bismuth manganite ceramics doped with 5 wt% of Fe, which has been produced by standard high-temperature sintering, in the laboratory in Riga University. The sintering conditions were slightly different from those applied for pure Bi12MnO20–BiMn2O5 ceramics sintered formerly [12, 15]. Mössbauer spectroscopy could confirm the symmetry of the Fe ions environment and structural disorder, deduced from XRD analysis. Moreover, we tried to correlate the small polaron models of electric conduction and the presumed occurrence of electrical relaxation to the charge transfer and structural disorder related to the self-composite features.
Experimental details
Sintering
Fe-doped bismuth manganite ceramics was prepared by standard high-temperature dry sintering method. The chemicals from Aldrich were used: Bi2O3 (99.5 %), MnO2 (99.5 %), and Fe2O3 (purity 99.5 %). The Bi2O3 and MnO2 powders were weighed in accordance to chemical formula stoichiometry, and 5 % of Fe2O3 was added. The components were mixed in ethanol and homogenized in an agate ball-mill for 24 h. After drying at 400 K, they were calcined for 2 h. Then the calcined powders were ground, pressed under the pressure of 15 MPa at room temperature in the form of pellets having 8 mm in diameter, and sintered for 6 h at T S = 1130 K, in ambient air. The samples in form rectangular plates were cut off for electrical measurements. The powder samples were prepared for the XRD and Mössbauer tests. The powdered sample was additionally annealed and/or sintered at T A = 1130 K for 8 h in an open-tube quartz oven, to control the stability of the structure.
X-ray diffraction test
The powdered sample was studied using a powder diffractometer (Kristalloflex-4, SIEMENS), using filtered CuKα radiation (λ = 0.154056 nm; U = 25 kV; I = 15 mA) and the θ–θ scan technique. The diffraction pattern was collected in the 2θ range (20°–100°) with scan step of 0.02°, and the time count was 15 s for each point, at the room temperature of T ≈ 300 K. The intensity and position of each measured line were fitted using the least squares method, by means of the X-ray Reflection Profiler software [34]. The crystal structure refinement was performed with the Rietveld profile method using the FullProf software [35]. The occurrence of two phases, I23 (No. 197) and Pbam (No. 55), was checked for the powdered sample [12].
Dielectric impedance
Impedance was measured in f = 20 Hz–1 MHz and 100–690 K ranges. The samples—in the form the platelet capacitor, with Ag electrodes—were suspended on two silver wires. Electric capacitance C, conductance G, and resistance R DC were measured using a LCR metre (Wayne Kerr 4300). The DC electric resistance R DC was measured in 200–690 K range, at the measuring voltage of U DC = 1 V. The measurements were conducted on heating and cooling at the constant rate of 2 K min−1, using an Unipan 680 temperature controller. The results were analysed with the use of electric modulus formalism \( M^{*} \left( {T,f} \right) = \left( {\varepsilon^{*} } \right)^{ - 1} = M ^{\prime} + M^{\prime\prime} \), where ε *—dielectric permittivity; \( M ^{\prime},M^{\prime\prime} \)—real and imaginary part of electric modulus, respectively.
Mössbauer spectroscopy
The sample was ground into powder and prepared in the shape of a thin disc. The 57Fe Mössbauer spectrum was recorded at room temperature using a constant acceleration spectrometer with 57Co:Cr source, a multichannel analyser with 1024 channels and linear arrangement of the 57Co source, an absorber, and a detector. The values of isomer shifts (IS) and quadrupole splitting (QS), for all identified sub-spectra, were determined with reference to the centroid of the spectrum of a standard α-Fe foil. The numerical analysis of the Mössbauer spectrum was performed with the use of WMOSS program.
Results
XRD determination of the crystal structure
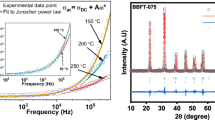
The XRD pattern lines have been successfully identified using the two sets of indices listed in our previous paper, concerning bismuth manganite ceramics [12]. The analysis of X-ray powder diffraction data (Fig. 1a) allowed us to confirm that the Fe-doped bismuth manganite ceramics consists of two centro-symmetric phases: the orthorhombic Pbam (No. 55) [14, 16, 17, 31] and the sillenite cubic I23 (No. 197) [2, 6]. The cubic sillenite structure of Bi12MnO20 phase can be described as discrete M 4+O4 tetrahedrons (M = Mn or Fe) separated by bismuth-oxygen framework. In case of the orthorhombic BiMn2O5 phase, the M 4+O6 octahedrons form linear chains and the square pyramids M 3+O5 interconnect the octahedrons via oxygen ions. In accordance to literature data, we presumed that Fe ions randomly replace Mn ions [29, 31, 32].
a X-ray powder diffraction pattern of Bi12MnO20–BiMn2O5–Fe ceramics obtained at room temperature: experimental (circles) and calculated (continuous line) spectrum; vertical ticks show 2θ Bragg positions, the curve at the bottom shows the difference between experimental pattern; and spectrum calculated for the superposition of Pbam and I23 space groups. b The XRD patterns obtained for the as sintered sample and for the sample after annealing at 1130 K for 8 h
The analysis of the room temperature XRD data of Fe-doped bismuth manganite shows the following superstructure: \( \left( {2\sqrt {2a_{p} } \times 2\sqrt {2a_{p} } \times 2\sqrt {2a_{p} } } \right) \) for I23 phase, and \( \left( {2a_{p} \times 2 b_{p} \times \sqrt {2c_{p} } } \right) \) for Pbam phase. Atoms are shifted from their ideal positions (see x, y, and z values in Table 1), which corresponds to deformation or distortion of the unit cell. Crystal lattice parameters for these phases are shown in Table 1.
The occurrence of two stable phases was not affected by the additional sintering conducted at T A = T S = 1130 K for 8 h, because of the set of diffraction lines remaining in the XRD pattern (Fig. 1b). However, the line placed at ~32° in the XRD pattern vanished. We deduce that a residual amount of additional compound, resulting probably from not fully reacted substrates, most likely bismuth carbonate (BiO)2CO3, that were removed after the sample was thermally treated [15, 36, 37]. Moreover, the disorder increased slightly, since the FWHM of the (112) line from Pbam symmetry and (400) line from I23 symmetry, e.g., placed at 35.77(2)° changed by 0.08.
Mössbauer study
In accordance to literature data, Fe ions randomly replace Mn ions in the manganite structures [29–32]. Mössbauer spectroscopy provides an insight to the local structure that enabled us to verify the variety of Fe environments in the Bi12MnO20–BiMn2O5 self-composite.
The 57Fe Mössbauer spectrum at room temperature is shown in Fig. 2, and the hyperfine parameters derived from the fitting procedure are collected in Table 2. This spectrum shows pure electronic quadrupolar interactions. It was fitted with three paramagnetic doublets. The observed isomer shift values are characteristic for Fe3+ ions placed at all sites. The QS observed in the Mössbauer spectrum, corresponds to the asymmetrical part of the electronic hyperfine interaction between the iron nucleus and its surrounding charges. Doublets labelled 1 and 2 represent iron Fe3+ ions distributed in the two sites of the BiMn2O5 structure, octahedral one and square pyramidal one, with a preferential occupation of the octahedral site (see Table 2). The isomer shift values of these two doublets are comparable with those presented in literature [30]. The quadrupole splitting value obtained for the octahedral site, QS = 1.131 mm s−1, is close to that of Fe-doped BiMnO3 (1.18 mm s−1) [30]. The large QS value indicates strong Jahn–Teller distortion of the octahedrons.
There is a third doublet with hyperfine parameters, visible in the Mössbauer spectrum. It originates from a small admixture of another crystal phase with iron Fe3+ in tetrahedral coordination. It can be related to the Bi12MnO20 phase.
Thus, the Mössbauer test confirmed the occurrence of three types of sites in the studied ceramics. The octahedral, pyramidal, and tetrahedral sites correspond to the Bi12MnO20 and the BiMn2O5 structures of the self-composite determined using XRD analysis.
Electric properties
The resistivity ρ DC decreased with increasing temperature that indicated thermally activated electric conductivity. It should be noted that several compounds containing Mn ions show polaronic conduction [12, 23, 24, 27, 28, 38, 39]. There are two models of small polaron conductivity, which include the potential energy landscape determined by the degree of crystal lattice disorder [25, 26]. Nearest-neighbours hopping (NNH) occurs for ordered solids and the Arrhenius law is fulfilled
Solids disordered, at least locally, show deviation from the Arrhenius law. In such a case, VRH of small polaron occurs [24]
where the parameter T 0 denotes Mott temperature and is measure of disorder, exponent equals to ¼ in case of three-dimensional conductivity. Moreover, T 0 relates to density of states in the vicinity of Fermi level, N (E F).
The Bi12MnO20–BiMn2O5–Fe ceramics has shown structural disorder; hence both models were checked. The ρ DC temperature dependence was shown both in the ρ DC versus T −1 plot, which corresponds to the NNH of small polaron, and in the ρ DC versus T −1/4 plot, which corresponds to the VRH small polaron model (Fig. 3).
In case of Arrhenius plot, the experimental points in the ρ DC (T −1) plot were not aligned in a straight line that corresponded to the monotonic change in E a value. Therefore, one could not determine the same value of activation energy in the whole temperature range. The activation energy values were estimated in narrower ranges: E a,1 = 0.37 eV (coefficient of determination, R 2 = 0.9996) in 358–568 K; E a,2 = 0.28 eV (R 2 = 0.9996) in 197–253 K; E a,3 = 0.22 eV (R 2 = 0.9956) in 151–173 K, respectively.
The use of the VRH model, ρ DC = ρ 0 exp [(T 0,DC/T)1/4], allowed us to determine that it is applicable below ~300 K (see the straight-line segment in Fig. 3). The value T 0,DC = 2.5 × 109 K (R 2 = 0.9999) was determined. Hence, the VRH of small polaron model fitted the resistivity with higher accuracy in the low-temperature range (compare R 2 values). Such a result was consistent with the structural disorder of the studied structural Bi12MnO20–BiMn2O5–Fe self- composite.
In case of lossy or conductive dielectric materials, the measured permittivity is the sum of three components:
where ε (ω) is dielectric permittivity, σ h is AC conductivity related to charge carriers hopping, and σ DC is DC conductivity contribution [40]. The same data can also be shown in the electric modulus representation, \( M^{*} = (\varepsilon^{*} )^{ - 1} = M^{\prime} + M^{\prime\prime} \). In this representation, the increase of losses in low-frequency range, related to conductivity, \( \varepsilon^{\prime\prime} \sim \sigma \omega^{ - 1} \), is transformed into the relaxation peak in the M″(ω) spectra. This transformation allows us to discern dipole relaxations covered in the dielectric loss ε″ spectra by the conductivity part [41–43].
The dielectric permittivity, ε *(T,ω), of the studied ceramics reached values of the order of 104 when it was measured in high-temperature range. It was dominated by conductivity contribution. Therefore, the imaginary part of electric modulus M *(T,f) temperature dependence for Bi12MnO20–BiMn2O5–Fe has been shown (Fig. 4). There are two different anomalies in M″(T) dependence, marked by frames. These anomalies shift toward higher temperatures with increasing frequencies, and hence, they can be assigned to relaxation processes. The most probable relaxation times, τ = (2π f max ) −1, were estimated from the M″ peak coordinates.
One process (I) occurs in the 90–200 K range. The details of this peak anomaly are shown in the inset (Fig. 4b). The M″(T) peak amplitude is constant in the 90–120 K range and increases in the 120–200 K range. The other process (II) occurs in the ~170–400 K range. However, the explicit peak in the M″(T) dependence occurs only in the narrower range, ~170–220 K, and a step-like anomaly manifests at higher temperature.
The relaxation times relate to conductivity for many disordered solids via the Barton–Nakajima–Namikawa (BNN) relation [26]:
where ω* is the frequency marking the onset of AC conduction, σ DC is the DC conductivity, p is the constant of the order of unity, and Δε is the dielectric strength, i.e., the difference between static and high-frequency relative dielectric permittivity.
The most probable relaxation times were estimated from the peak coordinates in the M″(T,f) dependence, τ = 1/2πf. We presumed that the relaxation times would reflect the structural disorder, in accordance to the BNN relation, τ (T) = ξ ρ DC(T). Therefore, the relaxation times were plotted in temperature scales appropriate for the NNH and the VRH models. The relaxation times related to processes (I) and (II) are shown in Fig. 5a and b, respectively. The numerical fit was performed in the same temperature ranges for adequate comparison, both for the NNH dependence, τ (T −1), and the VRH dependence, τ (T −1/4).
In case of process (I), the relaxation times were fitted, in accordance to thermally activated NNH hopping of small polaron, to Arrhenius law: τ = τ 0 exp (E A/kT). Activation energy values changed from E A,I,1 = 0.14 eV in the 90–120 K range to E A,I,2 = 0.20 eV in the 125–200 K range. The crossover in the activation energy at T = 120 K (see Fig. 5a) corresponded to the temperature T m where an offset in modulus amplitude manifests (compare Fig. 4b). The characteristic time values were τ 0,I,1 = 10−10 s and τ 0,I,2 = 10−12 s, respectively. We would like to mention that a nonlinear dependence in the relaxation times in the Arrhenius plot could be distinguished, which reflected in the E A value change. Such a curve indicated that activation energy depended on temperature, and the variable range hopping of small polaron model could be concerned [28, 42, 43]. Therefore, the most probable relaxation times have been also fitted in accordance to the VRH of small polaron model: τ = τ 0 exp [(T 0/T)¼]. The common value, T 0,I,VRH = 1.8 × 109 K, was determined for both temperature ranges.
The high-temperature anomaly (II) in M″(T,f) plots occurred in the 170–400 K range (see Fig. 4a). However, the determination of the most probable relaxation times, related to the peak position in the M″(T,f) plot, was effective only in the 170–220 K range (Fig. 5b). The determined relaxation times were fitted in accordance to the thermally activated dependence presumed for the nearest-neighbour hopping of small polaron model. The activation energy value was E A,II = 0.27 eV, and the characteristic time was τ 0,II = 10−11 s. Consequently, the VRH polaron model was also applied to this relaxation process (see Fig. 5b). The value T 0,II,VRH = 3.5 × 109 K was determined.
It would be noticed that the fitting performed in accordance to the VRH of small polaron model has shown better accuracy [R 2 = 0.9948 in the 90–120 K range and R 2 = 0.9995 in the range of 125–200 K for process (I) and R 2 = 0.9997 for process (II)], than the accuracy determined from fitting performed for the NNH of polaron model [R 2 = 0.9944 and R 2 = 0.9988 for the process (I) and R 2 = 0.9981 for the process (II)], respectively. Therefore, we deduce that relaxation times reflect a structural disorder.
Discussion
Fe-doped Bi12MnO20–BiMn2O5 ceramics was prepared by high-temperature sintering in air, at slightly different sintering temperature and time, in comparison to the non-doped Bi12MnO20–BiMn2O5 samples [12, 39]. Despite this difference, the XRD patterns exhibited the occurrence of the cubic I23 Bi12MnO20 phase and orthorhombic Pbam BiMn2O5 phases, for both the non-doped and Fe-doped samples. These phases remained in thermodynamic equilibrium and their ratio depended slightly on the temperature and time of sintering [13–15]. The superstructure lines occurred in XRD pattern for both phases. Such an effect corresponded to the crystal lattice deformation or distortion (the parameters of unit cells are listed in Table 1). The obtained values of the refinement parameters suggested the presence of structural disorder. This effect might correspond to the unit cells, which consist of tetrahedrons, octahedrons, and square pyramids.
It should be noted that “bismuth manganite” denotes the general content of the elements [39] and not the true local composition. Moreover, our research has shown different symmetries of the two determined phases, in contrary to the BiMnO3–Fe samples produced under high hydrostatic pressure by Belik et al. [8, 30, 33].
The Mössbauer spectroscopy study confirmed the variance in the surrounding of Fe3+ ions. The Fe3+ ions accommodated preferentially in the FeO6 octahedrons (~70 %). The minor amount placed in the pyramids FeO5 and FeO4 tetrahedrons. It has been shown by Retuerto et al. [31] that Fe ions preferentially occupy the pyramidal Fe3+O5 sites; however, the disorder related to anti-site occupancy of the octahedral sites was also determined in the BiMn2O5 compound. It should be noticed that the occurrence of Fe3+ ions in the octahedral and tetrahedral environments needed charge compensation when they replaced manganese ions in the Mn4+O6 and Mn4+O4 units. The charge compensation could be fulfilled by the induced oxygen vacancies, VO, in such cases.
We presume that structural and chemical non-homogeneity provides the necessary background for the occurrence of dielectric dispersion and relaxation. One possibility might originate from the misfit strains induced by different radii of the Fe and Mn ions and also induced by interfaces, which are formed between the structures of the two phases with different symmetries. The more plausible possibility corresponds to the Mn4+, Mn3+, and Fe3+ charge states, randomly distributed in oxygen tetrahedrons, octahedrons and square pyramids. The formation of either Fe3+–VO or/and of Fe3+–Mn3+/4+ pairs in the crystal lattice also can increase local disorder. The O 2p states hybridize with Mn 3d and Fe 3d states, which form the valence band. Therefore, a disordered environment of Mn and Fe ions can affect the electric transport features.
The permittivity relaxor-like dispersion is different from the ferroelectric mechanism [23, 27, 28, 38, 39]. It would be noticed that two relaxation processes occurred also in the non-doped Bi12MnO20–BiMn2O5 self-composite [12]. The low-temperature relaxation has shown E A = 0.20 eV and characteristic time τ 0 = 1.8 × 10−12 s. The high-temperature relaxation has shown E A = 0.24 eV and τ 0 = 1.5 × 10−8 s. The low values of activation energy are consistent with polaron hopping.
The manifestation of VRH polaron mechanism of conductivity, in the low-temperature range, indicated a significant role of the structural and chemical disorder, related to the occurrence of two phases and additionally affected by doping with Fe ions. Therefore, we propose that low-temperature relaxation (I) relates to charge hopping or charge transfer between the Mn3+ and Mn4+ sites.
We would also like to comment upon the dielectric anomaly visible in the M″(T,f) spectrum in the vicinity of 120 K (see Fig. 4). One may note the vague coincidence between this dielectric anomaly and magnetic phase transition, reported in literature. The antiferromagnetic transition at T Néel = 110 K for BiMnO3 [44] and ferromagnetic cluster-like behaviour below T C = 100–110 K for Fe-doped BiMnO3 [8, 33] have been reported for these materials, which have shown perovskite symmetry and composition. The antiferromagnetic order below T Néel = 40 K has been reported for BiMn2O5 polycrystalline samples [10]. The ceramics obtained from NaNbO3 mixed with the Bi12MnO20–BiMn2O5 compound also exhibited magnetic ordering below 40 K, most probably related to the BiMn2O5 phase contribution [45]. On the other hand, a dielectric anomaly has been induced in the BiMn1−x Ti x O5 compound at ~120 K by Ti ions substitution [11]. Hence, we deduce that the anomaly visible in the M″(T,f) spectrum originated from non-magnetic defects.
Conclusions
We note that electric conductivity dispersion and relaxation corresponds to the disorder related to a variety of structural items in Fe-doped Bi12MnO20–BiMn2O5 self-composite. The split of the Mössbauer spectrum enabled us to determine the Fe3+ sites with tetrahedral, octahedral, and square pyramidal symmetry. The occurrence of these three environments corresponds to the variable range hopping of small polaron model, which was fitted successively in low-temperature range. Oxygen vacancies can provide conditions for charge compensation of Fe3+ ions, which replace Mn4+ ions. Electric relaxation was attributed to charge transfer between the Mn3+ and Mn4+ sites. Hence, such electric transport features are consistent with structural disorder, which was identified with the use of XRD and the Mössbauer spectroscopy studies.
References
Han JT, Huang YH, Wu XJ, Wu CL, Wei W, Peng B, Huang W, Goodenough JB (2006) Tunable synthesis of bismuth ferrites with various morphologies. Adv Mater 18:2145–2148
Valant M, Suvorov D (2002) A stoichiometric model for sillenites. Chem Mater 14:3471–3476
Xiong Y, Wu M, Peng Z, Jiang N, Chen Q (2004) Hydrothermal synthesis and characterization of Bi2Fe4O9 nanoparticles. Chem Lett 33:502–503
Hur N, Park S, Sharma PA, Ahn JS, Guha S, Cheong SW (2004) Electric polarization reversal and memory in a multiferroic material induced by magnetic fields. Nature 429:392–395
Nippolainen E, Kamshilin AA, Prokofiev VV, Jaaskelainen T (2001) Combined formation of a self-pumped phase-conjugate mirror and spatial subharmonics in photorefractive sillenites. Appl Phys Lett 78:859–861
Wang Y, He R, Yang M, Wen T, Zhang H, Liang J, Lin Z, Wang Y, Li G, Lin J (2012) Hydrothermal growths, optical features and first-principles calculations of sillenite-type crystals comprising discrete MO4 tetrahedra. CrystEngComm 14:1063–1068
Montanari E, Righi L, Calestani G, Migliori A, Gilioli E, Bolzoni F (2005) Room temperature polymorphism in metastable BiMnO3 prepared by high-pressure synthesis. Chem Mater 17:1765–1773
Belik AA (2012) Polar and nonpolar phases of BiMnO3: a review. J Solid St Chem 195:32–40
Jia R-J, Han J-T, Wu X-J, Wu C-L, Huang Y-H, Huang W (2008) Controllable synthesis and magnetic property of BiMn2O5 crystals. Mater Res Bull 43:1702–1708
Liu Q, Sallagoity D, Josse M, Toulemonde O (2013) On the anomalous magnetic behavior and the multiferroic properties in BiMn2O5. Inorg Chem 52:7853–7861
Shukla DK, Mollah S, Kumar R, Thakur P, Chae KH, Choi WK, Banerjee A (2008) Effect of Ti substitution on multiferroic properties of BiMn2O5. J Appl Phys 104:033707-1–03370710
Molak A, Leonarska A, Szeremeta A (2015) Electric current relaxation and resistance switching in non-homogeneous bismuth manganite. Ferroelectrics 486:161–172
Sedmidubský D, Leitner J, Beneš O (2006) Phase equilibria modeling in Bi2O3–SrO–MnO x system. CALPHAD 30:179–184
Huo G, Gu Z, Qiu M (2004) Phase relations in the Bi2O3–Fe2O3–MnO y system at room temperature. J Alloy Compd 381:317–319
Pilch M, Molak A, Koperski J, Zajdel P (2016) Influence of nitrogen flow during sintering of bismuth manganite ceramics on grain morphology and their surface disorder. Phase Transit. doi:10.1080/01411594.2016.1219737
Nguyen N, Legrain M, Ducouret A, Raveau B (1999) Distribution of Mn3+ and Mn4+ species between octahedral and square pyramidal sites in Bi2Mn4O10—type structure. J Mater Chem 8:731–734
Munoz A, Alonso JA, Casais MT, Martinez-Lope MJ, Martinez JL, Fernandez-Diaz MT (2002) Magnetic structure and properties of BiMn2O5 oxide: a neutron diffraction study. Phys Rev B 65:144423-1–144423-8
Mohaideen KK, Joy PA (2012) Enhancement in the magnetostriction of sintered cobalt ferrite by making self-composites from nanocrystalline and bulk powders. ACS Appl Mater Interfaces 4:6421–6425
Bhowmik RN, Panda MR, Yusuf SM, Mukadam MD, Sinha AK (2015) Structural phase change in Co2.55Fe0.75O4 spinel oxide by vacuum annealing and role of coexisting CoO phase on magnetic properties. J Alloy Compd 646:161–169
Zhang J, Zuo R (2016) A novel self-composite property-tunable LaTiNbO6 microwave dielectric ceramics. Mat Res Bull 83:568–572
Zhang J, Xu B, Li XF, Yao KL, Liu ZL (2011) Origin of the multiferroicity in BiMn2O5 from first–principles calculations. J Magn Magn Mater 323:1599–1605
Goian V, Kamba S, Savinov M, Nuzhnyy D, Borodavka F, Vanek P, Belik AA (2012) Absence of ferroelectricity in BiMnO3 ceramics. J Appl Phys 112:074112-1–074112-6
Dar MS, Akram KB (2014) Evidence of variable range hopping (VRH) and exchange interaction in Co-doped multiferroic BiMnO3 nanoparticles. J Supercond Nov Magn 27:613–623
Hunt A (1991) The ac conductivity of variable range hopping systems such as amorphous-semiconductors. Philos Mag B 64:579–589
Wubbenhorst M, Turnhout J (2002) Analysis of complex dielectric spectra. I. One-dimensional derivative techniques and three-dimensional modeling. J Non-Cryst Solids 305:40–49
Dyre JC, Maass P, Roling B, Sidebottom DL (2009) Fundamental questions relating to ion conduction in disordered solids. Rep Prog Phys 72:046501-1–04650115
Pal S, Banerjee A, Chatterjee P, Chauduri BK (2003) Evidence of non-adiabatic conduction in Bi0.1A0.9MnO3 (A=Ca, Sr, Pb). Phys Status Solid B 237:513–522
Volkov NV, Eremin EV, Sablina KA, Sapronova NV (2010) Dielectric properties of a mixed-valence Pb3Mn7O15 manganese oxide. J Phys 22:375901-1–375901-6
Yang T, Abakumov AM, Hadermann J, Van Tendeloo G, Nowik I, Stephens PW, Hemberger J, Tsirlin AA, Ramanujachary KV, Lofland S, Croft M, Ignatov A, Sun J, Greenblatt M (2010) BiMnFe2O6, a polysynthetically twinned hcp MO structure. Chem Sci 1:751–762
Belik AA, Hayashi N, Azuma M, Muranaka S, Takano M, Takayama-Muromachi E (2007) Magnetic and Mössbauer studies of 5 % Fe–doped BiMnO3. J Solid State Chem 180:3401–3407
Retuerto M, Martinez-Lope MJ, Krezhov K, Fernández-Díaz MT, Alonso JA (2011) Structural and magnetic characterization of BiFexMn2-xO5 oxides (x = 0.5, 1.0). J Solid State Chem 184:2428–2433
Selbach SM, Tybell T, Einarsrud MA, Grande T (2009) Structure and properties of multiferroic oxygen hyperstoichiometric BiFe1−xMnxO3+δ. Chem Mater 21:5176–5186
Belik AA, Takayama-Muromachi E (2007) Effects of isovalent substitution in the manganese sublattice on magnetic, thermal, and structural properties of BiMnO3: BiMn1-xO3 (M = Al, Sc, Cr, Fe, Ga; 0 ≤ x ≤ 0.2). Inorg Chem 46:5585–5590
Kachel A (1995) XP Program Guide
Rodriguez–Carvajal J (2006) Introduction to the Program Fullprof
Grice JD (2002) A solution to the crystal structures of bismutite and beyerite. Can Mineral 20:693–698
Cao J, Li X, Lin H, Xu B, Chen S, Guan Q (2013) Surface acid etching (BiO)2CO3 to construct (Bi)2CO3/BiOX (X = Cl, Br, I) heterostructure for methyl orange removal under visible light. Appl Surf Sci 266:294–299
Woo H, Tyson TA, Croft M, Cheong S-W, Woicik JC (2001) Correlation between the magnetic and structural properties of Ca-doped BiMnO3. Phys Rev B 63:134412-1–134412-12
Molak A, Ujma Z, Pilch M, Gruszka I, Pawełczyk M (2014) Resistance switching induced in BiMnO3 ceramics. Ferroelectrics 464:59–71
Bokov AA, Ye Z-G (2000) Phenomenological description of dielectric permittivity peak in relaxor ferroelectrics. Solid State Commun 116:105–108
Bello A, Laredo E, Grimau M (2007) Comparison of analysis of dielectric spectra of PCL in the ε* and the M* formalism. J Non-Cryst Solids 353:4283–4287
Molak A, Paluch M, Pawlus S, Ujma Z, Pawełczyk M, Gruszka I (2006) Properties of (Bi1/9Na2/3)(Mn1/3Nb2/3)O3 analysed within dielectric permittivity, conductivity, electric modulus and derivative techniques approach. Phase Transit 79:447–460
Molak A, Paluch M, Pawlus S (2008) Electrical properties of Pb(Mn1/3Nb2/3)O3 ceramics under hydrostatic pressure: relaxation dynamics investigation and its relation to subsystem of defects. Phys Rev B 78:34207-1–3420714
Kimura T, Kawamoto S, Yamada I, Azuma M, Takano M, Tokura Y (2003) Magnetocapacitance effect in multiferroic BiMnO3. Phys Rev B 67:180401-1–180401-4
Bujakiewicz-Korońska R, Nalecz DM, Balanda M, Molak A, Ujma Z (2014) Electronic and magnetic properties of (Bi0.5Na0.5)(Mn0.5Nb0.5)O3. Phase Transit 87:1096–1104
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
We declare that there are no conflicts of interests. There were no research grants or funds from external companies. The work has been performed in accordance to our duties in the University of Silesia and Pedagogical University.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Leonarska, A., Kądziołka-Gaweł, M., Szeremeta, A.Z. et al. Electric relaxation and Mn3+/Mn4+ charge transfer in Fe-doped Bi12MnO20–BiMn2O5 structural self-composite. J Mater Sci 52, 2222–2231 (2017). https://doi.org/10.1007/s10853-016-0515-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10853-016-0515-2