Introduction

Abnormal grain growth (AGG) in polycrystalline materials is defined by a small fraction of grains that grow larger than the vast majority of their neighbors, resulting in a bimodal grain size distribution that does not evolve in a self-similar manner over time. The precise mechanism for AGG is a topic of ongoing debate [1], although the most common argument centers on a few grain boundaries that have exceptionally high mobility under special conditions [2, 3]. The microstructural heterogeneities created by AGG can be both detrimental and beneficial. Perhaps the most famous example of a beneficial use of AGG traces back to Goss’ 1935 work on Fe–Si where certain thermomechanical processes were found to produce extreme crystallographic texture (the ‘Goss texture’), enabled by AGG [4]. These alloys, now known as electrical steels, have seen extensive industrial use for decades due to their high magnetic anisotropy associated with the strong texture. AGG is problematic in the sintering of undoped alumina ceramics to achieve densities >97 %, an issue that was resolved in the 1960s by the introduction of MgO [5].

There is interest in AGG phenomenon, especially in the case of nanocrystalline metals which appear to be particularly susceptible. While nanocrystalline metals can exhibit AGG during thermal exposure (e.g., [6, 7]), they also often show a strong propensity for AGG under mechanical loading, such as tension [8], indentation [9], wear [10, 11], and fatigue [12, 13]. Our previous studies of fatigue-induced grain growth in nanocrystalline Ni alloys [12] suggest that a vanishingly small fraction of grains can grow abnormally under fatigue loading from ~50 to ~500 nm resulting in crack initiation and eventual catastrophic failure. Current understanding of mechanically driven AGG in nanocrystalline metals is limited due to challenges in direct non-destructive observation. Therefore, there is an urgent need for fast non-destructive in situ survey methods to identify the onset and progression of AGG. While AGG is generally considered problematic for nanocrystalline metals, the resulting bimodal grain size may also provide beneficial properties, such as improved ductility and corrosion resistance, if properly controlled [14, 15].

X-ray diffraction methods are ideal in many ways for in situ non-destructive grain size measurement. There is substantial literature describing the relevant theory (e.g., [16]), as well as many documented examples of the application of these methods to in situ experiments (e.g., [17]). All of the common methods for grain size determination of polycrystals using diffraction, including the 100-year old Scherrer method, Williamson–Hall’s [18] adaptation, and the more sophisticated Warren–Averbach [19] approach, are based on the analysis of the widths of diffraction peaks. These techniques can be used to determine average grain sizes typically in the <500 nm regime. Determination of the width of a diffraction peak for grain sizes of 1–50 nm is straight-forward, but as the grain sizes surpass 50 nm, contributions from instrumental broadening to the peak width are considerable and need to be carefully taken into account; for this reason, grain size determination above ~200 nm can be particularly challenging. Furthermore, Williamson–Hall only provides the average value for crystallite size. For this reason, it may not be sensitive enough to identify the presence of a diffracting volume of coarse grains which only represents a small fraction (<0.1 %) of the total volume of diffracting grains. Warren–Averbach analysis, by contrast, can estimate the entire grain size distribution, but it requires not only the widths but also the shape of several higher order diffraction peaks [19]. For this reason, the technique is applicable to only extremely high resolution, low noise diffraction data with many high-Q diffraction peaks. Warren–Averbach analysis is particularly challenging for small unit cell, high symmetry lattices, such as that of many structural metals. Furthermore, overlapping peaks additionally confound analysis. Conventional methods of grain size determination for grains larger than 100 nm, therefore, require high resolution diffractometers operating at high energies (to reach high-Q range). Even with the best diffractometer configuration, they often fail for samples with very low symmetry and large unit cell, where peak overlap is significant, or samples with high symmetry and a small unit cell, where only a few peaks are accessible. These high resolutions are almost always achieved by sacrificing intensity and they are also not very compatible with parallel detection using large area detectors. These systems, therefore, are slow, laborious and not well suited for quick in situ detection of AGG.

The difficulty in characterizing a bimodal grain size distribution by X-ray diffraction has been discussed in several previous publications (e.g., [20]). It is noted in that prior work that a minority of “coarse grains do not produce measurable profile broadening” [20]. Therefore, it is necessary to consider alternative analysis methods to determine bimodal grain size distributions, such as those caused by AGG.

The total (integrated) scattered intensity from a given volume of material is independent of the grain size (under a kinematic approximation). As the grains grow, the scattered intensity gets focused into sharper peaks. Thus, the diffraction peak width decreases with grain size, as suggested by Scherrer, Williamson, Warren, etc., but it also grows in height proportional to the grain size (e.g., see Fig. 4 in [21]). For a small fraction of abnormally large grains among a larger volume of much finer grains, anomalous intensity spikes are much easier to detect than sharpening of the peak width. Based on this observation, we propose a new approach to identify very small fractions of abnormally large grains in a matrix of much finer grains. To demonstrate this approach, we use a previously prepared sample of nanocrystalline Ni–Fe where cyclic fatigue loading of the material resulted in the presence of a few abnormally large grains. A series of X-ray transmission diffraction experiments are described, which investigate the conditions for the use of such a non-destructive method in both post-mortem and in situ analysis. In our proposed approach to an in situ AGG investigation, the sample would be subjected to gradually increasing external stimulus (e.g., temperature, strain, or impact), or increasing repetition of cyclic loading. The sample would be continuously surveyed to find new pockets of AGG by a technique similar to the one suggested below. As soon as the survey detects initiation of AGG, the in situ experiment would be halted and the microstructure, grain orientation, grain size distribution, and strain in the pocket of AGG and its surroundings would be investigated in detail, including Warren–Averbach and Williamson–Hall methods, if needed.

Experimental method

Material

The material used for the demonstration of this technique was nanocrystalline Ni–Fe, which had been known from previous studies to form isolated abnormal large grains during fatigue loading [12]. Electroplated Ni–Fe thin film tensile dogbone samples with an average initial grain size of 49 nm were fatigued in tension–tension loading to failure and analyzed in a previous study. The nominal thickness and gage width of the samples were 10 and 1000 μm, respectively. Previous texture measurements using a lab diffractometer on the same batch of samples revealed a weak (111) + (200) texture along the deposition (through thickness) direction. The grain size distribution of the as-deposited material is shown in Fig. 1 with a corresponding log-normal fit to the histogram. The average grain diameter was 49 nm and the largest grains were more than 125 nm, but <150 nm in diameter. After fatigue testing to failure, an isolated zone of large grains was associated with the point of crack initiation on the fracture surface [12]. This cluster of large grains contained highly textured grains, each ~500 nm in size, with the overall cluster being as large as 5 μm in size. Figure 2 shows cross-sectional TEM and an accompanying grain orientation map (collected from EBSD measurements of the same area) from a nominally identical sample, tested in the same way and observed to fail after AGG. The crystallographic texture of these large grains was near (220) parallel to the deposition direction and (111) parallel to the tensile axis. Based on previous focused ion beam dissection, it is believed that this zone of large grains on the fracture surface is the only such pocket of large grains in the entire sample, and our previous work speculated that these large grains were not present from electrodeposition, but instead were formed by fatigue-induced recrystallization and/or grain growth. Because this cluster of large grains was associated with blocky features on the fracture surface, it was relatively easy to find post-mortem. The future challenge, however, is to locate such an AGG cluster before fracture initiation.

Fig. 1
figure 1

Empirical probability density function of grain size and log-normal fit for the NC Ni–Fe material used in these experiments

Full size image
Fig. 2
figure 2

(left) Cross-sectional TEM and (right) EBSD grain orientation map of typical coarse-grained microstructure formed at the point of fatigue-crack nucleation. Black lines indicate 1° misorientation across pixels. Fatigue coarsened grains are surrounded by the original matrix of nanocrystalline grains. The blocky region viewed as part of the fracture surface would be visible from the left. The coarse-grained region is all essentially a single crystallite with low-angle subgrain boundaries and a (220) texture along the through-thickness, or deposition, direction

Full size image

X-ray diffraction measurements

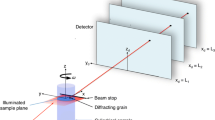
Transmission diffraction experiments were performed using a 12.7 keV collimated X-ray beam at the Stanford synchrotron radiation lightsource (SSRL) beamline 11–3. A MAR345 area detector was positioned at 200 mm from the sample to collect the full (111), (200), and (220) Ni diffraction rings. A specialized sample holder was fabricated to position the broken half of a thin film fatigue sample in an x–y stage perpendicular to the incoming X-ray beam (Fig. 3). Calibrations of the incident X-ray energy, diffractometer geometry, and instrumental resolution were performed periodically by translating the fatigue sample out of the beam and replacing it with a polycrystalline LaB6 transmission sample.

Fig. 3
figure 3

Schematic showing X-ray diffraction setup for locating abnormally large grains in the thin film fatigue sample

Full size image

The beam spot size was controlled by an aperture composed of horizontal and vertical slits which could be independently positioned at micron intervals. The experiments described here utilized equal horizontal and vertical slit spacings of 50, 100, or 200 µm. With the 10 μm sample thickness, these slits correspond to nominal sampling volumes of 2.5 × 104, 1 × 105, and 4 × 105 μm3. Since the sample itself was much larger than the X-ray footprint, the sample was rastered in-plane at increments equal to the nominal X-ray beam size defined by the size of the slits. The sample was known to have at least one cluster of abnormally large grains, so at least one position during rastering was expected to produce an anomalous X-ray peak.

The selected beamline was configured for transmission powder diffraction with a monochromatic beam and a 2-circle goniometer holding the broken fatigue sample. This configuration is not ideally suited for identifying the single-crystal signature associated with the anomalous large grain region. A single large grain will create a lattice array of intensity spikes in reciprocal space (actually a few depending on the multiplicity of that reflection [22]). However, in a monochromatic experiment, the single-crystal spikes may not intersect the permissible Bragg diffraction rings. Stated from the perspective of a Ewald-sphere construction, there is no guarantee that the thin shell of the Ewald-sphere will intersect the single-crystal lattice spots in reciprocal space. There are three possible strategies for identifying the presence of abnormal single crystals: (1) interrogate many diffraction rings through either high-energy X-rays and/or close detector working distance, (2) span X-ray energy either through a polychromatic beam or rastering a monochromator, and (3) rotate or tilt the sample during the measurement. While any of these three options are viable, the limitations of the beamline in the current study only afforded the ability to tilt the specimen with respect to the incoming beam. Unlike most conventional single-crystal diffraction studies, it is not necessary to capture many diffraction spots from the single crystal: while more diffraction spots provide further confirmation, only one definitive diffraction spike is needed to identify the presence of an abnormally large grain.

Results

Anomalous intensity determination

Raw data from a detector scan, such as that shown in Fig. 4, were processed using the Area Diffraction Machine (ADM), an open source code for analyzing area powder diffraction data. After applying the appropriate LaB6 calibration, each diffraction ring was extracted separately and transformed to a Cartesian grid for easier analysis (“caking”). To accomplish this cake, ADM interpolates the original pixel intensity values onto a polar coordinate grid with bin sizes defined by the user. The (111), (200), and (220) rings were processed in this way using 200 Q-divisions and 6300, 7500, and 10400 χ-divisions, respectively. Adjusting χ-divisions in this way keeps the size of the bins used for the caking process approximately equal to the original pixel dimensions. Only a portion of the data around each ring was included in this process, centered at the ring peak location (shown in Table 1) with dQ = ±0.3 Å−1. An example of a caked diffraction ring is shown in Fig. 5a.

Fig. 4
figure 4

Example of diffraction rings for the Ni–Fe sample as collected by the MAR area detector. The white box inset shows a higher magnification of a portion of the (111) ring which contained anomalous dark red (high intensity) spots superimposed on the ring (arrow in inset) (Color figure online)

Full size image
Table 1 Q data for the (111), (200), and (220) peaks
Full size table
Fig. 5
figure 5

a Example of (111) caked intensity data extracted from a (111) diffraction ring. Arrow indicates a possible anomalous peak at χ = 158°. b Plot showing local peak intensities at each value of χ. Colored regions indicate 3 or 6 standard deviations from the mean, which is shown by the red curve. The gap in data at χ = 260° is due to the beam stop (Color figure online)

Full size image

The caked diffraction ring data were then analyzed using a MATLAB script to automatically find potential diffraction peaks due to large crystallites in the diffracting volume. For this step, the caked data, imported as row (χ), column (Q), and intensity values, were searched to find the intensity maximum for each χ value. The peak intensity values were then plotted as a function of χ and fitted with a smoothing spline to establish a local mean of the dataset, as shown in Fig. 5b.

The local peak intensity values are assumed to follow a homoscedastic normal distribution around a mean, µ, which varies as a function of χ. The standard deviation, σ, is then calculated according to

$$ \sigma = \sqrt {\frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {Y_{i} } \right)^{2} } , $$
(1)

where Y i  = I(χ i ) − µ(χ i ). For each local peak intensity value, I(χ i ), the ratio of Y i to σ indicates how many standard deviations away from the mean a particular peak lies

$$ z_{i} = \frac{{Y_{i} }}{\sigma }. $$
(2)

The z-ratio can be related to the confidence interval, by the error function

$$ {\text{CI}} = {\text{erf}}\left( {z/\sqrt 2 } \right). $$
(3)

For example, an intensity spike that stands three standard deviations above the average intensity has a z-ratio of z = 3 and a confidence interval of 99.73 %. The interpretation of such a result would be that the intensity spike is statistically distinguished as an outlier that is not a result of Gaussian noise, with a confidence of 99.73 %.

The plots shown in Fig. 5 represent typical ways of viewing analyzed data to both interpret results and validate assumptions. Figure 5b shows the local peak intensity plot with the spline fit as well as 3σ (z = 3) and 6σ (z = 6) deviations. The plot in Fig. 6 shows another way of presenting the same data, wherein the z-ratio is plotted versus χ. The ratios should be randomly distributed around a value of zero, except for any potential positive peaks associated with a diffracting large crystallite.

Fig. 6
figure 6

An example of z-ratio versus χ showing three confidence intervals. Note the statistically anomalous peak at χ = 158°

Full size image

Statistical assessment

The use of basic statistical tools described in the previous section allows the objective identification of statistical outliers in the z-ratio data. The confidence interval defines how likely it is that a datum is a true outlier in the statistical sense. Defined inversely, the CI represents the odds of a datum not belonging to the normal distribution. As an example, consider a datum which lies just outside the threshold of a CI of 99.9999 %, corresponding to a z-ratio of 4.9. The value is a statistical outlier with 99.9999 % certainty—conversely, the odds of it not being anomalous are 1/(1 − CI) or approximately 1000000–1. These types of measures should not be considered just in themselves, but in relation to the distribution size. A CI of 99.99 % (z = 3.9) implies that approximately 1 out of 10000 data points would be expected to fall outside the normal distribution. Therefore, if several values fall outside this range, and they occur adjacent to each other, there is a high statistical likelihood that a large crystallite is causing the diffraction anomaly. Due to the difficulty in establishing an accurate representation of the true varying mean of local maximum intensities with χ, a more conservative CI threshold may be set to prevent mistakenly identifying outliers in lower quality datasets. For this purpose, a CI of 99.9999 % (z = 4.9) was used for the anomalous peak identification in the current study.

ϕ-Tilt measurements

As described in the method section, definitive identification of the single-crystal signature from the AGG region under the constraints of a monochromatic 2-circle goniometer requires rotating/tilting of the sample relative to the incoming beam. This was demonstrated by tilting the sample with respect to the ϕ axis as shown in the schematic, Fig. 3. Z-ratio versus χ results from ϕ-tilting experiments are shown in Fig. 7. Each plot represents a significance test of the local maximums from the (111) caked ring data at different sample tilts with respect to the incoming X-ray beam, ranging from ϕ = −45° to +45° in 2° increments. The emergence and disappearance of a significant peak at χ = 95° between ϕ = −3° and ϕ = +3° and also at χ = 330° between ϕ = +15° and ϕ = +21° suggest that either two different large crystallites were diffracting or two spots from the same crystallite were tilted to satisfy the Bragg condition. For each of these intensity spikes, the Bragg condition seems to show an angular misorientation tolerance of approximately 6°. To maintain the same region of interest during these tilting experiments, it is necessary to carefully calibrate the eucentric height.

Fig. 7
figure 7

Z-ratio versus χ plots for a series of diffraction measurements at different ϕ-tilts. Aperture size was 200 μm with the beam centered on the blocky region and the sample set to the eucentric height

Full size image

Grid measurements and efficiency tradeoffs

Time is of the essence in an in situ experiment. One strategy for reducing the survey time to locate a region of AGG is to scan the sample very quickly with a large beam and a coarse grid. If such a coarse grid indicated the presence of AGG, then progressively finer grid scans with smaller beams could be used to locate the large grain(s) more precisely. But such a strategy is valid only if both the coarse grid scan and higher resolution grid scan can identify the AGG region with statistical certainty. A series of spatial grid scans were performed with 50, 100, and 200 μm beam aperture sizes over a rectangular grid of locations in and around the location of known AGG. For this grid survey, the specimen was translated in the x–y plane with respect to the incoming beam (arriving along the z-axis). The nominal spot size and grid layouts are shown in Fig. 8.

Fig. 8
figure 8

Nominal layouts used for grid measurements with 50, 100, and 200 μm aperture openings

Full size image

The smallest interrogation spot size of 50 μm not only suffered from reduced intensity associated with the partitioned beam, but also exhibited poor spatial discrimination. Specifically, while the anomalous spike was present in the expected location, the same anomalous peak with identical diffraction coordinates (Q, χ, ϕ) was present at neighboring grid locations above, below, or to the side of the expected location. This is most likely due to beam spillover. While the slit aperture set a beam size of 50 μm, beam divergence and/or Fresnel diffraction from the slit sides caused the projected beam on the sample to be larger. This is a limit of the spatial selectivity of the beamline in use, as other beamlines are capable of defining X-ray spot sizes of 1μm or smaller.

The larger interrogation spot sizes of 100 and 200 μm were both able to uniquely identify the region of grain growth distinct from the neighboring regions. A single anomalous spike was present in both the (111) and (200) diffraction rings at χ = 95° and 317°, respectively. An example from (111) diffraction ring and the 200 μm aperture size is shown in Fig. 9. In both the (111) and (200) ring measurements, the only significant peak that occurs is in the central grid location, where AGG was expected. The large grain region, which is estimated to be ~350 nm in diameter, occupies <0.00001 % of the 200 × 200 × 10 μm sampling volume. Yet this isolated region of abnormally large grains is identified in the sea of smaller grains with far better than 4.9σ confidence. This anomalous peak was much more intense than the background: typically, the spike intensity was a factor of 50–100 % above the background polycrystalline diffraction ring intensity. In regions away from the expected location of grain growth, there were no other anomalous spikes that were distinctly above background. A minor intensity spike rising only ~5 % above background was found at several grid locations away from the expected grain growth region using both the 100 and 200 μm aperture. This minor spike was present at the same diffraction coordinates (χ = 185°) in several different grid locations that were >500 μm apart. Therefore, it was not coming from the specimen itself, but likely from a diffracting particle on the aperture.

Fig. 9
figure 9

An example grid scan of nine different physical locations using a spot size of 200 μm, and a translation distance between locations of 200 μm. The red circles at the (0,0) location indicate the statistically significant anomalous peak that was only present in the location of abnormal grain growth at the fatigue-crack initiation site. The intensity drops to zero in the left 3 scans where the beam no longer intersects the sample. The ϕ-tilt for these examples was 0°

Full size image

Aperture size and count time directly affect the measured intensity of diffraction data in an experiment, which in turn affect the statistical discriminating power to identify anomalous peaks associated with unusually large grains. For fast initial scans, a short duration per diffraction pattern is desirable so as to cover a large area on the sample quickly to determine whether to continue heating/straining or stop to perform a more detailed scan. The following series of diffraction experiments examine the impact of aperture size and counting statistics using a single sample location containing known abnormally large grains. 50 µm aperture openings were paired with durations of 300, 800, and 1200 s, while 100 μm aperture openings were paired with durations of 60 and 300 s. Since there was a fixed 120 s delay associated with the detector readout and transmitting detector data after a diffraction measurement, durations shorter than 60 s do not result in a significant time savings for the current experimental setup.

Intensity and z-ratio results from the (111) ring are shown in Fig. 10. It is clear that both duration and aperture size have a strong effect on the peak diffraction intensity (see Fig. 10a). Despite this fact, the significance of the peak is quite strong for even the shortest counting durations, as demonstrated by the 50 μm/300 s and 100 μm/60 s conditions. There is a clear tradeoff between interrogation volume, count time, and statistical discriminating power for a given volumetric ratio of the anomalous grain growth region. These tradeoffs could be parameterized and explored in more detail to improve efficiency in time-resolved studies—such an effort could be particularly rewarding for other beamlines that were not constrained by 120 s readout time or 200 μm maximum beam size.

Fig. 10
figure 10

a Local peak intensity versus χ and b z-ratio versus χ comparing 50 and 100 µm apertures for different collection times

Full size image

Confirmation experiments

The preceding proof-of-concept results were collected on a sample that was broken in half from fatigue testing. This sample was suspected to have pre-existing fatigue-induced grain growth based on a prior destructive-focused ion beam imaging on similar samples [12]. The technique was repeated on a second similar test coupon with comparable anomalous spikes in the diffraction pattern that exists only at the site of crack initiation, as was suspected due to AGG. However, for both of these cases, one could rightfully argue that this ‘needle-in-a-haystack’ technique was biased by prior awareness of the ‘needle.’ In a subsequent experiment, a virgin untested nanocrystalline Ni–Fe fatigue sample was imaged using this new mode of interrogation at periodic intervals throughout a fatigue test. This allowed the technique to be evaluated in its ability to detect the onset of AGG, rather than the aftermath. The diffraction pattern was first scanned on the virgin untested part, at ϕ-tilts from −10° to +10°. In this virgin condition, none of the diffraction patterns contained an anomalous spike. After fatigue testing for 63000 cycles but before fatigue failure, new anomalous diffraction spots emerged on the diffraction rings. Figure 11 shows both the untested reference condition and the fatigued condition of a caked slice of the diffraction ring in the location where an anomalous intensity spike emerged. After eventual fracture, the specimen was confirmed to have suffered from AGG at that location. This proof-of-concept experiment lays the groundwork for a detailed study of the loading conditions and microstructural configurations that give rise to fatigue-induced grain growth with this new mode of interpretation.

Fig. 11
figure 11

A wedge of the caked (111) diffraction ring showing the emergence of an intense peak due to fatigue loading of Ni–Fe. This sharp peak is associated with the single-crystal signature of abnormal grain growth during fatigue loading. Sample tilt ϕ = −10°

Full size image

Discussion

Optimal configurations for this method

While the present paper describes a new concept in observing AGG phenomenon, the experiments were not conducted under ideal circumstances. The beamline employed had been selected for the ill-advised purpose of conducting traditional grain size determination. This monochromatic 2-circle configuration was clearly not well suited for a detailed single-crystal study. A more ideal configuration would involve a 4-circle goniometer, polychromatic or scannable monochromatic X-rays, and a close working distance, high-pixel-count, fast area detector. Such a setup is more commonly found in a microdiffraction beamline, although the small size of a typical micron-sized microdiffraction beam would render large area surveys difficult or impossible. Actually, the new method performed admirably well with even a 200 μm spot size, the largest size available on the beamline—even with a 1 min count time, there was ample signal to identify the presence of abnormal grains. For the purposes of surveying a larger swath of microstructure (a larger ‘haystack’), it appears to be feasible to use even a 1 mm or larger spot size.

Scalability

The present study examines AGG in nanocrystalline alloys. Pure nanocrystalline metals have notoriously unstable grain boundaries—as such, there are concerted efforts to develop stabilized nanocrystalline alloys (e.g., [23]). However, the technique described in this proof-of-concept demonstration should also extend to other scenarios that involve AGG, even in the conventional microcrystalline regime. The technique relies on a sufficiently distinct populations of crystallographic texture. In the present scenario, the parent grains had a relatively modest texture, whereas the grain growth region was populated with essentially a perfect single-crystal texture. A similar distinctly bimodal structure at the macroscale is that of the Goss texture in secondary recrystallized Fe–Si alloys. Indeed, numerous prior studies have shown the emergence of special orientations as a result of heat treatments in X-ray pole figure texture maps (e.g., [24]). The distinction here is that with an intense X-ray source to provide sufficient counting statistics, it is possible to identify even one or a few abnormal grains, rather than relying on distributed bimodal grain growth. A related concern with scaling the technique to microcrystalline grains is that the sampling volume defined by the beam size should scale accordingly to maintain similar counting statistics. In the present scenario, the beam size was ~4000 times larger than the parent grain size. For a hypothetical microcrystalline metal with 25 μm grain size, the scaled beam size should be 100 mm, roughly an order of magnitude larger than conventional X-ray diffraction instruments. With reduced number of grain sampled, the powder ring will be more heterogeneous, rendering discrimination of abnormal events more difficult.

A mode of bimodal grain determination distinct from existing methods

There are several well-established techniques for grain size determination including Warren–Averbach, Williamson–Hall, and even the simplistic Scherrer formulation. These traditional formulations were applied to the integrated diffraction patterns described in the current study and were not able to detect the presence of these isolated abnormally large grains. This result is not surprising, since the peak breadth changes only infinitesimally due to the presence of a single large grain, as do the average grain size and the breadth of grain sizes integrated over a large volume of material. The current technique is also distinguished from conventional peak breadth techniques in that this new technique is conceptually scalable to be used for bimodal grain growth in the microcrystalline regime, a regime where instrumental broadening overwhelms grain size determination by breath measurements. The current proof-of-concept offers an alternative analysis methodology for identifying the onset of AGG. The initial motivation and the confirmation experiments in this study focused on AGG associated with high-cycle fatigue of nanocrystalline metals. However, the technique clearly will apply to thermally induced grain growth in nanocrystalline metals [25], and could likely provide better understanding of AGG phenomena in both metals (e.g., [26]) and ceramics (e.g., [27]). Unlike transmission electron microscopy studies of AGG (e.g., [28]) which are constrained to a relatively small sampling volume, the current technique provides the ability to identify exceptionally rare events in a much larger volume.

Conclusions

Based on the results presented, the use of X-ray synchrotron diffraction to identify abnormal coarse grains in a nanocrystalline matrix shows great potential as a non-destructive and in situ technique. The method presented here of identifying statistically anomalous peak intensities is very different from the line broadening analysis associated with Warren–Averbach or other traditional methods. While those methods can be used to obtain average grain size, and in some cases information regarding the breadth of the grain size distribution, the present method is better suited to identify an astonishingly small fraction of abnormally large grains. The method has been shown to be capable of identifying 350 nm coarse grains in a matrix with an average grain size of 49 nm. In this demonstration, the large (abnormal) grains are identified despite occupying merely ~0.00001 % of the interrogation volume, and are identified with a statistical confidence ≫99.9999 % (5σ). In the method demonstrated in this work, it is possible to miss a large crystallite when it is not properly oriented to diffract, but that limitation can be overcome through several very tractable pathways. The use of statistical methods provides confidence in the measurements, while the incorporation of programming scripts greatly aids in automating the search for coarse grains in a microstructure and helps avoid user bias in identifying significant peaks. The choice of large apertures and short collection times per scan makes the method suitable for in situ experiments when the onset of coarsening is unclear and the location of the coarse grains lends to a “needle in a haystack” problem.