Three-scale analysis of BaTiO₃ piezoelectric thin films fabrication process and its experimental validation

Abstract

A three-scale analysis of crystal growth process is newly proposed based on the first-principles calculation and on the finite element analysis in order to generate a new biocompatible piezoelectric thin film. Crystal growth process of lead-free BaTiO₃ thin films was designed and experimentally generated on SrTiO₃(100), (110), (111), and MgO(100) substrates using the radio-frequency magnetron sputtering method. Crystal structures of BaTiO₃ were measured by X-ray diffraction (XRD) θ/2θ scan. We used Pt for the electrode and measured piezoelectric strain constants d ₃₃ using the ferroelectric measurement system. As a result, analytical crystal orientation fractions on SrTiO₃(110) and (111) substrates had good quantitative agreement with experimental ones, and ones on SrTiO₃(100) and MgO(100) substrates corresponded with these experimental crystal structures. Furthermore, analytically determined piezoelectric strain constants d ₃₃ qualitatively showed a good agreement with experimental ones. Especially, for SrTiO₃(100) and MgO(100) substrates, the differences of d ₃₃ depending on orientation fractions were analyzed by the three-scale simulation accurately. Consequently, it is confirmed that the three-scale analysis is a useful simulation tool to design new biocompatible piezoelectric thin films.

Introduction

Perovskite-type Piezoelectric materials, such as lead zirconate titanate (Pb(Zr,Ti)O₃: PZT) and barium titanate (BaTiO₃), are widely used to construct various sensors [1] and actuators [2], due to their excellent piezoelectricity and responsiveness. Atoms within the unit cells of these materials are stirred along the c-axis of the cubic structure, and these materials distinguish mechanical and electrical anisotropy.

Sputtering [3], chemical vapor deposition (CVD) [4], and molecular beam epitaxy (MBE) [5] are commonly used to fabricate PZT and BaTiO₃ thin films. These piezoelectric thin film fabrication techniques allow us to control the crystal orientation employing a proper choice of the substrate crystal and generate high piezoelectric constants [6, 7]. It is required to develop alternate piezoelectric materials due to the hazardous lead, which is contained in PZT-type piezoelectric materials.

In order to fabricate a new biocompatible piezoelectric thin film, a three-scale analysis was proposed based on the first-principles calculation [8]. The preferred orientations and dielectric properties of piezoelectric thin films were compared with experimental results reported in Ref. [9].

In this study, in order to verify our three-scale analysis, the existing lead-free BaTiO₃ thin films were designed and generated on SrTiO₃(100), (110), (111), and MgO(100) substrates using the radio-frequency (RF) magnetron sputtering processes. Crystal orientations were measured by the X-ray diffraction (XRD) 2θ/θ scan, and piezoelectric properties were measured using the ferroelectric testing system. Experimentally observed crystal orientations and piezoelectric strain constants were compared with analytical results.

Three-scale analysis scheme

Three simulation scales could be denoted as crystal structure, microstructure, and macrostructure, corresponding to the molecule, the crystal grain, and the continuum structure, respectively. Figure 1 shows a flow chart of the analysis algorithm. The specific analysis procedure has been reported previously [8–11]; therefore, only a summary is presented in this article.

Fig. 1

The flowchart of the three-scale simulation based on the first-principles calculation

Simulation of the crystal structure using the first-principles calculation

We focus on a perovskite oxide ABO₃, as shown in Fig. 2, which is expected to have a high piezoelectric constant. The perovskite oxide ABO₃ is constructed from A cation with 12-fold coordination, B cation with sixfold coordination and oxygen. All cationic metals without poisonous elements are selected to candidate elements A and B. The biocompatibility of candidate elements is evaluated by hard and soft acid and bases (HSAB) theory [12]. The interaction energy between biological molecules and candidate elements is estimated by HSAB theory, such HSAB theory can be used to determine biocompatible atoms.

Fig. 2

The cubic structure of the perovskite oxide ABO₃

In order to construct the perovskite structure, the combination of elements is searched by the tolerance factor t as follows:

$$ t = {\frac{{r_{\text{A}} + r_{\text{O}} }}{{\sqrt 2 \left( {r_{\text{B}} + r_{\text{O}} } \right)}}} $$

(1)

where, $r_{\text{A}}$, $r_{\text{B}}$ and $r_{\text{O}}$ are the ionic radii of A, B elements, and oxygen atom, respectively. The ideal perovskite cubic structure indicates $t = 1.00$ , and stable perovskite structures have tolerance factor values approximately $0.75 \le t \le 1.10$.

The stable structures of the perovskite cubic are calculated by the first-principles calculation based on the density functional theory (DFT) [13] using the CASTEP code [14]. The stable structures are, then, computed using an ultra-soft pseudo potential method under the local density approximation (LDA) for exchange and correlation terms. A plane-wave basis set with 450 eV cutoff energy is used, and special k-points are generated by a $8 \times 8 \times 8$ Monkhorst-pack mesh [15].

Recently, many perovskite cubic crystals such as SrTiO₃ and LaNiO₃ have been reported. However, most of these could not be transformed into a tetragonal structure below Curie temperature, because most of perovskite cubic crystals are more stable than tetragonal crystals. Therefore, the tetragonal structure indicates a soft-mode of the phonon oscillation in cubic structure. Lattice parameters and piezoelectric constants of the tetragonal structure are calculated using the DFT.

Prediction of the microstructure using crystallography simulation

We calculate the microstructure consisted of inhomogeneous crystal grains using the process crystallography simulation [8]. Figure 3 shows two examples of analytical results of BaTiO₃ crystal clusters on SrTiO₃(100) substrate, which have (a) [001] and (b) [100] orientations. In the case of [001] orientation of BaTiO₃, at first, we determined the lattice constants a and b calculated by lattice mismatch between BaTiO₃ and the substrate under the condition of c-axis aligned on the substrate. Fixing the values of a and b, we found lattice constant c by minimizing the total energy of strained BaTiO₃ crystal through the DFT. On the other hand, in the case of [100] orientation, at first, we determined b and c calculated by lattice mismatch between BaTiO₃ and the substrate under the condition of a-axis aligned on the substrate. Fixing b and c, we found the lattice constant a by using the same manner.

Fig. 3

Schematic diagrams for some conformations of BaTiO₃ crystal cluster of a [001] and b [100] orientations on SrTiO₃(100) substrate

Total energy increments of strained crystal clusters are calculated by the difference of total energy between stable cluster and strained crystal. We assume that a particular crystal cluster with the lower total energy increment can be grown on the substrate. The crystal orientation fraction $P_{i}$ is calculated under the canonical distribution assumption [16] as follows:

$$ P_{i} = {\frac{{\exp \left[ {{{ - \Updelta E_{i} } \mathord{\left/ {\vphantom {{ - \Updelta E_{i} } {k_{\text{B}} T}}} \right. \kern-\nulldelimiterspace} {k_{\text{B}} T}}} \right]}}{{\sum\limits_{n} {\exp \left[ {{{ - \Updelta E_{n} } \mathord{\left/ {\vphantom {{ - \Updelta E_{n} } {k_{\text{B}} T}}} \right. \kern-\nulldelimiterspace} {k_{\text{B}} T}}} \right]} }}} $$

(2)

where, $n$ means total number of crystal cluster and $\Updelta E$ means total energy increments. $k_{\text{B}}$ is the Boltzmann coefficient and $T$ is the absolute temperature.

Simulation of the macrostructure using the crystallographic homogenization theory

The macrostructure analysis is carried out using the two-scale finite element analysis based on the crystallographic homogenization theory [11]. A microscopic structure is defined as a small periodic region Y at every point in a macroscopic structure Ω, and it is described by unit cells that are characterized by an inhomogeneous structure composed of crystal grains and domains as shown in Fig. 4.

Fig. 4

Hierarchical structure of polycrystalline piezoelectric materials

The microscopic and the macroscopic equations can be obtained to satisfy the principle of virtual work in the overall structure, which combines the microstructure and the macrostructure, for the arbitrary virtual displacement and the electrical potential defined at the microscopic scale. The macroscopic homogenized coefficients, which include the elastic stiffness at zero electric field $C_{ijmn}^{EH}$, the piezoelectric stress constant tensor $e_{pij}^{H}$ , and the dielectric constant tensor at zero strain $\in_{ip}^{SH}$, are described as follows:

$$ C_{ijmn}^{EH} = {\frac{1}{\left| Y \right|}}\int\limits_{\;Y} {\left( {C_{ijmn}^{E} + C_{ijkl}^{E} {\frac{{\partial \chi_{k}^{mn} \left( {x,y} \right)}}{{\partial y_{l} }}} + e_{kij} {\frac{{\partial \phi^{mn} \left( {x,y} \right)}}{{\partial y_{k} }}}} \right)} {\text{d}}Y $$

(3)

$$ \begin{gathered} e_{pij}^{H} = {\frac{1}{\left| Y \right|}}\int\limits_{\;Y} {\left( {e_{pij} + e_{kij} {\frac{{\partial R^{P} \left( {x,y} \right)}}{{\partial y_{k} }}} + C_{ijkl}^{E} {\frac{{\partial \Upphi_{k}^{p} \left( {x,y} \right)}}{{\partial y_{l} }}}} \right)} {\rm d}Y \hfill \\ \quad \;\; = {\frac{1}{\left| Y \right|}}\int\limits_{\;Y} {\left( {e_{pij} + e_{pkl} {\frac{{\partial \chi_{k}^{ij} \left( {x,y} \right)}}{{\partial y_{l} }}} - \in_{pk}^{S} {\frac{{\partial \phi^{ij} \left( {x,y} \right)}}{{\partial y_{k} }}}} \right)} {\rm d}Y \hfill \\ \end{gathered} $$

(4)

$$ \in_{ip}^{SH} = {\frac{1}{\left| Y \right|}}\int\limits_{\;Y} {\left( { \in_{ip}^{S} + \in_{ik}^{S} {\frac{{\partial R^{P} \left( {x,y} \right)}}{{\partial y_{k} }}} - e_{ikl} {\frac{{\partial \Upphi_{k}^{p} \left( {x,y} \right)}}{{\partial y_{l} }}}} \right)} {\rm d}Y $$

(5)

where, $\chi_{k}^{mn} \left( {x,y} \right)$ is the characteristic displacement of the unit cell, $R^{P} \left( {x,y} \right)$ is the characteristic electrical potential of the unit cell and $\phi^{mn} \left( {x,y} \right)$ and $\Upphi_{i}^{P} \left( {x,y} \right)$ is the characteristic coupling function of the unit cell. In addition, $\left| Y \right|$ is the volume of the unit cell and $C_{ijkl}^{E}$, $e_{kij}^{{}}$ , and $\in_{ik}^{S}$ are the microscopic piezoelectric coefficients, which are defined by the piezoelectric properties of the single domain as follows:

$$ C_{ijkl}^{E} = R_{im} R_{jn} R_{kp} R_{lq} C_{mnpq}^{\text{ECrystal}} $$

(6)

$$ e_{kij} = R_{kp} R_{im} R_{jn} e_{pmn}^{\text{Crystal}} $$

(7)

$$ \in_{ik}^{S} = R_{im} R_{jn} \in_{mn}^{\text{SCrystal}} $$

(8)

where, $R_{ij}$ means the coordinate transform tensor from the crystallographic coordinate to the microscopic coordinate, and $C_{mnpq}^{\text{ECrystal}}$, $e_{pmn}^{\text{Crystal}}$ , and $\in_{mn}^{\text{SCrystal}}$ are the piezoelectric coefficients of the single crystal.

In this study, we employ the isoparametric solid finite element with eight nodes and the linear interpolation function is used to obtain the displacement and the electrical potential in the microscopic and macroscopic structures.

RF magnetron sputtering system

In order to fabricate the high quality piezoelectric thin film, the RF magnetron sputtering is adopted seven deposition conditions for the crystal growth control [17]. Three conditions, which include (i) the electric power, (ii) the pressure of argon and oxygen atmosphere, and (iii) the sputtering time, affect the deposition speed and surface condition. (iv) The flux fraction of sputtering gases affects the crystal structure and the composition of BaTiO₃. Crystal growth during deposition is affected by (v) the substrate temperature, (vi) the buffer layer, and (vii) the composition of the substrate. The crystallographic orientation of the thin film is measured by X-ray diffractometer (XRD) using Cu K _α (λ = 0.1541 nm) radiation and compared with analytically determined crystal orientations. In general, the ferroelectric material possesses the spontaneous polarization, which can be switched at 90 or 180 degree by loading external electric field. Consequently, its voltage–displacement curve shows butterfly-type hysteresis loop, as shown in Fig. 5.

Fig. 5

The Voltage–displacement curve of the piezoelectric material

In this study, in order to measure the voltage–displacement curves, the platinum was deposited on the substrate and BaTiO₃ was used as the electrode. The piezoelectric strain constant d ₃₃ is calculated by the gradient at the zero voltage regions in these curves. Analytically determined values of d ₃₃ are compared with experimental ones, and the validity of the three-scale analysis scheme is confirmed.

Three-scale analysis of BaTiO₃ thin films

Lead-free BaTiO₃ thin films were designed by our three-scale analysis. At first, the crystal structure of the tetragonal with minimum total energy was calculated using the DFT. Calculated stable structure of tetragonal BaTiO₃ is shown in Fig. 6. Lattice parameters, a = b = 0.3932 nm and c = 0.3972 nm, were obtained. These lattice parameters had −1.55% and −1.63% errors by comparison with the experimental results, a = b = 0.3992 nm and c = 0.4035 nm, which were reported by Jaffe et al. [18].

Fig. 6

The stable structure of tetragonal BaTiO₃ calculated by first-principles calculation

The process crystallography simulation algorithm was applied to the cases of SrTiO₃(100), (110), (111), and MgO(100) substrates. Lattice constants of SrTiO₃ with the perovskite cubic structure were employed as a = b = c = 0.3905 nm, and lattice constants of MgO with the rocksalt cubic structure were employed as a = b = c = 0.4210 nm. The piezoelectric strain constants of BaTiO₃ single crystal, d ₃₃ = 85.60 pm/V and d ₃₁ = −34.50 pm/V, were employed.

Table 1 shows the crystal orientation, their typical lattice constants and orientation fraction calculated by the process crystallography simulation. [001] and [100] orientations of BaTiO₃ were grown 58.5% and 41.5% on SrTiO₃(100) substrate, and they were grown 46.4% and 53.6% on MgO(100) substrates. In the case of SrTiO₃(110) substrate, BaTiO₃ [110] orientation was grown preferentially, because fractions of [001] and [100] orientations were less than 5%. Furthermore, [111] orientation was grown on SrTiO₃(111) substrate. In general, lattice constants of tetragonal structure have the relationship as a = b ≠ c. However, lattice constants of our results as shown in Table 1 were not shown as a = b ≠ c. In our calculation, we fixed c-axis to coincide with the spontaneous polarization axis of the crystal. But, we did not fixed the equi-length axes as a and b. It means that the normal direction of the substrate plane did not coincide with the c-axis of BaTiO₃ crystal. At first, two lattice constants, which axes formed the plane and lied on the substrate plane, were determined. Next, the third lattice constant was found by minimizing the total energy of strained BaTiO₃ crystal through the DFT.

Table 1 Analytical results of preferred orientations, lattice constants, and their fraction for BaTiO₃ thin films generated on various substrates

Homogenized piezoelectric strain constants d ₃₃ and d ₃₁ of macrostructure obtained by finite element analysis based on the crystallographic homogenization method are shown in Fig. 7. For both constants on SrTiO₃(111) substrate, highest values of d ₃₃ = 156.5 pm/V and d ₃₁ = −125.2 pm/V were obtained. In contrast, for both constants on SrTiO₃(110) substrate, lowest values of d ₃₃ = 8.5 pm/V and d ₃₁ = −9.5 pm/V were obtained. In comparison between SrTiO₃(100) and MgO(100) substrate, d ₃₃ on SrTiO₃(100) was higher and d ₃₁ was lower than those values of MgO(100) substrate. This was because [001] orientation fraction of BaTiO₃ thin film on SrTiO₃(100) substrate was larger than that of MgO(100) substrate.

Fig. 7

The numerical results of piezoelectric strain constants d ₃₃ and d ₃₁

Validation with the RF magnetron sputtering

BaTiO₃ thin films were generated on SrTiO₃(100), (110), (111), and MgO(100) substrates using the RF magnetron sputtering in order to verify the validity of our three-scale analysis scheme.

Table 2 shows the sputtering conditions. The substrate temperature was kept at 800 °C during the sputtering. Argon and oxygen gases were introduced under the pressure of 1.0 Pa in the chamber, and their flux fraction was kept at the ratio of 4:1. The electric powers vary for each substrate, because sputtering conditions are affected by the substrate material and its facets. Therefore, we selected the best power levels for SrTiO₃(100), (110), (111), and MgO(100) substrates, such as 50 W, 100 W, 150 W, and 50 W, respectively. Here, thicknesses of BaTiO₃ thin films on SrTiO₃(100), (110), (111), and MgO(100) substrates were 700 nm, 1100 nm, 1950 nm, and 700 nm, respectively.

Table 2 Sputtering conditions for generation of BaTiO₃ thin films using the RF magnetron sputtering

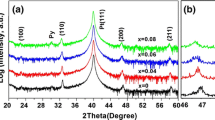
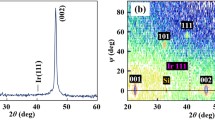
Figure 8 shows the XRD patterns for BaTiO₃ thin films on (a) SrTiO₃(100), (b) SrTiO₃(110), (c) SrTiO₃(111), and (d) MgO(100) substrates, respectively. As shown in Fig. 8b, because only [hh0] orientation of BaTiO₃ on SrTiO₃(110) substrate was observed, it could be concluded that the orientation fraction of [110] was 100%. In addition, Fig. 8c indicates [111] orientation of BaTiO₃ was grown on SrTiO₃(111) at 100% probability. Figure 9 shows the XRD patterns for BaTiO₃ thin films deposited on (a) SrTiO₃(100) and (b) MgO(100) substrates ranged from 43 to 46. In the case of SrTiO₃(100) substrate, 2θ/θ values of [002] and [200] orientations were obtained as 43.88 and 44.08, respectively. On the other hand, 2θ/θ values of [002] and [200] orientations on MgO(100) were 44.13 and 44.27, respectively. Therefore, we concluded that even though differences of 2θ/θ values of [002] and [200] orientations on SrTiO₃(100) and MgO(100) substrates were small, two orientations of [002] and [200] of BaTiO₃ crystal were grown. However, we could not indicate their orientation fractions by XRD measurement.

Fig. 8

XRD patterns for BaTiO₃ thin films: deposited on a SrTiO₃(100), b SrTiO₃ (110), c SrTiO₃(111), and d MgO(100)

Fig. 9

XRD patterns ranged from 43 to 46 for BaTiO₃ thin films: deposited on a SrTiO₃(100) and b MgO(100)

Table 3 shows comparison between analytically determined 2θ/θ angles calculated by lattice constants as shown in Table 1 and experimentally determined 2θ/θ angles observed by using XRD patterns. Errors between analytically and experimentally determined orientations ranged from 1.59 to 2.76%. It means that the process crystallography simulation could predict the epitaxial growth accurately.

Table 3 Comparison between analytically determined and experimentally measured 2θ/θ

In order to compare between analytically determined piezoelectric properties and experimental results and to confirm the preferred orientations, voltage–displacement curves were measured by the ferroelectric testing system as shown in Fig. 10. Here, BaTiO₃ thin films were deposited on platinum-coated substrates, and XRD patterns were confirmed to indicate same peaks, such as [00h] and [h00] orientations of BaTiO₃ on SrTiO₃(100) and MgO(100), [hh0] orientation on SrTiO₃(110) and [111] orientation on SrTiO₃(111), as shown in Fig. 8 Consequently, all films were confirmed to have the piezoelectric properties, because hysteresis loops were observed.

Fig. 10

Voltage–displacement curves of BaTiO₃ thin films: deposited on a SrTiO₃(100), b SrTiO₃(110), c SrTiO₃(111), and d MgO(100)

Figure 11 shows the comparison of piezoelectric strain constants d ₃₃ between experimental and analytical results. Analytically calculated values of d ₃₃ showed errors with a range 18.3–26.9%. This is because we could not calculate the effect of the temperature in the DFT, which was used in the first-principles calculation. Therefore, calculated lattice constants were generally smaller than the experimentally observed lattice constants. In addition, piezoelectric properties were affected by the strain, which was caused by the lattice mismatch with the substrate crystal, but we calculated macro-homogenized piezoelectric strain constants by employing a non-strained single crystal property. Even though the above-indicated reasons might cause the error of the piezoelectric property, our analysis could provide the crystallographic orientation and the piezoelectric property. Especially, d ₃₃ on SrTiO₃(100) substrate in particular was observed to have higher value than the case of MgO(100). It indicated that [001] orientation fraction of BaTiO₃ on SrTiO₃(100) substrate was larger than that of MgO(100). Therefore, it was concluded that our three-scale analysis was able to predict difference of piezoelectric properties with a very small difference of orientation fraction on the particular substrate, and it was useful tool to predict the crystal growth and the piezoelectric properties of the thin film.

Fig. 11

Comparison of piezoelectric strain constants d ₃₃ between analytical and experimental results

Conclusion

In this article, we analyzed BaTiO₃ thin film growth on SrTiO₃(100), (110), (111), and MgO(100) substrates using a three-scale analysis based on the first-principles calculation and crystallographic homogenization theory. BaTiO₃ thin film was generated on these substrates using the RF magnetron sputtering. Analytically determined orientation fractions and piezoelectric properties were compared with XRD results of crystal structure and piezoelectric strain constants d ₃₃ measured by the ferroelectric measurement system.

Consequently, analytically determined crystal orientations grown on SrTiO₃(110) and (111) substrates show good quantitative agreement with experimental results, and ones on SrTiO₃(100) and MgO(100) substrates coincide qualitatively. Furthermore, analytically determined piezoelectric strain constants d ₃₃ coincide with experimentally determined d ₃₃ constant. Especially, from the comparison of SrTiO₃(100) and MgO(100) substrates, it has been suggested that the piezoelectric strain constant d ₃₃ strongly depends on orientation fractions. We also succeeded in the reproduction of this difference. Therefore, it is confirmed that our three-scale analysis based on first-principles calculation can be a useful simulation tool to design a new biocompatible piezoelectric thin film.