Abstract
The refinement order on partitions corresponds to the operation of merging blocks in a partition, which is relevant to image segmentation and filtering methods. Its mathematical extension to partial partitions, that we call standard order, involves several operations, not only merging, but also creating new blocks or inflating existing ones, which are equally relevant to image segmentation and filtering techniques. These three operations correspond to three basic partial orders on partial partitions, the merging, inclusion and inflating orders. There are three possible combinations of these three basic orders, one of them is the standard order, the other two are the merging-inflating and inclusion-inflating orders. We study these orders in detail, giving in particular their minimal and maximal elements, covering relations and height functions. We interpret hierarchies of partitions and partial partitions in terms of an adjunction between (partial) partitions (possibly with connected blocks) and scalars. This gives a lattice-theoretical interpretation of edge saliency, hence a typology for the edges in partial partitions. The use of hierarchies in image filtering, in particular with component trees, is also discussed. Finally, we briefly mention further orders on partial partitions that can be useful for image segmentation.














Similar content being viewed by others
References
Adams, R., Bischof, L.: Seeded region growing. IEEE Trans. Pattern Anal. Mach. Intell. 16(6), 641–647 (1994)
Benzécri, J.P.: L’Analyse de Données, I: la Taxinomie. Dunod, Paris (1973)
Birkhoff, G.: Lattice Theory, 8th printing, 3rd edn. American Mathematical Society Colloquium Publications, vol. 25. American Mathematical Society, Providence (1995)
Blyth, T.: Lattices and Ordered Algebraic Structures. Springer, London (2005)
Cousty, J., Bertrand, G., Couprie, M., Najman, L.: Collapses and watersheds in pseudomanifolds of arbitrary dimension. J. Math. Imaging Vis. (2013, to appear)
Grätzer, G.: General Lattice Theory, 2nd edn. Birkhäuser, Basel (2003)
Guigues, L., Cocquerez, J.P., Le Men, H.: Scale-sets image analysis. Int. J. Comput. Vis. 68(3), 289–317 (2006)
Janowitz, M., Schweizer, B.: Ordinal and percentile clustering. Math. Soc. Sci. 18, 135–186 (1989)
Johnson, S.: Hierarchical clustering schemes. Psychometrika 32(3), 241–254 (1967)
Kiran, B.R., Serra, J.: Ground truth energies for hierarchies of segmentations. In: Luengo Hendriks, C.L., Borgefors, G., Strand, R. (eds.) Mathematical Morphology and Its Applications to Signal and Image Processing. Lecture Notes in Computer Science, vol. 7883, pp. 123–134. Springer, Berlin (2013). doi:10.1007/978-3-642-38294-9_11
Krasner, M.: Nombres semi-réels et espaces ultramétriques. C. R. Hebd. Séances Acad. Sci. 219, 433–435 (1944)
Meyer, F., Najman, L.: Segmentation, minimum spanning tree and hierarchies. In: Najman, L., Talbot, H. (eds.) Mathematical Morphology: From Theory to Applications, pp. 229–261. ISTE/Wiley, New York (2010). Chap. 9
Najman, L.: On the equivalence between hierarchical segmentations and ultrametric watersheds. J. Math. Imaging Vis. 40(3), 231–247 (2011). doi:10.1007/s10851-011-0259-1
Najman, L., Couprie, M.: Building the component tree in quasi-linear time. IEEE Trans. Image Process. 15(11), 3531–3539 (2006)
Najman, L., Schmitt, M.: Watershed of a continuous function. Signal Process. 38(1), 99–112 (1994)
Najman, L., Schmitt, M.: Geodesic saliency of watershed contours and hierarchical segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 18(12), 1163–1173 (1996)
Ore, O.: Theory of equivalence relations. Duke Math. J. 9, 573–627 (1942)
Ore, O.: Chains in partially ordered sets. Bull. Am. Math. Soc. 49, 558–566 (1943)
Pavlidis, T.: Structural Pattern Recognition. Springer, Berlin (1980)
Ronse, C.: A topological characterization of thinning. Theor. Comput. Sci. 43, 31–41 (1986)
Ronse, C.: Set-theoretical algebraic approaches to connectivity in continuous or digital spaces. J. Math. Imaging Vis. 8(1), 41–58 (1998)
Ronse, C.: Partial partitions, partial connections and connective segmentation. J. Math. Imaging Vis. 32(2), 97–125 (2008). doi:10.1007/s10851-008-0090-5
Ronse, C.: Adjunctions on the lattices of partitions and of partial partitions. Appl. Algebra Eng. Commun. Comput. 21(5), 343–396 (2010). doi:10.1007/s00200-010-0129-x
Ronse, C.: Idempotent block splitting on partial partitions, I: isotone operators. Order 28(2), 273–306 (2011). doi:10.1007/s11083-010-9171-3
Ronse, C.: Idempotent block splitting on partial partitions, II: non-isotone operators. Order 28(2), 307–339 (2011). doi:10.1007/s11083-010-9190-0
Ronse, C.: Orders on partial partitions and maximal partitioning of sets. In: Soille, P., Ouzounis, G., Pesaresi, M. (eds.) Proceedings of ISMM 2011, the 10th International Symposium on Mathematical Morphology. Lecture Notes in Computer Science, vol. 6671, pp. 49–60. Springer, Berlin (2011)
Ronse, C., Serra, J.: Algebraic foundations of morphology. In: Najman, L., Talbot, H. (eds.) Mathematical Morphology: From Theory to Applications, pp. 35–80. ISTE/Wiley, New York (2010). Chap. 2
Salembier, P., Oliveras, A., Garrido, L.: Anti-extensive connected operators for image and sequence processing. IEEE Trans. Image Process. 7(4), 555–570 (1998)
Salembier, P., Wilkinson, M.H.F.: Connected operators: a review of region-based morphological image processing techniques. IEEE Signal Process. Mag. 26(6), 136–157 (2009)
Serra, J.: Mathematical morphology for Boolean lattices. In: Serra, J. (ed.) Image Analysis and Mathematical Morphology, II: Theoretical Advances, pp. 37–58. Academic Press, London (1988). Chap. 2
Serra, J.: Morphological segmentations of colour images. In: Ronse, C., Najman, L., Decencière, E. (eds.) Mathematical Morphology: 40 Years on. Computational Imaging and Vision, vol. 30, pp. 151–176. Springer, Dordrecht (2005)
Serra, J.: A lattice approach to image segmentation. J. Math. Imaging Vis. 24(1), 83–130 (2006)
Serra, J.: Ordre de la construction et segmentations hiérarchiques. Tech. rep., ESIEE/A2SI/IGM (2010)
Serra, J.: Grain buiding ordering. In: Soille, P., Ouzounis, G., Pesaresi, M. (eds.) Proceedings of ISMM 2011, the 10th International Symposium on Mathematical Morphology. Lecture Notes in Computer Science, vol. 6671, pp. 37–48. Springer, Berlin (2011)
Serra, J.: Hierarchies and optima. In: Debled-Rennesson, I., Domenjoud, E., Kerautret, B., Even, P. (eds.) DGCI 2011, 16th International Conference on Discrete Geometry for Computer Imagery. Lecture Notes in Computer Science, vol. 6607, pp. 35–46. Springer, Berlin (2011)
Serra, J., Kiran, B.R.: Optima on hierarchies of partitions. In: Luengo Hendriks, C.L., Borgefors, G., Strand, R. (eds.) Mathematical Morphology and Its Applications to Signal and Image Processing. Lecture Notes in Computer Science, vol. 7883, pp. 147–158. Springer, Berlin (2013). doi:10.1007/978-3-642-38294-9_13
Soille, P.: Constrained connectivity for hierarchical image partitioning and simplification. IEEE Trans. Pattern Anal. Mach. Intell. 30(7), 1132–1145 (2008)
Author information
Authors and Affiliations
Corresponding author
Additional information
This work received funding from the Agence Nationale de la Recherche, contract ANR-2010-BLAN-0205-01.
Appendix: Local Knowledge: Truncation and Restriction
Appendix: Local Knowledge: Truncation and Restriction
We introduced numerous binary relations on Π ∗(E), most of them being partial order relations, cf. Table 1. We will now consider how such relations are preserved by the following two operations on partial partitions, for any \(A \in\mathcal{P}(E)\): truncation by A:
and restriction to A:
These operations are relevant to the problem of local knowledge, what Serra [32] calls class permanency: given a partial partition π and a restricted window A, viewing π through A means either truncating all blocks of π, that is, taking π∧1 A , or restricting π to blocks inside A, that is, taking \(\pi\cap\mathcal{P}(A)\); then it becomes interesting to know if these two operations of truncation and restriction preserve a given order on partial partitions.
We first consider compatibility with truncation. The following relations are preserved by truncation by A:
-
The support inclusion, support containment and support equality relations, since supp(π i ∧1 A )=supp(π i )∩A.
-
The standard order: standard lattice theory gives π 1≤π 2 ⇒ π 1∧1 A ≤π 2∧1 A .
-
The merging order, since it is the intersection of the standard order and the support equality relation.
-
The inclusion order: for π 1⊆π 2, the blocks of π 1∧1 A are all non-void B∩A for B∈π 1, so they belong to π 2∧1 A .
-
The inclusion-inflating order, that is, the intersection of the standard order and of the singularity relation. Indeed, let π 1≤π 2 and π 1⇚π 2. Then π 1∧1 A ≤π 2∧1 A . The blocks of π 1∧1 A (resp., π 2∧1 A ) are the non-void B∩A for B∈π 1 (resp., for B∈π 2). If C∩A (C∈π 2) contains B 1∩A and B 2∩A (B 1,B 2∈π 1), then B 1 and B 2 intersect C, and as π 1≤π 2, B 1,B 2⊆C, but as π 1⇚π 2, we deduce that B 1=B 2, so B 1∩A=B 2∩A. Thus π 1∧1 A ⇚π 2∧1 A .
The following relations are not preserved by truncation by A:
-
The singularity relation: take π 1={B,C} and π 2={A}, where B≬A≬C but B,C⊈A, then π 1⇚π 2 but \(\pi_{1} \wedge\mathbf{1}_{A} = \{ A \cap B, A \cap C \} \not\Lleftarrow\pi_{2} = \pi_{2} \wedge\mathbf{1}_{A}\).
-
The building order: take B⊃A⊃∅, π 1=1 B∖A and π 2=1 B , then π 1⋐π 2 but
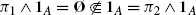 .
. -
The inflating order: take the counterexample given for the building order.
-
The merging-inflating order: take the same counterexample.
We now consider compatibility with restriction. The following relations are preserved by restriction to A:
-
The singularity relation: this is a special case of (12).
-
The building order, see (7).
-
The inclusion order: standard set theory gives \(\pi_{1} \subseteq \pi_{2} \ \Rightarrow\ \pi_{1} \cap\mathcal{P}(A) \subseteq\pi_{2} \cap\mathcal{P}(A)\).
The following relations are not preserved by restriction to A:
-
The support inclusion, support containment and support equality relations; indeed, the support does not tell anything about the existence of blocks included in A.
-
The standard order.
-
The merging order.
-
The inflating order.
-
The merging-inflating order.
-
The inclusion-inflating order.
In fact, any order included in the standard order, that is compatible with restriction, must be included in the inclusion order. Indeed, if π 1≤π 2 but π 1⊈π 2, then there is B∈π 1 and C∈π 2 such that B⊂C, so \(B \in\pi_{1} \cap\mathcal{P}(B)\) but \(\pi_{2} \cap \mathcal{P}(B) \subseteq\pi_{2} \setminus\{C\}\), and B is not included in a block of π 2∖{C}, thus \(\pi_{1} \cap\mathcal{P}(B) \not\le \pi_{2} \cap\mathcal{P}(B)\).
Rights and permissions
About this article
Cite this article
Ronse, C. Ordering Partial Partitions for Image Segmentation and Filtering: Merging, Creating and Inflating Blocks. J Math Imaging Vis 49, 202–233 (2014). https://doi.org/10.1007/s10851-013-0455-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10851-013-0455-2




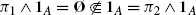 .
.