An Epistemic Separation Logic with Action Models

Abstract

In this paper we present an extension of (bunched) separation logic, Boolean BI, with epistemic and dynamic epistemic modalities. This logic, called action model separation logic ($\mathrm {AMSL}$), can be seen as a generalization of public announcement separation logic in which we replace public announcements with action models. Then we not only model public information change (public announcements) but also non-public forms of information change, such as private announcements. In this context the semantics for the connectives $*$ and $\mathrel {-*}$ from separation logic are epistemic versions of their usual semantics. This is because formulas are interpreted in states, not in resources, and agents may be uncertain between different states representing the same resource. We present the logic $\mathrm {AMSL}$ and its semantics, with a detailed case study that highlights its interest for modeling. We also prove the elimination of the dynamics modalities and discuss some alternative epistemic semantics for the separation connectives.

1 Introduction

Epistemic Logic is the logic of knowledge and belief, which models and expresses properties of knowledge that multiple agents may have about themselves and about each other (Hintikka, 1962; van Ditmarsch et al., 2015). The models of epistemic logic are based on possible worlds, that encode the possible states/configurations of a considered system. The analysis of Moorean phenomena (Moore, 1942) played an important role, for example that you cannot know that some fact p is true and that you do not know this. On the one hand, this multi-agent logic of knowledge was extended with group epistemic notions such as common knowledge (Aumann, 1976; McCarthy, 1990) and distributed knowledge (Hilpinen, 1977). On the other hand, there was increased interest in the analysis of multiple agents informing each other of their ignorance and knowledge, often inspired by logic puzzles (McCarthy, 1990; Moses et al., 1986). This culminated in public announcement logic (PAL) (Plaza, 1989), wherein such informative actions became full members of the logical language besides the knowledge modalities; parallel developments of dynamic but not epistemic logics of information change are van Emde Boas et al. (1984) and van Benthem (1989). A further generalization was to non-public information change such as private or secret announcements to some agents while other agents only partially observe that, in Action Model Logic (AML) (Baltag et al., 1998); parallel, now lesser known, developments are Gerbrandy and Groeneveld (1997) and van Ditmarsch (2000). Extensions of action model logic with factual change have been proposed in van Benthem et al. (2006) and van Ditmarsch and Kooi (2008). An independent quite successful line of research involving knowledge dynamics, that we will bypass in this investigation, is the runs-and-systems approach (Fagin et al., 1995, 1997).

In this context we want to enrich the models of such logics with more structure, namely by considering the possible worlds as resources that can be combined or separated. For that we consider the logic of Bunched Implications (BI) and its variants, like Boolean BI (BBI) (O’Hearn & Pym, 1999; Pym, 2002), that mainly focus on resource sharing and separation. The logics BI and BBI combine propositional classical additive ($\wedge$, $\rightarrow$, $\vee$) and multiplicative ($*$, $\mathrel {-*}$) connectives. The multiplicative conjunction $*$ expresses separation of resources and the multiplicative implication $\mathrel {-*}$ expresses resource update (Galmiche et al., 2005; Pym, 2002).¹ The semantics for BI and BBI is interpreted on resources rather than states, where the main idea is that resources, unlike states, can be used up, so to speak. To satisfy a standard implication $p \rightarrow q$ in a given state it is sufficient to satisfy either $\lnot p$ or q in that state. In particular $p \rightarrow p$ is trivial, a tautology. Whereas to satisfy $p \mathrel {-*}p$ it is far from guaranteed that after having satisfied p in a resource, p is still satisfied in an updated resource. Let us remark that we use here the term “separation logics” to denote the class of logics based on BI and BBI and their modal extensions, even if originally separation logic (SL) is a bunched logic, based on BBI, with resources being memory areas (Ishtiaq & O’Hearn, 2001), and that successfully improved verification of programs with mutable data structures (Reynolds, 2002).

Among extensions of separation logics with other modalities we can mention Dynamic Modal BI (DMBI) (Courtault & Galmiche, 2018) and Epistemic Resource Logic (ERL) (Galmiche et al., 2019). The first one is a BBI extension with the modalities $\Box$, $\Diamond$, and a dynamic modality $\langle a \rangle$, that allows us to investigate how resource properties change when dynamic processes are taking place, with an emphasis on concurrent processes (Courtault & Galmiche, 2018). The second one is a BBI extension with epistemic modalities, that makes a modelling difference between ambient resources and local resources (assigned to each agent), and investigates their composition (Galmiche et al., 2019).

Two other extensions of separation logic are Epistemic separation logic (ESL) (Courtault et al., 2015) and the related Public announcement separation logic (PASL) (Courtault et al., 2019). These works present resource semantics including ways to model uncertainty about resources and to model information updates reducing such uncertainty. The first extends the language of separation logic with knowledge modalities $K_a$ (where a is one out of a finite set of agents), and the second extends it as well with public announcement modalities representing reliable public observations, as in PAL. In these logics the states or worlds represent resources, and the members of the domain should represent a resource monoid. The monoidal structure entails inclusion of a neutral element (neutral, or unit resource). The PASL semantics of public announcement are therefore different from the usual model restricting PAL semantics. A domain restriction risks eliminating the state representing the neutral resource, in which case the domain of the resulting updated model would no longer correspond to a resource monoid. However, as dynamic processes are carried out it is vital that—in any case—the structure of our updated model still contains the neutral element, so that the monoidal structure is preserved. In $\mathrm {PASL}$ the issue was resolved by a so-called refinement semantics for public announcement (van Benthem & Liu, 2007), that ensures that no state (and therefore no resource) is ever removed from the model.

In action model separation logic (AMSL) that we present in this paper we generalize the dynamic aspects of $\mathrm {PASL}$  by replacing public announcements with action models. In $\mathrm {AMSL}$ we not only model public information change (public announcements) but also non-public forms of information change, such as private announcements, multi-casts, etc. Also, we can model factual change. Unlike in $\mathrm {PASL}$, we cannot identify states with resources, as uncertainty about the actual state may involve uncertainty between different states representing the same resource. As a consequence, our semantics for $*$ and $\mathrel {-*}$ cannot be as in BBI but are necessarily ‘epistemic’ versions of that, where we detailedly motivate different choices. In the semantics of AMSL a state still represents a resource, as in PASL, but different states can now be mapped to the same resource. The updated epistemic model—obtained after action model execution—preserves all state-to-resource mappings. But even if in some initial model only a single state was mapped to some resource, the updated model may contain several copies of that state still mapped to that same resource. Additionally, to preserve the resource monoid part of our structure we also require that our action model is covering, a technical requirement ensuring that the updated model always contains a state assigned to the neutral resource. Just as for $\mathrm {PASL}$, for this logic $\mathrm {AMSL}$ we show that we can eliminate the dynamic modalities. In other words: every formula in the language with dynamic modalities is equivalent to a formula in the language without these modalities. We also provide a detailed case study of the use of our logic.

Section 2 presents the logic $\mathrm {AMSL}$, its syntax, semantics, and associated structures, with a focus on the motivation for the proposed semantics in comparison with the BBI semantics. The expressivity is also analyzed. Section 3 provides a modelling example in which we compare $\mathrm {PASL}$ and $\mathrm {AMSL}$ with regard to their abilities to model public and private communications. Section 4 provides a reduction of dynamic modalities for action models, thus demonstrating that $\mathrm {AMSL}$ and ESL have the same expressivity. Section 5 investigates alternative epistemic semantics for resource composition and separation. Finally, Sect. 6 gives some conclusions and perspectives.

2 Action Model Separation Logic

Throughout the contribution, given are a finite set of agents A (with members denoted $a,b,c,\dots$) and a countable set of propositional variables (atoms) P (with members denoted $p,q,p',q',p_1,p_2,\dots$).

2.1 Syntax

The language ${\mathcal {L}}_{*{K}\otimes }(A,P)$ of action model separation logic ($\mathrm {AMSL}$) is defined as

$$\begin{aligned} \psi \, {::=} \, p \mid \bot \mid I \mid \lnot \psi \mid (\psi \wedge \psi ) \mid (\psi *\psi ) \mid (\psi \mathrel {-*}\psi ) \mid K_a \psi \mid [{\mathcal {E}}_e] \psi \end{aligned}$$

where ${\mathcal {E}}_e$ is an epistemic action (for language ${\mathcal {L}}_{*{K}\otimes }(A,P)$) as defined below. Members of a language are denoted formulas and denoted with lower case Greek letters $\varphi ,\psi ,\eta , \varphi ',\dots$.

Other propositional connectives are defined by abbreviation, such as $\varphi \rightarrow \psi := \lnot (\varphi \wedge \lnot \psi )$. Dual modalities are also defined by abbreviation, such as ${\hat{K}}_a \varphi := \lnot K_a \lnot \varphi$ and $\langle {\mathcal {E}}_e \rangle \varphi := \lnot [{\mathcal {E}}_e]\lnot \varphi$. Connective $*$ (resp. $\wedge$) is the multiplicative (resp. additive) conjunction and connective $\mathrel {-*}$ (resp. $\rightarrow$) is the multiplicative (resp. additive) implication. Expression $K_a \psi$ stands for “agent a knows that $\psi$.” Expression $[{\mathcal {E}}_e]\varphi$ stands for “after execution of action ${\mathcal {E}}_e$, $\varphi$ is true.”. Parentheses in formulas, and parameters A and P in ${\mathcal {L}}_{*{K}\otimes }(A,P)$, are omitted unless confusion results. The $K_a$ in formula $K_a \psi$ is an epistemic modality and the $[{\mathcal {E}}_e]$ in formula $[{\mathcal {E}}_e]\psi$ is a dynamic modality.

The following language fragments are also of interest. The fragment of the language without the $[{\mathcal {E}}_e]$ modalities is denoted ${\mathcal {L}}_{*{K}}$, and without $K_a$ modalities as well it is denoted ${\mathcal {L}}_{*}$ (the language of separation logic). The fragment without $*$ and $\mathrel {-*}$ is denoted ${\mathcal {L}}_{K\otimes }$ (the language of action model logic) and without $[{\mathcal {E}}_e]$ as well we get ${\mathcal {L}}_K$ (the language of epistemic logic).

2.2 Structures

Definition 1

(Resource monoid) A partial resource monoid (or resource monoid) is a structure ${\mathcal {R}}= (R, \circ , n)$ where R is a set of resources (with members denoted $r,r',r_1,r_2,\dots$) containing a neutral element n, and where $\circ : R \times R \rightarrow R$ is a resource composition operator that is associative, that may be partial and such for all $r \in R$, $r \circ n = n \circ r = r$. If $r \circ r'$ is defined we write $r \circ r' \!\downarrow$ and if $r \circ r'$ is undefined we write $r \circ r' \!\uparrow$. When writing $r \circ r' = r''$ we assume that $r \circ r' \!\downarrow$.

Definition 2

(Epistemic frame) An epistemic frame (frame) is a structure $(S,\sim )$ such that S is a set of states (with members denoted $s,t,s',t', \dots$) and ${\sim } : A \rightarrow {{\mathcal {P}}}(S\times S)$ is a function that maps each agent a to an equivalence relation $\sim \!\!(a)$ denoted as $\sim _{a}$.

Definition 3

(Epistemic resource model) Given a resource monoid ${\mathcal {R}}= (R,\circ ,n)$, an epistemic resource model (or plainly model) is a structure ${\mathcal {M}}= (S,\sim ,\varvec{r}_{},V)$ such that S is a domain of states (or worlds), ${\sim } : A \rightarrow {{\mathcal {P}}}(S\times S)$ is a function that maps each agent a to an equivalence relation $\sim _{a}$, surjection $\varvec{r}_{} : S \rightarrow R$ is a resource function, that maps each state to a resource and where we write $\varvec{r}_{s}$ for $\varvec{r}_{}(s)$, and $V: P \rightarrow {{\mathcal {P}}}(S)$ is a valuation function, where V(p) denotes the set of states where variable p is true. Given $s \in S$, the pair $({\mathcal {M}},s)$ is a pointed epistemic resource model, denoted ${\mathcal {M}}_s$.

Definition 4

(Action model) Given a logical language ${\mathcal {L}}$, an action model ${\mathcal {E}}$ is a structure ${\mathcal {E}}= (E,\approx , pre , post )$, such that E is a finite domain of actions (denoted $e,f,g,\dots$), $\approx _a$ an equivalence relation on E for all $a \in A$, $pre : E \rightarrow {\mathcal {L}}$ is a precondition function, and $post : E \rightarrow P \rightarrow {\mathcal {L}}$ is a postcondition function such that every $post (e)$ is only finitely different from the identity: we can see its domain as a finite set of variables $Q \subseteq P$. Given $e \in E$, a pointed action model (or epistemic action) is a pair $({\mathcal {E}},e)$, denoted ${\mathcal {E}}_e$. An action model is covering if $\bigvee _{e \in E} pre (e)$ is a validity of the logic of ${\mathcal {L}}$. We require all action models to be covering.

2.3 Motivation for the Semantics

Before we present the epistemically motivated semantics for $*$ and $\mathrel {-*}$, we first wish to motivate our deviation from the standard BBI semantics. In this subsection, for extra clarity, instead of mathematical English terminology we write $\forall$ for ‘for all’, $\exists$ for ‘there is’, & for ‘and’ and $\Rightarrow$ for ‘implies’.

The standard BBI semantics for $*$ and $\mathrel {-*}$ is as follows. Let a resource monoid ${\mathcal {R}}= (R, \circ , n)$ be given and let $r \in R$ and let $\varphi ,\psi \in {\mathcal {L}}_*$ (by ‘$\exists r'r''$’ we mean $\exists r'r''\in R$, etc.):

$$ \begin{aligned} \begin{array}{lll} r \models \varphi *\psi &{}\quad \text {iff} &{}\; \exists r'r'': r = r' \circ r'' \ \& \ r' \models \varphi \ \& \ r'' \models \psi \\ r \models \varphi \mathrel {-*}\psi &{}\quad \text {iff} &{} \; \forall r': r \circ r'\!\downarrow \ \& \ (r' \models \varphi \Rightarrow r\circ r' \models \psi ) \end{array} \end{aligned}$$

The AMSL semantics that we will propose is for states (worlds), not for resources. This means that $r \models \varphi$ is replaced by ${\mathcal {M}}_s \models \varphi$. Multiple states can be mapped to a single resource. This implies that we can either require all states mapped to a resource to satisfy a given formula or that we require some state mapped to this resource to satisfy that formula. Any $r \models \varphi$ under the scope of a declared resource r can thus be replaced by either $\forall s: \varvec{r}_{s} = r \Rightarrow {\mathcal {M}}_s \models \varphi$ or by $\exists s: \varvec{r}_{s} = r \ \& \ {\mathcal {M}}_s \models \varphi$.²

This straightforwardly gives us four versions for the $*$ semantics, denoted $*^{\forall \forall }$, $*^{\forall \exists }$, $*^{\exists \forall }$, $*^{\exists \exists }$, and four versions for the $\mathrel {-*}$ semantics, denoted $\mathrel {-*}^{\forall \forall }$, $\mathrel {-*}^{\forall \exists }$, $\mathrel {-*}^{\exists \forall }$, $\mathrel {-*}^{\exists \exists }$.

Let us make this computation for $*^{\exists \exists }$, as an example. Assume ${\mathcal {M}}= (S,\sim ,\varvec{r}_{},V)$ with $\varvec{r}_{} : S \rightarrow R$, and $s \in S$. By ‘$\exists t$’ we mean $\exists t \in S$, etc.

$$ \begin{aligned} \begin{array}{lll} &{}&{}{\mathcal {M}}_s \models \varphi *^{\exists \exists } \psi \\ &{} \text {iff} &{}\; \exists r'r'' : \varvec{r}_{s} = r' \circ r'' \ \& \ (\exists t: \varvec{r}_{t} = r' \ \& \ {\mathcal {M}}_{t} \models \varphi ) \ \& \ (\exists u: \varvec{r}_{u} = r'' \ \& \ {\mathcal {M}}_{u} \models \psi ) \end{array}\end{aligned}$$

There are different ways to write this. For a compositional semantics specifiying what is true in a state it seems preferable that the decomposition is also by quantifying over states and not over resources. One can easily transform the above into an equivalent description in terms of states. For the final paraphrase we revert to mathematical English again.

$$ \begin{aligned} \begin{array}{lll} &{}&{} {\mathcal {M}}_s \models \varphi *^{\exists \exists } \psi \\ &{} \text {iff} &{}\quad \exists r'r'' : \varvec{r}_{s} = r' \circ r'' \ \& \ (\exists t: \varvec{r}_{t} = r' \ \& \ {\mathcal {M}}_{t} \models \varphi ) \ \& \ (\exists u: \varvec{r}_{u} = r'' \ \& \ {\mathcal {M}}_{u} \models \psi ) \\ &{} \text {iff} &{}\quad \exists r'r''tu : \varvec{r}_{s} = r' \circ r'' \ \& \ \varvec{r}_{t} = r' \ \& \ \varvec{r}_{u} = r'' \ \& \ {\mathcal {M}}_{t} \models \varphi \ \& \ {\mathcal {M}}_{u} \models \psi \\ &{}\text {iff} &{}\quad \exists tu : \varvec{r}_{s} = \varvec{r}_{t} \circ \varvec{r}_{u} \ \& \ {\mathcal {M}}_t \models \varphi \ \& \ {\mathcal {M}}_u \models \psi \\ &{}\text {iff} &{}\quad \text {there are } t,u \in S \text { such that } \varvec{r}_{s} = \varvec{r}_{t} \circ \varvec{r}_{u}, {\mathcal {M}}_t \models \varphi \text { and } {\mathcal {M}}_u \models \psi \end{array} \end{aligned}$$

For $\mathrel {-*}^{\exists \exists }$ we get this.

$$ \begin{aligned} \begin{array}{lll} &{}&{} {\mathcal {M}}_s \models \varphi \mathrel {-*}^{\exists \exists } \psi \\ &{} \text {iff} &{}\;\, \forall r' : (\varvec{r}_{s} \circ r' \!\downarrow \ \& \ (\exists t: \varvec{r}_{t} = r' \ \& \ {\mathcal {M}}_{t} \models \varphi )) \ \Rightarrow \ (\exists u: \varvec{r}_{u} = \varvec{r}_{s} \circ r' \ \& \ {\mathcal {M}}_{u} \models \psi ) \\ &{} \text {iff} &{}\;\, \forall r't : (\varvec{r}_{s} \circ r' \!\downarrow \ \& \ \varvec{r}_{t} = r' \ \& \ {\mathcal {M}}_{t} \models \varphi ) \ \Rightarrow \ (\exists u: \varvec{r}_{u} = \varvec{r}_{s} \circ r' \ \& \ {\mathcal {M}}_{u} \models \psi ) \\ &{}\text {iff} &{}\;\, \text {for all } t\in S \text { such that } \varvec{r}_{s} \circ \varvec{r}_{t} \downarrow \text { and } {\mathcal {M}}_t \models \varphi \\ &{}&{}\;\, \text {there is } u \in S \text { such that } \varvec{r}_{u} = \varvec{r}_{s} \circ \varvec{r}_{t} \text { and } {\mathcal {M}}_u \models \psi \end{array} \end{aligned}$$

Not all versions of $*$ and $\mathrel {-*}$ have such straightforward paraphrases in terms of states and epistemic models, and not all versions of $*$ and $\mathrel {-*}$ seem to make modelling sense. We privilege the combination of $*^{\exists \exists }$ with $\mathrel {-*}^{\exists \exists }$ in the continuation, and we therefore continue to write $*$ and $\mathrel {-*}$ for those, as usual in BBI. In a later section we also discuss the combination of $*^{\forall \forall }$ with $\mathrel {-*}^{\forall \forall }$. The $\exists \exists$ pair models the intuition that we separate/update the resources as well as the epistemics, where the $\forall \forall$ version models that we separate/updates resource despite the uncertainty about resources. Section 5 will explain the difference in detail.

2.4 Semantics

In this section we present the semantics. Note that $*$ means $*^{\exists \exists }$, and $\mathrel {-*}$ means $\mathrel {-*}^{\exists \exists }$.

Definition 5

(Satisfaction relation) The satisfaction relation $\models$ between pointed epistemic resource models ${\mathcal {M}}_s$, where ${\mathcal {M}}= (S,\sim ,\varvec{r}_{},V)$, for resources ${\mathcal {R}}= (R,\circ ,n)$, and where $s \in S$, and formulas in ${\mathcal {L}}_{*{K}\otimes }(A,P)$, is defined by induction on formula structure.

$$\begin{aligned} \begin{array}{lll} {\mathcal {M}}_s \models p &{}\quad \text {iff} &{}\;\, s \in V(p) \\ {\mathcal {M}}_s \models \bot &{}\quad \text {iff} &{}\;\, \text {false} \\ {\mathcal {M}}_s \models I &{}\quad \text {iff} &{}\;\, \varvec{r}_{s} = n \\ {\mathcal {M}}_s\models \lnot \varphi &{}\quad \text {iff} &{}\;\, {\mathcal {M}}_s\not \models \varphi \\ {\mathcal {M}}_s\models \varphi \wedge \psi &{}\quad \text {iff} &{}\;\, {\mathcal {M}}_s\models \varphi \ \text {and} \ {\mathcal {M}}_s\models \psi \\ {\mathcal {M}}_s \models \varphi *\psi &{}\quad \text {iff} &{}\;\, \text { there exist } t,u \in S \text { s.t. } \varvec{r}_{s} = \varvec{r}_{t} \circ \varvec{r}_{u}, {\mathcal {M}}_t \models \varphi \text { and }{\mathcal {M}}_u \models \psi \\ {\mathcal {M}}_s \models \varphi \mathrel {-*}\psi &{}\quad \text {iff} &{}\;\, \text {for all } t\in S \text { such that } \varvec{r}_{s} \circ \varvec{r}_{t} \downarrow \text { and } {\mathcal {M}}_t \models \varphi , \\ &{}&{}\;\, \text {there exists } u \in S \text { such that } \varvec{r}_{u} = \varvec{r}_{s} \circ \varvec{r}_{t} \text { and } {\mathcal {M}}_u \models \psi \\ {\mathcal {M}}_s\models K_a\varphi &{}\quad \text {iff} &{}\;\, {\mathcal {M}}_t\models \varphi \text { for all } t\in S \text { such that } s \sim _a t \\ {\mathcal {M}}_s \models [{\mathcal {E}}_e]\varphi &{}\quad \text {iff} &{}\;\, {\mathcal {M}}_s \models pre (e) \text {implies } ({\mathcal {M}}\otimes {\mathcal {E}})_{(s,e)} \models \varphi \end{array} \end{aligned}$$

where in the clause for $[{\mathcal {E}}_e]\varphi$, ${\mathcal {E}}$ is a covering action model, $({\mathcal {M}}\otimes {\mathcal {E}})$ is defined below, and $(s,e) \in {\mathcal {D}}({\mathcal {M}}\otimes {\mathcal {E}})$. A formula $\varphi$ is valid on model ${\mathcal {M}}$, notation ${\mathcal {M}}\models \varphi$, iff for all $s \in S$, ${\mathcal {M}}_s \models \varphi$, and $\varphi$ is valid, notation $\models \varphi$, iff $\varphi$ is valid on all models ${\mathcal {M}}$.

Definition 6

Given are resource monoid ${\mathcal {R}}= (R,\circ ,n)$, epistemic resource model ${\mathcal {M}}= (S, \sim , \varvec{r}_{}, V)$, and covering action model ${\mathcal {E}}= (E, \approx , pre , post )$. The updated epistemic resource model ${\mathcal {M}}\otimes {\mathcal {E}}= (S',\sim ',\varvec{r}_{}',V')$ is defined as

$$\begin{aligned} \begin{array}{lll} S' &{}\;\, =&{}\;\, \{(s,e) \mid {\mathcal {M}}_s \models pre (e) \} \\ (s,e) \sim '_a (t,f) &{}\;\, \text {iff} &{}\;\, s \sim _a t \text { and } e \approx _a f \\ (s,e) \in V'(p) &{}\;\, \text {iff} &{}\;\, {\mathcal {M}}_s \models post (e)(p) \\ \varvec{r}_{(s,e)}' &{}\;\, = &{}\;\, \varvec{r}_{s} \end{array}\end{aligned}$$

Note that ${\mathcal {M}}\otimes {\mathcal {E}}$ is again an epistemic resource model for monoid $({\mathcal {R}},\circ ,n)$. In particular, let $t \in S$ be the state such that $\varvec{r}_{t} = n$. As ${\mathcal {E}}$ is a covering action model, there is $f \in E$ such that ${\mathcal {M}}_t \models pre (f)$ so that (t, f) is in the domain of ${\mathcal {M}}\otimes {\mathcal {E}}$. This is important, as $\varvec{r}_{(t,f)}=\varvec{r}_{t}=n$.

2.5 Public and Private Announcement as Action Models

Three common epistemic actions are the public announcement (Plaza, 1989), the semi-private announcement (also known as semi-public announcement) (van Ditmarsch, 2002), and a version of the semi-private announcement where the non-informed agents are uncertain if the announcement has been made (as described in for example (van Ditmarsch et al., 2008), that we denote the suspected semi-private announcement. The last epistemic action is non-deterministic so that multiple states in updated models may then map to the same resource.

For the public announcement we use the ‘refinement’ semantics of van Benthem and Liu (2007), also employed in Courtault et al. (2019). The standard semantics of Plaza (1989) that restricts the domain is unsuitable as we require the action model to be covering. Whereas the refinement semantics for public announcement makes it a covering action model.

Given some domain of states S, the identity relation is the binary relation on S defined as $I := \{ (s,s) \mid s \in S \}$, and the universal relation is the relation defined as $U := \{ (s,t) \mid s,t \in S \}$ (that is, $U = S \times S$).

We define the public announcement ${\mathcal {E}}_e$ where ${\mathcal {E}}= (E,\approx , pre , post )$ and $e \in E$, the semi-private announcement ${\mathcal {E}}'_{e'}$ where ${\mathcal {E}}' = (E',\approx ', pre ', post ')$ and $e' \in E'$, and the suspected semi-private announcement ${\mathcal {E}}''_{e''}$ where ${\mathcal {E}}'' = (E'',\approx '', pre '', post '')$ and $e'' \in E''$. In all three cases the postconditions are trivial, i.e., for any action point e of their respective domains $E,E',E''$, we have that $post (e)(p)=p$ for any $p \in P$. Postconditions are therefore omitted from the definitions.

Let $\varphi \in {\mathcal {L}}_{*{K}\otimes }$, $a \in A$, $B \subseteq A$, $b \in B$ and $c \in A \!\setminus \! B$.

$$\begin{aligned} \begin{array}{lll|lll|lll} E &{} = &{} \{e,f\} \;&{}\; E' &{} = &{} \{e',f'\} \;&{} \;E'' &{} = &{} \{e'',f'',g''\} \\ \approx _a &{} = &{} I \;&{}\; \approx '_b &{} = &{} I \;&{}\; \approx ''_b &{} = &{} I \\ &{}&{} &{}\; \approx '_c &{} = &{} U \;&{}\; \approx ''_c &{} = &{} U \\ pre (e) &{}=&{} \varphi \;&{}\; pre '(e') &{}=&{} \varphi \;&{}\; pre ''(e'') &{}=&{} \varphi \\ pre (f) &{}=&{} \lnot \varphi \;&{}\; pre '(f') &{}=&{} \lnot \varphi \;&{}\; pre ''(f'') &{}=&{} \lnot \varphi \\ &{}&{} &{} &{}&{} &{}\; pre ''(g'') &{}=&{} \top \end{array} \end{aligned}$$

By notational abbreviation for their respective modalities binding formulas, we denote public announcement of $\varphi$ binding $\psi$ as $[\varphi ]\psi$, semi-private announcement (to subgroup $B \subseteq A$ of agents) as $[\varphi ]_B\psi$ and where $[\varphi ]_{\{a\}}\psi$ is written $[\varphi ]_a\psi$, and suspected semi-private announcement as $[\varphi ]^+_{B}\psi$ ($[\varphi ]^+_{a}\psi$), where $[\varphi ]^-_{B}\psi$ represents that nothing happened (precondition $\top$); and similarly for their diamond versions: $\langle \varphi \rangle \psi$, $\langle \varphi \rangle _B\psi$, $\langle \varphi \rangle ^+_{B}\psi$, $\langle \varphi \rangle ^-_{B}\psi$. Note that $[\varphi ]^-_{B}\psi$ has the same meaning as $[\lnot \varphi ]^-_{B}\psi$ and that $\langle \varphi \rangle ^-_{B}\psi$ has the same meaning as $\langle \lnot \varphi \rangle ^-_{B}\psi$: either way, the precondition is $\top$, the notation is merely to evoke the preconditions for the informative part of the action model.

2.6 Expressivity

The extension of the epistemic language with $*$ and $\mathrel {-*}$ enhances the expressivity. Given two logical languages ${\mathcal {L}}$ and ${\mathcal {L}}'$ (and a logical semantics), ${\mathcal {L}}$ is at least as expressive as ${\mathcal {L}}'$ if for every formula in ${\mathcal {L}}$ there is an equivalent formula in ${\mathcal {L}}'$, notation ${\mathcal {L}}\ge {\mathcal {L}}'$. If ${\mathcal {L}}\ge {\mathcal {L}}'$ and ${\mathcal {L}}' \ge {\mathcal {L}}$, then ${\mathcal {L}}$ and ${\mathcal {L}}'$ are equally expressive (as expressive). If ${\mathcal {L}}\ge {\mathcal {L}}'$ and ${\mathcal {L}}' \not \ge {\mathcal {L}}$, then ${\mathcal {L}}$ is more expressive than ${\mathcal {L}}'$.

As ${\mathcal {L}}_{K}$ is a sublanguage of ${\mathcal {L}}_{*{K}}$, it is trivial that ${\mathcal {L}}_{*{K}}$ is at least as expressive as ${\mathcal {L}}_K$. By example we now show that ${\mathcal {L}}_K$ is not at least as expressive as ${\mathcal {L}}_{*{K}}$. And from both then follows that ${\mathcal {L}}_{*{K}}$ is more expressive then ${\mathcal {L}}_K$.

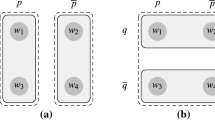
Consider the following epistemic resource model ${\mathcal {M}}= (S,\sim ,\varvec{r}_{},V)$ for a single agent a and a single atom p, with $S = \{s,t,u\}$, ${\sim _a} = {S^2}$, $\varvec{r}_{s}=0$, $\varvec{r}_{t}=1$, $\varvec{r}_{u}=2$, and $V(p) = \{1\}$. The resource monoid ${\mathcal {R}}= \{\{0,1,2\},\circ \}$ represents agent a (Alice) being allowed to borrow 0, 1, or 2 books from a library, where 2 is the maximum (we anticipate on a more detailed subsequent example in Sect. 3). Unfortunately Alice forgot how many books she still has at home, and she is therefore uncertain between all three options. The resource composition $\circ$ is defined as: $r \circ r' \uparrow$ if $r+r' > 2$, and otherwise $r \circ r' = r+r'$. Note that 0 is the neutral element n. A depiction of the model is:

We now have, for example, that:

$$\begin{aligned} \begin{array}{l} M_s \models \lnot p \wedge \lnot (p *p) \\ M_t \models p \\ M_u \models p *p \end{array} \end{aligned}$$

However, in the language without $*$ and $\mathrel {-*}$, we cannot distinguish the states s and u. It is easy to show by formula induction that for all $\varphi \in {\mathcal {L}}_{K}$, ${\mathcal {M}}_s \models \varphi$ iff ${\mathcal {M}}_u \models \varphi$, where we note that for the inductive case ‘knowledge’ according to the semantics both s and u satisfy the same formulas of form $K_a \varphi$, because: ${\mathcal {M}}_s \models K_a \varphi$, iff ${\mathcal {M}}_u \models K_a \varphi$, iff ${\mathcal {M}}_s \models \varphi$ and ${\mathcal {M}}_t \models \varphi$ and ${\mathcal {M}}_u \models \varphi$. On the other hand we can distinguish state t from states s and u, namely by the atom p that is only true in t: ${\mathcal {M}}_s \not \models p$ and ${\mathcal {M}}_u \not \models p$, whereas ${\mathcal {M}}_t \models p$.

Therefore ${\mathcal {L}}_K$ is not at least as expressive as ${\mathcal {L}}_{*{K}}$.

3 The Library Example

In this section we illustrate the semantics with a detailed example. It recalls the ‘library’ example from Courtault et al. (2019), where we now can give a much greater variety of dynamics, not only for public information change (public announcements) as in Courtault et al. (2019) but for any type of epistemic action, such as also private announcements.

Alice and Bob want to borrow books from a library. They are allowed to borrow at most two books. Their book requests are known to the librarian. The librarian can carry at most two requested books.

Formally, there two agents a, b (Alice and Bob) and three propositional variables $p_a,p_b,c$, standing for ‘Alice requests one book and Bob requests no books’, ‘Alice requests no books and Bob requests one book’, and ‘the librarian can carry the requested books’. Resources are pairs (i, j) representing that Alice requests i books and Bob requests j books. The resource monoid ${\mathcal {R}}= (R,\circ ,n)$ is such that: $R = \{ (i,j) \mid 0 \le i,j \le 2 \}$, the neutral element $n = (0,0)$, and resource composition $\circ$ is defined as: $(i_1,j_1) \circ (i_2,j_2)=(i_1+i_2,j_1+j_2)$ if these sums are both at most 2 and otherwise $(i_1,j_1) \circ (i_2,j_2) \!\uparrow$. The initial epistemic model is ${\mathcal {M}}= (S,\sim ,\varvec{r}_{,}V)$ where

$$\begin{aligned} S= & {} \{ ij \mid i,j \in {\mathbb {N}}, 0 \le i,j \le 2 \} \\ \sim _a= & {} \{ (ij,i'j') \mid i = i' \} \\ \sim _b= & {} \{ (ij,i'j') \mid j = j' \} \\ \varvec{r}_{ij}= & {} (i,j) \\ V(p_a)= & {} \{ 10 \}\\ V(p_b)= & {} \{ 01 \}\\ V(c)= & {} \{ ij \mid i+j \le 2 \} \end{aligned}$$

It encodes that agents are aware of the previous scenario and otherwise only know how many books they requested themselves.

The model is depicted in Fig. 1. In the figure we use the following conventions. Links for Alice (a) are solid and links for Bob (b) are dashed. Grey means ‘cannot carry’. States are labelled with resources they map to. Model ${\mathcal {M}}^1$ is the initial model; ${\mathcal {M}}^2$ is the result of the public announcement whether the librarian can carry the books; ${\mathcal {M}}^3$ is the result of the semi-private announcement of that to Alice; ${\mathcal {M}}^4$ is the result of the suspected semi-private announcement of that to Alice. The dashes between the two submodels of ${\mathcal {M}}^4$ represent that states mapping to the same resource are indistinguishable for Bob.

Fig. 1

Alice and Bob request at most two books from a librarian who can carry at most two requested books. Visual conventions are explained in the main text

We now model check some formulas in this setting, in particular involving dynamics.

• Alice and Bob both request one book.

  $$\begin{aligned} {\mathcal {M}}^1_{11} \models p_a *p_b \end{aligned}$$

  Note that ${\mathcal {M}}^1_{11} \not \models p_a \wedge p_b$. The ordinary conjunction is not satisfied here, only the multiplicative conjunction. The ordinary conjunction is unsatisfiable on this model for the given set of resources, as a state cannot be mapped to (0, 1) and (1, 0) simultaneously.

• ...but neither Alice nor Bob knows that! For example:

  $$\begin{aligned} {\mathcal {M}}^1_{11} \not \models K_a (p_a *p_b) \end{aligned}$$

  This is because Alice does not know that Bob has requested one book, although she knows that she has one book herself. Alice also considers it possible that Bob has requested two books, that is: ${\mathcal {M}}^1_{11} \models {\hat{K}}_a (p_a *(p_b *p_b))$. Or that Bob has not requested any book.

• Even if Alice and Bob request one book, they are both uncertain whether the librarian will be able to handle (carry) their request. Let us abbreviate $K_a \varphi \vee K_a \lnot \varphi$ (Alice knows whether $\varphi$) by $Kw _a \varphi$, and similarly for $Kw _b\varphi$ (Bob knows whether $\varphi$).

  $$\begin{aligned} {\mathcal {M}}^1 \models (p_a *p_b) \rightarrow (\lnot Kw _a c \wedge \lnot Kw _b c) \end{aligned}$$

  Note that this is a model validity (only a single state, 11, satisfies the antecedent).

• However, after the librarian informed them whether can he carry the requested books, they know that (where the resulting model is ${\mathcal {M}}^2$).

  $$\begin{aligned} {\mathcal {M}}^1 \models [c]( Kw _a c \wedge Kw _b c) \quad \text { as well as } \quad {\mathcal {M}}^1 \models [\lnot c]( Kw _a c \wedge Kw _b c)\end{aligned}$$

  In our public announcement semantics, the update due to some $\varphi$ (such as c) is the same as the update due to $\lnot \varphi$. The $[\varphi ]$ versions of the announcement modality are conditional to the truth of the announcement. Only the dual versions of the announcement modality assume the truth of the announcement. So, for example:

  $$\begin{aligned} {\mathcal {M}}^1_{11} \models \langle c \rangle ( Kw _a c \wedge Kw _b c) \quad \text { as well as } \quad {\mathcal {M}}^1_{21} \models \langle \lnot c \rangle ( Kw _a c \wedge Kw _b c)\end{aligned}$$

• Let Alice request two books and Bob one book, as above. We will now illustrate the different ways for the librarian to inform them. The public announcement way is as above: shouting “Are you out of your mind, I cannot carry that”. This has other interesting consequences as well, for example:

  $$\begin{aligned} {\mathcal {M}}^1_{21} \models \langle \lnot c \rangle (p_b *K_a c) \end{aligned}$$

  We can decompose the resource 21 into 01 and 20, and the (state labelled with the) 01 satisfies $p_b$ whereas 20 satisfies $K_a c$, formally: ${\mathcal {M}}^2_{01}\models p_b$ and ${\mathcal {M}}^2_{20} \models K_a c$, because 20 is the only state Alice considers possible in ${\mathcal {M}}_2$.

• However, the librarian might also have chosen to inform Alice privately that he cannot carry the requested books. For example, because the librarian might find it more reasonable that Alice changes her order and requests fewer books than that Bob changes his order. We now get:

  $$\begin{aligned} {\mathcal {M}}^1_{21} \models \langle \lnot c \rangle _a (p_b *K_a c) \end{aligned}$$

  Again, afterwards $p_b *K_a c$ is true in the state labeled 21, however this is now in model ${\mathcal {M}}^3$. A difference between ${\mathcal {M}}^2$ and ${\mathcal {M}}^3$ is, of course, that Bob does not know that Alice knows that the librarian cannot carry the books:

  $$\begin{aligned} {\mathcal {M}}^1_{21} \models \langle \lnot c \rangle _a\lnot K_b K_a \lnot c, \end{aligned}$$

  but he knows that Alice now knows whether c:

  $$\begin{aligned} {\mathcal {M}}^1_{21} \models \langle \lnot c \rangle _a K_b Kw _a c.\end{aligned}$$

• For a further complication, Bob may be uncertain whether Alice is privately informed, what we defined as ‘suspected semi-private announcement’. We now again have that:

  $$\begin{aligned} {\mathcal {M}}^1_{21} \models \langle \lnot c \rangle _a^+ (p_a *K_a c) \end{aligned}$$

  The model resulting from this action is ${\mathcal {M}}_4$, with as designated state the right one from the two labelled with (2, 1) in Fig. 1. Similarly, we obtain

  $$\begin{aligned} {\mathcal {M}}^1_{21} \models \langle \lnot c \rangle _a^+ (p_a *\lnot K_a c) \end{aligned}$$

  in which case $\lnot K_a c$ is validated by the left state labelled with (2, 1) in the figure.

  Let the ‘name’ of suspected semi-private announcements with modality $\langle \varphi \rangle ^+_B$ be $\varphi ^+_B$, and analogously for $\varphi ^-_B$. Then in accordance with our notational conventions the right (2, 1) is formally state $(21,{\lnot c}^+_a)$ in the modal product and the left (2, 1) is is formally state $(21,{\lnot c}^-_a)$.

  Again, ${\mathcal {M}}^4_{(21,{\lnot c}^-_a)} \models p_b *\lnot K_a c$, because $(2,0) \circ (0,1) = (2,1)$, ${\mathcal {M}}^4_{(01,c^-_a)} \models p_b$ and ${\mathcal {M}}^4_{(20,c^-_a)} \not \models K_a c$ because Alice is uncertain between (2, 0), (2, 1) and (2, 2) in that part of the model.

  Also, to continue our previous example, unlike before we now have that Bob does not know that Alice knows whether c, because Bob is uncertain which of $\langle c \rangle ^+_a$ and $\langle c \rangle ^-_a$ took place. That is:

  $$\begin{aligned} \begin{array}{l} {\mathcal {M}}^1_{21} \models \langle \lnot c \rangle _a K_b Kw _a c\\ {\mathcal {M}}^1_{21} \models \langle \lnot c \rangle ^+_a \lnot K_b Kw _a c \end{array}\end{aligned}$$

• If Alice and Bob both did not request a book, then if they both were to request a book, the librarian can carry the requested books:

  $$\begin{aligned} {\mathcal {M}}^1_{00} \models (p_a *p_b) \mathrel {-*}c \end{aligned}$$

  Consider ${\mathcal {M}}^1_{00}$. The unique resource satisfying $p_a *p_b$ is (1, 1), $(0,0) \circ (1,1) = (1,1)$, and indeed ${\mathcal {M}}^1_{11} \models c$. However, Alice does not know this, nor does Bob:

  $$\begin{aligned} {\mathcal {M}}^1_{00} \models \lnot K_a ((p_a *p_b) \mathrel {-*}c) \wedge \lnot K_b ((p_a *p_b) \mathrel {-*}c) \end{aligned}$$

  because in fact they consider it possible that the librarian is the unable to carry the books:

  $$\begin{aligned} {\mathcal {M}}^1_{00} \models {\hat{K}}_a ((p_a *p_b) \mathrel {-*}\lnot c) \wedge {\hat{K}}_b ((p_a *p_b) \mathrel {-*}\lnot c) \end{aligned}$$

  This is because Alice and Bob both consider it possible that the other agent already requested as least one book. For example, Alice considers possible that the actual state is (0, 1), and $(0,1) \circ (1,1) = (2,1)$, in which case $(p_a *p_b) \mathrel {-*}\lnot c$ is true.

  For another example, $(p_a *p_a *p_a) \mathrel {-*}\bot$ is a model validity, as $(1,0) \circ (1,0) \circ (1,0) \uparrow$.

Expressivity revisited The library example of this section is not so different from the example in the previous section demonstrating that $*$ and $\mathrel {-*}$ increase the expressivity of the logical language. Like in that example, also here we have few atoms, namely only $p_a$ and $p_b$ representing the request of one book by a respectively b, where all other states can be described by composition of these ‘basic’ resources; and additionally atom c. A fair question is whether without $*$ and $\mathrel {-*}$ we can still distinguish all the states of the models involved in the library example. It is easy to see that if we can distinguish all states in the initial model, then also in any of its subsequent updates due to announcements.

Like before, we can distinguish all states in the initial model ${\mathcal {M}}$ by a formula in the language of separation logic ${\mathcal {L}}_{*}$. In other words, for all states ij in domain S of ${\mathcal {M}}$ there is unique formula in ${\mathcal {L}}_{*}$ that is only true in ij. This is elementary, as any ij has a (not necessarily unique) decomposition into other resources distinguishing it from all other resources. For example:

$$\begin{aligned}\begin{array}{l} {\mathcal {M}}_{22} \models p_a *p_a *p_b *p_b \\ {\mathcal {M}}_{12} \models p_a *p_b *p_b \\ \dots \end{array}\end{aligned}$$

Unlike before, all states in the initial model ${\mathcal {M}}$ can also be distinguished by a (purely) epistemic formula, that is, in the language ${\mathcal {L}}_{K}$ (without $*$ and $\mathrel {-*}$). This is maybe not so evident. Note the (diagonal) mirror symmetry in the formulas below.

$$\begin{aligned}\begin{array}{l|l|l} {\mathcal {M}}_{00} \models K_a c \wedge K_b c &{} {\mathcal {M}}_{10} \models p_a &{} {\mathcal {M}}_{20} \models K_b c \wedge {\hat{K}}_a \lnot c \wedge \lnot p_a \\ {\mathcal {M}}_{01} \models p_b &{} {\mathcal {M}}_{11} \models {\hat{K}}_a p_a \wedge {\hat{K}}_b p_b &{} {\mathcal {M}}_{21} \models \lnot c \wedge {\hat{K}}_b p_b \\ {\mathcal {M}}_{02} \models K_a c \wedge {\hat{K}}_b \lnot c \wedge \lnot p_b &{} {\mathcal {M}}_{12} \models \lnot c \wedge {\hat{K}}_a p_a &{} {\mathcal {M}}_{22} \models \lnot c \wedge K_a \lnot p_a \wedge K_b \lnot p_b \end{array}\end{aligned}$$

Postconditions and factual change The reader may observe that we did not model factual change in our examples, although our logical semantics allow for that, as the action models have postconditions that can change the value of factual propositions. The presence of factual change seems slightly more suitable for different combinations of resource update and information update, wherein the resource functions $\varvec{r}_{}$ can map states to different resources before and after the update (thus reflecting a simultaneous resource update). This is deferred to future research. As a mere example of factual change, and to ponder about the consequences this may have, consider a singleton action model with trivial precondition, accessible for all agents, and with postcondition (for the single event e): $post (e)(p_a) = p_a *p_a$. This has the effect that the denotation of $p_a$ is changed, for example, in the model ${\mathcal {M}}^1$ above it was (1, 0) but it now becomes (2, 0). In such an updated model, it is now the case that $p_a *p_a \mathrel {-*}\bot$, unlike above, because the truth of $p_a *p_a$ no longer means that Alice wants $1+1 = 2$ books but that she wants $2+2=4$ books, which, as we know, is definitely not permitted by the librarian: $(2,0)\circ (2,0)\uparrow$.

4 Eliminating Dynamic Modalities

In this section we show that every formula in ${\mathcal {L}}_{*{K}\otimes }$ is equivalent to a formula in ${\mathcal {L}}_{*{K}}$ wherein therefore no action model modality occurs. In order words, we reduce any given formula to an equivalent formula without dynamic modalities. From this it follows that the expressivity of the two languages is the same.

The usual strategy for such reductions is to show that whenever a dynamic modality x binds a given formula with a main logical connective y, this is equivalent to some formula wherein the main connective is y but where the constituent or constituents bound by y may involve dynamic modality x. If we then also have some basic case where x binds an propositional variable that can be shown to be equivalent to some formula not containing x, we can formally define some recursive rewriting procedure for which we ‘merely’ have to show termination in the fragment without modalities x. To prove termination one defines a complexity or weight measure on formulas, which allows to compare a formula with formulas that are not subformulas of it.

A first step towards such a proof for our current logic is to show that whenever an action model modality binds a multiplicative conjunction $*$ or multiplicative implication $\mathrel {-*}$, this is equivalent to a formula with main connective $*$ or $\mathrel {-*}$, respectively, and where the action models occur in the constituents of that. This is formalized in the following lemma, wherein we use diamond versions of the modalities to obtain a smoother proof. We recall that $*$ means $*^{\exists \exists }$ and that $\mathrel {-*}$ means $\mathrel {-*}^{\exists \exists }$. By ‘$\bigvee _f$’ we mean ‘$\bigvee _{f \in E}$’, etc.

Lemma 1

The following schemas are valid in $\mathrm {AMSL}$:

$$\begin{aligned}\begin{array}{lll} \langle {\mathcal {E}}_e \rangle (\varphi *\psi ) &{} \leftrightarrow &{} pre (e) \wedge \bigvee _{f,g} (\langle {\mathcal {E}}_f \rangle \varphi *\langle {\mathcal {E}}_g \rangle \psi ) \\ \langle {\mathcal {E}}_e \rangle (\varphi \mathrel {-*}\psi ) &{} \leftrightarrow &{} pre (e) \wedge \bigwedge _{f} (\langle {\mathcal {E}}_f \rangle \varphi \mathrel {-*}\bigvee _{g} \langle {\mathcal {E}}_g \rangle \psi ) \end{array}\end{aligned}$$

Proof

We first show the validity for $*$. Let ${\mathcal {M}}= (S,\sim ,\varvec{r}_{},V)$ and $s \in S$ be arbitrary.

($\Rightarrow$)    

Assume ${\mathcal {M}}_s \models \langle {\mathcal {E}}_e \rangle (\varphi *\psi )$. Then ${\mathcal {M}}_s \models pre (e)$ and $({\mathcal {M}}\otimes {\mathcal {E}})_{(s,e)} \models \varphi *\psi$. Therefore, there are $(t,f), (u,g) \in {\mathcal {D}}({\mathcal {M}}\otimes {\mathcal {E}})$ such that $\varvec{r}_{(s,e)} = \varvec{r}_{(t,f)}\circ \varvec{r}_{(u,g)}$, $({\mathcal {M}}\otimes {\mathcal {E}})_{(t,f)} \models \varphi$ and $({\mathcal {M}}\otimes {\mathcal {E}})_{(u,g)} \models \psi$. Also, as $(t,f), (u,g) \in {\mathcal {D}}({\mathcal {M}}\otimes {\mathcal {E}})$, we may conclude that ${\mathcal {M}}_t \models pre (f)$ and ${\mathcal {M}}_u \models pre (g)$. From $({\mathcal {M}}\otimes {\mathcal {E}})_{(t,f)} \models \varphi$ and ${\mathcal {M}}_t \models pre (f)$ it follows that ${\mathcal {M}}_t \models \langle {\mathcal {E}}_f \rangle \varphi$. From $({\mathcal {M}}\otimes {\mathcal {E}})_{(u,g)} \models \psi$ and ${\mathcal {M}}_u \models pre (g)$ it follows that ${\mathcal {M}}_u \models \langle {\mathcal {E}}_g \rangle \psi$. Then, from $\varvec{r}_{(s,e)} = \varvec{r}_{(t,f)}\circ \varvec{r}_{(u,g)}$, $\varvec{r}_{(s,e)} = \varvec{r}_{s}$, $\varvec{r}_{(t,f)} = \varvec{r}_{t}$ and $\varvec{r}_{(u,g)}=\varvec{r}_{u}$ we obtain that $\varvec{r}_{s} = \varvec{r}_{t}\circ \varvec{r}_{u}$. Finally, from $\varvec{r}_{s} = \varvec{r}_{t}\circ \varvec{r}_{u}$, ${\mathcal {M}}_t \models \langle {\mathcal {E}}_f \rangle \varphi$, and ${\mathcal {M}}_u \models \langle {\mathcal {E}}_g \rangle \psi$ we obtain that ${\mathcal {M}}_s \models \langle {\mathcal {E}}_f \rangle \varphi *\langle {\mathcal {E}}_g \rangle \psi$, so that also ${\mathcal {M}}_s \models \bigvee _{f,g} (\langle {\mathcal {E}}_f \rangle \varphi *\langle {\mathcal {E}}_g \rangle \psi )$ and together with the already obtained ${\mathcal {M}}_s \models pre (e)$ we get the required ${\mathcal {M}}_s \models pre (e) \wedge \bigvee _{f,g} (\langle {\mathcal {E}}_f \rangle \varphi *\langle {\mathcal {E}}_g \rangle \psi )$.

($\Leftarrow$)    

Assume ${\mathcal {M}}_s \models pre (e) \wedge \bigvee _{f,g} (\langle {\mathcal {E}}_f \rangle \varphi *\langle {\mathcal {E}}_g \rangle \psi )$. We follow a fairly similar argument but now in the other direction. From the assumption we obtain that ${\mathcal {M}}_s \models pre (e)$ and that there are $f,g \in E$ such that ${\mathcal {M}}_s \models \langle {\mathcal {E}}_f \rangle \varphi *\langle {\mathcal {E}}_g \rangle \psi$. Therefore there are $t,u \in S$ such that $\varvec{r}_{s} = \varvec{r}_{t}\circ \varvec{r}_{u}$, ${\mathcal {M}}_t \models \langle {\mathcal {E}}_f \rangle \varphi$ and ${\mathcal {M}}_u \models \langle {\mathcal {E}}_g \rangle \psi )$. From that we obtain, as before, that $({\mathcal {M}}\otimes {\mathcal {E}})_{(t,f)} \models \varphi$ and $({\mathcal {M}}\otimes {\mathcal {E}})_{(u,g)} \models \psi$. From ${\mathcal {M}}_s \models pre (e)$ we get that $(s,e) \in {\mathcal {D}}({\mathcal {M}}\otimes {\mathcal {E}})$ and from that and $\varvec{r}_{s} = \varvec{r}_{t}\circ \varvec{r}_{u}$ we now obtain $\varvec{r}_{(s,e)} = \varvec{r}_{(t,f)}\circ \varvec{r}_{(u,g)}$. Therefore $({\mathcal {M}}\otimes {\mathcal {E}})_{(s,e)} \models \varphi *\psi$ so that with ${\mathcal {M}}_s \models pre (e)$ we also have ${\mathcal {M}}_s \models \langle {\mathcal {E}}_e \rangle (\varphi *\psi )$, as required.

We now show the validity for $\mathrel {-*}$. Again, let ${\mathcal {M}}= (S,\sim ,\varvec{r}_{},V)$ and $s \in S$ be arbitrary.

($\Rightarrow$)

Assume ${\mathcal {M}}_s \models \langle {\mathcal {E}}_e \rangle (\varphi \mathrel {-*}\psi )$. Then ${\mathcal {M}}_s \models pre (e)$ as well as $({\mathcal {M}}\otimes {\mathcal {E}})_{(s,e)} \models \varphi \mathrel {-*}\psi$. In order to prove the required, let $f \in E$ and let $t \in S$ be such that $\varvec{r}_{s}\circ \varvec{r}_{t}\!\downarrow$, and assume that ${\mathcal {M}}_t \models \langle {\mathcal {E}}_f \rangle \varphi$. We now wish to prove that there is a $u \in S$ such that $\varvec{r}_{u}=\varvec{r}_{s}\circ \varvec{r}_{t}$ and ${\mathcal {M}}_u \models \bigvee _{g} \langle {\mathcal {E}}_g \rangle \psi$, where the latter means that there is a $g \in E$ such that ${\mathcal {M}}_u \models \langle {\mathcal {E}}_g \rangle \psi$. We prove this as follows.

From ${\mathcal {M}}_t \models \langle {\mathcal {E}}_f \rangle \varphi$ we obtain that ${\mathcal {M}}_t \models pre (f)$ and $({\mathcal {M}}\otimes {\mathcal {E}})_{(t,f)} \models \varphi$. From $\varvec{r}_{s}\circ \varvec{r}_{t}\!\downarrow$ and $(s,e),(t,f) \in {\mathcal {D}}({\mathcal {M}}\otimes {\mathcal {E}})$ we obtain that $\varvec{r}_{(s,e)}\circ \varvec{r}_{(t,f)}\!\downarrow$. We recall that t and f were arbitrary and therefore (t, f) as well. From $({\mathcal {M}}\otimes {\mathcal {E}})_{(s,e)} \models \varphi \mathrel {-*}\psi$ and $\varvec{r}_{(s,e)}\circ \varvec{r}_{(t,f)}\!\downarrow$ for arbitrary (t, f) we obtain that there is a $(u,g) \in {\mathcal {D}}({\mathcal {M}}\otimes {\mathcal {E}})$ (which implies that ${\mathcal {M}}_u\models pre (g)$) such that $\varvec{r}_{(u,g)}=\varvec{r}_{(s,e)}\circ \varvec{r}_{(t,f)}$ and $({\mathcal {M}}\otimes {\mathcal {E}})_{(u,g)} \models \psi$. From ${\mathcal {M}}_u\models pre (g)$ and $({\mathcal {M}}\otimes {\mathcal {E}})_{(u,g)} \models \psi$ it follows that ${\mathcal {M}}_u \models \langle {\mathcal {E}}_g \rangle \psi$, which fulfils the proof requirement.

($\Leftarrow$)

Assume ${\mathcal {M}}_s \models pre (e) \wedge \bigwedge _{f} (\langle {\mathcal {E}}_f \rangle \varphi \mathrel {-*}\bigvee _{g} \langle {\mathcal {E}}_g \rangle \psi )$. In order to prove ${\mathcal {M}}_s \models \langle {\mathcal {E}}_e \rangle (\varphi \mathrel {-*}\psi )$, and given that ${\mathcal {M}}_s \models pre (e)$, it remains to prove $({\mathcal {M}}\otimes {\mathcal {E}})_{(s,e)}\models \varphi \mathrel {-*}\psi$. In order to prove that, let us assume arbitrary $(t,f)\in {\mathcal {D}}({\mathcal {M}}\otimes {\mathcal {E}})$ (such that ${\mathcal {M}}_t\models pre (f)$) for which $\varvec{r}_{(s,e)}\circ \varvec{r}_{(t,f)}\!\downarrow$, and that ${\mathcal {M}}\otimes {\mathcal {E}})_{(t,f)}\models \varphi$. From the assumption ${\mathcal {M}}_s \models \bigwedge _{f} (\langle {\mathcal {E}}_f \rangle \varphi \mathrel {-*}\bigvee _{g} \langle {\mathcal {E}}_g \rangle \psi )$ we obtain that in particular ${\mathcal {M}}_s \models \langle {\mathcal {E}}_f \rangle \varphi \mathrel {-*}\bigvee _{g} \langle {\mathcal {E}}_g \rangle \psi$. From $\varvec{r}_{(s,e)}\circ \varvec{r}_{(t,f)}\!\downarrow$ we obtain that $\varvec{r}_{s}\circ \varvec{r}_{t}\!\downarrow$ (and that t is also arbitrary). Also, from ${\mathcal {M}}\otimes {\mathcal {E}})_{(t,f)}\models \varphi$ and ${\mathcal {M}}_t \models pre (f)$ we get ${\mathcal {M}}_t \models \langle {\mathcal {E}}_f \rangle \varphi$. Then, from that, from $\varvec{r}_{s}\circ \varvec{r}_{t}\!\downarrow$ and from ${\mathcal {M}}_s \models \langle {\mathcal {E}}_f \rangle \varphi \mathrel {-*}\bigvee _{g} \langle {\mathcal {E}}_g \rangle \psi$ it follows that there is $u\in S$ such that $\varvec{r}_{u}= \varvec{r}_{s}\circ \varvec{r}_{t}$ and ${\mathcal {M}}_u \models \bigvee _{g} \langle {\mathcal {E}}_g \rangle \psi$. Choose such $g \in E$. Then ${\mathcal {M}}_u \models \langle {\mathcal {E}}_g \rangle \psi$, so that (as before) $({\mathcal {M}}\otimes {\mathcal {E}})_{(u,g)}\models \psi$. As we also have $\varvec{r}_{(u,g)}= \varvec{r}_{(s,e)}\circ \varvec{r}_{(t,f)}$, this fulfils our requirement. $\square$

Although the lemma is formulated for the diamond version of the modalities, this is—nearly, but not quite—irrelevant. There are equivalent versions using the box version primitive modalities of the logical language. Now to get these box versions we cannot simply use that $\langle {\mathcal {E}}_e \rangle \varphi$ is equivalent to $\lnot [{\mathcal {E}}_e]\lnot \varphi$, thus getting:

$$\begin{aligned}\begin{array}{lll} \lnot [{\mathcal {E}}_e]\lnot (\varphi *\psi ) &{} \leftrightarrow &{} pre (e) \wedge \bigvee _{f,g} (\lnot [{\mathcal {E}}_f]\lnot \varphi *\lnot [{\mathcal {E}}_g]\lnot \psi ) \\ \lnot [{\mathcal {E}}_e]\lnot (\varphi \mathrel {-*}\psi ) &{} \leftrightarrow &{} pre (e) \wedge \bigwedge _{f} (\lnot [{\mathcal {E}}_f]\lnot \varphi \mathrel {-*}\bigvee _{g} \lnot [{\mathcal {E}}_g]\lnot \psi ) \end{array}\end{aligned}$$

There are no axioms in BBI for the interaction between negation and the multiplicative conjunction and implication: $\lnot (\varphi *\psi )$ is not equivalent to a formula with main connective $*$, and $\lnot (\varphi \mathrel {-*}\psi )$ is not equivalent to a formula with main connective $\mathrel {-*}$. Therefore, it is also unclear how, for example, $[{\mathcal {E}}_e]\lnot (\varphi *\psi )$ is equivalent to a formula where $[{\mathcal {E}}_e]$ binds a formula with main connective $*$. And therefore, the iteratively defined reduction cannot proceed.

As pointed action models are deterministic programs, like public announcement, there is however an alternative road leading to our goal. We then use that for any ${\mathcal {E}}_e$ and $\varphi$, $\langle {\mathcal {E}}_e \rangle \varphi$ is equivalent to $pre (e) \wedge [{\mathcal {E}}_e]\varphi$, and $[{\mathcal {E}}_e]\varphi$ is equivalent to $pre (e)\rightarrow \langle {\mathcal {E}}_e \rangle \varphi$. Thus we obtain

$$\begin{aligned}\begin{array}{lll} {[}{\mathcal {E}}_e](\varphi *\psi ) &{} \leftrightarrow &{} pre (e) \rightarrow \bigvee _{f,g} (( pre (f)\wedge [{\mathcal {E}}_f]\varphi ) *( pre (g)\wedge [{\mathcal {E}}_g]\psi )) \\ {[}{\mathcal {E}}_e](\varphi \mathrel {-*}\psi ) &{} \leftrightarrow &{} pre (e) \rightarrow \bigwedge _{f} (( pre (f)\wedge [{\mathcal {E}}_f]\varphi ) \mathrel {-*}\bigvee _{g} ( pre (g)\wedge [{\mathcal {E}}_g]\psi )) \end{array}\end{aligned}$$

which have the required shape of reduction axioms. As the diamond formulation is more elegant, we stick to that. Later proofs by formula induction require us to show that the right equivalent of the above box version is less complex than the left equivalent, and we will then use the box formulation again.

Proposition 2

(Reduction axioms for action models) The following schemas are valid.

$$\begin{aligned}\begin{array}{lll} {[{\mathcal {E}}_e]p} &{} \leftrightarrow &{} pre (e) \rightarrow post (e)(p) \\ {[{\mathcal {E}}_e]\bot } &{} \leftrightarrow &{} pre (e) \\ {[{\mathcal {E}}_e]I} &{} \leftrightarrow &{} pre (e) \rightarrow I \\ {[{\mathcal {E}}_e](\varphi \wedge \psi )} &{} \leftrightarrow &{} [{\mathcal {E}}_e]\varphi \wedge [{\mathcal {E}}_e]\psi \\ {[{\mathcal {E}}_e]\lnot \varphi } &{} \leftrightarrow &{} pre (e) \rightarrow \lnot [{\mathcal {E}}_e]\varphi \\ {[{\mathcal {E}}_e]K_a \psi } &{} \leftrightarrow &{} pre (e) \rightarrow \bigwedge _{e \sim _a f} K_a [{\mathcal {E}}_f] \psi \\ \langle {\mathcal {E}}_e \rangle (\varphi *\psi ) &{} \leftrightarrow &{} pre (e) \wedge \bigvee _{f,g} (\langle {\mathcal {E}}_f \rangle \varphi *\langle {\mathcal {E}}_g \rangle \psi ) \\ \langle {\mathcal {E}}_e \rangle (\varphi \mathrel {-*}\psi ) &{} \leftrightarrow &{} pre (e) \wedge \bigwedge _{f} (\langle {\mathcal {E}}_f \rangle \varphi \mathrel {-*}\bigvee _{g} \langle {\mathcal {E}}_g \rangle \psi ) \end{array}\end{aligned}$$

Proof

The validities involving $*$ and $\mathrel {-*}$ were shown in Lemma 1. All the remaining are well-known validities of action model logic, see for example van Ditmarsch et al. (2008, Table 6.1, page 165) and van Ditmarsch and Kooi (2008) for the case $[{\mathcal {E}}_e]p$. $\square$

We note that the instantiation of the reductions of $*$ and $\mathrel {-*}$ for public announcement are therefore those already reported before in Courtault et al. (2019). They are as follows.

$$\begin{aligned} \langle \chi \rangle (\varphi *\psi )&\leftrightarrow&\chi \wedge ( \\&(\langle \chi \rangle \varphi *\langle \chi \rangle \psi ) \vee \\&(\langle \chi \rangle \varphi *\langle \lnot \chi \rangle \psi ) \vee \\&(\langle \lnot \chi \rangle \varphi *\langle \chi \rangle \psi ) \vee \\&(\langle \lnot \chi \rangle \varphi *\langle \lnot \chi \rangle \psi ) \\&) \\ \langle \chi \rangle (\varphi \mathrel {-*}\psi )&\leftrightarrow&\chi \wedge ( \\&(\langle \chi \rangle \varphi \mathrel {-*}\langle \chi \rangle \psi \vee \langle \lnot \chi \rangle \psi ) \wedge \\&(\langle \lnot \chi \rangle \varphi \mathrel {-*}\langle \chi \rangle \psi \vee \langle \lnot \chi \rangle \psi ) \\&) \end{aligned}$$

Next, we define the complexity $c: {\mathcal {L}}_{*{K}\otimes } \rightarrow {\mathbb {N}}$ and the translation $t: {\mathcal {L}}_{*{K}\otimes } \rightarrow {\mathcal {L}}_{*{K}}$. These extend similarly defined c and t in van Ditmarsch et al. (2008, p. 194–196).

Definition 7

(Translation) The translation $t: {\mathcal {L}}_{K*\otimes } \rightarrow {\mathcal {L}}_{K*}$ is defined by induction on the structure of formulas.

$$\begin{aligned}\begin{array}{lll} t(p) &{}=&{} p \\ t(\bot ) &{}=&{} \bot \\ t(I) &{}=&{} I \\ t(\lnot \varphi ) &{}=&{} \lnot t(\varphi ) \\ t(\varphi \wedge \psi ) &{}=&{} t(\varphi ) \wedge t(\psi ) \\ t(K_a\varphi ) &{}=&{} K_a t(\varphi ) \\ t(\varphi *\psi ) &{}=&{} t(\varphi ) *t(\psi ) \\ t(\varphi \mathrel {-*}\psi ) &{}=&{} t(\varphi ) \mathrel {-*}t(\psi ) \\ t([{\mathcal {E}}_e]p) &{}=&{} t(pre(e) \rightarrow post(e)(p)) \\ t([{\mathcal {E}}_e]\lnot \varphi ) &{}=&{} t(pre(e) \rightarrow \lnot [{\mathcal {E}}_e]\varphi ) \\ t([{\mathcal {E}}_e](\varphi \wedge \psi )) &{}=&{} t([{\mathcal {E}}_e]\varphi \wedge [{\mathcal {E}}_e]\psi ) \\ t([{\mathcal {E}}_e]K_a\varphi ) &{}=&{} t(pre(e) \rightarrow \bigwedge _{e \sim _a f} K_a [{\mathcal {E}}_f] \varphi ) \\ t([{\mathcal {E}}_e](\varphi *\psi )) &{}=&{} t( pre (e) \rightarrow \bigvee _{f,g} (( pre (f)\wedge [{\mathcal {E}}_f]\varphi ) *( pre (g)\wedge [{\mathcal {E}}_g]\psi ))) \\ t([{\mathcal {E}}_e](\varphi \mathrel {-*}\psi )) &{}=&{} t( pre (e) \rightarrow \bigwedge _{f} (( pre (f)\wedge [{\mathcal {E}}_f]\varphi ) \mathrel {-*}\bigvee _{g} ( pre (g)\wedge [{\mathcal {E}}_g]\psi ))) \end{array}\end{aligned}$$

Note that the translation only meaningfully affects formulas with action model modalities. It is also easy to see that also $t(\varphi \vee \psi )= t(\varphi ) \vee t(\psi )$ and $t(\varphi \rightarrow \psi )= t(\varphi )\rightarrow t(\psi )$.

Definition 8

(Complexity) The complexity measure $c: {\mathcal {L}}_{K*\otimes } \rightarrow {\mathbb {N}}$ is defined by induction on the structure of formulas.

$$\begin{aligned}\begin{array}{lll} c(x) &{} = &{} 1 \text {for } x \in P \text { or } x = \bot ,I \\ c(\lnot \varphi ) &{}= &{} 1 + c(\varphi ) \\ c(\varphi @ \psi ) &{}= &{} 1 + \max \{c(\varphi ), c(\psi ) \} \text {for } @ = \wedge , *,\mathrel {-*}\\ c(K_a\varphi ) &{}=&{} 1 + c(\varphi )\\ c([{\mathcal {E}}_e]\varphi ) &{}=&{} c({\mathcal {E}}) \cdot c(\varphi ) \\ c({\mathcal {E}}) &{}=&{} 2+ 2|E|^2 + \max \{c( pre (e)), c( post (e)(p)) \mid e \in E, p \in P\} \end{array} \end{aligned}$$

For the connectives that are defined by abbreviation, and that occur in the reduction axioms, we have to calculate derived complexities by way of their definitional abbreviations. For disjunction we have that $c(\varphi \vee \psi ) = c(\lnot (\lnot \varphi \wedge \lnot \psi )) = \max \{c(\varphi ), c(\psi )\} +4$. For implication we have that $c(\varphi \rightarrow \psi ) = c(\lnot (\varphi \wedge \lnot \psi )) = \max \{c(\varphi ), c(\psi )\} +3$. This complicates the calculations somewhat. Below, we may change the names of the actions and atoms quantified over in the set $\max \{c( pre (e)), c( post (e)(p)) \mid e \in E, p \in P\}$, to clearly distinguish them from already declared actions e and atoms p. Note that for any ${\mathcal {E}}$, $c({\mathcal {E}}) \ge 5$ as $|E|\ge 1$ and $\max \{c( pre (e)), c( post (e)(p)) \mid e \in E, p \in P\} \ge 1$.

Lemma 3

For all $p,\varphi ,\psi \in {\mathcal {L}}_{*{K}}$:

$$\begin{aligned}\begin{array}{lll} c([{\mathcal {E}}_e]p) &{}>&{} c(pre(e) \rightarrow post(e)(p)) \\ c([{\mathcal {E}}_e]\lnot \varphi ) &{}>&{} c(pre(e) \rightarrow \lnot [{\mathcal {E}}_e]\varphi ) \\ c([{\mathcal {E}}_e](\varphi \wedge \psi )) &{}>&{} c([{\mathcal {E}}_e]\varphi \wedge [{\mathcal {E}}_e]\psi ) \\ c([{\mathcal {E}}_e]K_a\varphi ) &{}>&{} c(pre(e) \rightarrow \bigwedge _{e \sim _a f} K_a [{\mathcal {E}}_f] \varphi ) \\ c([{\mathcal {E}}_e](\varphi *\psi )) &{}>&{} c( pre (e) \rightarrow \bigvee _{f,g} (( pre (f)\wedge [{\mathcal {E}}_f]\varphi ) *( pre (g)\wedge [{\mathcal {E}}_g]\psi ))) \\ c([{\mathcal {E}}_e](\varphi \mathrel {-*}\psi )) &{}>&{} c( pre (e) \rightarrow \bigwedge _{f} (( pre (f)\wedge [{\mathcal {E}}_f]\varphi ) \mathrel {-*}\bigvee _{g} ( pre (g)\wedge [{\mathcal {E}}_g]\psi ))) \end{array}\end{aligned}$$

Proof

We successively show all different cases.

For the final two cases, first note that for any action f and formula $\varphi$, $c( pre (f)\wedge [{\mathcal {E}}_f]\varphi )= 1+c({\mathcal {E}})c(\varphi )$ $(*)$, which can be shown as follows:

$$\begin{aligned} \begin{array}{lll} c( pre (f)\wedge [{\mathcal {E}}_f]\varphi ) &{}=&{} 1+ \max \{c( pre (f)), c([{\mathcal {E}}_f]\varphi )\} \\ &{}=&{} 1+ \max \{c( pre (f)), c({\mathcal {E}})\cdot c(\varphi )\} \\ &{}=&{} 1+ c({\mathcal {E}}) c(\varphi ) \quad \text {as } c( pre (f))< c({\mathcal {E}}) \text { and } 1 < c(\varphi ) \\ \end{array}\end{aligned}$$

We proceed with case $[{\mathcal {E}}_e](\varphi *\psi )$:

$$\begin{aligned}&c([{\mathcal {E}}_e](\varphi *\psi )) \\&\quad = c({\mathcal {E}}) \cdot c(\varphi *\psi ) \\&\quad = c({\mathcal {E}}) \cdot (1+\max \{c(\varphi ), c(\psi )\}) \\&\quad = c({\mathcal {E}}) + c({\mathcal {E}}) \cdot \max \{c(\varphi ), c(\psi )\} \\&\quad> 2+c( pre (e)) + 2|E|^2 + c({\mathcal {E}})\cdot \max \{ c(\varphi ), c(\psi )\} \quad \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \text {as } c({\mathcal {E}}) > 2+c( pre (e)) + 2|E|^2 \\&\quad = 2+c( pre (e)) + 2|E|^2-1 + \max \{ 1+ c({\mathcal {E}})c(\varphi ), 1+ c({\mathcal {E}})c(\psi )\} \\&\quad = 2+c( pre (e)) + 2|E|^2-1 + \max \{ 1+ c({\mathcal {E}})c(\varphi ), 1+ c({\mathcal {E}})c(\psi ) \mid f,g \in E \} \\&\quad = 2+c( pre (e)) + 2|E|^2-1 + \\ \quad&\qquad \max \{ c(( pre (f)\wedge [{\mathcal {E}}_f]\varphi ) *( pre (g)\wedge [{\mathcal {E}}_g]\psi ))) \mid f,g \in E \} \ \ (*) \\&\quad = 2+c( pre (e)) + c\left( \bigvee _{f,g} (( pre (f)\wedge [{\mathcal {E}}_f]\varphi ) *( pre (g)\wedge [{\mathcal {E}}_g]\psi ))\right) \\&\quad = c( pre (e) \rightarrow \bigvee _{f,g} (( pre (f)\wedge [{\mathcal {E}}_f]\varphi ) *( pre (g)\wedge [{\mathcal {E}}_g]\psi ))) \end{aligned}$$

The final case $[{\mathcal {E}}_e](\varphi \mathrel {-*}\psi )$ is very similar to the preceding case $[{\mathcal {E}}_e](\varphi *\psi )$, except that instead of weight $2|E|^2-1$ apported by $\bigvee _{f,g}$ we have weight $2|E|^2-3|E|+1$ apported by $\bigwedge _f$ and $\bigvee _g$. As the conjunction is a primitive operator, the $\bigwedge _f$ conjuncts contribute only $|E|-1$, this has to be multiplied by the $\bigvee _g$ disjuncts contributing $2|E|-1$, which makes $2|E|^2-3|E|+1$. As $2|E|^2-3|E|+1 < 2|E|^2-1$, the proof can then proceed as in the case $*$. $\square$

The eye-catching weight in the proof is of course

$$\begin{aligned} c({\mathcal {E}}) = 2+ 2|E|^2 + \max \{c( pre (e)), c( post (e)(p)) \mid e \in E, p \in P\}. \end{aligned}$$

It seems appropriate to explain why this seemingly haphazard weight is exactly right, that is, the minimum needed.

• The 2 is needed to show the cases atoms p, I and negation. We note that 1 would be insufficient. The minimum weight of an action model is 5, as $|E|\ge 1$ and $\max \{c( pre (e)), c( post (e)(p)) \mid e \in E, p \in P\}\ge 1$.

• The $2|E|^2$ is needed to show the case $*$. We note that $2|E|^2-1$ would be insufficient, a big disjunction with |E| disjuncts, by notational abbreviation, contributes with $2|E|^2-1$ to the weight.

• The $\max \{c( pre (e)), c( post (e)(p)) \mid e \in E, p \in P\}$ is needed in any case where a precondition or postcondition occurs (all but the case conjunction), as we then need that $c( pre (e)) < c({\mathcal {E}})$, which is guaranteed by $c( pre (e)) \le \max \{c( pre (e)), c( post (e)(p)) \mid e \in E, p \in P\} < c({\mathcal {E}})$; and similarly for $c( post (e)(p)$. So this is also minimal.

Lemma 4

For all $\varphi \in {\mathcal {L}}_{*{K}\otimes }$: $c(\varphi ) \ge c(t(\varphi )$.

Proof

This is an easy proof by induction on the structure of $\varphi$. All the clauses of the translation t that commute with the connectives ensure that $c(\varphi ) \ge c(t(\varphi ))$, for example $c(\varphi \wedge \psi ) = 1+ \max \{c(\varphi ),c(\psi )\} \ge \text {(IH) } 1+ \max \{c(t(\varphi )),c(t(\psi ))\} = c(t(\varphi \wedge \psi ))$. Whereas all the clauses of the translation t involving an action model modality ensure that $c(\varphi ) \le c(t(\varphi ))$ because we already have $c(\varphi ) < c(t(\varphi ))$ by Lemma 3, and induction. For example, $c([{\mathcal {E}}_e](\varphi \wedge \psi )) = c({\mathcal {E}})\cdot (1+\max \{c(\varphi ),c(\psi )\}) \ge \text {(IH) } c(t({\mathcal {E}}))\cdot (1+\max \{c(t(\varphi )),c(t(\psi ))\}) = c(t([{\mathcal {E}}_e](\varphi \wedge \psi )))$, where we note that $c({\mathcal {E}}) \ge c(t({\mathcal {E}}))$ is because of the inductive assumption for all preconditions and postconditions occurring in ${\mathcal {E}}$, so that: $\max \{c( pre (e)), c( post (e)(p)) \mid e \in E, p \in P\} \ge \max \{c(t( pre (e))), c(t( post (e)(p))) \mid e \in E, p \in P\}$. $\square$

We are now fully prepared to show the following proposition.

Theorem 5

Every formula in ${\mathcal {L}}_{*{K}\otimes }$ is equivalent to a formula in ${\mathcal {L}}_{*{K}}$.

Proof

Let $\varphi \in {\mathcal {L}}_{*{K}\otimes }$.

Consider an innermost dynamic modality in $\varphi$, that is, a formula of shape $[{\mathcal {E}}_e]\psi$ that is a subformula of $\varphi$ and such that $\psi \in {\mathcal {L}}_{*{K}}$ and also all preconditions and postconditions in ${\mathcal {E}}$ are in ${\mathcal {L}}_{*{K}}$. Using the reduction axioms we obtain $t([{\mathcal {E}}_e]\psi )\in {\mathcal {L}}_{*{K}}$. Lemmas 3 and 4 guarantee that the translation is a terminating procedure: either the translation clause uses subformula structure, which is obviously terminating as the number of subformulas is limited (also note that $c(\xi ) > c(\eta )$ if some $\eta$ is a strict subformula of some $\xi$), or the translation clause involves an action model modality in which case we have that $c(\xi ) > c(\eta )$ because of Lemma 3. This race to the bottom is bounded by 0.

Repeat the procedure on the formula $\varphi '$ wherein subformula $[{\mathcal {E}}_e]\psi$ of $\varphi$ is replaced by $t([{\mathcal {E}}_e]\psi )$. Note that this formula $\varphi '$ contains one less dynamic modality, and that it is equivalent to $\varphi$. We continue to repeat the procedure for all of the (remaining) finite number of action model modalities originally in $\varphi$.

Let the resulting formula be $\varphi ''$. It is clear that $\varphi ''$ is equivalent to $\varphi$, and that the construction terminates. $\square$

The above proof is a bit sneaky, as the translation is defined outside-in whereas the proof finds the dynamic modalities inside-out. So it is unclear (and even unlikely) that the $\varphi ''$ we find is identical to $t(\varphi )$, although it will of course be equivalent to it. We can get away with this, because our result is in semantics and not in proof theory. We are not proving the completeness of a Hilbert-style axiomatization of a logic. In that case we would be obliged to have an outside-in proof which requires an additional reduction axiom $[{\mathcal {E}}_e][{\mathcal {E}}'_{'e}]\varphi \leftrightarrow [{\mathcal {E}}_e \circ {\mathcal {E}}'_{'e}]\varphi$. That would have been possible but would have resulted in a technically more complex proof. Our inside-out proof assumes ‘replacement of equivalents’ (from $\varphi \leftrightarrow \psi$, infer $\chi [p/\varphi ] \leftrightarrow \chi [p/\psi ]$), by all means validity preserving, but required as an additional derivation rule for inside-out proof theoretical arguments.

Despite the main result of Theorem 5 that every formula with action model modalities is equivalent to a formula without action model modalities, in the language of ESL, a puzzling observation remains. A sound and complete tableau system for PASL is a main result of Courtault et al. (2019). It is therefore also sound and complete for its fragment ESL. Does this mean we could contemplate a tableau system for AMSL that is a direct extension of the tableau system for ESL? Not really. Here we recall that the ESL and PASL semantics are with respect to a class of models X where states exactly correspond to resources: the resource function is a bijection. But our reduction of AMSL to ESL is with respect to a class of models Y where the resource function is a surjection. As an X model is also a Y model, it is clear that ESL-valid with respect to Y implies ESL-valid with respect to X. But it is unclear to us if ESL-valid with respect to X always implies ESL-valid with respect to Y.³

5 Other Semantics for $*$ and $\mathrel {-*}$

So far our results were for $*^{\exists \exists }$ and $\mathrel {-*}^{\exists \exists }$. We recall that for each connective we could choose between no less than four different semantics. In this section we argue that there are sound modelling reasons for the above combination and for (only) one other combination, namely $*^{\forall \forall }$ and $\mathrel {-*}^{\forall \forall }$, but not for any other of the 16 different combinations. We also give a reduction for this $^{\forall \forall }$ version of the multiplicative connectives, merely to demonstrate the complex interactions when quantifying over states as well as resources.

5.1 Semantics for $*^{\forall \forall }$ and $\mathrel {-*}^{\forall \forall }$

We first recall the semantics for the ${\exists \exists }$ version (Definition 5 on page 6), now using the prior semi-formal notation again.

$$ \begin{aligned} \begin{array}{lll} {\mathcal {M}}_s \models \varphi *^{\exists \exists } \psi &{}\;\, \text {iff} &{}\;\, \exists tu : \varvec{r}_{s} = \varvec{r}_{t} \circ \varvec{r}_{u} \ \& \ {\mathcal {M}}_t \models \varphi \ \& \ {\mathcal {M}}_u \models \psi \\ {\mathcal {M}}_s \models \varphi \mathrel {-*}^{\exists \exists } \psi &{}\;\, \text {iff} &{}\;\, \forall t : (\varvec{r}_{s} \circ \varvec{r}_{t} \!\downarrow \ \& \ {\mathcal {M}}_{t} \models \varphi ) \ \Rightarrow \ (\exists u: \varvec{r}_{u} = \varvec{r}_{s} \circ \varvec{r}_{t} \ \& \ {\mathcal {M}}_{u} \models \psi ) \end{array}\end{aligned}$$

We get the following for the ${\forall \forall }$ version.

$$ \begin{aligned} \begin{array}{lll} &{}&{} {\mathcal {M}}_s \models \varphi *^{\forall \forall } \psi \\ &{} \text {iff} &{}\;\, \exists r'r'' : \varvec{r}_{s} = r' \circ r'' \ \& \ (\forall t': \varvec{r}_{t'} = r' \Rightarrow {\mathcal {M}}_{t'} \models \varphi ) \ \& \ (\forall u': \varvec{r}_{u'} = r'' \Rightarrow {\mathcal {M}}_{u'} \models \psi ) \\ &{}\text {iff} &{} \;\,\exists tu : \varvec{r}_{s} = \varvec{r}_{t} \circ \varvec{r}_{u} \ \& \ (\forall t': \varvec{r}_{t'} = \varvec{r}_{t} \Rightarrow {\mathcal {M}}_{t'} \models \varphi ) \ \& \ (\forall u': \varvec{r}_{u'} = \varvec{r}_{u} \Rightarrow {\mathcal {M}}_{u'} \models \psi ) \\ &{}&{} \\ &{}&{} {\mathcal {M}}_s \models \varphi \mathrel {-*}^{\forall \forall } \psi \\ &{} \text {iff} &{}\;\, \forall r' : (\varvec{r}_{s} \circ r' \!\downarrow \ \& \ (\forall t': \varvec{r}_{t'} = r' \Rightarrow {\mathcal {M}}_{t'} \models \varphi )) \ \Rightarrow \ (\forall u: \varvec{r}_{u} = \varvec{r}_{s} \circ r' \Rightarrow {\mathcal {M}}_{u} \models \psi ) \\ &{} \text {iff} &{}\;\, \forall t : (\varvec{r}_{s} \circ \varvec{r}_{t} \!\downarrow \ \& \ (\forall t': \varvec{r}_{t'} = \varvec{r}_{t} \Rightarrow {\mathcal {M}}_{t'} \models \varphi )) \ \Rightarrow \ (\forall u: \varvec{r}_{u} = \varvec{r}_{s} \circ \varvec{r}_{t} \Rightarrow {\mathcal {M}}_{u} \models \psi ) \end{array}\end{aligned}$$

Intuitively the difference between the ${\exists \exists }$ and the ${\forall \forall }$ versions is clear. The reductions for $*^{\forall \forall }$ also display the perfect duality with $\mathrel {-*}^{\exists \exists }$ one might expect:

Proposition 6

The following schemas are valid in $\mathrm {AMSL}$:

$$\begin{aligned} \begin{array}{lll} {[}{\mathcal {E}}_e](\varphi *^{\forall \forall }\psi ) &{} \leftrightarrow &{} pre (e) \rightarrow \bigwedge _{f,g}([{\mathcal {E}}_f]\varphi *^{\forall \forall } [{\mathcal {E}}_g]\psi ) \\ {[}{\mathcal {E}}_e](\varphi \mathrel {-*}^{\forall \forall } \psi ) &{} \leftrightarrow &{} pre (e) \rightarrow \bigvee _{f} ([{\mathcal {E}}_f]\varphi \mathrel {-*}^{\forall \forall } \bigwedge _{g} [{\mathcal {E}}_g]\psi ) \end{array}\end{aligned}$$

Proof

We first show the validity for $*^{\forall \forall }$. Let ${\mathcal {M}}= (S,\sim ,\varvec{r}_{,}V)$ and $s \in S$ be given. On the assumption that ${\mathcal {M}}_s \models pre (e)$, it is sufficient to prove:

$$\begin{aligned} {\mathcal {M}}\otimes {\mathcal {E}}_{(s,e)} \models \varphi *^{\forall \forall }\psi \text { \ \ iff \ \ for all } f,g \in E, {\mathcal {M}}_s \models [{\mathcal {E}}_f]\varphi *^{\forall \forall } [{\mathcal {E}}_g]\psi \end{aligned}$$

By definition, ${\mathcal {M}}\otimes {\mathcal {E}}_{(s,e)} \models \varphi *^{\forall \forall }\psi$ is equivalent to:

• 1. there are $(t,f),(u,g) \in {\mathcal {D}}({\mathcal {M}}\otimes {\mathcal {E}})$ such that $\varvec{r}_{(s,e)} = \varvec{r}_{(t,f)} \circ \varvec{r}_{(u,g)}$;

• 2. for all $(t',f') \in {\mathcal {D}}({\mathcal {M}}\otimes {\mathcal {E}})$, if $\varvec{r}_{(t',f')} = \varvec{r}_{(t,f)}$ then ${\mathcal {M}}_{(t',f')} \models \varphi$;

• 3. for all $(u',g') \in {\mathcal {D}}({\mathcal {M}}\otimes {\mathcal {E}})$, if $\varvec{r}_{(u',g')} = \varvec{r}_{(u,g)}$ then ${\mathcal {M}}_{(u',g')} \models \psi$.

Concerning item 1, we recall that for any t, f, u, g: $\varvec{r}_{(s,e)} = \varvec{r}_{(t,f)} \circ \varvec{r}_{(u,g)}$ iff $\varvec{r}_{s} = \varvec{r}_{t} \circ \varvec{r}_{u}$, where from the right to the left equivalent it is implicit that (t, f) and (u, g) are in the domain of ${\mathcal {M}}\otimes {\mathcal {E}}$ (where we note that it was a given that (s, e) is in that domain). Therefore, 1 is equivalent to

There are $t,u \in S$ such that $\varvec{r}_{s} = \varvec{r}_{t} \circ \varvec{r}_{u}$ and there are $f,g \in E$ such that ${\mathcal {M}}_t \models pre (f)$ and ${\mathcal {M}}_u \models pre (g)$.

As action models are required to be covering (the disjunction of all preconditions of actions in the domain is a validity) there always are such f and g. As this part of the requirement is therefore always fulfilled in our semantics it can be removed from the above formulation, we thus we have shown that item 1 is equivalent to

• 1. there are $t,u \in S$ such that $\varvec{r}_{s} = \varvec{r}_{t} \circ \varvec{r}_{u}$.

Item 2 is equivalent to

For all $f' \in E$, for all $t' \in S$, if $\varvec{r}_{t'} = \varvec{r}_{t}$ then ${\mathcal {M}}_{t'} \models pre (f')$ implies ${\mathcal {M}}\otimes {\mathcal {E}}_{(t',f')} \models \varphi$.

and therefore also to—where for convenience we renamed $f'$ as f

For all $f \in E$, for all $t' \in S$, if $\varvec{r}_{t'} = \varvec{r}_{t}$ then ${\mathcal {M}}_{t'} \models [{\mathcal {E}}_f]\varphi$.

Similarly to item 2, item 3 can be rephrased as

For all $g \in E$, for all $u' \in S$, if $\varvec{r}_{u'} = \varvec{r}_{u}$ then ${\mathcal {M}}_{u'} \models [{\mathcal {E}}_g]\varphi$.

Combining the three items again, and moving the quantification over $f \in E$ and over $g \in E$ to the beginning of the statement, we obtain

For all $f,g \in E$:

• 1. there are $t,u \in S$ such that $\varvec{r}_{s} = \varvec{r}_{t} \circ \varvec{r}_{u}$;

• 2. for all $t' \in S$, if $\varvec{r}_{t'} = \varvec{r}_{t}$ then ${\mathcal {M}}_{t'} \models [{\mathcal {E}}_f]\varphi$;

• 3. for all $u' \in S$, if $\varvec{r}_{u'} = \varvec{r}_{u}$ then ${\mathcal {M}}_{u'} \models [{\mathcal {E}}_g]\psi$.

By definition of the semantics of $*^{\forall \forall }$ this is equivalent to

For all $f,g \in E$, ${\mathcal {M}}_s \models [{\mathcal {E}}_f]\varphi *^{\forall \forall } [{\mathcal {E}}_g]\psi$.

as required to fulfil the proof obligation.

We now show the validity for $\mathrel {-*}^{\forall \forall }$ (wherein we use somewhat more succinct notation on the meta-level). On the assumption of ${\mathcal {M}}_s \models pre (e)$, this time we have to show that: ${\mathcal {M}}\otimes {\mathcal {E}}_{(s,e)} \models \varphi \mathrel {-*}^{\forall \forall } \psi$ iff ${\mathcal {M}}_s \models \bigvee _f ([{\mathcal {E}}_f]\varphi \mathrel {-*}^{\forall \forall } \bigwedge _g [{\mathcal {E}}_g]\psi )$. By definition, the first is equivalent to:

• $\forall (t,f) : \varvec{r}_{(s,e)} \circ \varvec{r}_{(t,f)} \!\downarrow$ and

• $\forall (t',f'): \varvec{r}_{(t',f')} = \varvec{r}_{(t,f)} \Rightarrow {\mathcal {M}}\otimes {\mathcal {E}}_{(t',f')} \models \varphi$, implies

• $\forall (u,g): \varvec{r}_{(u,g)} = \varvec{r}_{(s,e)} \circ \varvec{r}_{(t,f)} \Rightarrow {\mathcal {M}}\otimes {\mathcal {E}}_{(u,g)} \models \psi$

The second is equivalent to:

There is $f \in E$ such that:

• $\forall t : \varvec{r}_{s} \circ \varvec{r}_{t} \!\downarrow$ and

• $\forall t': \varvec{r}_{t'} = \varvec{r}_{t} \Rightarrow {\mathcal {M}}_{t'} \models [{\mathcal {E}}_f]\varphi$, imply

• $\forall g, u: \varvec{r}_{u} = \varvec{r}_{s} \circ \varvec{r}_{t} \Rightarrow {\mathcal {M}}_{u} \models [{\mathcal {E}}_g]\psi$.

and therefore, internalizing f into the antecedent of the second item and replacing f for $f'$, to:

• $\forall t : \varvec{r}_{s} \circ \varvec{r}_{t} \!\downarrow$ and

• $\forall f', t': \varvec{r}_{t'} = \varvec{r}_{t} \Rightarrow {\mathcal {M}}_{t'} \models [{\mathcal {E}}_{f'}]\varphi$, imply

• $\forall g, u: \varvec{r}_{u} = \varvec{r}_{s} \circ \varvec{r}_{t} \Rightarrow {\mathcal {M}}_{u} \models [{\mathcal {E}}_g]\psi$.

Similarly to the proof of the previous validity, the second and third items of these transcriptions are equivalent (on the implicit assumption that ${\mathcal {M}}_t \models pre (f)$), and concerning the first item we note that

$$\begin{aligned} \forall (t,f) : \varvec{r}_{(s,e)} \circ \varvec{r}_{(t,f)} \!\downarrow \end{aligned}$$

is equivalent to

$$ \begin{aligned} \forall f,t : {\mathcal {M}}_t \models pre (f) \ \& \ \varvec{r}_{s} \circ \varvec{r}_{t} \!\downarrow \end{aligned}$$

where the part $\forall f: {\mathcal {M}}_t \models pre (f)$ can just as well be an explicit assumption in the second item, so that we can replace the above by

$$\begin{aligned} \forall t : \varvec{r}_{s} \circ \varvec{r}_{t} \!\downarrow \end{aligned}$$

and we again obtain equivalent descriptions, as required to close the proof. $\square$

5.2 Comparing the ${\exists \exists }$ Semantics to the ${\forall \forall }$ Semantics

The remainder of this section compares the modelling advantages of the ${\exists \exists }$ and ${\forall \forall }$ versions, illustrated by the library example from Sect. 3.

All versions of the multiplicative connectives $*$ and $\mathrel {-*}$ go beyond the original BI semantics, as they combine aspects of separation of resources with aspects of uncertainty about resources. It seems that the $\exists \exists$ version emphasizes the epistemic aspect of the semantics whereas the $\forall \forall$ version emphasizes the separation aspect of the semantics. For example, consider $*^{\forall \forall }$.

A formula $\varphi *^{\forall \forall } \psi$ is true in a state s mapped to resource r if r can be decomposed in resources $r'$ and $r''$ such that all states mapped to $r'$ satisfy $\varphi$ and all states mapped to $r''$ satisfy $\psi$, disregarding their possibly different epistemic properties. As (really) different states mapped to the same resource typically differ in epistemic properties, the requirements to satisfy $\varphi *^{\forall \forall } \psi$ are stronger than the requirements to satisfy $\varphi *^{\exists \exists } \psi$. Given s and t both mapped to $r'$, maybe s satisfies that agent a knows that the resource is $r'$, exemplified in $K_a p$ for some p interpreted as $r'$, whereas in t the same agent does not know that. In that case, a separation in a given state (world) u such that $K_a p *^{\forall \forall } \psi$ cannot be satisfied, nor $\lnot K_a p *^{\forall \forall } \psi$. The left multiplicative conjunct must be satsfied in s and in t. Whereas neither $K_a p *^{\exists \exists } \psi$ nor $\lnot K_a p *^{\exists \exists } \psi$ are problematic. In the first case we choose s and in the second case we choose t, and p is true because both map to $r'$.

Dually, in order to satisfy some $\varphi *^{\exists \exists } \psi$ we focus on the epistemic differences between states, while satisfying the resource separation requirements. In applications focussing on ‘epistemic’ safety requirements the $\forall \forall$ version seems more appropriate whereas ‘epistemic’ liveness appears to favour the liberty from the $\exists \exists$ version. This is illustrated in the further developed library example below.

For any other of the 16 semantic variations we could not think of obvious modelling advantages. However, their might be certain technical logical advantages, for example if the reductions for the different versions are most elegantly formulated in axioms combining several versions. However, this is not born out by our experience so far.

For restricted language fragments the difference between the semantic variations vanishes. We make two observations on that count, in the form of propositions without (elementary) proof. As we need to be explicit on the syntax, let for any $\varphi \in {\mathcal {L}}_{*{K}\otimes }$ the formula $\varphi ^\exists$ be $\varphi$ wherein all $*$ and $\mathrel {-*}$ are substituted for $*^{\exists \exists }$ and $\mathrel {-*}^{\exists \exists }$ and let $\varphi ^\forall$ be $\varphi$ wherein all $*$ and $\mathrel {-*}$ are substituted for $*^{\forall \forall }$ and $\mathrel {-*}^{\forall \forall }$.

The first observation is that for non-epistemic formulas, it does not matter which version we use.

Proposition 7

Let $\varphi \in {\mathcal {L}}_{*}$. Then $\varphi ^\exists$ is equivalent to $\varphi ^\forall$.

The second observation concerns public announcements. In the semantics of PASL, if we restrict the language to action models that are public announcements, and if we restrict the models to those where the domain of the epistemic resource model corresponds to the domain of the resource monoid, there is no difference between $\exists \exists$ and $\forall \forall$ (or any other version). Let us call an epistemic resource model with a one–one correspondence between states and resources rigid.

Proposition 8

Let ${\mathcal {M}}$ be a rigid epistemic resource model, let state s be in the domain of ${\mathcal {M}}$, and let $\varphi \in {\mathcal {L}}_{*{K}\otimes }$ only contain dynamic modalities for public announcements. Then ${\mathcal {M}}_s \models \varphi ^\exists$ iff ${\mathcal {M}}_s \models \varphi ^\forall$.

This is because the PASL semantics required a one–one correspondence between states and resources. So if there is one state satisfying a given formula, all states mapped to that resource satisfy that formula, and if all states mapped to a certain resource satisfy a certain formula, there must be at least one because the carrier set of the resource monoid is the entire domain of the model. As long as this property of ‘rigidity’ is preserved after update, any $\varphi ^\exists$ is equivalent to $\varphi ^\forall$.

This does not imply that in AMSL there is no difference between the $\exists \exists$ and $\forall \forall$ semantics for public announcements, not even in the comforting presence of public announcement, because in general its models need not be rigid.

We now continue by demonstrating these issues in the library example. We recall that

$$\begin{aligned} {\mathcal {M}}^1_{21} \models \langle \lnot c \rangle _a^+ (p_a *^{\exists \exists } K_a c) \end{aligned}$$

as well as

$$\begin{aligned} {\mathcal {M}}^1_{21} \models \langle \lnot c \rangle _a^+ (p_a *^{\exists \exists } \lnot K_a c) \end{aligned}$$

and in both cases we now have made explicit that $*$ means $*^{\exists \exists }$. We further recall that the former is justified by ${\mathcal {M}}^4_{(21,\lnot c_a^+)} \models K_a c$ whereas the latter is justified by ${\mathcal {M}}^4_{(21, \lnot c_a^-)} \models \lnot K_a c$.

As a consequence, this plays out differently for $*^{\forall \forall }$. We then have, for example:

$$\begin{aligned} \begin{array}{l} {\mathcal {M}}^1_{21} \not \models \langle \lnot c \rangle _a^+ (p_b *^{\forall \forall } K_a c) \\ {\mathcal {M}}^1_{21} \not \models \langle \lnot c \rangle _a^+ (p_b *^{\forall \forall } \lnot K_a c) \end{array}\end{aligned}$$

The truth of that would require both states mapping to (2, 0) in ${\mathcal {M}}_4$ to satisfy $K_a c$, or both to satisfy $\lnot K_a c$.

For a different example, consider ${\mathcal {M}}^4$ (the model resulting from the suspected semi-private announcementof c) once more. For the convenience of the reader this example is quite dual to the previous one, but formulated in terms of resource update instead of resource separation. We now have:

$$\begin{aligned}\begin{array}{l} {\mathcal {M}}^4_{(01,c^+_a)} \models (p_a *^{\exists \exists } p_a) \mathrel {-*}^{\exists \exists } K_a c \\ {\mathcal {M}}^4_{(01,c^+_a)} \models (p_a *^{\exists \exists } p_a) \mathrel {-*}^{\exists \exists } \lnot K_a c \\ {\mathcal {M}}^4_{(01,c^+_a)} \not \models (p_a *^{\forall \forall } p_a) \mathrel {-*}^{\forall \forall } K_a c \\ {\mathcal {M}}^4_{(01,c^+_a)} \not \models (p_a *^{\forall \forall } p_a) \mathrel {-*}^{\forall \forall } \lnot K_a c \end{array}\end{aligned}$$

The first is true because

$$\begin{aligned}\begin{array}{l} {\mathcal {M}}^4_{(21,\lnot c^+_a)} \models K_a c \end{array}\end{aligned}$$

Whereas the second is false because

$$\begin{aligned}\begin{array}{l} {\mathcal {M}}^4_{(21, \lnot c^-_a)} \models \lnot K_a c \end{array}\end{aligned}$$

Therefore neither is true in the $\forall \forall$ semantics for $\mathrel {-*}$, and the third and fourth are both false. As a point of evaluation in ${\mathcal {M}}^4$, instead of $(01,c^+_a)$ we could also have chosen $(01,c^-_a)$: for any of the $*$ and $\mathrel {-*}$ versions, it does not matter for their truth what the epistemic properties are of the state of evaluation s, it only matters what resource it maps to, in this case: (0, 1).

6 Conclusion and Further Research

We proposed a dynamic epistemic separation logic with action models, $\mathrm {AMSL}$, containing modalities to reason about knowledge, multiplicative conjunctions and implications as in separation logic, as well as dynamic modalities (parameterized by action models) for uncertainty about knowledge and resources. We have shown that the dynamic modalities can be eliminated from the logical language: every formula containing them is equivalent to a formula not containing them. Our proposal is the expected generalization of public announcement separation logic, $\mathrm {PASL}$ (Courtault et al., 2019), that indeed now is a special case in our logic.

In our proposal the separation aspects are completely orthogonal to the dynamic aspects: we only model uncertainty about resources and their composition and update. A very different approach to combining change of knowledge with change of resources is to let the resource update correspond to the information update (the action model execution). In that case, while updating states, we can simultaneously update resources, that is, map the resulting states in the modal product to different resources. We expect to pursue this in subsequent research.

Another perspective consists in designing a tableaux calculus with labels and constraints for $\mathrm {AMSL}$  from the semantics, in the spirit of the labelled calculi developed for Modal BI and $\mathrm {PASL}$ (Courtault & Galmiche, 2018; Courtault et al., 2019), with a study of its soundness and completeness from a countermodel extraction method. It could be also interesting to define a Hilbert-style axiomatization of BBI and its modal extensions, including $\mathrm {AMSL}$, and to relate them to the existing proof calculi. Finally, even if BBI has been proved undecidable (Larchey-Wendling & Galmiche, 2010, 2013), a complementary perspective is the study of some sublogics of $\mathrm {AMSL}$ that would be expressive enough to model systems, but that would still be decidable.