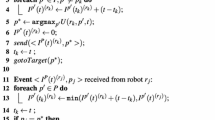Abstract
Multi-robot patrolling represents a fundamental problem for many monitoring and surveillance applications and has gained significant interest in recent years. In patrolling, mobile robots repeatedly travel through an environment, capture sensor data at certain sensing locations and deliver this data to the base station in a way that maximizes the changes of detection. Robots move on tours, exchange data when they meet with robots on neighboring tours and so eventually deliver data to the base station. In this paper we jointly consider two important optimization criteria of multi-robot patrolling: (i) idleness, i.e. the time between consecutive visits of sensing locations, and (ii) delay, i.e. the time between capturing data at the sensing location and its arrival at the base station. We systematically investigate the effect of the robots’ moving directions along their tours and the selection of meeting points for data exchange. We prove that the problem of determining the movement directions and meeting points such that the data delay is minimized is NP-hard. For this purpose, we define a structure called tour graph which models the neighborhood of the tours defined by potential meeting points. We propose two heuristics that are based on a shortest-path-search in the tour graph. We provide a simulation study which shows that the cooperative approach can outperform an uncooperative approach where every robot delivers the captured data individually to the base station. Additionally, the experiments show that the heuristic which is computational more expensive performs slightly better on average than the less expensive heuristic in the considered scenarios.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Acevedo, J.J., Arrue, B.C., Diaz-Banez, J.M., Ventura, I., Maza, I., Ollero, A.: Decentralized strategy to ensure information propagation in area monitoring missions with a team of UAVs under limited communications. In: Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), pp. 565–574. IEEE (2013)
Acevedo, J.J., Arrue, B.C., Maza, I., Ollero, A.: Cooperative perimeter surveillance with a team of mobile robots under communication constraints. In: Proceedings of the IEEE International Conference on Intelligent Robots and Systems (IROS), pp. 5067–5072. IEEE (2013)
Anisi, D.A., Ógren, P., Hu, X.: Cooperative minimum time surveillance with multiple ground vehicles. IEEE Trans. Autom. Control 55(12), 2679–2691 (2010)
Banfi, J., Basilico, N., Amigoni, F.: Minimizing communication latency in multirobot situation-aware patrolling. In: Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 616–622 (2015)
Chang, C.Y., Chen, G., Yu, G.J., Wang, T.L., Wang, T.C.: TCWTP: Time-constrained weighted targets patrolling mechanism in wireless mobile sensor networks. IEEE Trans. Syst. Man Cybern.: Syst. 45(6), 901–914 (2015)
Chevaleyre, Y.: Theoretical analysis of the multi-agent patrolling problem. In: Proceedings of the IEEE/WIC/ACM International Conference on Intelligent Agent Technology (IAT), pp. 302–308. IEEE (2004)
Erdelj, M., Natalizio, E., Chowdhury, K.R., Akyildiz, I.F.: Help from the sky: Leveraging UAVs for disaster management. IEEE Pervasive Comput. 16(1), 24–32 (2017)
Fargeas, J.L., Hyun, B., Kabamba, P., Girard, A.: Persistent visitation under revisit constraints. In: Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), pp. 952–957. IEEE (2013)
Flushing, E.F., Gambardella, L.M., Di Caro, G.A.: Simultaneous task allocation, data routing, and transmission scheduling in mobile multi-robot teams. In: Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 1861–1868. IEEE (2017)
Frederickson, G.N., Hecht, M.S., Kim, C.E.: Approximation algorithms for some routing problems. In: Proceedings of the Annual Symposium on Foundations of Computer Science, pp. 216–227. IEEE (1976)
Garey, M.R., Johnson, D.S.: Computers and Intractability - A Guide to the Theory of NP-Completeness. W. H. Freeman & Co., New York (1979)
Ghamry, K.A., Zhang, Y.: Cooperative control of multiple UAVs for forest fire monitoring and detection. In: Proceedings of the IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), pp. 1–6. IEEE (2016)
Grotli, E.I., Johansen, T.A.: Path- and data transmission planning for cooperating UAVs in delay tolerant network. In: Proceedings of the IEEE Globecom Workshops, pp. 1568–1573. IEEE (2012)
Hollinger, G.A., Singh, S.: Multirobot coordination with periodic connectivity: Theory and experiments. IEEE Trans. Robot. 28(4), 967–973 (2012)
Kantaros, Y., Guo, M., Zavlanos, M.M.: Temporal logic task planning and intermittent connectivity control of mobile robot networks. IEEE Trans. Autom. Control PP(c), 1–1 (2019)
Kantaros, Y., Zavlanos, M.M.: Distributed intermittent connectivity control of mobile robot networks. IEEE Trans. Autom. Control 62(7), 3109–3121 (2017)
Khan, A., Rinner, B., Cavallaro, A.: Cooperative robots to observe moving targets: Review. IEEE Trans. Cybern. 48(1), 187–198 (2018)
Kingston, D., Beard, R., Holt, R.: Decentralized perimeter surveillance using a team of UAVs. IEEE Trans. Robot. 24(6), 1394–1404 (2008)
Lauri, F., Créput, J.C., Koukam, A.: The multi-agent patrolling problem theoretical results about cyclic strategies. In: Lecture Notes in Computer Science, vol. 8473, pp. 171–182. Springer (2014)
Liu, B., Dousse, O., Nain, P., Towsley, D.: Dynamic coverage of mobile sensor networks. IEEE Trans. Parallel Distrib. Syst. 24(2), 301–311 (2013)
Machado, A., Ramalho, G.: Multi-Agent Patrolling: An Empirical Analysis of Alternative Architectures, Lecture Notes in Computer Science, vol. 2581. Springer, Berlin (2003)
Magnanti, T.L., Wolsey, L.A.: Optimal trees. In: Handbooks in Operations Research and Management Science, vol. 7, pp. 503–615. Elsevier B.V (1995)
Manyam, S.G., Rasmussen, S., Casbeer, D.W., Kalyanam, K., Manickam, S.: Multi-UAV routing for persistent intelligence surveillance & reconnaissance missions. In: Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), pp. 573–580. IEEE (2017)
Masehian, E., Jannati, M., Hekmatfar, T.: Cooperative mapping of unknown environments by multiple heterogeneous mobile robots with limited sensing. Robot. Auton. Syst. 87, 188–218 (2017)
Mosteo, A.R., Montano, L.: Concurrent tree traversals for improved mission performance under limited communication range. In: Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 2840–2845. IEEE (2009)
Nigam, N., Bieniawski, S., Kroo, I., Vian, J.: Control of multiple UAVs for persistent surveillance: Algorithm and flight test results. IEEE Trans. Control Syst. Technol. 20(5), 1236–1251 (2012)
Pasqualetti, F., Durham, J.W., Bullo, F.: Cooperative patrolling via weighted tours: Performance analysis and distributed algorithms. IEEE Trans. Robot. 28(5), 1181–1188 (2012)
Pasqualetti, F., Franchi, A., Bullo, F.: On cooperative patrolling: Optimal trajectories, complexity analysis, and approximation algorithms. IEEE Trans. Robot. 28(3), 592–606 (2012)
Ponda, S.S., Johnson, L.B., Kopeikin, A.N., Choi, H.L., How, J.P.: Distributed planning strategies to ensure network connectivity for dynamic heterogeneous teams. IEEE J. Selected Areas Commun. 30(5), 861–869 (2012)
Portugal, D., Pippin, C., Rocha, R.P., Christensen, H.: Finding optimal routes for multi-robot patrolling in generic graphs. In: Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 363–369. IEEE (2014)
Rossi, M., Brunelli, D.: Autonomous gas detection and mapping with unmanned aerial vehicles. IEEE Trans. Instrum. Meas. 65(4), 765–775 (2016)
Santos, J.M., Krajník, T., Duckett, T.: Spatio-temporal exploration strategies for long-term autonomy of mobile robots. Robot. Auton. Syst. 88, 116–126 (2017)
Scherer, J., Rinner, B.: Persistent multi-UAV surveillance with energy and communication constraints. In: Proceedings of the IEEE International Conference on Automation Science and Engineering (CASE), pp. 1225–1230 (2016)
Scherer, J., Rinner, B.: Short and full horizon motion planning for persistent multi-UAV surveillance with energy and communication constraints. In: Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 230–235. IEEE (2017)
Scherer, J., Rinner, B., Yahyanejad, S., Hayat, S., Yanmaz, E., Andre, T., Khan, A., Vukadinovic, V., Bettstetter, C., Hellwagner, H.: An autonomous multi-UAV system for search and rescue. In: Proceedings of the First Workshop on Micro Aerial Vehicle Networks, Systems, and Applications for Civilian Use - DroNet ’15, pp. 33–38 (2015)
Smith, S.L., Schwager, M., Rus, D.: Persistent robotic tasks: Monitoring and sweeping in changing environments. IEEE Trans. Robot. 28(2), 410–426 (2012)
Funding
Open access funding provided by University of Klagenfurt.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: MILP formulation of MDTD
The mixed integer linear programming (MILP) model of MDTD is based on a multi-commodity flow formulation for trees on a graph G = (V, A) with n + 1 vertices V (including a vertex 0 for a virtual base station tour) and arc set A [22]. The base station is the source of a commodity flow \(f^c_e\) for each vertex (constraint (8)). A flow of commodity c represents the path of the data from robot c towards the base station (though the flow originates at the base station in this formulation). For each vertex the sum of incoming flows is equal to the sum of outgoing flows for each commodity not dedicated to that vertex (constraint (9)), and each vertex c consumes the commodity of type c (constraint (10)). There can be only a flow on an edge if this edge is selected in the tree (constraint (11)) and the sum of the edges must be n (constraint (12)).
The data which robot j gets at the meeting point between i and j and is forwarded at meeting point between j and k has to travel the distance \(l_{ik}^{j,ccw}\) or \(l_{ik}^{j,cw}\) on tour j, depending on the direction robot j traverses its tour. Therefore, two flow variables \(f_{ij}^c\) and \(f_{jk}^c\) are involved in the cost calculation in constraint (15) for data originating from c and traversing the tour j. The separation of the flows in this formulation allows the definition of a min-max objective. For each commodity c, zc models the delay of data originating at robot c and the objective is to minimize z. The decision variables \(u_j^{ccw}\) and \(u_j^{cw}\) determine the direction robot j traverses its tour.
The products, e.g. \(f_{ij}^c f_{jk}^c u_j^{ccw}\), can be linearized (likewise \(f_{ij}^c f_{jk}^c u_j^{cw}\)) with an additional variable \(f_{ijk}^{c, ccw}\) and the constraints:
Appendix B: List of symbols
- Symbol :
-
Meaning
- X :
-
set of points of environment
- P S :
-
sensing locations
- Y :
-
communication relation
- R = {1,…,n}:
-
set of n robots/tours
- π ∈π:
-
patrolling strategy/schedule (from the set of all strategies π)
- π + :
-
repeated schedule (repetition of schedule π)
- \(\mathbb {R}_{\geq 0}\) :
-
set of real numbers larger or equal 0
- \(I_t^{\pi }(x)\) :
-
instantaneous idleness of x at time t (using π)
- \(D_t^{\pi }(x, t^{\prime }, t^{\prime \prime })\) :
-
instantaneous delay of x at time t (using π)
- \(WI_t^{\pi }(x)\) :
-
instantaneous worst idleness at time t (using π)
- \(WD_t^{\pi }(x)\) :
-
instantaneous worst delay at time t (using π)
- WI, WD:
-
worst idleness, worst delay
- G = (V, E):
-
(tour) graph with vertex set V and edge set E
- G = (V, A):
-
(tour) graph with vertex set V and arc set A
- T = (V, E):
-
(tour) tree with vertex set V and edge set E
- [v, w] ∈ E:
-
(undirected) edge between v and w
- (v, w) ∈ A:
-
(directed) arc from v to w
- \(G^{\prime }=(V^{\prime },E^{\prime },W)\) :
-
converted graph of tour graph G
- v k l :
-
vertex of converted tour graph
- v0 or 0:
-
base station
- l v :
-
minimum traversal time (without stops) of tour v
- \(l_v^S\) :
-
minimum time any sensing location can be reached from a point on tour v
- L :
-
\(\max \limits _{v\in V}\{l_v\}\)
- d v :
-
direction (cw or ccw) robot v traverses its tour (cw or ccw)
- pr(t):
-
position of robot r at time t
- timev(p, q, d):
-
minimum travel time on tour v from point p to point q with direction d
- \(p_v^{start}\) :
-
start position of robot v on its tour v
- \(p_v^{meet}(w)\) :
-
meeting point of robot v on tour v with robot w
- waitv(p):
-
waiting time for robot v on meeting point p
- Δwv:
-
time difference between the starts of robots v and w at their start positions, \(wait_w(p_w^{start})-wait_v(p_{v}^{start})\)
- P(v):
-
set of all positions on tour v
- τ v :
-
traversal time plus waiting times on tour v
- distG(s, d):
-
length of shortest path between vertices s and d in (weighted) graph G
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Scherer, J., Rinner, B. Multi-Robot Patrolling with Sensing Idleness and Data Delay Objectives. J Intell Robot Syst 99, 949–967 (2020). https://doi.org/10.1007/s10846-020-01156-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10846-020-01156-6