A hybrid genetic algorithm for parallel machine scheduling with setup times

Abstract

This paper addresses the unrelated parallel machine scheduling problem with sequence and machine dependent setup times and machine eligibility constraints. The objective is to minimize the maximum completion time (makespan). Instances of more than 500 jobs and 50 machines are not uncommon in industry. Such large instances become increasingly challenging to provide high-quality solutions within limited amount of computational time, but so far, have not been adequately addressed in recent literature. A hybrid genetic algorithm is developed, which is lean in the sense that is equipped with a minimal number of parameters and operators, and which is enhanced with an effective local search operator, specifically targeted to solve large instances. For evaluation purposes a new set of larger problems is generated, consisting of up to 800 jobs and 60 machines. An extensive comparative study shows that the proposed method performs significantly better compared to other state-of-the-art algorithms, especially for the new larger instances. Also, it is demonstrated that calibration is crucial and in practice it should be targeted at a narrower set of representative instances.

Introduction

Scheduling concerns the allocation of tasks, usually called jobs, to different resources, often referred to as machines, optimizing a given objective function. Despite the abundant literature, there is a noticeable gap between theory and the application of developed methods. The proposed methods often neglect important real-world aspects and focus on relatively small problem instances. As a consequence manual scheduling is still relatively common in practice. On the other side, scheduling is becoming an increasingly complex task, as technological advancement leads to companies with ever growing product portfolios.

This work deals with the scheduling of n independent jobs on m unrelated parallel machines. Each job needs to be processed on exactly one machine. Jobs are non-preemptive and require a given process and setup time. In case of identical machines the processing time of a job is the same on all machines. Machines are considered unrelated when the processing time of a job depends on the machine to which it is assigned. Additionally, not every machine is eligible to process all jobs. This setting closely resembles real-world scenarios, where a large machine dependency is common due to the presence of multiple machines from different ages and with various technologies. A setup is a set of operations that must be performed on a machine to prepare it for processing a job. In many cases the required operations depend on the job that was previously processed and on the machine itself, i.e. setup times are sequence and machine dependent. Setup times play an important role in many modern industrial and manufacturing environments and need to be explicitly considered while making scheduling decisions in order to improve resource utilization.

The optimization criterion most frequently studied for this scheduling problem is the minimization of the maximum completion time, also known as the makespan or $C_\text {max}$. Lenstra et al. (1977) demonstrated that minimization of the makespan, even for the simple case with identical parallel machines and no setup times, is a non-deterministic polynomial (NP) hard problem. Therefore, it is not surprising that many of the developed solution methods are based on heuristic and metaheuristic algorithms. In summary, according to the standard notation for scheduling problems, the problem addressed in this work is denoted by $R/s_{i,j,k},M_j/C_\text {max}$ (Graham et al. 1979). In the $R/s_{i,j,k},M_j/C_\text {max}$ scheduling problem there is a set of jobs $J = \{j_1,j_2,\ldots ,j_{|J|}\}$ to be scheduled on one of k unrelated parallel machines from the set $M = \{m_1,m_2,\ldots ,m_k\}$. The setup time between the subsequent processing of job i and j on machine m is $s_{i,j,m}$. Each job j is associated with a processing time $p_{j,m}$ that depends on the machine m to which it is assigned, and $M_j$ denotes the specific subset of machines that is eligible to process job j. The objective is to find the schedule $S = \{S_1,S_2,\ldots ,S_k\}$ that minimizes the makespan $C_\text {max} = \max _{1 \le i \le k} C_i$, where $S_i$ denotes the process sequence and $C_i$ is the completion time of the last job on machine $m_i$. Moreover, as is common in literature that focuses on the same problem, it is assumed that:

• Jobs are non-preemptive;

• All jobs and machines are available at time zero;

• There are no precedence constraints among jobs;

• The setup time prior to the first job in the sequence is zero.

Although the parallel machine scheduling problem has been extensively studied over the past decades, most work focuses on scenarios with identical machines (Cheng et al. 2004). Moreover, the vast majority of the literature ignores setup times completely or assumes they are independent of job sequence and machine (Zhu and Wilhelm 2006; Allahverdi et al. 2008; Allahverdi 2015; Ezugwu et al. 2018). In this paper, only the literature that focuses on the more complex setting with machine dependent processing times, as well as machine and sequence dependent setup times, is considered. Moreover, the scope is constrained to work that considers the objective to minimize the makespan.

Fig. 1

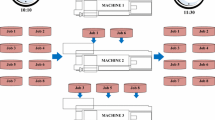
For simplicity one machine is considered. Colored blocks indicate jobs. When jobs have the same color it means their requirements are identical. Dashed blocks in between represent setup time. a Two sets of jobs are subsequently released and scheduled. b The two sets are simultaneously released and scheduled

Several algorithms have been developed to solve the unrelated parallel machine scheduling problem with sequence and machine dependent setup times for makespan minimization, i.e. $R/s_{i,j,k}/C_\text {max}$. Rabadi et al. (2006) published a set of synthetic problem instances and proposed a randomized priority search metaheuristic. Arnaout et al. (2010) provided an ant colony optimization (ACO) algorithm and Ying et al. (2012) presented a restricted simulated annealing algorithm for the same problem. Both showed that this method outperforms the method of Rabadi et al. (2006) for the same problem instances. Later, Arnaout et al. (2014) proposed an enhanced ACO algorithm and showed that this approach outperforms its predecessor as well as the method proposed by Ying et al. (2012). Chang and Chen (2011) derived dominance properties and used these heuristics to provide good initial solutions for a genetic algorithm. Lin and Ying (2014) provided a hybrid artificial bee colony (HABC) algorithm and compared its performance with several other algorithms, including the methods of Rabadi et al. (2006), Chang and Chen (2011) and Ying et al. (2012). Vallada and Ruiz (2011) introduced another challenging set of randomly generated problem instances and proposed a hybrid genetic algorithm (HGA) with a local search enhanced crossover mechanism. This set of problems received considerable attention in literature. Avalos-Rosales et al. (2015) proposed a multi start algorithm that outperforms the HGA of Vallada and Ruiz (2011). Also, they provided a novel mixed integer formulation for the problem that allows instances up to 60 jobs and 5 machines to be solved in two to three hours. Cota et al. (2017) proposed an adaptive large neighborhood search metaheuristic. Their results generally improved the original results of Vallada and Ruiz (2011), presenting better solutions for most instances. Santos et al. (2019) proposed various stochastic local search methods and showed that simulated annealing significantly outperforms the methods of Vallada and Ruiz (2011) and Cota et al. (2017). New mixed integer formulations and an algorithm based on mathematical programming were presented by Fanjul-Peyro et al. (2019). A worm optimization algorithm was applied by Arnaout (2020). Later, de Abreu and de Athayde Prata (2020) applied a hybdrid metaheuristic based on a genetic algorithm. Ezugwu and Akutsah (2018) proposed a firefly algorithm and later Ewees et al. (2021) proposed a salp swarm algorithm, based on the firefly algorithm. More recently, a fixed set search method was proposed by Jovanovic and Voß (2021) and a whale optimization algorithm was presented by Al-qaness et al. (2021).

Due to a lack of real-world problem instances, the aforementioned studies are all based on artificially generated problem instances. The majority of these studies focus on two sets of problem instances. The first set is provided by Rabadi et al. (2006), where the largest instances consider scenarios where the number of machines m is 12 and the number of jobs n is 120. The second set is provided by Vallada and Ruiz (2011) and considers scenarios up to $m=30$ and $n=250$. Nonetheless, significantly larger instances are frequently encountered in many industrial sectors. Problems twice the size of the largest instances mentioned above are not uncommon. Furthermore, another motivation to consider larger problems is that they provide more potential in creating efficient schedules. In practice, new sets of jobs are released repeatedly, for example in weekly buckets. This way, scheduling remains manageable for manual planning. If instead, when jobs are released biweekly, the potential benefit increases, especially in the presence of sequence and machine dependent setup times. This is illustrated in Fig. 1. When two sets of jobs are combined into one larger set, a sequence that corresponds to a better overall objective (e.g. $C_\text {max}$) may exist.

Recently, Fanjul-Peyro et al. (2019) provided a third set of larger problem instances, the largest of which considers $n=1000$ and $m=8$. The computational time depends on various factors, such as the CPU, the compiler and the termination criterion (for metaheuristics). Among the mentioned methodologies, the metaheuristics often require a computational time in the order of magnitude of minutes for the largest instances considered. Not surprisingly, the exact methods (Avalos-Rosales et al. 2015; Fanjul-Peyro et al. 2019) require computational times in the order of magnitude of hours. Yilmaz Eroglu and Ozmutlu (2017) proposed a hybrid genetic algorithm to solve the unrelated parallel machine scheduling problem with sequence dependent but machine independent setup times, that incorporates machine eligibility constraints, i.e. $R/s_{j,k},M_j/C_\text {max}$. The algorithm is used to solve a real-world, large-scale loom scheduling problem where $m=133$ and $n=1100$. However, a computational time in the order of magnitude of numerous hours is reported to solve this problem. This large computational time is most likely caused by the local search constituent of the algorithm. Local search neighborhoods are known to scale non-linearly with the number of machines m and jobs n. For practical applications, computational times of this magnitude may be infeasible due to the fact that frequent re-scheduling is required, e.g. due to unforeseen disturbances. Hence, there is a need for methods that can efficiently handle large industry sized problem instances.

In this work, a new hybrid genetic algorithm is proposed to solve the unrelated parallel machine scheduling problem, including sequence and machine dependent setup times, as well as machine eligibility constraints: as is the setting in many real-world scenarios. The main novelty of this algorithm is that it is lean, as it employs a minimal number of parameters and operators, which eases parameter calibration, and it is enhanced with an effective local search procedure, specifically designed to solve large problem instances. The balance between exploration and exploitation is clearly defined through a limited number of parameters. A new set of larger challenging problem instances is generated based on the same principle as the existing set from Vallada and Ruiz (2011). This new set of instances contains problems with up to 60 machines and 800 jobs and is made publicly available to encourage future research. Furthermore, an extensive and accurate comparative study is done by implementing the methods of Vallada and Ruiz (2011), Avalos-Rosales et al. (2015) and Santos et al. (2019). Additionally, the proposed algorithm is applied to the real-world instance published by Yilmaz Eroglu and Ozmutlu (2017).

The remainder of this paper is structured as follows: the proposed hybrid genetic algorithm is presented in “” section. The computational experiments are presented in “” section. The problem instances are described in “” section. In “” section the parameters of the algorithm are calibrated. The comparative studies are discussed in “” section. Finally, conclusions and recommendations for further research are given.

Hybrid genetic algorithm

A genetic algorithm (GA) is a bio-inspired metaheuristic optimization method that simulates the process of natural evolution. The basic principles of this technique were first laid down by Holland (1992). Nowadays, the technique is widely used to obtain high quality solutions for optimization problems (Goldberg 1989; Blum et al. 2011; Binitha et al. 2012).

In a genetic algorithm a population of candidate solutions within the search space, so-called individuals, evolves toward better solutions through an iterative evolutionary process. The population in each iteration is referred to as a generation. In each generation, the fitness of the individuals is evaluated, which is usually the value of the objective function in the optimization problem. Then, a subset of the individuals is selected (the parents) and a cross-over mechanism is applied to obtain a new generation of individuals (the offspring). Moreover, a mutation operator may be applied to maintain genetic diversity.

The performance of any search algorithm depends on the balance between two conflicting objectives: exploiting the best solutions found so far (local search) and at the same time exploring the search space for other promising solutions (global search). Genetic algorithms have proven to perform well as a global search technique, i.e. they can rapidly determine the region in which the global optimum exists. However, they can take a relatively long time to determine the exact local optimum in the region of convergence (Booker et al. 2005). Application of local search techniques within a GA can improve its exploiting ability. Such hybrid genetic algorithms (HGAs) were first introduced by Corne et al. (1999) and can be viewed as a hybridization of a genetic algorithm with an individual learning procedure.

Fig. 2

Hybrid genetic algorithm flow chart. The diamonds represent conditional decisions. The parameter P denotes the population size and the parameters $d_{ins}$, $d_{swap}$ and $d_{nn}$ define the extent of the respective local search operators, as will be explained in “”

As for any metaheuristic method, the parameter setting of the genetic algorithm is important to its performance. Parametric tuning is itself a tough optimizatiom problem. In essence, it is a hyperoptimization problem, i.e. the optimization of optimization. Eiben and Smit (2011) provided a comprehensive summary of existing studies on parametric tuning. Clearly, the effort required to calibrate the algorithm considerably increases with the number of parameters. Hence, in the design of the genetic algorithm in the current paper, an attempt is made to keep the number of parameters limited, i.e. to develop a lean algorithm.

In Fig. 2 a schematic overview of the proposed algorithm is shown. After initialization, an evolutionary cycle begins with selection of the parents. Then, based on the parents, the crossover mechanism generates two offspring. Three local search methods are applied to the offspring sequentially. Key features of these local search operators are that they are fast yet effective, and that they scale well with the problem size. If one of these local search methods improved the offspring, all three local search operators are repeated. This search continues until a local minimum is reached. The offspring are accepted into the population if (i) there are no identical individuals already in the population, i.e. they are unique, and (ii) they are fitter than the weakest individual in the population. If they are accepted, the offspring replaces the weakest individuals, otherwise they are discarded. These evolutionary cycles are repeated as long as the termination criterion remains unsatisfied. Contrary to other algorithm designs, in each evolutionary cycle the same operations are performed. No probabilities are required to select these operations. Moreover, a mutation operator is not included. As mentioned, such operator is often applied to maintain genetic diversity, i.e. exploration. However, preliminary experimentation showed that this framework provides sufficient exploratory capabilities through the diversity of the population itself and the crossover mechanism, hence it was decided not to include a mutation operator. A mutation operator is often applied with a certain probability, and requires the number of mutations to be specified. Thus, not including a mutation operator prevents the need for two additional parameters to be specified. Furthermore, the selection and crossover operators used in this framework rely completely on randomness and do not require any parameters to be set, contrary to other well-known alternatives. The only design parameters in this algorithm are the population size P, and three parameters ($d_{ins}$, $d_{swap}$ and $d_{nn}$) that specify the extent of three different local search methods (“” section). These parameters specify the balance between exploration (population size) and exploitation (local search). This limited number of parameters allows facile calibration, as will be demonstrated in “” section. In the subsequent sections, a detailed description of the components of this hybrid genetic algorithm is presented.

Fig. 3

Local search enhanced one-point crossover mechanism, cf. (Vallada and Ruiz 2011)

Solution representation

In parallel machine scheduling problems, solutions are typically represented by an array of jobs for each machine that reflects the processing sequence of the jobs assigned to that machine. The population consists of P individuals, where each individual is composed of |M| arrays of jobs. This way, each array can be viewed as a chromosome constituent of the individuals genome. In the context of this optimization problem, the fitness of an individual refers to the makespan.

Initialization

Although it is common to randomly generate the initial population, there is a recent trend to include some strong individuals that are generated by some heuristic. In this algorithm, the initial population is generated by first creating a random permutation of the list of jobs to be assigned through the Fisher-Yates shuffle mechanism (Fisher and Yates 1953). Then, all jobs in the list are subsequently scheduled as follows: for each job all possible insertion positions are evaluated, respecting machine eligibility constraints. The position that is most favorable in terms of the fitness function is selected. All initial individuals are generated according to this heuristic. This way, an initial population that is both strong and diverse is obtained.

Selection

The selection operator selects two individuals from the population: the parents. Various selection mechanisms are often applied in genetic algorithms, e.g. random, roulette-wheel and tournament selection. After short experimentation with several operators none proved significantly more effective. Therefore, in this algorithm the simplest and computationally most efficient method is applied, namely random selection.

Crossover

Once parents are selected, the crossover mechanism is applied. Many crossover operators are reported in literature, one of the most common being the one-point crossover technique. Here, a local search enhanced one-point crossover operator is applied, cf. Vallada and Ruiz (2011). In Fig. 3 an example is given for a simple case with 10 jobs and 2 machines. After two parents are selected, one point is randomly determined in the job sequence of each machine of parent 1 (a). Jobs to the left-hand side of this point are copied to offspring 1 and jobs to the right are copied to offspring 2 (b). Then, for each machine of parent 2, the jobs that are not yet assigned to the offspring are inserted (c). This is moment where the local search procedure comes into play: when a missing job is inserted into the offspring, it is inserted in every position at the same machine, and finally it is placed at the position that results in the earliest completion time (d). Although in the work of Vallada and Ruiz (2011) machine eligibility constraints are not considered, it is important to note that this mechanism is perfectly applicable in scenarios with machine eligibility constraints without any necessary modifications.

Local search

The genetic algorithm is combined with a fast local search operator to speed up the search towards a local optimum. Arguably, two common local search neighborhoods for parallel machine scheduling problems are the insertion and swap neighborhood. Both have been proven powerful for the considered problem (Wesley Barnes and Laguna 1993; Avalos-Rosales et al. 2015; Cota et al. 2017). The proposed local search operator includes variants of both neighborhoods. As stated earlier, when the size of the problem increases, the size of search neighborhoods (and thus the computational effort) usually increases stronger. Therefore, with increasing problem size, the design of effective search strategies becomes critical. Before describing the specifics of this local search operator, it is important to stress several aspects of the problem at hand:

• Only improvements on the busiest machine improve the makespan.

• Attempting to move a job from a machine with an early completion time to a busier machine is unlikely to decrease the makespan.

With this in mind, three local search neighborhoods are developed to exploit the search space. The insertion and swap neighborhoods focus mainly on machine assignments, i.e. inter-machine movements of jobs. The third neighborhood attempts to improve the job sequence at a single machine, i.e. intra-machine movements of jobs.

Fig. 4

An example of a swap move. Swapping jobs $j_7$ and $j_5$ on the left (a), while maintaining the positions of all other jobs, results in the schedule on the right (b)

Insertion neighborhood search

An insertion move removes one job from a machine and inserts it into another machine. Thus, the entire insertion neighborhood consists of all solutions obtained when each job is extracted from its current position and inserted in all possible positions on all other eligible machines. Given the size of this neighborhood is $O(n^2)$, it is divided into smaller sub-neighborhoods. Specifically, a sub-neighborhood is defined for each machine. The sub-neighborhood of machine i consists of all solutions obtained when each job in the sequence of machine i is extracted from its current position and inserted in all positions on all other eligible machines that have an earlier completion time. Recall that attempting to move a job from a machine with an early completion time to a busier machine is unlikely to decrease the makespan. Thus, the size of the sub-neighborhood of the busiest machine is expected to be $O(n/m\cdot (n - n/m))$, while the size of the least busy machine is 0. Furthermore, the sub-neighborhoods are evaluated starting with the busiest machine, then the second busiest, and so on. The total number of sub-neighborhoods that are evaluated is constrained by a certain fraction of the machines that signifies the degree of exploitation and is denoted by the parameter $d_{ins}$. This way, the number of sub-neighborhoods that are evaluated scales with the problem size, i.e. the number of machines.

During the search in a sub-neighborhood, it needs to be decided when a move is accepted, applying a certain acceptance criterion. At the start, all machine are placed in descending order according to their completion times. Let $G = \{m_1,m_2,\ldots ,m_k\}$ denote the ordered set of machines, where the machine indices are renumbered according to their position in the set, starting with the busiest machine $m_1$. The sub-neighborhood of a certain machine at position i in G is evaluated by picking up each job from its current position and inserting it at all other possible positions on all other eligible machines $m_j$, where $j > i$. Let $C_i$ and $C_j$ denote the completion time of machine $m_i$ and $m_j$ respectively. A movement is accepted (though not implemented yet) if the maximum completion time of $m_i$ and $m_j$ does not increase, i.e.

$$\begin{aligned} \max \big (C_i^{before}, C_j^{before}\big ) \ge \max \big (C_i^{after}, C_j^{after}\big ) \end{aligned}$$

(1)

Note that implicitly this ensures that a move never worsens $C_\text {max}$. Since multiple movements may be accepted, a is defined as the value of the move, i.e.

$$\begin{aligned} a = \big (C_i^{before} - C_i^{after}\big ) +\big (C_j^{before} - C_j^{after}\big ) \end{aligned}$$

(2)

After all moves in the sub-neighborhood of machine $m_i$ are evaluated, the move that corresponds to the minimum value of a is finally implemented. This acceptance strategy resembles a steepest descent method. Among several preliminary experiments with different acceptance criteria and strategies, e.g. with any descent, this combination yielded the best results. After a move is implemented the same machine is searched again. The search within this sub-neighborhood continues until no more improvements can be found at machine $m_i$, i.e. until a local minimum. Then, while $i + 1 < \lfloor k \cdot d_{ins} \rfloor$, the sub-neighborhood of the machine at position $i+1$ in G is explored.

Swap neighborhood search

A swap move interchanges the machine assignment of two jobs, maintaining the positions on these machines. An example of a swap move is shown in Fig. 4. Similarly, the swap neighborhood is divided into smaller sub-neighborhoods. The sub-neighborhood of machine $m_i$ consists of all solutions obtained when each job in the sequence of machine $m_i$ is swapped with every job on all other eligible machines that have an earlier completion time. Given the sequence dependency of the setup times, the position of the jobs after the swap move may not be optimal. Therefore, the search is further intensified by placing the job at machine $m_j$ at the best position in terms of completion time. The swap sub-neighborhoods are evaluated in the same sequence as for the insertion sub-neighborhoods: first the machines are ordered in descending way according to their completion times. Then, the sub-neighborhoods are searched starting with the busiest machine, then the second busiest, and so forth. As for the insertion neighborhood search, the total number of sub-neighborhoods that are evaluated is constrained by a certain fraction of the machines that signifies the degree of exploitation and is denoted by the parameter $d_{swap}$. The same acceptance strategy using Equations (1) and (2) is applied to determine which move is finally implemented. After a move is implemented, the same sub-neighborhood is searched again before continuing to the sub-neighborhood of the next machine.

To reduce the computational effort as much as possible, the number of calculations needed to generate a neighbor should be kept to a minimum. This can be achieved through computation of the changes that occur due to a move, instead of reevaluating the entire sequence. When a job is removed from a sequence, the change of its completion time can be calculated with three subtractions and one addition (or two subtraction when the job is first or last in the sequence). The processing time of this job and the setup time with both adjacent jobs must be subtracted. Then, the setup time between its predecessor and successor must be added. In case the removed job is last in the sequence, only the processing time of this job and the setup time with its predecessor must be subtracted. When the removed job is first in the sequence, only the processing time of this job and the setup time with its successor must be subtracted. Similarly, when a job is inserted into a given sequence, the change can be calculated with only one subtraction and three additions, or two additions when the job is inserted at the end of the sequence. This fast calculation method is applied to both moves in the insertion and swap neighborhood.

Nearest neighbor search

The third neighborhood structure focuses on intra-machine movements. It attempts to optimize the job sequence of a certain machine by evaluating its so-called nearest neighbors. Given a machine $m_i$ with a certain job sequence $S_i$, a nearest neighbor sequence is generated as follows: one job from $S_i$ is taken as the start of the neighbor sequence. Then, all the jobs in $S_i$ that are not yet in the neighbor sequence are inserted at all positions. At each position the change in total setup time of the neighbor sequence is evaluated. Finally, the job that results in the smallest change in total setup time is inserted into the neighbor sequence at the corresponding position. This greedy procedure continues until all jobs are inserted into the neighbor sequence. Another neighbor is generated by taking a different job as the start of the neighbor sequence and assigning the remaining jobs in the same greedy manner. All jobs are taken as a start once, thus, the number of neighbors is equal to the number of jobs in the sequence. Finally, the neighbor with the minimum total setup time replaces the original sequence if its total setup time is smaller. Note that in the current problem the processing time of a job only depends on the machine to which it is assigned and does not depend on the process sequence. Hence, intra-machine movements can only change the total setup time of a sequence and never alter the total processing time. Also note that the number of calculations needed to determine the best position to insert a job is even smaller than for the insertion and swap neighborhoods because the processing time can be omitted. This way, a neighbor sequence can be generated with minimal computational effort. Similar as for the insertion and swap neighborhoods, this nearest neighbor search is only applied to a fraction of the machines. First, the machines are arranged in descending order according to their completion times. Then, the nearest neighbor search is applied to the busiest machine, then the second busiest, and so forth. The total number of machine sequences that are optimized in this manner is constrained by a certain fraction of the machines denoted by the parameter $d_{nn}$.

Local search operator

The offspring generated by the crossover mechanism is subjected to a local search operator that combines the developed search neighborhoods (Fig. 2). Within this operator, the three search neighborhoods are exploited sequentially, as described in Algorithm 1. The nearest neighbor search is exploited first, then the insertion neighborhood and finally the swap neighborhood. When one of the neighborhoods improves the fitness of the individual the iteration is repeated, and when neither of the neighborhoods is able to improve the solution the operator is terminated. As stated before, the offspring is accepted into the population when (i) there are no identical individuals already in the population, i.e. they are unique, and (ii) they are fitter than the weakest individual in the population. If they are accepted, the offspring replaces the weakest individuals, otherwise they are discarded.

The reason that the neighborhoods are evaluated in this particular sequence is related to the computational effort required to evaluate a move. Moves in the nearest neighbor search can be evaluated with minimal computational effort, followed by moves in the insertion neighborhood and movements in the swap neighborhood are the most expensive. Given the steepest descent acceptance strategy, when a move in a swap sub-neighborhood is accepted, the entire sub-neighborhood is searched again. To limit the number of relatively more expensive moves, the swap neighborhood is searched last. Furthermore, the degree by which each individual neighborhood is exploited can be tuned by the parameters $d_{nn}$, $d_{ins}$ and $d_{swap}$ that were introduced before. Together, these parameters define the degree of exploitation of the HGA as a whole. On the other hand, the degree of exploration is defined by a single parameter, namely the population size P. In “” section the calibration of these parameters will be discussed elaborately.

Computational experiments

A detailed description of the instances used in this work is given in the next section. Thereafter, the parameters of the proposed algorithm are calibrated. Then, in “” section, the calibration is validated and the algorithm is benchmarked against methods previously reported in the literature for the problem without eligibility constraints. To make a fair comparison between different methods, all algorithms are coded in C# 6.0 and all experiments are run on a computer with an Intel Core i5-540M (2.53 GHz) processor and 4 GB of memory. Finally, in “” section the algorithm is applied to a large real-world instance of the problem that includes eligibility constraints.

Fig. 5

In the synthetic problem instances the setup times between jobs are completely random. If job $j_2$ is removed from the favourable sequence on the left (a), this may result in an extremely large setup time between job $j_1$ and $j_3$ as is shown on the right (b). Such occurrences are unrealistic in practice

Instances

Recently, Yilmaz Eroglu and Ozmutlu (2017) provided a large-scale real-world instance of the $R/s_{i,j,k},M_j/C_\text {max}$ problem. Here, $m=133$, $n=2111$, setup times range between 1 and 1440 minutes, processing times range between 38 and $10\,955$ minutes and eligibility constraints restrict the number of machines that can be used to process certain jobs. The most technically constrained machine can only process 211 of the jobs, while the least constrained machine can process 1740 jobs. In “” section an attempt to solve this instance is made. This is one of the very few instances available in the literature that include machine eligibility constraints. Hence, although the algorithm proposed here is capable to solve the generalized $R/s_{i,j,k},M_j/C_\text {max}$ problem, the main part of this work focuses on synthetic instances of the more widely studied $R/s_{i,j,k}/C_\text {max}$ problem. Two sets of instances are used: large and extra large.

The large instances are available at http://soa.iti.es and consider the following combinations of number of machines m and jobs n: $m \in \{10, 15, 20, 25, 30\}$ and $n \in \{50, 100, 150, 200, 250\}$. Processing times are integer values uniformly distributed between 1 and 99. The setup times are integer values uniformly distributed between four ranges: 1–9, 1–49, 1–99, 1–124. There are 10 instances for each combination of machines, jobs and setup times, yielding a total of 1000 large instances.

The extra large instances were newly generated in an identical manner. The following combinations of number of machines m and jobs n were considered: $m \in \{20, 40, 60\}$ and $n \in \{400, 600, 800\}$. The same process and setup time ranges were used. Similarly, 5 instances for each combination of machines, jobs and setup times were generated, yielding a total of 240 new instances. These instances are made publicly available at https://git.io/JvCnC.

Furthermore, a separate set of instances is used to calibrate the parameters of the algorithm (“” section). The use of a separate set for calibration prevents a bias in the final results. As mentioned, this research is specifically targeted to solve new extra large problem instances. Hence, the parameters are calibrated on a set of extra large instances. This set consists of two instances for each combination of the number of machines, number of jobs, processing time and setup time range. Thus, the calibration set consists of 72 instances in total, which are also made publicly available at https://git.io/JvCnC.

It is important to make a remark concerning these synthetic instances. In practice, the sequence dependency of the setup times often arises from the fact that certain settings on a machine need to be changed before a job can be processed. In Fig. 5 an example is given of three jobs on one machine. If all three jobs require similar settings, the setup times between the jobs will be small. In the synthetic instances it is well possible that $s_{1,3,1}$ is much larger than $s_{1,2,1} + s_{2,3,1}$. However, this is very unlikely in the real world. In practice, there is often a clear explainable relation between $s_{1,2,1}$, $s_{2,3,1}$ and $s_{1,3,1}$, and in particular the setup times will obey the triangular inequality $s_{1,3,1} \le s_{1,2,1} + s_{2,3,1}$ (Kim et al. 2002). This randomness makes it more difficult for any scheduling algorithm to find favourable clusters of jobs that are alike. On top of this, consider moving such a favourable cluster of jobs entirely from one machine to another. Although the setup times may change to some extent, in practice, this remains a somewhat favourable cluster. In these synthetic instances, this may change completely. Though the instances clearly do not reflect practical aspects in a correct manner, there are two important reasons to use them, namely (i) the limited availability of real-world instances and (ii) other studies focused on the same instances so they provide a way to benchmark with other algorithms.

Fig. 6

Pareto chart that displays the effects in decreasing order of significance. The vertical dashed line indicates the significance level $\alpha$, after standardization. Effects above $\alpha$ are statistically significant

Calibration

The performance of any metaheuristic algorithm depends largely on the setting of its parameters. Calibration of these parameters is itself a very tough optimization problem (Yang 2020). Here, the parameter calibration is done using Design of Experiments (DOE), similar as in Chang and Chen (2011) and Vallada and Ruiz (2011). The performance of the proposed algorithm for a given problem instance is evaluated by means of the relative proportional deviation (RPD), which is computed according to:

$$\begin{aligned} \text {RPD} = \frac{A - B}{B} \cdot 100\% \end{aligned}$$

(3)

where A is the objective value found for a certain problem instance with a specific method and B is the best solution known for this problem instance. Note that in essence the RPD measure is similar to the optimality gap that is generally reported by optimization software. Here the lower bound, or best possible solution, is the best solution ever found for a particular instance. The population size, the depth of the nearest neighbor search, and the depth of the insertion and swap neighborhoods are identified as tuneable parameters in the proposed algorithm. The calibration of these parameters is done as follows: first, for each of the parameters two levels (low and high) are considered, as is shown in Table 1. Rather than setting extreme values for these two levels, the choice of these levels is based on insights obtained through manual experimentation. From several experiments with a hand-full of problem instances, values for each of the parameters were found that result in acceptable performance. The lower and upper levels are chosen slightly below and above these values, respectively. As stated before, calibrating over the same set of instances that are later used to test the tuned algorithm results in a unrealistic estimate of the performance. For this reason, a separate set of instances is used to calibrate the parameters. This set contains two instances for each combination of the number of machines, number of jobs, processing time and setup time range, and is limited to the extra large combinations only. This results in a selection of 72 instances. The termination criterion is set to a maximum elapsed computational time of $n \cdot m \cdot 50$ milliseconds. This way, the computational time scales with both the number of jobs n and the number of machines m. Furthermore, for each instance 5 independent runs are performed. Thus, the computational time required to evaluate one parameter configuration is 30 hours. To evaluate all the possible parameter configurations $30 \cdot 2^4 = 480$ hours are required. Instead of using a full factorial experimental design, a properly chosen fractional factorial design is often sufficient (Montgomery et al. 2009). Since there are four parameters, a half-fraction design suffices to estimate the main effects. Interaction effects cannot be independently estimated. However, it is still possible to sense the presence of interaction effects. If these interactions appear to significantly affect the performance, additional experiments can be performed at a later stage to identify these effects individually.

Fig. 7

The estimated effect of each of the four tuneable parameters on the average RPD

For each parameter configuration the average RPD over all instances is calculated. The results are analysed by means of analysis of variance (ANOVA). In Fig. 6 a Pareto chart is provided that shows the effects in decreasing order of statistical significance. The length of each bar is proportional to the value of a t-statistic calculated for the corresponding effect. Any bars beyond the vertical dashed line are statistically significant at the selected significance level $\alpha$, which is set to 5%. When effects are not independently estimated this is indicated by a ‘+’ sign in Fig. 6. In this case all 4 main effects appear to be significant. The combined interaction effect between the population size and the depth of the nearest neighbor search, and the depths of the swap and insertion neighborhood appears to be significant as well. However, from these results it is not possible to conclude whether one or both of the interactions are significant. As mentioned, to identify individual interaction effects additional experiments are required. Due to the fact that the significance of the combined effect is rather small, these steps are left outside the scope of this research.

Figure 7 shows how each of the 4 parameters affect the average RPD. The lines indicate the estimated change in average RPD as each parameter is moved from its low to its high level, with all other parameters held constant at a value midway between their lows and their highs. Note that the parameters with a higher significance have a larger impact on the average RPD than the others. For each parameter the level that yields the lowest RPD is selected. In Table 1 these values are indicated in bold face. In order to validate the calibration, in the next section the algorithm is applied to the set of test instances using the calibrated parameters values as well as the values found through manual experimentation.

Table 1 Tuneable parameters in the proposed algorithm and tested values for the calibration

Comparative study ($R/s_{i,j,k}/C_\text {max}$)

The proposed algorithm is benchmarked against several methods previously reported in literature for the same problem and the same optimization objective. The first comparison is made with the hybrid genetic algorithm proposed by Vallada and Ruiz (2011). A second comparison is made with the multi-start algorithm (MS) proposed by Avalos-Rosales et al. (2015), which is in essence local search with restarts. Thirdly, a comparison is made to the simulated annealing method proposed by Santos et al. (2019). These methods all focus on the $R/s_{i,j,k}/C_\text {max}$ problem. All methods (i.e. the logic of these methods) have been implemented using the guidelines and descriptions of the original papers. The methods are all coded in C# 6.0 and make use of the same data structures. In this comparative evaluation, all three methods are applied to the large and the extra large instances. As in the original papers, in all cases the termination criterion is set to a maximum elapsed computational time of $n \cdot m \cdot 50$ milliseconds. For each instance 5 independent runs, with different random seeds, are performed (which appeared to be enough as the variability of $C_{max}$ over the runs proved to be sufficiently low). The results are averaged over the runs and instances for each $n \times m$ combination. Recall that there are 10 large and 5 extra large instances for each combination of size and setup time range. There are 4 different setup time ranges. Thus, for each large instance size the average value is computed over $10 \times 4 \times 5 = 200$ executions, and for each extra large instance size it is calculated over $5 \times 4 \times 5 = 100$ executions. The results obtained for the large and extra large instances are shown in Tables 2 and 3 respectively. The algorithms are in chronological order based on publication date, starting with the earliest on the left and the current method on the right.

It can be seen that the genetic algorithm of Vallada and Ruiz (2011) is clearly outperformed by the MS algorithm. Furthermore, both are significantly outperformed by SA and HGAI. This holds for both the large and the extra large instances. Both the VR and especially the MS algorithm make use of relatively large local search neighborhood structures. As stated before, with increasing problem size, the size of these search neighborhoods tends to grow stronger. Consequently, both algorithms do not scale well with the problem size, as can be seen by comparing the average RPD for the large instances with the extra large instances. On the contrary, both SA and HGAI appear to scale much better with the problem size.

A crucial difference between the HGA proposed here and the one of Vallada and Ruiz (2011) is the local search component. The results obtained with HGAI indicate that a hybrid genetic algorithm can be a powerful method, if however, the local search operator is designed effectively. Specifically, VR applies local search to the entire schedules, whereas HGAI only applies it to the sequences that dictate the objective, which proves to be much more effective.

For relatively small sized instances SA performs better than the other algorithms. This is especially the case for the instances with 50 jobs. It is important to note that for these instances the objective values lie around 20 time units. As a result, a small absolute difference translates to a large RPD. As the size of the problem increases, the dominance of simulated annealing diminishes and for instances with 200 jobs and more the HGAI outperforms the other algorithms. For the large instances, HGAI outclasses the other algorithms in 14 of the 25 cases (as is shown in bold face), and for the extra large instances, it outperforms the other methods in 7 of the 9 cases.

Table 2 Average relative proportional deviation (RPD) for the non-calibrated (HGAI) compared to three other methods: VR (Vallada and Ruiz 2011), MS (Avalos-Rosales et al. 2015) and SA (Santos et al. 2019) for the large instances

Table 3 Average relative proportional deviation (RPD) for the non-calibrated (HGAI) and calibrated algorithm (HGAII) compared to three other methods (VR, MS and SA) extracted from literature for the extra large instances

Another interesting observation is that the RPD tends to increase as the expected number of jobs per machine (n/m) decreases. This is true for all algorithms except for SA, where the opposite is true. In fact, the instances where SA performs better than HGAI are all cases where the n/m ratio is relatively low. However, this difference diminishes with increasing problem size, which is an indication that HGAI is more suitable to solve larger problems. The contrasting response related to the n/m ratio is likely due to a different balance between intra- and inter-machine movements in the local search constituents of these algorithms. In both algorithms this balance is largely defined by the setting of its parameters.

Lastly, the calibrated algorithm (HGAII) is compared to the non-calibrated algorithm (HGAI). As mentioned in “” section, the calibration procedure is targeted at the extra large problems. It appears that the algorithm with the calibrated parameters performs significantly better on average when compared to the non-calibrated algorithm (– 0.76%). Even so, this is not the case for all instance sizes. The calibration procedure prescribes that if, for example, a certain parameter setting significantly minimizes the RPD for $800 \times 60$ instances, while the RPD of $400 \times 40$ instances slightly worsens, this parameter setting is regarded better. The observation that for some instance sizes the calibrated parameters worsen the performance indicates that a certain instance size requires different parameters. Hence, a better performance can be achieved by tuning the parameters for a smaller selection of instance sizes. In practice, the number of machines will probably remain constant for a long time and the amount of jobs that are scheduled will probably vary within a certain range. Therefore, for practical applications, it is advised to calibrate the parameters for a narrower selection of problem instances.

Tables 2 and 3 indicate the average performance of the algorithms, however, these values do not provide much insight in the distribution of the results. To visualize how the results are distributed, the results are summarized in a box-and-whisker plot. Figure 8 displays a box plot for all of the large problem instances (i.e. all instances and runs), whereas Fig. 9 shows a box plot for the extra large instances. An RPD value that is larger than 1.5 times the interquartile range is defined as an outlier, which are indicated by the solitary data points. For the large instances the variation appears to follow the same trend as the average performance, i.e. it is high for VR and MS algorithms, and significantly lower for SA and HGAI. The same is observed for the extra large instances: the better the average performance, the lower the variability.

There are two main causes for the observed variations, namely (i) the randomness in the algorithms themselves and (ii) the observation that particular instances or groups of instances are more difficult to solve compared to others. For example, in case of the large instances (Fig. 8), a number of the results obtained with SA as well as with HGAI are marked as outliers. In case of the former, the vast majority of the outliers correspond to instances with 250 jobs, whereas in case of the latter the outliers are dominated by instances with 50 jobs.

Fig. 8

Box-and-whisker plot for the non-calibrated (HGAI) compared to three other methods: VR (Vallada and Ruiz 2011), MS (Avalos-Rosales et al. 2015) and SA (Santos et al. 2019) for the large instances

Fig. 9

Box-and-whisker plot for the non-calibrated (HGAI) and calibrated algorithm (HGAII) compared to three other methods (VR, MS and SA) extracted from literature for the extra large instances

Fig. 10

Box-and-whisker plot for the non-calibrated (HGAI) compared to three other methods: VR (Vallada and Ruiz 2011), MS (Avalos-Rosales et al. 2015) and SA (Santos et al. 2019) for the large instances

Fig. 11

Average RPD values of HGAII versus the setup time ranges for the large instances (red) and the extra large instances (blue)

Based on Fig. 8 alone, SA and HGAI appear similar in terms of the first quartile, median and the third quartile. However, HGAI is clearly worse in terms of outliers. It is important to make a remark regarding the RPD performance measure. This work focuses on the RPD as it is a common measure in related literature (Vallada and Ruiz 2011; Avalos-Rosales et al. 2015; Santos et al. 2019). For small instances, say all instances with 50 jobs, the average RPD for SA and HGAI is 1.39% and 6.31%, respectively (see Table 2). This appears as a major difference in performance. However, for these small instances, where the best known solution B (see Equation (3)) is small, the average absolute deviation from B for SA and HGAI is 0.87 and 2.04, respectively, which is only a minor difference. On the contrary, for all instances with 250 jobs, the difference in terms of RPD appears to be small: 4.82% and 2.35% for SA and HGAI respectively. Although this is a minor difference in terms of RPD, the average absolute deviation from the best known solution is much more pronounced, namely 9.15 and 3.68, for SA and HGAI respectively. Figure 10 shows a box-and-whisker plot of the absolute deviation for all of the large problem instances (i.e. all instances and runs). This shows a different picture compared to the box-and-whisker plot of the RPD in Fig. 8, and hence caution is required when the RPD is the only measure taken into consideration.

Another observation, which is not visible in the box plots, nor in Tables 2 and 3, is the following: if instead of averaging over all instances of the same size, the average is taken over all instances with the same setup time range, an interesting trend is observed. Given the 4 different setup time ranges, for the large instances the average is now calculated over 900 executions, whereas for the extra large instances it is computed over 450 executions. For HGAII the results are depicted in Fig. 11. The average RPD values for the large and extra large instances from Tables 2 and 3 respectively are indicated by the dashed lines. It can be seen that problems with a wide setup time range (i.e. a large variation) are much harder to solve compared to ones where the range is narrow, as anticipated in “” section. The same trend is observed for all other algorithms. Such observations are valuable insights, as they reaffirm the earlier statement, that certain instances demand specific parameter settings in order to maximize performance.

In summary, this comparative study shows that the proposed HGA outperforms other state-of-the-art algorithms in most cases. This is mainly due to the local search constituent of the HGA. Also, calibration has proven to be important since it enables a significant decrease of the average RPD. Although the overall performance increase is positive, some instances clearly demand different parameters. Hence, it is advisable that for practical applications the calibration is targeted at a narrower set of representative instances.

Real-world instance ($R/s_{i,j,k},M_j/C_\text {max}$)

Thus far, the proposed algorithm is applied to hypothetical instances of the $R/s_{i,j,k}/C_\text {max}$ problem. However, as discussed in “” section, these instances are not necessarily an accurate representation of real-world manufacturing environments. Additionally, machine eligibility constraints often appear in real-world environments. As mentioned, the proposed HGA is capable to solve the generalized $R/s_{i,j,k},M_j/C_\text {max}$ problem. Here, the proposed HGA is applied to the real-world loom (jacquard) scheduling instance recently provided by Yilmaz Eroglu and Ozmutlu (2017). Recall, this problem instance consists of 2111 jobs and 133 machines, refer to “” section for further details. Additionally, the authors proposed a hybrid genetic algorithm to solve this problem and reported that a computational time of 2.69 days is required to solve this large-scale instance. Furthermore, the best solution found by Yilmaz Eroglu and Ozmutlu (2017) has a maximum completion time of 784 hours. Although this method is not implemented here, the authors also coded it in C# 6.0 and ran it on a similar computer as the one used in this experimentation.

Here, the calibrated HGA (HGAII) is applied to this real-world instance. Initially, the termination criterion was $n \cdot m \cdot 50$ milliseconds, as for the other experiments in this work. For this problem instance, this corresponds to around 234 minutes. Preliminary experiments indicated that this appears to be unnecessary. Hence, in this case the termination criterion is set to $n \cdot m \cdot 5$ milliseconds. In total 5 independent executions are performed, all of which resulted in a final solution with $C_\text {max} = 650$ hours. Although one instance is not sufficient to draw any definitive conclusion, at least it appears that the HGA is able to solve this particular real-world instance very efficiently and robust. In fact, despite its size, this instance contains eligibility constraints and real setup times. Eligibility constraints clearly simplify the problem as the possibilities are limited. Real setup times are far less random compared to the setup times in the synthetic instances, which makes it easier for the HGA to converge.

Conclusions

In this work a hybrid genetic algorithm is proposed for the unrelated parallel machine scheduling problem with sequence and machine dependent setup times and machine eligibility constraints with the objective to minimize the maximum completion time $C_\text {max}$. The algorithm incorporates a local search operator specifically designed to solve large problem instances. The number of operators and parameters is kept to a minimum to allow facile calibration. This parameter calibration is done by means of Design of Experiments. The results indicate that the calibration is effective. An extensive comparison with other state-of-the-art algorithms shows that the proposed HGA outperforms other algorithms for the largest problems considered. Furthermore, the results also indicate that the proposed method scales well with the size of the problem.