Introduction

Additive manufacturing (AM) is an emerging technology in the advanced fabrication sector. As a sub-category of metallic AM systems, Wire arc additive manufacturing (WAAM) is a wire-feed system that typically makes use of electric arc welding equipment to fabricate a component by depositing metallic consumable in a layer-by-layer fashion (Frazier, 2014). WAAM can be classified into three common types according to its heat source: Gas Tungsten Arc Welding (GTAW)-based, Gas Metal Arc Welding (GMAW)-based, and Plasma Arc Welding (PAW)-based. Key benefits of the WAAM process include high deposition rate, large working volume, and low equipment costs (Derekar, 2018). Compared with other AM systems such as laser or electron beam-based systems, the high deposition rate makes WAAM more appropriate to fabricate large components (Xia et al., 2020a, 2020b). Compared with other metallic AM systems such as powder-feed or powder-bed systems, WAAM also features a higher buy-to-fly ratio, lower equipment costs (Reisch et al., 2020), and reduced porosity of fabricated parts (Taşdemir & Nohut, 2020), making WAAM a more cost-effective manufacturing technique.

GMAW based WAAM often adopts the controlled dip transfer welding process to improve (amongst other things) process stability, deposition accuracy, and material properties, whilst reducing overall power and heat inputs (Derekar, 2018). CMT is a modified metal inert gas (MIG) welding process based on short-circuiting (dip) transfer process developed by Fronius of Austria in 2004 (Selvi et al., 2018). CMT processes allow for control of arc length and thermal input by utilizing an innovative wire feed system integrated with high-speed digital control (Pickin & Young, 2013; Robert et al., 2018). Additionally, the CMT process also improves the porosity (Derekar, 2018) and geometric qualities (Feng et al., 2009; Zhao et al., 2019) of fabricated parts compared with other conventional GMAW processes.

In recent times, research activity in WAAM has increased rapidly and developed systems to dynamically control the deposited bead geometry is one of key focal areas (Liu et al., 2020). In a conventional WAAM setup, welding parameters that control deposition rates for a particular layer are pre-programmed. However, for components featuring changing geometry, such as areas with high variance of curvature or large overhanging angles with the layer below. Ideally, the deposition rates should be dynamically altered in a controlled fashion during the deposition to ensure an even distribution of material across the entire layer. Consequently, fluctuations in deposited components’ surface evenness become apparent without effective control, especially when fabricating large components featuring complex freeform geometry (Lam et al., 2019). Smaller geometric errors within each layer will accumulate as the build process continues, eventually leading to unacceptable differences between the design CAD model and the fabricated product (Xiong et al., 2020). This will cause serious build quality issues. The unwanted material accumulation can lead to adverse fluctuations in the weld torch contact tip to work distance (CTWD) throughout the build process, causing welding arc instability and associated defects (porosity, for example) (Zhu & Xiong, 2020).

Current research efforts on improving geometric properties of deposited material in WAAM focus mainly on controlling the heat input (Xiong et al., 2020; Zhao et al., 2020), travel velocity (Lam et al., 2019; Yildiz et al., 2020), torch posture (Venkatarao, 2021), path-planning (Ding et al., 2016; Evjemo et al., 2019), and active cooling (da Silva et al., 2020; Scotti et al., 2020). As a summary of these studies, commonly applied control algorithms include the error-based controller, model-based controller, and various advanced controllers involving machine learning and/or neural networks. For example, Xiong et al. (2020) optimized surface flatness of bead geometry at intersection points by controlling the welding heat inputs through an integral-separation PID controller. Xia et al., (2020a, 2020b) achieve bead width control by adjusting wire feed rates via a real-time model-based controller with the feedback of bead width. Ding et al. (2021) developed an automatic system based on machine learning technologies to control multiple welding parameters to improve geometric accuracy of deposited components. Although many approaches have improved the accuracy of deposited bead geometry in simple deposition tasks, they provide limited control performance in practical applications. For example, although control of bead geometry has been demonstrated through mathematical modelling, this often comes at the expense of relatively long processing times and a requirement for large sets of training data to set up the model properly (Ding et al., 2021). In comparison, a real-time control strategy can feature reduced training costs, however, the control accuracy is then limited by reaction speeds and system latency (Abe et al., 2020).

Accuracy, stability, robustness, and processing time are key objectives when designing an online control system for the WAAM deposition process. As a means to achieve this, a layer-by-layer online control strategy employing offline process planning and real-time control is presented. Data collection and computational processing steps are performed during the downtime between the interlayer welding processes, whilst the real-time control action is executed during welding. In this configuration, calculations can be processed during inter-layer cooling time, relaxing requirements for rapid data processing. Thus, the control accuracy can be improved by increasing the complexity of model or control algorithm, while stability and robustness are enhanced by iterative updates to the control algorithm from provided feedback as the build process continues. In this work, a model predictive control (MPC) algorithm, identified for its high degree of flexibility and robustness is proposed to handle the control task. Furthermore, a conventional real-time control approach based on the PID algorithm proposed by Xiong et al. (2020) is developed alongside to provide a comparative analysis.

Model-based predictive control is a control technique popular in research due to its performance in the control of constrained systems with multiple inputs and outputs. Theoretically, it can minimize the control error depending on the implemented model, however, it requires a longer processing time than conventional error-based controllers such as PID. Controlled outputs are generated by minimizing a cost function constructed by calculating discrepancies between predicted responses and desired reference trajectories within a finite time interval. There are several bead geometry control systems that employ an MPC approach in conventional welding areas (Li & Zhang, 2014; Stoyanov & Bailey, 2017). MPC approaches have also been employed in non-metal AM, powder-based metal AM and conventional gas tungsten arc welding (GTAW) processes to achieve a similar action of layer-by-layer control (Inyang-Udoh et al., 2020; Liu et al., 2019). These approaches are extended in this work by implementing a multi-input multi-output (MIMO) MPC strategy to output welding parameters between each layer of the fabrication process.

The model implemented inside the MPC is a key factor in determining the overall accuracy of the system. In this work, an autoregressive model (ARX) is utilized. The ARX model estimates outputs based on a sequence of previous inputs and output responses. There are many examples in the literature of the ARX model used for simulating complex systems. Sumalatha et al. (2015) designed a MIMO ARX model to simulate input–output data with noise. Hu and Kaloop (2015) simulate the thermal response of a bridge by associating a nonlinear ARX model with wavelet networks. These research efforts indicate that, compared to conventional regression techniques, the ARX model features high flexibility, stability, and accuracy in the simulation of complex systems (Hu & Kaloop, 2015; Sumalatha et al., 2015).

This study aims to develop an online layer-by-layer bead geometry controller to achieve higher deposition accuracy for the WAAM process. The rest of the paper is organized as follows: In Sect. 2, an overview of the control system architecture is presented. In Sect. 3, the mathematical model of the control system is presented. In Sect. 4, simulations and experiment case studies are introduced. In Sect. 5, experiments are implemented and discussed to verify the performance of the control strategy. Section 6 provides a conclusion for this work.

System overview

The control system architecture (shown in Fig. 1) presents three key modules: robot path generation module, bead geometry identification module, and control module. Inputs to the system are the CAD model of the component to be fabricated along with layer height data for each deposition process and initial welding parameters (which are later altered by the control algorithm). The system slices the model according to the input layer height and generates robot tool paths for the selected layer. This data is sent to the robotic welding system for execution. After the deposition process for the given layer is complete, the surface of the deposited material is manually cleaned with a wire brush and the robotic scanning program is then executed. The control system processes the scanned data and the peak layer height values are calculated. If the height of the deposited layer exceeds the acceptable given range, the CAD model will be resliced based on the fabricated part’s height.

Fig. 1
figure 1

Flowchart of the control system, composed of A: robot path generation module, B: bead geometry identification module, C: control module

Full size image

Robot path generation module

Initially, the input CAD model is converted to a generic mesh format consisting of vertexes and the straight edges which connect them. Then this mesh is sliced into several layers according to the input layer height. For each layer, the outer perimeter of the CAD model is simplified somewhat (if required) and converted into a robot trajectory through inverse kinematic algorithm. This trajectory forms the welding path for the given layer. No infill is used in this work.

Welding path generation

Each welding path consists of robot target points and control points. Robot target points consist of coordinates that define the cartesian path for the welding torch to follow. Control points are a subset of the robot target points, they provide additional information relating to the welding parameters to be used from that location and onwards. The sequence of control points is defined as:

$$ C\left( i \right) = W\left( {4*\left( {i - 1} \right) + 1} \right) $$
(1)

where W is the sequence of weld path and C is the sequence of control points, i is the index of a point on weld path, j is the index of a control point. To reduce the impact of arc-instability and irregular deposition rates during arc ignition and extinguishing, the starting point for each welding path is randomly selected from the set of robot target points that make up the welding path loop.

Scanning path generation

The scanning path is generated by selecting the midpoint between two control points on the welding path. Additionally, the orientation of the scanner is defined perpendicular to the weld path, thus allowing the bead width to be processed. The sequence of scanned points is defined as:

$$ S\left( k \right) = W\left( {{\text{round}}\left[ {\frac{{\left( {{\text{where}}\left( {W\left( i \right) = C\left( j \right)} \right) + {\text{where}}\left( {W\left( i \right) = C\left( {j + 1} \right)} \right)} \right)}}{2} } \right]} \right) $$
(2)

where W is the sequence of weld path and C is the sequence of control points, S is the scanned points, i is the index of point on weld path, j is the index of control point, k is the index of scanned point.

Welding parameter identification

The welding parameters transmitted to the robot are stored as a sequence of values. When the welding torch passes a particular control point, the corresponding welding parameter set stored in the control point is used from that point onwards. The control algorithm generates these welding parameter sets for a given control point by gathering associated data from the position directly below it on the previous layer. To correctly gather this data, a matching algorithm was developed. The principle of the matching algorithm is to calculate the position of the current control point relative to the centroid of the welding path and its starting point (before randomization). This information is used to find the associated control point below the currently selected one. This data is then input into the control algorithm and the new set of welding parameters for the particular control point are then generated.

Bead geometry module

The bead geometry identification module calculates the bead height and width at a given position from laser sensor data. If the measured bead height exceeds an acceptable value (i.e., 4 mm in this study), the CAD mesh is resliced with the new height information. Processing of the collected scan data provides the bead height h and width w, which are defined as follows:

$$ h = \max \left[ {Z\left( i \right)} \right] $$
(3)
$$ w = \max \left[ {X\left( i \right)} \right] - \min \left[ {X\left( i \right)} \right], {\text{where}}\left| {\frac{{Z\left( {i + 1} \right) - Z\left( i \right)}}{{X\left( {i + 1} \right) - X\left( i \right)}}} \right| < {\text{Threshold}} $$
(4)

where Z and X are arrays that contain scanned height and width data, respectively. Threshold is defined as the inclined angle of the bead’s surface.

Control module

The control module calculates the welding parameters during the inter-layer cooling time of the deposition process. Two controllers (i.e., PID and MPC) are implemented in this study to achieve a layer-by-layer control strategy. The first several layers are classified as base layers, which are deposited without control to initialise the modelling and control process. After each layer’s deposition, the bead geometry and welding inputs are saved into a database for training and updating the ARX model. The detailed controller design will be introduced in Sect. 3.

Control strategy design

Generally speaking, the influential parameters relating to the WAAM process include the wire feed speed (WFS), robot travel speed (TS), welding voltage, current, contact tip to work distance (CTWD), welding interpass temperature, and the bead geometry of previously deposited layers. The CMT welding process is used in this work due to its low heat input and suitability for welding aluminum structures (Derekar, 2018). With regards to the CMT process, both current and voltage levels are determined by WFS through the control algorithm integrated into the welding machine (synergic control). During experimentation, recorded variation in deposited bead height is relatively small (generally within 2 mm) compared to the CTWD, so its effect is deemed neglectable [33]. Thus, in this study, the mean value for height of all scanned points in a given layer is calculated and the CTWD is then set to 12 mm above this value. A CTWD of 12 mm is based on the previous research [33]. In between the welding of each layer, the deposition surface is allowed to air cool to room temperature (around 25 degrees Celsius, monitored by a thermal camera). This ensures minimal variance in interpass temperatures as the build process continues. Consequently, the control variables selected for the control strategies design in this work are WFS, TS, and the bead geometry of previously deposited layers.

A bead-on-plate test was conducted to estimate the relationships between deposited bead geometry and the WFS and TS input variables. A 5-by-5 result matrix is produced in this experiment, with WFS varying from 3 to 7 m/min and TS varying from 0.3 to 0.7 m/min. This range of welding parameter sets is based on experimental limits which were found to reliably produce acceptable bead geometries for the WAAM process featured in these experiments. A 50 mm single-layer bead was deposited for each combination of WFS and TS. After deposition, resultant bead geometries were measured and are presented in Fig. 2.

Fig. 2
figure 2

Relationship between bead height (a) and width (b) and welding parameters

Full size image

MIMO linear ARX model

The robustness and control accuracy of an MPC system depends largely on the model implemented inside it. For simulating dynamic systems, a linear ARX model with multiple inputs and outputs features a high degree of robustness and control accuracy (Hu & Kaloop, 2015; Sumalatha et al., 2015). This control process can be modelled in a linear ARX form as:

$$ \mathop \sum \limits_{i = 1}^{{n_{y} }} A_{i} \left( q \right)y_{i} \left( t \right) = \mathop \sum \limits_{j = 1}^{{n_{u} }} B_{j} \left( q \right)u_{j} \left( {t - nk_{i} } \right) + e\left( t \right) $$
(5)

where y is the output sequence, u is the input sequence, e is the noise, nki is the delay of ith input, nu is the number of inputs, ny is the number of outputs, t is the time instant, and A, B are polynomials, which can be written as follows:

$$ A_{i} \left( q \right) = 1 + a_{i1} q^{ - 1} + a_{i2} q^{ - 2} + \cdots + a_{{in_{ai} }} q^{{ - n_{ai} }} $$
(6)
$$ B_{j} \left( q \right) = b_{j1} q^{ - 1} + b_{j2} q^{ - 2} + \cdots + b_{{jn_{bj} }} q^{{ - n_{bj} }} $$
(7)

where na and nb represent the number of coefficients in A and B respectively and q refers to the layer number. Because of the nonlinear relationship between WFS, TS, and bead geometry, a linear regression analysis based on the bead-on-plate test was conducted to linearize the relationship between inputs and outputs for the linear ARX model. Three inputs are selected in the linear regression analysis: WFS, TS, and the ratio of WFS and TS. As for the nonlinear relationship between the output and inputs, they can be linearized by logarithmic and exponential operations. To select the best linearization result, the p-value and R-Squared values are calculated for each combination of inputs. Ultimately, the derived ARX model becomes:

$$ A_{1} \log \left[ {h\left( t \right)} \right] = B_{1,1} \left( q \right){\text{WFS}}\left( {t - nk_{i} } \right) + B_{1,2} \left( q \right)\log \left[ {{\text{TS}}\left( {t - nk_{i} } \right)} \right] + B_{1,3} \left( q \right)\frac{{{\text{WFS}}\left( {t - nk_{i} } \right)}}{{ts\left( {t - nk_{i} } \right)}} + {\text{bias}} $$
(8)
$$ A_{2} \log \left[ {w\left( t \right)} \right] = B_{2,1} \left( q \right){\text{WFS}}\left( {t - nk_{i} } \right) + B_{2,2} \left( q \right)\log \left[ {TS\left( {t - nk_{i} } \right)} \right] + {\text{bias}} $$
(9)

where h and w are the bead height and width, respectively. The bias term is held constant, which can improve the accuracy and robustness of the ARX model. For this application, calculated p values for Eqs. 8 and 9 both fall below 0.001, corresponding R-Squared values were above 95%, verifying the theoretical accuracy of the model. The mean squared error between practical and predicted bead geometry is also presented in Sect. 5.

MIMO MPC design

The MPC algorithm produces welding parameters by minimizing a cost function consisting of a desired reference trajectory, predicted system dynamics, change in future inputs, and boundary conditions. When combined with the ARX model, the predicted system dynamics at layer k after m layers can be derived from Eqs. 8 and 9:

$$\begin{aligned} h\left( {k + m} \right) = &\exp \left\{ -\mathop \sum \limits_{i = 1}^{{n_{a} }} a\left( 1, i \right)\log \left[{h\left( {k + m - i} \right)} \right]\right.\\& + \mathop \sum \limits_{j =1}^{{n_{b} }} B_{1,1} \left( j \right){\text{WFS}}\left( {k + m - j - nk} \right)\\& + \mathop \sum \limits_{j = 1}^{{n_{b} }} B_{1,2}\left( j \right)\log \left[ {{\text{TS}}\left( {k + m - j - nk}\right)} \right]\\&\left. + \mathop \sum \limits_{j = 1}^{{n_{b} }} B_{1,3}\left( j \right)\frac{{{\text{WFS}}\left( {k + m - j - nk}\right)}}{{{\text{TS}}\left( {k + m - j - nk} \right)}} +{\text{bias}} \right\}\end{aligned} $$
(10)
$$\begin{aligned} w\left( {k + m} \right) = &\exp \left\{ -\mathop \sum \limits_{i = 1}^{{n_{a} }} a_{2,i} \log \left[ {w\left({k + m - i} \right)} \right]\right.\\& + \mathop \sum \limits_{j = 1}^{{n_{b}}} B_{2,1} \left( j \right){\text{WFS}}\left( {k + m - j - nk}\right) \\&\left.+ \mathop \sum \limits_{j = 1}^{{n_{b} }} B_{2,2} \left( j \right)\log \left[ {{\text{TS}}\left( {k + m - j - nk} \right)}\right] + {\text{bias}} \right\}\end{aligned}$$
(11)

The future change of inputs at layer k after m layers can be expressed as:

$$ \Delta u\left( k \right) = \left[ {\begin{array}{*{20}c} {u\left( k \right) - u\left( {k - 1} \right)} \\ {\vdots} \\ {u\left( {k + m - 1} \right) - u\left( {k + m - 2} \right)} \\ \end{array} } \right] $$
(12)

At the core of the MPC is a cost function that reflects the control objectives. According to the research from (Raghavan & Thomas, 2016), the generalized cost function for a MIMO MPC can be formulated as:

$$ J\left( k \right) = \mathop \sum \limits_{m = 1}^{{n_{p} }} \parallel y\left( {k + m|k} \right) - y_{ref} \left({k + m} \right)\parallel_{Q}^{2} + \mathop \sum \limits_{m =0}^{{n_{c} - 1}} \parallel \Delta u\left( {k + m|k}\right)\parallel_{R}^{2} $$
(13)

where J is the cost function, y is the response of the system,yref is the desired reference trajectory, u is the system inputs, np is the prediction horizon, nc is the control horizon, and Q and R are the weighting matrices for system response and input,respectively. To format the equations into matrix form, the change of input variables from Eq. 13 can be expressed as:

$$ \mathop \sum \limits_{m = 0}^{{n_{c} - 1}}\left\| \Delta u\left( {k + m|k} \right)\right\|_{R}^{2} =\left\| \left[ {\begin{array}{*{20}c} {R_{{{\text{WFS}}}} } \\{R_{{{\text{TS}}}} } \\ \end{array} } \right] \odot \left[{\begin{array}{*{20}c} {\Delta {\text{WFS}}\left( k \right)\left.\right|_{{m = n_{c} }} } \\ {\Delta {\text{TS}}\left( k \right)\left. \right|_{{m = n_{c} }} } \\ \end{array} }\right]\right\|^{2} $$
(14)

where RWFS and RTS are nc-by-1 weighting matrices.

The matrix forms of the height and width response within the prediction horizon are derived from Eqs. 10 and 11, which is expressed as follows:

$$\begin{aligned}{h}_{\text{predict}}\left(k\right)=&\left[\begin{array}{*{20}c}h\left(k\right)\\ {\vdots} \\h\left(k+{n}_{p}-1\right)\end{array}\right]\\=&{\text{exp}}\left\{{\left[\begin{array}{*{20}c}\begin{array}{*{20}c}1\\{a}_{1}\\ {\vdots} \end{array}\\{a}_{{n}_{p}-1}\end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}0\\ 1\\ {\vdots} \end{array}\\{a}_{{n}_{p}-2}\end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}\cdots \\ {\dots} \\ {\ddots} \end{array}\\ {\dots} \end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}0\\ 0\\ {\vdots} \end{array}\\ 1\end{array}\right]}_{{n}_{p}\times {n}_{p}}^{-1}\right.\\&\times \left[-{\left[\begin{array}{*{20}c}\begin{array}{*{20}c}{a}_{1}\\ {a}_{2}\\ {\vdots} \end{array}\\{a}_{{n}_{p}}\end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}{a}_{2}\\{a}_{3}\\ \vdots \end{array}\\{a}_{{n}_{p}+1}\end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}\cdots \\ {\dots} \\ \ddots \end{array}\\ \dots \end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}{a}_{{n}_{a}}\\ 0\\ {\vdots} \end{array}\\ 0\end{array}\right]}_{{n}_{p}\times {n}_{a}}\left[\begin{array}{*{20}c}h\left(k-1\right)\\ \vdots \\h\left(k-{n}_{a}\right)\end{array}\right]\right.\\&+\sum\limits_{i=1}^{3}\left({\left[\begin{array}{*{20}c}\begin{array}{*{20}c}{b}_{i1}\\{b}_{i2}\\ \vdots \end{array}\\{b}_{{i(n}_{p}-1)}\end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}0\\{b}_{i1}\\ \vdots \end{array}\\{b}_{{i(n}_{p}-2)}\end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}\cdots \\ \dots \\ \ddots \end{array}\\ \dots \end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}0\\ 0\\ \vdots \end{array}\\ {b}_{i,1}\end{array}\right]}_{{n}_{p}\times {n}_{p}}\right.\\&\left[\begin{array}{*{20}c}{u}_{i}\left(k\right)\\ \vdots \\{u}_{i}\left(k+{n}_{p}-1\right)\end{array}\right]+{\left[\begin{array}{*{20}c}\begin{array}{*{20}c}{b}_{i2}\\{b}_{i3}\\ \vdots \end{array}\\{b}_{{in}_{p}}\end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}{b}_{i3}\\{b}_{i4}\\ \vdots \end{array}\\0\end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}\cdots \\ {\dots} \\ {\ddots} \end{array}\\ \dots \end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}{b}_{i{n}_{bi}}\\ 0\\ {\vdots} \end{array}\\ 0\end{array}\right]}_{{n}_{p-1}\times {(n}_{bi}-1)}\\&\left.\left.\left.\left[\begin{array}{*{20}c}{u}_{i}\left(k-1\right)\\ \vdots\\{u}_{i}\left(k-{n}_{bi}-1\right)\end{array}\right]\right)+bia{s}_{h}\right]\right\},\end{aligned}$$
(15)

where \({u}_{1}\;\mathrm{is\, WFS},\, {u}_{2}\;\mathrm{is\, log\,}\left(\mathrm{TS}\right), {u}_{3}\;\mathrm{is}\;\frac{\mathrm{WFS}}{\mathrm{Ts}}\)

$$\begin{aligned}{w}_{\text{predict}}\left(k\right)=&\left[\begin{array}{*{20}c}w\left(k\right)\\ {\vdots} \\w\left(k+{n}_{p}-1\right)\end{array}\right]\\=&{\text{exp}}\left\{{\left[\begin{array}{*{20}c}\begin{array}{*{20}c}1\\{a}_{1}\\ \vdots \end{array}\\{a}_{{n}_{p}-1}\end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}0\\ 1\\ {\vdots} \end{array}\\{a}_{{n}_{p}-2}\end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}\cdots \\ {\dots} \\ \ddots \end{array}\\ \dots \end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}0\\ 0\\ \vdots \end{array}\\ 1\end{array}\right]}_{{n}_{p}\times {n}_{p}}^{-1}\right.\\&\times \left[-{\left[\begin{array}{*{20}c}\begin{array}{*{20}c}{a}_{1}\\ {a}_{2}\\ {\vdots} \end{array}\\{a}_{{n}_{p}}\end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}{a}_{2}\\{a}_{3}\\ \vdots \end{array}\\{a}_{{n}_{p}+1}\end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}\cdots \\ {\dots} \\ \ddots \end{array}\\ \dots \end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}{a}_{{n}_{a}}\\ 0\\ \vdots \end{array}\\ 0\end{array}\right]}_{{n}_{p}\times {n}_{a}}\left[\begin{array}{*{20}c}w\left(k-1\right)\\ \vdots \\w\left(k-{n}_{a}\right)\end{array}\right]\right.\\&+\sum\limits_{i=1}^{2}\left({\left[\begin{array}{*{20}c}\begin{array}{*{20}c}{b}_{i1}\\{b}_{i2}\\ \vdots \end{array}\\{b}_{{i(n}_{p}-1)}\end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}0\\{b}_{i1}\\ \vdots \end{array}\\{b}_{{i(n}_{p}-2)}\end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}\cdots \\ \dots \\ \ddots \end{array}\\ \dots \end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}0\\ 0\\ \vdots \end{array}\\ {b}_{i,1}\end{array}\right]}_{{n}_{p}\times {n}_{p}}\right.\\&\left[\begin{array}{*{20}c}{u}_{i}\left(k\right)\\ \vdots \\{u}_{i}\left(k+{n}_{p}-1\right)\end{array}\right]+{\left[\begin{array}{*{20}c}\begin{array}{*{20}c}{b}_{i2}\\{b}_{i3}\\ \vdots \end{array}\\{b}_{{in}_{p}}\end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}{b}_{i3}\\{b}_{i4}\\ \vdots \end{array}\\0\end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}\cdots \\ \dots \\ \ddots \end{array}\\ \dots \end{array}\begin{array}{*{20}c}\begin{array}{*{20}c}{b}_{i{n}_{bi}}\\ 0\\ \vdots \end{array}\\ 0\end{array}\right]}_{{n}_{p-1}\times ({n}_{bi}-1)}\\&\left.\left.\left.\left[\begin{array}{*{20}c}{u}_{i}\left(k-1\right)\\ \vdots \\{u}_{i}\left(k-{n}_{bi}-1\right)\end{array}\right]\right)+{\text{bias}}_{w}\right]\right\},\end{aligned}$$
(16)

where \({u}_{1}\,\mathrm{ is \,WFS}, \,{u}_{2}\,\mathrm{is\,log}\,\left(\mathrm{TS}\right)\)

To simplify the calculation,na and nb were set equal to np. Then, the predicted system dynamics in Eq. 13 are as follows:

$$\begin{aligned} &\mathop \sum \limits_{m = 1}^{{n_{p} }}\left\| y\left( {k + m|k} \right) - y_{{{\text{ref}}}} \left( {k +m} \right)\right\|_{Q}^{2} \\&\quad= \left\| \left[{\begin{array}{*{20}c} {Q_{h} } \\ {Q_{w} } \\ \end{array} } \right]\odot \left( {\left[ {\begin{array}{*{20}c} {h_{{{\text{predict}}}}\left( k \right)} \\ {w_{{{\text{predict}}}} \left( k \right)} \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c}{h_{{{\text{ref}}}} \left( k \right)} \\ {w_{{{\text{ref}}}} \left(k \right)} \\ \end{array} } \right]} \right) \right\|^{2}\end{aligned}$$
(17)

where href and wref are the desired reference trajectory for height and width, respectively. In this study, both the available range and maximum rate of change for input variables are limited according to the result from bead-on-plate test. Finally,the optimal values for inputs to minimize the MPC cost function are solved by a series MATLAB control toolbox function.

During the fabrication process, the welding and geometric data is input to the ARX model, and the weighting coefficients for ARX model keep iterating according to previous control results, thus the adaptiveness of the control system is increased further.

PID control strategy design

The PID control strategy is a conventional online control strategy. This work controls welding parameters based on measured errors between reference geometry (from the CAD model) and actual deposited geometry. The control procedure is the same as MPC, the PID controller outputs the welding inputs for a whole layer during the cooling time. A simple PID algorithm with multiple inputs can be expressed as:

$$ \Delta u = kp * ep + ki * ei + kd * ed $$
(17)

where u is the controlled output parameter and kp, ki and kd are 2-by-2 weighting matrices. Error variables ep, ei, and ed can be written as follows:

$$ ep\left( k \right) = \left[ {\begin{array}{*{20}c} {h_{ref} - h\left( k \right)} \\ {w_{ref} - w\left( k \right)} \\ \end{array} } \right] $$
(18)
$$ ei\left( k \right) = \left[ {\begin{array}{*{20}c} {h\left( {k - 1} \right) - h\left( k \right)} \\ {w\left( {k - 1} \right) - w\left( k \right)} \\ \end{array} } \right] $$
(19)
$$ ed\left( k \right) = \left[ {\begin{array}{*{20}c} {2*h\left( {k - 1} \right) - h\left( k \right) - h\left( {k - 2} \right)} \\ {2*w\left( {k - 1} \right) - w\left( k \right) - w\left( {k - 2} \right)} \\ \end{array} } \right] $$
(20)

where k represents current time instant, href and wref are the reference height and width, respectively, and h and w are the bead height and width responses, respectively. The PID is tuned in the simulation via the ARX model. Detailed procedures are presented in Sect. 3.4, below.

PID tuning

PID tuning is an important process to ensure control accuracy. In general, a MIMO PID controller can be broken up into several SISO PID controllers, thus the tuning of MIMO PID controller is similar to a SISO PID and can be further simplified with the assistance of the ARX model. Firstly, the ki and kd gain parameters were set to zero. Then, kp is set according to the coefficients in the ARX model. The weighting coefficients in the ARX model represent the relationship between welding inputs and bead geometry. When increasing kp, the control action becomes more aggressive, introducing a degree of instability to the controller. The overshoot increases and the rise time is reduced. When a suitable value for kp is found, ki is then increased to eliminate steady-state error. When increasing ki, the overshoot and settling time will increase, and the rise time will decrease. Increasing both kp and ki will lead to a negative effect on the control stability. This is addressed by finally adjusting kd to achieve a similar control performance as the MPC. When increasing kd, both overshoot and settling time will decrease and the control stability is improved. The control performance of PID controller is verified and discussed in Sect. 5.

Experimental Case Studies

Experimental system

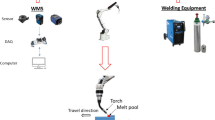
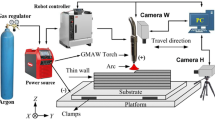
A conventional WAAM system, shown in Fig. 3, was used to deposit the components featured in these tests. It consists of an ABB IRB 2600 robot, a positioning table, a Fronius CMT welder, a shielding gas cylinder, a laser scanner, and a computer used for WAAM process planning and control. The parameters of the laser scanner are listed in Table 1. The material of wire and baseplate is a 4043-aluminum, and other experiment parameters are listed in Table 2. The control algorithms are developed based on MATLAB and its relevant toolboxes. The process control program is developed with Python and features modules for path-planning, data processing, and communication between robot and computer.

Fig. 3
figure 3

The WAAM system. (1) IRB 2600; (2) TransPuls Synergic 5000 CMT welder; (3) VR 7000 CMT wire feeder; (4) CMT torch; (5) Aluminium base plate; (6) 2-DOF workpiece positioner; (7) 2D laser scanner; (8) infrared temperature sensor

Full size image
Table 1 Parameters of the laser scanner
Full size table
Table 2 Experimental condition of WAAM
Full size table

Procedure

A simulation exercise and three practical case studies are proposed. The simulation exercise is designed to compare the control performance of the MPC and PID approaches in a theoretical context. These results are then validated through a series of practical case studies.

Simulation

The simulation process aims to explore the theoretical control performance for MPC and compare it with PID control strategy. Parameters for the ARX model and MPC (i.e., weighting coefficients, control horizon, prediction horizon, etc.) are also tuned during this process. The detailed data flow for the simulation process is shown in Fig. 4.

Fig. 4
figure 4

Data flow for the simulation process at kth layer (np: prediction horizon)

Full size image

Bead heights for the first few (typically 2 to 3) layers of the WAAM deposition process feature an large degree of variance. This instability can be attributed to several disparate factors (e.g., heat conduction condition) and is difficult to reliably control. So the first few layers are usually removed after deposition as sacrificing layers and don’t need to be controlled. In both simulation and practical experiments, the input parameter set for the first six (prediction horizon) layers is kept constant in order to establish the ARX model. The output variable set, which is the predicted bead geometry, is taken from previous layers. Then, the MPC (or the PID algorithm) calculates the welding inputs for the 7th layer which are sent to the ARX model. The ARX model simulates the bead geometry for the 7th layer, which is in-turn sent back to the MPC to complete the iteration loop. The welding inputs and geometric control responses of the simulation process are recorded and analyzed. To investigate the theoretical difference between the two control strategies, several groups of reference output geometries are set and compared with the simulation outputs. The best performing (i.e., most stable) group of reference geometry is then be selected as the reference for the practical experiments performed later. The parameters of both controllers are listed in Tables 3, 4 and 5 and results from these simulations are presented in Sect. 5.1, below.

Table 3 Parameters of PID controller
Full size table
Table 4 Parameters of ARX model
Full size table
Table 5 Parameters of MPC
Full size table

Inclined thin-wall structure

In the first case study, three inclined thinwall structures (55 mm in length, 30 degrees of overhang angle, 20 build layers) were deposited to evaluate the relative performance between the PID and MPC control strategies. For reference, a third wall was built with no control (i.e., a static welding parameter set for the entire build process). The flowchart for the MPC control process is shown in Fig. 5.

Fig. 5
figure 5

Overview of the physical process

Full size image

Initial values for TS and WFS are set to 0.4 m/min and 4 m/min respectively for all three walls. Because of the initialization process required by the ARX model, control starts from the 7th layer of deposition. Scanning routines measure deposition geometry and generate new sets of welding parameters at the start of each layer. The controllers work to make corrections for geometric errors caused by the overhang through generating new parameter sets for the future layers, while the reference wall maintains a static build strategy. For each wall, 10 control points are distributed evenly along the length of the thinwall. Results from this test are presented in Sect. 5.2, below.

Inclined tube structure

In the second case study, two inclined tubes are fabricated to further compare PID algorithm and MPC control performance. Both tubes are designed to have the same geometry (incline angle, radius, and height), however, the variance in overhang angle in each layer will test the adaptiveness of each strategy. In a similar fashion to the previous thinwall test, the welding parameter sets for the first six layers remain constant (build with static welding parameters: WFS: 4 m/min, TS: 0.4 m/min) and the control starts from the 7th layer. For each deposited layer, 12 control points are distributed uniformly across the welding path. Comparative results between the two tubes are presented in Sect. 5.3, below.

Free-form structure

To present a practical and challenging test for the developed control system, the third case study involving the manufacture of a free-from tube structure, shown in Fig. 6, was conducted. The first six layers are built with the static welding parameter set of WFS: 4 m/min and TS: 0.4 m/min. From the 7th layer on, these parameters are then generated by the MPC algorithm. For each deposition path, control points are defined between 10 to 6 mm depending on the curvature of local geometry. Comparative results between the two tubes are presented in Sect. 5.4, below.

Fig. 6
figure 6

Example of free-form tube with complex geometry

Full size image

Result and Discussions

Simulation results

Optimal welding parameters and reference geometry generated from the simulation are shown in Fig. 7 below. The parameters which define the control action are adjusted to achieve the most accurate and stable response. For the WFS input of 4 m/min and TS of 0.4 m/min, the reference geometry is 2.2 mm and 5.5 mm for bead height and width, respectively. Both strategies satisfy their control requirements in bead height and width within 20 and 15 layers, respectively. Steady-state errors were found to be negligible. Large variation in both height and width was encountered during early iterations, which results in long settling times for both controllers. This is caused by the relatively large error between the reference and initial widths. The controller initially sacrifices control of bead height to address bead width first in order to achieve what it determines is the best overall control accuracy. Over the later iterations, the control action eventually leads to convergence. For bead height control, the MPC shows better steady-state error, overshoot, and settling time than the PID strategy. With regards to bead width control, the PID strategy performs slightly better than MPC. This could be attributed to the complexity of inputs and the challenge of accurately setting weighting coefficients in the control algorithm.

Fig. 7
figure 7

Simulated control performance of bead height (a) and width (b)

Full size image

Inclined thin-wall structure

The three thinwall structures deposited in these tests are shown in Fig. 8. Data relating to the as-deposited layer-by-layer bead geometries are shown in Fig. 9, where it is clear to see trends forming with regards to fluctuation of bead height and width. Whilst the CMT welding process (with no control) does indeed work to smooth the geometric errors over preceding layers, this action is limited, and bead heights fluctuate within a relatively large range (2 mm) and present an increasing trend. As a comparison, both PID and MPC can significantly decrease the range (less than 0.5 mm), and greatly improve the flatness of the wall, which is reflected in the decrease in standard deviation of wall height (from 0.7 to 0.2). Wall widths are kept within satisfactory ranges for all walls, however, fluctuations in widths are significantly reduced by both control strategies, which is reflected in the decrease of the standard deviation of wall width (generally less than 0.5). Maintaining geometric accuracy of the deposition process is critical when manufacturing complex geometries that require varying deposition rates along the path. For example, the inclined tube structure cannot be adequately manufactured without an active control strategy in place, and as such, only the control performance of the PID and MPC strategies will be evaluated in the next case study.

Fig. 8
figure 8

Uncontrolled (a), PID controlled (b), and MPC controlled (c) thin-wall structure

Full size image
Fig. 9
figure 9

Comparison of standard deviation of bead height and width at each layer

Full size image

Average calculation times for the PID and MPC controllers are 0.21 and 6.83 s, respectively. In addition, the calculating time of MPC at the 7th layer (which is the 1st controlled layer) reaches 37.4 s due to the initializing of ARX model, and when the weighting coefficients have been generated, the calculating time dropped to 6.20 s at the 8th layer (which is the 2nd controlled layer) and kept decreasing as the deposition continues.

During the deposition process, the feedback data was recorded for the iteration of ARX model to further improve the prediction accuracy, as shown in Fig. 10. The MSE of bead height and width both fall below 1 after 6 layers’ iteration and are 0.5801 and 0.2631, respectively.

Fig. 10
figure 10

Iteration of ARX model during deposition process

Full size image

Inclined tube structure

Results from this test are shown in Figs. 11 and 12. The average calculation time at each layer for PID and MPC controller is 0.23 and 8.16 s, respectively. The overall calculating time at each layer compared to the thinwall structure increased as the number of control points increased. After the deposition of 30 layers, the welding process guided by the MPC features an increased surface evenness. The measured standard deviation and range of both bead height and width are reduced significantly. Height differences between the highest and the lowest point are 4.44 mm in the PID controlled tube and 1.50 mm for the MPC controlled tube, representing a 296% improvement. The standard deviations of heights at the control points are 1.20 for the PID controlled tube and 0.51 and MPC controlled tube, representing a 235% improvement. The standard deviations of widths at each of the control points are 0.29 for the PID controlled tube and 0.40 for the MPC controlled tube, they are both within an acceptable range, but the width of MPC controlled tube is closer to the reference width. The PID controlled component has a higher range and standard deviation which becomes more pronounced as the layer numbers increase. This suggests that if PID controlled deposition of this tube were to continue, these errors between desired and actual build geometries may become unacceptable.

Fig. 11
figure 11

Fabricated inclined tubes controlled by PID (a) and MPC (b)

Full size image
Fig. 12
figure 12

Comparison of PID and MPC: a standard deviation of bead height, b standard deviation of bead width, c tube height, and d average material deposition rate

Full size image

12 control points are spread evenly across the weld path for each layer of the tube structure and the MPC strategy generates a new set of welding parameters at each control point. Figure 12d shows that material deposition rate increases at control points located where overhang angles are greater and are conversely minimized where no overhang exists, which helps to improve layer evenness. Although the control algorithm is not designed to directly adjust material deposition rates (in a synergically controlled welding process, deposition rate is a function of TS and WFS) based on the geometry of the input CAD model, this result is achieved by machine learning from previously deposited layers, which demonstrates the adaptivity of the employed MPC and ARX models. The deposition rate change of MPC is more aggressive compared to the PID. This can be explained by the working principle of the controller: The PID controller achieves control based on the errors between feedback values and a reference value, thus it cannot predict the future responses and can only make limited adjustments to the welding parameters. Instead, the model implemented in MPC can predict several layers’ geometries in the future and output more efficient welding parameters to suit. The accuracy of predictions is then ensured by model updates. Consequently, PID is not suitable for the control of a free-form structure due to the lack of adaptiveness. The control accuracy and adaptiveness of MPC are further investigated in Sect. 5.4.

Free-form structure

The fabrication of more complex free-form structures highlights the need for adaptive geometry control. The parts’ non-uniform surface profile means that surface evenness and consistency in layer height rapidly deteriorate. The designed control system achieves a notable degree of overall geometric accuracy (shown as Fig. 13 a) and also demonstrates good control of connection geometry (shown as Fig. 13b). As shown in Fig. 14, the standard deviation of both height and width were at first stable but then became unstable when the connection occurred from layer 9 to 11. This is caused by the non-uniform gap between the approaching deposited beads, which leads to welding arc instability. Nevertheless, the MPC successfully controlled the bead geometry within 2 layers after connection and maintained the standard deviation of height and width under 1.6 and 2, respectively. Except for layers 10 to 12 (where the connection occurs), the range of height was controlled within 4 mm for the manufacturing process. Processing times for calculations equated to, on average, 12.28 s/layer.

Fig. 13
figure 13

Fabricated free-form part (a) and its connection point (b)

Full size image
Fig. 14
figure 14

Bead height and width analysis of free-form structure (green dot: connection layer)

Full size image

When the welding torch is held in a vertical orientation, the overhang angle was found a significant impact on the resultant bead geometry. If the overhang exceeds half of the weld seams width, the molten pool will form at the edge of the fabricated, spilling downwards with the effect of gravity. This significantly lowers the layer height in these regions, which produces a larger effective CTWD when welding the next layer. These larger CTWD’s will reduce the arc power input, which further affects formation of the next layer geometry or even lead to arc irregularities or extinguishment.

As the overhang angle of the fabricated model is the main limitation to improving geometric accuracy for the bead geometric control system, several approaches can be investigated in future work. One is modifying the torch angle according to the overhang angle; thus, the direction of arc force is changed, and the effect of gravity can be reduced. Another solution is modifying the fabricated bead width according to the overhang angle. These approaches are to be explored and implemented in future work on the MPC control strategy.

Discussion

The idea of a layer-by-layer online controller is for the first time investigated and implemented in the geometry control during the WAAM process. With the current research focus moving towards the implementation of the artificial intelligence and digital twin technologies to achieve smart manufacturing, the developed adaptive MPC controller presents an effective and realistic solution for improving the geometrical accuracy of the WAAM system.

Current models-based controllers for WAAM are highly relied on accurate bead modelling, which is rarely available due to the resultant deposition path usually requiring a combination of varying torch angle, travel speed, and wire feed speed, which is rarely used in practice. Most of the existing planning algorithms only account for accurate bead height through slicing while maintaining the bead width within a reasonable range. In this study, the investigated layer-by-layer controller can significantly increase the model accuracy and stability due to the iterative adjustment and self-training of the parameters in the ARX model through the feedback geometry. In addition, the proposed controller does not require a very complex bead modelling, which is usually combined with artificial intelligence or machine learning techniques, while maintaining the control error within an acceptable range.

The control accuracy of conventional error-based real-time feedback control for WAAM is usually limited by the reacting time. In this study, the calculation time for the PID strategy falls within 1 s, while the MPC strategy typically requires more than ten times this. However, the layer-by-layer implementation of the MPC, where calculation is performed during the protracted cooling down period between layers, largely negates perceived drawbacks of long processing times. Consequently, the hybrid nature of the layer-by-layer model-based adaptive controller takes advantage of both modelling and real-time control.

Conclusion

In this work, an online layer-by-layer ARX model-based adaptive MPC controller was developed to improve the geometric accuracy of the WAAM process. After the deposition of a given layer, the as-deposited bead geometry is measured using a laser scanner and compared to the CAD model of the component. This information is used by the ARX model to predict bead geometries at specific welding conditions. Then, a MIMO MPC generates a set of welding parameters for the next layer of the deposition process. During the fabricating process, control results have been saved for iterations of the ARX model to ensure model accuracy.

The experimental results reveal that the layer-by-layer controller is capable of controlling bead height and width of WAAM deposited parts with complex geometries.

  • Compared to the uncontrolled approach, PID and MPC approach presented 266% and 548% improvement of layer morphology, respectively. Furthermore, the MPC approach presented a 235% improvement of layer morphology for complex geometries compared to the PID strategy.

  • Calculations associated with the MPC strategy are far more time-consuming. The calculation time for MPC strategy is 35 times of PID strategy and will increase with the number of control points in a given layer.

  • The adaptiveness of the controller is achieved by the ARX model iterating its control action after each layer’s deposition. The model becomes stable after 5 layers’ iteration.

Further research aims to implement error-based controller during the model establishing phase and combine artificial intelligence techniques with both forward and backward models to increase the control accuracy and adaptiveness. This work will also expand reliable and robust model of interpass beads and overlap to implement the layer-by-layer control of solid structures in WAAM.