Abstract
Remanufacturing includes disassembly and reassembly of used products to save natural resources and reduce emissions. While assembly is widely understood in the field of operations management, disassembly is a rather new problem in production planning and control. The latter faces the challenge of high uncertainty of type, quantity and quality conditions of returned products, leading to high volatility in remanufacturing production systems. Traditionally, disassembly is a manual labor-intensive production step that, thanks to advances in robotics and artificial intelligence, starts to be automated with autonomous workstations. Due to the diverging material flow, the application of production systems with loosely linked stations is particularly suitable and, owing to the risk of condition induced operational failures, the rise of hybrid disassembly systems that combine manual and autonomous workstations can be expected. In contrast to traditional workstations, autonomous workstations can expand their capabilities but suffer from unknown failure rates. For such adverse conditions a condition-based control for hybrid disassembly systems, based on reinforcement learning, alongside a comprehensive modeling approach is presented in this work. The method is applied to a real-world production system. By comparison with a heuristic control approach, the potential of the RL approach can be proven simulatively using two different test cases.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Given the continuously growing world population, reducing resource consumption and global waste are great challenges of our time (World Economic Forum 2019). One piece of the solution lies in reusing products and their resources in closed-loops. Compared to conventional, linear production approaches, up to 90 % of raw materials and energy consumption as well as the proportional amount of CO2 emissions can be saved (Tolio et al. 2017). Remanufacturing realizes a circular and closed-loop economy by reprocessing used products, whereby according to Lund (1984), in contrast to repair, not just the broken but all components of a returned product are disassembled and either reprocessed or replaced by new ones. Therefore, remanufactured products are by no means of inferior quality compared to new products after reassembly. Due to their high quality and lower price, remanufactured products receive a high acceptance rate by distributors and users (Tolio et al. 2017). In addition, it is a possible means for parts suppliers, e.g. in the automotive industry, to meet delivery promises once series production has been discontinued.
Today, the high proportion of manual labor in the remanufacturing value chain reduces its economic feasibility, in particular in high-wage countries. Especially for disassembly, uncertain product specifications and non-deterministic production processes require a large degree of flexibility that conventional, rigidly automated production systems cannot provide (Junior and Filho 2012). Due to an increasing product variety, so far only human operators show the necessary flexibility in mainly manual operations (Vongbunyong and Chen 2015).
As in assembly, automated resources can potentially be operated more cost-effectively in disassembly. In the last decades there were many research attempts to automate disassembly processes for various kinds of products, e.g. televisions (Scholz-Reiter et al. 1999), mobile phones (Kopacek and Kopacek 2003), printed circuit boards (Kopacek and Kopacek 2006) or car wheels (Büker et al. 2001). So far, however, full automation of the disassembly process has not been established in industry (Poschmann et al. 2020). There are only few applications for automated disassembly that are operated on an industrial scale. The only one known to the authors is a robot-based disassembly line for smartphones called Liam (Rujanavech et al. 2016) and its successor for destructive disassembly called Daisy, both introduced by the technology company Apple Inc. (Apple Inc. 2019). Daisy is able to dismantle up to 200 phones per hour using destructive disassembly techniques. However, there are still human operators conducting the downstream component sorting process. There is a consensus in research that hybrid production systems consisting of manual and automated workstations offer the greatest potential for a productive and economically reasonable industrial application (Kim et al. 2007a). Besides a high number of variants and low quantities, the main reason is the high fluctuation of product conditions. Even if a station is capable of automatically disassembling a product type in general, severe wear and tear can prevent disassembly according to the standard procedure, especially in non-destructive disassembly.
However, thanks to advances in the field of artificial intelligence (AI) and robotics, flexible and autonomous production systems are now within reach (Poschmann et al. 2020; World Economic Forum and Accenture Strategy 2019; Wurster et al. 2021). Furthermore, human-robot-collaboration can help to combine the strengths and compensate the weaknesses of humans and robots in order to improve disassembly productivity. Machine learning is enabling robots to self-learn how to solve specific problems (World Economic Forum and Accenture Strategy 2019). In particular deep reinforcement learning (RL) can enable robots to think and learn in a similar way to human operators. These developments will further increase the effectiveness and efficiency of robotically performed disassembly tasks and likewise allow robots to adapt to changing requirements when dealing with uncertainty (Vongbunyong et al. 2013; Vongbunyong et al. 2017; Bdiwi et al. 2016). Autonomous disassembly robots can play a vital role in maintaining the required flexibility as a part of an entire disassembly system (Poschmann et al. 2020).
Poschmann et al. (2020) argue that automated disassembly will be part of the industrial state-of-the-art within the next ten years. Thus, the research question arises how a resource, such as an autonomous robot, can be integrated effectively into a production system. In fact, the advancement towards autonomous workstations as a new type of resource in production impacts how production systems are planned and controlled today. Hence, in the production planning phase the important decision of deploying autonomous, conventionally automated or manual stations, their quantity as well as their layout has to be considered. Furthermore, production planning must strategically allocate processes to individual resources and their types. While learning robots possess the ability to learn and adapt to new situations, they also come with a probability to fail that is, in general, unpredictable. This new type of uncertainty is further aggravated by fluctuating quality conditions of used products, easily leading to rescheduling decisions in the daily operations.
In this paper a novel type of hybrid disassembly system consisting of manual, autonomous and rigidly automated workstations that are combined in a job shop, is introduced. The system is designed to deal with product variance and uncertainty. It is based on the approach of robot-based learning disassembly stations. Besides that a RL-based approach as a solution for controlling the material flow in the system is developed.
The remainder of this paper is organized as follows: In Section “Related work”, relevant and recent approaches in the literature on disassembly control including product information and failing processes are reviewed. Furthermore, a short wrap-up on the most recent approaches on deploying reinforcement learning in production control is provided. Section “Disassembly system model” then describes the considered production system with its characteristic processes and its implementation as a model. This is followed by a description of the RL-based control logic in Section “Production control approach”. In Section “Application in a hybrid disassembly factory” the control system is tested and compared with benchmarks before concluding with a discussion of the results and an outlook on further research in Section “Conclusion and Outlook”.
Related work
The following section provides an overview of disassembly planning and control. In addition, existing research on the control of production systems using product information, considering the chance of failing operations and by means of reinforcement learning are reviewed.
Disassembly describes the process of dismantling a product into its components and/or subassemblies. Because of challenges that include diverging material flow and uncertain condition or product type of the returned products—also called cores—disassembly planning is not comparable with classical production planning and, therefore, represents its own research direction (Lee et al. 2001). Although there has been a great deal of research in the field of disassembly production planning and control in recent decades, many important questions remain unsolved, not least because of the high level of complexity. In addition, existing research questions are adapted to new forms of production systems for disassembly, such as hybrid systems. Relevant work originates from the field of scheduling and deals with allocation of orders and operations to available resources of the disassembly system over time (Kim et al. 2007b). The first authors to describe the basic problem of disassembly scheduling had been Gupta and Taleb (1994). In a literature review, Slama et al. (2019) arrange the latest approaches in the field of disassembly scheduling. In general, they distinguish the approaches by specific attributes or features which are considered in the problem and have an impact on its complexity. These are the number of levels of the product structure, the number of items, parts communality, consideration of capacities and consideration of stochastic processes. Another characteristic problem in disassembly planning is the representation of the product structure and disassembly processes modeling. Solutions to the product representation problem are disassembly-specific, e.g. disassembly precedence graphs, disassembly trees, state diagrams, logical AND/OR graphs (Vongbunyong and Chen 2015) or Disassembly Petri Nets (Moore et al. 1998).
Dynamic control approaches
Production control, often abbreviated as just control in this paper, describes the determination of the disassembly sequence as well as the allocation of the disassembly operations to available resources.
Many characteristics of the disassembly job scheduling problem as well as the product representation are relevant within this work. However, while classical job scheduling determines a corresponding schedule in advance, problems in the real world tend to have a dynamic character. New jobs may be added unpredictably and at short notice, machines may break down, jobs may be cancelled or completion dates and priorities may change (Madureira et al. 2013). Therefore, production control gains importance, in order to adjust operations in production at run time.
Tang et al. (2001) develop a heuristic, consisting of three Petri nets, for the real-time adaptation of disassembly operations in running disassembly systems. Their approach is integrated since disassembly sequence planning and assignment to a workstation are done simultaneously. However, the exact assignment plans are determined in a second, downstream inspection station. Kim et al. (2006) develop a concept for a flexible disassembly system that reevaluates the planned disassembly sequences almost in real-time. For the rescheduling, the update algorithm takes not only the capabilities of the system but also the state of the disassembly system and the current disassembly status of products into account. Beyond that and similar to our approach, Kim et al. examine a hybrid system structure, consisting of automated and manual disassembly stations. Duta et al. (2007) present a stochastic algorithm to control a disassembly line with multiple product types. They aim for a solution, enabling quick adaptions when perturbations occur. Their optimization problem comprises decisions, such as the disassembly level of a product, the assignment of workstations, or whether to select destructive or non-destructive operations. The authors’ algorithm delivers optimal solutions in real-time. In a work by Kim et al. (2009), the authors identify the difference between disassembly planning and the actual situation at shop floor level as a major problem. Therefore, they design a dynamic process planning system to adapt the planning to the actual conditions of the system considering the availability of devices and tools.
Product-condition-based planning and control
Products that have been exposed to greater stress during their life show greater signs of wear and tear, signs of aging or other types of devaluation. Furthermore, these products tend to be more difficult to disassemble. More specific, the condition of a discarded product has a decisive influence on the type and duration of the necessary disassembly operations (Colledani and Battaïa 2016). By viewing and processing product information in the planning and control phase, uncertainty can be reduced, disturbances can be avoided and more accurate production plans can be generated. Most relevant approaches in literature, in which an integrated consideration of the product condition is conducted, can be assigned to production planning.
Gao and Zhou (2001) develop an approach for product-condition-based disassembly sequence selection. They assume that the value of each subassembly/part and the cost of disassembly are known, while the condition of the returned products is subject to a high degree of uncertainty. Therefore, the authors develop a fuzzy reasoning Petri-Net model to represent such products and evaluate which further procedure is most suitable. Reuse, remanufacturing, recycling or direct disposal are available for selection. A similar approach for an adaptive process planner aiming on maximizing the total remanufacturing value while considering the product condition is given by Zussman and Zhou (2000). In their approach, Tang et al. (2001) consider the product condition in a way that products in a very bad condition are directly disposed. Moreover, the authors also consider real-time resource capacities.
Ullerich and Buscher (2013) propose an approach to solve the flexible disassembly planning problem while taking into account the condition of a product on the component level. They distinguish a core and its items by genuineness, functionality and the presence of damage. Furthermore, they introduce a graph-based condition model, which enables to determine the probability that a core contains only reusable items. This information is then used to decide whether an item can be reused, recycled or has to be disposed. The condition model is integrated into a mixed-integer program model to solve the flexible disassembly planning problem.
Riggs et al. (2015) propose an approach with multiple quality classes for End-of-Life products to cope with varying task times more accurately and improve disassembly line balancing. Colledani and Battaïa (2016) introduce a decision support system for disassembly systems in a similar approach. Specific quality criteria for electronic braking systems are defined which allows the classification of cores and to assign them to one out of six possible quality classes. Task times are specific for each class, so is the economic feasibility to perform them. A comparison with a decision support system neglecting quality classes shows that the quality class-based approach shows a higher probability of meeting the target takt time for each quality class.
To the best of the authors’ knowledge, the only control approach with an integrated view on the product condition is proposed by Kim et al. (2006). To collect relevant product information, they introduce a concept of a modular sensing system called Life Cycle Unit. These units are integrated into products over their whole life cycle to gather and deliver relevant data, which then can be used for disassembly control. The information is used to select appropriate devices, tools and workstations according to technical feasibility and availability. If no suitable automated process can be matched, a manual or mechanized workstation is selected.
Controlling production systems with the chance of failing processes
In a production environment where products, whose condition is a determinant for the success of a process operation, have to be processed, a control system must be able to cope with failing operations. This capability is especially important in the closed-loop domain, as discarded products with uncertain product conditions are disassembled by automated systems. However, only very limited research has regarded the present problem statement. One field of research from manufacturing that has similarities with failing processes is the so-called flow control problem, where machines are unreliable. Kimemia and Gershwin (1983) are one of the first authors to propose production control for such problems. There is a branch of extensions, which also include defective parts, as for example from Mhada et al. (2011) who investigate the influence of defective parts on the optimal stock.
Regarding disassembly systems, almost all control approaches generally exclude defective parts and failing processes because of the otherwise significantly increased complexity (Kim et al. 2007a). On the other hand, it is undisputed that in any reverse logistics system, where discarded products are collected and disassembled, the aforementioned variance in the condition of products brings enormous uncertainty into the disassembly process and can, thus, lead to an even increased chance of errors (Altekin and Akkan 2012). Therefore, the problem of failing processes in disassembly plants is of particular importance, especially for practical applications. Hence, current solutions are not capable of dealing with the complexity of the problem.
Gungor and Gupta (2001) noticed that the chance for failure of single process steps can significantly complicate the flow within a disassembly line. For instance, after a failed operation, downstream operations cannot continue to operate normally. The authors define anomalies in comparison to the classical material flow, which result from failed processes. These include prematurely leaving the line, skipping stations and re-entering a predecessor station.
The only research area that explicitly addresses resource allocation considering failures are line balancing problems of disassembly lines (Altekin and Akkan 2012; Aytug et al. 2005). However, these approaches differ significantly from the control approach for flexible job shops considered in this work.
Reinforcement learning applications in production control
Reinforcement learning (RL) applies behavior-based learning. Each RL model has an agent within an environment, which is perceived through an environment state \({s}_{t}\in S\) at time \(t\) and manipulated through a selected action \({a}_{t}\in A\). This influences the next environment state \({s}_{t+1}\) and the obtained reward \({r}_{t}\). The agent targets optimizing the cumulative reward, that serves as feedback to support the agent in learning a desired control policy \(\pi\). RL is based on a Markov Decision Process \(MDP=(S,A,P,R)\) with the Markov property stating, that the next state \({s}_{t+1}\) only depends on state \({s}_{t}\) and the selected action \({a}_{t}\) but not any previously visited states or selected actions.
There is a rising interest in the use of (deep) reinforcement learning for the control and scheduling of conventional production plants. Cunha et al. (2020) present a review paper on the use of evolutionary algorithms and deep reinforcement learning to solve job shop scheduling, as they believe that the use of deep reinforcement learning could revolutionize scheduling. Also Kuhnle and Lanza (2019) discuss possible applications of reinforcement learning in the area of production planning and control. The authors note that the complexity in production has increased significantly due to increased product diversity, lower quantities and higher quality requirements. Waschneck et al. (2018) specifically use a Deep Q-Network (DQN) in production scheduling in the semiconductor industry. Kuhnle et al. (2019a) implement an autonomous order dispatching system based on reinforcement learning in a real application case from semiconductor manufacturing. Furthermore, Kuhnle et al. (2019b) present a methodical approach for the design, implementation and evaluation of RL algorithms for adaptive order allocation that can be improved with robust design principles (Kuhnle et al. 2021a) and through the application of explainable reinforcement learning techniques (Kuhnle et al. 2021b). The authors specifically address production engineers. Lately Altenmüller et al. (2020) designed a RL-control for job scheduling under time constraints in complex job shop problems. To the best of the authors’ knowledge, there are no papers that apply reinforcement learning for disassembly process planning or control. However, the existing body of literature suggest, that the application of model-free RL, i.e. DQN, in event discrete simulations to learn superior scheduling or dispatching strategies is feasible across different simulations.
Research deficit
In the future, production systems, especially for disassembly, are increasingly supported by autonomous workstations. In production planning and control, though, the integration of corresponding resources into industrial production systems has not yet been studied. With the breakthrough of disassembly automation on an industrial scale, however, there is a need for adaptive control solutions. Within this section further characteristics were identified, which affect the material flow during disassembly and therefore are to be considered. These are the products’ conditions and the possibility of a disassembly operation to fail. Both characteristics are related to the introduction of autonomous learning stations and further increase the problem complexity. The few existing approaches consider the characteristics only incidentally or can be assigned to predictive production planning. The use of autonomous learning stations originates in the robotics domain and has not yet been investigated in the context of production system planning and control. In particular, there are no approaches, neither scheduling nor dispatching approaches that consider operation failures due to a lack of skill by autonomous robots. If product information is taken into account, this is conducted not in a quantitative but a qualitative manner and by classifying products and assigning them to quality classes. The few existing approaches in disassembly planning and control usually proceed sequentially, so that the optimal disassembly sequence is first determined during planning and later only an allocation to resources takes place during control (Lee et al. 2001; Kim et al. 2006). There are no approaches where the operation sequence and resource allocation is conducted completely reactive by an integrated dispatcher, which is particularly suitable regarding uncertainty and ineffective planning horizons that are inherent to remanufacturing (Kurilova-Palisaitiene and Sundin 2014). Most approaches are neither real-time nor condition-based, and if so they are based on an already existing master plan (Kim et al. 2009).
In this paper a model of a disassembly factory and a simulation-based control system for the latter are introduced. Four shortcomings within the current state of research are tackled specifically. Besides manual and rigidly automated stations, the production system includes autonomous stations (1) that are prone to operation failure based on a lack of experience or skill (2). Product conditions (3) are modelled and have an influence on the success rate of disassembly operations. The production control dispatching system conducts a condition-based integrated determination of the disassembly sequence and resource allocation (4) in real-time.
Disassembly system model
In our approach we deliberately refrain from determining the optimal dismantling sequence in advance. Hence, the determination of the disassembly sequence is left open in order to select the individually best sequence depending on the respective product condition, but also on the machines’ availabilities and capabilities. The actual schedule results from the collective individual actions and may only be evaluated retrospectively. The decision which of the next disassembly operations and on which machine it is to be performed are made simultaneously and in real-time. Thus, the control challenge constitutes an integrated dispatching.
To develop and evaluate such a control logic, an appropriate test-bed is required. In our approach a discrete-event simulation model is deployed as a digital twin to simulate the production and logistic processes which are triggered and controlled by a single decision agent. However, we extend this model by various disassembly-specific assumptions and additional conventions according to the proposed system including autonomous stations.
Basic problem statement
Our shop floor layout is comparable in its basic features to a flexible job shop that is well established in the scheduling domain (Pinedo 2016). The production system consists of loosely coupled disassembly stations. Its basic goal is to process \(N\) incoming orders \(O={\{O}_{1},{O}_{2},\ldots ,{O}_{N}\}\). An order is a specific instance of a product which is supposed to be disassembled. This is done by performing disassembly operations which may be a subject of a specific sequence. Let \({Op}_{i}={\{Op}_{i,1},{Op}_{i,2},\ldots ,{Op}_{i,g}\}\) be the set of all disassembly operations that theoretically can be performed during the disassembly of order \({O}_{i}\). However, some operations may not have to be performed at all due to alternative parallel disassembly paths and some operations may be invalid in a specific state.
Orders enter the system at sources \(So={\{So}_{1},{So}_{2},\dots ,{So}_{J}\}\). The transport of the orders is done by \(M\) transport units \(T={\{T}_{1},{T}_{2},\dots ,{T}_{M}\}\).
The disassembly operations are performed at the stations \(S={\{S}_{1},{S}_{2},\ldots ,{S}_{K}\}\) in the production system. Each station is able to perform a certain amount of disassembly operations – the so-called capability space. The capability space \({F}_{k}={\{Op}_{1},{Op}_{2},\ldots ,{Op}_{O}\}\) of a station \(k\) is the set of all executable operations \({Op}_{O}\). In addition to the working space, each station has an input buffer of the capacity \({EP}_{k}\), where orders can be stored before they are processed. After processing, orders are stored in an output buffer with unlimited capacity, where they remain waiting for further operations. An order is disassembled until the desired disassembly depth is reached. If there are no more disassembly operations to be performed, orders, or more specifically their components, are eventually transported to a sink \(Si={\{Si}_{1},{Si}_{2},\dots ,{Si}_{L}\}\). This assumption complies with remanufacturing, since the machines, e.g. for cleansing, are specific for the individual components or subassemblies, which are usually processed batch wise.
With this basic model, it is possible to map a wide variety of configurations of disassembly production systems.
Modelling disassembly processes
To provide a thorough representation of the disassembly steps, the following properties are defined as prerequisites:
-
1.
Representation of priority conditions of disassembly operations,
-
2.
Modeling of diverging product structure and material flows,
-
3.
Description of the current disassembly state of the cores.
An adapted approach of the Disassembly Petri Net (DPN) is selected. DPNs fulfill all three requirements. Using edges and transitions, logical AND as well as logical OR relations can be represented (Zussman and Zhou 1999).
A Petri net is a directed graph with two different types of nodes: places and transitions. A place describes a state and is represented by a circle. A transition describes a process and is represented by a bar. Places and transitions are connected by directed edges. An edge never connects two places or two transitions, but always a place with a transition or vice versa. Dynamic systems can be represented by moving so-called tokens through the system. Tokens occupy places and stand by their position for the current state of the system. By “firing” the transitions, the tokens are moved through the system and thus model the dynamic behavior of a system. (Reisig 2013)
Following Zussman & Zhou, Moore & Gungor et al. and Tang & Zhou et al. a disassembly Petri net is defined in this paper as follows (Moore et al. 1998; Zussman and Zhou 1999; Tang et al. 2001):
A disassembly Petri net is defined as 6-tuples:
with
-
1.
Let \(P = \left\{{p}_{i}\right\}\) be a finite set of places, \(i = 1,\dots ,m\). Here \({p}_{1}\) is the root representing the product and has no incoming edges. Let the subset of \({P}^{{\prime}}\subset P\) of the set of places be the set of all places without outgoing edges. These are called leaves and represent the components. The remaining places correspond to subassemblies.
-
2.
Let \(T = \left\{{t}_{j}\right\}\) be a finite set of transitions, \(j = 1,\ldots,n\); A transition corresponds to a disassembly operation. Each transition has at least one incoming and one outgoing edge.
-
3.
Let \(I:P \times T\to \left\{\text{0,1}\right\}\) be an input function defining the set of directed edges from \(P\) to \(T\). Let \({I}_{ij}=1\), if there is an edge from location \({p}_{i}\) to transition \({t}_{j}\); otherwise \({I}_{ij}=0\).
-
4.
Let \(O:T \times P\to \left\{\text{0,1}\right\}\) be an output function describing the directed edges from \(T\) to \(P\). Let \({O}_{ij}=1\), if \({p}_{i}\) is the initial point of transition \({t}_{j}\); otherwise \({O}_{ij}=0\).
-
5.
Let \({m}_{0}\) be the initial mark with \({m}_{0}\left({p}_{1}\right)=1\) and \({m}_{0}\left({p}_{i}\right)=0\,\forall {p}_{i} \in P\setminus \left\{{p}_{1}\right\}\)
-
6.
Let \(\rho :T \to \left[\text{0,1}\right]\) be a probability value indicating the success probability of a transition.
A mark corresponds to a specific allocation of tokens and represents the current state of the Petri net. In the case of DPNs, this encodes the current state of disassembly of a product. The state changes when a transition “fires”. When “firing”, tokens are moved from one state via a transition to one or more subsequent states. Consequently, a transition can fire only if a token is present in the input state. With successful firing the token disappears at the input point and is added at the output points. Modeling with multiple input points is also possible. However, in the context of the disassembly Petri net defined here, one input point is assumed (Reisig 2013).
In the completely disassembled state, all leaves are occupied by at least one token and all other places are not occupied. If there are several outgoing edges from one place to correspondingly several transitions, a logical OR is encoded. In this case several alternative disassembly operations are available, from which one can be selected. Several outgoing edges from a transition to accordingly several places encode a logical AND. This enables the modelling of divergent product structures (Zussman and Zhou 1999).
Thereby, even complex priority relationships like alternative disassembly sequences can be mapped. This is a decisive advantage over simpler representations, such as disassembly precedence graphs (Tumkor and Senol 2007). Another advantage is the representation of the subassemblies as places (see (Lambert and Gupta 2004)). Due to this property and the possible multiplication of tokens, the divergence of material flows can be modeled intuitively. Furthermore, the current token assignment automatically describes the disassembly state.
A further crucial added value of the Petri net is its compact representation form, in particular for complex product structures. This generates a significant advantage over dismantling trees (Lambert and Gupta 2004).
In Fig. 1, an illustrative DPN of a simple assembly consisting of 4 components is displayed. When completely assembled, the assembly allows for two alternative disassembly sequences. Given the allocation of the tokens, the current disassembly state can be derived: two components (C and D) are completely disassembled while the remaining components (A and B) require one more disassembly operation.
The chance for operation failures and the product condition
Stations from the type autonomous station consists of robots which carry out disassembly operations autonomously. The robots are not rigidly programmed but derive their capabilities e.g. through transfer learning from virtual simulation or learning by demonstration from human workers. Recent concepts are summarized in (Poschmann et al. 2020) or in (Vongbunyong and Chen 2015). The robot applies the learned capabilities to disassemble products. Since these capabilities are implicitly specified and adaptive rather than rigidly determined, the robot achieves a higher flexibility than conventional automated resources. However, on the other hand it is assumed that unlike a trained worker autonomous stations can fail when performing a disassembly operation. Furthermore, it is assumed, that in case of a failed disassembly operation, the same operation can be repeated on a manual disassembly station.
Having the choice to select between stations with redundant process capabilities leads to an extended decision problem.
As described in Section “Introduction”, disassembly automation is particularly motivated by the reduction of manual workload to reduce costs for disassembly. According to Fig. 2, the central control task is to decide, depending on the condition of the respective core, whether an autonomous station or a manual station should be visited next. The capabilities of both are partially redundant. However, as a basic assumption in this paper, the operating costs at an autonomous station are significantly lower compared to a manual station where the core is manually dismantled. On the other hand, it may not make sense in terms of resource utilization to use only the autonomous station type. Furthermore, there is the risk of failure at these stations, which would mean that a manual station would have to be visited eventually for the same operation. Therefore, it is essential to allocate those products with the “right” condition to the autonomous station. However, the “right” condition changes depending on the balancing of the entire system, the cost rates and the distribution of the order conditions for a product type.
Whether an operation fails depends on the condition of the order. Like discarded products in closed-loop production, an incoming order has a certain condition that varies from order to order. Against the background of remanufacturing, part of the condition could be the degree of corrosion or other properties that are specific for degradation. In our model, the condition property (Eq. 1) is modelled as an abstract \(p\)-dimensional order condition vector:
The individual elements of this vector, the condition properties \({q}_{p}\), are normalized values and represent a relative specification of a certain attribute of the product in percent, while 1 corresponds to flawless condition or highest-possible quality. This generic representation makes it possible to map a wide variety of product features that depend on the product family and are selected according to their process relevance, when applied in an industrial use-case.
In contrast to assembly, where the material flow converges, components can diverge after disassembly. This means that when performing a disassembly operation, an assembly can be divided into multiple independent subassemblies or components. These separated subassemblies and components are moved individually through the system. To enable this, a parent order such as the main order \({O}_{n}\) can be split into several sub-orders \({O}_{n.1},\dots ,{O}_{n.i}\), which themselves can be further subdivided by extending the index. The main order itself has no parent order. Assuming a main order \({O}_{n}\) has remaining disassembly operations to be performed from \({Op}_{n,Rest}={\{Op}_{1},{Op}_{2},\dots ,{Op}_{j}\}\), then the sets of all disassembly operations \({Op}_{n.1},\dots ,{Op}_{n.i}\) of the suborders are disjoint and the union of the sets corresponds to the set of the main order.
Another important feature of the production system model is scrap. There is a chance that an order becomes scrap after a disassembly operation based on its condition \(q\). As stated before, an increased probability for scrap is assumed after a failed operation at an autonomous station.
General assumptions that are not described in detail yet but support in understanding better the modelling approach, are summarized in the following:
-
Orders must be disassembled completely.
-
Products are treated individually (One-Piece-Flow), no batch formation.
-
Only one order at a time can be processed at a station.
-
A station is considered available (even when processing) until its input buffer is full.
-
Once reaching an input buffer of a station, orders are processed FIFO.
Performance target figures
In production planning and control, target figures determine the optimization goal and vary depending on the specific problem. In scheduling, typical figures are time-related target figures such as lead time, adherence to due dates or machine utilization. However, the aforementioned extensions require a re-evaluation of these measures. In the following, suitable performance measures are defined that are developed in the present work.
One objective function that reflects the aforementioned dilemma of resource redundancy very well is an adapted approach of machine hour calculation. The basic idea behind this approach is to convert all resource-dependent costs to the productive hours of the resource (Eisele and Knobloch 2014). Therefore, the first objective function (Eq. 2) of the model is defined as the sum of the processing costs including labor costs and idling costs of each station in the disassembly system that is to be minimized:
\({c}_{k,working}\) is the processing cost rate, \({c}_{k,idling}\) the idling cost rate, \({t}_{k,working}\) the total working time and \({t}_{k,idling}\) the total idling time for station \(k\).
The second objective function (Eq. 3) considers the makespan \({t}_{MS}\), which indicates how long the system needs to process all orders \(O={\{O}_{1},{O}_{2},\dots ,{O}_{N}\}\):
If \({c}_{k,idling}\ne 0\) is assumed, the makespan is implied within the resource cost objective.
The third optimization goal explicitly refers to the number of failed operations \({n}_{failures}\) and should be minimized as follows in Eq. (4):
Production control approach
For the selection of the next disassembly operation and the next station at which the operation is to be performed, a decision agent is used called allocation agent in the following.
An allocation for an order \({\text{O}}_{\text{i}}\) is a 2-tuple \(({Op}_{i,j}; {S}_{k})\), combining a feasible operation \({Op}_{i,j}\) and a station \({S}_{k}\) that is capable of \({Op}_{i,j}\). When no further disassembly operations can be selected, a leaf of the DPN is reached. Then just a sink \({Si}_{l}\) needs to be chosen and the decision is reduced to a 1-tuple: (\({Si}_{l})\). An order needs to be allocated after its arrival in a source or after being processed at a station. If the material flow diverges, a separate allocation decision is made for each generated suborder.
A decisive aspect that the control system has to consider when reaching redundant disassembly stages (see Section “Disassembly system model”) is whether an operation should be performed on a cheaper autonomous learning station. On such stations, however, it is possible that operations fail. An alternative is to proceed on a manual station, which generally has higher machine-hour rates, mainly due to wage costs, but on which the success of the disassembly operation is assured.
The product condition characteristic correlates strongly with the probability of failure. It is therefore particularly important that the product condition is considered by the allocation agent. Nevertheless, this trade-off is only one aspect of the complex allocation decision at hand. The present problem can be classified as a modified flexible job-shop problem.
Selection of control algorithm
Finding a solution to job-shop scheduling problems is known to be among the hardest NP-hard problems (Pinedo 2016). So, conventional mathematical programming or rule-based approaches reach their limits in job-shop scheduling (Csáji et al. 2006). Due to their static nature and their model-based implementation, both approaches require a high degree of manual adaptation in case of system changes (Kuhnle et al. 2019b). Disadvantages of often used metaheuristics are the difficult problem generalization, the runtime, and the required development effort (Cunha et al. 2018; McKay et al. 1988; Lawler et al. 2005). Besides, most of the available scheduling tools are tailored exactly to one specific use-case (Dios and Framinan 2016). Furthermore, in the modeled system at hand, the dependency between a specific system state and the quality of selectable actions is not tangible or unknown in the beginning so that conventional approaches such as priority rules are hard to derive, especially in a multi objective set up. In contrast, an RL-agent, that learns circumstances implicitly, is much more generic. Even if the system changes, an RL-algorithm can be retrained and, thus, can adapt to constantly changing conditions (Waschneck et al. 2018). This is particularly useful in end-of-life product treatment were quantities are low, product variety is high and new product types are introduced on a regular basis. The exact product condition-based operation failure probability might not be known from the beginning but can be anticipated by a RL-based control logic at run-time.
Reinforcement learning is particularly well suited to deal with complex production systems. Moreover, the digitalization of production lays the foundation to apply reinforcement learning, as production systems provide relevant data in real-time, including, for example, the tracking of orders, inventories and machine statuses (Kuhnle et al. 2019a). This database is an ideal basis for the applying RL-algorithm.
In the following, a state space, action space and reward function are designed as a prerequisite to apply reinforcement learning.
State space
The state space consists solely of decision-relevant information. The state space can be divided into two parts. One part is the order state, which contains state information about the order to be allocated. The second part comprises the states of the \(K\) Stations \({S}_{1},{S}_{2},\dots ,{S}_{K}\) the so-called station states. All elements of the state space are normalized values between zero and one.
The order state is a vector including the following information:
-
Completion of the job (binary; one digit).
-
Information whether the last operation failed (binary; one digit).
-
Condition characteristics \({q}_{1},{q}_{2}\dots {q}_{p}\) (decimal proportion, \(P\) digits for \(\varvec{q}=\left(\begin{array}{c}{q}_{1}\\ {q}_{2}\\ {\cdots }\\ {q}_{p}\end{array}\right)\))
-
Scrap probability of the order (decimal proportion; one digit).
-
Information whether the order is scrap (binary; one digit).
-
Location of the order (binary one-hot encoding; \(K\) digits for \(K\) stations)
-
Product type of the order (binary one-hot encoding; \(J\) digits for \(J\) product types)
-
Position in the DPN (binary one-hot encoding; \(X\)+1 digits for a maximum of \(\text{X}\) subcomponents and a digit for the progress of disassembly).
The order state therefore has the total length: \(5+P+K+J+X\). The respective station state consists of five digits and is composed as follows:
-
Input buffer utilization as a percentage of its total capacity (decimal proportion; 1 digit).
-
Output buffer utilization as a percentage of the total capacity of the source (decimal proportion; 1 digit).
-
Information whether the station is broken (binary; 1 digit).
-
Information whether the station is working or idling (binary; 1 digit).
-
Basic probability for the failure of an operation at the station (decimal proportion; 1 digit, 0 for conventional stations).
Thus, the vector, which consists of the individual \(K\) station state vectors, has the length \(6K\). This results in a length of \(5+P+7K+J+X\) for the entire state vector with a \(P\)-dimensional condition characteristic, \(K\) stations, \(J\)different product types as well as the possibility of displaying products with up to \(X\) components.
Action space
The agent’s goal is to choose an action based on the current state that maximizes the cumulative discounted reward. Characteristic for the integrated approach of the control logic is the simultaneous determination of the next operation and the station on which the operation should be conducted. This two-dimensional decision is reflected in the action space: Selection of an operation \({Op}_{i,j}\) and a station \({S}_{k}\): \(({Op}_{i,j}; {S}_{k})\). An exception is made if the maximum dismantling depth has already been reached. In this case no more operation has to be selected, but only a suitable sink \({Si}_{l}\).
Feasible actions per given state depend on disassembly precedence conditions extracted from the DPN and the compatibility of next targeted stations or sinks. However, first of all it is checked whether a vacant order is scrap or the maximum disassembly depth has been reached after the current node in the DPN was identified. In both cases, the only available action is to transport the order to a sink. If the previous operation failed, the operation is repeated or the order is send for idling. If none of this is the case, next operations are derived from the existing transitions of the current node. The action space results from all valid combinations of next possible operations and available stations. A process flow on how the action space is specified is illustrated in Fig. 3.
Reward function
The objective is to obtain an RL-agent that optimizes according to the predefined target figures, i.e. total resource costs, makespan and number of failed operations. A weighted reward function \({r}_{total}\) is designed so that the RL-agent minimizes all three figures. The reward is given to the agent immediately after each allocation step.
The resource cost reward (Eq. 5) penalizes utilized resource capacities depending on the respective resource costs. For each station \(k\) the required operating time since the last allocation \({t}_{k,diff}\) is calculated. For the reward of a single station, this duration is multiplied by the cost rate \({c}_{k,working}\). The resource cost reward is the sum of the costs over all stations K:
The time reward \({r}_{time}\) (Eq. 6) punishes the agent for the required time to process the given number of jobs. The level of the penalty equals the time difference between the last allocation \({t}_{Allocation x-1}\) and the current allocation \({t}_{Allocation x}\). Thereby, the penalty equals the total duration of an episode. However, the agent receives the reward sequentially after each step:
Finally, the fail reward \({r}_{fail}\) (Eq. 7) punishes for the failure of an operation:
The total reward \({r}_{\text{total}}\) (Eq. 8) is calculated as a weighted sum of the individual rewards. The individual rewards are assigned weights \({w}_{RC}\), \({w}_{time}\) and \({w}_{fail}\). Depending on the disassembly system, this ensures that individual rewards are not over- or underrepresented. In addition, preferences for certain objectives in training can be highlighted, by favoring rewards that correspond to the desired targets for the entire system according to Eq. 8:
Besides this penalties, the agent is rewarded +1 for each completed order.
Software implementation
We implemented an event-discrete simulation model using Python, adapted from the SimRLFab by Kuhnle (2020). The generic simulation can be specified by a JSON initialization file. Five different types of processes run in the simulation. An order creation process simulates the arrival of orders in the sources. Therefore, new orders with a corresponding product type and DPN are instantiated. When creating each order, the order processing is started. The first step is to select the next disassembly operation and station at which it will be performed. Furthermore, the order processing is responsible for triggering transport and processing. Suborders are created in case of a diverging product structure. Each transport resource has a transporting process that simulates the execution of transport requests. Finally, the processing of orders at stations is simulated.
A DQN algorithm is deployed as an established deep reinforcement learning algorithm. For the implementation, the Tensorforce library is used (Kuhnle et al. 2017).
Figure 4 provides an overview of the involved subsystems and implementation architecture. The illustration is based on generic reinforcement learning. The allocation agent interacts with the simulation model introduced in Section “Disassembly system model”. Accordingly, the simulation model corresponds to the environment. The simulation transfers states and rewards to the allocation agent. On the other hand, the agent makes allocation decisions that are passed to the simulation. The simulation model can be instantiated with product and production system specific parameters such as the number of orders etc.
Application in a hybrid disassembly factory
In the previous sections, we presented a modeling approach for hybrid production systems for disassembly with autonomous and manual stations as well as a logic to control the material flow. The model and the applicability of the control approach are evaluated in this section.
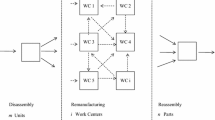
Since considering the condition of returned cores and dealing with autonomous stations is an unexplored area in the field of disassembly planning and control, dealing with complex problem instances is not initially useful. Instead, we limit our investigations to the core of this work: dispatching orders on disassembly stages with redundant station types and proofing the suitability of reinforcement learning as a control approach. For this purpose, we assume a problem instance consisting of three conventional stations (\({S}_{1}, {S}_{2.1}\),\({S}_{3})\), one autonomous station \({(S}_{2.2})\), one source \(\left(So\right)\) and six sinks \(\left(S{i}_{1}, S{i}_{2}, S{i}_{3}, S{i}_{4}, S{i}_{5}, S{i}_{6}\right)\) (see Fig. 5).
This instance is based on the structure of the AgiProbot disassembly factory located at the Karlsruhe Institute of Technology (Häfner 2020)). In the factory, various types of automotive electric actuators and real remanufacturing products are disassembled. These end-of-life products, representing each a main order, pass through the factory as follows. An incoming order is first examined at a measuring station \({S}_{1}\) (conventional). Afterwards there are two redundant stations (comprising a redundant disassembly stage) to conduct the upcoming operations: a manual station \({\text{S}}_{2.1}\), which is considered a conventional station in this work, and an autonomous station \({S}_{2.2}\) prone to failure. The system is supplemented by a conventional station \({S}_{3}\), which is automated but not autonomous learning. When all parts and subcomponents have reached their associated sink, the disassembly process is considered complete.
In order to concentrate on the influence of the product condition, the test case is limited to only one product type to be disassembled. The DPN of this product type, which consists of six components, is shown in Fig. 5b). For further simplification, the product type comprises only three operations \({Op}_{1}\), \({Op}_{2}\) and \({Op}_{3 }\) and only one possible disassembly sequence. The components diverge after the last disassembly operation.
An essential simplification is made regarding the product condition and its influence on operation failures. First, the product condition vector \(\varvec{q}\) is assumed as one-dimensional \(q\). A static failure threshold \({q}_{fail}= 0.5\) is assumed so that \(({Op}_{i,2}; {S}_{2})\) fails if \(q\le 0.5\). Further simplifications are the following: there are no breakdowns, no scrap, unlimited number of available transport entities, unified transport effort for each transport operation (5 time units), deterministic operation times, and \({q}_{i}\) is uniformly distributed for all orders.
The analyses are conducted on two different test cases, whose parameters and configurations are displayed in Table 1. The first experiment is to proof that the agent is able to recognize product information. So, the test case is characterized by operation times, chosen in a way that a bottleneck is caused at the measuring station \({S}_{1}\). The makespan cannot be influenced and, hence, is neglected for the reward. In test case 2, operation times are roughly balanced. Thus, dispatching decisions affect the makespan as an additional opposing optimization goal besides resource costs. In both cases, the autonomous station \({S}_{1}\) is characterized by significantly lower processing costs. Since test case 2 is more sophisticated than test case 1 including probabilistic failure rates and multiple objectives, the RL agent was slightly optimized by a dynamic exploitation-exploration ratio that decreases the exploration proportion over time to improve its performance.
Three different allocation agents are tested and compared. First, the previously described DQN-agent is trained on the basis of the use case. The network consists of two dense fully connected hidden layers. The first layer is twice as large as the state space and the second layer is twice as large as the action space. The further specification details of the DQN-agent for both cases are attached in Table A1 in the Appendix.
Second, two heuristics are deployed for order dispatching. First of all, there is a random heuristic that takes random decisions regardless of the condition of the order or the production system. The second heuristic is more advanced and decides based on the order condition. If \(q\le {q}_{fail}\), \(({Op}_{i,2}; {S}_{2.1})\) is chosen. \(\left({Op}_{i,2}; {S}_{2.2}\right)\) is chosen otherwise. While \({q}_{fail}\) is unknown to the DQN-agent, the advanced heuristic is aware of \({q}_{fail}\) which is a clear advantage. Both, the random heuristic and the more advanced heuristic serve as benchmarks for the performance of the DQN-agent.
The training phase includes the processing of 50,000 orders in test case 1 and 125,000 orders in test case 2 followed by 5,000 orders in evaluation mode. An episode is defined as the completion of 50 orders. Depending on the hardware, the duration of the training phase takes several hours. However, the training phase is not critical to real-time application. The actual reaction time of the agent after training, meaning the time to take one individual allocation decision, is lower than one second. This makes the agent suitable as a decision tool for reactive dispatching in dynamic shopfloor environments.
Test case 1
Figure 6a shows the course of the DQN’s resource cost reward over more than 1000 episodes for test case 1. The average training reward achieved is plotted for all ten episodes. The random heuristic serves as a benchmark. Initially, the agent allocates even worse than the random heuristic. However, the DQN-agent can significantly improve the average episode reward in the first 400 episodes. The agent learns to dispatch orders in the redundant disassembly stage according to their condition. After initial fluctuations, the agent manages to significantly reduce the number of failed operations to an average of around 4.0 failures per episode compared to 12.5 failed operations per episode by the random heuristic (Fig. 6b). By avoiding to repeat \(O{p}_{2}\), the utilization of the manual station is significantly reduced. This leads to lower resource costs of the entire system.
Test case 2
Two major changes are made in test case 2. First, the operation failure rate is modeled probabilistically (\({p}_{fail}=1-q)\) to test whether the agent can learn, while dealing with a higher degree of uncertainty. Second, as stated before, the system is roughly balanced and, thus, the control logic can influence the makespan. While it is advantageous in terms of costs (\({min}{f}_{1}\)) to select station \({S}_{2.2}\) solely if order conditions q are suitable, it may nevertheless be beneficial concerning makespan optimization (\({min}{f}_{2})\) to disassemble orders in good condition at station \({S}_{2.1}\) to avoid a bottleneck at \({S}_{2.2}\). Therefore, the time reward \({r}_{time}\) is observed and the total reward \({r}_{total}\) is made up of the two rewards \({r}_{RC}\) with \({w}_{RC}=0.05\) and \({r}_{time}\) with \({w}_{time}=0.5\). The reward \({r}_{time}\) harms to send each order via station \({S}_{2.2}\), because otherwise makespan will increase significantly. In this case, the reward \({r}_{time}\) penalizes the agent for the additional time, but rewards it for completing orders.
The course of the total reward is shown in Fig. 6c. The DQN-agent succeeds in increasing the reward significantly during the training. It quickly rises above the average level of the random heuristic (\({{r}}_{{random},{avg}}=-{315,13}\)). Once the DQN-agent is in evaluation mode, it even achieves a slightly higher average reward than the advanced heuristic (\({{r}}_{{DQN},{avg}}=-{254,58}\), \({{r}}_{{heuristic,avg}}= -259,63\)). Both rewards \({r}_{RC}\) (Fig. 6d) and \({r}_{time}\) (Fig. 6e) increase significantly during training. While the \({r}_{RC}\) performance of the DQN-agent does not reach the level of the heuristic, in terms of \({r}_{time}\) it exceeds the heuristic. The DQN-agent consciously takes the trade-off of the higher resource costs by allocating more orders to the autonomous station. The result of this strategy is more frequent failure with associated multiple processing, but a significant makespan reduction.
Conclusion and Outlook
Productive disassembly systems are crucial to the success of closed-loop production as in remanufacturing (Guide 2000; Duflou et al. 2008; Priyono et al. 2016). Flexible automated production systems that include autonomous robots have the potential to improve or replace traditional remanufacturing factories, which are characterized by a high share of manual work. In the field of production planning and control, however, there are yet no approaches to efficiently manage and operate such remanufacturing production systems. More specifically, in this work, the control-side consideration is identified as an important research gap and investigated in detail. A production model of a hybrid disassembly system and a comprehensive description of an optimization problem including appropriate target criteria was developed. Thereby the aim was to map production systems were human workers are complemented by autonomous robots that are prone to product condition-dependent operation failures in redundant disassembly stages. With the overall aim to unburden human workers from repetitive standard tasks while remaining productive, an all-new order allocation problem arised. Three control logics were implemented to test the model. Thereby, reinforcement learning was identified as particularly suitable for the order dispatching control task. A control logic based on a DQN-agent was implemented and tested on two test cases.
The DQN-agent successfully manages to allocate individual orders to appropriate stations based on the respective product condition, thus reducing resource costs. Against the background of probabilistic failure in a balanced scenario, the RL-control succeeds in dispatching orders in such a way that both resource costs and the makespan can be optimized simultaneously. This shows that a simple RL-based dispatcher is capable of achieving results comparable to a rule-based dispatcher, but also that it is able to outperform a heuristic, especially when target variables cannot be traced back to a single priority rule and a wide variety of influencing factors have to be taken into account. After a thorough sensitivity analysis followed by an adjustment of rewards and weights and some further parameter tuning, the RL agent should develop its full potential.
This paper lays a foundation for addressing the problem of dealing with redundant workstations and failing operations from a production control perspective. However, some simplifying assumptions had to be made that require additional investigation in future works. For instance, the product condition is modeled very generically. Further research should be used to adapt the condition vector and investigate the effects of vastly differing simulation probability distributions. Moreover, the applicability should be tested more widely and for real products. In addition to a real product structure, an instantiation of a multi-dimensional order condition vector with product features relevant to the disassembly process should be carried out. In this course, the influence of the identified characteristics on the failure probability has to be examined and subsequently incorporated. Besides that, another goal is to develop improved heuristics for benchmarking. Finally, multi-agent RL-systems should be investigated. In conclusion, we expect that reinforcement learning will develop its full strength to improve the operational performance in complex systems.
References
Altekin, F. T., & Akkan, C. (2012). Task-failure-driven rebalancing of disassembly lines. International Journal of Production Research, 50, 4955–4976. https://doi.org/10.1080/00207543.2011.616915.
Altenmüller, T., Stüker, T., Waschneck, B., Kuhnle, A., & Lanza, G. (2020). Reinforcement learning for an intelligent and autonomous production control of complex job-shops under time constraints. Production Engineering, 14, 319–328. https://doi.org/10.1007/s11740-020-00967-8.
Apple Inc. (2019). Environmental Responsibility Report: 2019 Progress Report, covering fiscal year 2018. Cupertino, CA. https://www.apple.com/environment/pdf/Apple_Environmental_Responsibility_Report_2019.pdf. Accessed 21 November 2020.
Aytug, H., Lawley, M. A., McKay, K., Mohan, S., & Uzsoy, R. (2005). Executing production schedules in the face of uncertainties: A review and some future directions. European Journal of Operational Research, 161, 86–110. https://doi.org/10.1016/j.ejor.2003.08.027.
Bdiwi, M., Rashid, A., & Putz, M. (2016). Autonomous disassembly of electric vehicle motors based on robot cognition. In A. Okamura & A. Menciassi (Eds.), 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 5/16/2016 - 5/21/2016 (pp. 2500–2505). Piscataway, NJ: IEEE. https://doi.org/10.1109/ICRA.2016.7487404.
Büker, U., Drüe, S., Götze, N., Hartmann, G., Kalkreuter, B., Stemmer, R., et al. (2001). Vision-based control of an autonomous disassembly station. Robotics and Autonomous Systems, 35, 179–189. https://doi.org/10.1016/S0921-8890(01)00121-X.
Colledani, M., & Battaïa, O. (2016). A decision support system to manage the quality of End-of-Life products in disassembly systems. CIRP Annals, 65, 41–44. https://doi.org/10.1016/j.cirp.2016.04.121.
Csáji, B. C., Monostori, L., & Kádár, B. (2006). Reinforcement learning in a distributed market-based production control system. Advanced Engineering Informatics, 20, 279–288. https://doi.org/10.1016/j.aei.2006.01.001.
Cunha, B., Madureira, A., Fonseca, B., & Coelho, D. (2018). Deep Reinforcement Learning as a Job Shop Scheduling Solver: A Literature Review. In Ana Maria Madureira, Ajith Abraham, Niketa Gandhi, Maria Leonilde Varela, & Janusz Kacprzyk (Eds.), Hybrid Intelligent Systems (pp. 350–359).
Cunha, B., Madureira, A. M., Fonseca, B., & Coelho, D. (2020). Deep Reinforcement Learning as a Job Shop Scheduling Solver: A Literature Review. In A. Abraham (Ed.), Hybrid intelligent systems: 18th International Conference on Hybrid Intelligent Systems (HIS 2018) held in Porto, Portugal, December 13-15, 2018 (Vol. 923, pp. 350–359, Advances in Intelligent Systems and Computing, volume 923). Cham: Springer International Publishing.
Dios, M., & Framinan, J. (2016). A review and classification of computer-based manufacturing scheduling tools. Computers & Industrial Engineering, 99, 229–249. https://doi.org/10.1016/j.cie.2016.07.020.
Duflou, J. R., Seliger, G., Kara, S., Umeda, Y., Ometto, A., & Willems, B. (2008). Efficiency and feasibility of product disassembly: A case-based study. CIRP Annals, 57, 583–600. https://doi.org/10.1016/j.cirp.2008.09.009.
Duta, L., Henrioud, J. M., & Caciula, I. (2007). A real time solution to control disassembly processes. IFAC Proceedings Volumes, 40, 789–794. https://doi.org/10.3182/20070927-4-RO-3905.00130.
Eisele, W., & Knobloch, A. P. (2014). Technik des betrieblichen Rechnungswesens: Buchführung und Bilanzierung, Kosten- und Leistungsrechnung, Sonderbilanzen (8th ed., Vahlens Handbücher). München: Verlag Franz Vahlen.
Gao, M., & Zhou, M. C. (2001). Fuzzy reasoning Petri nets for demanufacturing process decision. In 2001 IEEE International Symposium on Electronics and the Environment. 2001 IEEE ISEE, Denver, CO, USA, 7-9 May 2001 (pp. 167–172). Piscataway, N.J: IEEE. https://doi.org/10.1109/ISEE.2001.924521.
Guide, V. D. R. (2000). Production planning and control for remanufacturing: industry practice and research needs. Journal of Operations Management, 18, 467–483. https://doi.org/10.1016/S0272-6963(00)00034-6.
Gungor, A., & Gupta, S. M. (2001). A solution approach to the disassembly line balancing problem in the presence of task failures. International Journal of Production Research, 39, 1427–1467. https://doi.org/10.1080/00207540110052157.
Gupta, S. M., & Taleb, K. N. (1994). Scheduling disassembly. International Journal of Production Research, 32, 1857–1866. https://doi.org/10.1080/00207549408957046.
Häfner, B. (2020). AgiProbot. http://agiprobot.de/. Accessed 31 July 2020.
Junior, M. L., & Filho, M. G. (2012). Production planning and control for remanufacturing: literature review and analysis. Production Planning & Control, 23, 419–435. https://doi.org/10.1080/09537287.2011.561815.
Kim, H. J., Chiotellis, S., & Seliger, G. (2009). Dynamic process planning control of hybrid disassembly systems. The International Journal of Advanced Manufacturing Technology, 40, 1016–1023. https://doi.org/10.1007/s00170-008-1407-7.
Kim, H. J., Ciupek, M., Buchholz, A., & Seliger, G. (2006). Adaptive disassembly sequence control by using product and system information. Robotics and Computer-Integrated Manufacturing, 22, 267–278. https://doi.org/10.1016/j.rcim.2005.06.003.
Kim, H. J., Harms, R., & Seliger, G. (2007a). Automatic Control Sequence Generation for a Hybrid Disassembly System. IEEE Transactions on Automation Science and Engineering, 4, 194–205. https://doi.org/10.1109/TASE.2006.880538.
Kim, H. J., Lee, D. H., & Xirouchakis, P. (2007b). Disassembly scheduling: literature review and future research directions. International Journal of Production Research, 45, 4465–4484. https://doi.org/10.1080/00207540701440097.
Kimemia, J., & Gershwin, S. B. (1983). An Algorithm for the Computer Control of a Flexible Manufacturing System. IIE Transactions, 15, 353–362. https://doi.org/10.1080/05695558308974659.
Kopacek, P., & Kopacek, B. (2003). Robotized Disassembly of Mobile Phones. IFAC Proceedings Volumes, 36, 103–105. https://doi.org/10.1016/S1474-6670(17)37669-3.
Kopacek, P., & Kopacek, B. (2006). Intelligent, flexible disassembly. The International Journal of Advanced Manufacturing Technology, 30, 554–560. https://doi.org/10.1007/s00170-005-0042-9.
Kuhnle, A. (2020). SimRLFab: Simulation and reinforcement learning framework for production planning and control of complex job shop manufacturing systems. GitHub.
Kuhnle, A., Kaiser, J. P., Theiß, F., Stricker, N., & Lanza, G. (2021a). Designing an adaptive production control system using reinforcement learning. Journal of Intelligent Manufacturing, 32, 855–876. https://doi.org/10.1007/s10845-020-01612-y.
Kuhnle, A., & Lanza, G. (2019). Application of Reinforcement Learning in Production Planning and Control of Cyber Physical Production Systems. In J. Beyerer (Ed.), Machine learning for cyber physical systems: Selected papers from the international conference ML4CPS 2018 (Vol. 9, pp. 123–132, Technologien für die intelligente Automation: technologies for intelligent automation, Band 9). Berlin, Germany: Springer Vieweg.
Kuhnle, A., May, M. C., Schäfer, L., & Lanza, G. (2021b). Explainable reinforcement learning in production control of job shop manufacturing system. International Journal of Production Research, 24, 1–23. https://doi.org/10.1080/00207543.2021.1972179.
Kuhnle, A., Röhrig, N., & Lanza, G. (2019a). Autonomous order dispatching in the semiconductor industry using reinforcement learning. Procedia CIRP, 79, 391–396. https://doi.org/10.1016/j.procir.2019.02.101.
Kuhnle, A., Schaarschmidt, M., & Fricke, K. (2017). Tensorforce: a TensorFlow library for applied reinforcement learning. https://github.com/tensorforce/tensorforce.
Kuhnle, A., Schäfer, L., Stricker, N., & Lanza, G. (2019b). Design, Implementation and Evaluation of Reinforcement Learning for an Adaptive Order Dispatching in Job Shop Manufacturing Systems. Procedia CIRP, 81, 234–239. https://doi.org/10.1016/j.procir.2019.03.041.
Kurilova-Palisaitiene, J., & Sundin, E. (2014). Challenges and Opportunities of Lean Remanufacturing. International Journal of Automation Technology, 8, 644–652. https://doi.org/10.20965/ijat.2014.p0644.
Lambert, A. J. D., & Gupta, S. M. (2004). Disassembly Modeling for Assembly, Maintenance, Reuse and Recycling. CRC Press
Lawler, E. L., Lenstra, J. K., Kan, R., & Shmoys, D. B., A. H.G., &. (2005). Chapter 9 Sequencing and scheduling: Algorithms and complexity. In Graves, S. C. (Ed.), Logistics of production and inventory (Vol (4 vol., pp. 445–522). Handbooks in Operations Research and Management Science, Vol. 4). Amsterdam: Elsevier
Lee, D. H., Kang, J. G., & Xirouchakis, P. (2001). Disassembly planning and scheduling: Review and further research. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 215, 695–709. https://doi.org/10.1243/0954405011518629.
Lund, R. T. (1984). Remanufacturing: The experience of the United States and implications for developing countries (1st ed., Integrated resource recovery, Vol. 2). Washington, DC: The World Bank.
Madureira, A., Pereira, I., & Falcao, D. (2013). Dynamic adaptation for scheduling under rush manufacturing orders with case-based reasoning. In Int. Conf. on Algebraic and Symbolic Computation.
McKay, K. N., Safayeni, F. R., & Buzacott, J. A. (1988). Job-Shop Scheduling Theory: What Is Relevant? Interfaces, 18, 84–90. https://doi.org/10.1287/inte.18.4.84.
Mhada, F., Hajji, A., Malhamé, R., Gharbi, A., & Pellerin, R. (2011). Production control of unreliable manufacturing systems producing defective items. Journal of Quality in Maintenance Engineering, 17, 238–253. https://doi.org/10.1108/13552511111157362.
Moore, K. E., Gungor, A., & Gupta, S. M. (1998). A Petri net approach to disassembly process planning. Computers & Industrial Engineering, 35, 165–168. https://doi.org/10.1016/S0360-8352(98)00051-5.
Pinedo, M. L. (2016). Scheduling. Cham: Springer International Publishing
Poschmann, H., Brüggemann, H., & Goldmann, D. (2020). Disassembly 4.0: A Review on Using Robotics in Disassembly Tasks as a Way of Automation. Chemie Ingenieur Technik, 92, 341–359. https://doi.org/10.1002/cite.201900107.
Priyono, A., Ijomah, W., & Bititci, U. (2016). Disassembly for remanufacturing: A systematic literature review, new model development and future research needs. Journal of Industrial Engineering and Management, 9, 899. https://doi.org/10.3926/jiem.2053.
Reisig, W. (2013). Understanding Petri Nets. Berlin, Heidelberg: Springer Berlin Heidelberg
Riggs, R. J., Battaïa, O., & Hu, S. J. (2015). Disassembly line balancing under high variety of end of life states using a joint precedence graph approach. Journal of Manufacturing Systems, 37, 638–648. https://doi.org/10.1016/j.jmsy.2014.11.002.
Rujanavech, C., Lessard, J., Chandler, S., Shannon, S., Dahmus, J., & Guzzo, R. (2016). Liam - An Innovation Story. Cupertino, CA. https://www.apple.com/environment/pdf/Liam_white_paper_Sept2016.pdf. Accessed 21 November 2020.
Scholz-Reiter, B., Scharke, H., & Hucht, A. (1999). Flexible robot-based disassembly cell for obsolete TV-sets and monitors. Robotics and Computer-Integrated Manufacturing, 15, 247–255. https://doi.org/10.1016/S0736-5845(99)00022-8.
Slama, I., Ben-Ammar, O., Masmoudi, F., & Dolgui, A. (2019). Disassembly scheduling problem: literature review and future research directions. IFAC-PapersOnLine, 52, 601–606. https://doi.org/10.1016/j.ifacol.2019.11.225.
Tang, Y., Zhou, M., & Caudill, R. J. (2001). An integrated approach to disassembly planning and demanufacturing operation. IEEE Transactions on Robotics and Automation, 17, 773–784. https://doi.org/10.1109/70.975899.
Tolio, T., Bernard, A., Colledani, M., Kara, S., Seliger, G., Duflou, J., et al. (2017). Design, management and control of demanufacturing and remanufacturing systems. CIRP Annals, 66, 585–609. https://doi.org/10.1016/j.cirp.2017.05.001.
Tumkor, S., & Senol, G. (2007). Disassembly Precedence Graph Generation. In Assembly and Manufacturing, 2007. ISAM ‘07. IEEE International Symposium on (pp. 70–75). https://doi.org/10.1109/ISAM.2007.4288451.
Ullerich, C., & Buscher, U. (2013). Flexible disassembly planning considering product conditions. International Journal of Production Research, 51, 6209–6228. https://doi.org/10.1080/00207543.2013.825406.
Vongbunyong, S., & Chen, W. H. (2015). Disassembly automation: Automated systems with cognitive abilities (Sustainable production. life cycle engineering and management). Cham: Springer
Vongbunyong, S., Kara, S., & Pagnucco, M. (2013). Basic behaviour control of the vision-based cognitive robotic disassembly automation. Assembly Automation, 33, 38–56. https://doi.org/10.1108/01445151311294694.
Vongbunyong, S., Vongseela, P., & Sreerattana-aporn, J. (2017). A Process Demonstration Platform for Product Disassembly Skills Transfer. Procedia CIRP, 61, 281–286. https://doi.org/10.1016/j.procir.2016.11.197.
Waschneck, B., Reichstaller, A., Belzner, L., Altenmuller, T., Bauernhansl, T., Knapp, A., et al. (2018). Deep reinforcement learning for semiconductor production scheduling. In 2018 29th Annual SEMI Advanced Semiconductor Manufacturing Conference (ASMC), Saratoga Springs, NY, USA, 30.04.2018 - 03.05.2018 (pp. 301–306). IEEE. https://doi.org/10.1109/ASMC.2018.8373191.
World Economic Forum (2019). A New Circular Vision for Electronics: Time for a Global Reboot. http://www3.weforum.org/docs/WEF_A_New_Circular_Vision_for_Electronics.pdf. Accessed 12 February 2021.
World Economic Forum, & Accenture Strategy (2019). Harnessing the Fourth Industrial Revolution for the Circular Economy: Consumer Electronics and Plastics Packaging. http://www3.weforum.org/docs/WEF_Harnessing_4IR_Circular_Economy_report_2018.pdf. Accessed 3 February 2021.
Wurster, M., Häfner, B., Gauder, D., Stricker, N., & Lanza, G. (2021). Fluid Automation—A Definition and an Application in Remanufacturing Production Systems. Procedia CIRP, 97, 508–513. https://doi.org/10.1016/j.procir.2020.05.267.
Zussman, E., & Zhou, M. (1999). A methodology for modeling and adaptive planning of disassembly processes. IEEE Transactions on Robotics and Automation, 15, 190–194. https://doi.org/10.1109/70.744614.
Zussman, E., & Zhou, M. C. (2000). Design and implementation of an adaptive process planner for disassembly processes. IEEE Transactions on Robotics and Automation, 16, 171–179. https://doi.org/10.1109/70.843173.
Acknowledgements
The project AgiProbot is funded by the Carl Zeiss Foundation.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wurster, M., Michel, M., May, M.C. et al. Modelling and condition-based control of a flexible and hybrid disassembly system with manual and autonomous workstations using reinforcement learning. J Intell Manuf 33, 575–591 (2022). https://doi.org/10.1007/s10845-021-01863-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10845-021-01863-3