Disassembly line optimization with reinforcement learning

Abstract

As the environmental aspects become increasingly important, the disassembly problems have become the researcher’s focus. Multiple criteria do not enable finding a general optimization method for the topic, but some heuristics and classical formulations provide effective solutions. By highlighting that disassembly problems are not the straight inverses of assembly problems and the conditions are not standard, disassembly optimization solutions require human control and supervision. Considering that Reinforcement learning (RL) methods can successfully solve complex optimization problems, we developed an RL-based solution for a fully formalized disassembly problem. There were known successful implementations of RL-based optimizers. But we integrated a novel heuristic to target a dynamically pre-filtered action space for the RL agent (dlOptRL algorithm) and hence significantly raise the efficiency of the learning path. Our algorithm belongs to the Heuristically Accelerated Reinforcement Learning (HARL) method class. We demonstrated its applicability in two use cases, but our approach can also be easily adapted for other problem types. Our article gives a detailed overview of disassembly problems and their formulation, the general RL framework and especially Q-learning techniques, and a perfect example of extending RL learning with a built-in heuristic.

1 Introduction

The increasing environmental pressures caused by human activities drive governments and organizations to limit or decrease their footprints. As an outcome, the European Commission declared this a strategic goal. A new Circular Economy Action Plan for a cleaner and more competitive Europe has been announced to sustainably transform the economy and society. There is a wide range of recommendations and proposals on how these kinds of issues should be handled, and the key point is to reduce consumption and increase the recycling rate. The efforts led to the creation of the concept of circular economy, which is more complex than just a manufacturing optimization because it also covers the supply chain, disassembly, and recycling optimization steps (Loiseau et al. 2016; Camacho-Otero et al. 2018). A process flow overview diagram of the circular economy is shown in Fig. 1 (Kalmykova et al. 2018).

Fig. 1

Schematic flow of circular economy Kalmykova et al. (2018)

Every step in the circular process has practices and methods to optimize the operation. Still, the primary goal of the circular economy is to optimize the whole supply chain up to recycling. The classical problem of manufacturing supply chain optimization is a deeply researched topic (Beamon 1999; de Koster et al. 2007; Hervani et al. 2005). The circular economy optimization goal also covers the recollection and recycling processes that can be a bit more complex because these are more stochastic and less controlled processes. Disassembly line design and balancing problems describe the methodological background of the relevant segment of the whole circle (Jovane et al. 1993; Duflou et al. 2008; Sasikumar and Kannan 2008). The most basic models assumed deterministic inputs but the advanced models started to handle the uncertainty observed in real problems. Among others, the source materials and their distributions are described by stochastic variables. Similarly, the disassembly tasks, their required process times, and the demand values of recycling steps can also be stochastic attributes in some models.

The supply chain optimization and assembly line balancing topics have been intensively studied issues since the 1950s years, while the focused analysis of disassembly lines started almost 40 years later (Gupta and McLean 1996). A detailed historical overview of disassembly methods (Kim et al. 2007) delivered a summary table of the different solutions, which was extended by using a comprehensive classification (Chand and Ravi 2023) in Table 1. It shows a wide range of machine-learning methods for solving the disassembly line balancing problem. There are already successful RL-based solutions with attractive learning performance, but it needs to be explained in detail how to construct an effective implementation for a given problem.

Table 1 Overview of disassembly line balancing solutions

The above-collected facts strengthened our motivation to prepare an effective self-learning RL-based solution that is easy to adapt to different disassembly problems. We present a general guide on how to define the reward function from problem parameters. Furthermore, we highlight the importance of customizing the action-taking method, which will be relevant whenever a general RL framework is parameterized. According to the current outlook, the number of disassembly lines and their optimization requirements will increase significantly, and such a self-learning solution will explain this adequately.

Our first experiences with an RL-based solution show that the most basic version of training an RL agent is not obviously efficient: after declaring the state- and action spaces the central task is to define the reward function. Most of the RL frameworks support this approach without the option of customizing the action-taking method. But a huge portion of infeasible state-action pairs should not be learned. For disassembly line balancing problems, it is an obvious option to dynamically filter for the possible uncompleted actions by considering the precedence graph. We found that integrating such an efficient state-dependent action-restriction method can radically reduce the learning path. The same conclusion has been found (Woo and Sung 2020). The major idea was to apply the identical constraints that were set up in mixed-integer quadratic problem (MIQP) formulation, and hence to deliver a systematic method to define an appropriate restriction for action-selection step. The key result of our article is to present a Q-learning solution with an integrated heuristic for dynamic state-dependent action restriction. The dlOptRL algorithm is described and explained in detail. From a higher aspect, our algorithm belongs to the class of Heuristically Accelerated Reinforcement Learning (HARL) methods, which is highlighted by an appropriate formulation as well.

Our article stands for the following major parts:

• First, in Sect. 2.1, we will give a problem formulation of disassembly line optimization problems. We will summarize the notations, declare the objective function components, and present an MIQP formulation with fewer decision variables. It enables solving larger-size problems with the widely used solvers by keeping the limitations of decision variables.

• Sect. 3 will present the general framework of Reinforcement Learning solutions. We will describe the Q-learning method in detail that was applied in our development. We will also summarize all the necessary steps that should be prepared for an RL solution to the previously defined disassembly problem.

• Then, in Sect. 3.2, we will describe a novel algorithm called dlOptRL. It contains a built-in heuristic to minimize applicable action space and speed up the learning of an RL agent. Our algorithm highlights how RL methods can be combined with problem-specific heuristics to get an efficient self-learning solution. We will also point out that our algorithm belongs to the Heuristically Accelerated Reinforcement Learning class.

• Sect. 4 will describe two commonly used use cases for which we will summarize a MIQP solution as a reference and the results of our dlOptRL learning path. We will show that our solution approximates the optimal solution effectively without any prior preparations.

• Finally, in Sect. 5, we will take an overview of our results and summarize some potential directions for further research.

2 Optimization of disassembly line balancing

In this section, we will summarise the general notations of disassembly problems. Then we will overview the solution methods, including the problem formulation as a linear programming task.

2.1 Problem formulation

We consider a disassembly line balancing model for a single product with a finite supply. There are $N^c$ elementary components in each product to remove. The task of eliminating component i is specified by its processing time $T_i^{rm}$, while a boolean flag of $h_i$ indicates its hazardousness. The general problem is to assign every task to workstations of the disassembly line to optimize the objective function. We will make the following additional assumptions:

• There are $N_{a}^{ws}$ available workstations that are preliminarily prepared.

• All workstations are identical, and they are capable of performing any component removal tasks.

• The cycle time is denoted by $T^{c}$. Each workstation should finish its allocated removal tasks on the current product in the disassembly line. The cycle time is preliminarily defined.

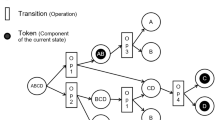
• A precedence graph describes the logical dependencies of component removal tasks. The vertices represent the components to be removed. The edges are directed, and there are two types of edges: AND type and OR type edges. The removal process of a component i can be started, only if all the components from which a directed AND-type path goes to the vertex of i are already removed, and at least one of the components from which a directed OR-type path goes to the vertex of i is removed. Typically the precedence graph is used in its transitive reduced form.

• A solution is described by a sequence of the component removal tasks, where $C_k$ denotes the kth component in the disassembly sequence.

• A workstation will perform a continuous range of component removal tasks.

• The total time for workstation j to perform all of its assigned tasks is denoted by $T_j^{ws}$.

• $N_{u}^{ws}$ denotes the number of workstations used.

The major attributes of the disassembly line balancing problem are summarised in Table 2.

Table 2 Notations of disassembly line balancing problems

2.2 Objective function

There are several ways to measure how well is a disassembly line balanced. Based on the different disassembly optimization solutions collected in Table 1, there are two major approaches for the objective: one is cost-benefit-based, and the other one is based on the processed quantities. By following the mixed objective approach (Tuncel et al. 2014), we used a combination of three components in our analysis.

• $F_1= \min \{ \sum _{j=1}^{N_u^{ws}} (T^c-T_{j}^{ws})^2 \}$ minimizes the total idle time of workstations used,

• $F_2= \min \{ \sum _{k=1}^{N^c} (k\cdot h_{C_k}) \}$ forces to remove hazardous components as early as it can,

• $F_3= \min \{ \sum _{k=1}^{N^c} (k\cdot d_{C_k}) \}$ supports removing components with higher demand earlier.

The preliminary defined circle time and the total sum of components’ removal times and the number of used workstations determine the total idle time: $N_u^{ws}\cdot T_c-\sum _{i=1}^{N^c}T_i^{rm}$. The shorter idle time results a higher processed quantity. The objective function $F_1$ amplifies the imbalance and contains the corresponding items in a quadratic term. Hence it supports not only minimizing the idle times but also decreasing the imbalance. Objective functions $F_2$ and $F_3$ depend on the component property and disassembly sequence. The component’s hazardousness requires additional care or causes extra risk, which motivates removal as early as possible. A binary boolean indicator describes the Hazardousness property. $F_2$ prefers to remove hazardous components earlier than non-hazardous ones. $F_3$ is similar to $F_2$ construction except that demand values are not binary but non-negative figures, and they represent the disassembled components’ importance in remanufacturing due to the benefit values. It was reviewed and shown (Laili et al. 2020) that using the multi-objective approach for disassembly optimization problems is quite general. Further aspects can also be taken into account by adding other components to the objective for minimizing the disassembly cost, maximizing the profit obtained from disassembly, or minimizing environmental pollution.

In our article, according to the analyzed use cases, we will use a linear combination of the three selected objectives: $w_1 F_1 + w_2 F_2 + w_3 F_3$. In this context, weights of $w_1$, $w_2$, and $w_3$ have double roles. These should compensate for the scaling discrepancies of the objectives, and the weights can determine the relative importance of the objectives based on external preferences. The first role could be substituted by normalizing or standardizing the objectives. However the second aspect cannot be replaced with an autonomous solution, although the relative importance constantly changes in real-world problems. A dynamic weighting optimization that reflects the external conditions is out of the scope of our article. Hence we assume that weights of $w_1$, $w_2$, and $w_3$ are preliminarily defined as external parameters.

2.3 Linear programming problem formulation

There are already described formulations of the disassembly problem in the literature (Kalaycilar et al. 2016), but we will present a new formulation with a decreased size of decision variables. It stands for six significant types of decision variables:

• Type 1 decision variables describe which of the removable component is assigned to a disassembly sequence order number:

  $$\begin{aligned} x_{i,j}^{Type 1} = \left\{ \begin{array}{ll} 1 &{} \begin{array}{l} \text {if component } i \text { will be removed } \\ \text {as } j\text {th task in the removal sequence}\end{array}\\ 0 &{} \text {otherwise}\\ \end{array} \right. \end{aligned}$$

  (1)

• Type 2 decision variables determine the process times of every step in the disassembly sequence:

  $$\begin{aligned} x_{j}^{Type 2} = T_{C_k}^{rm}. \end{aligned}$$

  (2)

• Type 3 decision variables describe the workstation on which the component will be removed:

  $$\begin{aligned} x_{i,k}^{Type 3} = \left\{ \begin{array}{ll} 1 &{} \text {if component } i \text { will be removed on workstation } k\\ 0 &{} \text {otherwise} \end{array} \right. \end{aligned}$$

  (3)

• Type 4 decision variables determine whether a workstation will be in use or not:

  $$\begin{aligned} x_{k}^{Type 4} = \left\{ \begin{array}{ll} 1 &{} \text {if workstation } k \text { will be in use }\\ 0 &{} \text {otherwise} \end{array} \right. \end{aligned}$$

  (4)

• Type 5 decision variables determine the total idle time of each workstation if it is in use:

  $$\begin{aligned} x_{k}^{Type 5} = T^c x_k^{Type 4} \sum _{i}x_{i,k}^{Type 3}C_i. \end{aligned}$$

  (5)

• Type 6 decision variables describe the workstation assignments in the disassembly sequence order:

  $$\begin{aligned} x_{j}^{Type 6} = \left\{ \begin{array}{ll} k &{} \text {if workstation } k \text { will be assigned the } j\text {th component in the disassembly sequence}\\ 0 &{} \text {otherwise}\\ \end{array} \right. \end{aligned}$$

  (6)

Then we need to set up constraints to satisfy all the requirements collected in Sect. 2.1:

• Constraints guarantee that each component is listed exactly once in the removal sequence:

  $$\begin{aligned} \sum _{j=1}^{N^{ws}} x_{i,j}^{Type 1} = 1 \qquad \forall i\in \{1,\dots ,N^c\} \end{aligned}$$

  (7)

• The workstation’s process time should not exceed the cycle time limit:

  $$\begin{aligned} \sum _{i=1}^{N^c} T_i^{rm}\cdot x_{i,k}^{Type 3} \le T^c \qquad \forall k\in \{1,\dots ,N^{ws}\} \end{aligned}$$

  (8)

Before declaring the constraints of the precedence graph, we need to declare the two types of predecessor relations:

• Predecessor AND relation ($P_{AND}(i)$) declares a set of predecessor tasks that all need to be finished before starting task i.

• Predecessor OR relation ($P_{OR}(i)$) declares a set of predecessor tasks of which at least one needs to be finished before starting task i.

Figure 2 shows examples of predecessor AND and OR relations.

Fig. 2

Predecessor relation types

In this context, we can continue to define the required constraints:

• All the predecessor tasks with AND relation should be assigned earlier in the sequence than the particular one:

  $$\begin{aligned} \sum _{j=1}^{N^{c}} j\cdot x_{l,j}^{Type 1} \le \sum _{j=1}^{N^{c}} j\cdot x_{i,j}^{Type 1} \qquad \forall i\in \{1,\dots ,N^c\}; \forall l\in P_{AND}(i) \end{aligned}$$

  (9)

• At least one of the predecessor tasks with OR relation should be assigned earlier in the sequence than the particular one:

  $$\begin{aligned} x_{i,j}^{Type 1} \le \sum _{h=1}^{j} \sum _{l\in P_{OR}(i)} j\cdot x_{l,h}^{Type 1} \qquad \forall i\in \{1,\dots ,N^c\}; \forall j\in \{1,\dots ,N^c\} \end{aligned}$$

  (10)

• Assuring that a disassembly task is assigned to exactly one workstation:

  $$\begin{aligned} \sum _{k=1}^{N^{ws}} x_{i,k}^{Type 3} = 1 \qquad \forall i\in \{1,\dots ,N^c\} \end{aligned}$$

  (11)

• The workstation assignments should be in a monotone sequence:

  $$\begin{aligned} 0 \le x_j^{Type 6} - x_{j-1}^{Type 6} \le 1 \qquad \forall j\in \{2,\dots ,N^c\} \end{aligned}$$

  (12)

• Integer and non-negative properties:

  $$\begin{aligned} \begin{array}{ll} x_{i,j}^{Type 1} \in \{0, 1\} &{}\quad \forall i,j \in \{1,\dots ,N^c\} \\ 0 \le x_{j}^{Type 2}\le T^c &{}\quad \forall j \in \{1,\dots ,N^c\} \\ x_{i,k}^{Type 3} \in \{0, 1\} &{}\quad \forall i \in \{1,\dots ,N^c\} \\ &{}\quad \forall k \in \{1,\dots ,N^{ws}\} \\ 0 \le x_{k}^{Type 4}\le T^c &{}\quad \forall k \in \{1,\dots ,N^{ws}\} \\ x_{k}^{Type 5} \in \{0, 1\} &{}\quad \forall k \in \{1,\dots ,N^{ws}\} \\ x_{j}^{Type 6} \in \{1, \dots ,N^{ws}\} &{}\quad \forall j \in \{1,\dots ,N^c\} \\ \end{array} \end{aligned}$$

  (13)

By solving the MIQP problem, we can conduct an optimal solution, but in practice, it can be a heavily resource-intensive process for mid and large-scale problems. A former analysis of a profit-oriented linear objective shows that an exact MILP solution cannot be reached in a reasonable time limit for disassembly problems over 60 components (Kalaycilar et al. 2016). In this formulation, the number of decision variables was quadratic to the number of components. We used a modified formulation with $2(N^c)^2+4N^c$ decision variables for an $N^c$-component disassembly problem. Moreover, our weighted objective leads to a quadratic optimization problem. We used a Gurobi-based solver from Matlab, and experienced the same issue: no solution was found within the same time limit.¹ This fact may bring alternative solutions to the fore, especially reinforcement learning methods.

3 Formulation of the disassembly line balancing problem as an RL-based optimization task

Reinforcement learning (RL) refers to learning problems. An agent takes observations of the environment, and based on that, it executes an action ($A_t$). As a result of the action in the environment, the agent will get a reward ($R_t$), and it can take a new observation ($O_t$) from the environment, and the cycle is repeated. The problem is to let the agent learn to maximize the total reward. Figure 3 shows the general reinforcement learning framework.

Fig. 3

Reinforcement learning framework

Reinforcement learning is based on the reward hypothesis which states that all goals can be described by the maximization of expected cumulative rewards.

Formally the history is the sequence of observations, actions, and rewards: $H_t = O_1, T_1, A_1, \dots , A_{t-1}, O_t, R_t$. The state is the information used to determine what happens next. Formally, state is a function of the history: $S_t = f (H_t)$. A state is Markov if and only if ${\mathbb {P}}[S_{t+1} \mid S_{t}] = {\mathbb {P}}[S_{t+1} \mid S_{1}, \dots , S_{t}]$. Markov property is fundamental to the theoretical basis of RL methods. $G_t$ denotes the total discounted reward from time-step t: $G_t = R_{t+1} + \gamma R_{t+2} + \dots = \sum _{k=0}^{\infty }\gamma ^k R_{t+k+1}$.

The state value function v(s) gives the expected total discounted return if starting from state s: $v(s) = {\mathbb {E}} [G_t \mid S_t = s]$. The Bellman Equation practically states that the state value function (VF) can be decomposed into two parts: immediate reward ($R_{t+1}$) and the discounted value of successors states $\gamma v(S_{t+1})$.

The policy covers the agent’s behavior in all possible cases, so it is essentially a map from states to actions. There are two major categories in it: deterministic policy ($a = \pi (s)$) and stochastic policy ($\pi (a\mid s) = {\mathbb {P}}[A_t = a\mid S_t = s]$).

We will focus on using an action-value function to determine the current optimal action. However, for large state- and/or action spaces it can be a very slow process to keep the value function updated (and hence optimal).

There are several situations when the learning process is not based on just own experience. Formally this means that action-value function $q_\pi (s;a)$ is determined by observing results of an external behavior policy $\mu (a\vert s)$.

A possible way to handle the difference between target and behavior policy is to modify the value-function update logic as Q-learning does (Sutton and Barto 2018, Section 6.5). Assume that in state $S_t$ the very next action is derived by using behavior policy: $A_{t+1}\sim \mu (\cdot \vert S_t)$. By taking action $A_{t+1}$ immediate reward $R_{t+1}$ and the next state $S_{t+1}$ will be determined. But for value-function update let’s consider an alternative successor action based on target policy: $A'\sim \pi (\cdot \vert S_t)$. Then the Q-learning value-function update will look like: $Q(S_t;A_t) \leftarrow Q(S_t;A_t) + \alpha \Big (R_{t+1}+\gamma Q(S_{t+1};A') - Q(S_t;A_t)\Big )$.

In a special case if target policy $\pi$ is chosen as a pure greedy policy and behavior policy $\mu$ follows $\epsilon$-greedy policy then so-called SARSAMAX update can be defined as follows: $Q(S;A) \leftarrow Q(S;A) + \alpha \Big (R+\gamma \max _{a'}Q(S';a') - Q(S;A)\Big )$. Last, but not least it was proven that Q-learning control converges to the optimal action-value function: $Q(s;a)\rightarrow q_*(s;a)$.

3.1 Design of reinforcement learning solution

In this section, we will present a reinforcement learning-based solution design.

• State space: A state needs to contain all the relevant information from the past and be identical for equivalent situations. Hence, the current state should contain the set of removed and remaining components as well as the utilization of the active workstation. So we can declare the state vector in a similar way to the multi-type decision variable in the MIQP formulation:

  • the performed removal steps and the remaining ones:

    $$\begin{aligned} {\hat{x}}_{i}^{Type 1} = \left\{ \begin{array}{ll} 1 &{} \text {if component } i \text { has been removed }\\ 0 &{} \text {otherwise}\\ \end{array} \right. \end{aligned}$$

    (14)

  • the current utilization of the active workstation:

    $$\begin{aligned} {\hat{x}}^{Type 2} = \text {total assigned removal time of last active workstation}. \end{aligned}$$

    (15)

• Action space: The next action is determined by considering both the current status and the constraints defined by the precedence graph. Formally, it will be described by the component’s identifier which one needs to be removed next. It is essential to highlight that a built-in heuristic to limit the potential actions to the feasible ones can significantly speed up the solution.

• Reward: Reward function is defined as the reciprocal of the weighted sum of objective components:

  $$\begin{aligned} \frac{1}{w_1F_1+w_2F_2+w_3F_3}. \end{aligned}$$

  (16)

• Reinforcement Learning method: Considering that both state- and action spaces are discrete, we decided to use the Q-learning method. Triplets of the single state vector, the next action, and cumulative discounted rewards will determine Q-table rows (practically Q-table structure).

• Q-table growth: Some approaches suggest declaring the Q-table structure initially, and during the learning phase its rows need to be updated. By having a precedence graph determining the total number of feasible states is not trivial. Hence, we applied a dynamic Q-table growth mechanism (Viharos and Jakab 2021): the learning phase starts with an empty Q-table, and whenever a new state-action pair is observed, it should be inserted into the Q-table. Therefore, the Q-table contains only visited rows.

• Knowledge transition: Whenever the RL agent experiences a better reward from a visited state than the former best one, the Q-table needs to be updated accordingly. The learning process can be sped up by using the knowledge transition process. In this case, the Q-table updates are made backward from the latter visited states of the episode to the former ones. The key idea is to update not only the visited state-action pairs of the episode but all further state-action pairs that lead to the visited route. In other words, the rewards of those state-action pairs, which partially overlap with the visited episode, can also be updated.

• If the agent should make the optimal action and not a random one, but it is not known (not listed in Q-table yet) because the current state has never been visited before, then a random decision will be made as a fallback action.

• A disabling discount factor can simplify the Q-learning method. The reason is that the state defines how many actions are required to finish the episode, so the discount factor value could be easily calculated from the state. On the other hand, its ability to differentiate between potential routes by considering their lengths also breaks off.

• Q-learning method works with $\epsilon$-Greedy decisions: the RL agent takes a random action with $\epsilon$ probability or the best-known action based on the Q-table with $(1-\epsilon$) probability. There are different $\epsilon$-strategies, from which we tested the following four:

  • 1. Pure $\epsilon$-Greedy approach: during the whole simulation, the value of $\epsilon$ is constant in all the episodes.

  • 2. Two-step $\epsilon$-Greedy approach: in the first phase of the simulation $\epsilon$ has a value of $100\%$, and hence the RL agent takes only random actions, while in the second phase of the simulation $\epsilon$ switches to a lower reasonable constant.

  • 3. Linearly decreasing $\epsilon$ approach: the value of $\epsilon$ starts from $100\%$ at the beginning and linearly decreases to $0\%$ proportionally to the progress of the simulation.

  • 4. Sigmoid-shape $\epsilon$ approach: $\epsilon$ value goes from $100\%$ to $0\%$, but in contrast to the linear version, it follows a sigmoid-shape curve.

  Figure 4 shows the tested $\epsilon$-functions by the progress of the simulation (in proportion of scheduled episodes).

Fig. 4

$\epsilon$ functions tested in $\epsilon$ strategies

3.2 Disassembly optimization algorithm with reinforcement learning

This section will describe a reinforcement learning-based method for disassembly optimization with a built-in heuristic to determine the following action.

Algorithm 1

Procedure for disassembly line optimization with reinforcement learning

Generally, in reinforcement learning applications, all the feedback arrives in the reward, which means that the agent takes a sequence of actions and will experience whether it works fine or not. In this approach, the agent is not restricted to preserving itself from an easily foreseeable bad action. Instead, it will realize the badness of the actions only afterward by getting the low reward values. Our algorithm implemented a heuristic within the action-choosing process to significantly decrease the potential action space’s size. The principal idea was that all the restrictions we declared in the MIQP formulation could be used to pre-filter possible actions before the agent chooses the final one. Such an approach helps the agent discover only the feasible part of the action space and not waste time exploring irrelevant paths, which significantly speeds up the learning phase.

dlOptRL algorithm requires the following inputs:

• $P_{AND}$ is an $n\times n$ matrix representing the predecessor AND relations of the disassembly problem’s precedence graph, where $n=\vert P\vert$ is the total number of parts to remove. According to the edge types of a precedence graph, the matrix elements have a binary applicable value set. The value of P(i, j) is defined by the type of $e(v_i,v_j)$ as follows: 0 means no direct predecessor AND dependencies between part i and j (represented by $v_i$ and $v_j$ in the precedence graph) during the disassembly process; 1 describes an existing predecessor AND relation between part i and j.

• $P_{OR}$ is an $n\times n$ matrix representing the predecessor OR relations of the disassembly problem’s precedence graph similar to $P_{AND}$ construction.

• ${\textbf{t}}$ is an n-length vector that describes part removal times

• ${\textbf{h}}$ is an n-length binary vector that indicates hazardousness of each component

• ${\textbf{d}}$ is an n-length vector that determines the demand values of parts

• c is a constant that describes cycle-time

• ${\textbf{o}}$ is a 3-length vector that contains the objective components’ weights

After entering into an outer loop that iterates the episodes, we should initialize some technical variables (counters and pointers), and an inner loop is started that represents a single episode. We should first determine the applicable steps by considering the current disassembly status. Then a decision should be made about how will be determined the next action. The agent will try to follow the known best option that will be successful in the case of a double condition will be met, namely:

• we are on a known track, and hence at least one applicable step is known, and

• the generated standard uniform random number is over the uniformly decreasing threshold

If both the conditions above are satisfied, we will exploit our cumulative knowledge and the optimal action will be chosen that will result in the highest reward for it. Otherwise, the next action will be chosen randomly out of the applicable actions. The chosen action will be registered into the short-term episode history.

After the episode ends, we will retrieve the reward. Then, we need to check whether the visited state-action pairs are already registered in the long-term Q-table. If an appropriate row is available in the Q-table, then the discounted reward value will be compared to the one stored in the Q-table. If we realize that the newly experienced path provides a greater reward than the known best one, it needs to be updated. This is also a minor modification to the original Q-learning method, where the Q-table rows contain the average reward values. For a deterministic disassembly problem, we can use a MAX aggregation function and let the agent immediately learn whenever a new best route is visited. Finally, if the observed state-action pair is not listed yet in the Q-table, then we should add it to the table.

3.3 Formulating dlOptRL algorithm as a HARL method

Since finding an optimal solution by using RL methods can be very time-consuming, in recent years many researchers made efforts to speed up the learning process by improving the action selection method (Bianchi et al. 2012). There are successful references for extracting domain knowledge by integrating special heuristics into an RL method (Cheng et al. 2021). It was shown (Bianchi et al. 2015) that the value function can be mathematically combined with a heuristic function if $\left[ F_t(s_t, a_t) \bowtie \xi H_t(s_t, a_t)^\beta \right]$, where $\mathcal {F}:\mathcal {S}\times \mathcal {A}\rightarrow {\mathbb {R}}$ is an estimate of a value function, while $\mathcal {H}:\mathcal {S}\times \mathcal {A}\rightarrow {\mathbb {R}}$ is the heuristic function. It can be easily seen that a sufficiently large negative $\xi$ value can practically avoid selecting inappropriate actions. Regarding dlOptRL algorithm, the heuristic function can be defined as 0 when the component is disassembled according to the precedence graph and $-\Omega$ otherwise, where $\Omega$ is larger than the theoretical maximum objective value of the concrete disassembly problem.

4 Application examples

There are several benchmark problems analyzed in the literature. In this section, we will present two of them and summarise the performance of our reinforcement learning-based solution by comparing them to classical methods. Then we will highlight the main advantages of RL-based optimizations on further problems.

4.1 Small scale benchmark problem–personal computer disassembly

There is a small-scale problem in the literature (Tuncel et al. 2014; Lambert and Gupta 2004) regarding disassembling personal computers. There are identified 8 salvageable components of a PC. The parts themselves, their removal times, demand values, and hazardousness indicators are collected in Table 3.

Table 3 Personal computer disassembly tasks and parameters

A precedence graph describes the logical dependencies of the disassembly task’s order in Fig. 5.

Fig. 5

Precedence graph of personal computer disassembly problem

By choosing a combined objective function of $F=\frac{1}{w_1F_1+w_2F_2+w_3F3}$, where the components are the same as defined in Sect. 2.2, the optimal global solution can be determined by using a MIQP solver. We want to highlight that the weights allow for prioritizing the objective components to align with the user’s needs. Therefore, the concrete weighting values are less important from a scientific perspective, and hence the researchers often set them equally. Although there are multiple reasons not to follow this, to let the results compare, we also applied equal weights in this use case. The published global optimum to remove the components is presented in Table 4.

Table 4 Optimal solution for personal computer disassembly problem

First, by solving the MIQP problem, we found that the optimal objective value is $F_{opt}=(3^2+2^2+4^2+2^2)+7+19025=19065$. Now we can evaluate the result of dlOptRL by comparing it to the known optimal objective as a reference value.

As a first approach, we implemented a simple Q-learning-based algorithm controlled purely by the reward function and has only a single restriction to choosing the upcoming part for removal. Every component needs to be selected exactly once in the disassembly sequence. We realized that this approach practically results in very low efficiency, like testing a random permutation of the parts whether it meets the criterion of the precedence graph or not.

This kind of experience motivated us to integrate the constraints (that were collected at MIQP formulation) into the next action determination step by restricting the set of potential actions only to the applicable ones, which is practically the intersection of three sets:

• parts that are not removed yet,

• parts of which all AND type predecessor parts are already removed,

• parts of which at least one OR type predecessor part is removed.

Such a limitation of action space indicates a significant change in the learning speed: the agent found the optimal solution after very few steps in our small-scale use case.

4.2 Mid scale benchmark problem–cell phone disassembly

Another case study problem is about disassembling cell phones. There are identified 25 salvageable components of a cell phone. The parts themselves, their removal times, the demand values, and hazardousness indicators are collected in Table 5.

Table 5 Cell phone disassembly tasks and parameters

A precedence graph describes the logical dependencies of the disassembly order in Fig. 6. This drives to a less trivial solution than in the previous use case (Tuncel et al. 2014). This led us to highlight our new formulation that works with significantly smaller decision variable vector size as it was described in Sect. 2.3.

Fig. 6

Precedence graph of cell phone disassembly problem

The degraded MIQP problem solution is presented in Table 6. In this case, the optimal objective value is: $F_{opt}=15+75+815=905$. The pure Q-learning algorithm could not deliver a feasible solution without limiting the action space to the applicable actions. In contrast, the dlOptRL algorithm provides a feasible solution from the very first episode. Of course, this fact does not mean that the early solutions are efficient enough. By performing multiple simulations, we found that the dlOptRL algorithm could find a reasonably good approximation for the optimal solution. As we described in Sect. 3.1, we tested four different static $\epsilon$-strategies for the RL agent’s decision. Figure 7 shows the learning performance results by following the different approaches.

Fig. 7

Learning performance of the tested $\epsilon$-strategies

For easier interpretation, the weighted total objective values are plotted instead of the cumulative rewards. Although the continuous $\epsilon$-Greedy approach presents the best performance with the lowest objective values in the first phase of the simulation, it reaches the worst solution at the end of the simulation. The other methods start with a high $\epsilon$-value to discover the search space more intensively. The linearly decreasing $\epsilon$ approach gets the best overall objective value, and hence we will use that one further. Another advantage is that it does not need a custom parameter for its operation, which simplifies the dlOptRL algorithm.

Fig. 8

Objective values (reciprocal reward values) by iterations

In contrast to the small-scale use case presented in Sect. 4.1, the dlOptRL algorithm does not reach the global optimal solution of the mid-scale benchmark problem. We executed 100 identically parameterized simulations to provide cross-validated results. Figure 8 shows the empirical results by presenting:

• the range of the observed objectives,

• 50-episode moving averages of median objectives,

• 50-episode moving averages of upper/lower quartiles of objectives,

• best objective of learned routes by episodes.

Although the global optimum was not found, all the simulations show a stable convergence in objective values. The median value of the objectives is 985, which is 8.8% worse than the global optimum. The best solution of dlOptRL method has an objective of 917, and it is presented in Table 7 in detail. A widely used indicator comparing two sequences is the concordance ratio. It is calculated by counting all of the item pairs that are in the same order in both sequences and dividing by the total number of item pairs. Out of the $\left( {\begin{array}{c}25\\ 2\end{array}}\right) =300$ different item pairs 293 have concordant orders and 7 have discordant orders, and hence the concordance ratio is 97.67%. So the RL solution delivered a strongly similar solution to the optimal one. As the multiple steps of the best objective curve show, the learning process is continuous. There is a significant difference between the moving average values and the known best reward value, which highlights the “cost-of-learning”: if we decide to explore an unknown path instead of the known best one, it will cause some loss in the overall performance, but it leaves open the chance to find a better path than the current best one.

Table 6 Optimal solution for cell phone disassembly problem

Table 7 Best RL solution for cell phone disassembly problem

4.3 Comparison of RL-based solution to the mixed-integer solution and further research directions

In this section, we will summarize the major experiences of the two described solution methods for disassembly line balancing problems, and further research directions, which can have significant potential to improve the solution’s robustness and adaptivity.

As the disassembly line balancing problem is NP-hard (Chand and Ravi 2023), it cannot be guaranteed, that an optimal solution will be found in polynomial calculation time. In our formulation, the number of decision variables in the MIQP problem is quadratic to the number of components. We validated the formulation on the small-size PC disassembly problem, and the MIQP solver provided the optimal solution within a second. However, for the mid-size cell phone disassembly problem the MIQP solver processed 983,557 branches in 3,600 s. The first feasible solution was found after 539,992 iterations. In contrast, the RL-based solution reached a complete Q-table in 2 s for the small size problem. Furthermore, it performed 10,000 episodes of the mid-size problem in 382 s, and it grew a Q-table with 8,845 rows. Table 8 summarizes the key performance measures of the simulations.

Table 8 Summary of use case solutions

The difference between the two solutions is that the MIQP solver requires a preliminary training process, while the RL-based solution learns online. As our MIQP formulation shows the component removal times, the hazardous indicators, the demands, the cycle time and the objective component weights are all necessary to start the MIQP solver. In practice, it is often easier to set up an empirical reward function by measuring idle times and component removal orders and then letting the RL agent start learning. Furthermore, it is a complex task to implement an efficient MIQP solver, and costly to buy one, while our RL solution is easy to implement. In case of having multiple identical disassembly lines or if there is a virtual twin of it, the RL learning process is easy to parallel. Our results show that the RL agent reliably converges to the optimal solution. The dlOptRL algorithm delivers feasible solutions from the beginning and finds a competitive disassembly setup within a reasonable training time limit.

We identified further research directions, which can have significant potential to improve the solution’s robustness and adaptivity.

• The dlOptRL algorithm can be extended to a multi-agent approach for parallelizing the learning process by updating a central Q-table.

• A new indicator for measuring the proportion of undiscovered routes (actions) would be worth introducing, and an adaptive episode length determination process could help to approach better the global optimum.

• Disassembly components’ removal times have higher uncertainty than assembly process times because the condition of a used product is more heterogeneous than a uniform new one. This implies applying stochastic removal times instead of deterministic ones.

• Using a moving time window or resetting the Q-table periodically can raise the adaptivity of the RL solution.

• The RL-based solution is less sensitive to measurement inconsistencies and one-time issues. Therefore, even if these observations are involved in the Q-value aggregations, their effects will be marginal in the long term.

• By measuring the rewards directly, the cumulative measurement errors can decrease compared to an MIQP formulation, where the errors will be accumulated.

We want to analyze the RL-based solution’s behavior in the above contexts in the next phase of our ongoing research to verify them. We also recommend such analysis for other researchers in the disassembly domain.

5 Summary and conclusions

Disassembly line optimization problems become more important, leading researchers to pay more attention to developing dedicated solutions. The optimization challenges have many problem formulations, objectives, and restrictions, and a wide range of problem sizes. We presented a compact formulation for the disassembly optimization problem that requires fewer decision variables to solve larger problems with the same solver limitations.

We showed that the standard approach of reinforcement learning application when only the reward function must be declared, has a low convergence rate in the learning path. We described a Q-learning-based solution with an integrated heuristic named dlOptRL algorithm that lets the reinforcement learning agent learn the solution very effectively. We demonstrated the learning capability of our algorithm in two selected use cases that proved the real-life applicability of our approach.

We believe that the presented solution shows a possible way to fine-tune reinforcement learning algorithms to increase their learning performance for disassembly problems and other fields.

Furthermore, we have shown that our algorithm formally belongs to the Heuristically Accelerated Reinforcement Learning class. It delivers a working example of translating an MIQP problem into a heuristic function.

Our algorithm has further potential for adapting to slowly changing disassembly environments or completely stochastic problems. The presented method can be used for other problem classes that need ordering complex actions into a sequence, such as the Travelling Salesman Problem (TSP), network/map discovery, or Vehicle Routing Problem (VRP), especially in stochastic cases when the state space is mixed continuous-discrete.