Abstract
This paper examines entry deterrence and signaling when an incumbent firm experiences capacity constraints. Our results show that if the costs that constrained and unconstrained incumbents incur when expanding their facilities are substantially different, separating equilibria can be supported under large parameter values whereby information is perfectly transmitted to the entrant. If, in contrast, both types of incumbent face similar expansion costs, subsidies that reduce expansion costs can help move the industry from a pooling to a separating equilibrium with associated efficient entry. Nonetheless, our results demonstrate that if subsidies are very generous entry patterns remain unaffected, suggesting a potential disadvantage of policies that significantly reduce firms’ expansion costs.



Similar content being viewed by others
Notes
As documented for each of these industries by the U.S. Energy Information Administration, BioPlan Associates Inc. in a survey among European and U.S. firms, and the University of Denver’s Intermodal Transportation Institute, respectively.
In addition, both the separating and pooling equilibria survive standard equilibrium refinements in signaling games, i.e., the Cho and Kreps’ (1987) Intuitive Criterion, under relatively general parameter conditions.
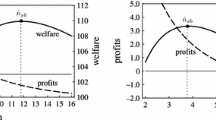
Our results depend on the severity of the capacity constraint. In particular, when capacity constraints are not severe, no type of incumbent significantly benefits from breaking her capacity constraint. In this case, a policy reducing financial costs would only switch the particular pooling equilibrium being played, namely, from one where no type of incumbent expands to one where both firms expand. Hence, under weak capacity constraints our paper suggests that a policy reducing both firms’ financial costs is futile, since it does not modify the entry patterns that arise in the pooling equilibria of the game.
Bloomberg, for instance, reported a 5.5 % increase in sales among U.S. retailers (see Bloomberg.com on December 28th, 2010), while the Wall Street Journal recorded a 4.2 % sales increase among chain-stores (December 21st, 2010), relative to the same period in 2009.
Arvan (1986) considers an incomplete information version of Dixit’s (1980) model but focuses on type-dependent strategy profiles, unlike our paper that examines both type-dependent and type-independent strategy profiles. In addition, our model allows for capacity constraints to originate from both the incumbent’s efficiency level and market demand.
In an extension to Milgrom and Roberts’ (1982), Harrington (1986) allows for the possibility that the entrant is uncertain about his own costs after entry. Interestingly, this article shows that when the costs of the entrant and the incumbent are sufficiently positively correlated then Milgrom and Roberts’ (1982) results are reversed. That is, the incumbent’s production is below the simple monopoly output in order to strategically deter entry. Our model is different from Harrington (1986) because in our setting both firms know each other’s costs, but the entrant is uninformed about the incumbent’s capacity constraint.
Essentially, the constrained incumbent experiences a larger increase in profits from expanding her facility than her unconstrained counterpart if entry is deterred, but may experience a smaller increase if entry follows. As we show in the paper, this result holds even when the constrained incumbent can finance her expansion at a lower cost than the unconstrained incumbent.
Poitevin (1990) also examines an entry-deterrence game, where an incumbent strategically chooses her capital structure in order to signal her production costs to two uninformed audiences: a potential entrant and the financial market. Our paper, in contrast, analyzes an incumbent who uses her expansion decision in order to convey information to a single audience (the potential entrant), but we allow for the incumbent’s capacity constraint to originate from two sources: the incumbent’s low production costs or the high level of market demand, showing similar results in both information contexts.
For compactness, we do not include posterior beliefs about the incumbent’s type being low, i.e., μ(L|Exp)and μ(L|NoExp), since they are already captured by the case in which μ(H|Exp) = 0 and μ(H|NoExp) = 0, respectively.
This information structure resembles that in standard entry-deterrence games, such as Milgrom and Roberts (1982), whereby the incumbent’s costs are unobserved by the potential entrant, but the entrant’s can be anticipated by the incumbent given her experience in the industry.
Expansion costs might be weakly lower for the most efficient incumbent, i.e., K H ≥ K L . Intuitively, this might occur when the incumbent uses a share of previous period profits to finance her expansion decision. We elaborate on this specific case in our discussion of the equilibrium results (Section 5).
Note that if, rather than fixed entry costs, the incumbent faced variable capacity costs, our results would be qualitatively unaffected; see our discussion of the Single-Crossing property in this section.
Note that we use superscript NE in first period profits since the incumbent has not expanded her facility yet. In our description of output and profit decisions during the second period, however, this superscript can either be E or NE to denote that the incumbent expands (does not expand, respectively).
This implies that the unconstrained monopolist does not modify her sales after expanding her facility and, as suggested below, her benefits from expansion arise only if entry is deterred.
At the end of Section 3 we relax this assumption and show that our equilibrium results are not qualitatively affected. In particular, we allow for the capacity constraint to be binding (not binding) under monopoly (duopoly, respectively). Thus, the capacity constraint will not be as severe as in our current analysis, where it affects the incumbent both under monopoly and duopoly. Note that this assumption can alternatively be interpreted in terms of the efficiency of the low-cost incumbent. Specifically, for a given capacity constraint, a decrease in her marginal cost c L implies that the incumbent finds the capacity constraint limiting under both market structures.
Nonetheless, the above two conditions can be summarized as \( \pi_{{ent,H}}^{{D,NE}} > F > \pi_{{ent,L}}^{{D,NE}} \). In particular, the entrant’s profits satisfy \( \pi_{{ent,H}}^{{D,E}} = \pi_{{ent,H}}^{{D,NE}} \) since the high-cost incumbent is not affected by the capacity constraint —and therefore the expansion decision does not modify her production capacity in the second period— but \( \pi_{{ent,L}}^{{D,NE}} > \pi_{{ent,L}}^{{D,E}} \) given that the entrant’s duopoly profits decrease when the low-cost incumbent eliminates her capacity constraint. Intuitively, the incumbent can fully use her more efficient production process (as if she was committing to a substantial production level in case of entry), further reducing the entrant’s competitiveness.
Note that the profit loss from entry for the high-cost incumbent when she expands, \( PLE_H^E = \pi_{{inc,H}}^{{M,E}} - \pi_{{inc,H}}^{{D,E}} \), coincides with that when he does not, \( PLE_H^{{NE}} = \pi_{{inc,H}}^{{M,NE}} - \pi_{{inc,H}}^{{D,NE}} \), since \( \pi_{{inc,H}}^{{M,E}} = \pi_{{inc,H}}^{{M,NE}} \) under monopoly and \( \pi_{{inc,H}}^{{D,E}} = \pi_{{inc,H}}^{{D,NE}} \) under duopoly.
Note that \( PLE_L^{{NE}} = {{{5}} \left/ {{{36}}} \right.} - {{{1}} \left/ {{{12}}} \right.} = {{{1}} \left/ {{{18}}} \right.} \) for the low-cost incumbent, and that \( PLE_H^E = PLE_H^{{NE}} = {{4} \left/ {{25}} \right.} - {{{16}} \left/ {{225}} \right.} = {{4} \left/ {{48}} \right.} \) for the high-cost incumbent.
Note that \( \pi_{{inc,L}}^{{D,E}} > \pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right) \) is a sufficient condition whereas \( \pi_{{inc,L}}^{{D,E}} - \pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right) > \pi_{{inc,H}}^{{D,E}} - \pi_{{inc,H}}^{{M,E}} \) is a necessary condition for the single-crossing property to hold. Hence, if \( \pi_{{inc,L}}^{{D,E}} > \pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right) \) is not satisfied, condition \( \pi_{{inc,L}}^{{D,E}} - \pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right) > \pi_{{inc,H}}^{{D,E}} - \pi_{{inc,H}}^{{M,E}} \) can still hold if, for instance, the profit loss due to entry for the high-cost incumbent, \( PLE_H^E \), is relatively large.
A similar argument would also be valid if the incumbent’s efficiency, rather than being drawn from only from two levels, high and low, was drawn from a continuum of expansion investments. In general, when expansion is followed by entry, the low-cost incumbent does not necessarily obtain a larger benefit from marginally increasing her investment in comparison to a high-cost incumbent.
Recall that the entrant obtains zero profits on the alternative perfectly competitive market where information is readily available to any potential entrants.
The expressions for p NE and p E are obtained by solving for p in these indifference conditions. They are both included in the proof of Lemma 1 in the appendix. We show that p E, p NE ∊ [0, 1], and that these expressions satisfy p E > p NEunder all parameter values.
Under complete information, the high-cost incumbent does not expand since entry ensues and such an expansion does not bring any direct benefit. Hence, in such an information context the low (high)-cost incumbent expands (does not expand) if K L < BCC L and for any K H > 0.
Note that if incumbent and entrant’s costs were correlated, the incumbent’s expansion decision could signal that not only the incumbent’s costs are low, but that the entrant’s are also low, attracting this firm to enter the market, thus ultimately reducing the incentives of the incumbent to expand.
This implies that \( BC{{C}_L} < PLE_L^{{NE}} \) when the incumbent is not very efficient (c L is relatively high), but \( BC{{C}_L} > PLE_L^{{NE}} \) when her efficiency increases (c L is relatively low).
Note that the figure depicts the case where \( PLE_H^E > PLE_L^{{NE}} \). An analogous figure can be constructed otherwise.
In addition, Appendix 2 shows that, under relatively general conditions, a semiseparating equilibrium can be sustained, whereby one or both types of incumbent randomize their expansion decision.
Appendix 1 shows that the pooling equilibrium described in Proposition 2b violates the Cho and Kreps’ (1987) Intuitive Criterion for all expansion costs lower than the benefits that the low-cost incumbent obtains from breaking her capacity constraint and protecting the market, i.e., \( {{K}_L} < BC{{C}_L} + PLE_L^E \)
Note that from our above discussion, only the profit loss from entry is reduced. In particular, \( PLE_L^{{NE}} \) decreases, but cutoffs \( BC{{C}_L},{ }PLE_H^{{NE}}{\text{ and }}PLE_K^E \) are unaffected.
Similarly as in our previous model, each capacity constraint \( \overline q \) can be interpreted as a maximum production level that the high-demand incumbent cannot exceed, but also as an increase in the incumbent’s marginal costs of production when her output exceeds \( \overline q \), as in Dixit (1980).
For simplicity, the figure considers p < p NE as in Fig. 1. Analogous figures can be applied to different prior probabilities.
One example of this type of policies is, for instance, the subsidy programs of several European countries (such as Germany and Spain) that reduce the production cost of firms installing solar cell panels; as documented in The Economist (2010), on December 9th 2010.
However, note that in order to guarantee that the entrant stays out of the market where the efficient incumbent operates the above policy might have to be accompanied by an increase in the administrative costs of entry, F.
Graphically, this implies that cutoff \( BC{{C}_L} - PLE_L^E \) would cross cutoff \( PLE_H^E \) above the main diagonal K H = K L in Fig. 3.
Both separating and pooling equilibria might still emerge in this context, since when expansion is followed by entry, the constrained incumbent does not necessarily obtain a larger benefit from marginally increasing her investment than the unconstrained incumbent does, as suggested in our discussion of the single-crossing property.
References
Albaek S, Overgaard PB (1994) Advertising and pricing to deter or accommodate entry when demand is unknown: Comment. Int J Ind Organ 12:83–87
Arvan L (1986) Sunk capacity costs, long-run fixed costs, and entry deterrence under complete and incomplete information. RAND J Econ 17:105–1211
Bagwell K, Ramey G (1990) Advertising and pricing to deter or accommodate entry when demand is unknown. Int J Ind Organ 8:93–113
Cho I, Kreps D (1987) Signaling games and stable equilibrium. Q J Econ 102:179–222
Dixit A (1979) A model of duopoly suggesting a theory of entry barriers. Bell J Econ 10(1):20–32
Dixit A (1980) The role of investment in entry-deterrence. Econ J 90:95–106
Espinola-Arredondo A, Gal-Or E, Munoz-Garcia F (2011) When should a firm expand its business? the signaling implications of business expansion. Int J Ind Organ 29:729–745
Formby, J, Smith WJ (1984) Collusion, entry, and market shares. Review of Industrial Organization, pp 15–25
Harrington J (1986) Limit pricing when the entrant is uncertain about its cost function. Econometrica 54:429–437
Mason C, Nowell C (1992) Entry, collusion, and capacity constraints. South Econ J 58(4):1002–1014
Matthews S, Mirmann L (1983) Equilibrium limit pricing: the effects of private information and stochastic demand. Econometrica 51:981–996
Milgrom P, Roberts J (1982) Limit pricing and entry under incomplete information. Econometrica 50:443–466
Poitevin M (1990) Strategic financial signaling. Int J Ind Organ 8:499–518
Ridley D (2008) Herding versus hotelling: market entry with costly information. J Econ Manag Strateg 17:607–631
The Economist (2010) Shining a light. Solar cells are getting cheaper as subsidies subside, December 9th
Ware R (1984) Sunk costs and strategic commitment: a proposed three-stage equilibrium. Econ J 94(374):370–378
Author information
Authors and Affiliations
Corresponding author
Additional information
We would like to especially thank Ana Espinola-Arredondo, Jia Yan, Jill McCluskey and Levan Elbakidze for their insightful comments and suggestions. We also thank participants at the 86th Annual Conference of the Western Economic Association International in San Diego for their useful comments.
Appendices
Technical appendix
1.1 Proof of Lemma 1
We need to show that p NE < p E. Indeed, \( {{p}^{{NE}}} \equiv \frac{{F - \pi_{{ent,L}}^{{D,NE}}}}{{\pi_{{ent,H}}^{{D,NE}} - \pi_{{ent,L}}^{{D,NE}}}} < \frac{{F - \pi_{{ent,L}}^{{D,E}}}}{{\pi_{{ent,H}}^{{D,E}} - \pi_{{ent,L}}^{{D,E}}}} \equiv {{p}^E} \), and solving for the entry cost, F, we obtain
and since \( \pi_{{ent,H}}^{{D,NE}} = \pi_{{ent,H}}^{{D,E}} \)we can reduce the above expression to \( F < \pi_{{ent,H}}^{{D,E}} \), which holds by definition.
1.2 Proof of Propositions 1, 2 and 3
Pooling equilibrium with no expansion
Let us investigate if the strategy profile {NoExp H ,NoExp L } can be supported as a pooling PBE of this signaling game. First, the entrant’s beliefs are μ(H|NExp) = p after observing no expansion (in equilibrium) and μ(H|Exp) = μ ∊ [0,1]after observing expansion (off-the-equilibrium). Given these beliefs after observing no expansion (in equilibrium) the entrant enters if and only if
where the right-hand side represents the entrant’s profits from staying in the perfectly competitive market (with zero profits). Solving for p, we obtain that the entrant enters if \( p \geqslant \frac{{F - \pi_{{ent,L}}^{{D,NE}}}}{{\pi_{{ent,H}}^{{D,NE}} - \pi_{{ent,L}}^{{D,NE}}}} \equiv {{p}^{{NE}}} \). Note that this cutoff is positive and smaller than one, 1 > p NE > 0, since entry costs, F, satisfy \( \pi_{{ent,H}}^{{D,NE}} > F > \pi_{{ent,L}}^{{D,NE}} \) by definition. Hence, after observing no expansion (in equilibrium) the entrant enters the market if p ≥ p NEand stays out otherwise. Similarly, after observing expansion (off-the-equilibrium), the entrant enters if and only if
Solving for μ, we find that the entrant enters if \( \mu \geqslant \frac{{F - \pi_{{ent,L}}^{{D,E}}}}{{\pi_{{ent,H}}^{{D,E}} - \pi_{{ent,L}}^{{D,E}}}} \equiv {{p}^E} \). Note that this cutoff is positive and smaller than one, 1 > p NE > 0, since \( \pi_{{ent,H}}^{{D,E}} > F > \pi_{{ent,L}}^{{D,E}} \) is satisfied by definition. Indeed, \( \pi_{{ent,H}}^{{D,NE}} = \pi_{{ent,H}}^{{D,E}} > F > \pi_{{ent,L}}^{{D,NE}} > \pi_{{ent,L}}^{{D,E}} \) given that the entrant’s profits are not affected by the (unconstrained) high-cost incumbent decision to expand, \( \pi_{{ent,H}}^{{D,NE}} = \pi_{{ent,H}}^{{D,E}} \), and the entrant’s profits are higher when the low-cost incumbent does not expand than when she does, \( \pi_{{ent,L}}^{{D,NE}} > \pi_{{ent,L}}^{{D,E}} \). Hence, after observing expansion (off-the-equilibrium) the entrant enters if μ ≥ p E and stays out otherwise. Given the entrant’s strategies let us now analyze the incumbent:
-
If p < p NE and μ ≥ p E then the entrant does not enter after observing no expansion (in equilibrium) but enters otherwise. Hence, the low-cost incumbent prefers not to expand (as prescribed) if and only if \( \matrix{ {\pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right) > \pi_{{inc,L}}^{{D,E}} - {{K}_L},}{\text{or}\;}{{{K}_L} > \pi_{{inc,L}}^{{D,E}} - \pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right)} \\ }<!end array> \), where \( BC{{C}_L} - PLE_L^E \equiv \pi_{{inc,L}}^{{D,E}} - \pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right) \). Similarly, the high-cost incumbent does not expand if \( \matrix{ {\pi_{{inc,H}}^{{M,NE}} > \pi_{{inc,H}}^{{D,E}} - {{K}_H},} \hfill &{\text{or}} \hfill &{{{K}_H} > \pi_{{inc,H}}^{{D,E}} - \pi_{{inc,H}}^{{M,NE}} < 0} \hfill \\ }<!end array> \)is satisfied, which holds for any expansion cost K H > 0. Thus, the strategy profile in which both types of incumbent do not expand their facility can be supported as a pooling PBE in the signaling game if \( {{K}_L} > BC{{C}_L} - PLE_L^E \); as described in Proposition 1, Part 3a.
-
If p < p NE and μ < p E then the entrant does not enter after observing any action from the incumbent. Therefore, the low-cost monopolist prefers not to expand (as prescribed) if and only if \( \matrix{ {\pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right) > \pi_{{inc,L}}^{{M,E}} - {{K}_L},} \hfill &{\text{or}} \hfill &{{{K}_L} > \pi_{{inc,L}}^{{M,E}} - \pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right) \equiv BC{{C}_L}} \hfill \\ }<!end array> \). Similarly, the high-cost incumbent prefers not to expand since \( \matrix{ {\pi_{{inc,H}}^{{M,NE}} > \pi_{{inc,H}}^{{M,E}} - {{K}_H}} \hfill &{\text{or}} \hfill &{{{K}_H} > \pi_{{inc,H}}^{{M,E}} - \pi_{{inc,H}}^{{M,NE}} < 0} \hfill \\ }<!end array> \) which is satisfied for any K H > 0. Thus, this strategy profile can be sustained as a pooling PBE in the signaling game if expansion costs satisfy K L > BCC L ; as described in Proposition 1, Part 3b.
-
If p ≥ p NE and μ < p Ethen the entrant enters after observing no expansion (in equilibrium) but does not enter otherwise. Hence, the low-cost incumbent does not expand (attracting entry) if and only if \( \matrix{ {\pi_{{inc,L}}^{{D,NE}}\left( {\overline q } \right) > \pi_{{inc,L}}^{{M,E}} - {{K}_L},} \hfill &{\text{or}} \hfill &{{{K}_L} > \pi_{{inc,L}}^{{M,E}} - \pi_{{inc,L}}^{{D,NE}}\left( {\overline q } \right) \equiv BC{{C}_L} + PLE_L^{{NE}}} \hfill \\ }<!end array> \). Similarly, the high-cost incumbent does not expand if and only if \( \matrix{ {\pi_{{inc,H}}^{{D,NE}} > \pi_{{inc,H}}^{{M,E}} - {{K}_H}} \hfill &{,{\text{or}}} \hfill &{{{K}_H} > \pi_{{inc,H}}^{{M,E}} - \pi_{{inc,H}}^{{D,NE}} = \pi_{{inc,H}}^{{M,E}} - \pi_{{inc,H}}^{{D,E}} = PLE_H^E} \hfill \\ }<!end array> \), since \( \pi_{{inc,H}}^{{D,E}} = \pi_{{inc,H}}^{{D,NE}} \)given that the high-cost incumbent is unaffected by the capacity constraint. Thus, this strategy profile can be supported as a pooling PBE in the signaling game under expansion costs \( \matrix{ {{{K}_L} > BC{{C}_H} + PLE_H^{{NE}}} \hfill &{\text{and}} \hfill &{{{K}_H} > PLE_L^E} \hfill \\ }<!end array> \); as described in Proposition 2a, and Proposition 3.
-
If p ≥ p NE and μ ≥ p E then the entrant enters after observing any action from the incumbent. Therefore, the low-cost incumbent does not expand (as prescribed) if and only if \( \matrix{ {\pi_{{inc,L}}^{{D,NE}}\left( {\overline q } \right) > \pi_{{inc,L}}^{{D,E}} - {{K}_L}} \hfill &{,{\text{or}}} \hfill &{{{K}_L} > \pi_{{inc,L}}^{{D,E}} - \pi_{{inc,L}}^{{D,NE}}\left( {\overline q } \right) \equiv BC{{C}_L} + PLE_L^{{NE}} - PLE_L^E} \hfill \\ }<!end array> \). Similarly, the high-cost incumbent does not expand since \( \matrix{ {\pi_{{inc,L}}^{{D,NE}} > \pi_{{inc,L}}^{{D,E}} - {{K}_L},} \hfill &{\text{or}} \hfill &{{{K}_L} > \pi_{{inc,L}}^{{D,E}} - \pi_{{inc,L}}^{{D,NE}} = 0} \hfill \\ }<!end array> \), which holds for any K H >0. Thus, this strategy profile can be supported as a pooling PBE for expansion costs \( {{K}_L} > BC{{C}_L} + PLE_L^{{NE}} - PLE_L^E \) and K H > 0; as described in Proposition 2b, and Proposition 3.
Separating equilibrium
Let us now consider the separating strategy profile where only the low-cost incumbent expands, i.e., {NotExpand H , Expand L }. First, entrant’s updated beliefs becomeμ(H|NExp) = 1 and μ(H|Exp) = 0. Given these beliefs, the entrant enters after observing no expansion since \( \matrix{ {\pi_{{ent,H}}^{{D,E}} - F > 0,} \hfill &{\text{or}} \hfill &{\pi_{{ent,L}}^{{D,NE}} < F} \hfill \\ }<!end array> \),, which satisfies our initial assumptions. On the other hand, after observing expansion the entrant stays out since \( \matrix{ {\pi_{{ent,L}}^{{D,E}} - F < 0,} \hfill &{\text{or}} \hfill &{\pi_{{ent,L}}^{{D,E}} < F} \hfill \\ }<!end array> \), which also holds by definition. Therefore, given the entrant’s responses, the high-cost incumbent does not expand (as prescribed) if and only if \( \matrix{ {\pi_{{inc,H}}^{{D,NE}} > \pi_{{inc,H}}^{{M,E}} - {{K}_H},} \hfill &{\text{or}} \hfill &{{{K}_H} > \pi_{{inc,H}}^{{M,E}} - \pi_{{inc,H}}^{{D,NE}}} \hfill \\ }<!end array> \). Since \( \pi_{{inc,H}}^{{M,E}} - \pi_{{inc,H}}^{{D,NE}} = \pi_{{inc,H}}^{{M,E}} - \pi_{{inc,H}}^{{D,E}} \equiv PLE_H^E \) given that \( \pi_{{inc,H}}^{{D,NE}} = \pi_{{inc,H}}^{{D,E}} \), we can then conclude that the high-cost incumbent does not expand if \( {{K}_H} > PLE_H^E \). By contrast, the low-cost incumbent expands (as prescribed) if and only if \( \matrix{ {\pi_{{inc,L}}^{{D,NE}}\left( {\overline q } \right) < \pi_{{inc,L}}^{{M,E}} - {{K}_L}} \hfill &{\text{or}} \hfill &{{{K}_L} < \pi_{{inc,L}}^{{M,E}} - \pi_{{inc,L}}^{{D,NE}}\left( {\overline q } \right) \equiv BC{{C}_L} + PLE_L^{{NE}}} \hfill \\ }<!end array> \). Thus, this strategy profile can be sustained as a separating PBE for expansion costs \( \matrix{ {{{K}_H} > PLE_H^E} \hfill &{\text{and}} \hfill &{{{K}_L} < BCC_L + PLE_L^{{NE}}} \hfill \\ }<!end array> \); as described in Proposition 1 (Part 1) and Proposition 3.
For completeness, let us check that the opposite separating strategy profile {Exp H , NoExp L } cannot be supported as a PBE of the signaling game. In this case, the entrant’s updated beliefs become μ(H|NExp) = 0 and μ(H|Exp) = 1. Given these beliefs, the entrant enters after observing expansion since \( \pi_{{ent,H}}^{{D,E}} - F > 0\,{\text{or}}\,\pi_{{ent,H}}^{{D,E}} > F \), which holds by definition. However, the entrant does not enter after observing no expansion given that \( \matrix{ {\pi_{{ent,L}}^{{D,NE}} - F < 0,} \hfill &{\text{or}} \hfill &{\pi_{{ent,L}}^{{D,NE}} < F} \hfill \\ }<!end array> \), which is satisfied by definition. Given the entrant’s responses, the low-cost incumbent does not expand (as prescribed) if and only if \( \matrix{ {\pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right) > \pi_{{inc,L}}^{{D,E}} - {{K}_L},} \hfill &{\text{or}} \hfill &{{{K}_L} > \pi_{{inc,L}}^{{D,E}} - \pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right)} \hfill \\ }<!end array> \). On the other hand, the high-cost incumbent expands (as prescribed) if \( \matrix{ {\pi_{{inc,H}}^{{M,NE}} < \pi_{{inc,H}}^{{D,E}} - {{K}_H},} \hfill &{\text{or}} \hfill &{{{K}_H} < \pi_{{inc,H}}^{{D,E}} - \pi_{{inc,H}}^{{M,NE}} = \pi_{{inc,H}}^{{D,E}} - \pi_{{inc,H}}^{{M,E}} < 0} \hfill \\ }<!end array> \) (since \( \pi_{{inc,H}}^{{M,E}} = \pi_{{inc,H}}^{{M,NE}} \)), which cannot hold for any K H > 0. Thus, this strategy profile cannot be supported as a separating PBE of the signaling game.
Pooling equilibrium with expansion
Let us investigate if the pooling strategy profile in which both types of incumbent expand their facility, i.e., {Exp H , Exp L }, can be supported as a PBE of the signaling game. First, the entrant’s beliefs are μ(H|Exp) = p after observing expansion (in equilibrium) and μ(H|NExp) = γ ∊ [0,1] after observing no expansion (off-the-equilibrium). Given these beliefs, after observing expansion, the entrant enters if
Solving for p, we obtain \( p \geqslant \frac{{F - \pi_{{ent,L}}^{{D,E}}}}{{\pi_{{ent,H}}^{{D,E}} - \pi_{{ent,L}}^{{D,E}}}} \equiv {{p}^E} \), where 0 ≤ p E ≤ 1 from our above discussion. Hence, entry ensues after observing expansion if p > p E, but does not otherwise. If, instead, the entrant observes no expansion, she enters if
Solving for γ, we find \( \gamma \geqslant \frac{{F - \pi_{{ent,L}}^{{D,NE}}}}{{\pi_{{ent,H}}^{{D,NE}} - \pi_{{ent,L}}^{{D,NE}}}} \equiv {{p}^{{NE}}} \), where 0 ≤ p NE ≤ 1 holds from our above discussion. Therefore, the entrant enters after observing no expansion if γ ≥ p NE, but does not otherwise. Given the entrant’s strategies let us now examine the incumbent:
-
If p ≥ p E and γ ≥ p NEthen the entrant enters both after observing expansion and no expansion. Therefore, the low-cost incumbent expands (as prescribed) if and only if \( \matrix{ {\pi_{{inc,L}}^{{D,NE}}\left( {\overline q } \right) < \pi_{{inc,L}}^{{D,E}} - {{K}_L},} \hfill &{\text{or}} \hfill &{{{K}_L} < \pi_{{inc,L}}^{{D,E}} - \pi_{{inc,L}}^{{D,NE}}\left( {\overline q } \right)} \hfill \\ }<!end array> \). However, the high-cost incumbent does not expand since \( \matrix{ {\pi_{{inc,H}}^{{D,NE}} > \pi_{{inc,H}}^{{D,E}} - {{K}_H},} \hfill &{\text{or}} \hfill &{{{K}_H} > \pi_{{inc,H}}^{{D,E}} - \pi_{{inc,H}}^{{D,NE}} = 0} \hfill \\ }<!end array> \), which holds for any expansion costs K H > 0. Thus, the strategy profile in which both types of incumbent expand cannot be supported as a pooling PBE of the signaling game.
-
If p ≥ p E but γ < p NEthen the entrant enters after observing expansion (in equilibrium), but does not enter otherwise. Hence, the low-cost incumbent expands (as prescribed) if and only if \( \matrix{ {\pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right) < \pi_{{inc,L}}^{{D,E}} - {{K}_L},} \hfill &{\text{or}} \hfill &{{{K}_L} < \pi_{{inc,L}}^{{D,E}} - \pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right) \equiv BC{{C}_L} - PLE_L^E} \hfill \\ }<!end array> \). By contrast, the high-cost incumbent does not expand since \( \matrix{ {\pi_{{inc,H}}^{{M,NE}} > \pi_{{inc,H}}^{{D,E}} - {{K}_H},} \hfill &{\text{or}} \hfill &{{{K}_H} > \pi_{{inc,H}}^{{D,E}} - \pi_{{inc,H}}^{{M,NE}} < 0} \hfill \\ }<!end array> \), which holds for all expansion costs K H > 0. Therefore, this strategy profile cannot be sustained as a pooling PBE of the signaling game.
-
If p < p E but γ ≥ p NE then the entrant does not enter after observing expansion (in equilibrium), but enters otherwise. Hence, the low-cost incumbent expands (as prescribed) if and only if \( \matrix{ {\pi_{{inc,L}}^{{D,NE}}\left( {\overline q } \right) < \pi_{{inc,L}}^{{M,E}} - {{K}_L},} \hfill &{\text{or}} \hfill &{{{K}_L} < \pi_{{inc,L}}^{{M,E}} - \pi_{{inc,L}}^{{D,NE}}\left( {\overline q } \right)} \hfill \\ }<!end array> \). Since
$$ BC{{C}_L} + PLE_L^{{NE}} = \left( {\pi_{{inc,L}}^{{M,E}} - \pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right)} \right) + \left( {\pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right) - \pi_{{inc,L}}^{{D,NE}}\left( {\overline q } \right)} \right) = \pi_{{inc,L}}^{{M,E}} - \pi_{{inc,L}}^{{D,NE}}\left( {\overline q } \right), $$the low-cost incumbent expands if \( {{K}_L} < BC{{C}_L} + PLE_L^{{NE}} \). Similarly, the high-cost incumbent expands (as prescribed) if and only if \( \matrix{ {\pi_{{inc,H}}^{{D,NE}} < \pi_{{inc,H}}^{{M,E}} - {{K}_H},} \hfill &{\text{or}} \hfill &{{{K}_H} < \pi_{{inc,H}}^{{M,E}} - \pi_{{inc,H}}^{{D,NE}} \equiv PLE_H^{{NE}}} \hfill \\ }<!end array> \), since \( \matrix{ {\pi_{{inc,H}}^{{M,NE}} = \pi_{{inc,H}}^{{M,E}}} \hfill &{\text{and}} \hfill &{\pi_{{inc,H}}^{{D,NE}} = \pi_{{inc,H}}^{{D,E}}} \hfill \\ }<!end array> \) for the unconstrained high-cost incumbent under monopoly and duopoly, respectively. Thus, this strategy profile can be supported as a pooling PBE under expansion costs \( \matrix{ {{{K}_L} < BC{{C}_L} + PLE_L^{{NE}}} \hfill &{\text{and}} \hfill &{{{K}_H} < PLE_H^E} \hfill \\ }<!end array> \); as described in Proposition 1, Part 2.
-
If p < p E and γ < p NE then the entrant does not enter after observing any action from the incumbent. Therefore, the low-cost incumbent expands (as prescribed) if and only if \( \matrix{ {\pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right) < \pi_{{inc,L}}^{{M,E}} - {{K}_L},} \hfill &{\text{or}} \hfill &{{{K}_L} < \pi_{{inc,L}}^{{M,E}} - \pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right) \equiv BC{{C}_L}} \hfill \\ }<!end array> \). By contrast, the high-cost incumbent does not expand since \( \matrix{ {\pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right) < \pi_{{inc,L}}^{{M,E}} - {{K}_L},} \hfill &{\text{or}} \hfill &{{{K}_L} < \pi_{{inc,L}}^{{M,E}} - \pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right) \equiv BC{{C}_L}} \hfill \\ }<!end array> \), which holds for any expansion cost K H >0. Thus, this strategy profile cannot be sustained as a pooling PBE.
1.3 Proof of Proposition 4
Pooling equilibrium with no expansion
Let us investigate if the pooling strategy profile {NoExp H ,NoExp L } can be supported as a pooling PBE of this signaling game. First, the entrant’s beliefs are μ(H|NExp) = p after observing no expansion (in equilibrium) and μ(H|Exp) = μ ∊ [0,1] after observing expansion (off-the-equilibrium). Given these beliefs after observing no expansion (in equilibrium) the entrant enters if and only if
where the right-hand side represents the entrant’s profits from staying in the perfectly competitive market (with zero profits). Solving for p, we obtain that the entrant enters if \( p \geqslant \frac{{F - \pi_{{ent,L}}^{{D,NE}}}}{{\pi_{{ent,H}}^{{D,NE}} - \pi_{{ent,L}}^{{D,NE}}}} \equiv {{p}^{{NE}}} \). Note that this cutoff is positive and smaller than one, 1 > p NE > 0, since entry costs, F, satisfy \( \pi_{{ent,H}}^{{D,NE}} > F > \pi_{{ent,L}}^{{D,NE}} \) by definition. Hence, after observing no expansion (in equilibrium) the entrant enters the market if p ≥ p NEand stays out otherwise. Similarly, after observing expansion (off-the-equilibrium), the entrant enters if and only if
Solving for μ, we find that the entrant enters if \( \mu \geqslant \frac{{F - \pi_{{ent,L}}^{{D,E}}}}{{\pi_{{ent,H}}^{{D,E}} - \pi_{{ent,L}}^{{D,E}}}} \equiv {{p}^E} \). Note that this cutoff is positive and smaller than one, 1 > p NE > 0, since \( \pi_{{ent,H}}^{{D,E}} > F > \pi_{{ent,L}}^{{D,E}} \) is satisfied by definition. Indeed, \( \pi_{{ent,H}}^{{D,NE}} > \pi_{{ent,H}}^{{D,E}} > F > \pi_{{ent,L}}^{{D,NE}} = \pi_{{ent,L}}^{{D,E}} \) given that the entrant’s profits are not affected by the (unconstrained) low-demand incumbent decision to expand, \( \pi_{{ent,L}}^{{D,NE}} = \pi_{{ent,L}}^{{D,E}} \), and the entrant’s profits are higher when the high-demand incumbent does not expand than when she does, \( \pi_{{ent,H}}^{{D,NE}} > \pi_{{ent,H}}^{{D,E}} \). Hence, after observing expansion (off-the-equilibrium) the entrant enters if μ ≥ p E and stays out otherwise. Finally, note that p NE < p E as it shown in the proof of Proposition 1.
Given the entrant’s strategies let us now analyze the incumbent:
-
If p < p NE and μ ≥ p E then the entrant does not enter after observing no expansion (in equilibrium) but enters otherwise. Hence, the high-demand incumbent prefers not to expand (as prescribed) if and only if \( \matrix{ {\pi_{{inc,H}}^{{M,NE}}\left( {\overline q } \right) > \pi_{{inc,H}}^{{D,E}} - {{K}_H},} \hfill &{\text{or}} \hfill &{{{K}_H} >\pi_{{inc,H}}^{{D,E}} - \pi_{{inc,H}}^{{M,NE}}\left( {\overline q } \right)} \hfill \\ }<!end array> \), where \( BC{{C}_H} - PLE_H^E \equiv \pi_{{inc,H}}^{{D,E}} - \pi_{{inc,H}}^{{M,NE}}\left( {\overline q } \right) \). Similarly, the low-demand incumbent does not expand if \( \matrix{ {\pi_{{inc,L}}^{{M,NE}} > \pi_{{inc,L}}^{{D,E}} - {{K}_L},}{\text{or}}\;{{{K}_L} > \pi_{{inc,L}}^{{D,E}} - \pi_{{inc,L}}^{{M,NE}} < 0} \\ }<!end array> \). is satisfied, which holds for any expansion cost K L > 0. Thus, the strategy profile in which both types of incumbent do not expand their facility can be supported as a pooling PBE if \( {{K}_H} > BC{{C}_H} - PLE_H^E \).
-
If p < p NE and μ < p E then the entrant does not enter after observing any action from the incumbent. Therefore, the high-demand monopolist prefers not to expand (as prescribed) if and only if \( \matrix{ {\pi_{{inc,H}}^{{M,NE}}\left( {\overline q } \right) > \pi_{{inc,H}}^{{M,E}} - {{K}_H},} \hfill &{\text{or}} \hfill &{{{K}_H} > \pi_{{inc,H}}^{{M,E}} - \pi_{{inc,H}}^{{M,NE}}\left( {\overline q } \right) \equiv BC{{C}_H}} \hfill \\ }<!end array> \). Similarly, the low-demand incumbent prefers not to expand since \( \matrix{ {\pi_{{inc,L}}^{{M,NE}} > \pi_{{inc,L}}^{{M,E}} - {{K}_L}} \hfill &{\text{or}} \hfill &{{{K}_L} > \pi_{{inc,L}}^{{M,E}} - \pi_{{inc,L}}^{{M,NE}} < 0} \hfill \\ }<!end array> \) which is satisfied for any K L > 0. Thus, this strategy profile can be sustained as a pooling PBE in the signaling game if expansion costs satisfy \( {{K}_H} > BCC_H \).
-
If p ≥ p NE and μ < p Ethen the entrant enters after observing no expansion (in equilibrium) but does not enter otherwise. Hence, the high-demand incumbent does not expand (attracting entry) if and only if \( \matrix{ {\pi_{{inc,H}}^{{D,NE}}\left( {\overline q } \right) > \pi_{{inc,H}}^{{M,E}} - {{K}_H},} \hfill &{\text{or}} \hfill &{{{K}_H} > \pi_{{inc,H}}^{{M,E}} - \pi_{{inc,H}}^{{D,NE}}\left( {\overline q } \right) \equiv BC{{C}_H} + PLE_H^{{NE}}} \hfill \\ }<!end array> \). Similarly, the low-demand incumbent does not expand if and only if \( \matrix{ {\pi_{{inc,L}}^{{D,NE}} > \pi_{{inc,L}}^{{M,E}} - {{K}_L},} \hfill &{\text{or}} \hfill &{{{K}_L} > \pi_{{inc,L}}^{{M,E}} - \pi_{{inc,L}}^{{D,NE}} = PLE_L^E} \hfill \\ }<!end array> \). Thus, this strategy profile can be supported as a pooling PBE in the signaling game under expansion costs \( \matrix{ {{{K}_H} > BC{{C}_H} + PLE_H^{{NE}}} \hfill &{\text{and}} \hfill &{{{K}_L} > PLE_L^E} \hfill \\ }<!end array> \).
-
If p ≥ p NE and μ ≥ p E then the entrant enters after observing any action from the incumbent. Therefore, the high-demand incumbent does not expand (as prescribed) if and only if \( \matrix{ {\pi_{{inc,H}}^{{D,NE}}\left( {\overline q } \right) > \pi_{{inc,H}}^{{D,E}} - {{K}_H},} \hfill &{\text{or}} \hfill &{{{K}_H} > \pi_{{inc,H}}^{{D,E}} - \pi_{{inc,H}}^{{D,NE}}\left( {\overline q } \right) \equiv BC{{C}_H} + PLE_H^{{NE}} - PLE_H^E} \hfill \\ }<!end array> \). Similarly, the low-demand incumbent does not expand since \( \matrix{ {\pi_{{inc,L}}^{{D,NE}} > \pi_{{inc,L}}^{{D,E}} - {{K}_L},} \hfill &{\text{or}} \hfill &{{{K}_L} > \pi_{{inc,L}}^{{D,E}} - \pi_{{inc,L}}^{{D,NE}} = 0} \hfill \\ }<!end array> \), which holds for any K L >0. Thus, this strategy profile can be supported as a pooling PBE for expansion costs \( {{K}_H} > BC{{C}_H} + PLE_H^{{NE}} - PLE_H^E \) and K L > 0.
Separating equilibrium
Let us now consider the separating strategy profile where only the high-demand incumbent expands, i.e., {Expand H , NotExpand L }. First, entrant’s updated beliefs becomeμ(H|NExp) = 0 and μ(H|Exp) = 1. Given these beliefs, the entrant enters after observing expansion since \( \matrix{ {\pi_{{ent,H}}^{{D,E}} - F > 0,} \hfill &{\text{or}} \hfill &{\pi_{{ent,H}}^{{D,E}} > F} \hfill \\ }<!end array> \). On the other hand, after observing no expansion the entrant stays out since \( \matrix{ {\pi_{{ent,L}}^{{D,NE}} - F < 0,} \hfill &{\text{or}} \hfill &{\pi_{{ent,L}}^{{D,NE}} < F} \hfill \\ }<!end array> \), which also holds by definition. Therefore, given the entrant’s responses, the low-demand incumbent does not expand (as prescribed) if and only if \( \matrix{ {\pi_{{inc,L}}^{{D,NE}} > \pi_{{inc,L}}^{{M,E}} - {{K}_L},} \hfill &{\text{or}} \hfill &{{{K}_L} > \pi_{{inc,L}}^{{M,E}} - \pi_{{inc,L}}^{{D,NE}}} \hfill \\ }<!end array> \). Since \( \pi_{{inc,L}}^{{M,E}} - \pi_{{inc,L}}^{{D,NE}} = \pi_{{inc,L}}^{{M,E}} - \pi_{{inc,L}}^{{D,E}} \equiv PLE_L^E \) given that \( \pi_{{inc,L}}^{{D,NE}} = \pi_{{inc,L}}^{{D,E}} \), we can then conclude that the high-demand incumbent does not expand if \( {{K}_L} > PLE_L^E \). By contrast, the high-demand incumbent expands (as prescribed) if and only if \( \matrix{ {\pi_{{inc,H}}^{{D,NE}}\left( {\overline q } \right) < \pi_{{inc,H}}^{{M,E}} - {{K}_H}} \hfill &{\text{or}} \hfill &{{{K}_H} < \pi_{{inc,H}}^{{M,E}} - \pi_{{inc,H}}^{{D,NE}}\left( {\overline q } \right) \equiv BC{{C}_H} + PLE_H^{{NE}}} \hfill \\ }<!end array> \). Thus, this strategy profile can be sustained as a separating PBE for expansion costs \( \matrix{ {{{K}_L} > PLE_L^E} \hfill &{\text{and}} \hfill &{{{K}_H} < BC{{C}_H} + PLE_H^{{NE}}} \hfill \\ }<!end array> \).
For completeness, let us check that the opposite separating strategy profile {NoExp H , Exp L } cannot be supported as a PBE of the signaling game. In this case, the entrant’s updated beliefs become μ(H|NExp) = 1 and μ(H|Exp) = 0. Given these beliefs, the entrant does not enter after observing expansion since \( \matrix{ {\pi_{{ent,L}}^{{D,E}} - F < 0} \hfill &{\text{or}} \hfill &{\pi_{{ent,L}}^{{D,E}} < F} \hfill \\ }<!end array> \), which holds by definition. However, the entrant enters after observing no expansion given that \( \matrix{ {\pi_{{ent,L}}^{{D,NE}} - F < 0,} \hfill &{\text{or}} \hfill &{\pi_{{ent,L}}^{{D,NE}} < F} \hfill \\ }<!end array> \), which is satisfied by definition. Given the entrant’s responses, the high-demand incumbent does not expand (as prescribed) if and only if \( \matrix{ {\pi_{{inc,H}}^{{M,NE}}\left( {\overline q } \right) > \pi_{{inc,H}}^{{D,E}} - {{K}_H},} \hfill &{\text{or}} \hfill &{{{K}_H} > \pi_{{inc,H}}^{{D,E}} - \pi_{{inc,H}}^{{M,NE}}\left( {\overline q } \right)} \hfill \\ }<!end array> \). On the other hand, the low-demand incumbent expands (as prescribed) if \( \matrix{ {\pi_{{inc,L}}^{{M,NE}} < \pi_{{inc,L}}^{{D,E}} - {{K}_L},} \hfill &{\text{or}} \hfill &{{{K}_L} < \pi_{{inc,L}}^{{D,E}} - \pi_{{inc,L}}^{{M,NE}} = \pi_{{inc,L}}^{{D,E}} - \pi_{{inc,L}}^{{M,E}} < 0} \hfill \\ }<!end array> \) (since \( \pi_{{inc,H}}^{{M,E}} = \pi_{{inc,H}}^{{M,NE}} \)), which cannot hold for any K L > 0. Thus, this strategy profile cannot be supported as a separating PBE of the signaling game.
Pooling equilibrium with expansion
Let us investigate if the pooling strategy profile in which both types of incumbent expand their facility, i.e., {Exp H ,Exp L }, can be supported as a PBE of the signaling game. First, the entrant’s beliefs are μ(H|Exp) = p after observing expansion (in equilibrium) and μ(H|NExp) = γ ∊ [0,1] after observing no expansion (off-the-equilibrium). Given these beliefs, after observing expansion, the entrant enters if
Solving for p, we obtain \( p \geqslant \frac{{F - \pi_{{ent,H}}^{{D,E}}}}{{\pi_{{ent,L}}^{{D,E}} - \pi_{{ent,H}}^{{D,E}}}} \equiv {{p}^E} \), where 0 ≤ p E ≤ 1 from our above discussion. Hence, entry ensues after observing expansion if p ≥ p E, but does not otherwise. If, instead, the entrant observes no expansion, she enters if
Solving for γ, we find \( \gamma \geqslant \frac{{F - \pi_{{ent,H}}^{{D,NE}}}}{{\pi_{{ent,L}}^{{D,NE}} - \pi_{{ent,H}}^{{D,NE}}}} \equiv {{p}^{{NE}}} \), where 0 ≤ p NE ≤ 1holds from our above discussion. Therefore, the entrant enters after observing no expansion if γ ≥ p NE, but does not otherwise. Given the entrant’s strategies let us now examine the incumbent:
-
If p ≥ p E and γ ≥ p NEthen the entrant enters both after observing expansion and no expansion. Therefore, the high-demand incumbent expands (as prescribed) if and only if \( \matrix{ {\pi_{{inc,H}}^{{D,NE}}\left( {\overline q } \right) < \pi_{{inc,H}}^{{D,E}} - {{K}_H},} \hfill &{\text{or}} \hfill &{{{K}_H} < \pi_{{inc,H}}^{{D,E}} - \pi_{{inc,H}}^{{D,NE}}\left( {\overline q } \right)} \hfill \\ }<!end array> \). However, the low-demand incumbent does not expand since \( \matrix{ {\pi_{{inc,H}}^{{D,NE}} > \pi_{{inc,H}}^{{D,E}} - {{K}_H},} \hfill &{\text{or}} \hfill &{{{K}_H} > \pi_{{inc,H}}^{{D,E}} - \pi_{{inc,H}}^{{D,NE}} = 0} \hfill \\ }<!end array> \), which holds for any expansion costs K L > 0. Thus, the strategy profile in which both types of incumbent expand cannot be supported as a pooling PBE of the signaling game.
-
If p ≥ p E but γ < p NE then the entrant enters after observing expansion (in equilibrium), but does not enter otherwise. Hence, the high-demand incumbent expands (as prescribed) if and only if \( \matrix{ {\pi_{{inc,H}}^{{M,NE}}\left( {\overline q } \right) < \pi_{{inc,H}}^{{D,E}} - {{K}_H},} \hfill &{\text{or}} \hfill &{{{K}_H} < \pi_{{inc,H}}^{{D,E}} - \pi_{{inc,H}}^{{M,NE}}\left( {\overline q } \right) \equiv BC{{C}_H} - PLE_H^E} \hfill \\ }<!end array> \). By contrast, the low-demand incumbent does not expand since \( \matrix{ {\pi_{{inc,L}}^{{D,NE}} > \pi_{{inc,L}}^{{D,E}} - {{K}_L},} \hfill &{\text{or}} \hfill &{{{K}_L} > \pi_{{inc,L}}^{{D,E}} - \pi_{{inc,L}}^{{D,NE}} = 0} \hfill \\ }<!end array> \), which holds for all expansion costs K L > 0. Therefore, this strategy profile cannot be sustained as a pooling PBE of the signaling game.
-
If p < p E but γ ≥ p NE then the entrant does not enter after observing expansion (in equilibrium), but enters otherwise. Hence, the high-demand incumbent expands (as prescribed) if and only if \( \matrix{ {\pi_{{inc,H}}^{{D,NE}}\left( {\overline q } \right) < \pi_{{inc,H}}^{{M,E}} - {{K}_H},} \hfill &{\text{or}} \hfill &{{{K}_H} < \pi_{{inc,H}}^{{M,E}} - \pi_{{inc,H}}^{{D,NE}}\left( {\overline q } \right)} \hfill \\ }<!end array> \). Since
$$ BC{{C}_H} + PLE_H^{{NE}} = \left( {\pi_{{inc,H}}^{{M,E}} - \pi_{{inc,H}}^{{M,NE}}\left( {\overline q } \right)} \right) + \left( {\pi_{{inc,H}}^{{M,NE}}\left( {\overline q } \right) - \pi_{{inc,H}}^{{D,NE}}\left( {\overline q } \right)} \right) = \pi_{{inc,H}}^{{M,E}} - \pi_{{inc,H}}^{{D,NE}}\left( {\overline q } \right), $$the high-demand incumbent expands if \( {{K}_H} < BC{{C}_H} + PLE_H^{{NE}} \). Similarly, the low-demand incumbent expands (as prescribed) if and only if \( \matrix{ {\pi_{{inc,L}}^{{D,NE}} < \pi_{{inc,L}}^{{M,E}} - {{K}_L},} \hfill &{\text{or}} \hfill &{{{K}_L} < \pi_{{inc,L}}^{{M,E}} - \pi_{{inc,L}}^{{D,NE}} \equiv PLE_L^{{NE}}} \hfill \\ }<!end array> \), since \( \matrix{ {\pi_{{inc,L}}^{{M,NE}} = \pi_{{inc,L}}^{{M,E}}} \hfill &{\text{and}} \hfill &{\pi_{{inc,L}}^{{D,NE}} = \pi_{{inc,L}}^{{D,E}}} \hfill \\ }<!end array> \) for the unconstrained low-demand incumbent under monopoly and duopoly, respectively. Thus, this strategy profile can be supported as a pooling PBE under expansion costs \( \matrix{ {{{K}_H} < BC{{C}_H} + PLE_H^{{NE}}} \hfill &{\text{and}} \hfill &{{{K}_L} < PLE_L^E} \hfill \\ }<!end array> \).
-
If p < p E and γ < p NE then the entrant does not enter after observing any action from the incumbent. Therefore, the high-demand incumbent expands (as prescribed) if and only if \( \matrix{ {\pi_{{inc,H}}^{{M,NE}}\left( {\overline q } \right) < \pi_{{inc,H}}^{{M,E}} - {{K}_H},}{\text{or}}\;{{{K}_H} < \pi_{{inc,H}}^{{M,E}} - \pi_{{inc,H}}^{{M,NE}}\left( {\overline q } \right) \equiv BC{{C}_H}} \\ }<!end array> \). By contrast, the low-demand incumbent does not expand since \( \matrix{ {\pi_{{inc,L}}^{{M,NE}} > \pi_{{inc,L}}^{{M,E}} - {{K}_L},} \hfill &{\text{or}} \hfill &{{{K}_L} > \pi_{{inc,L}}^{{M,E}} - \pi_{{inc,L}}^{{M,NE}} = 0} \hfill \\ }<!end array> \), which holds for any expansion cost K L > 0. Thus, this strategy profile cannot be sustained as a pooling PBE.
Appendix 1-Equilibrium refinement
Proposition A
All equilibria identified in Propositions 1 and 2 survive the Cho and Kreps’ (1987) Intuitive Criterion, except for:
-
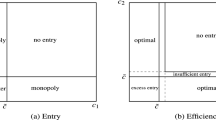
1.
the pooling equilibrium of no expansion followed by [NoEnter NoExp , Enter Exp ] as described in Proposition 1(part 3a), if expansion costs satisfy \( BCC_L > {{K}_L} > BCC_L - PLE_L^E \) and K H > 0;
-
2.
the pooling equilibrium of no expansion followed by [NoEnter NoExp , NoEnter Exp ]as described in Proposition 1(part 3b), if expansion costs satisfy \( \matrix{ {BC{{C}_L} + PLE_L^{{NE}} > {{K}_L} > BC{{C}_L}} \hfill &{and} \hfill &{PLE_H^{{NE}} > {{K}_H} > 0} \hfill \\ }<!end array> \) ;
-
3.
the pooling equilibrium of no expansion followed by [Enter NoExp , Enter Exp ]as described in Proposition 2b, if expansion costs satisfy \( \matrix{ {BC{{C}_L} + PLE_L^{{NE}} > {{K}_L} > BC{{C}_L}} \hfill &{and} \hfill &{PLE_H^{{NE}} > {{K}_H} > 0} \hfill \\ }<!end array> \) ; and if expansion costs satisfy \( \matrix{ {BC{{C}_L} + PLE_L^E > {{K}_L} > BC{{C}_L} + PLE_L^{{NE}} - PLE_L^E} \hfill &{and} \hfill &{{{K}_H} > PLE_H^{{NE}}} \hfill \\ }<!end array> \) .
2.1 Proof
Pooling equilibrium (Proposition 2b)
If the high-cost incumbent deviates towards expansion, the highest payoff she can obtain is \( \pi_{{inc,H}}^{{M,E}} - {{K}_H} \), which strictly exceeds her equilibrium payoff of \( \pi_{{inc,H}}^{{D,NE}} \) if and only if \( \pi_{{inc,H}}^{{M,E}} - \pi_{{inc,H}}^{{D,NE}} > {{K}_H} \), and since \( \pi_{{inc,H}}^{{M,E}} = \pi_{{inc,H}}^{{M,NE}} \) this condition implies \( PLE_H^{{NE}} \equiv \pi_{{inc,H}}^{{M,NE}} - \pi_{{inc,H}}^{{D,NE}} > {{K}_H} \). Hence, considering the equilibrium condition for the high-cost incumbent (K H > 0), she deviates towards expansion if and only if \( PLE_H^{{NE}} > {{K}_H} > 0 \). Similarly, if the low-cost incumbent deviates towards expansion, the highest payoff she can obtain is \( \pi_{{inc,L}}^{{M,E}} - {{K}_L} \), which strictly exceeds her equilibrium payoff of \( \pi_{{inc,L}}^{{D,NE}} \) if and only if \( {{K}_L} < \pi_{{inc,L}}^{{M,E}} - \pi_{{inc,L}}^{{D,NE}}\left( {\overline q } \right) \equiv BC{{C}_L} + PLE_L^E \). Considering the equilibrium condition for the low-cost incumbent (K L > BCC L ), she deviates towards expansion if and only if \( BCC_L + PLE_L^{{NE}} - PLE_L^E < {{K}_L} < BCC_L + PLE_L^E \). Hence, the following cases can arise:
-
If \( \matrix{ {BC{{C}_L} + PLE_L^{{NE}} - PLE_L^E < {{K}_L} < BC{{C}_L} + PLE_L^E} \hfill &{\text{and}} \hfill &{0 < {{K}_H} < PLE_H^{{NE}}} \hfill \\ }<!end array> \) for the low-cost and high-cost incumbent, respectively, then both types of incumbent deviate towards expansion. Then the entrant’s off-the-equilibrium beliefs are updated to μ(H|Exp) = p, where p NE ≤ p < p E, leading the entrant to stay out after observing this expansion. But then both types of incumbent have incentives to deviate towards expansion, and the pooling equilibrium without expansion violates the Intuitive Criterion for all \( \matrix{ {BC{{C}_L} + PLE_L^{{NE}} - PLE_L^E < {{K}_L} < BC{{C}_L} + PLE_L^E} \hfill &{\text{and}} \hfill &{0 < {{K}_H} < PLE_H^{{NE}}} \hfill \\ }<!end array> \)and intermediate priors p NE ≤ p < p E. If, instead, priors are relatively high, p ≥ p E, the entrant enters after observing the deviation towards expansion. Hence, the high-cost incumbent does not deviate since its profit from deviating towards expansion, \( \pi_{{inc,H}}^{{D,E}} - {{K}_H} \), is lower than her equilibrium profit from not expanding, \( \pi_{{inc,H}}^{{D,NE}} \), since \( \pi_{{inc,H}}^{{D,E}} = \pi_{{inc,H}}^{{D,NE}} \). Similarly, the low-cost incumbent does not deviate towards expansion either if her profits from doing so, \( \pi_{{inc,L}}^{{D,E}} - {{K}_L} \), is lower than her equilibrium profit, \( \pi_{{inc,L}}^{{D,NE}}\left( {\overline q } \right) \) or \( {{K}_L} > \pi_{{inc,L}}^{{D,E}} - \pi_{{inc,L}}^{{D,NE}}\left( {\overline q } \right) \equiv BC{{C}_L} + PLE_L^{{NE}} - PLE_L^E \), which holds in this pooling equilibrium. Therefore, no type of incumbent deviates and the pooling equilibrium without expansion of Proposition 2b survives the Intuitive Criterion for all \( \matrix{ {BC{{C}_L} + PLE_L^{{NE}} - PLE_L^E < {{K}_L} < BC{{C}_L} + PLE_L^E} \hfill &{\text{and}} \hfill &{0 < {{K}_H} < PLE_H^{{NE}}} \hfill \\ }<!end array> \) and priors are relatively high, i.e., p ≥ p E.
-
If \( {{K}_H} > PLE_H^{{NE}} \) but \( BCC_L + PLE_L^{{NE}} - PLE_L^E < {{K}_L} < BCC_L + PLE_L^E \), then the high-cost incumbent does not deviate towards expansion, but the low-costs incumbent does deviate. The entrant’s off-the-equilibrium beliefs (after observing a expansion) become μ(H|Exp) = 0, whereas his beliefs after observing no expansion are μ(H|NoExp) = p ∊ [0,1]. Since p > p NE holds in this equilibrium, the entrant does not enter after observing expansion, but enters otherwise, i.e., [NoEnter exp, Enter noexp]. Given this response by the entrant after updating his off-the-equilibrium beliefs, the high-cost incumbent does not deviate towards expansion if \( \matrix{ {\pi_{{inc,H}}^{{D,NE}}\left( {\overline q } \right) > \pi_{{inc,H}}^{{M,E}} - {{K}_H}} \hfill &{\text{or}} \hfill &{{{K}_H} > PLE_H^{{NE}}} \hfill \\ }<!end array> \), which is satisfied in the case we consider. However, the low-cost incumbent deviates towards expansion since \( \pi_{{inc,L}}^{{D,NE}}\left( {\overline q } \right) < \pi_{{inc,L}}^{{M,E}} - {{K}_L} \), or
$$ 0 < {{K}_L} < \pi_{{inc,L}}^{{M,E}} - \pi_{{inc,L}}^{{D,NE}}\left( {\overline q } \right) \equiv BC{{C}_L} + PLE_L^E. $$ -
Considering, in addition, this incumbent’s equilibrium conditions \( \left( {BC{{C}_L} + PLE_L^{{NE}} - PLE_L^E < {{K}_L}} \right) \), the above condition becomes \( BCC_L < {{K}_L} < BCC_L + PLE_L^E \), which indeed holds in the case we consider. As a consequence, the low-cost incumbent deviates towards expansion. Hence, the pooling equilibrium (NoExpH, NoExpL) with (EnterNoExp, EnterExp), as described in Proposition 2b, violates the Intuitive Criterion when expansion costs satisfy\( \matrix{ {{{K}_H} > PLE_H^{{NE}}} \hfill &{\text{and}} \hfill &{BC{{C}_L} + PLE_L^{{NE}} - PLE_L^E < {{K}_L} < BC{{C}_L} + PLE_L^E} \hfill \\ }<!end array> \).
-
If \( \matrix{ {{{K}_L} > BC{{C}_L} + PLE_L^{{NE}}} \hfill &{\text{and}} \hfill &{{{K}_H} > PLE_H^{{NE}}} \hfill \\ }<!end array> \), then no incumbent deviates towards expansion. This implies that the entrant does not update his beliefs and therefore he responds by using the prescribed strategy (EnterEXP, EnterNEXP). Hence, the pooling (NoExpH;NoExpL) with (EnterEXP; EnterNEXP) survives the Intuitive Criterion.
-
If \( \matrix{ {{{K}_L} > BC{{C}_L} + PLE_L^{{NE}}} \hfill &{\text{but}} \hfill &{0 < {{K}_H} < PLE_H^{{NE}}} \hfill \\ }<!end array> \), then the low-cost incumbent does not deviate towards expansion, but the high-cost incumbent does deviate. The entrant’s off-the-equilibrium beliefs become μ(H|Exp) = 1, whereas his beliefs after observing no expansion (in equilibrium) are μ(H|NoExp) = p ∊ [0,1]. Since p > p NE holds in this equilibrium, the entrant enters after observing expansion, and also enters after observing no expansion, i.e., [Enter Exp , Enter NoExp ]. Hence, the entrant’s strategy coincides with that in equilibrium, and therefore both types of incumbent’s equilibrium strategy are unaffected. Thus, this pooling equilibrium survives the Intuitive Criterion under expansion costs \( \matrix{ {{{K}_L} > BC{{C}_L} + PLE_L^{{NE}}} \hfill &{\text{and}} \hfill &{0 < {{K}_H} < PLE_H^{{NE}}} \hfill \\ }<!end array> \).
Pooling equilibrium (Proposition 1, Part 3a)
If the low-cost incumbent deviates towards expansion the highest payoff she can obtain is \( \pi_{{inc,L}}^{{M,E}} - {{K}_L} \), which strictly exceeds her equilibrium payoff of \( \pi_{{inc,L}}^{{M,NE}} \) if and only if \( {{K}_L} < \pi_{{inc,L}}^{{M,E}} - \pi_{{inc,L}}^{{M,NE}} \equiv BCC_L \). Combining this condition with the parameter values under which this equilibrium is supported \( \left( {{{K}_L} > BC{{C}_L} - PLE_L^E} \right) \), we obtain that the low-cost incumbent deviates towards expansion if \( BC{{C}_L} > {{K}_L} > BC{{C}_L} - PLE_L^E \). Similarly, if the high-cost incumbent deviates towards expansion, the highest payoff she can obtain is \( \pi_{{inc,H}}^{{M,E}} - {{K}_H} \), which does not exceed her equilibrium payoff of \( \pi_{{inc,H}}^{{M,NE}} \) since \( \pi_{{inc,H}}^{{M,E}} - {{K}_H} > \pi_{{inc,H}}^{{M,NE}} \) implies \( 0 = \pi_{{inc,H}}^{{M,E}} - \pi_{{inc,H}}^{{M,NE}} > {{K}_H} \). As consequence, the high-cost incumbent does not deviate under any parameter values. The following two cases can hence arise:
-
If \( BC{{C}_L} > {{K}_L} > BC{{C}_L} - PLE_L^E \)only the low-cost incumbent has incentives to deviate towards expansion, which helps the entrant restrict his off-the-equilibrium beliefs to μ(H|Exp) = 0. These beliefs induce no entry after observing expansion (and no entry after expansion either since μ(H|NoExp) = p < p NEin this equilibrium), i.e., [NoEnter NoExp , NoEnter Exp ]. Given this strategy for the entrant, the low-cost incumbent deviates towards expansion since \( \pi_{{inc,L}}^{{M,E}} - {{K}_L} > \pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right) \)given that K L < BCC L holds in this case. By contrast, the high-cost incumbent does not deviate towards expansion since \( \pi_{{inc,H}}^{{M,E}} - {{K}_H} < \pi_{{inc,H}}^{{M,NE}} \)for all K H > 0. Therefore, only the low-cost incumbent deviates towards expansion, and the pooling PBE where (NoExpH, NoExpL) with (NEnterNoExp, EnterExp), as described in Proposition 1, Part 3a, violates the Intuitive Criterion if expansion costs satisfy\( BC{{C}_L} > {{K}_L} > BC{{C}_L} - PLE_L^E \)and K H > 0.
-
If, instead, \( {{K}_L} > BC{{C}_L} > BC{{C}_L} - PLE_L^E \), then no type of incumbent has incentives to deviate towards no expansion. Hence, the entrant’s beliefs are unaffected, his strategy still coincides with that in the pooling equilibrium, i.e., [NEnter NoExp , Enter Exp ], and this pooling equilibrium survives the Intuitive Criterion.
Pooling equilibrium (Proposition 2a)
If the low-cost incumbent deviates towards expansion the highest payoff she can obtain is \( \pi_{{inc,L}}^{{M,E}} - {{K}_L} \), which strictly exceeds her equilibrium payoff of \( \pi_{{inc,L}}^{{D,NE}}\left( {\overline q } \right) \) if and only if \( {{K}_L} < \pi_{{inc,L}}^{{M,E}} - \pi_{{inc,L}}^{{D,NE}}\left( {\overline q } \right) \equiv BC{{C}_L} + PLE_L^{{NE}} \). This inequality, however, contradicts the parameter condition for the low-cost incumbent supporting this pooling PBE. As a consequence, she does not deviate towards expansion. Similarly, if the high-cost incumbent deviates towards expansion, the highest payoff she can obtain is \( \pi_{{inc,H}}^{{M,E}} - {{K}_H} \), which strictly exceeds her equilibrium payoff of \( \pi_{{inc,H}}^{{D,NE}} \) if and only if \( {{K}_H} < \pi_{{inc,H}}^{{M,E}} - \pi_{{inc,H}}^{{D,NE}} \equiv PLE_H^E \). This inequality also contradicts the parameter condition for the high-cost incumbent supporting this pooling PBE. Therefore, she does not deviate towards expansion either. Hence, no type of incumbent has incentives to deviate towards expansion, and the pooling equilibrium (NoExpH, NoExpL) with (ENEXP; NEEXP) survives the Intuitive Criterion.
Pooling equilibrium (Proposition 1b)
If the low-cost incumbent deviates towards expansion the highest payoff she can obtain is \( \pi_{{inc,L}}^{{M,E}} - {{K}_L} \), which strictly exceeds her equilibrium payoff of \( \pi_{{inc,L}}^{{M,NE}} \) if and only if \( {{K}_L} < \pi_{{inc,L}}^{{M,E}} - \pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right) \equiv BC{{C}_L} \). This inequality, however, contradicts the parameter condition for the high-cost incumbent supporting this pooling PBE (K L > BCC L ). As a consequence, she does not deviate towards expansion. Similarly, if the high-cost incumbent deviates towards expansion, the highest payoff she can obtain is \( \pi_{{inc,H}}^{{M,E}} - {{K}_H} \), which does not exceed her equilibrium payoff of \( \pi_{{inc,H}}^{{M,NE}}\left( {\overline q } \right) \)for any K H > 0. Therefore, the high-cost incumbent does not deviate towards expansion either, and the pooling equilibrium (NoExpH, NoExpL) with (NoEntryNEXP; NoEntryEXP) survives the Intuitive Criterion.
Pooling equilibrium (Proposition 1, Part 3b)
If the high-cost incumbent deviates towards no expansion, the highest payoff she can obtain is \( \pi_{{inc,H}}^{{M,NE}} \), which strictly exceeds her equilibrium payoff of \( \pi_{{inc,L}}^{{M,E}} - {{K}_L} \) for any K H > 0, i.e., \( \pi_{{inc,H}}^{{M,NE}} > \pi_{{inc,H}}^{{M,E}} - {{K}_H},{\text{or}}\,{{K}_H} > \pi_{{inc,H}}^{{M,E}} - \pi_{{inc,H}}^{{M,NE}} = 0 \). Considering the equilibrium condition for the high-cost incumbent \( \left( {{{K}_H} < PLE_H^{{NE}}} \right) \), this implies that she deviates towards no expansion if and only if \( 0 < {{K}_H} < PLE_H^{{NE}} \). Regarding the low-cost incumbent, if she deviates towards no expansion the highest payoff she can obtain is \( \pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right) \), which strictly exceeds her equilibrium payoff of \( \pi_{{inc,L}}^{{M,E}} - {{K}_L} \) if and only if \( {{K}_L} > \pi_{{inc,L}}^{{M,E}} - \pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right) \equiv BC{{C}_L} \). Considering the equilibrium condition for the low-cost incumbent \( \left( {{{K}_L} < BC{{C}_L} + PLE_L^{{NE}}} \right) \), she deviates towards no expansion if and only if \( BCC_L < {{K}_L} < BCC_L + PLE_L^{{NE}} \). Hence, the following cases can arise:
-
If \( \matrix{ {BC{{C}_L} < {{K}_L} < BC{{C}_L} + PLE_L^{{NE}}} \hfill &{\text{and}} \hfill &{0 < {{K}_H} < PLE_H^{{NE}}} \hfill \\ }<!end array> \), then both incumbents deviate towards no expansion, and the entrant’s off-the-equilibrium beliefs become μ(H|NoExp) = p, where p < p NE (the pooling equilibrium of Proposition 1, part 3b holds only for relatively low priors). The entrant hence stays out after observing a deviation towards no expansion. Therefore, both types of incumbents have incentives to deviate towards no expansion if \( \matrix{ {\pi_{{inc,H}}^{{M,NE}} > \pi_{{inc,H}}^{{M,E}} - {{K}_H},} \hfill &{\text{or}} \hfill &{{{K}_H} > \pi_{{inc,H}}^{{M,E}} - \pi_{{inc,H}}^{{M,NE}} = 0} \hfill \\ }<!end array> \) for the high-cost incumbent and \( \matrix{ {\pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right) > \pi_{{inc,L}}^{{M,E}} - {{K}_L},} \hfill &{\text{or}} \hfill &{{{K}_L} > \pi_{{inc,L}}^{{M,E}} - \pi_{{inc,L}}^{{M,NE}}\left( {\overline q } \right) \equiv BC{{C}_L}} \hfill \\ }<!end array> \) for the low-cost incumbent. Since both conditions on the expansion costs of the low and high-cost incumbent are satisfied, both types of incumbent deviate towards no expansion, and the pooling equilibrium with expansion of Proposition 1 (part 3b) violates the Intuitive Criterion for all: \( \matrix{ {BC{{C}_L} < {{K}_L} < BC{{C}_L} + PLE_L^{{NE}}} \hfill &{\text{and}} \hfill &{0 < {{K}_H} < PLE_H^{{NE}}} \hfill \\ }<!end array> \).
-
If, instead, \( \matrix{ {{{K}_L} < BC{{C}_L} < BC{{C}_L} + PLE_L^{{NE}}} \hfill &{\text{but}} \hfill &{0 < {{K}_H} < PLE_H^{{NE}}} \hfill \\ }<!end array> \), then the low-cost incumbent does not deviate towards no expansion, while the high-cost incumbent does deviate. The entrant’s off-the-equilibrium beliefs become μ(H|NExp) = 1, whereas his beliefs after observing expansion are μ(H|Exp) = p ∊ [0,1]. Since in this equilibrium priors satisfyp <p E, the entrant stays out after observing expansion but enters after observing no expansion, i.e., (NoEnter Exp ,Enter NExp ). The optimal response by the entrant after updating his beliefs, however, coincides with his response in this pooling equilibrium. As a consequence, the incumbent’s expansion decision is unaffected, and we can conclude that this pooling equilibrium survives the Intuitive Criterion if expansion costs satisfy \( \matrix{ {{{K}_L} < BC{{C}_L} < BC{{C}_L} + PLE_L^{{NE}}} \hfill &{\text{and}} \hfill &{0 < {{K}_H} < PLE_H^{{NE}}} \hfill \\ }<!end array> \).
Appendix 2-Semiseparating equilibria
Proposition B
The following strategy profiles can be supported as semi-separating PBEs of the game:
-
1.
A strategy profile where the incumbent expands her facility when her costs are low, p L = 1, but expands with probability p H ∊ (0,1)when her costs are high, where \( {{p}_H} = \frac{{{{p}^E}}}{{1 - {{p}^E}}}\frac{{1 - p}}{p}. \) In this equilibrium, after observing no expansion the entrant enters, s = 1, and after observing expansion, the entrant enters with probability \( r = 1 - \frac{{{{K}_H}}}{{PLE_H^E}} \) , given beliefs μ(H|NoExp) = 1 and μ(H|Exp) = p E . This equilibrium can be only supported if priors are relatively high, p > p E , and expansion costs satisfy \( 0 < {{K}_H} < \min \left\{ {PLE_H^E,{{K}_H}^1} \right\} \) , where \( \matrix{ {K_H^1 \equiv - \frac{B}{{PLE_L^E}} + \frac{{PLE_H^E}}{{PLE_L^E}}{{K}_L}} \hfill &{and} \hfill &{B \equiv PLE_H^E\left[ {BC{{C}_L} + \left( {PLE_L^{{NE}} - PLE_L^E} \right)} \right]} \hfill \\ }<!end array> \) .
-
2.
A strategy profile where the incumbent expands her facility when her costs are high, p H = 1, but expands with probability p L ∊ (0,1)when her costs are low, where \( {{p}_L} = \frac{p}{{1 - p}}\frac{{1 - {{p}^E}}}{{{{p}^E}}}. \) In this equilibrium, after observing no expansion the entrant stays out, s = 0, and after observing expansion, the entrant enters with probability \( r = 1 - \frac{{{{K}_H}}}{{PLE_H^E}} \) , given beliefs μ(H|NoExp) = 0 and μ(H|Exp) = p E . This equilibrium can be only supported if priors are relatively high, p > p E , and expansion costs satisfy \( {{K}_L} < PLE_L^E \) .
-
3.
A strategy profile where the high-cost incumbent expands with probability \( {{p}_H} = \frac{{{{p}^E}\left( {p - {{p}^{{NE}}}} \right)}}{{\left( {{{p}^E} - {{p}^{{NE}}}} \right)p}} \) ,and the low-cost incumbent expands with probability \( {{p}_L} = \frac{{\left( {1 - {{p}^E}} \right)\left( {p - {{p}^{{NE}}}} \right)}}{{\left( {{{p}^E} - {{p}^{{NE}}}} \right)\left( {1 - p} \right)}} \) , where \( {{p}_H},{{p}_L} \in \left( {0,1} \right) \) After observing expansion (no expansion) the entrant enters with probability r (s, respectively), where
$$ r = \left[ {{{K}_L} - BC{{C}_L} - \frac{{{{K}_H} \times PLE_L^{{NE}}}}{{PLE_H^E}}} \right] \times \frac{1}{{PLE_L^{{NE}} - PLE_L^E}}\,and\, s = \left[ {{{K}_L} - BC{{C}_L} - \frac{{{{K}_H} \times PLE_L^E}}{{PLE_H^E}}} \right] \times \frac{1}{{PLE_L^{{NE}} - PLE_L^E}} $$given beliefs μ(H|NoExp) = p NE and μ(H|Exp) = p E . This equilibrium can be only supported if priors are intermediate, p NE ≥ p > p E , and: (1) expansion costs satisfy \( \matrix{ {0 < {{K}_H} < \frac{C}{{PLE_L^{{NE}}}}} \hfill &{and} \hfill &{0 < {{K}_L} < \frac{{PLE_L^E}}{{PLE_H^E}}{{K}_H} + \frac{B}{{PLE_H^E}}} \hfill \\ }<!end array> \) if \( PLE_L^{{NE}} > PLE_L^E \) ; (2) expansion costs satisfy K H > 0 for all K L ≤ BCC L and \( {{K}_H} > \frac{C}{{PLE_L^E}} \) otherwise if \( PLE_L^{{NE}} \leqslant PLE_L^E \) , where \( \matrix{ {B \equiv PLE_H^E\left[ {BC{{C}_L} + \left( {PLE_L^{{NE}} - PLE_L^E} \right)} \right]} \hfill &{and} \hfill &{C \equiv PLE_H^E\left( {{{K}_L} - BC{{C}_L}} \right)} \hfill \\ }<!end array> \) .
-
4.
A strategy profile where the incumbent does not expand her facility when her costs are high, p H = 0, but expands with probability p L ∊ (0,1)when her costs are low, where \( {{p}_L} = \frac{{{{p}^{{NE}}} - p}}{{{{p}^{{NE}}}\left( {1 - p} \right)}} \) In this equilibrium, after observing expansion the entrant stays out, r = 0, and after observing no expansion the entrant enters with probability \( s = \frac{{BC{{C}_L}}}{{PLE_L^E}} + \frac{{{{K}_L}}}{{PLE_L^E}} \) , given beliefs μ(H|Exp) = 0 and μ(H|NoExp) = p NE . This equilibrium can be only supported if priors are relatively low, p < p NE , and expansion costs satisfy \( PLE_L^E - BC{{C}_L} > {{K}_L} > \frac{{PLE_L^E}}{{PLE_H^E}}{{K}_H} - BC{{C}_L} \) .
-
5.
A strategy profile where the incumbent does not expand her facility when her costs are low, p L = 0, but expands with probability p H ∊ (0,1)when her costs are low, where \( {{p}_H} = \frac{{p - {{p}^{{NE}}}}}{{p\left( {1 - {{p}^{{NE}}}} \right)}} \) In this equilibrium, after observing expansion the entrant enters, r = 0, and after observing no expansion the entrant enters with probability \( s = \frac{{{{K}_H}}}{{PLE_H^E}} \) , given beliefs μ(H|Exp) = 1 and μ(H|NoExp) = p NE . This equilibrium can be only supported for priors, p > p NE , and expansion costs satisfying
$$ PLE_H^E > {{K}_H} > \frac{{PLE_H^E}}{{PLE_L^E}}{{K}_L} + \frac{{BC{{C}_L} \times PLE_H^E}}{{PLE_L^E}} $$
3.1 Proof
p L = 1 and p H ∊ (0,1)
In this equilibrium, the entrant’s beliefs after observing no expansion become μ(H|NoExp) = 1, which leads him to enter since \( \pi_{{ent,H}}^{{D,NE}} > F \). In the case that the entrant observes expansion, he mixes if his beliefs μ(H|Exp) satisfy
and solving for μ(H|Exp), we obtain \( \mu \left( {H|Exp} \right) = \frac{{F - \pi_{{ent,H}}^{{D,E}}}}{{\pi_{{ent,L}}^{{D,E}} - \pi_{{ent,H}}^{{D,E}}}} \equiv {{p}^E} \). We can now use the entrant’s posterior beliefs μ(H|Exp) = p Ein order to find the probability, p H , with which the high-cost incumbent randomizes, by using Bayes’ rule as follows
Solving for p H we obtain \( {{p}_H} = \frac{{{{p}^E}}}{{\left( {1 - {{p}^E}} \right)}} \times \frac{{\left( {1 - p} \right)}}{p} \), where p H ∊ (0,1) for all p E < p. In addition, note that p H is decreasing in p since \( \frac{{\partial {{p}_H}}}{{\partial p}} = \frac{{{{p}^E}}}{{\left( {{{p}^E} - 1} \right) \times {{p}^2}}} < 0 \), starting from \( \mathop{{\lim }}\limits_{{p \to {{p}^E}}} {{p}_H} = 1 \) and converging to \( \mathop{{\lim }}\limits_{{p \to 1}} {{p}_H} = 0 \).
Regarding the incumbent, when her costs are high, she mixes as prescribed, p H ∊ (0,1), if and only if
where r is the probability with which the entrant enters after observing expansion. Solving for r, we obtain \( r = \frac{{\pi_{{inc,H}}^{{M,E}} - \pi_{{inc,H}}^{{D,NE}} - {{K}_H}}}{{\pi_{{inc,H}}^{{M,E}} - \pi_{{inc,H}}^{{D,E}}}} \), and since \( \matrix{ {PLE_H^E = \pi_{{inc,H}}^{{M,E}} - \pi_{{inc,H}}^{{D,E}}} \hfill &{\text{and}} \hfill &{\pi_{{inc,H}}^{{D,E}} = \pi_{{inc,H}}^{{D,NE}}} \hfill \\ }<!end array> \), we can rewrite this probability as \( r = 1 - \frac{{{{K}_H}}}{{PLE_H^E}} \), where r ∊ (0,1) only if expansion costs satisfy \( {{K}_H} < PLE_H^E \). On the other hand, the low-cost incumbent expands as prescribed (p L = 1) if and only if
which implies
Hence, probability r must satisfy \( r > \widehat{r} \)which implies \( {{K}_H} < - \frac{B}{{PLE_L^E}} + \frac{{PLE_H^E}}{{PLE_L^E}}{{K}_L} \equiv {{K}^1}_H \) where\( B \equiv PLE_H^E\left[ {BC{{C}_L} + \left( {PLE_L^{{NE}} - PLE_L^E} \right)} \right] \). Hence, this semiseparating strategy profile can be supported as an equilibrium if expansion costs satisfy \( 0 < {{K}_H} < \min \left\{ {PLE_H^E,{{K}_H}^1} \right\} \) and priors are relatively high, i.e. p > p E.
p H = 1 and p L ∊ (0,1)
In this equilibrium, the entrant’s posterior beliefs after observing no expansion are μ(H|NoExp) = 0, which leads him to stay out since \( \pi_{{ent,L}}^{{D,NE}} < F \). In the case that the entrant observes expansion, he mixes if his beliefs μ(H|Exp) satisfy
and solving for μ(H|Exp), we obtain μ(H|Exp) = p E. Using Bayes’ rule, \( \mu \left( {H|Exp} \right) = {{p}^E} = \frac{p}{{p + \left( {1 - p} \right){{p}_L}}} \) and solving for p L we obtain \( {{p}_L} = \frac{p}{{1 - p}} \times \frac{{1 - {{p}^E}}}{{{{p}^E}}} \), where p L ∊ (0,1) for all p < p E. In addition, p L is increasing in p since \( \frac{{\partial {{p}_L}}}{{\partial p}} = \frac{{1 - {{p}^E}}}{{{{p}^E}{{{\left( {1 - p} \right)}}^2}}} > 0 \), starts at \( \mathop{{\lim }}\limits_{{p \to 0}} {{p}_L} = 0 \)and converges to \( \mathop{{\lim }}\limits_{{p \to {{p}^E}}} {{p}_L} = 1 \).
Regarding the incumbent, when her costs are high, she expands as prescribed (p H = 1) if and only if
solving for r, and using the property that \( \pi_{{inc,H}}^{{M,NE}} = \pi_{{inc,H}}^{{M,E}} \), we find
where cutoff \( \widetilde{r} < 0 \) for all parameter values. On the other hand, the low-cost incumbent randomizes as prescribed, p L ∊ (0,1), if and only if
which implies
where r ∊ (0,1) if \( {{K}_L} < PLE_L^E \). Finally, since cutoff \( \widetilde{r} < 0,r > \widetilde{r} \)under all parameter values. Hence, this semiseparating strategy profile can be supported as an equilibrium if expansion costs satisfy \( {{K}_L} < PLE_L^E \)for low and intermediate priors, i.e., p < p E.
p L , p H ∊ (0,1)
In this equilibrium, after observing an expansion, the entrant is indifferent between entering and not entering the incumbent’s market if and only if his posterior beliefs μ(H|Exp) satisfy
and solving for μ(H|Exp), we obtain \( \mu \left( {H|Exp} \right) = \frac{{F - \pi_{{ent,H}}^{{D,E}}}}{{\pi_{{ent,L}}^{{D,E}} - \pi_{{ent,H}}^{{D,E}}}} \equiv {{p}^E} \). We can then use the entrant’s posterior beliefs μ(H|Exp) = p Ein order to find probability, p H , with which the incumbent randomizes when her costs are high, by using Bayes’ rule, as follows
Solving for p H we obtain \( {{p}_H}\left( {{{p}_L}} \right) = \frac{{{{p}^E} \times {{p}_L} \times \left( {1 - p} \right)}}{{p \times \left( {1 - {{p}^E}} \right)}} \). Similarly, after observing that the incumbent does not expand, the entrant is indifferent between entering and not entering the incumbent’s market if and only if his posterior beliefs μ(H|NoExp) satisfy
and solving for μ(H|NoExp) we obtain \( \mu \left( {H|NoExp} \right) = \frac{{F - \pi_{{ent,L}}^{{D,NE}}}}{{\pi_{{ent,H}}^{{D,NE}} - \pi_{{ent,L}}^{{D,NE}}}} \equiv {{p}^{{NE}}} \). We can hence use the entrant’s posterior beliefs μ(H|NoExp) = p NEin order to find probability, p L , with which the incumbent randomizes when her costs are low, by using Bayes’ rule, as follows
Solving for p L we obtain \( {{p}_L}\left( {{{p}_H}} \right) = \frac{{{{p}^{{NE}}} + \left( {{{p}_H} - 1} \right)p - {{p}_H} \times {{p}^{{NE}}} \times p}}{{{{p}^{{NE}}} \times \left( {1 - p} \right)}} \). Solving for p H and p L simultaneously, we obtain \( \matrix{ {{{p}_L} = \frac{{\left( {1 - {{p}^E}} \right) \times \left( {p - {{p}^{{NE}}}} \right)}}{{\left( {{{p}^E} - {{p}^{{NE}}}} \right) \times \left( {1 - p} \right)}}} \hfill &{\text{and}} \hfill &{{{p}_H} = \frac{{{{p}^E} \times \left( {p - {{p}^{{NE}}}} \right)}}{{\left( {{{p}^E} - {{p}^{{NE}}}} \right) \times p}}} \hfill \\ }<!end array> \). First, note that p L ≥ 0 if and only if p ≥ p NE, given that p E > p NE and p, p E, p NE ∊ (0,1) under all parameter values. In addition, p L < 1 for all p < p E. Therefore, p L ∊ (0,1) if and only if priors are intermediate, i.e., p NE ∊ p < p E. Second, note that p H ≥ 0if and only if p ≥ p NE. Furthermore, p H < 1 for all p < p E. Therefore, p H ∊ (0,1) only if priors are intermediate, i.e., p NE ≤ p < p E. We can therefore conclude that under intermediate priors both types of incumbent randomize their expansion decisions, p H , p L ∊ (0,1), where note that p H ≥ p L for all p < p E, which holds in this regime of intermediate priors. We next show that these probabilities are both increasing in p, since
Finally, note that at the lower bound of p ∊ [p NE, p E), the incumbent’s randomization becomes \( \mathop{{\lim }}\limits_{{p \to {{p}^{{NE}}}}} {{p}_L} = \mathop{{\lim }}\limits_{{p \to {{p}^{{NE}}}}} {{p}_H} = 0 \) whereas at the upper bound, we obtain \( \mathop{{\lim }}\limits_{{p \to {{p}^E}}} {{p}_L} = \mathop{{\lim }}\limits_{{p \to {{p}^E}}} {{p}_H} = 1 \).
Let us now examine the incumbent’s strategy in this equilibrium. If the high-cost incumbent expands with probability p H ∊ (0,1), as prescribed, it must be that the entrant makes her indifferent between expanding and not expanding her facility,
where r and s are the probability with which the entrant enters after observing expansion and no expansion, respectively. Solving for r, we obtain
and since \( \matrix{ {\pi_{{inc,H}}^{{M,E}} = \pi_{{inc,H}}^{{M,NE}}} \hfill &{\text{and}} \hfill &{\pi_{{inc,H}}^{{D,E}} = \pi_{{inc,H}}^{{D,NE}}} \hfill \\ }<!end array> \), the above expression simplifies to \( r(s) = s - \frac{{{{K}_H}}}{{PLE_H^E}} \).
Similarly, when the incumbent’s costs are low, the entrant makes the incumbent indifferent between expanding and not expanding her facility,
Solving for s, we obtain
which simplifies to \( s(r) = \frac{{{{K}_L} - BC{{C}_L}}}{{PLE_L^{{NE}}}} + r\left( {\frac{{PLE_L^E}}{{PLE_L^{{NE}}}}} \right) \). Solving for probabilities s and r simultaneously, we obtain
First, note, that probability s is positive if and only if \( \matrix{ {PLE_L^{{NE}} > PLE_L^E} \hfill &{\text{and}} \hfill &{\frac{{PLE_H^E \times \left( {{{K}_L} - BC{{C}_L}} \right)}}{{PLE_L^E}} > {{K}_H}} \hfill \\ }<!end array> \) hold. Secondly, s < 1 if and only if
Similarly, note that probability r is positive if and only if \( \matrix{ {PLE_L^{{NE}} > PLE_L^E} \hfill &{\text{and}} \hfill &{\frac{{PLE_H^E \times \left( {{{K}_L} - BC{{C}_L}} \right)}}{{PLE_L^{{NE}}}} > {{K}_H}} \hfill \\ }<!end array> \)hold. Finally, note that r < 1 if and only if
Let us first analyze the case in which condition\( PLE_L^{{NE}} > PLE_L^E \)holds. In this case, probabilities r,s ∊ (0,1) if expansion costs satisfy
where
First, note that \( \frac{C}{{PLE_L^E}} > \frac{C}{{PLE_L^{{NE}}}} \)since \( PLE_L^{{NE}} > PLE_L^E \) in the case we consider. Hence \( \frac{C}{{PLE_L^{{NE}}}} > {{K}_H} \) is more restrictive than \( \frac{C}{{PLE_L^E}} > {{K}_H} \). In order to rank expressions\( \matrix{ {\frac{{PLE_H^E}}{{PLE_L^E}} \times {{K}_L} - \frac{B}{{PLE_L^E}}} \hfill &{\text{and}} \hfill &{\frac{{PLE_H^E}}{{PLE_L^{{NE}}}} \times {{K}_L} - \frac{B}{{PLE_L^{{NE}}}}} \hfill \\ }<!end array> \), note that vertical intercepts satisfy \( 0 > \frac{B}{{PLE_L^{{NE}}}} > \frac{B}{{PLE_L^E}} \) and the equation in condition (2) is flatter than that in (1) since \( \frac{{PLE_H^E}}{{PLE_L^E}} > \frac{{PLE_H^E}}{{PLE_L^{{NE}}}} \). Hence, condition (1) is more restrictive than (2). Thus, we only need to use \( {{K}_H} > \frac{{PLE_H^E}}{{PLE_L^E}}{{K}_L} - \frac{B}{{PLE_L^E}} \). Regarding condition \( \frac{C}{{PLE_L^{{NE}}}} > {{K}_H} \), note that it can be expressed as
which is flatter than condition (1) since \( \frac{{PLE_H^E}}{{PLE_L^{{NE}}}} < \frac{{PLE_H^E}}{{PLE_L^E}} \), and the vertical intercept is also smaller (absolute value) than that of condition (1) since \( \matrix{ {BC{{C}_L} \times PLE_H^E < B} \hfill &{\text{and}} \hfill &{PLE_L^{{NE}} < PLE_L^E} \hfill \\ }<!end array> \), as depicted in Fig. 4.
Hence, when condition\( PLE_L^{{NE}} > PLE_L^E \)holds, this semiseparating equilibrium with p H , p L ∊ (0,1) can be supported for intermediate priors p NE ≥ p > p E and expansion costs satisfying
If, by contrast, \( PLE_L^{{NE}} < PLE_L^E \)holds, probabilities r,s∊ (0,1) if expansion costs satisfy
and
From our previous discussion, \( \frac{C}{{PLE_L^E}} > \frac{C}{{PLE_L^{{NE}}}} \). In addition, \( {{K}_H} > \frac{C}{{PLE_L^E}} \) is more restrictive than \( {{K}_H} > \frac{{PLE_H^E}}{{PLE_L^E}}{{K}_L} - \frac{B}{{PLE_L^E}} \) since both expressions have the same slope but the former originates at a higher vertical intercept than the latter since \( BC{{C}_L} \times PLE_H^E < B \). Therefore, when \( PLE_L^{{NE}} < PLE_L^E \)holds this semiseparating equilibrium with p H , p L ∊ (0,1) can be supported for intermediate priors p NE ∊ p > p E and expansion costs satisfying K H > 0 for all K L ≤ BCC L , and \( {{K}_H} > \frac{C}{{PLE_L^E}} \) otherwise.
p H =0 and p L ∊ (0,1)
We now check other semiseparating strategy profiles where either type of incumbent does not expand her facility. Let us first analyze the case where p H =0 and p L ∊ (0,1). In this case, the entrant’s posterior beliefs become μ(H|Exp) = 0 after observing an expansion, which leads him to stay out since \( \pi_{{ent,L}}^{{D,E}} < F \). In the case that the entrant observes no expansion from the incumbent, the entrant mixes if and only if his beliefs μ(H|Exp) satisfy
and solving for μ(H|NoExp), we obtain μ(H|NoExp) = p NE. We can hence use Bayes’ rule to find
Solving for p L we obtain \( {{p}_L} = \frac{{{{p}^{{NE}}} - p}}{{{{p}^{{NE}}}\left( {1 - p} \right)}} \), where p L ∊ (0,1) for low priors, i.e., p < p NE. In addition, p L is decreasing in p since \( \frac{{\partial {{p}_L}}}{{\partial p}} = \frac{{{{p}^{{NE}}} - 1}}{{{{p}^{{NE}}}{{{\left( {1 - p} \right)}}^2}}} < 0 \) starting at \( \mathop{{\lim }}\limits_{{p \to {{p}^{{NE}}}}} {{p}_L} = 0 \)and converging to \( \mathop{{\lim }}\limits_{{p \to 0}} {{p}_L} = 1 \).
Regarding the high-cost incumbent, she does not expand as prescribed, p H = 0, if
Solving for s, we obtain
and since \( \matrix{ {PLE_H^{{NE}} = \pi_{{inc,H}}^{{M,NE}} - \pi_{{inc,H}}^{{D,NE}},} \hfill &{\pi_{{inc,H}}^{{M,NE}} = \pi_{{inc,H}}^{{M,E}}} \hfill &{\text{and}} \hfill &{PLE_H^{{NE}} = PLE_H^E} \hfill \\ }<!end array> \), then this expression reduced to \( s > \frac{{{{K}_H}}}{{PLE_H^E}} \equiv \hat{s} \). On the other hand, the low-cost incumbent mixes as prescribed, p L ∊ (0,1), if and only if
Solving for s, we obtain
and since \( \matrix{ {BC{{C}_L} = \pi_{{inc,L}}^{{M,NE}} - \pi_{{inc,L}}^{{M,E}}} \hfill &{\text{and}} \hfill &{PLE_L^{{NE}} = \pi_{{inc,L}}^{{M,NE}} - \pi_{{inc,L}}^{{D,NE}}} \hfill \\ }<!end array> \), this expression becomes \( s = \frac{{BC{{C}_L}}}{{PLE_L^E}} + \frac{{{{K}_L}}}{{PLE_L^E}} \equiv \widetilde{s} \), where probability cutoff \( \widetilde{s} \)satisfies \( \widetilde{s} \in \left( {0,1} \right) \) if \( {{K}_L} < PLE_L^E - BC{{C}_L} \). Hence, we need \( \widetilde{s} > \widehat{s} \), or \( {{K}_L} > \frac{{PLE_L^E}}{{PLE_H^E}}{{K}_H} - BC{{C}_L} \). Hence, this semiseparating equilibrium can be sustained for relatively low priors, p < p NE, and expansion costs satisfying \( PLE_L^E - BC{{C}_L} > {{K}_L} > \frac{{PLE_L^E}}{{PLE_H^E}}{{K}_H} - BC{{C}_L} \).
p L =0 and p H ∊ (0,1)
Let us finally check the strategy profile where only the high-cost incumbent randomizes and the low-cost incumbent does not expand. In this case, the entrant’s posterior beliefs after observing expansion are μ(H|Exp) = 1, which leads him to enter since \( \pi_{{ent,H}}^{{D,E}} > F \). In the case that the entrant observes no expansion from the incumbent, the entrant mixes if his beliefs μ(H|NoExp) are such that
and solving for μ(H|NoExp), we obtain μ(H|NoExp) = p NE. Using Bayes’ rule we have \( \mu \left( {H|NoExp} \right) = {{p}^{{NE}}} = \frac{{p\left( {1 - {{p}_H}} \right)}}{{p\left( {1 - {{p}_H}} \right) + \left( {1 - p} \right)}} \), and solving for p H we obtain \( {{p}_H} = \frac{{p - {{p}^{{NE}}}}}{{p\left( {1 - {{p}^{{NE}}}} \right)}} \), where p H ∊ (0,1) for all p > p NE. In addition, p H is increasing in p since \( \frac{{\partial {{p}_H}}}{{\partial p}} = \frac{{{{p}^{{NE}}}}}{{\left( {1 - {{p}^{{NE}}}} \right) \times {{p}^2}}} > 0 \), starting at \( \mathop{{\lim }}\limits_{{p \to {{p}^{{NE}}}}} {{p}_H} = 0 \)and converging to \( \mathop{{\lim }}\limits_{{p \to 1}} {{p}_H} = 1 \).
Regarding the low-cost incumbent, she does not expand as prescribed (p L = 0) if and only if
and solving for s, we find \( s > \frac{{BC{{C}_L}}}{{PLE_L^E}} + \frac{{{{K}_L}}}{{PLE_L^E}} \equiv \widetilde{s} \). On the other hand, the high-cost incumbent mixes as prescribed, p H ∊ (0,1), if and only if
Solving for s, we obtain \( s = \frac{{{{K}_H}}}{{PLE_H^E}} \equiv \widehat{s} \), where \( \widehat{s} \in \left( {0,1} \right) \)for all \( {{K}_H} < PLE_H^E \). Hence, we need that \( \matrix{ {\widehat{s} > \widetilde{s},} \hfill &{\text{or}} \hfill &{{{K}_H} > \frac{{PLE_H^E}}{{PLE_L^E}}{{K}_L} + \frac{{BC{{C}_L} \times PLE_H^E}}{{PLE_L^E}}} \hfill \\ }<!end array> \). Hence, this semiseparating strategy profile can be sustained for priors p > p NE and expansion costs satisfying
Rights and permissions
About this article
Cite this article
Munoz-Garcia, F., Zaynutdinova, G. Capacity Constrained Firms and Expansion Subsidies: Should Governments Avoid Generous Subsidies?. J Ind Compet Trade 13, 563–597 (2013). https://doi.org/10.1007/s10842-012-0135-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10842-012-0135-8