Introduction

The great Capricorn beetle, Cerambyx cerdo L. (1758), (Coleoptera, Cerambycidae), is the largest of the European obligate saproxylic (wood-dwelling) insects, and is associated with old, sun-exposed oak trees and other deciduous trees dominating open and semi-open landscapes (e.g., Buse et al. 2007; Albert et al. 2012; Torres-Vila 2017). On the one hand, Cerambyx cerdo is considered an important umbrella species—meaning that by protecting it, many other species are indirectly protected—as well as an ecosystem engineer, which together with the stag beetle Lucanus cervus influences other species by modifying habitats (Buse et al. 2008; Drag and Čižek 2015; Torres-Vila 2017). On the other hand, there are also reports about this beetle’s harmful impact on oak trees, particularly in the context of global warming (Sallé et al. 2014).

Three subspecies of Cerambyx cerdo have been recognized on the basis of geographic distribution and morphological characteristics (Horák et al. 2010). Here, we focus on Cerambyx cerdo cerdo, which is present in most of Europe (western, central, and southern parts), but gradually declines toward the northern and southwestern parts of its range, being absent from Britain and Ireland (Bílý and Mehl 1989; Luce 1997; Buse et al. 2007; Sama 2013). In Poland, since the 1930s, C. cerdo populations have gradually decreased, particularly in the southern and southeastern parts of the country. Adamski et al. (2004) reported only 29 localities in the country. The most abundant populations occur along the Vistula and Odra river basins, but the actual distribution requires new observations to confirm it (Sama 2002; Makomaska-Juchiewicz and Baran 2012). In Poland its census population size was estimated as 1000–10,000 individuals (Starzyk 2004), but its current population size is probably much smaller, mainly due to fragmentation and degradation of habitats (e.g., loss of veteran oaks, deadwood removal), and deaths caused by birds coupled with poor dispersal power and long juvenile stages of the beetle (see also Warren and Key 1991; Geiser 1998; Miklȋn and Čižek 2014; Ceia and Ramos 2016; Torres-Vila 2017. Despite these threats and the fact that this species has been protected since 1952, protection programs have not yet been developed or implemented in Poland (Makomaska-Juchiewicz and Baran 2012).

Based on collected evidence, threatened species show less genetic diversity, and small and declining populations are subjected more frequently to founder events and bottlenecking, resulting in reduced adaptive potential and fitness (Charlesworth et al. 1993; Hedrick 1994; Franklin and Frankham 1998). To increase the beetle populations, conservation actions have been undertaken which involve techniques such as protective legislation, habitat restoration, translocation, and monitoring. Cerambyx cerdo is legally protected under the EU Habitats Directive (Annexes II and IV and Appendix II of the Bern Convention), and it is also included as a globally vulnerable species in the IUCN red list of threatened species (IUCN 2013). Improving habitat quality is another management action occasionally undertaken. This includes creating openings within forests to remove shadows cast from trees and shrubs growing around old oaks, because one of the most important habitat requirements for this species is proper tree insolation (Buse et al. 2007; Stachowiak 2012). Moreover, relocation of individuals is another strategy in C. cerdo conservation. One type of such relocation is supplementation, understood as the release of animals taken from a source population to enhance the survival probability of a recipient population (see also Weeks et al. 2011). However, insects have rarely been considered a conservation target despite the relatively low cost of such an action as compared to actions involving large vertebrates (Fischer and Lindenmayer 2000; Dunn 2005). So far, one successful translocation of C. cerdo was reported by Drag and Čižek (2015). Despite the conservation actions undertaken, the isolation of C. cerdo populations and their small census size make them highly vulnerable to environmental threats.

No information about the genetic makeup of Polish populations of C. cerdo is available, which is necessary to ensure their successful supplementation and further monitoring and evaluation. We collected genetic and field data from one of the best-preserved but isolated populations in the Polish distribution area (hereafter Rogalin) and one of the southernmost populations from the area (hereafter Ispina) to develop an optimal strategy to preserve these populations (see also Stachowiak 2012). The Ispina population, characterized by a small census size, is interesting from a geographical perspective because it is the only population of this species on the right side of the Vistula and is remote from the nearest populations of C. cerdo by 150–287 km.

A population viability analysis (PVA) summarizing genetic data as well as site- and species-specific information was performed to predict the populations’ fate in the context of their genetic makeup and survival. This validation under the theoretical framework of PVA seems to be a necessary step before practical application of population harvesting and supplementation (Reed et al. 2002). Our PVA simulations were restricted to four major parameters that could affect estimates of population growth and extinction risk according to different levels of (1) supplementation, (2) carrying capacity, (3) inbreeding depression (decreased reproductive fitness in inbred individuals; Hedrick and Kalinowski 2000; see also Fox and Scheibly 2006), and (4) mortality rates. Specifically, we aimed to answer the following questions: (1) what is the level of genetic variability and genetic differentiation between analyzed populations and within each of the populations? (2) How long are the populations likely to exist without human intervention and under different levels of supplementation? (3) What is the most important variable affecting projected population persistence? To realize the study’s objectives, we performed a two-step analysis beginning by recognizing demographic features and genetic variation within and between populations and finishing with a PVA risk assessment of extinction and recommendations for conservation and management of the C. cerdo populations.

Materials and methods

Study areas

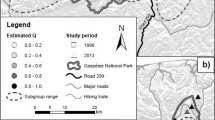
This study focused on two Polish populations of C. cerdo. One population occurs in the western part of the country, in the Warta River floodplain terraces near the small town of Rogalin (Fig. 1, Rogalin). This population, described for the first time by Schumann in 1906, inhabits the Rogalin Landscape Park (RLP), established in 1997, where the largest sanctuary of putatively 1000-year-old English oak trees (Quercus robur L.) occurs in Europe. These monumental ancient oaks, which have a trunk circumference over 2 m, grow as a single trees or small groups. These trees occur on managed, periodically flooded meadows, in a very rare, endangered community of floodplain forest Populetum albae BR.-BL. 1931 on fertile alluvial sandy soils, which are currently rarely flooded, and in a riparian ash-elm forest Ficario-Ulmetum minoris Knapp 1942 em J. Mat 1976 (see also Ratyńska and Wachowiak 2014). These ancient, living trees are often weakened; sometimes their tops die, they suffer bark losses and cavities, and they have some dead, thick branches. No active management actions, such as pollarding, small-branch trimming, mulching, or impregnating the hollows with pesticides, have been undertaken, but the competing low vegetation around the ancient trees has been cleared. Nevertheless, large, decayed branches litter the site. For our research, we collected Cerambyx cerdo specimens from a 210-ha area (out of the total 12,750-ha area of the RLP) at a minimum distance of 70 m from each other (Fig. 1; Table 1).

Fig. 1
figure 1

A Geographical location of samples examined in this study (black). Distribution of Cerambyx cerdo in Poland after Głowaciński and Nowacki (2004), Stachowiak (2012), and a map of Biodiversity (2017), http://baza.biomap.pl/pl/taxon/species-cerambyx_cerdo_cerdo/mapb, modified by MP (grey—actual localities; grey contour—localities presently not confirmed); UPGMA dendrograms on geographic distances between sampling locations coming from UTM coordinates for Rogalin (B) and Ispina (C). (Color figure online)

Full size image
Table 1 Diversity indices of seven microsatellite loci and two populations of Cerambyx cerdo based on data of 62 individuals
Full size table

The second population, which is small and highly isolated, is located on the right side of the Vistula River floodplain near the Ispina village in southern Poland (Starzyk 1973, 1976, 1979, Fig. 1, Ispina). This C. cerdo population, described by Jabłoński in 1869, currently inhabits six groups of oaks and solitary oaks (Quercus robur) scattered on the 7.5-ha area. These old trees occur in the lime-oak-hornbeam forest (i.e., Tilio cordatae-Carpinetum betuli Tracz.1962) at the woodland edge of the transition zone between a freshwater meadow and agricultural land and at the property borders. Three oaks are considered monumental. In the forest, clear cuttings are undertaken every 10–15 years, whereas arable lands are managed, but the current land use does not influence the suitability of oaks as breeding habitats. The minimum distance between our samples was 15 m.

DNA extraction

For DNA sources, we noninvasively collected part of one foreleg from living insects as well as remnants of insects (i.e., insect heads) from a circle on the ground with a radius extending from the tree’s trunk to a point no more than 0.5 m away at a given site. To show geographical distances between sample locations, we built UPGMA dendrograms on distances coming from UTM coordinates with the help of the PHYLogeny Inference Package 3.695, option neighbor. We displayed the dendrograms resulting from this analysis in the program TreeView v. 1.6.6. Detailed references are available upon request.

We extracted DNA from the tissue of Cerambyx cerdo preserved in 70% ethanol with the NucleoSpin Tissue XS genomic DNA extraction kit (MACHEREY–NAGEL) following the manufacturer’s protocol (MACHEREY–NAGEL 2014). The DNA is currently preserved at the Department of Genetics, Adam Mickiewicz University, in Poznań, Poland.

PCR protocol for microsatellite markers

We genotyped the extracted DNA for two markers: mitochondrial DNA (COI) and polymorphic microsatellite loci. We tested the amplification of 10 microsatellite loci, and, finally, in the subsequent analyses, we included seven of the most polymorphic loci. We carried out PCR amplification of microsatellites from the beetles in 5-μl reaction volume containing 1 × Type-it Microsatellite Kit (Qiagen), 0.2 μM forward primer, 0.2 μM fluorescent-labeled primer, and 1 μl (> 5 to 20 ng) of DNA template using a thermocycling profile of one cycle of 4 min at 94 °C followed by 34 steps of 30 s at 94 °C, 60 s at 54 °C, and 60 s at 72 °C, with a final step of 5 min at 72 °C (see also Drag et al. 2013). We performed multiplex reactions with four primer sets labeled using different fluorescent dyes: 6-FAM (Cc-01, Cc-03, Cc-18), VIC (Cc-11, Cc-13), PET (Cc-10, Cc-07), NED (Cc-08, Cc-06, Cc-20). For the final analysis we used the following loci: Cc-01, Cc-03, Cc-06, Cc-07, Cc-08, Cc-18, and Cc-20. We separated the amplified alleles on an ABI PRISM® 3130XL (Applied Biosystems) with GeneScan® 600LIZ size standard. We scored the amplicons with Peak Scanner™ v.1.0 (Applied Biosystems). We repeated the amplification procedure at least twice and compared the results between amplifications to test for consistency. We removed all individuals from the data if amplification failed at one or more loci.

Sequencing of COI

To check for the existence of new haplotypes in Cerambyx cerdo and define relationships between populations, we amplified and sequenced a part of subunit I of cytochrome c oxidase (COI) for 59 individuals. We used universal forward and reverse primers: (1) CI-J-2183 and TL2-N-3014 (Simon et al. 1994). We performed DNA fragment assembly and a quality assessment using SeqTrace (Stucky 2012). To identify amino acid substitutions in this region and to check for the presence of stop codons and nonfunctional coding sequences, we translated DNA sequences into amino acid sequences using Geneious (http://www.geneious.com). We performed NCBI-BLAST comparisons to known sequence databases to determine matches to the collected sequences. We conducted a statistical parsimony analysis with the program TCS v. 1.21 (Clement et al. 2000) to generate a haplotype network between mtDNA sequences. We performed a visualization of the network using the program tcsBU (Santos et al. 2015). We deposited the COI sequences into the GenBank database (http://www.ncbi.nlm.nih.gov/GenBank) using the submission tool BankIt (http://www.ncbi.nlm.nih.gov/BankIt/) under the following accessions no MF434579‒MF434637. We computed standard genetic indices for the analyzed region using MEGA v.7.0.21 (Kumar et al. 2016).

Data analysis

Loci characteristics

We used MICRO-CHECKER v.2.2.3 (Van Oosterhout et al. 2004) to test for the presence of null alleles and unexpected mutation steps. We calculated a mean allelic error rate, e a as described by Pompanon et al. (2005) for the final data set. We tested genotypic disequilibrium for each pair of loci in each population and for each locus pair across populations assuming heterozygote deficit with the help of Genepop v.4.2 (Raymond and Rousset 1995; Rousset 2008) using default parameters. For multiple tests we employed a sequentially rejective Bonferroni correction as described by Holm (1979).

We calculated the number of alleles, observed and expected heterozygosity, and Weir and Cockerham (1984) estimations of F ST (theta), F IT, and F IS over all loci using FSTAT v.2.9.3.2 (Goudet 2002) and GenAlEx v. 6.5 (Peakall and Smouse 2006, 2012). Moreover, with the help of the program FreeNa, we employed an excluding null alleles method (ENA; Chapuis and Estoup 2007) to calculate F ST. We evaluated measures of allelic richness and private allelic richness in ADZE v.1.0 (Allelic Diversity Analyzer; Szpiech et al. 2008) and HP-Rare (Kalinowski 2005). These programs use a rarefaction framework to correct the number of alleles when unequal sample sizes are present in the analyzed data set. We also calculated the inbreeding coefficient F IS (Weir and Cockerham 1984) with a correction for null alleles. For this purpose, we used the Bayesian method (model IIM) as is implemented in INEST v.2.1 (Chybicki 2017) with Markov chain Monte Carlo (MCMC) iterations 500,000, thinning 1000, and burn-in 50,000. Based on the lowest value of the deviance information criterion (DIC), we chose the model that best fits the data. We calculated polymorphic information contents (PICs) with CERVUS v.3.0.7 (http://www.fieldgenetics.com).

Population structure

To detect population structure and assign individuals into populations, we employed STRUCTURE v.2.3.4 (Pritchard et al. 2000; Falush et al. 2003) three times for K values from 1 to 15 and with 10 replicates for each K value, using a burn-in period of 104 and 106 MCMC iterations and incorporating the “no LOCPRIOR” option (without information about sampling locations). The high number of K was employed to detect a potential structure in C. cerdo populations resulting from trees’ distribution patterns, see also Fig. 1b, c. We carried out the analyses under the admixture model (i.e., individuals were allowed to have ancestry from multiple populations) assuming dependent allele frequencies. The program sorts individuals into K clusters according to their genetic similarity. To infer the K value that best fits the data, we estimated a statistic delta K (Evanno et al. 2005) via the online application STRUCTURE HARVESTER (Earl and van Holdt 2012). We analyzed the assignment of individuals to the genetic clusters according to the highest Q-values (probability of membership). We visualized the population structure with POPHELPER v.1.0.10 (http://www.pophelper.com; Francis 2017).

We assessed a spatial genetic structure (SGS) within analyzed geographic populations using INEST based on two genetic relatedness coefficients: Queller and Goodnight’s r (Queller and Goodnight 1989) and Moran’s I-value (estimated as in Streiff et al. 1998, after Chybicki 2017). We obtained correlograms by averaging these relatedness coefficients within distance classes, each containing an equal number of pairs. A significance of the correlogram was determined based on 9999 permutations.

Demographic factors

Because effective population size (Ne) is the most important conservation parameter indicating the adaptive potential of the population under study, we calculated the parameter using the method based on linkage disequilibrium, which is powerful for small populations (Waples and Do 2010). An algorithm is implemented in the program NE ESTIMATOR v.2.01 (Do et al. 2013). The critical values are set as a default to 0.05, 0.02, and 0.01, but we analyzed results for P crit 0.02, which provides an acceptable balance between precision and bias from rare alleles (England et al. 2010). We used a private allele method, as implemented in the program GenePop, to estimate the number of migrants per generation between the populations.

To assess whether the numbers of collected individuals provided sufficient statistical power to detect a population structure (if it existed), we calculated expected F ST by simulations with the help of POWSIM (Ryman and Palm 2006). We assumed a large and constant effective population size (Ne = 5000), varied time of separation (t), and three different sampling efforts: (1) 18 and 44 individuals (as in this study), (2) 30 and 44 individuals, and (3) 50 individuals sampled from each population; allele frequencies were taken from the observed data. We ran simulations using default parameter values for dememorization, batches, and iterations per batch (1000, 100, and 1000, respectively).

To detect a severe reduction in population size through bottleneck events, we employed BOTTLENECK v. 1.2.02 (Piry et al. 1999). We performed a comparison of the allele frequency distribution of analyzed samples with the expected L-shape distribution in a stable population under mutation-drift equilibrium (see Luikart et al. 1998a). The distribution of expected heterozygosity was obtained through simulations of the coalescent process of genes under two mutation models: the stepwise mutational model (SMM; Kimura and Ohta 1978) and the two-phase model (TPM). For the latter model, we used the default parameters as implemented in INEST (proportion of multistep mutations 0.22 and average multistep mutation size 3.1). We tested departures from the mutation-drift equilibrium using the Wilcoxon signed-rank test. To approximate the exact value, we determined P values based on 1,000,000 permutations. The procedure implemented in INEST does not require the assumption of normality (Chybicki 2017).

Estimation of viability and extinction risk of the Rogalin and Ispina populations

We used a simulation modeling approach to evaluate the viability of the populations with the help of Vortex v.10.2.7.0 (Lacy and Pollak 2017). We ran 24 individual-based scenarios, simulating 20 years of population dynamics, Table 2. We assumed the environment was relatively stable during this period to make the data obtained more realistic. The following demographic, environmental, and genetic parameters were considered: (1) supplementation, (2) mortality, (3) inbreeding depression, and (4) carrying capacity. If nothing else is noted, only one parameter was changed at a time. We ran simulations at realistic values of supplementation of the Ispina population by 10 or 30 individuals each year across 3 years. These individuals were added to Ispina through harvesting of the Rogalin population. Additionally, our scenarios simulated what will happen to the Ispina and Rogalin populations if no supplementation/harvest is done. By taking into account habitat stability and extent, distribution patterns of habitats, and data from other cerambycids (López-Pantoja et al. 2008, 2011), we set the mortality rate at two levels: (1) 10% females and 10% males in all age classes, and (2) 20% females and 30% males at the imago stage, keeping mortality rates unchanged in the remaining age classes (10%), all with a standard deviation of 3%. We evaluated the impact of inbreeding on survival, quantified as different numbers of lethal equivalents (LE), 3.14 and 6.29, assuming 50% inbreeding depression due to recessive lethal alleles (Brook et al. 2002; O’Grady et al. 2006), although the exact number of LE for C. cerdo is unknown (but see Pray et al. 1994; Pray and Goodnight 1995). We also considered habitat improvement scenarios, with potentially high carrying capacities (Car. cap.) for both populations, Car. cap. = 5000 and with highly constrained carrying capacities (Car. cap.Ispina = 420 and Car. cap.Rogalin = 1818 individuals), by taking into account the number of inhabited and uninhabited old oaks at both sites to ensure that the local carrying capacity did not become a limiting factor to population growth.

Table 2 Summary of parameter input values used in the models (1–24) of the great Capricorn beetle (Cerambyx cerdo; vortex “year” for C. cerdo is defined as 365 days)
Full size table

The remaining parameters, which were stable in all scenarios, are characterized below; see also Table 2. The estimation of initial population size (IPS) is based on the results of the August 2016 Cerambyx cerdo count of entrance holes and observable individuals in both populations. We estimated 10 oaks were inhabited by 100 individuals in Ispina, and 77 oaks were occupied by 1350 individuals in Rogalin. We hypothesized that reproduction occurred after short-distance dispersal, but zero net migration between populations was assumed due to the lack of corridors connecting both populations. We also assumed density-dependent reproduction with default values provided by the program (100% breeding at low densities and 75% at carrying capacity, Allee parameter 1, and steepness parameter 2) due to the lack of reliable life-history data for Cerambyx cerdo. We simulated the effect of a bottleneck by assuming one environmental catastrophic event, but not all individuals in the population were affected by environmental variation (e.g., weather or predators; Lacy et al. 2017); see Table 2. Allele frequencies on the C. cerdo analyzed populations were used as starting allele frequencies. We evaluated the results of simulations with STATISTICA v.12 (Statsoft).

Results

We used a total of 62 individuals out of the 81 samples initially included in this project for the final genetic analyses. PCR amplification reactions failed for most loci for 19 individuals and probably did so because of highly degraded DNA, insufficient DNA quality, or a combination of these factors. These problems apply especially to individuals for which we could retrieve only remnant samples.

COI characteristics

The region of COI (837-bp) diverged into six haplotypes that differed by one or two point mutations (more common transitions A→G and C→T and less common transversions A→C and T→G) in the Rogalin population. One geographically widespread haplotype (88.135%) occurs in both analyzed populations, Fig. S1. We found only this haplotype in the Ispina population. This haplotype was also previously published for samples originating from the Czech Republic (NCBI nt database: KM 516109, Drag and Čižek 2015), Fig. S1. The amino acid translations produced four unique protein sequences for COI, similar to those previously described in the GenBank protein database (identities ranged from 99 to 100%). The alignment of coding sequences appears to be in frame; in other words, the alignment does not contain premature and terminal stop codons or nonfunctional coding sequences. Table S1 presents basic mtDNA statistics.

Data characteristics and estimation of heterozygosity

We removed three loci (Cc10, Cc11, and Cc 13) from the final analysis because of a high proportion of missing values (e.g., locus Cc 13: 30.6%) and difficulties in determining the sample’s true allele composition (despite optimization of PCR conditions), and the occurrence of alleles with only small size differences. Based on the number of mismatches between duplicated genotypes, we found that the mean allelic error rate for the final data set is low and equal to e a = 0.01.

All seven SSR loci were variable in samples originating from each site (18 and 44 individuals) and amplified a total of 28 alleles. For the combined data, the highest number of alleles (5) was detected at loci Cc-01, 06, 18, and only two alleles were detected at locus Cc-20. The number of alleles per locus ranged from 2 to 5 in both populations. Also, mean allelic richness and private allelic richness were similar in both populations, Table 1.

Observed heterozygosity (Ho) is lower than expected (He) for six out of seven loci, and ranged from 0.197 (Cc-08) to 0.696 (Cc-18) and from 0.341 (Cc-20) to 0.676 (Cc-06), with averages of 0.402 and 0.574, respectively. No significant differences in observed and expected heterozygosity between Ispina and Rogalin were detected. After the sequential Bonferroni correction (SBC) for multiple tests, four loci were in HWE across populations, except for Cc-03, Cc-06, and Cc-08. Deviations from HWE for the Ispina and Rogalin populations are shown in Table 1. After the SBC, we detected no linkage disequilibrium between pairs of loci when we pooled sampling localities and considered populations separately.

An estimated frequency of null alleles per locus > 20% was detected in locus Cc-08 in Ispina (25%) and Rogalin (26%), and in locus Cc-06 (23 and 29%, respectively). No systematic distribution of null alleles in analyzed populations was found. The inbreeding coefficient Rhois was high (not shown), but may be overvalued due to the presence of null alleles. Therefore, we used a Bayesian approach (see “Materials and methods”) to calculate the sample mean inbreeding coefficient, taking into account the frequency of null alleles. The average values of F i null avg were much lower for both considered populations than those without the correction. A higher mean value of F i null was observed for Rogalin than for Ispina (Table 1). The effect of inbreeding for the Ispina population is known relatively precisely (95% confidence interval is narrow), whereas for Rogalin, the CI is much wider.

Population structure

STRUCTURE reveals that two clusters (K = 2) provide the most probable representation of the overall genetic structure of the C. cerdo populations when no LOCPRIOR option is employed; see Fig. 2. There was a weak but significant positive correlation between genetic and geographic boundaries (Spearman’s R Correlation Test: r 2 = 0.376, P < 0.05). Based on a Q-matrix, 33.3% of individuals had a coefficient of membership equal to or higher than 0.80 in the first genetic cluster (individuals from Ispina), whereas it was 43.18% in the second cluster (individuals from Rogalin), indicating those individuals can be considered residents. For the remaining individuals, the coefficient of membership was much lower, and these were assigned almost equally to two clusters.

Fig. 2
figure 2

Bayesian clustering analysis, inferred from STRUCTURE and STRUCTURE HARVESTER, of the Cerambyx cerdo data (62 individuals/7 SSR loci) collected from Poland (see Fig. 1). A Different colors indicate the assignment probability to different demes (K = 2); each individual is represented by vertical bars shaded in proportion to its ancestry; B Evanno’s delta K values of the K values tested. (Color figure online)

Full size image

We employed an ENA correction method, as described in Chapuis and Estoup (2007), to estimate the F ST parameter. Estimated values of F ST were relatively low both with and without ENA correction, but slightly overvalued without correction: F ST(ENA) = 0.027 (95% CI 0.00–0.119) and F ST(−ENA) = 0.032 (95% CI 0.00–0.136); see also Carlsson (2008).

Migration

The private allele-based estimation of the number of migrants is 0.785. This apparent contradiction (low values of F ST and low values of Nm) may be due to the low sample size of the Ispina population. POWSIM suggests that with seven loci and the number of individuals collected, we have 90% power to detect significant genetic differentiation when F ST = 0.0296, 80% when F ST = 0.025, and 40% when F ST = 0.01. When the sample size is increased to 50 individuals collected from each population, we have 100% power to detect significant genetic differentiation when F ST = 0.0247 and 60% when F ST = 0.01.

A relationship coefficient for distance classes under the “equal number of pairs” criterion revealed no significant positive r value in either studied population; a significant positive r value means the pairs of individuals within a distance class have more alleles in common than would be expected by chance. Instead, we observe a random distribution of genetic variation among individuals within populations (nonsignificant r values).

Demographic factors

A high uncertainty in the Ne estimates due to an infinite confidence limit was observed in both populations; thus, inferences about Ne are highly problematic (see Table 1). For example, depending on the minimal threshold of rare allele frequency, the effective population size (Ne) estimates for Rogalin ranged from 117 to 149 individuals, but even if the point estimate is 120.7, we cannot exclude values lower than 31.1 or higher than infinity with 95% confidence.

Significant heterozygosity excess under both mutation models (TPM, SMM), and a distribution of alleles with a shifted mode indicate that the Ispina population has gone through a bottleneck. A recent bottleneck was also evidenced for Rogalin, assuming a mixed mutation model (TPM) and the mode-shift test; see Table 3.

Table 3 Results of Wilcoxon’s sign-rank test (P-values) under the stepwise mutation model (SMM) and two-phase model (TPM), along with the shape of the allelic distribution inferred from the mode-shift test based on seven microsatellite loci
Full size table

Future of the Ispina and Rogalin populations—a simulation study

Assuming a rather optimistic level of mortality rates in our simulations, the exponential rate of increase r is negative and varied from r = − 0.08 to r = − 0.11, depending on the scenario (Table 2, S2). This means the populations are in deterministic decline. However, in the majority of simulations they are likely to survive over the next 20 years. According to the worst simulations (assuming no supplementation, higher levels of the mortality rate, and lethal equivalents), the Ispina population will become extinct in approximately 19 years. This overall negative trend is also visible in the net replacement rate (i.e., the average number of offspring produced by a female, which varies from r 0 = 0.58 to r 0 = 0.90), indicating the populations are not able to maintain themselves. In our models, which incorporate random catastrophic events, the stochastic r ranged from r = − 0.06 to − 0.18. After 20 years, the number of individuals decreased to 5.58 in Ispina and 110.68 individuals in Rogalin populations, and the probability of extinction is equal to 0% (Rogalin) and 65.8% (Ispina) in the worst scenarios; thus, modeled populations do not reach even the lower level of carrying capacity assumed in this study (K = 420 and K = 1818 in Ispina and Rogalin, respectively). Thus, changes in K did not affect analyzed demographic parameters in either population.

For the Ispina supplementation, we sourced 10 or 30 individuals each year across 3 years from the Rogalin population (30 or 90 total individuals). The initial size of the Ispina population was 100 individuals. Assuming the lower mortality rate and 3.14 lethal equivalents, after 20 years the number of extant individuals (N-extant) was low (29.99 and 200.06 individuals in Ispina and Rogalin populations, respectively). After supplementation by 90 individuals, the N-extant increased by 167% in the Ispina population compared with the nonsupplemented population, whereas in the Rogalin population, the harvest of these individuals caused a decrease of N-extant by 16.05%. The probability of extinction of the Ispina population declined to 0.4% after supplementation by 90 individuals and to 6.4% after supplementation by 30 individuals (see Fig. 3). Considering the higher level of mortality and 6.29 lethal equivalents and supplementation by 90 individuals, the N-extant was lower by 46.11 and 56.53% in Ispina and Rogalin populations, respectively, compared with the scenarios presented above (see Fig. 4). The probability of extinction of the Ispina population declined to 33% after supplementation by 30 individuals and to 6.8% after supplementation by 90 individuals.

Fig. 3
figure 3

The influence of supplementation on the probability of extinction of the simulated Ispina population of Cerambyx cerdo; scenarios 1, 5, 9: mortality rate: 10% (females) and 10% (males) in all age classes, 3.14 lethal equivalents and carrying capacity of N = 5000 individuals; scenario 1 assumes no supplementation; scenario 5: supplementation by 10 individuals each year across 3 years; scenario 9: supplementation by 30 individuals each year across 3 years

Full size image
Fig. 4
figure 4

The influence of supplementation/harvest on the mean number of extant individuals of the simulated Ispina and Rogalin populations of Cerambyx cerdo; scenarios: 4, 8, 12: number of lethal equivalents 6.29; mortality rate: 20% (females) and 30% (males) at the imago stage and 10% in the remaining age classes; carrying capacity 5000 individuals; scenario 4 assumes no supplementation/harvest; scenario 8: supplementation/harvest by 10 individuals each year across 3 years; scenario 12: supplementation/harvest by 30 individuals each year across 3 years

Full size image

For our small initial population sizes, the higher level of mortality had dramatic consequences on the probability of extinction, even with a high supplementation. As an example, we present a detailed analysis of the Ispina population for four scenarios assuming no supplementation, different levels of mortality rates, and different numbers of lethal equivalents (see Fig. 5). The probability of extinction (PE) was over two times higher for Ispina assuming the higher mortality rate of individuals than it was for the population of individuals characterized by the lower mortality rate. Based on 24 scenarios, increasing number of lethal equivalents had no significant effect on the analyzed parameters (N-extant, P = 0.85; PE, P = 0.47).

Fig. 5
figure 5

The influence of mortality and different number of lethal equivalents on the probability of extinction of simulated Ispina population of Cerambyx cerdo; scenarios 1–4 assume no supplementation and carrying capacity of N = 5000 individuals; scenario 1: mortality rate: 10% (females) and 10% (males) in all age classes, 3.14 lethal equivalents; scenario 2: mortality rate: 20% (females) and 30% (males) at the imago stage and 10% in the remaining age classes, and 3.14 lethal equivalents; scenario 3: mortality rate: 10% (females) and 10% (males) in all age classes, 6.29 lethal equivalents; scenario 4: mortality rate: 20% (females) and 30% (males) at the imago stage and 10% in the remaining age classes, and 6.29 lethal equivalents

Full size image

Discussion

Pattern of genetic variation in analyzed populations of C. cerdo

Data about the level and distribution of genetic diversity in threatened Cerambyx cerdo populations are crucial for planning conservation strategies for this species (see e.g., Lande and Barrowclough 1987). For the first time, we assessed genetic properties of Polish C. cerdo populations with seven out of the 10 initially analyzed microsatellite loci and one fragment of a subunit I of the mitochondrial gene COI. Our results demonstrated patterns of genetic diversity and differentiation of the C. cerdo populations in the context of their supplementation/harvesting and provide information that can be incorporated into future management actions to aid in the conservation of this beetle.

In both Polish populations of C. cerdo we detected the pattern of genetic variation consistent with other species that have suffered from genetic drift, founder effect, and inbreeding. Both populations showed a shift in allele frequency distribution, suggesting that the populations had experienced one or more bottleneck events in the recent past, which might have led to reduced heterozygosity, loss of rare alleles, and significant inbreeding (see e.g., Maruyama and Fuerst 1985; Luikart et al. 1998b). We found evidence of reduced genetic diversity within the Polish populations compared to the populations of C. cerdo from the Czech Republic. In the Polish populations, Ho = 0.402 and He = 0.574 (Table 1), and in the Czech populations, Ho = 0.57 and He = 0.63 (see Drag et al. 2013). Differences in the panels of marker loci available and the number of individuals studied hindered direct comparison of our results to those related to other Cerambycidae from Carter et al. (2010), Oleksa et al. (2013, 2015), and Drag et al. (2015).

In the Polish populations, allelic size variations are limited (up to five alleles per locus) and could be derived from a small number of founding individuals or drift. Polish populations are also almost fixed (88.135%) for a single mitochondrial haplotype (COI) in contrast to the Czech populations, which have more diverse haplotypes, including a haplotype found in Polish populations (Drag and Čižek 2015; NCBI databases, Fig. S1). This finding might suggest that Poland was colonized through the expansion of a single lineage. Postglacial colonization (founder effect) and bird predators, including the following insectivores, could cause C. cerdo populations to decrease (see also Ceia and Ramos 2016): tits—Lophophanes cristatus and Aegithalus caudatus caudatus; woodpeckers—Dendrocopos major and D. minor; nuthatch—Sitta europea; or the short-toed treecreeper—Certhia brachydactyla. In summary, the possible explanation for the reduced He—the low number of alleles seen for the number of SSR loci and the presence of predominantly one specific mtDNA variant in the Polish populations of the “southern” C. cerdo—is that a founder event(s) was followed by genetic bottleneck(s). However, we cannot also exclude the possibility that limited sampling might influence our results.

The private allele-based estimation of the number of migrants (0.785) is low and considered insufficient to make gene flow overcome genetic drift (Wright 1931). Also, the number of optimal genetic clusters, as inferred from STRUCTURE, was equal to the number of sampled populations, but genetic boundaries are only roughly linked to geographic locations (Spearman’s R Correlation Test, P < 0.05), (see also Fig. 2a, b). The long distance between populations (481 km), a relatively weak dispersal power of the beetles (only 0.1% of adults disperse beyond 2000 m) (Torres-Vila 2017, see also Nilsson and Baranowski 1997), and a lack of connectivity via ecological corridors indicate that the observed weak populations differentiation (as shown by the F ST value and the mitochondrial network, Fig. S1) could be attributed to shared ancestral polymorphism and stochasticity of retained alleles.

In spite of generally limited dispersal of C. cerdo, we did not find a spatial structure of genetic variation within geographic populations, which may indicate that a distance of the scale of few kilometers (up to 2.1 km), human-made or natural barriers, and selective forces do not affect distribution of alleles of analyzed loci (see also Beaumont and Nichols 1996; Beaumont and Balding 2004). We also speculate that a possible primary fine-scale genetic structure in C. cerdo populations could be deteriorated by random natural disturbance (e.g., felling of overly mature trees), anthropogenic activity, or biotic interactions. Because we analyzed the remnants of insects collected under trees, we cannot also exclude the possibility that this is a consequence of migratory journeys made by birds that feed on insects. Contrary results were found for a few species of beetles living in old-growth hollow trees, Elater ferrugineus, O. barnabita, and P. marmorata, for which restricted dispersal appeared to be the main factor driving population differentiation (Oleksa et al. 2013, 2015). This apparent contradiction might, for example, reflect different population histories such as different effects of genetic drift in different population sizes. However, in our study the best estimates of Ne are infinitely large and have very low precision (see also Wang 2005). Hence, further research is needed to increase the power and precision of various genetic properties of C. cerdo populations by analyzing more populations and increasing sample sizes.

Supplementation and outbreeding depression

The most important factors for demographic conditions of analyzed populations are supplementation/harvesting and the levels of mortality; however, both deterministic and stochastic r, although increased by up to 62% with the decreasing level of mortality and the increasing level of supplementation, are still negative, indicating that the population is in the decline phase, and continuous supplementation is needed to compensate for the loss of individuals. The genetic properties of transplanted individuals may positively affect the restored population through enrichment of genetic variation and removal of inbreeding effects. On the other hand, both source and recipient populations should exhibit genetic and environmental similarity to limit maladaptation of transplanted individuals in the site of release (Allendorf and Luikart 2007). Because the risk of outbreeding depression increases with greater genetic and geographical distances, the threat that individuals transplanted to the Ispina population may become maladapted appears limited in light of our results and main conclusions from previous studies (see Frankham 2015). Although one can argue that the number of marker loci used here is not sufficient to conclusively prove that analyzed populations are genetically distinct, Rosenberg et al. (2001) stated that such discrete populations can be defined based on how difficult it is to separate them from others. In other words, if some populations were easier to separate with only a small number of markers, then this could imply the genetic distinctness of those populations. That, however, is not our case.

What is the point of saving the Ispina population?

We did not find evidence (genetic distinctness) to suggest that the analyzed populations should be treated as evolutionary significant units (Moritz 1994). However, the distribution of C. cerdo in Poland is fragmented, and known beetle density is relatively low (Adamski et al. 2004; Starzyk 2004, and field observations of the authors of this study MP and EB). Moreover, in Poland, the southern and eastern populations of the beetle have experienced the greatest decline, thus raising concerns over their future conditions. The southern Ispina population, the largest and only one on the right side of the Vistula River, is likely to be extirpated if it is not supplemented. However, supplementation cannot succeed unless followed by habitat protection and restoration. Our habitat Ispina conservation project aims to protect ancient oaks inhabited by C. cerdo, evaluating habitats’ suitability over the long term, identifying other suitable habitats for the beetle in surrounding areas, and monitoring the release.

Quality data evaluation

The exhaustion of the Polish Cerambyx cerdo population influenced our sampling and calculations of population-level parameters. This is a common problem in declining populations of endangered species for which management decisions and status assessments must be made. Three microsatellite loci showed evidence for departure from Hardy–Weinberg expectations in a pooled sample, which could result from several factors: (1) inbreeding (Wright 1921); (2) sampling from cryptic isolated reproductive units, called the Wahlund effect, (see Castric et al. 2002); and (3) technical issues related to the PCR reaction or null alleles (Dharmarajan et al. 2013). Multiple signs indicate the Wahlund effect is not the main cause of departure from the Hardy–Weinberg equilibrium. First, we did not observe a consistent signature of heterozygote deficits across loci (Dakin and Avise 2004, but see also Dharmarajan et al. 2013). Second, we observed random spatial patterns of relatedness among individuals, which may indicate no restriction in gene flow across a few kilometers (see also Smouse and Peakall 1999; Peakall et al. 2003; Chybicki 2017). Third, the population structure, as inferred from STRUCTURE, was only partially consistent with geography, nevertheless STRUCTURE clustering may be biased due to a low number of loci analyzed (Silva et al. 2012). The observed departures from Hardy–Weinberg equilibrium could thus be rather attributed to substantial inbreeding (F i null avg. > 0) or the locus-specific effect caused by null alleles. The presence of null alleles has also been reported for populations of C. cerdo from the Czech Republic for the Cc-03, Cc-06, and Cc-08 loci analyzed in this study (Drag et al. 2013; Drag and Čižek 2015).

We admit that the sample size from Ispina is small, and both populations experienced recent reductions in size, and thus the assessed F ST value, the number of alleles, and Ne might be biased (Pearse and Crandall 2004; England et al. 2006). For the latter parameter, the results did not improve, contrary to expectation, when low frequency alleles were omitted from NEESTIMATOR analyses. Our results agree also well with the findings of Drag and Čižek (2015) for C. cerdo from the Czech Republic and indicate that rather temporal estimators should be used to calculate Ne (Pollak 1983). Moreover, population-level parameters are probably influenced by a combination of sampling error and stochasticity in survivorship and fecundities of such small groups of individuals in the year-to-year transition (e.g., Holmes 2001). The necessity of greater sampling efforts is obvious. But currently, in the case of the Ispina population, certain constraints are impossible to remove (e.g., small population size, the unobservability of juveniles, and low peaks of maximum seasonal emergence).

Researchers working on threatened species occurring in extremely small populations often face the dilemma of whether to obtain high-quantity samples to examine those populations or minimize the risk of their extinction. High-quantity samples from the Ispina population are currently unavailable because more exhaustive data acquisition might lead to the extinction of the population within years. Nevertheless, our genetic data summarize a declining trajectory of such small populations.

Conservation implications

A given population is considered viable if the extinction risk is 5–10% over a 30-year period (IUCN Standards and Petitions Subcommittee 2011). Because our scenarios showed the Ispina population cannot be considered demographically viable, even when supplemented, it is likely to go extinct within the next 19 years under the worst simulation scenarios. The negative trend can be reversed if efforts are made to improve survival of individuals, particularly in the last stages (imago)––for example, by habitat improvement involving netting of tree trunks to protect beetles from birds and shade removal around old oaks. Habitat improvement should be combined with population supplementation to create a long-term self-sustained population. Because the effect of a different number of lethal equivalents is insignificant on the considered demographic parameters, we recommend demographic supplementation instead of genetic supplementation, in which new genetic material may potentially cause outbreeding depression. Preferably, individuals should be sourced from populations with high heterozygosity, allelic richness, and low inbreeding––for example, from Czech populations that share the same COI haplotype. Translocation of individuals from the Rogalin population would also be effective in increasing the time to extinction of the Ispina population. At least 30 individuals should be released every year across 3 years, and this treatment should be repeated periodically because the population is in the decline phase. Postrelease monitoring should be established, and its results should determine subsequent management decisions. The results of our study provide information that can be incorporated into future management actions to aid in the conservation of Cerambyx cerdo cerdo.