A Systematic Method for Arranging Diagnostic Tests in Linear Analog DC and AC Circuits

Abstract

The paper deals with multiple soft fault diagnosis of linear analog circuits. The basic problem of arranging diagnostic tests performed in DC or AC states is considered in detail. A systematic method is developed that allows finding values of the sources applied to the excitation nodes as well as the measurement nodes at which the voltage variations due to the parameter deviations are sufficiently large. For this purpose the sensitivity analysis and the nonlinear programming technique, with appropriate objective function and constraints, are used. Four numerical examples reveal effectiveness of the proposed method for arranging the diagnostic tests.

1 Introduction

Fault diagnosis of analog circuits plays a key role in electronic circuit design. In integrated circuits it represents the main cost factor of the production process. In consequence, the subject is of considerable interest, leading to numerous publications, e.g. [1–25]. Generally, fault diagnosis includes detection of the circuit, location of the faulty elements, and evaluation of their parameters. If a faulty parameter is drifted from its tolerance range, but does not lead to some topological changes, the fault is said to be soft or parametric. If the fault is open circuit or short circuit, it is classified as catastrophic or hard. In some cases, physical imperfections such as near–opens and near–shorts may occur.

This paper is focused on soft fault diagnosis of linear analog circuits and offers a method for arranging diagnostic tests that allow effective performing of the multiple fault diagnosis. During the last years a number of methods for soft fault diagnosis have been proposed, e.g. [1–4, 7, 10–13, 15–20, 23, 25]. They exploit various concepts and techniques, e.g. neural networks [1], linear programming [20], fuzzy approach [3, 25], wavelet transform [2], frequency response function [11, 23], support vector machine [10, 12], V-transform of polynomial coefficients [13], evolutionary algorithm [7], Volterra series [4], block relaxation method [16]. Several papers have been devoted to soft fault diagnosis of the process parameters in analog integrated circuits, e.g. [17–19].

Methods for fault diagnosis of analog circuits exploit various measurement tests which constitute a preliminary step of the diagnostic process. To determine the optimal set of the test points required by the dictionary approach, different tools have been proposed, e.g. evolutionary computations [6] and fault–pair isolation tables [24]. A method for selection of optimal test frequencies, used by soft and hard fault diagnoses, is developed in reference [22]. A test that finds a set of optimal sampling points in CMOS circuits with ramp input signal is proposed in reference [14].

Certain methods devoted to multiple fault diagnosis, e.g. [15, 18, 19], exploit a test leading to a system of algebraic equations expressing some measured node voltages in terms of the diagnosis parameters p ₁ ,   …  ,  p _n . The circuit under test is driven by voltage or current sources applied to the nodes accessible for excitation. In general, to arrange the test several sets of the source values are applied in succession and every time voltages at some nodes are measured. The total number of the measured voltages is equal to n. Thus, the final result of the test is a system of n nonlinear algebraic type equations in n unknown variables p ₁ ,   …  ,  p _n

$$ \begin{array}{c}\hfill {v}_1={f}_1\left({p}_1,\kern0.5em \dots, \kern0.5em {p}_n\right)\hfill \\ {}\hfill {v}_2={f}_2\left({p}_1,\kern0.5em \dots, \kern0.5em {p}_n\right)\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill {v}_n={f}_n\left({p}_1,\kern0.5em \dots, \kern0.5em {p}_n\right)\kern0.5em ,\hfill \end{array} $$

(1)

where v ₁ ,   …  ,  v _n are the measured node voltages. The above mentioned diagnostic methods do not require the functions f ₁ ,   …  ,  f _n in explicit analytical form, which in real circuits either do not exist or are very complex and costly to obtain. To arrange an effective test the measurement voltages whose variations due to deviations of the diagnostic parameters are sufficiently large should be selected. Thus, the deviations of the parameters must considerably influence the tested voltages. The influence is specified by the sensitivities of the voltages with respect to the parameters. Because the sensitivities due to different parameters may vary enormously we will operate with semi–relative sensitivities of the form ${p}_k\frac{\partial {v}_i}{\partial {p}_k}$, where v _i is a voltage and p _k is a parameter.

In this paper linear DC and AC circuits, with real and positive parameters p ₁ ,   …  ,  p _n , are considered. The circuit has N nodes, except the datum one, including m nodes accessible for excitation. Let all N nodes be considered to select appropriate measurement nodes, which can be exploited in the diagnostic test. Thus, the circuit under test will be driven by m current sources, labelled b ₁ ,   …  ,  b _m , and some node voltages from among v ₁ ,   ⋯  ,  v _N will be measured. We want to select the measurement nodes and the sets of the input currents ${B}^{(i)}=\left\{\;{b}_1^{(i)},\kern0.5em \cdots, \kern0.5em {b}_m^{(i)}\right\}$ so that the magnitudes of the semi–relative sensitivities of the voltages at these nodes with respect to all the parameters are greater than a threshold value γ > 0 and the node voltages do not exceed a maximum value μ.

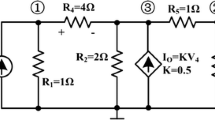
To shed more light on the discussed problem we consider a very simple example. Some details of full diagnosis process are presented in Section 5 (Example 1). In the circuit shown in Fig. 1 [20], where nominal values of the parameters are indicated, we want to identify the faulty resistors R ₃, R ₄. For this purpose the method developed in reference [18] will be used. To estimate the values of the unknown parameters (R ₃ and R ₄) this method needs two diagnostic tests: the principal test (test A) and the validation one (test B). To arrange these tests the circuit is supplied with current sources i ₁ and i ₂ at the accessible for excitation nodes 1 and 2 and all three nodes are taken into account to select the measurement nodes. To construct a proper test that satisfies the above described requirements the values of the current sources and the measurement nodes must be selected. Using the systematic method described in Sections 2–4, with γ = 0.1 V, μ = 5 V, and assuming the initial currents ${i}_1^{(0)}=0.1\kern0.5em \mathrm{A}$, ${i}_2^{(0)}=0.1\kern0.5em \mathrm{A}$ several tests can be applied. On the basis of the obtained results (see Section 5) we choose the measurement nodes 2 and 3 and the source currents i ₁ = 5.7855 A, i ₂ =  − 1.2127 A (test A). To verify the correctness of the selected tests we assume the actual values R ₃ = 2.60 Ω and R ₄ = 2.80 Ω. On the basis of the test A, with the measurement accuracy 1 mV, the diagnostic method proposed in reference [18] determines the parameter values R ₃ = 2.6058 Ω, R ₄ = 2.8050 Ω which are very close to the actual ones and they are confirmed by the verification test B. On the other hand, if ad hoc test with the current sources equal to the initial values i ₁ = 0.1 A, i ₂ = 0.1 A and the same measurement nodes 2 and 3, is exploited by the diagnostic method presented in [18], then the computed parameter values are R ₃ = 2.6296 Ω, R ₄ = 10077.9389 Ω. Resistance R ₄ is completely incorrect and the method, on the basis of the validating test B, discards the obtained result. Thus, the diagnostic method based on this test fails.

Fig. 1

An exemplary circuit

The main idea of the proposed method will be presented using DC linear circuits driven by current sources b ₁ ,   ⋯  ,  b _m . Next it will be extended to AC circuits. The method exploits the sensitivity analysis with respect to the diagnostic parameters and the nonlinear programming (NLP) technique. It should be emphasized that the proposed in this paper systematic method for arranging the diagnostic tests is dedicated to linear analog circuits only. The tests can be arranged in DC or AC states and used by different methods devoted to multiple fault parametric diagnosis, including location and identification of the faulty parameters. The systematic method, described in Sections 2–4, simplifies and improves creation of the test and increases its quality.

2 The Main Idea of the Method

This section brings a foundation of the systematic method for arranging diagnostic tests presented in Section 4.

Let us consider a linear DC circuit with n positive parameters p ₁ ,   …  ,  p _n considered as potentially faulty. They form an n-vector p = [p ₁  ⋯  p _n ] ^T, where T denotes transposition. The circuit is described by the node equation in symbolic form

$$ \mathbf{Y}\left(\mathbf{p}\right)\mathbf{v}=\mathbf{b} $$

(2)

where v = [v ₁  ⋯  v _N ] ^T is the node voltage vector, b = [b ₁  ⋯  b _N ] ^T is the source vector, consisting of the current sources entering the nodes 1 ,   ⋯  ,  N, and Y(p) = [y _ij (p)]  _NxN is the node admittance matrix, whose elements depend on the parameters p ₁ ,   …  ,  p _n . Using the solution of eq. (2)

$$ \mathbf{v}={\left[\mathbf{Y}\left(\mathbf{p}\right)\right]}^{-1}\mathbf{b} $$

(3)

we calculate the sensitivity vector $\frac{\partial \boldsymbol{v}}{\partial {p}_k}={\left[\frac{\partial {v}_1}{\partial {p}_k}\kern0.5em \cdots \kern0.5em \frac{\partial {v}_N}{\partial {p}_k}\right]}^{\;\mathrm{T}}$ with respect to a parameter p _k

$$ \frac{\partial \mathbf{v}}{\partial {p}_k}=\frac{\partial {\left[\mathbf{Y}\left(\mathbf{p}\right)\right]}^{-1}}{\partial {p}_k}\mathbf{b} $$

(4)

Since Y(p)[Y(p)]⁻¹ = 1, we write

$$ \frac{\partial \mathbf{Y}\left(\mathbf{p}\right)}{\partial {p}_k}{\left[\mathbf{Y}\left(\mathbf{p}\right)\right]}^{-1}+\mathbf{Y}\left(\mathbf{p}\right)\frac{\partial {\left[\mathbf{Y}\left(\mathbf{p}\right)\right]}^{-1}}{\partial {p}_k}=\mathbf{0} $$

(5)

and find

$$ \frac{\partial {\left[\mathbf{Y}\left(\mathbf{p}\right)\right]}^{-1}}{\partial {p}_k}=-{\left[\mathbf{Y}\left(\mathbf{p}\right)\right]}^{-1}\frac{\partial \mathbf{Y}\left(\mathbf{p}\right)}{\partial {p}_k}{\left[\mathbf{Y}\left(\mathbf{p}\right)\right]}^{-1} $$

(6)

Substituting (6) into (4) yields

$$ \frac{\partial \mathbf{v}}{\partial {p}_k}=-{\left[\mathbf{Y}\left(\mathbf{p}\right)\right]}^{-1}\frac{\partial \mathbf{Y}\left(\mathbf{p}\right)}{\partial {p}_k}{\left[\mathbf{Y}\left(\mathbf{p}\right)\right]}^{-1}\mathbf{b} $$

(7)

Let p be ${\mathbf{p}}^{\mathrm{nom}}={\left[{p}_1^{\mathrm{nom}}\kern0.5em \cdots \kern0.5em {p}_n^{\mathrm{nom}}\right]}^{\;\mathrm{T}}$, where ${p}_j^{\mathrm{nom}}$ (j = 1,  …,  n) means the nominal value of p _j , then it holds

$$ \frac{\partial \mathbf{v}}{\partial {p}_k}={\mathbf{C}}^{(k)}\mathbf{b} $$

(8)

where ${\mathbf{C}}^{(k)}={\left.-{\left[\mathbf{Y}\left({\mathbf{p}}^{\mathrm{nom}}\right)\right]}^{-1}\frac{\partial \mathbf{Y}\left(\mathbf{p}\right)}{\partial {p}_k}\right|}_{{\mathbf{p}}^{\mathrm{nom}}}{\left[\mathbf{Y}\left({\mathbf{p}}^{\mathrm{nom}}\right)\right]}^{-1}={\left[{c}_{ij}^{(k)}\right]}_{\; NxN}$. Equation (8) allows finding sensitivity vectors $\frac{\partial \mathbf{v}}{\partial {p}_k}$ for k = 1 ,   …  ,  n. For this purpose we need [Y(p ^nom)]⁻¹ and $\frac{\partial \mathbf{Y}\left(\mathbf{p}\right)}{\partial {p}_k}$ at p ^nom for all k. The derivatives $\frac{\partial \mathbf{Y}\left(\mathbf{p}\right)}{\partial {p}_k}$ can be efficiently computed if Y(p) is given in symbolic form.

Since the circuit is driven by the sources b ₁ ,   …  ,  b _m , the source vector b can be presented in the form b = [b ₁  ⋯  b _m  0  ⋯ 0] ^T. The sensitivities of the node voltages v _i for i = 1 ,   ⋯  ,  N, on the basis of (8), are given by the equations

$$ \left[\begin{array}{c}\hfill \frac{\partial {v}_1}{\partial {p}_k}\hfill \\ {}\hfill \frac{\partial {v}_2}{\partial {p}_k}\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill \frac{\partial {v}_N}{\partial {p}_k}\hfill \end{array}\right]=\left[\begin{array}{cccc}\hfill {c}_{11}^{(k)}\hfill & \hfill {c}_{12}^{(k)}\hfill & \hfill \cdots \hfill & \hfill {c}_{1 m}^{(k)}\hfill \\ {}\hfill {c}_{21}^{(k)}\hfill & \hfill {c}_{22}^{(k)}\hfill & \hfill \cdots \hfill & \hfill {c}_{2 m}^{(k)}\hfill \\ {}\hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ {}\hfill {c}_{N1}^{(k)}\hfill & \hfill {c}_{N2}^{(k)}\hfill & \hfill \cdots \hfill & \hfill {c}_{N m}^{(k)}\hfill \\ {}\hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right]\left[\begin{array}{c}\hfill {b}_1\hfill \\ {}\hfill {b}_2\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill {b}_m\hfill \end{array}\right], k=1,\dots, n $$

(9)

The set of eqs. (9), for k = 1 ,   …  ,  n, allows writing the following systems of equations

$$ \begin{array}{l}\left\{\begin{array}{c}\hfill {p}_1^{\mathrm{nom}}\frac{\partial {v}_1}{\partial {p}_1}={p}_1^{\mathrm{nom}}\left({c}_{11}^{(1)}{b}_1+\cdots +{c}_{1 m}^{(1)}{b}_m\right)\hfill \\ {}\hfill {p}_2^{\mathrm{nom}}\frac{\partial {v}_1}{\partial {p}_2}={p}_2^{\mathrm{nom}}\left({c}_{11}^{(2)}{b}_1+\cdots +{c}_{1 m}^{(2)}{b}_m\right)\hfill \\ {}\hfill \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \hfill \\ {}\hfill {p}_n^{\mathrm{nom}}\frac{\partial {v}_1}{\partial {p}_n}={p}_n^{\mathrm{nom}}\left({c}_{11}^{(n)}{b}_1+\cdots +{c}_{1 m}^{(n)}{b}_m\right)\hfill \end{array}\right.\\ {}\begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \begin{array}{cc}\hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \vdots \hfill & \hfill \hfill & \hfill \hfill \end{array}\kern1.5em \\ {}\left\{\begin{array}{c}\hfill {p}_1^{\mathrm{nom}}\frac{\partial {v}_N}{\partial {p}_1}={p}_1^{\mathrm{nom}}\left({c}_{N1}^{(1)}{b}_1+\cdots +{c}_{N m}^{(1)}{b}_m\right)\hfill \\ {}\hfill {p}_2^{\mathrm{nom}}\frac{\partial {v}_N}{\partial {p}_2}={p}_2^{\mathrm{nom}}\left({c}_{N1}^{(2)}{b}_1+\cdots +{c}_{N m}^{(2)}{b}_m\right)\hfill \\ {}\hfill \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \hfill \\ {}\hfill {p}_n^{\mathrm{nom}}\frac{\partial {v}_N}{\partial {p}_n}={p}_n^{\mathrm{nom}}\left({c}_{N1}^{(n)}{b}_1+\cdots +{c}_{N m}^{(n)}{b}_m\right)\hfill \end{array}\right.\end{array} $$

(10)

Each of the N systems of n eqs. (10) relates to semi–relative sensitivities of one of the voltages v ₁ ,   ⋯  ,  v _N with respect to all parameters p ₁ ,   …  ,  p _n , at the nominal values of the parameters. Using the first set of n equations of the representation (10) we wish to find the excitations ${b}_1={b}_1^{(1)},\kern0.5em \dots, \kern0.5em {b}_m={b}_m^{(1)}$ so that the magnitude of each of the semi–relative sensitivities of the voltage v ₁ at node 1, ${p}_1^{n om}\frac{\partial {v}_1}{\partial {p}_1},{p}_2^{n om}\frac{\partial {v}_1}{\partial {p}_2},\dots, {p}_n^{n om}\frac{\partial {v}_1}{\partial {p}_n}$ is greater than or equal to the threshold value γ. Furthermore, the excitations should cause the magnitudes of the node voltages not to exceed some maximum value μ. For this purpose we use the nonlinear programming technique with an objective function f(b ₁,  …,  b _m ) = (b ₁ b ₂  ⋯  b _m )² and constraint functions as follows

$$ \begin{array}{c}\hfill \max {\left({b}_1{b}_2\kern0.5em \cdots \kern0.5em {b}_m\right)}^2\hfill \\ {}\hfill \mathrm{subject}\kern0.5em \mathrm{to}\hfill \\ {}\hfill \gamma - {p}_1^{\mathrm{nom}}\left|{c}_{11}^{(1)}{b}_1+\cdots +{c}_{1 m}^{(1)}{b}_m\right|\le 0\hfill \\ {}\hfill \gamma - {p}_2^{\mathrm{nom}}\left|{c}_{11}^{(2)}{b}_1+\cdots +{c}_{1 m}^{(2)}{b}_m\right|\le 0\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill \gamma - {p}_n^{\mathrm{nom}}\left|{c}_{11}^{(n)}{b}_1+\cdots +{c}_{1 m}^{(n)}{b}_m\right|\le 0\hfill \\ {}\hfill \left|\sum_{j=1}^m{z}_{ij}{b}_j\right|-\mu \le 0,\kern1em i=1,\kern0.5em \dots, \kern0.5em N\hfill \end{array} $$

(11)

where z _ij are elements of the matrix [Y(p ^nom)]⁻¹.

The maximization of the objective function is to counteract very small values of the current sources, whereas $\left|\sum_{j=1}^m{z}_{i j}{b}_j\right|-\mu =\left|{v}_i\right|-\mu \le 0,\kern1em$ i = 1 ,   …  ,  N, ensure the magnitudes of the node voltages against exceeding μ. To solve the NLP problem, the procedure ‘fmincon’ implemented in MATLAB 2013b is used, where max(b ₁ b ₂  ⋯  b _m )² is replaced by min(−(b ₁ b ₂  ⋯  b _m )²).

The set of excitations ${B}^{(1)}=\left\{\;{b}_1^{(1)},\kern0.5em \dots, \kern0.5em {b}_m^{(1)}\right\}$ provided by the nonlinear programming (11) guarantees that magnitudes of all the semi–relative sensitivities of voltage v ₁ at node 1, with respect to all the parameters p ₁ ,   …  ,  p _n , are sufficiently large. Similar approach is applied to the other systems of n equations of the representations (10). As a result the sets of excitations ${B}^{(2)}=\left\{\;{b}_1^{(2)},\kern0.5em \dots, \kern0.5em {b}_m^{(2)}\right\},\kern0.5em \dots, \kern0.5em {B}^{(N)}=\left\{\;{b}_1^{(N)},\kern0.5em \dots, \kern0.5em {b}_m^{(N)}\right\}$, which satisfy the sensitivity requirements at nodes 2 ,   …  ,  N, are determined. However, the number of useful test nodes and the corresponding sets B ⁽ⁱ⁾ may be smaller than N because in some cases NLP fails. The actual number of the nodes will be labelled $\hat{N}$.

3 Extension to AC Circuits

Let us consider a linear AC circuit with real and positive diagnostic parameters p ₁ ,   …  ,  p _n . In the frequency domain sinusoidal current sources acting in the circuit are represented by their phasors. Let all initial phases of the sources be either zero or π, then the phasors are real numbers (positive or negative). The node equation describing the circuit has the form (2), were b = [b ₁  ⋯  b _m  0  ⋯ 0] ^T, v = [v ₁  ⋯  v _N ] ^T, with v _i (i = 1,  …,  N) being complex numbers (phasors) ${v}_i={\tilde{v}}_i+\mathrm{j}{\tilde{\tilde{v}}}_i$, (i = 1,  …,  N) ,where ${\tilde{v}}_i$ is the real part of v _i and ${\tilde{\tilde{v}}}_i$ is the imaginary part of v _i . Hence, it holds

$$ \frac{\partial {v}_i}{\partial {p}_k}=\frac{\partial {\tilde{v}}_i}{\partial {p}_k}+\mathrm{j}\frac{\partial {\tilde{\tilde{v}}}_i}{\partial {p}_k} $$

(12)

and

$$ \left|\frac{\partial {v}_i}{\partial {p}_k}\right|=\sqrt{{\left(\frac{\partial {\tilde{v}}_i}{\partial {p}_k}\right)}^2+{\left(\frac{\partial {\tilde{\tilde{v}}}_i}{\partial {p}_k}\right)}^2} $$

(13)

Also elements of matrix Y(p) are complex. In consequence, elements ${c}_{ij}^{(k)}$ of matrix C ^(k) (see(8)) are complex ${c}_{ij}^{(k)}={\tilde{c}}_{ij}^{(k)}+\mathrm{j}{\tilde{\tilde{c}}}_{ij}^{(k)}$. As a result the equations of the representation (10) have to be modified as it is explained using the first of them

$$ {p}_1^{\mathrm{nom}}\left(\frac{\partial {\tilde{v}}_1}{\partial {p}_1}+\mathrm{j}\frac{\partial {\tilde{\tilde{v}}}_1}{\partial {p}_1}\right)= p{}_1{}^{\mathrm{nom}}\left[\left({\tilde{c}}_{11}^{(1)}{b}_1+\cdots +{\tilde{c}}_{1 m}^{(1)}{b}_m\right)+\mathrm{j}\left({\tilde{\tilde{c}}}_{11}^{(1)}{b}_1+\cdots +{\tilde{\tilde{c}}}_{1 m}^{(1)}{b}_m\right)\right] $$

(14)

and

$$ {p}_1^{\mathrm{nom}}\left|\frac{\partial {v}_1}{\partial {p}_1}\right|={p}_1^{\mathrm{nom}}\sqrt{{\left({\tilde{c}}_{11}^{(1)}{b}_1+\cdots +{\tilde{c}}_{1 m}^{(1)}{b}_m\right)}^2+{\left({\tilde{\tilde{c}}}_{11}^{(1)}{b}_1+\cdots +{\tilde{\tilde{c}}}_{1 m}^{(1)}{b}_m\right)}^2} $$

(15)

Hence, the nonlinear programming corresponding to (11) becomes

$$ \begin{array}{c}\hfill \max {\left({b}_1\kern0.5em {b}_2\kern0.5em \cdots \kern0.5em {b}_m\right)}^2\hfill \\ {}\hfill \mathrm{subject}\kern0.5em \mathrm{to}\hfill \\ {}\hfill \gamma - {p}_1^{\mathrm{nom}}\sqrt{{\left({\tilde{c}}_{11}^{(1)}{b}_1+\cdots +{\tilde{c}}_{1 m}^{(1)}{b}_m\right)}^2+{\left({\tilde{\tilde{c}}}_{11}^{(1)}{b}_1+\cdots +{\tilde{\tilde{c}}}_{1 m}^{(1)}{b}_m\right)}^2}\le 0\hfill \\ {}\hfill \gamma - {p}_2^{\mathrm{nom}}\sqrt{{\left({\tilde{c}}_{11}^{(2)}{b}_1+\cdots +{\tilde{c}}_{1 m}^{(2)}{b}_m\right)}^2+{\left({\tilde{\tilde{c}}}_{11}^{(2)}{b}_1+\cdots +{\tilde{\tilde{c}}}_{1 m}^{(2)}{b}_m\right)}^2}\le 0\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill \gamma - {p}_n^{\mathrm{nom}}\sqrt{{\left({\tilde{c}}_{11}^{(n)}{b}_1+\cdots +{\tilde{c}}_{1 m}^{(n)}{b}_m\right)}^2+{\left({\tilde{\tilde{c}}}_{11}^{(n)}{b}_1+\cdots +{\tilde{\tilde{c}}}_{1 m}^{(n)}{b}_m\right)}^2}\le 0\hfill \\ {}\hfill {}\sqrt{{\left(\sum_{j=1}^m{r}_{ij}{b}_j\right)}^2+{\left(\sum_{j=1}^m{x}_{ij}{b}_j\right)}^2}-\mu \le 0,\kern1em i=1,\kern0.5em \dots, \kern0.5em N\hfill \end{array} $$

(16)

where r _ij  = Re (z _ij ) and x _ij  = Im (z _ij ).

4 Method for Arranging the Diagnostic Tests

Diagnostic test asks for n equations with n unknown variables p ₁ ,   …  ,  p _n . If $\hat{N}\ge n$ then the simplest way to arrange a test leading to n equations with n unknown variables p ₁ ,   …  ,  p _n is choosing n measurement nodes from the set of $\hat{N}$ nodes and the corresponding excitation sets. To write the test equations we consider n circuits, each driven by one of the excitation sets and measure the voltages at the appropriate nodes. As a result the system of n equations, expressing the measured voltages in terms of the parameters p ₁ ,   …  ,  p _n , can be written. Thus, n measurement nodes and n sets of excitations are exploited to arrange the test. However, usually less number of nodes and/or sets of excitations may be used to arrange a test and the test can be organized even if $\hat{N}< n$. To make possible creating different tests, on the basis of the obtained results, we take into account one of the nodes ${k}_l\in \left\{\;1,\kern0.5em \dots, \kern0.5em \hat{N}\right\}$ and the corresponding set of excitations ${B}^{\left({k}_l\right)}$. We check whether the set ${B}^{\left({k}_l\right)}$ also meets the constraints required by any other NLP corresponding to other node. This checking is performed for each ${B}^{\left({k}_l\right)}$, $l=1,\kern0.5em \dots, \kern0.5em \hat{N}$ and all the nodes. The results are summarized in a table consisting of rows corresponding to the sets ${B}^{\left({k}_l\right)}$ and columns corresponding to the nodes. If a set ${B}^{\left({k}_l\right)}$ meets the constraints required by the NLP relating to node k _j , we insert x at the crossing of l-th row and j-th column. The table allows arranging different tests. For example, let us consider Table 1 corresponding to n = 3 and $\hat{N}=2$. Although $\hat{N}< n$the test leading to three equations, can be arranged by measurement of the voltages at nodes k ₁ and k ₂ in the circuit driven by the excitations belonging to ${B}^{\left({k}_2\right)}$ and measurement of the voltage at node k ₁ in the circuit driven by the excitations belonging to ${B}^{\left({k}_1\right)}$.

Table 1 Exemplary results provided by the method

If Table 2 is obtained, with n = 3, $\hat{N}=3$, then several tests, leading to three equations, can be arranged. For this purpose three nodes k ₁, k ₂, k ₃ and the set of excitations ${B}^{\left({k}_3\right)}$ or three sets of excitations ${B}^{\left({k}_1\right)}$, ${B}^{\left({k}_2\right)}$, ${B}^{\left({k}_3\right)}$ and one node k ₁ can be used. Several other tests can be generated on the basis of Table 2.

Table 2 Exemplary results provided by the method

More marks in the table, more different tests can be arranged. Thus, the crucial point of arranging the diagnostic test, suitable to the diagnosis problem, is constructing the table having the above described structure. The table, labelled DT, contains information about possibility of arranging a test and forming various alternative tests. It provides the set of the measurement nodes and the excitations (current source values), which can be exploited in the diagnostic tests. If several of the obtained sets of excitations are identical, the corresponding rows of the DT table are the same. Then, only one of them is essential and the others repeat the information contained in this row. Therefore, such redundant rows are discarded and the size of the DT table is reduced.

5 Numerical Examples

5.1 Example 1

Consider again the simple DC circuit shown in Fig. 1. This example is exhibited to compare the systematic and ad hoc methods and to manifest the influence of the test on the diagnostic process carried out using the method of reference [18] at different levels of the measurement uncertainty. In work [18] no systematic method for arranging the tests is proposed. They were created by performing many numerical experiments.

In this exemplary circuit we concentrate on the location and identification of the faulty resistors R ₃ and R ₄, as described in Section 1, with the parameters γ = 0.1 V and μ = 5 V. The value of γ guarantees that in the selected test the measurements can be executed with proper accuracy. The value of μ prevents the voltages from exceeding the threshold values, e.g. from the breaking down of some devices. The nodes 1 and 2 are considered as the excitation ones and DC current sources i ₁ and i ₂ are applied to them. Thus, the elements b ₁ ,   ⋯  ,  b _m (m = 2) of the vector b are b ₁ = i ₁, b ₂ = i ₂. It is assumed that all the nodes of the circuit are accessible for measurement. To solve the nonlinear programming problem we pick the initial values ${b}_k^{(0)}={i}_k^{(0)}=0.1\kern0.5em \mathrm{A}$, where k = 1 ,  2. The NLP technique applied in succession to the nodes 1, 2, and 3 leads to the sets of excitations B ⁽¹⁾, B ⁽²⁾, and B ⁽³⁾ comprising the input current sources, gathered in the first column of the Table 3.

Table 3 DT table relating to the set of parameters {R ₃,  R ₄}

The information contained in this table allows arranging six diagnostic tests. They are specified by B ^(k) and the numbers of the corresponding measurement nodes: B ⁽³⁾, 2, 3; B ⁽¹⁾, 1 and B ⁽²⁾, 2; B ⁽¹⁾, 1 and B ⁽³⁾, 2; B ⁽²⁾ and B ⁽³⁾, 2; B ⁽¹⁾, 1 and B ⁽³⁾, 3; B ⁽²⁾, 2 and B ⁽³⁾, 3. Let us concentrate on two of them, as follows. To arrange test A of [18] we choose the set of excitation B ⁽³⁾ and the measurement nodes 2 and 3. In the case of test B of [18] we choose the set of excitations B ⁽¹⁾ and the measurement node 1 and B ⁽²⁾ with the measurement at node 2. The actual values of the faulty parameters are R ₃ = 2.60 Ω, R ₄ = 2.80 Ω. Alternatively, ad hoc tests A and B are arranged with the current sources i ₁ = i ₂ = 0.1 A in test A and i ₁ = 0.2 A, i ₂ = 0.5 A in test B with the measurement nodes 2 and 3. In all the tests the measurements were performed with three levels of the uncertainty: case (i) – 1 mV, case (ii) – 0.1 mV, and case (iii) – 0.01 mV.

The results provided by the method proposed in reference [18], exploiting the test arranged with the help of the systematic method (SM) and the ad hoc (AH) method are summarized in Table 4. They reveal that the method of [18] with the test SM gives correct values of the faulty parameters at all levels of the measurement uncertainty. The influence of the measurement accuracy on the values of the parameters is not essential in this case. When the test AH is applied the method of [18] gives correct results only with the highest measurement accuracy (0.01 mV) and fails in the other cases, (i) and (ii).

Table 4 The comparison results of the diagnosis process of the circuit shown in Fig. 1

5.2 Example 2

Let us consider the DC circuit shown in Fig. 2, containing the operational amplifiers that operate in the linear region. We wish to construct DT tables that allow arranging the tests suitable to multiple fault diagnosis of the following sets of three parameters: P ⁽¹⁾ = {R ₁,  R ₂,  R ₃}, P ⁽²⁾ = {R ₁,  R ₄,  R ₇}, P ⁽³⁾ = {R ₁,  R ₃,  R ₆}, P ⁽⁴⁾ = {R ₂,  R ₄,  R ₆}, P ⁽⁵⁾ = {R ₄,  R ₅,  R ₆}. For this purpose the nodes 1, 2, 3 are chosen as the excitation nodes and all the nodes 1 ,   …  ,  8 are taken into account to select the measurement nodes. The current sources i ₁, i ₂, i ₃ with the internal resistors ${R}_{g_1}$, ${R}_{g_2}$, ${R}_{g_3}$ are applied to nodes 1, 2, 3.

Fig. 2

An exemplary DC circuit

Thus, elements b ₁ ,   …  ,  b _m (where m = 3) of vector b are: b ₁ = i ₁, b ₂ = i ₂, b ₃ = i ₃. To construct DT tables the method described in this paper is used with the constants γ = 1 V, μ = 12 V and the initial guess of the NLP ${\left[{b}_1^{(0)}\kern0.5em {b}_2^{(0)}\kern0.5em {b}_3^{(0)}\right]}^{\kern0.2em \mathrm{T}}$ is picked with ${b}_k^{(0)}={i}_k^{(0)}=0.1\kern0.5em \mathrm{A}$, k = 1 ,  2 ,  3. In the case P ⁽²⁾ the method leads to 1 × 1 matrix $\left(\hat{N}=1\right)$ and the test, which has to comprise three equations, cannot be arranged. In all the other cases the DT tables allow arranging one test. Two of them, relating to cases P ⁽³⁾ and P ⁽⁵⁾, are enclosed (Tables 5 and 6).

Table 5 DT table relating to the set of parameters P ⁽³⁾ = {R ₁,  R ₃,  R ₆}

Table 6 DT table relating to the set of parameters P ⁽⁵⁾ = {R ₄,  R ₅,  R ₆}

5.3 Example 3

Consider the AC circuit (http://www/ti.com/lit/an/snoa586d/snoa586d.pdf) shown in Fig. 3 containing the operational amplifiers operating in the linear region. In this circuit 11 sets consisting of three parameters selected from the capacitors C ₁ ,   …  ,  C ₄ and resistances R ₁ ,   …  ,  R ₈ are considered: S ⁽¹⁾ = {C ₁,  C ₂,  C ₃}, S ⁽²⁾ = {C ₁,  R ₂,  R ₈}, S ⁽³⁾ = {C ₁,  R ₃,  C ₃}, S ⁽⁴⁾ = {C ₁,  R ₄,  R ₆}, S ⁽⁵⁾ = {R ₁,  C ₁,  C ₂}, S ⁽⁶⁾ = {R ₁,  C ₁,  R ₇}, S ⁽⁷⁾ = {R ₁,  R ₂,  R ₃}, S ⁽⁸⁾= {R ₂,  C ₃,  C ₄}, S ⁽⁹⁾ = {R ₂,  C ₃,  R ₅}, S ⁽¹⁰⁾ = {R ₃,  C ₃,  C ₄}, S ⁽¹¹⁾ = {R ₆,  R ₈,  C ₄}. We want to construct the DT tables which allow arranging the tests suitable to the diagnoses of these sets of three parameters. For this purpose the nodes 1 and 2 are chosen as the excitation nodes and all nine nodes are considered to select the measurements nodes. The sinusoidal current sources i ₁, i ₂ at the frequency 80 Hz with internal resistors ${R}_{g_1}$, ${R}_{g_2}$ are connected to nodes 1 and 2. The sinusoidal currents are chosen so that their phasors I ₁, I ₂ are real numbers. They are elements of the source vector, I ₁ = b ₁, I ₂ = b ₂. To construct DT tables we use the method proposed in this paper with the constants γ = 0.1 V, μ = 12 V. The initial guess of each NLP is ${\left[{b}_1^{(0)}\kern0.5em {b}_2^{(0)}\right]}^{\kern0.2em \mathrm{T}}$ where ${b}_1^{(0)}={I}_1^{(0)}={b}_2^{(0)}={I}_2^{(0)}=0.1\kern0.5em \mathrm{A}$. In the cases S ⁽¹⁾, S ⁽²⁾, S ⁽³⁾, S ⁽⁵⁾ the method leads to DT tables that allow arranging proper tests. One of them is Table 7. In the other cases the method does not allow arranging a test consisting of three equations. However, if the restriction concerning the minimal values of the semi–relative sensitivities is weakened, by choosing γ = 0.01 V, the method enables us to create the tests in seven cases S ⁽¹⁾, S ⁽²⁾, S ⁽³⁾, S ⁽⁵⁾, S ⁽⁷⁾, S ⁽⁸⁾, S ⁽¹¹⁾. For example the results relating to the case S ⁽¹⁾ is presented in Table 8. However, if γ is decreased then the higher measurement accuracy is necessary. Both Tables 7 and 8 have been obtained after discarding the redundant rows corresponding to B ⁽⁷⁾ and B ⁽⁸⁾. They allow arranging different tests, e.g. on the basis of Table 8 the tests can be created in the circuit supplied with the sources of the set B ⁽⁶⁾ by measurement of the voltages at three nodes from among the nodes 6, 7, 8, 9 or at two of these nodes and voltage measurement at node 9 in the circuit driven by the sources of set B ⁽⁹⁾.

Fig. 3

Pre-amplifier with accurate RIAA response

Table 7 DT table relating to the set of parameters S ⁽⁵⁾ = {R ₁,  C ₁,  C ₂}

Table 8 DT table relating to the set of parameters S ⁽¹⁾ = {C ₁,  C ₂,  C ₃} with weakened γ = 0.01 V

5.4 Example 4

In the AC circuit, being the subwoofer filter, shown in Fig. 4 we wish to construct DT tables which allow arranging the tests suitable to multiple diagnoses of the following sets of three, four or five parameters: Q ⁽¹⁾ = {R ₁,  R ₉,  C ₅}, Q ⁽²⁾ = {C ₅,  C ₇,  C ₈}, Q ⁽³⁾ = {R ₉,  R ₁₁,  C ₅}, Q ⁽⁴⁾ = {R ₁,  R ₈,  R ₁₀,  C ₆}, Q ⁽⁵⁾ = {R ₁,  R ₈,  R ₁₇,  C ₅,  C ₇}. For this purpose the nodes 1 and 2 are chosen as the excitation nodes and all the 18 nodes are considered to select the measurement nodes. The sinusoidal current sources i ₁, i ₂ at the frequency 100 Hz with real phasors I ₁, I ₂ are connected to nodes 1 and 2. They constitute the elements of the source vector, b ₁ = I ₁, b ₂ = I ₂. To construct DT tables we use the method proposed in this paper with the constants γ = 0.1 V, μ = 12 V. The initial guess ${\left[{b}_1^{(0)}\kern0.5em {b}_2^{(0)}\right]}^{\kern0.2em \mathrm{T}}={\left[{I}_1^{(0)}\kern0.5em {I}_2^{(0)}\right]}^{\kern0.2em \mathrm{T}}$ of the NLP is picked with ${I}_1^{(0)}={I}_2^{(0)}=0.1\kern0.5em \mathrm{A}$. In each of the cases the method provides DT table that allows arranging several tests satisfying the requirements. Three of them, relating to cases Q ⁽³⁾, Q ⁽⁴⁾, Q ⁽⁵⁾ are enclosed (Tables 9, 10, 11). All the tables have been obtained after discarding redundant rows. In the case specified by Table 11 the tests leading to five equations can be arranged using the current supply sources of the set B ⁽¹³⁾ and measuring the voltages at five nodes from among the nodes 13, 14, 15, 16, 17, 18.

Fig. 4

The subwoofer filter

Table 9 DT table relating to the set of parameters Q ⁽³⁾ = {R ₉,  R ₁₁,  C ₅}

Table 10 DT table relating to the set of parameters Q ⁽⁴⁾ = {R ₁,  R ₈,  R ₁₀,  C ₆}

Table 11 DT table relating to the set of parameters Q ⁽⁵⁾ = {R ₁,  R ₈,  R ₁₇,  C ₅,  C ₇}

6 Conclusion

Various methods for fault diagnosis of analog circuits are based on diagnostic test performed in DC or AC state. The test is the preliminary step of these methods. To arrange an effective test the excitations and the measurement nodes should be selected so that the voltages at these nodes considerably react to deviations of the diagnostic parameters. The proposed in this paper approach exploits the sensitivities of the node matrix elements with respect to the parameters and NLP technique with appropriate constraints. The constraints guarantee that the magnitudes of the semi–relative sensitivities of the selected node voltages due to all the diagnostic parameters are not smaller then a threshold value and the magnitudes of the node voltages do not exceed a maximum value. Furthermore, the maximization of the objective function of the NLP counteract very small values of the current sources. The final result of the proposed approach are DT tables. They contain information about the possible tests and usually allow arranging several tests for given set of the parameters. In this way we can choose the best one taking into account, for example, the number of the excitation sets, the number of measurement nodes, the values of the measured voltages and the values of the sensitivities. In AC case the method can be extended by considering, in addition, different frequencies of the input signals. Numerical examples show that the approach allows effective arranging of the tests performed in DC and AC states.