Study of GABAergic extra-synaptic tonic inhibition in single neurons and neural populations by traversing neural scales: application to propofol-induced anaesthesia

Abstract

Anaesthetic agents are known to affect extra-synaptic GABAergic receptors, which induce tonic inhibitory currents. Since these receptors are very sensitive to small concentrations of agents, they are supposed to play an important role in the underlying neural mechanism of general anaesthesia. Moreover anaesthetic agents modulate the encephalographic activity (EEG) of subjects and hence show an effect on neural populations. To understand better the tonic inhibition effect in single neurons on neural populations and hence how it affects the EEG, the work considers single neurons and neural populations in a steady-state and studies numerically and analytically the modulation of their firing rate and nonlinear gain with respect to different levels of tonic inhibition. We consider populations of both type-I (Leaky Integrate-and-Fire model) and type-II (Morris-Lecar model) neurons. To bridge the single neuron description to the population description analytically, a recently proposed statistical approach is employed which allows to derive new analytical expressions for the population firing rate for type-I neurons. In addition, the work shows the derivation of a novel transfer function for type-I neurons as considered in neural mass models and studies briefly the interaction of synaptic and extra-synaptic inhibition. We reveal a strong subtractive and divisive effect of tonic inhibition in type-I neurons, i.e. a shift of the firing rate to higher excitation levels accompanied by a change of the nonlinear gain. Tonic inhibition shortens the excitation window of type-II neurons and their populations while maintaining the nonlinear gain. The gained results are interpreted in the context of recent experimental findings under propofol-induced anaesthesia.

1 Introduction

The neural mechanism of general anaesthesia is poorly understood. Despite its everyday application in hospital practice, it is far from being understood why the patients under general anaesthesia lose consciousness (hypnosis), do not feel pain (analgesia), can not move (immobility) and do not remember details of the surgery (amnesia) (Longnecker et al. 2008). In the last decades much experimental research has focused on the molecular effect of the anaesthetic drugs administered on the receptor targets in the brain while fewer studies have been devoted to more theoretical approaches. In the last years more and more theoretical mathematical and computational studies have been performed (Hutt et al. 2013; Foster et al. 2008) to understand better the experimental data obtained under anaesthesia, such as single cell recordings (Antkowiak 2002; Bai et al. 2001), Local Field Potentials (Sellers et al. 2013) and electroencephalogram (Gugino et al. 2001; Cimenser et al. 2011; Lewis et al. 2012; Purdon et al. 2013). Most of the previous theoretical studies (McCarthy et al. 2008; Ching et al. 2010; Bojak and Liley 2005; Steyn-Ross et al. 2001; Sleigh et al. 2011; Hutt and Longtin 2009; Hutt 2012) consider anaesthetic action on synaptic receptors neglecting extra-synaptic effects, cf. the review of Hutt et al. (2013) for more details.

The present work aims to link some recent insights from the experimental research on extra-synaptic GABAergic receptors (ESR) to the theoretical work on neural populations. The work provides major effects of ESRs on different description scales which may serve a basis for future extended theoretical studies. To be able to extract features on multiple scales, it is necessary to work out a link between the scales. Hence this link is the driving force to develop new analytical techniques to bridge the still distinct description levels of single neuron networks and neural populations. The gained results indicate how ESR activity modulates the neural population activity and hence may affect the encephalographic acitivity (EEG) measured in general anaesthesia.

Some experimental studies of the action of anaesthetic agents on neural GABAergic receptors revealed the existence of ESRs, which induce a tonic inhibitory current (Farrant and Nusser 2005; Semyanov et al. 2004; Nusser et al. 1997; Nusser et al. 1998; Brickley and Mody 2012). They have been found experimentally in the cerebellum, dentate gyrus, hippocampus, thalamus, striatum, hypthalamus and neocortex, see (Belelli et al. 2009; Kullmann et al. 2005) for review. Tonic inhibition is assumed to tune the level of excitation in neural population and is supposed to play a role, e.g. in the loss of consciousness, sleep or arousal (Kopanitsa 1997). Moreover, ESRs are very sensitive to small ambient concentrations of GABA and respond on a much larger time scale than synaptic receptors (Cavelier et al. 2005; Hamann et al. 2002). These specific properties are the sign of their possible importance in the context of slow consciousness phenomena (Kopanitsa 1997; Farrant and Nusser 2005). Further evidence for the importance of ESRs in anaesthesia is their high sensitivity to various clinically relevant anaesthetic agents (Farrant and Nusser 2005; Orser 2006). For instance, the anaesthetics midazolan and propofol enhance much more tonic inhibition than phasic inhibition in the thalamus (Belelli et al. 2009). Since the thalamus is supposed to play an important role in general anaesthesia (Alkire et al. 2008), ESRs receptors may mediate anaesthetic effects, such as loss of consciousness.

Tonic inhibition induced by ESRs represents a persistent increase in the cell membrane conductance of single cells, while ESRs affect the excitability of interneuron-pyramidal cell networks and thus modify network oscillations (Semyanov et al. 2003). To understand the effect of microscopic molecular action of anaesthetic agents on the encephalographic activity and behaviour, it is necessary to bridge the gap between a microscopic description at single neuron level and the mesoscopic level of neural populations where extracellular currents generate the encephalographic activity. Our work shows how to link the different description levels to take into account the ESR effect in two neuron types. To this end, the subsequent sections presents analytic and numerical studies of the neural firing rate and its corresponding nonlinear gain. We reveal that tonic inhibition induces both a subtractive and divisive effect in neural population of type-I and type-II neurons, i.e. tonic inhibition shifts the firing thresholds to higher values and modulates the nonlinear gain of the population firing rate function. In addition, we derive a new sigmoidal transfer function applicable in neural mass and neural field models involving tonic inhibition effects. In the context of anaesthesia, the theoretical findings in neural population dynamics can explain the origin of some spectral power changes in EEG under anaesthesia in the δ− and α− frequency bands.

To reveal the effects of anaesthetics by ESR action, we neglect the anaesthetic effect of anaesthetics on synaptic receptors. We are well aware that this approximation is strong, but the present work aims to extract features of of ESRs only. Future work will consider both synaptic and extra-synaptic action.

The Results section considers three description scales according to the brain structure ,namely single neurons, a single population of neurons and a network of populations. The present work considers both type-I and type-II neurons. In the first two partial studies of single neurons and their population, we reveal the effects of ESR activity on the firing rate and its nonlinear gain which are distinct in type-I and type-II neurons. Most parts of these studies show analytical calculations. The last partial study on the network of populations presents numerical results only and points out the relation of the gained network activity to experimental EEG.

2 Methods

Tonic inhibition occurs mainly due to the presence of ESRs, see (Houston et al. 2012; Glykys and Mody 2007; Farrant and Nusser 2005; Scimemi et al. 2005; Semyanov et al. 2004; Mody 2001) and references in (Hutt 2012). As these receptors are found on inhibitory as well as on excitatory neurons, tonic inhibition affects these two types of neurons and their populations in different brain areas (Song et al. 2011; Belelli et al. 2009; Kullmann et al. 2005). Hence the present work takes into account the effects of tonic inhibition on two different neuron types: type-I excitatory cells whose dynamics obey the equations of a Leaky-Integrate and Fire (LIF) neuron model and interneurons described by a type-II inhibitory cell which obeys the Morris-Lecar model equations.

Moreover, frequently tonic inhibition is called shunting inhibition, which occurs when the reversal potential of the inhibitory receptor is identical to the resting potential of the cell. Since GABAergic receptors exhibit a reversal potential close to the resting potential in pyramidal cells, tonic inhibition resembles shunting inhibition in excitatory neurons. For simplicity the present work adopts this equivalence in both excitatory and inhibitory cells and chooses the reversal potentials correspondingly.

In the next section, the different models used are presented: the single neuron models, the derived population model based on firing rates, and the spiking-neuron-based network.

2.1 Single neuron models

In general, the firing activity onset of neurons may exhibit two scenarios: if the membrane potential exceeds a certain threshold, the neuron firing sets in either at a very small firing frequency or at larger a firing frequency. The former case denotes neurons of type-I and the latter of type-II which are reasonable models e.g. of pyramidal or granular cells and interneurons, respectively.

2.1.1 Type-I neuron

To mathematically model the membrane potential of a type-I neuron in a steady state, we consider the Leaky Integrate-and-Fire model (Koch 1999; London et al. 2008; Mitchell and Silver 2003) with excitatory (e) and inhibitory (i) receptors and corresponding conductances:

$$\begin{array}{@{}rcl@{}} C\frac{dV}{dt} = g_{l}(E_{l}-V)+ g_{e}(t)(E_{e}-V) + g_{i}(t)(E_{i}-V) \\+ g_{ton}(E_{ton} - V) +I_{app}(t){\kern106pt} \end{array} $$

(1)

$$ g_{syn}(t)=\sum\limits_{n=i}^{T} w_{syn}e^{-(t-t_{i})/\tau_{syn}}\quad ,\quad \small{syn} = e,~i$$

(2)

where C is the membrane capacitance and t _i are the instances of incoming spikes that trigger a synaptic response with amplitude w _syn and decay time τ _syn , T is the number of occured spikes at time t. Consequently g _syn (t) is a stochastic process and, for temporally uncorrelated incoming Poisson spike trains with constant rate λ, its mean and variance is (Ross 1982)

$$E[g_{syn}](t)=w_{syn}\tau_{syn}\lambda\left(1-e^{-t/\tau_{syn}}\right) $$

(3)

$$ Var[g_{syn}](t)=\frac{w^{2}_{syn}}{2}\tau_{syn}\lambda\left(1-e^{-2t/\tau_{syn}}\right)~.$$

(4)

These expression will be very important inter alia in the context of mean field models of a population in section 3.2.

The differential equation (1) is accompanied by the reset to the membrane potential V _r if the membrane potential crosses the firing threshold V _th . After resetting, the model considers a refractory time interval Δ. The constant conductance g _ton induces a tonic current in the membrane at ESR, E _ton is the reversal potential of the receptors, g _l and E _l are the leaky membrane conductance and the resting potential in the absence of excitation and inhibition, respectively. Moreover E _e , E _i represent the reversal potentials of excitatory (e) and inhibitory (i) receptors, respectively. According to the equivalence of shunting and tonic inhibition, for single neurons and the single neural population we choose E _l = E _i = E _ton . To derive the population model, we consider granule cells with a surface of 100μm ², E _e = 0mV, E _l = −75mV, g _l = 0.385nS and V _r = −75mV and V _th = −49mV (Mitchell and Silver 2003).

The neuron emits a spike if the membrane potential exceeds the threshold. For constant membrane conductances g _e , g _ton and neglecting synaptic inhibition (g _i = 0), the steady state spike rate reads

$$\begin{array}{@{}rcl@{}} f(V_{m},V_{th})&=&\frac{1}{\Delta-\tau\ln\frac{V_{m}-V_{th}}{V_{m}-V_{r}}}\quad,\quad V_{m}\ge V_{th}\\ &=&0\quad,\quad V_{m}<V_{th} \end{array} $$

(5)

with

$$V_{m}(g_{e},g_{ton})=\frac{g_{e}E_{e}+g_{ton}E_{ton}+g_{l}E_{l}}{g_{e}+g_{ton}+g_{l}}~,~\tau=C/(g_{e}+g_{ton}+g_{l})~.$$

(6)

The membrane potential V _m would be reached for $t\to \infty$ if no threshold is present, τ is the effective membrane time constant which increases the membrane time constant and hence slows down the neural firing activity. For simplicity, this model does not consider nonlinear effects of dendritic integration as observed in theory and experiments (Zhang et al. 2013).

2.1.2 Type-II neuron

To model the membrane potential of a type-II neuron, we employ the Morris-Lecar model (Borisyuk 2005; Morris and Lecar 1981)

$$\begin{array}{@{}rcl@{}} C\frac{dV}{dt} &= & g_{Ca} m_{\infty}(V)(V_{Ca}-V)+g_{K} w(t)(V_{K}-V)+g_{L}(E_{L}-V)\\ & & +g_{e}(t)(E_{e}-V)+g_{i}(t)(E_{i}-V)+g_{ton}(E_{ton}-V) + I_{app}(t)\\ &&\\ \tau_{w}\frac{dw}{dt} &=&\phi(w_{\infty}-w) \end{array} $$

(7)

The functions $m_{\infty }=m_{\infty }(V), \, w_{\infty }=w_{\infty }(V), \,\tau _{w}(V)=\tau _{w}(V)$ are given by

$$\begin{array}{@{}rcl@{}} m_{\infty}(V)&=&0.5(1+\tanh((V-V_{1})/V_{2}) )\\ w_{\infty}(V)&=&0.5(1+\tanh((V-V_{3})/V_{4}) )\\ \tau_{w}(V) &=& 1/(\cosh((V-V_{3})/(2V_{4}) ) )\\ \end{array} $$

with constants V ₁ = −1.2mV, V ₂ = 18mV, V ₃ = 2mV, V ₄ = 30mV, ϕ = 0.04/s. Here, V and w are the membrane potential and the activation variable, respectively, see Borisyuk (2005) for details of the Morris-Lecar model. We also chose the reversal potential of potassium ion channels V _K = −84mV and calcium ion channels V _Ca = 120mV, and the external current I _app = 90μA.

The firing rate function for the Morris-Lecar model is not known analytically due to the nonlinear nature of the underlying Hopf bifurcation at the firing onset. Hence the present work investigates the firing activity of type-II neurons numerically only. The model is said to generate a spike if the neuron membrane crosses the threshold V = 0mV with dV/dt > 0.

2.1.3 Generalized firing rate

In biological neurons, synaptic receptors and ESRs are spatially distributed on the dendritic tree of each neuron. Their contribution to the membrane potential at the neurons’ soma depends strongly on their spatial location (Spruston 2008). Since the receptor locations are different on each neuron and currently there is no experimental technique with which one is able to extract the exact position of each receptor on each neuron in the population, we adopt a statistical approach and consider distributions of membrane conductances of synaptic receptors and ESRs (Hutt 2012). This approach implies the distribution of membrane conductances in the single neuron firing rate and the corresponding analytical model considers steady-state neural activity neglecting transient activity. The firing rate for both type-I and type-II neurons reads (Hutt 2012)

$$F_{s}({G},V_{th})={\int}_{-\infty}^{\infty}p_{s}(g-{G}){\Theta}(V(g)-V_{th})f(V(g),V_{th})dg $$

(8)

with the distribution p _s (g) of membrane conductances g with mean value G and the noiseless neuron firing rate f. Here Θ(x) is the Heaviside function with Θ(x)=0 for x < 0 and Θ(x)=1 for x≤0. In the case of type-I neurons, f is defined analytically in Eq. (5) and V(g) is the membrane potential defined in (6) dependent on the conductances g = {g _e , g _ton }.

Specifically, we assume Poisson-distributed independent spike trains of rate λ₀ arriving at excitatory synaptic receptors of number n on the dedritic tree of a single neuron and identical constant tonic inhibition induced at ESRs. In a first approximation, the position of the receptors on the dendritic branch is not considered. Then the total rate of the excitatory spike trains at the neuron is λ = nλ ₀. The synaptic receptors respond to incoming pulses according to Eq. (2) and the excitatory conductance g _e in the steady-state is a random variable with mean and variance

$$G_{E}=w_{e}\tau_{e} \lambda~\quad\mbox{ and }\quad {\sigma_{e}^{2}}=\frac{1}{2}{w_{e}^{2}}\tau_{e}\lambda~, $$

(9)

respectively, cf. Eq. (3) and (4). The constant w _syn is the synaptic weight and τ _e represents the decay time constant of the excitatory synaptic receptors. For a large number of receptors n the excitatory conductances obey a Gaussian distribution according to the central limit theorem and the inhibitory extra-synaptic conductance G _ton is constant leading to the probability density introduced in (8)

$$p_{s}(g_{e}-G_{E})=\frac{1}{\sqrt{2\pi}\sigma_{e}}e^{-(g_{e}-G_{E})^{2}/2{\sigma_{e}^{2}}}~. $$

(10)

The subsequent studies of single neurons and single populations neglect synaptic inhibition, i.e. g _i = 0.

2.2 A single neural population

The population firing rate is an input-output transfer function relating the membrane potential or synaptic activity as input and the firing rate of the neurons in the population as output. It is a major element in neural mass models which consider a mean potential V as the statistical average over the neuron population and a short time window. Consequently it is coarse-grained in time. Since the population firing rate depends on the number of neurons in the population, it is sufficient to consider the population firing rate per neuron which is called F in the following.

In biological neural populations, properties of single neurons are not identical. For instance, the firing threshold or resting membrane potential may vary between neurons. To consider such heterogeneities, the subsequent paragraph considers a large number of neurons in the population for which the central limit theorem guarantees the normal distribution of the corresponding properties. Specifically, for type-I neurons we assume a normal distribution N(V _th ) of firing thresholds V _th with mean $\bar {V}_{th}$ and variance $\sigma ^{2}_{th}$ (Wilson and Cowan 1972; Amit 1989). Here N(V _th ) is the percentage of neurons with threshold V _th that are ready to fire, i.e. which are out of their refractory period. Then, considering the firing rate F _s in Eq. (8) for a single stochastic neuron, the population firing rate reads (Hutt 2012)

$$\begin{array}{@{}rcl@{}} F(\bar{g},\bar{V}_{th})&=&{\int}_{-\infty}^{\infty}F_{s}(\bar{g},V_{th})N(V_{th}-\bar{V}_{th})dV_{th}\\ &=&{\int}_{-\infty}^{\infty}{\kern-1.5pt}p_{s}(g-\bar{g}){\int}_{-\infty}^{\infty}{\Theta}(V(g)-V_{th})f(V(g),V_{t}h)N(V_{th}-\bar{V}_{th})dV_{th}dg~. \end{array} $$

In type-II neurons, the firing threshold is defined by the external current and hence we assume a normal distribution of the external current I _app with mean $\bar {I}_{app}$ and variance $\sigma ^{2}_{app}$ yielding a distribution of the firing threshold.

In numerical simulations, the population of type-I and type-II neurons include 200 non-identical uncoupled neurons while receiving stationary uncorrelated input spike trains.

One of the simplest single neuron models is the McCulloch-Pitts neuron whose firing rate function f is the Heaviside-function. This standard choice yields the standard sigmoidal transfer function for populations (Wilson and Cowan 1972; Amit 1989; Hutt 2012). Since McCulloch-Pitts neurons neglect important physiological features of single neurons, such as conductance-based currents and refractory periods, the present work considers the more realistic single neuron firing rate functions of type-I and type-II neurons. This approach enables us to take into account tonic inhibition in the presence of a receptor distribution on dendrites and in neural populations.

2.3 Network of networks

After the study of single neurons and neural populations, the work examines numerically tonic inhibition action on a rather realistic network of excitatory and inhibitory neurons, see Fig. 1. Since tonic inhibition may be induced by a spill-over of neurotransmitters at synaptic receptors or the specific activation by anaesthetic agents such as propofol (Farrant and Nusser 2005; Semyanov et al. 2004), it is reasonable to assume a global inhibitory effect affecting both excitatory and inhibitory neurons.

Fig. 1

Topology of the network of networks. Arrows and dots denote excitatory and inhibitory connections, respectively, terminating at synaptic receptors with probability of connection sp (sparseness)

2.3.1 Neuron properties

In the population of Type-I neurons, we consider 750 pyramidal cells with a surface of 400μm ², the membrane capacitance is C = 33.181nF, E _ton = −76mV, g _L = 22.88nS, E _L = −76mV, V _T = −58mV, V _r = −68mV and the refractory period Δ=8ms (London et al. 2008). Their dynamics obey Eq. (2). The interneuron population exhibits 250 type-II neurons sharing the parameters E _ton = −60.9mV (which is the resting potential of the neuron), C = 20μF/cm ², V ₁ = −1.2mV, V ₂ = 18mV, g _K = 8mS/cm ², g _l = 2mS/cm ², V _Ca = 120mV, V _K = −84mV, V _l = −60mV, V ₃ = 2mV, V ₄ = 30mV, g _Ca = 4mS/cm ² and φ = 0.04. The dynamics of the interneurons obeys Eqs. (7). In the simulation, both excitatory and inhibitory synapses receive external input in the presence of ESRs.

Stochastic input

An external input current applied during the simulations to neuron i is stochastic

$$ I_{\text{app},i} = I_{0} + \beta_{i}(t)\quad,\quad i=1,\ldots,750 $$

where the random values β _i (t) are taken from the uniform distribution in the interval [−2.0μA;2.0μA] for Type I neurons and for Type-II neurons

$$ I_{\text{app},i} (t) = I_{1} + \alpha_{i}(t)\quad,\quad i=1,\ldots,250 $$

(11)

with the random variable α _i (t) taken from the uniform distribution in the interval [−60.0μA;60.0μA] for Type II neurons. Here I ₀ = 103μA and I ₁ are constants fixed for each simulation. Together with the physiological parameters of the models, I ₀ and I ₁ yield firing frequencies of the neurons between 0Hz and 17Hz, which reflects a rather high level of noise. The input current fluctuations reflect spontaenous ion channel activity.

Heterogeneity

Biological neural structures stipulate a certain level of randomness in the model, be it in the neurons themselves or the network. Specifically, we assume Gaussian distributed thresholds in the neurons which reflects neuron hetereogeneity. For Type-I neurons, the threshold of neuron i is Gaussian distributed by

$$\begin{array}{@{}rcl@{}} V_{th,i} = -49\text{mV} + \xi_{i}\quad,\quad i=1,\ldots,750 \end{array} $$

with random values ξ _i of zero mean and the variance 0.0001mV. In Type II-neurons the distribution of thresholds transforms into Gaussian distributed perturbations in the external input constant in Eq. (11)

$$I_{1,i} = I_{2} + \eta_{i}\quad,\quad i=1,\ldots,250~, $$

where I ₂ = 97μA is constant and identical in each simulation, η _i obeys a Gaussian distribution with zero mean and variance 1μA.

Connectivity

The neurons in each population are randomly connected to each other as well as the two populations. The time scales of all synapses are identically chosen to τ _e = 5ms and τ _i = 20ms corresponding to NMDA- and GABA _A -receptors, respectively. The network coupling constants are w _ee = 0.005mS, w _ie = 0.008mS, w _ei = 0.4mS, w _ii = 0.5mS where w _nm , n, m = {e, i} denotes the weight at synapse of type n on neurons of type m. The connectivity is sparse with probabilities p _ii = 0.05, p _ie = 0.02, p _ei = 0.01, p _ee = 0.005 reflecting cortical connectivity (Binzegger et al. 2004).

Tonic inhibition

The network considers tonic conductances g _ton = x⋅20μS for Type-I neurons and g _ton = x⋅100μS for Type-II neurons where x ∈ [0; 1]. These values are physiologically reasonable for GABA _A receptors (Song et al. 2011; Farrant and Nusser 2005). Hence the conductance of tonic inhibition in inhibitory cells may be higher than for excitatory cells. This is consistent with the experimental observation that the tonic GABA _A currents in pyramidal cells usually is significantly smaller than those in interneurons (Song et al. 2011; Scimemi et al. 2005).

All numerical simulations of neural activity were performed with the BRIAN simulator (Goodman and Brette 2009). Typically, the network is simulated for 5 s with integration time constant 0.5 ms while ensuring that transients do not affect the results.

2.3.2 Spike coherence measure

To analyse the coherence or correlation of spiking neural activity subject to the level of tonic inhibition, we make use of the spike coherence measure κ based on the normalized cross-correlation of spike trains of neuronal pairs in the network (Wang and Buzsáki 1996). The spike coherence of two neurons x and y is computed by the cross-correlation of their spike trains X and Y, respectively, within a time bin τ _bin over a time interval T:

$$ {\kappa}_{xy}(\tau_{\text{bin}}) = \frac{{\sum}_{l=1}^{K} X(l)Y(l)}{\sqrt{{\sum}_{l=1}^{K} X(l) {\sum}_{l=1}^{K} Y(l)}}\quad,\quad 0\le {\kappa}_{xy}\le 1~.$$

The spike trains are given by X(l), Y(l)∈{0,1}, l = 1, 2, …, K and K = τ _bin/T, i.e. X(l)=1 if there is at least one spike in the bin.

The present work computes the population spike coherence measure

$$\begin{array}{@{}rcl@{}} {\kappa}(\tau_{\mathrm{\tiny{bin}}})={\sum}_{i=1}^{N_{1}}{\sum}_{j=1}^{N_{2}}\frac{\kappa_{ij}(\tau_{\mathrm{\tiny{bin}}})}{M} \end{array} $$

which is the spike coherence measure of pairs averaged over M pairs of spike trains of the numbers N ₁, N ₂. For instance, M = N(N−1)/2 for intra-network spike coherence with N ₁ = N ₂ = N neurons, while M = N ₁ N ₂ for spike coherence measures between different networks of number N ₁, N ₂ neurons. When the time bin τ _bin is very small (as chosen in the subsequent analysis), strong synchrony renders κ(τ _bin) ≈ 1 and the smaller κ(τ _bin), the less synchronized is the network activity.

2.3.3 Power spectrum

Moreover, to learn more about the subthreshold activity in the neuron populations subject to tonic inhibition, the work considers the population membrane potential averaged over the ensemble of neurons. The corresponding power spectra of the averaged membrane potential are computed on sub-sampled data with a sample interval of 5ms applying the Welch-method with an average over 10 simulations of the network activity. These simulations are performed with different random initial conditions of the membrane potential and different values of temporal fluctuations, heterogeneity, and connectivity realizations. The δ−frequency band is defined in the frequency interval 0−4Hz, the 𝜃-band in the interval 4−8Hz, the α−band in 8−12Hz and the β-band in 12−25Hz. The power in the band is the integral of the power value function over the corresponding frequencies in the interval.

3 Results

To learn more about the action of propofol on neural population activity induced by ESRs, this section shows results on different neural description scales. We begin with a short study of tonic inhibition in single neurons and afterwards utilize the insights gained to study tonic inhibition effects on firing activity in a single population. These studies consider Type-I and Type-II neurons. Finally, to understand better how tonic inhibition affects the interaction in a network, the last part investigates a small network of excitatory and inhibitory neurons subject to tonic inhibition. This increase of the hierarchical level of structures from single neurons to a network of populations allows one to compare firing activity in small and large systems.

3.1 Tonic inhibition in single neurons

Anaesthetic agents like propofol enhance tonic currents in ESRs located on the dendritic branches of single neurons. To understand the neural activity of populations subject to tonic currents in ESRs, first we study the firing rate of a single neuron subject to conductance fluctuations induced by incoming Poisson-distributed spike trains and subject to two levels of tonic inhibition. The subsequent study of the nonlinear gain of such neurons reveals new insights into tonic inhibition action. Both studies consider both Type-I and Type-II neurons.

3.1.1 Firing rate

In Type-I neurons, it is well-known that tonic inhibition has a strong subtractive effect on the firing rate (Holt and Koch 1997; Gabbiani et al. 1994). According to our statistical approach the single neuron firing rate reads

$$\begin{array}{@{}rcl@{}} F_{s}(G_{E},G_{ton})={\int}_{-\infty}^{\infty}p_{s}(g_{e}-G_{E}){\Theta}(V_{m}(g_{e},G_{ton})-V_{th})\\ f(V_{m}(g_{e},G_{ton}))dg_{e} \end{array} $$

(12)

with V defined in Eq. (6) and f taken from Eq. (5). Figure 2 confirms the subtractive effect in the F−G _E curve for two levels of tonic inhibition G _ton in accordance to previous studies (Mitchell and Silver 2003; Ulrich 2003). In addition, Fig. 2 affirms the analytical description (12) in good accordance to numerical results.

Fig. 2

Tonic inhibition shifts the firing rate-curve to larger conductances in Type-I neurons. The statistical firing rate F _s in Eq. (8) is plotted with respect to the mean excitatory conductance G _E in the absence (control, G _ton 0nS) and presence of tonic inhibition (G _ton = 1nS). The symbols denote numerical results from simulations of the LIF-model (1) and the lines represent the analytical function Eq.(12) under control conditions (filled dots and solid line) and in the presence of tonic inhibition (filled diamonds and dashed line). Synaptic inhibition is neglected, i.e. g _i = 0

The shift to larger excitatory conductances while increasing the tonic inhibition can be understood simply by taking a close look at Eq. (6). For V _m = V _t h, dg _e /dg _i > 0 if E _e > E _i which holds in most cases, i.e. tonic inhibition increases the firing threshold. Moreover, tonic inhibition increases the effective time constant τ, cf. Eq. (6), and thus slows down the firing and decreases the firing rate.

Moreover, in Fig. 2 it seems that the slope of the F _s −G _E curve is different for the control and tonic inhibition condition. This indicates an additional divisive effect, see below.

Considering the same distributions of synaptic and extra-synaptic activity in Type-II neurons as in Type-I neurons, Fig. 3 shows the single neuron firing rate subject to the mean excitatory conductance G _E and reveals a rather different firing rate curve compared to Type-I neurons. First, the neuron does not fire outside a certain interval of excitatory conductances which confirms previous findings on the effect of the external current I _app in the absence of synaptic receptors and ESRs as known from isolated noiseless Morris-Lecar neurons (Borisyuk 2005), cf. Fig. 3 (control condition). Moreover adding tonic inhibition shrinks the interval of excitatory conductances for which the neuron fires, which, to our best knowledge, is a new finding. These findings reveal the fundamental difference between type-I and type-II neurons in their response to tonic inhibition.

Fig. 3

Tonic inhibition shrinks the firing interval in Type-II neurons. (a) The firing rate of the linearised model F _s , cf. Eq. (15), for non-distributed values of g _e (filled circles for G _ton = 0mS, open circles for G _ton = 1.0mS) and distributed values of g _e (solid line for G _ton = 0mS, dashed line for G _ton = 1.0mS). (b) The numerically determined firing rate subject to mean excitatory conductance G _E for G _ton = 0mS (solid line with filled dots for data points) and G _ton = 1.0mS (dashed line with diamonds for data points)

To better understand the results, let us consider analytically the resting state potential of the Morris-Lecar model Eq. (7) and its stability. For the constant conductance g _e the resting potential $\bar {V}$ stipulates dV/dt = 0, dw/dt = 0 in Eqs. (7) leading to the implicit equation

$$\begin{array}{@{}rcl@{}} &&I_{app}-g_{e}E_{e}-g_{ton}E_{ton}-g_{L}E_{L}\\ &&=g_{Ca}m_{\infty}(\bar{V})(\bar{V}-C_{Ca})+g_{K}w_{\infty}(\bar{V})(\bar{V}-V_{K})\\&&\quad+(g_{e}+g_{ton}+g_{L})\bar{V}~. \end{array} $$

(13)

Linearising Eqs. (7) about the resting state given by $\bar {V}$ and $\bar {w}=w_{\infty }(\bar {V})$ and assuming $\tau _{w}\approx \tau _{w}(\bar {V})$ (Borisyuk 2005) yields the condition for an oscillatory instability:

$$\begin{array}{@{}rcl@{}} &&K(g_{e},g_{ton})=\\ &&-\phi C/\tau_{w}-\left(g_{Ca}m_{\infty}^{\prime}(\bar{V})(\bar{V}-V_{Ca})+g_{Ca}m\infty(\bar{V})\right.\\ &&\kern5pt\left.+g_{K}w_{\infty}(\bar{V})+g_{e}+g_{ton}\right)>0~.\\ && \end{array} $$

(14)

The condition K(g _c , g _ton )=0 defines the critical frequency ν _c = ν _c (g _c , g _ton ) and for K(g _e , g _ton )>0 ν(g _e , g _ton ) is the frequency above the Hopf-bifurcation with which the system oscillates close to the stationary state. Hence the analytical firing rate reads:

$$\begin{array}{@{}rcl@{}} f_{ana}(g_{e},g_{ton})=\nu(g_{e},g_{ton}){\Theta}(g_{e}-g_{1}){\Theta}(g_{2}-g_{e}) \end{array} $$

with the lower and higher critical conductances g _c = g ₁ and g _c = g ₂, respectively. Figure 3(a) shows the f _ana −g _e -curve (symbols) for control and tonic inhibition. Considering Poisson-distributed input spike trains to the excitatory synapses, g _e and g _ton are taken from the distribution (10) and the resulting firing rate (based on the linear approximation above) is a convolution of f _ana (g _e , g _ton ) and p _s (g _e −G _E , g _ton )

$$F_{s}(G_{E},G_{ton})={\int}_{-\infty}^{\infty}p_{s}(g_{e}-G_{E},G_{ton})f_{ana}(g_{e},g_{ton})dg_{e} $$

(15)

Figure 3(a) shows the resulting firing rate function F _s (lines) from Eq. (15). We observe that the interval borders of the firing rate function are smoothed and increasing tonic inhibition decreases the firing rate. The numerically computed mean firing rate obtained from a single stochastic Type-II model neuron (Fig. 3(b)) shows good qualitative accordance to the analytical finding.

However, it is important to mention that the analytical result in Fig. 3(a) is based on the linear approximation of the Morris-Lecar model close to its stationary state, whereas the numerical solution shown in Fig. 3(b) involves the highly nonlinear dynamics of the model. This difference emerges in the firing rates of simulated neuron where it is slightly smaller compared to the analytical firing rate close to the Hopf bifurcation. In addition, increasing tonic inhibition slightly increases the firing rate in the interval center, whereas it decreases the firing rate in the full interval in the full model.

To understand the difference between the analytical and numerical result, Fig. 4 shows the system trajectories in phase space below (subthreshold) and beyond (superthreshold) the stability threshold for two tonic inhibition values. Most prominently, the trajectories evolve along a regular spiral close to the stationary state (spiral centers in Fig. 4, subthreshold) well below the firing threshold at V = 0mV, whereas the trajectories perform a deformed periodic orbit far from the stationary state beyond the stability threshold, cf. Fig. 4 (right panel). Equation (15) defines the frequency of the Hopf instability, i.e. the frequency with which the system oscillates close to the stationary state. Hence this description is correct if the trajectories remain close to the stationary state in the super-threshold condition. However, Fig. 4 (right panel) reveals that super-threshold activity exhibits a nonlinear orbit different from the linear spirals with a periodic time different from the (linear) Hopf frequency. The consecutive times the trajectory passes through the threshold with dV/dt > 0 is the interspike interval. Hence, the firing rate is different from the critical frequency as observed in Fig. 3.

Fig. 4

In Type-II neurons, the analytical frequency close to stability threshold is different from the spike rate. Left panel: the subthreshold trajectories show stable foci about the stable stationary state in the control condition (black, g _E = 1.0mS, G _ton = 0.0mS) and for tonic inhibition (red, g _E = 1.5mS, G _ton = 0.2mS). Right panel: superthreshold trajectories exhibit spirals close to the unstable resting state but nonlinear orbits far from the stationary states for the control condition (black, g _E = 1.1mS, G _ton = 0.0mS) and for tonic inhibition (red, g _E = 1.53mS, G _ton = 0.2mS). The numerical firing threshold is set to V = 0mV

3.1.2 Nonlinear gain

The slope of the firing rate, also called the nonlinear gain, is proportional to the neuron responsiveness to external stimuli or the afferent activity from other neurons. It is an important parameter to understand the dynamics of neurons in a network subject to modified receptor properties. Figure 5 presents the slopes for two levels of tonic inhibition in both neuron types. Firstly, the nonlinear gain is non-symmetric to the inflection point for Type-I neurons and exhibits a maximum value for a certain level of tonic inhibition. In contrast in Type-II neurons, the absolute value of the maximum gain value decreases slightly with increasing tonic inhibition.

Fig. 5

The nonlinear gain of the single neuron firing rate in the presence of tonic inhibition. Tonic inhibition may increase the nonlinear gain in Type-I neurons (Leaky-Integrate and Fire) but decreases its absolute value in Type-II neurons (Morris-Lecar). Parameters are taken from Fig. 2 and 3

To gain further insights, Fig. 6 shows the nonlinear gain of Type-I neurons subject to tonic inhibition levels for some specific mean excitatory conductances. Increasing tonic inhibition may decrease (G _E = 0.15nS) or first increase and then decrease (G _E = 0.4nS and G _E = 1.0nS) the nonlinear gain. In addition, there is an optimal combination of excitatory and tonic inhibition conductance for which the nonlinear gain is maximum. Analytical investigations (not shown) confirm this numerical finding.

Fig. 6

The nonlinear gain of Type-I neurons subject to tonic inhibition level for different excitatory conductances G _E = 0.15nS, G _E = 0.4nS and G _E = 1.0nS. Increasing tonic inhibition may decrease or increase the nonlinear gain subject to the excitatory conductance. Parameters are taken from Fig. 2

3.2 Tonic inhibition in a single neuron population

After the study of single neurons, the study of a population of such neurons promises to give some mor insight into the effect of anaesthetic drugs via ESRs. Similar to the previous section, the subsequent paragraphs shows tonic inhibition effects on the firing rate and nonlinear gain in neural populations. Moreover, the work considers the case of sparsely-coupled neurons and shows the link to neural mass models by deriving a new transfer function for Type-I neurons subject to tonic inhibition.

3.2.1 Population firing rate

Mathematically, for type-I neurons the population firing rate function reads

$$\begin{array}{@{}rcl@{}} F_{I}(G_{E},G_{ton},\bar{V}_{th})&=&{\int}_{-\infty}^{\infty}{\int}_{-\infty}^{\infty}p_{s}(g_{e}-G_{E},G_{ton}){\mathcal N}(V_{th}-\bar{V}_{th})\\ &&\times{\Theta}(V_{m}(g_{e},G_{ton})-V_{th})f(V_{m}(g_{e},G_{ton}))dg_{e}dV_{th}~. \end{array} $$

(16)

Since the further analytical treatment of populations of Type-II neurons would well exceed the major aim of this work, the subsequent paragraphs consider numerical simulations of Type-II neural populations only.

Figure 7 shows the population firing rate of Type-I neurons for two tonic inhibition levels and we observe a smoothing of the F _s −G _E curve by the distributed thresholds. Importantly, the numerical (symbols) and analytical (lines) results for the F−G _E -curve show very good accordance. Moreover, increasing the heterogeneity by an increased variance of the firing threshold distribution $\sigma ^{2}_{th}$ renders the F−G _E -curve flatter and hence decreases the nonlinear gain. Since the nonlinear gain determines the response of the population to external inputs, the heterogeneity reduces the responsiveness of the population. The figure also clearly reveals that the responsiveness of heterogeneous populations is well reduced in the presence of tonic inhibition because the nonlinear gain of the population firing rate is much smaller.

Fig. 7

Population firing rate of heterogeneous Type-I neural populations subject to tonic inhibition. Tonic inhibition induces a strong subtractive effect, while heterogeneity renders the F−G _E -curve more flat and yields a strong divisive effect. The circles (G _ton = 0mS) and diamonds (G _ton = 1.0mS) denote results obtained by numerical simulations of a set of N = 200 Leaky-Integrate and Fire model neurons. The solid (G _ton = 0mS) and dashed (G _ton = 1mS) lines represent the population firing rate given by the analytical expression in Eq. (16). The two levels of heterogeneity of firing threshold distributions are color-coded (black: σ _th = 0.1mV, blue: σ _th = 10.0mV). Black lines resemble well the results in Fig. 2 due to the low level of heterogeneity, whereas the blue lines show the effect of hetereogeneity

In a population of Type-II neurons, tonic inhibition is expected to shrink the firing interval in a way similar to the previous results (Fig. 3). Figure 8 affirms this finding in single neurons for two different levels of firing threshold heterogeneity. Moreover, increasing the heterogeneity smoothens the F−G _E -curve and thus, diminishes the population firing rate in the firing interval, increases it outside, and in total diminishes the nonlinear population gain. Mathematically this smoothing effect results from the convolution by the distributed firing thresholds. Hence heterogeneity reduces the responsiveness of the population. In addition, tonic inhibition does not seem to affect much the nonlinear population gain in contrast to type-I neurons and does change slightly the responsiveness of the population only. Although this aspect of tonic inhibition in type-II neurons needs a more detailed discussion, this would exceed the major aim of the present study and we refer to future work.

Fig. 8

Population firing rate of heterogeneous Type-II neural populations subject to tonic inhibition. Tonic inhibition shrinks the firing interval, while heterogeneity smoothens the F−G _E -curve and renders it more flat. The circle-solid line (G _ton = 0mS) and diamond-dashed line (G _ton = 1.0mS) denote numerical results of simulations of a set of N = 200 Morris-Lecar model neurons. The line color denotes the levels of heterogeneity of firing threshold distributions (black: low heterogeneity with σ _app = 0.1μA; blue: high heterogeneity with σ _app = 10.0μA)

3.2.2 Nonlinear population gain

The previous paragraphs have indicated that the nonlinear population gain may change with an increase of tonic inhibition. To quantify this gain change, Fig. 9 presents the nonlinear population gain for both neuron types and for two levels of tonic inhibition. For both Type-I and Type-II neurons, tonic inhibition decreases the nonlinear population gain and thus diminishes the responsiveness of the populations to external stimuli.

Fig. 9

The nonlinear gain of the population firing rate function F(G _E ) for Type-I (Leaky-Integrate and Fire) and Type-II (Morris-Lecar) neurons in the presence of tonic inhibition. The results for Type-I neurons are based on the analytical expression, the results of Type-II neurons are gained numerically by simulating the population firing rate from N = 200 neurons, and afterwards the derivative is computed numerically. For the other parameters, see Fig. 7 and 8

A more detailed study of Type-I populations (Fig. 10) reveals that the nonlinear population gain exhibits a maximum while increasing tonic inhibition, and the gain exhibits a global maximum at low levels of mean excitatory conductance. However, a similar maximum gain as revealed in single Type-I neurons for larger excitatory conductances (Fig. 6) has not been found.

Fig. 10

Tonic inhibition may maximize the nonlinear population gain dependent on the mean excitatory conductance. For parameters, see Fig. 9

The nonlinear population gain may be computed analytically by taking the derivative of F in Eq. (16) with respect to G _E . Here it is necessary to note that the variance of the incoming spike trains depends on the mean firing rate, and thus σ _e = σ _e (G _E ). We gain the expression:

$$\begin{array}{@{}rcl@{}} &&F^{\prime}=\frac{dF(G_{E},G_{ton},\bar{V}_{th})}{dG_{E}}=\\ &&{\int}_{-\infty}^{\infty}{\int}_{-\infty}^{\infty}q_{s}(g_{e},G_{E},G_{ton}){\mathcal N}(V_{th}-\bar{V}_{th}){\Theta}(V_{m}(g_{e},G_{ton})\\&&\kern6pc-V_{th})f(V_{m}(g_{e},G_{ton})dg_{e}dV_{th}~\\ \end{array} $$

(17)

with

$$\begin{array}{@{}rcl@{}} q_{s}(g_{e},G_{E},G_{ton})=w_{e}\left(-\tau_{e} \frac{\partial p_{s}(x,\sigma_{e})}{\partial x}|_{x=g_{e}-G_{E}}\right.\\ \left.+\sqrt{\frac{\tau_{e}}{8}}\frac{\partial p_{s}(g_{e}-G_{E},y)}{\partial y}|_{y=\sigma_{e}}\right)~\\ \end{array} $$

(18)

which will be helpful in the next section on connected neurons.

3.2.3 Connected neural population

In the previous paragraphs, we have assumed uncoupled neurons for simplicity while cortical neurons are sparsely connected (Binzegger et al. 2004). To render the previous analytical description more realistic, now the input to single neurons is a sum of external uncorrelated spike trains and the single neuron activity of other neurons in the same population. The subsequent paragraphs shows how to employ a mean-field approximation considering the input from other neurons as being small. This approach allows us to derive a modified population firing rate distribution.

In a first approximation, the input spike rate from other neurons of number N is:

$$\begin{array}{@{}rcl@{}} \lambda_{j}={\sum}_{j=1}^{N} w_{jl}F_{s,l}~, \end{array} $$

F _{s, l} is the spike rate (12) of neuron l in the same population and w _jl > 0 is the synaptic weight of input from neuron l to neuron j. Hence the mean input rate and its variance read

$$ {G_{e}^{j}}=G_{E}+w_{e}\tau_{e} \sum\limits_{l=1}^{N} w_{jl}F_{s,l} $$

(19)

$$\begin{array}{@{}rcl@{}} {\sigma_{e}^{j}}&=&\sqrt{\frac{{w_{e}^{2}}\tau_{e}}{2}\left(\lambda+\sum\limits_{l=1}^{N} w_{jl}F_{s,l}\right)}\\ &\approx&\sigma_{e}+w_{e}\sqrt{\frac{\tau_{e}}{8}}\sum\limits_{l=1}^{N} w_{jl}F_{s,l}~. \end{array} $$

(20)

with the assumption of weak coupling ${\sum }_{l=1}^{N} w_{jl}F_{s,l}/G_{E}\ll 1$ resulting either from strong sparseness or low synaptic weights. For Type-I neurons, re-writing the probability density function (10) of neuron j

$$\begin{array}{@{}rcl@{}} p_{s,j}(g_{e}-{G_{e}^{j}},{\sigma_{e}^{j}})&=&\frac{1}{\sqrt{2\pi}{\sigma_{e}^{j}}}e^{-(g_{e}-{G_{e}^{j}})^{2}/2({\sigma_{e}^{j}})^{2}}~ \end{array} $$

and expanding it about the uncoupled state we gain

$$\begin{array}{@{}rcl@{}} p_{s,j}(g_{e},{G_{e}^{j}})&\approx& p_{s,j}(g_{e}-G_{E},\sigma_{e})\\ &&+q_{j}(g_{e}-G_{E},\sigma_{e})\sum\limits_{l=1}^{N} w_{jl}F_{s,l} \end{array} $$

(21)

with ${\sigma _{e}^{j}}={\sigma _{e}^{j}}({G_{e}^{j}})$ and the nonlinear gain function q _l taken from (18). Then the population firing rate for Type-I neurons F reads

$$\begin{array}{@{}rcl@{}} \bar{F}(G_{E},G_{ton},\bar{V}_{th})&=&\frac{1}{N}\sum\limits_{j=1}^{N} F_{s,j}\\ &=&F_{I}(G_{E},G_{ton},\bar{V}_{th})+\frac{1}{N}\sum\limits_{j,l=1}^{N}Q_{j}w_{jl}F_{s,l}~ \end{array} $$

(22)

with

$$\begin{array}{@{}rcl@{}} Q_{j}({G_{e}^{j}},G_{ton},V_{th}^{j})={\int}_{-\infty}^{\infty}q_{j}(g_{e},{G_{e}^{j}},G_{ton}){\mathcal N}(V_{th}^{j}-\bar{V}_{th})\\{\Theta}(V_{m}(g_{e},G_{ton})-V_{th}^{j})f(V_{m}(g_{e},G_{ton}))dg_{e}~. \end{array} $$

and the population firing rate of uncoupled neurons (16). If the inter-neuron coupling is weak as assumed before, then the firing rate of each neuron is the mean-field firing rate of the population, i.e. $F_{s,l}\approx \bar {F}$. For identical small weights w _ij = γ/N > 0, finally we gain

$$\begin{array}{@{}rcl@{}} \bar{F}(G_{E},G_{ton},\bar{V}_{th})&=&F_{I}(G_{E},G_{ton},\bar{V}_{th})+\gamma\bar{F}\frac{1}{N}{\sum}_{j=1}^{N}Q_{j}\\~ &&=F_{I}(G_{E},G_{ton},\bar{V}_{th})+\gamma\bar{F}F^{\prime}_{I}(G_{E},G_{ton},\bar{V}_{th})~\\ \end{array} $$

and consequently

$$ \bar{F}(G_{E},G_{ton},\bar{V}_{th})=\frac{F_{I}(G_{E},G_{ton})}{1-\gamma F^{\prime}_{I}(G_{E},G_{ton})} $$

(23)

where $F^{\prime }$ is the nonlinear population gain taken from Eq. (17) and we used ${\sum }_{j} Q_{l}/N\approx \int Q(G_{E},G_{ton},V_{th}) dV_{th}$ which is valid for a large numnber of neurons in the population. Equation (23) shows that the larger the nonlinear gain, the larger the deviation of the mean-field population firing rate from the population rate of uncoupled neurons. In more details, if $F^{\prime }>0$ as in Type-I neurons, then the weak coupling of neurons yields an enhancement of the population firing rate. Because tonic inhibition enhances the nonlinear gain, it has a similar effect as an increased neural coupling in the network. In contrast, populations of Type-II neurons exhibit $F^{\prime }>0$ for smaller excitation and $F^{\prime }<0$ for larger excitation yielding an increase and decrease of the population firing rate by coupling of neurons. Since tonic inhibition reduces the nonlinear gain of Type-II neurons slightly only, it poorly modifies the effect of coupling.

3.2.4 Extended neural mass models

After studying the tonic inhibition effect in spiking neural networks, the question arises how one can use the gained insights in other neural population models, such as the neural mass or neural field models (Bressloff 2012). A major element in neural mass models is the nonlinear transfer function S, which is the population firing rate subject to the mean dendritic activity in the population. In the standard derivation of the function (Bressloff 2012), one assumes that the membrane potential at synaptic receptors V(t) is always close to the resting membrane potential V _rest . This assumption involves Type-I neurons in which the time constant of the neuron membrane is small compared to the time scale of the synaptic response given by the conductance g(t). Consequently, the voltage-gated current at the synapse I(t)=g(t)(V(t)−E) induced by an incoming spike with the reversal potential of the corresponding ion channel at the synaptic receptor E reads I(t)≈g(t)(V _rest −E), and the corresponding extracellular potential is approximately U(t)∼g(t). Considering many receptors and neurons, the spatial and temporal mean of this potential is one of the activity variables in neural mass models. The transfer function S depends on this mean variable U which, in a more general formulation, includes all potentials U _j generated by currents at synaptic receptors or ESRs, i.e. $S=S[{\sum }_{j} U_{j}]$. For instance, in the presence of excitatory and inhibitory receptors S = S[U _e −U _i ].

In the presence of incoming neural spike trains, g(t) is a stochastic process with mean and variance given in Eqs. (9). Excitatory synaptic responses and extra-synaptic tonic inhibition lead to corresponding mean conductances G _e and G _ton which are proportional to the corresponding currents which are proportional to mean extra-cellular potentials, i.e. U _e = k ₁ G _E and U _ton =k ₂ G _ton with constants k ₁, k ₂ > 0. Moreover, we identify the population firing rate in the neural mass model with the population firing rate F given by Eq. (16) derived from spiking neural networks of type-I neurons. This identification resembles very well the original derivation of the population firing rate (Amit 1989; Wilson and Cowan 1972; Hutt 2012) where neurons are considered as McCulloch-Pitts neurons, i.e. f(V _m (g _e , G _ton ))=Θ(V _m −V _th ). This identification extends neural mass models by considering type-I neurons by the specific choice of f(V _m (g _e , G _ton )) as discussed in a recent work (Hutt 2012). Consequently, the new transfer function in neural mass models for Type-I neurons reads

$$S_{I}=F_{I}[U_{e}/K_{1},U_{ton}/k_{2},\bar{V}_{th}] $$

(24)

However Eq. (24) is hardly useful in analytical studies since the integral involved is not solvable in a closed form. To this end, we suggest to simplify F, but keep major features of the F−G _E curve. A recent preliminary study (Hutt 2012) has shown that one of the most important differences of F compared to the original standard sigmoid function is its missing symmetry to its inflection point, i.e. the nonlinear gain is not symmetric as shown in Fig. 9. Moreover, tonic inhibition has a clear subtractive effect and neglecting the divisive effect of tonic inhibition is a reasonable first approximation. Taking these elements into account, we suggest a new single-neuron firing rate function f _approx :

$$\begin{array}{@{}rcl@{}} f(V_{m}(g_{e},G_{ton}))&\approx&f_{approx}(u_{e}/k_{1},U_{ton}/k_{2},V_{th})\\ &=&f_{max}\left(1-e^{-\gamma (u_{e}-U_{ton}-V_{th})}\right)\\&& {\Theta}\left(u_{e}-U_{ton}-V_{th}\right) \end{array} $$

(25)

with a suitable value of γ > 0. Then the new approximated transfer function reads:

$$\begin{array}{@{}rcl@{}} S_{I,approx}(U_{e},U_{ton},\bar{V}_{th})&=&\frac{1}{2\pi\sigma_{e}\sigma_{th}}{\int}_{-\infty}^{\infty}{\int}_{-\infty}^{\infty}e^{-(u_{e}-U_{e})^{2}/2{\sigma_{e}^{2}}-(V_{th}-\bar{V}_{th})^{2}/2\sigma^{2}_{th}}\\ &&\times f_{approx}(u_{e},U_{ton},V_{th})du_{e}dV_{th}~. \end{array} $$

(26)

Recall that ${\sigma _{e}^{2}}$ depends on G _e by Eqs. (9) and hence ${\sigma _{e}^{2}}=K_{3}U_{e}$ with K ₃ = w _e /2K ₁. The approximation (25) is motivated by its analytical simplicity and the limit case of standard neural mass models for $\gamma \to \infty$

$$ f_{approx}(u_{e}-U_{e},U_{ton},V_{th})\to f_{max}{\Theta}\left(U_{e}-U_{ton}-V_{th}\right)~,\quad \gamma\to\infty~. $$

(27)

Hence, $\gamma <\infty$ reflects biological properties of Type-I neurons. Computing analytically the new transfer function (26) leads to:

$$\begin{array}{@{}rcl@{}} &&S_{I,approx}(U_{e},U_{ton},\bar{V}_{th})=\frac{f_{max}}{2}\left(1+{\Phi}\left(\frac{U_{e}-U_{th}}{\sqrt{2}\sigma(U_{e})}\right)\right)\\ &&-\frac{f_{max}}{2}e^{-\gamma(U_{e}-U_{th})+\gamma^{2}\sigma^{2}(U_{e})/2}\left(1+{\Phi}\left(\frac{U_{e}-U_{th}-\gamma\sigma^{2}(U_{e})}{\sqrt{2}\sigma(U_{e})}\right)\right) \end{array} $$

(28)

with the effective variance $\sigma ^{2}(U_{e})={\sigma _{e}^{2}}(U_{e})+\sigma _{th}^{2}=K_{3}U_{e}+\sigma _{th}^{2}$, the mean firing threshold $U_{th}=U_{ton}+\bar {V}_{th}$ and the Gaussian error function Φ (see the Appendix for more details on the derivation). The first term in (28) represents the sigmoidal function for McCulloch-Pitts neurons subject to Poisson noise and the second term takes into account specifically the Type-I properties for $\gamma <\infty$. We observe that the tonic inhibition contribution U _ton shifts the mean firing threshold $\bar {V}_{th}$, i.e. increasing tonic inhibition increases the mean firing threshold of the population. For illustration, Fig. 11 shows the single neuron firing rate f _approx and the resulting new transfer function in the absence and presence of tonic inhibition.

Fig. 11

The reduced single neuron model and the resulting new transfer function. Panel (a) compares the single neuron firing rate of the Leaky-Integrate and Fire model (dotted line) given in Eq. (5) and the reduced model defined in Eq. (25). Panel (b) presents the resulting new transfer function given in Eq. (28) with $\sigma =\sqrt {18}m$V. Please note that U _e originates from the the dendritic current, it adds up on the resting potential without input E _l and the mean membrane potential in the population is E _l +U _e . Parameters are γ = 1/mV, $\sigma _{th}=\sqrt {2}m$V, K ₃ = 0.5

It is important to point out that the new transfer function allows to study tonic inhibition in neural mass and neural field models (Coombes 2006) that attracts much attention to model e.g. electroencephalographic activity measured during general anaesthesia (Bojak and Liley 2005; Steyn-Ross et al. 2001; Sleigh et al. 2011; Hutt and Longtin 2009; Hutt 2013; Hutt et al. 2013). In this context, one important hypothesis states that the loss of consciousness in subjects originates from a jump of high neural steady state activity to a neural resting state of low activity (Steyn-Ross et al. 2001). Making use of a recent neural field model (Hutt and Longtin 2009; Hutt et al. 2013) involving a fully-connected network of excitatory and inhibitory neurons and excitatory and inhibitory synapses, the spatially constant resting state potential U _rest is given implicitly by:

$$\begin{array}{@{}rcl@{}} U_{rest}=(a_{e}-a_{i}p)S_{I,approx}[U_{rest}-U_{ton}-\bar{V}_{th}]~. \end{array} $$

(29)

This resting state reflects a state of spatially constant population activity where all neurons are highly synchronized. This state contrasts to the activity states in sparsely-connected populations investigated in the sections above. For the sake of simplicity, here we assume an identical transfer function S _{I, approx} for excitatory and inhibitory neurons with identical mean firing thresholds $\bar {V}_{th}$. The constants a _e and a _i in Eq. (29) are the excitatory and inhibitory synaptic gain, resp., and p ≥ 1 reflects the synaptic action of the anaesthetic drug propofol on synaptic receptors. The value p = 1 reflects the absence of propofol while p−1 is proportional to the on-site concentration of propofol.

Propofol affects both synaptic and ESR action, but the relation of propofol on-site concentration and the level of tonic inhibition is not well-understood. Hence a first ansatz is the linear relationship U _ton = k⋅p for simplicity, where k > 0 represents the sensitivity of ESRs to propofol. Figure 12(a) presents the resting states U _rest subject to the drug concentration factor p for three different values of k. We observe the occurence of three resting states for smaller values of p where the center branch is linearly unstable (dashed line, analysis not shown). For larger p a single resting state at a low potential exist only revealing a saddle-node bifurcation. The plot illustrates the phase transition hypothesis: starting at a high activity level resting state before drug induction (p = 1), increasing the drug concentration leads to the loss of the resting state at high activity level and the neural system drops to the only existing stable low activity resting state reflecting the loss of consciousness. Moreover, the corresponding nonlinear gain at the upper stable stationary state (Fig. 12(b)) increases with larger tonic inhibition (k is larger with higher tonic inhibition level) and while the system approaches the saddle-node bifurcation point. The gain of the lower stationary state is close to zero. The gain enhancement reflects the increasing sensitivity of ESRs to external stimuli or input from other areas. Summarizing, increasing the tonic inhibition increases the nonlinear gain of the high-activity stationary state.

Fig. 12

The resting state potential (a) and the nonlinear gain (b) subject to the drug concentration factor p. Solid (dashed) lines encode stable (unstable) stationary states. Parameters are a _e = 0.17, a _i = 0.07, $\gamma =1.0/m\textit {V},~\sigma _{t}h=\sqrt {2}m$V, K ₃ = 0.5

3.3 Tonic inhibition in a network of networks: EEG and population firing patterns

The anaesthetic propofol modifies GABAergic receptor dynamics and changes neural firing activity, exerting either inhibition or even excitation (Borgeat et al. 1991; McCarthy et al. 2008; Ching et al. 2010; Lewis et al. 2012). It is also known that anesthetic agents such as propofol induce changes in the electroencephalographic recordings (EEG) (Purdon et al. 2013; Cimenser et al. 2011; Gugino et al. 2001) indicating that they alter the subthreshold activity of excitatory neurons since EEG is known to originate from subthreshold dendritic currents on spatially aligned apical cortical dendrites (Nunez and Srinivasan 2006). In order to investigate how tonic inhibition affects sub-threshold activity and hence induces changes in EEG and how it modifies neural firing activity in a biologically realistic network, we perform a numerical study of the population spiking activity and the power spectra of the subthreshold activity in excitatory neurons.

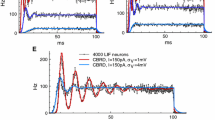
Figure 13 presents the behavior of the network shown in Fig. 1 when tonic inhibition is applied. Re-call that the network involves a population of excitatory type-I neurons and a population of inhibitory type-II neurons and all neurons are coupled sparsely to each other. Tonic inhibition affects all neurons. In the absence of tonic inhibition (Fig. 13(a)), the network displays synchronized patterns of oscillations in both networks at about 9.5Hz (α-band) visible in the raster plots of the two populations. This oscillation also shows up in the power spectrum of the subthreshold activity of the pyramidal neuronal population.

Fig. 13

Raster plots of inhibitory and excitatory populations and smoothed power spectrum of the membrane voltage of the excitatory cells. (a) without tonic inhibition. (b) tonic inhibition, x = 0.3, i.e. g _ton = 6μS and g _ton = 30μS in excitatory and inhibitory neurons. (c) tonic inhibition x = 0.8, i.e g _ton = 16μS and g _ton = 80μS in excitatory and inhibitory neurons

When weak tonic inhibition is added (Fig. 13(b)), the spiking activity slows down slightly in both networks while the synchrony visibly decreases. This can be thought of as a right-shift of the F−G _E curve of type-I neurons yielding a lower population firing rate. In type-II neurons the excitation window becomes smaller while neurons close to the excitation window center decrease their frequency slightly only. Moreover, the frequency of the maximum power spectral density shifts to lower values, i.e. the amplitude of the α−activity decreases. As the level of tonic inhibition keeps increasing (Fig 13(c)), the neurons fire less synchronized accompanied by an extinction of α-activity in the excitatory neuron firing. A detailed study on when the α−activity vanishes reveals that the frequency of the excitatory population decreases while increasing tonic inhibition whereas the inhibitory population retains its α−rhythm much longer (not shown). This is in line with the finding in the previous sections above on single type-II neurons and their populations: tonic inhibition decreases the excitation window, but almost maintains the firing frequency in the window center. In addition, the subthreshold activity of the excitatory population decreases in power as well.

Finally, when the level of tonic inhibition increases further (g _ton = 24μS for type-I neurons and g _ton = 120μS for type-II neurons, not shown), the firing of excitatory neurons stops and the inhibitory neurons remain active only for a transient period before its neuronal activity fully dies out as well. In this case, the F−G _E curve for excitatory (type-I) neurons is shifted much to the right to exhibit a low population firing rate and the excitation window for the inhibitory (type-II) neurons has vanished.

To further quantify the effect of tonic inhibition on the network activity, Fig. 14(a) presents the intra-population spike coherence in the excitatory and inhibitory population and the inter-population spike coherence between the excitatory and inhibitory population. The spike coherence in the excitatory population (dashed grey curve) decreases monotonically with the increase of tonic inhibition. In contrast the spike coherence of the inhibitory population (plain black curve) exhibits a minimum at x≈0.45 and increases as the activity of the excitatory population becomes more random for x > 0.45. The spike coherence between the pyramidal and the interneuron populations (plain grey curve) is maximum at about x = 0.16 (zoom in not shown), a further increase of tonic inhibition diminishes the spike coherence in conjunction with the reduction of the excitatory activity. A computation of the spike coherence measure κ for various bin sizes τ shows that it does not increase linearly with τ (not shown) and hence the latter interpretation holds, cf. (Wang and Buzsáki 1996).

Fig. 14

Summary of the effects of tonic inhibition on the synchrony and the subthreshold activity of the spiking neural network. (a) Spike coherence measure of the neuronal population as a function of propofol concentration (x). b) Ratio of the power values in the δ-, 𝜃− and β−band and the power in the α

Moreover, Fig. 14(b) shows that the ratio between the amplitude of δ-rhythms and the amplitude of α-rhythms (dashed black curve) increases as a sigmoid-like function of the propofol concentration x and becomes larger than 1 from x = 0.575, namely the quantity of α-rhythms is then smaller than the quantity of δ-rhythms. The ratio between the amplitude of 𝜃 and α-rhythms (plain grey curve) increases for x < 0.6, becoming larger than 1 for x > 0.49. The curve of the 𝜃-ratio crosses the curve of the δ-ratio at x = 0.65 where the amplitude of δ−activity remains higher. The ratio between β− and α−activity (dotted grey line) is larger than the 𝜃−α ratio for x < 0.19, and larger than the δ−α ratio for x < 0.32. For larger values of x the 𝜃 ratio then is smaller than the two other ratios reaching a maximum for x = 0.8.

4 Discussion

4.1 Decrease of population firing rate

Tonic inhibition induces a shunting effect and inhibits firing in both Type-I and Type-II neurons by a decrease of both the single neuron (cf. Figs. 2 and 3) and population firing rates (Figs. 7, 8 and 13). Such an effect is well-known in single neurons (Koch 1999; Mitchell and Silver 2003; Ulrich 2003; Brickley and Mody 2012) but, to our best knowledge, has not been found yet in populations. We mention that most previous studies investigate the effect of shunting inhibition on Type-I neurons, whereas the present work is one of the first to consider Type-II neurons as well. The most prominent difference between Type-I and Type-II neurons is the way how the diminuation of neural firing emerges. In Type-I neurons, tonic inhibition decreases the neuron excitation leading to a strong subtractive effect, whereas tonic inhibition in Type-II neurons shrinks the window of excitation level of the neuron. This latter specific effect leads to a strong diminuation of firing activity close to the border excitations, whereas the neurons excited in the center of the excitation interval decrease their firing much less. This stability towards tonic inhibition explains the robustness of Type-II tonic firing observed in Fig. 13.

4.2 Both subtractive and divisive effect by tonic inhibition

Figure 2 shows that tonic inhibition moves the firing rate curve horizontally in single Type-I neurons however synchronously affects the nonlinear gain as seen in Figs. 5 and 9 reflecting a divisive effect. This result is in good accordance with the literature on single Type-I neurons, pointing out a subtractive and divisive effect of inhibition (Carandini and Heeger 1994; Doiron et al. 2001). The present work contributes to this discussion and extends previous results by considering neural populations. Moreover, our results reveals a maximum nonlinear gain due to tonic inhibition in single neurons (Figs. 6) indicating an optimal level of tonic inhibition. This effect is also found in neural populations as shown in Figs. 9 and 10 and in the new neural mass model, cf. Fig. 12(b). The nonlinear gain is proportional to the neural firing response to small excitation variations originating from neurons in the same population or other neural structures. As experimental studies indicate that tonic inhibition is supposed to regulate the state of consciousness, e.g. via ESRs (Brickley and Mody 2012; Cavelier et al. 2005; Belelli et al. 2009) and potentiate the action of anaesthetic agents (Kretschmannova et al. 2013), the optimum gain seems to reflect one underlying neural mechanism in the regulation of anaesthetic action and consciousness.

Type-II neurons also exhibit such a local maximum and the absolute value of the nonlinear gain decreases with increasing level of tonic inhibition, cf. Figs. 5 and 9. However, in contrast to Type-I neurons, increasing tonic inhibition does not maximize the gain in Type-II neurons but decreases it only.

4.3 Analytical description of firing rates

The statistical approach employed resembles a previous approach of (Amit and Brunel 1997; Roxin et al. 2011) on Type-I neurons, which however is strongly based on the specific Leaky Integrate-and-Fire model. Our statistical approach promises to apply to more models, such as the Morris-Lecar model for a Type-II neuron.

The work presents both analytical and numerical simulations of tonic inhibition in single neurons and single populations and the analytical results match the numerical simulation results very well in the case of Type-I neurons. For Type-II neurons, the statistical approach is also valid but more difficult to apply because the single neuron firing rate is not known analytically due to the nonlinear dynamical nature for most models. However, the first attempt to consider the firing rate based on a linear approximation yields reasonable accordance with the nonlinear firing rate, cf. Fig. 3. These results point out the power of the statistical approach given in equations (12) and (16). The present work does not proceed the study of these new analytical models since this would exceed the major aim of the work, i.e. the study of tonic inhibition, the analytical insight promises a new avenue of analysis of population firing statistics.

In order to study the impact of tonic inhibition, the first analytical description of population activity neglects the interaction of neurons. A subsequent analytical study of the population firing rate of sparsely connected neurons in section 3.2.3 reveal that the sparse coupling affects the firing rate mainly about the maximum nonlinear gain, cf. Eq. 23, whereas low and high firing rate are poorly affected. Moreover the new population firing rate allows to re-derive the transfer function applied in neural mass and neural field models and gain a novel transfer function taking into account tonic inhibition. This bridge to neural mass models is supposed to have a strong impact on such models due to their growing popularity in computational neuroscience and the growing insight into the importance of tonic inhibition effects in biological neural structures. A first insight gives the study of stationary states in the presence of both phasic and tonic inhibition in the context of propofol anaesthesia, cf. Fig. 12(a). We observe that tonic inhibition lowers the propofol concentration (encoded by the factor p) for which a high-activity stationary state exists, i.e. the stronger the tonic inhibition, the more probable is a low-activity stationary state in neural populations. In addition, the increased sensitivity modeled by the nonlinear gain (Fig. 12(b)) is accompanied by an earlier destruction of the high-activity resting states. This finding is in good accordance with recent experimental findings close to the point of loss of consciousness (Lewis et al. 2012) revealing a dramatic drop of population firing rate. Hence tonic inhibition facilitates the destruction of high-activity resting states and the drop of neural activity to lower activity. Taking up the idea of loss of consciousness in general anaesthesia caused by a jump from high to low activity, as proposed by Steyn-Ross et al. (Steyn-Ross et al. 2001), the previous results indicate that the tonic inhibition facilitates the loss of consciousness.

4.4 Anaesthetic action

On the microscopic level, ESRs are sensitive to anaesthetic drugs such as propofol (Bai et al. 2001; McDougall et al. 2008; Bieda and MacIver 2004) and induce tonic currents at inhibitory GABA _A -receptors. On the macroscopic level, one of the major non-invasive indicators for the depth of anaesthesia in patient is the electroencephalogram (EEG) (Ballard et al. 2012; Sleigh et al. 2011) which is known to originate from electric population activity (Nunez and Srinivasan 2006). To learn more about the impact of tonic inhibition on EEG (see also (Kretschmannova et al. 2013)), Fig. 13 shows the power spectrum of the mean membrane potential which is supposed to be linked to EEG (Nunez and Srinivasan 2006). In the excitatory population, we observe a clear decrease of spectral power in the α−band with increasing tonic inhibition (Fig. 13) similar to previous experimental findings in occipital EEG-electrodes under propofol-anaesthesia (Cimenser et al. 2011; Gugino et al. 2001). Synchronously the decrease of α-power and the enhancement of spectral power in the δ−band in excitatory neurons (Fig. 14) reflect the experimental finding in occipital EEG-electrodes (Cimenser et al. 2011; Gugino et al. 2001).

Since the neural mechanism during loss of consciousness is unknown, several hypothesis have been put forward (Hutt et al. 2013).Besides the hypothesis of Steyn-Ross et al. discussed above, one other prominent hypothesis of (Tononi 2004) and (Mashour 2005) explains loss of consciousness by a loss of functional connectivity between brain areas as revealed experimentally (Boly et al. 2012; Mashour 2005; Murphy et al. 2011; Alkire et al. 2008; Liu et al. 2013; Purdon et al. 2013). Similar model results are found in our spiking neural network revealing clear effects of tonic inhibition on the spike coherence (Fig. 14): tonic inhibition diminishes spike coherence between neurons in the excitatory population (Fig. 14) and in the inter-neuron population for small propofol concentration reflecting a fragmentation of cortical areas as has been found in previous studies (Boly et al. 2012; Lewis et al. 2012; Purdon et al. 2013). Hence ESR action supports neural fragmentation as observed in experiments. Moreover, our study predicts a maximum of spike coherence between excitatory cells and inter-neurons at an intermediate level of anaesthesia what, to our best knowledge, has not been studied experimentally yet.

At a first glance the different EEG-spectral features and their explanations seem to contradict each other. However, we point out that frontal and occipital EEGs are generated in different brain areas involving different neural structures and possible neuron interactions, as revealed in a recent experimental animal study on the anaesthetic effect in prefrontal and occipital visual cortex (Sellers et al. 2013). Our results reveal an initial increase and then decrease of the nonlinear gain in single Type-I neurons and their sparsely-connected populations while increasing tonic inhibition and a gain increase in fully-connected and synchronized populations. The numerical simulations of sparsely-connected networks show a clear diminuation of spectral power in the excitatory population which can be explained by the loss of spike coherence in the population. In contrast, successful neural mass models of EEG (Hindriks and van Putten 2012; Hutt 2013) explain the power increase by an enhanced nonlinear gain. Consequently, the connectivity type of neuron networks and their ability to synchronize may decide whether tonic inhibition yields a diminuation or enhancement of the population gain.

We point out that previous theoretical studies on synaptic anaesthetic action (McCarthy et al. 2008; Ching et al. 2010; Bojak and Liley 2005; Steyn-Ross et al. 2001; Sleigh et al. 2011; Hutt and Longtin 2009; Hutt 2012) are able to describe more spectral phenomena in EEG than the present work. At a first glance this indicates that synaptic action should not be omitted in the description of spectral EEG features. However, these previous synaptic models are limited since they may consider cortex only (Bojak and Liley 2005; Steyn-Ross et al. 2001) or may take into account a cortico-thalamic feedback (McCarthy et al. 2008; Ching et al. 2010) but neglect various sub-cortical structures where the ESRs have been found primarily, such as areas in the reticular activating system (Vanini and Baghdoyan 2013). Hence synaptic models do not give the full picture of the anaesthetic action in the brain. For instance, the strong increase at low frequencies (<1Hz) (Lewis et al. 2012; Sellers et al. 2013) is poorly modeled by synaptic action, but may originate from the slow action of extra-synaptic receptors (Belelli et al. 2009). In addition, the dramatic drop of activity during loss of consciousness (Lewis et al. 2012) indicates a nonlinear jump in neural activity. This transition may be explained in synaptic models by nonlinear interactions (Steyn-Ross et al. 2001; Sleigh et al. 2011; Friedman et al. 2010), or much more simple by a shift of the population firing rate induced by ESR action, cf. Fig. 12.

Summarizing, ESRs supports the reduction of neural activity, be it diminished EEG power or drop of the population firing rate, but it does not explain the characteristic spectral power features observed in Local Field Potentials and EEG which may originate from synaptic anaesthetic action.

5 Conclusion

The experimental observation that extra-synaptic GABA-receptors may play an important role for the information processing in neural populations stimulated us to perform the present theoretical work. We elaborate on a recently proposed statistical approach that allows us to traverse the scales from single-neuron level to mesoscopic population level. This analytical link enables us to derive analytical expressions for the steady-state population firing rate based on the steady-state single neuron firing rate and hence allows to study analytically the effect of extra-synaptic tonic inhibition in neural populations. The present study shows this link for both Type-I (Leaky Integrate-and-Fire) and Type-II (Morris-Lecar) models.

Extra-synaptic GABA-receptors are highly sensitive to anaesthetic drugs and the present work highlights a strong effect of tonic inhibition on the nonlinear gain in single neurons and neural populations. Our work shows in detail different spectral features observed in EEG under anaesthesia induced by the tonic inhibition effect on the nonlinear gain. These findings are in line with previous studies on phasic inhibition (Hindriks and van Putten 2012; Hutt et al. 2013; McCarthy et al. 2008; Ching et al. 2010). We conclude that one of the major effects of tonic inhibition is the control of sensitivity and network interactions by tuning of the nonlinear gain. Future work will extend the analysis of population firing statistics to nonlinear dendritic integration effects of tonic inhibition in single neurons (Zhang et al. 2013) and further elaborate this aspect in the context of populations. This will allow to better explain different EEG-spectral features measured under anaesthesia and validate hypotheses on loss of consciousness.