Abstract
Significant inroads have been made to understand cerebellar cortical processing but neural coding at the output stage of the cerebellum in the deep cerebellar nuclei (DCN) remains poorly understood. The DCN are unlikely to just present a relay nucleus because Purkinje cell inhibition has to be turned into an excitatory output signal, and DCN neurons exhibit complex intrinsic properties. In particular, DCN neurons exhibit a range of rebound spiking properties following hyperpolarizing current injection, raising the question how this could contribute to signal processing in behaving animals. Computer modeling presents an ideal tool to investigate how intrinsic voltage-gated conductances in DCN neurons could generate the heterogeneous firing behavior observed, and what input conditions could result in rebound responses. To enable such an investigation we built a compartmental DCN neuron model with a full dendritic morphology and appropriate active conductances. We generated a good match of our simulations with DCN current clamp data we recorded in acute slices, including the heterogeneity in the rebound responses. We then examined how inhibitory and excitatory synaptic input interacted with these intrinsic conductances to control DCN firing. We found that the output spiking of the model reflected the ongoing balance of excitatory and inhibitory input rates and that changing the level of inhibition performed an additive operation. Rebound firing following strong Purkinje cell input bursts was also possible, but only if the chloride reversal potential was more negative than −70 mV to allow de-inactivation of rebound currents. Fast rebound bursts due to T-type calcium current and slow rebounds due to persistent sodium current could be differentially regulated by synaptic input, and the pattern of these rebounds was further influenced by HCN current. Our findings suggest that active properties of DCN neurons could play a crucial role for signal processing in the cerebellum.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The deep cerebellar nuclei (DCN) perform an important gateway function in the cerebellum, as they provide the sole source of cerebellar output to red nucleus, thalamus, and inferior olive after integrating inhibitory inputs from cerebellar cortical Purkinje cells with excitatory input from brain stem and cortical sources. DCN neurons projecting to the inferior olive are GABAergic (Fredette and Mugnaini 1991) while those projecting to red nucleus and thalamus are glutamatergic (Chan-Palay 1977; Daniel et al. 1987) and show a distinguishable morphology with a slightly larger size (Sultan et al. 2003). Nevertheless, both types of neurons have remarkably similar physiological properties characterized by spontaneous spiking in vitro and a robust postinhibitory rebound spike burst, but show a minor difference in the depth of fast spike afterhyperpolarization (Uusisaari et al. 2007). The hallmark behavior of strong post-hyperpolarization rebound spiking was identified already in early intracellular investigations of DCN intrinsic properties (Gardette et al. 1985a, b; Jahnsen 1986a, b). A T-type calcium current and a sodium plateau current were identified as important contributors to fast and slow components of depolarization underlying rebound spiking, respectively (Llinas and Muhlethaler 1988). The T-type current dependent fast rebound burst is particularly strong in DCN neurons with a high CaV3.1 expression, while it is much weaker in DCN neurons with a predominant expression of CaV3.3 channels (Molineux et al. 2006). Rebounds can also be elicited by strong inhibitory synaptic inputs in vitro (Aizenman and Linden 1999), suggesting that they may be triggered in vivo as well. A requirement of hyperpolarization and rebound spiking to elicit potentiation of mossy fiber synapses onto DCN neurons (Pugh and Raman 2006, 2008) suggests that rebounds might be directly linked to mechanisms of learning. Nevertheless, due to the limited level of hyperpolarization that is reached during GABAA mediated IPSPs and due to shunting of rebound currents in the presence of ongoing synaptic inputs, it is possible that in vivo conditions may not favor rebound behavior (Alvina et al. 2008) unless the inhibitory inputs are very intense (Tadayonnejad et al. 2009). Rebound behavior is certainly not the only possibility of transmitting information through the cerebellar output stage, as dynamic clamp studies in brain slices have shown that the rate of Purkinje cell inputs also results in a rate code of DCN output, and that very brief pauses in Purkinje cell input to DCN neurons reliably trigger individual DCN action potentials (Gauck and Jaeger 2000, 2003).
Computer modeling presents an ideal tool to determine the involvement of intrinsic cellular properties in controlling spike output during complex synaptic input patterns expected in vivo because all system variables can be simultaneously measured and because intrinsic properties can be precisely controlled and arbitrary input patterns can be constructed and repeatedly applied. In the present study we obtained a large sample of whole cell recordings from DCN neurons to characterize their behavior and to act as a template to construct a full morphological compartmental model of DCN projection neurons. The model incorporated active conductances previously established in DCN neurons (Jahnsen 1986b; Raman et al. 2000), and was tuned to replicate our current clamp recordings in vitro. Variants of the model were developed to reproduce the observed heterogeneity in the rebound responses across cells and the multiphasic rebound behavior. We then applied background synaptic input to the model as expected to exist in the in vivo condition (Gauck and Jaeger 2000) to examine how spike rates were affected by different balances of excitation and inhibition. Moreover, we determined how strong inhibitory bursts could engage rebound mechanisms in the presence of synaptic background input. We found that rebound currents can shape the response patterns following strong bursts of inhibition in a robust way, but only under conditions of a relatively hyperpolarized chloride reversal potential. Our study generates several predictions as to the possible role of DCN neuron properties in cerebellar coding.
2 Methods
2.1 Ethics statement
All animal procedures were conducted under an approved Emory IACUC protocol and fully complied with the NIH guidelines on animal care and use.
2.2 Whole cell recordings from brain slices
Whole cell slice recordings from DCN neurons were obtained following the protocol of our earlier dynamic clamp study (Gauck and Jaeger 2000). Here, we used a sample of 129 recorded DCN neurons, which included the neurons reported in our earlier study in regard to responses to dynamic clamp stimuli. We made use of additional traces of spontaneous spiking activity and traces showing responses to hyperpolarizing and depolarizing current injection pulses available for these neurons. Neurons accepted for analysis had spikes overshooting 0 mV and showed stable spontaneous spiking behavior without the injection of a bias current. Briefly, recordings were obtained at 32°C from 13 to 19 day old male Sprague-Dawley rats. The slice medium contained (in mM): NaCl 124, KCl 3, KH2PO4 1.2, NaHCO3 26, CaCl2 2, MgSO4 1.9, glucose 20. Electrodes were filled with: K-gluconate 140, HEPES 10, NaCl 10, EGTA 0.2, MgATP 4, NaGTP, 0.4, spermine 0.05, glutathione 5, 1% biocytin. Excitatory and inhibitory synapses were blocked with 100 μM AP-5, 10 μM CNQX and 40 μM picrotoxin. We calculated a junction potential of ~10 mV for our K-gluconate based intracellular solution (Gauck and Jaeger 2000) and subtracted 10 mV from our recordings to correct for this depolarizing shift.
2.3 Construction of DCN model
Morphology and passive model properties
The morphological reconstruction and fitting of passive parameters for this model were described in a previous publication (Steuber et al. 2004). Briefly, the DCN neuron on which the model morphology is based (Fig. 1(a)) was recorded for passive responses to positive and negative current injection pulses in the presence of blockers for voltage-gated ion channels (in mM: TTX 0.001, TEA 10, 4-AP 2, Cd2+ 0.2, Ni2+ 2, Cs+ 5, amiloride 0.5) and synaptic inputs (in mM: CNQX 0.01 and picrotoxin 0.02). After morphological reconstruction of the recorded neuron and preparation of a GENESIS morphology file a genetic algorithm was used to find the passive parameters of the model that provided an optimal fit to the voltage responses to current injection pulses injected into the original neuron. The passive parameter values we used for the present study were derived from this fitting procedure, and are given by uniform specific RM of 3.56 Ωm2 , RA of 2.35 Ωm, and CM of 0.0156 F/m2. We applied a small hyperpolarizing current pulse to the soma of this passive model to simulate the method by which membrane capacitance has been estimated for DCN neurons in slice experiments (Uusisaari et al. 2007). Fitting an exponential to the observed voltage decay and using the relationship that Cm = τm / RN, our model showed an apparent membrane capacitance (Cm) of 203 pF, which is in good agreement with the apparent Cm of glutamate decarboxylase (GAD) negative DCN neurons (Uusisaari et al. 2007). While remaining errors in the morphological reconstruction and passive parameters can not be excluded, the performance of the active model to moderate variations in passive parameters was quite stable, since the conductance amplitudes of voltage-gated currents dominated over the leak conductance. Using the parameters described here our model (soma and 485 dendritic compartments) had a total membrane resistance of 271 MΩ, a maximal electrotonic length of 0.53 λ from the soma to the most distal dendritic tip, and a mean dendritic electrotonic distance from the soma of 0.2 λ. Thus this model should be considered moderately electrotonically compact, as a voltage step applied to the soma will not decay much in the dendrites (Rall 1959). The axon of the original neuron was not reconstructed, but an artificial 30 compartment axon with nodal and internodal segments was pasted onto our reconstructed cell following a published method (Shen et al. 1999) to allow for an axonal spike initiation zone.
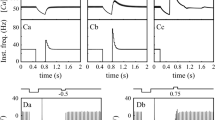
Match of DCN model neuron to physiological properties. (a) Morphology of reconstructed neuron used for our model. The artificially created axon attached to the soma is not shown. (b) (left column) Slice recording of typical DCN neuron. Voltages shown are junction potential corrected (see Section 2). (right column) Sample simulation traces show good match in spike shape and afterhyperpolarization properties with physiology. (c) Spike rates as a function of injected current for three recorded neurons (dotted lines), and the model (solid line). The f-I curve for the model was obtained with rebound conductance densities GNaP of 8 S/m2, GHCN of 1 S/m2, and GGCaT of 2 S/m2. These conductances, however, had little influence on spontaneous activity or on the f-I curve
Active conductances
The kinetics of voltage-gated and calcium-gated channels were modeled using the Hodgkin-Huxley formalism as implemented by the GENESIS tabchannel object (Bower and Beeman 1997). Channels chosen to be present were primarily based on published analyses of DCN neuron conductances (Aizenman and Linden 1999; Jahnsen 1986a, b; Llinas and Muhlethaler 1988; Raman et al. 2000). The model contained the following six active currents to allow baseline spiking behavior: A fast sodium current (INaF) based on DCN kinetics (Raman et al. 2000), a mixture of fast Kv3 family (IfKdr) and slow Kv2 (IsKdr) family delayed rectifiers (Baranauskas et al. 1999; 2003) which together form a TEA sensitive Kdr current that is present in DCN neurons (Raman et al. 2000), a tonic non-specific cation current (ITNC) providing inward current to allow baseline spiking (Raman et al. 2000), a high-voltage activated calcium current (ICaHVA) identified in DCN neurons (Gauck et al. 2001), a purely calcium-gated potassium current (ISK) present in DCN neurons (Aizenman and Linden 1999; Jahnsen 1986b; Raman et al. 2000) that creates a medium-duration spike-afterhyperpolarization (AHP) in DCN neurons (Jahnsen 1986b). The intracellular calcium concentration was modeled as a diffusion shell with calcium inflow from ICaHVA and an exponential decay with a time constant of 70 ms. This extrusion time constant leads to a baseline accumulation of calcium during fast spiking as observed experimentally in DCN neurons (Muri and Knopfel 1994). All channel kinetics were adjusted to a temperature of 32°C as used for our slice recordings by applying a Q10 value of 3.0 for all Hodgkin-Huxley rate constants (Hille 2001). Generally, the kinetics of these channels available from experiments were partly incomplete, and also prone to experimental errors due to space-clamp problems with voltage-clamping in whole neurons (Castelfranco and Hartline 2002). In addition ISK primarily depended on the concentration of calcium, which was modeled in a simplified way. Thus, adjustments of channel kinetics within the margins of experimental uncertainty were undertaken and deemed acceptable when the channel kinetics derived from published voltage-clamp data proved unsuitable to generate good matches with our DCN current clamp traces (see below). The full final parameters for all active conductances are given in the “Supplemental material”.
While the model was able to match physiological spontaneous spiking and responses to depolarizing current injection pulses with this set of six active conductances (see below), it needed three additional conductances to replicate physiological rebound behavior following periods of strong hyperpolarization. Unequivocal evidence exists for the presence of an IHCN in most but not all DCN neurons through the presence of a ‘sag’ in the response to hyperpolarizing stimuli (Aizenman and Linden 1999; Jahnsen 1986a; Raman et al. 2000; Uusisaari et al. 2007). This current has been linked to a depolarizing rebound current following the offset of hyperpolarization (Aizenman and Linden 1999), however, it is not present to a noticeable degree in some DCN neurons with considerable rebound behavior (Jahnsen 1986a). We modeled IHCN with a relatively negative half-activation voltage as demonstrated in DCN recordings (Raman et al. 2000), which excluded a participation of IHCN in ongoing spontaneous spiking behavior without strong hyperpolarizing stimuli. A second rebound conductance present in DCN neurons is given by low-voltage activated T-type calcium channels, which produce a fast spike burst in DCN neurons after strong hyperpolarization (Aizenman and Linden 1999; Llinas and Muhlethaler 1988). A recent study showed that the T-type current (ICaT) underlying strong fast rebound behavior in DCN neurons is of the CaV3.1 subtype (Molineux et al. 2006), for which a very thorough kinetic model was developed for thalamocortical neurons (Destexhe et al. 1998). We adopted these kinetics without further modification. Since CaV3.3 contributes only little to rebound behavior (Molineux et al. 2006) we omitted this channel type from our simulations, and generated weak fast rebounds by low densities of CaV3.1 conductance. We did not connect the inflow of calcium through CaV3.1 channels to the intracellular calcium pool, as all test simulations coupling CaV3.1 to this pool led to poor matches of rebound properties with physiological data due to an excess of ISK activation. This prediction of the model that CaV3.1 should not contribute to the calcium pool activating ISK was borne out in a recent experimental study (Alvina and Khodakhah 2008). Therefore our calcium pool should be viewed as a calcium concentration acting on ISK through a submembrane microdomain coupling it exclusively to ICaHVA.
Finally, a sodium plateau current has been observed in DCN neurons (Jahnsen 1986b; Llinas and Muhlethaler 1988), which in our recordings causes a prolonged (1–5 s) increase in spike rate following strong hyperpolarization (Sangrey and Jaeger 2005). This current is slowly inactivating, characteristic of persistent sodium currents (INaP) (Magistretti and Alonso 1999). We adapted a previous model of INaP (Purvis and Butera 2005) by slowing the activation and inactivation time constants so that current clamp data of the model matched our experimental prolonged rebound periods. In this Hodgkin-Huxley kinetic model, INaP is treated as a separate current from INaF, although experimental findings point to INaP as a special gating mode of the NaF channels (Alzheimer et al. 1993; Brown et al. 1994). There is no experimental support for a specific Markov model of the combined Na channel kinetics, however, and to date no Markov formalism is known that results in improved kinetics than can be obtained with two separate Hodgkin-Huxley formalisms.
The distribution of active conductances in the model was generally not uniform, but changed between the following major divisions of the neuron: axonal, somatic, proximal dendritic, and distal dendritic. Spike currents (INaF, IfKdr, IsKdr) were reduced in the proximal dendrite and absent in the distal dendrite as no experimental evidence points to dendritic spike current. The SK current was also predominantly somatic to generate a strong AHP local to the spike currents. Following the calcium imaging study by Gauck et al. (2001) we added a gradient of T-type calcium conductance with higher density in the dendrite than the soma (2-fold), and a similar gradient for HCN conductance, which is also likely to be predominantly dendritic in DCN neurons (Raman et al. 2000). The axonal, somatic, and dendritic densities for all active conductances in the model are listed in Table 1. Details on the kinetics are found in the supplemental on-line material as well as in the simulation scripts publicly available in the ModelDB repository (http://senselab.med.yale.edu/modeldb/).
Synaptic inputs
Synapses were modeled as biexponential postsynaptic conductance changes, and the times of synaptic activation were controlled by GENESIS timetable objects, which replace presynaptic neurons. Using the synaptic conductance kinetics we have previously employed in dynamic clamp studies of DCN neurons (Gauck and Jaeger 2000, 2003) excitatory (mossy fiber) input was modeled as a mixed AMPA and NMDA conductance while inhibitory (Purkinje cell) input was modeled as a pure GABAA conductance (see “Supplemental material” for detailed equations and parameters). We added mossy fiber inputs to 100 and Purkinje cell inputs to 400 randomly chosen dendritic compartments as well as the soma to reflect the dominance of inhibition on DCN neurons (Palkovits et al. 1977). The total number of synapses is much smaller than found on biological DCN neurons, and each synapse in the model should be considered as representing a population of synapses in the real neurons over a local area of membrane surface. To allow this computationally more efficient scheme, synapses in GENESIS (synchan elements) do not saturate when multiple input events overlap, so that a high rate of inputs to a simulated synapse can stand for a lower rate at multiple synapses in the biological neuron (De Schutter and Bower 1994). Given the larger number of inhibitory inputs expected on the soma than on dendritic compartments, the rate of inhibitory inputs to the soma was always multiplied by 50 with respect to each of the 400 inhibitory dendritic synapses. Thus a rate of 20 Hz used for inhibitory synapses resulted in an average of 8,000 dendritic and 1,000 somatic inhibitory inputs per second. Random synaptic inter-event interval distributions at the specified mean rates were drawn from a third degree Gamma distribution and obtained using the GENESIS timetable object. Control simulations were performed with a higher number of synapses (one excitatory and one inhibitory synapse on each compartment) and proportionally reduced input rates for each synapse. These simulations showed nearly identical spike trains as those with reduced numbers of synapses (see supplemental Fig. 1), thus excluding the possibility that massive input to particular compartments has a significant impact on simulations through local dendritic voltage saturation. While the synaptic conductances we used allow a direct comparison of model performance with our dynamic clamp results (Gauck and Jaeger 2000, 2003) and are based on an experimental study of DCN neurons (Anchisi et al. 2001), more recent publications describe faster unitary EPSC and IPSC kinetics and larger conductance amplitudes (Pugh and Raman 2006; Telgkamp et al. 2004). Thus we performed additional control simulations with synaptic parameters adjusted to these new findings. These control simulations revealed that the model predictions on spike rate control and rebounds with inhibitory bursts (see Section 3) remained robust for changes in unitary conductance parameters (supplemental Figs. 4 and 5).
2.4 Data analysis
To quantify different rebound behaviors after adding rebound currents, simulation data were analyzed using Matlab (MathWorks, Inc., Natick, MA). Traces of instantaneous spike rates were constructed by convolving action potentials (thresholded at −20 mV) with Gaussians to derive a local Gaussian rate code measure (Paulin 1995). In analogy to Paulin (1995), we used Gaussian kernels with a standard deviation inversely proportional to the neuronal firing frequency. Given that the firing rate of DCN neurons undergoes strong fluctuations, in particular during rebound responses, we set the Gaussian standard deviation σk for each spike k to \( {\sigma_k} = \min (IS{I_{{before}}},IS{I_{{after}}})/\sqrt {{2\pi }} \), where ISIbefore and ISIafter are the inter-spike intervals (ISIs) directly before and after the spike. This ensured that the individual contribution of each spike to the local Gaussian rate was limited to the maximum instantaneous rate just before or after it.
2.5 Model limitations
A model by nature presents a simplification of the real system, and thus will only replicate this system within limitations. To address specific questions, it is thus important to build a model that is adequate to match the level of complexity of the dynamics one intends to examine. There are clearly many features of DCN neuron physiology that we did not incorporate into the model described above, partly because they are not necessary at the level of questions we pose, and partly because the experimental literature has not yet adequately explored the necessary parameters to simulate such features with any level of accuracy. For example, we omitted processes from the model that determine slow dynamics such as pump currents, calcium release from stores, and channel phosphorylation. On the other side of the spectrum we omitted stochastic channel activation, full Markov descriptions of ion channels, ion channel subunit heterogeneity, etc. This level of detail would likely add little to the questions we examine and is problematic to model as the parameters specifying these processes remain mostly unknown. Parameters that we are uncertain about also include features that may have a significant impact on the questions we address, as for example the presence of spike currents in dendrites. In this and similar cases we applied the principle of Occam’s razor, i.e. we did not incorporate dendritic INaF and IKdr as they were not required to replicate our experimental data. Overall, our model thus presents a ‘working hypothesis’ of DCN neuron physiology at the time scale appropriate to examine short-term responses to current injection and synaptic input. It is intended to be updated as more experimental results become available, and different levels of dynamics are simulated. Nevertheless, this model presents to date the most complete replication of DCN neuron dynamics available and, as we hope to show convincingly in our results section, allows an exploration of interactions between synaptic and intrinsic conductances that leads to interesting insights about the possible role of DCN neuron conductances in vivo. Most important, the modeling process reveals those gaps in knowledge that are critical for a functional understanding of synaptic integration in the DCN, and can guide future experiments to fill in those gaps. The model will be made fully available on public databases such as ModelDB, including a simulator-independent version in NeuroML format (Gleeson et al. 2010), and we hope it will be adapted to include more processes and updated parameters as our understanding of the DCN improves.
3 Results
3.1 Spontaneous spiking properties of the full morphological DCN model and detailed comparison to slice recordings
DCN neurons in brain slices typically are spontaneously spiking when excitatory and inhibitory inputs are blocked (Gauck and Jaeger 2000). Principal excitatory DCN projection neurons exhibit characteristic features such as a spike waveform with a narrow half-width, distinct phases of fast and slow spike-afterhyperpolarization (AHP), and linear rate increases with current injection (Uusisaari et al. 2007). We acquired a sample of 36 slice recordings of DCN neurons with a discernible fast AHP and thus likely representing glutamatergic projection neurons (Uusisaari et al. 2007) to score the range of detailed spike properties found in this type of neuron (Fig. 1(b)). We found quite variable detailed spike waveforms and frequencies, indicating that the biological neurons may vary substantially in their relative densities of ion channels: 1) spontaneous firing frequency: 0–40 Hz, mean 10.6 ± 8.5 Hz; 2) spike rate during 100 pA current injection: 18–84 Hz, mean 38.4 ± 15.7 Hz; 3) spike amplitude (measured from spike peak to bottom of fast AHP): 54–85 mV, mean 66.4 ± 8.4 mV; 4) spike width at half amplitude: 0.4–1.35 ms, mean 0.74 ± 0.25 ms; 5) depth of fast AHP relative to subsequent afterdepolarization (ADP): 0–6.5 mV, mean 1.7 ± 1.6 mV; 6) delay from spike peak to ADP peak: 2.2–7.5 ms, mean 3.7 ± 1.2 ms; 7) depth of slow AHP from peak of ADP: 4.1–14.7 mV, mean 8.6 ± 2.9 mV.
The overall quality of the model match can be assessed by comparing the voltage traces and injected current—spike rate relationships from sample neurons and the model (Fig. 1(b, c)). When we varied parameters such as GNaF density, GKV3 density, or GSK density in steps as big as 50% increases or decreases we generally found a smooth change in model behavior that reached many values found in the experimental distributions of spike amplitude, spike width, slow AHP depth, etc. Thus, the solution space for this model with varied parameter settings contains a broadly distributed class of behaviors matching the physiological range, similar to observations in other conductance based compartmental models (Achard and De Schutter 2006; Gunay et al. 2008; Prinz et al. 2003). Our final baseline model was within the experimental range for each of the physiological measures listed above. However, there was a noticeable overall hyperpolarized shift by about 10 mV in the model membrane potential trajectory compared to experimental data even after junction potential correction (Fig. 1). This shift was due to a lower Na spike threshold in the model than in the experiments, and could be compensated by a 10 mV depolarizing shift in the activation and inactivation properties of INaF and IKdr compared to the literature values in dissociated neurons (supplemental Fig. 3). This compensation had no significant impact on other aspects of model behavior (supplemental Figs. 3, 4 and 5), again demonstrating the robustness of model behavior against small parameter variations.
Active properties underlying baseline spiking behavior
A plot of the currents underlying the voltage trajectory in the model (Fig. 2) clarifies how the different spike properties of the recorded neurons are matched. As the model lacks NaF and Kdr spike currents in most of its dendrite, action potentials attenuated and broadened as they propagated passively into the dendrite (Fig. 2(a)). The delayed depolarization of the dendrite with respect to the soma resulted in a push–pull mechanism of axial current similar to Purkinje cells (Jaeger and Bower 1999), by which the soma first pushes current into the dendrite during the action potential, but then a substantial current flows back during the AHP and creates the ADP following the fast AHP (Fig. 2(a, b)). These observations in the model lead to the prediction that a dissociated DCN neuron with predominantly a soma remaining would not exhibit the ADP following the AHP.
Somatic and dendritic voltages during an action potential in the model and currents underlying the spontaneous spike cycle. (a) Somatic voltage (red) shows the waveform of a narrow spike and a subsequent notch followed by a brief depolarizing transient characteristic for DCN neurons (see Section 2). As the spike propagates passively into the dendrite, the spike waveform becomes attenuated, delayed, and broadens. The somatic potential is truncated at −30 mV in order to enhance the y-axis resolution. (b) Somatic currents underlying the spontaneous spike cycle. The notch and depolarizing transient of each spike result from an interaction of delayed rectifier current (blue: fast and slow Kdr combined), HVA calcium current (red), and resurgent axial current flowing back from the dendrites into the soma (orange)
As previously observed in experimental studies (Raman et al. 2000) the total membrane current in the middle of the inter-spike-interval (ISI) during spontaneous activity in the model was quite small, and no single current exceeded 20 pA (Fig. 2(b)). In fact, the repolarization allowing rhythmic pacemaking was generated by a persistent inward tonic non-specific cation (TNC) current of an amplitude of only 10–20 pA (Fig. 2(b)), which is much smaller than expected synaptic currents in vivo (Gauck and Jaeger 2003) and thus is unlikely to dominate in vivo firing properties of DCN neurons. This low-conductance state of intrinsic channels therefore is likely to allow a high sensitivity to small synaptic steering conductances or applied currents.
3.2 Match of model with a range of physiological rebound behaviors by adjusting persistent sodium, T-type calcium, and HCN conductance densities
Physiological results
Because rebound behavior is a prominent feature of DCN current clamp recordings in cerebellar slices, we placed a special emphasis on reproducing heterogeneous rebound dynamics in our model. To accurately determine the experimental range of rebound behaviors, we acquired 129 recordings of DCN neurons in brain slices in the presence of the synaptic input blockers picrotoxin and CNQX and analyzed the data for rebound responses to negative current injection pulses. We found that rebound responses could be described by the combination of two prominent components, which we termed fast rebound burst and prolonged rebound period (Fig. 3). The fast burst consisted of two to six spikes with diminishing amplitude superposed on a depolarized plateau (Fig. 3, Neuron 1 and Neuron 2, blue inset). All fast bursts had an initial ISI below 7 ms. We found a fast burst for 91 of the 129 analyzed neurons (71%). The fast rebound burst was followed by a pause of an average duration of 106 ± 35.2 ms in 53 of the 91 neurons (58%), after which spiking resumed with an increased rate compared to baseline. The remaining 38 neurons with a fast burst directly transitioned into a prolonged rebound period without an intervening interval of increased duration. For these neurons the presence of a distinct fast burst was ascertained by the presence of an initial ISI of less than 7 ms and a clear transition to slower spiking after two to six spikes. In a large proportion of recorded neurons with a fast burst and a pause a second dampened fast burst occurred before the onset of a prolonged rebound period (Fig. 3, Neuron 1). For 39 neurons we quantified properties of the fast rebound further for a 1.5 s stimulus of −150 pA amplitude. We found that the mean number of fast rebound spikes was 4.2 ± 0.7, the mean latency from the offset of the negative current injection pulses to the first rebound spike was 29.5 ± 11 ms, and the peak rebound frequency (determined by the shortest ISI) was 274 ± 67 Hz.
Different typical rebound patterns of DCN neurons recorded in brain slices (Neurons 1–3, left column) and matching rebound types in the model (right column). Note that the HCN current activates well above −90 mV in our physiological data (dashed lines). Insets show an expanded waveform of a single spontaneous spike (red) and the initial portion of rebounds (blue). A current injection of −150 pA for 1.5 s elicited the hyperpolarization and following rebound in both the physiological traces and the model. Models using the combinations of rebound conductances replicating the rebound patterns of Neurons 1, 2 and 3 are referred to as models of these specific neurons in the remainder of the paper
In all neurons, a prolonged rebound period was found when a negative current that resulted in a strong hyperpolarization was injected for 1 or 1.5 s (Fig. 3, all neurons). The duration of the prolonged rebound period (spike rate above baseline) was always greater than 1 s and most often persisted until the end of our data acquisition period, which ended 1.4 s after the offset of stimulation in most cases. We quantified the spike rate increase for a 1.5 s current injection of −150 pA for 105 neurons with a non-zero baseline frequency. For these neurons the mean baseline spike frequency was 11.3 Hz, while the mean frequency of the slow spike rate increase (scored by the average of the first two successive ISIs 300 ms after current injection offset) was 21.9 Hz, indicating an average spike rate increase of 10.6 Hz over baseline in this time window. However, the magnitude of spike rate increase had a high standard deviation of 8.4 Hz, and reached a maximum of 48 Hz.
These data on fast bursts and prolonged rebound periods were taken as the target of rebound behavior in our compartmental model. We accomplished this goal by adding a T-type calcium current ICaT and a slowly inactivating persistent sodium current INaP to our model. These currents inactivate during baseline firing, but de-inactivate during a hyperpolarized period in membrane potential. Subsequent depolarization then leads to activation of these channels resulting in an inward rebound current. A third current contributing to rebound behaviors is given by the hyperpolarization-activated cyclic-nucleotide gated conductance IHCN, which activates during hyperpolarization and remains active for a short period after the offset of hyperpolarization. The densities of the three rebound conductances in the model were adjusted so that the range of rebound behaviors observed experimentally could be reproduced. We picked three specific neurons from our physiological recordings (Fig. 3), which showed representative examples of the rebound behaviors described in the preceding text, to serve as templates to be matched by the model. We refer to these ‘typical’ neurons as Neurons 1, 2, and 3 in the remainder of this study.
Matching the model to the heterogeneous physiological behaviors
Previous studies have shown that the fast rebound burst of DCN neurons is carried by a CaT conductance (Aizenman and Linden 1999; Molineux et al. 2006). Adding a variable CaT conductance density (GCaT, see Section 2) to our baseline simulation could indeed replicate the experimentally observed properties of the fast rebound burst of two to six spikes with a longer inter-spike interval between the second last and last spike in the burst (Fig. 3). The fastest spike rates (determined by the shortest ISI) in the burst for simulated Neuron 1 and 2 were 291 Hz and 321 Hz, respectively, which is within one standard deviation of the experimental data for the population mean. In fact, when the GCaT density in model Neuron 2 was varied from 2.5 to 5.5 S/m2, the number of fast rebound spikes increased from 3 to 5, and the fastest rate from 242 to 346 Hz. Thus, by adjusting the GCaT density in this range the simulation replicates the heterogeneity in our experimental data, and the simulation of two separate CaV3.1 and CaV3.3 CaT channels was not necessary.
The prolonged rebound period was attributed to a persistent sodium conductance in an early study (Llinas and Muhlethaler 1988), but has not been studied in much detail since then. We added a persistent sodium conductance GNaP to our model to determine whether it could account for the timing and intensity of our experimentally observed slow spike rate increases (see Section 2). Simulations with varying densities of GNaP could match the range of experimentally observed prolonged rebound period profiles well (Fig. 3). However, an interdependence of GNaP effects with other conductances was observed, as is typically seen when the effects of specific conductances on neural dynamics are analyzed (Gunay et al. 2008; Taylor et al. 2009). Most notably, we obtained a larger prolonged rebound in simulated Neuron 2 than in Neuron 3 despite a higher level of GNaP in the latter (Fig. 3). Upon inspection we found that this difference was due to a higher density of HCN conductance (GHCN) present in Neuron 3, which resulted in a diminished hyperpolarization and diminished de-inactivation of GNaP during the negative current injection. To match the overall rebound response of Neuron 3 a higher GHCN density was required because recordings of this neuron did not show a pause in firing after the fast rebound burst carried by GCaT, and only GHCN was capable of producing sufficient inward current at this time point to eliminate the pause in the simulations. Overall, these simulation results demonstrate that a combination of HCN, CaT and NaP conductances can replicate the physiologically observed heterogeneous rebound patterns, and that rebound profiles are shaped by interactions between these conductances as well as by the temporal and amplitude profile of preceding hyperpolarizations. This allows for a large degree of modulation of rebound properties by channel density variability and triggering conditions.
3.3 CaT and NaP conductances carry fast and slow rebound currents, respectively
The pronounced variability in rebounds between neurons can be understood most easily by examining differences in the strength of rebound currents for variable densities of the underlying rebound conductances (Fig. 4). In all cases, during baseline firing, the CaT and NaP rebound conductances were predominantly inactivated and they had only a small influence on baseline firing rate. Following the de-inactivation of ICaT and INaP during negative current injection, they each activated with a characteristic profile after the offset of hyperpolarization, and the strength of the respective rebound component was determined by the amount of conductance present (Fig. 4). ICaT provided a fast current of substantial amplitude (peak current of −1.85 nA for a GCaT density of 3.5 S/m2, Fig. 4b), which then rapidly inactivated and thus led to the transient fast rebound spike burst. INaP activated more slowly and gave rise to a much smaller peak current of 190 pA for a conductance density of 8 S/m2 (Fig. 4a). Due to its slow inactivation time constant this current persisted for over 1 s. Despite its small amplitude it led to a pronounced increase of spiking from the 11.9 Hz baseline to 32.1 Hz at 300 ms following the offset of the current injection (with 1.5 S/m2 GCaT and 2.0 S/m2 GHCN also present, Fig. 4a). This is due to the fact that the spike rate of the model neuron is sensitive to small currents as noted above.
Currents underlying rebound patterns in the model of Neuron 1 and Neuron 3. The T-type calcium current (ICaT, green) underlies the fast burst after the offset of hyperpolarization, while the persistent sodium current (INaP, red) underlies the subsequent prolonged rebound period of spiking. Depending on the relative density of GCaT and GNaP present, each component of the rebound can be more or less pronounced. Note that IHCN (blue) only makes a minor contribution to the rebound depolarization. This is due to the small driving force of IHCN (reversal potential of −45 mV) during the rebound depolarization. (b) A pronounced fast spike burst is present with high GCaT density. The peak of ICaT reaches −1.85 nA, and is shown truncated to allow visualization of smaller currents
3.4 The HCN current shortens rebound delays and smoothes oscillations
The HCN conductance has been suggested as a main contributing factor to rebound behavior in DCN neurons (Aizenman and Linden 1999) as it activates during hyperpolarization and can provide a remaining inward current following it. However, our simulations showed that the contribution of the HCN current to rebound spiking was limited by its small amplitude (Fig. 4) which was due to a small driving force during the rebound period when the membrane potential was close to the IHCN reversal potential of −45 mV. Nevertheless, IHCN had modulatory influences on the rebound properties in addition to diminishing hyperpolarization during negative current injection. To isolate effects of IHCN at a controlled level of hyperpolarization we simulated rebound responses induced by transient voltage clamp pulses to −90 mV for the different combinations of GNaP and GCaT present in Neurons 1 and 3 (Fig. 5). Using this protocol, we determined the effect of GHCN without modulating the de-inactivation of GCaT and GNaP. We found that the presence of GHCN had two additional influences on the rebound.
The role of IHCN in controlling rebound spiking. (a) In the presence of a high density of 8 S/m2 GNaP and a low density of 1.5 S/m2 GCaT (Neuron 3) increasing the GHCN density from 0 to 2 S/m2 resulted in an advance of the fast rebound by 50 ms while having little influence on the rebound pattern. The stimulus here was a 500 ms voltage clamp to −90 mV. The current plots show that IHCN activated gradually over the course of the voltage-clamp hyperpolarization, and that following stimulus offset this led to a substantial inward current that sped up depolarization. Due to the reversal potential of IHCN at −45 mV this current was much diminished during rebound spiking and turned into a transient outward current during each spike. Using a voltage clamp stimulus isolated the effect of IHCN activation on rebound rates, since a current injection stimulus with varying GHCN densities would also lead to varying hyperpolarization potentials and thus would change the de-inactivation of GNaP and GCaT. (b) Rebound rate histograms show the graded dependence of rebound delay on the level of GHCN present. These histograms are constructed by calculating an instantaneous spiking rate trace for each simulation (see Section 2), and by subtracting the spike rate in a simulation without hyperpolarizing stimulus from the otherwise identical simulation containing this stimulus. Thus, the spike rate before the stimulus subtracts to 0, during the hyperpolarizing stimulus the difference between background and stimulated trace drops to the negative of the spontaneous firing rate, and after the stimulus the rebound spike rate shows an increase in spiking above baseline. Insets show the graded delay of the fast rebound at a higher temporal resolution. (c) Dependence of rebound latency after stimulus offset on GHCN. (d–f) The same effects of GHCN were seen for a reduced GNaP and increased GCaT (Neuron 1). Note that GHCN in this case also significantly shaped the rebound pattern in that it suppresses the oscillatory nature of the ICaT rebound (see Section 3). A density of 2 S/m2 GHCN led to a current of −220 pA at 150 ms following stimulus offset, which presented the critical time window to prevent the ISK induced pause
First, GHCN reduced the onset latency of the fast rebound for both NaP and CaT conductance combinations in Neuron 1 and 3 (Fig. 5). This is because IHCN was already activated during the hyperpolarization and drove the initial depolarization following the offset of negative current injection or voltage clamp. In contrast, ICaT and INaP are activated by depolarization, and although they are de-inactivated during hyperpolarization they required another current to depolarize the neuron before they could create a rebound following hyperpolarization. This current was provided by IHCN activation, which reduced the rebound latency by up to 50 ms. Over a 4-fold range of GHCN levels from 0.5 to 2.0 S/m2, which resulted in matches with experimental variability in sag amplitudes with hyperpolarizing current injection (range 3.6 to 29.7 mV, N = 46 neurons analyzed), the difference in delay was about 15 ms (Fig. 5(c, f)). This difference in rebound delay covers a behaviorally relevant time scale; for example in the control of delay eye-blink conditioning (Choi and Moore 2003) or throwing movements (Timmann et al. 2001) the cerebellum is believed to control muscle coordination to a precision of only a few ms. Therefore, a modulation of IHCN in vivo, for example due to its modulation by cyclic nucleotides (Surges et al. 2006), could lead to a functionally significant adaptation of rebound timing.
A second modulation of rebounds by IHCN occurred by eliminating the pause between the fast rebound bursts and the prolonged rebound period that was most pronounced for neurons with high GCaT and low GNaP densities (Neuron 1, Fig. 5(d)). This pause was triggered by an increased activation of ISK during the initial spike burst, which could be counteracted by IHCN in the matching time window. In fact, IHCN could recover the early phase of the prolonged rebound period when INaP was otherwise deactivated due to the hyperpolarization associated with the pause (Fig. 5(d)). In the absence of any INaP and IHCN the model generated repetitive fast rebound bursts due to ICaT activation (supplemental Fig. 2), which we observed in two out of our 132 experimental recordings as well. The presence of IHCN suppressed such repetitive bursting following negative current injection by limiting the hyperpolarization and thus de-inactivation of ICaT during repetitive post-burst pauses.
3.5 Rebounds depend on hyperpolarization duration and depth
In vivo one would expect hyperpolarization due to strong inhibitory input to be of varying depth and duration. This raises the question how rebounds can be shaped by these parameters. In a first series of simulations, we investigated this by varying the duration and amplitude of current injection pulses.
We found that for our default current injection period of 250 ms the prolonged rebound increased gradually with the amount of negative current injected and the resulting level of hyperpolarization (shown for Neuron 3 in Fig. 6(a, b)). The fast burst was also much increased for −250 pA compared to −100 pA current injection (Neuron 1, Fig. 6(c, d)), though it was already more robustly expressed at lower injection levels than the prolonged rebound (Fig. 6(b)).
Dependence of rebound strength on depth of preceding hyperpolarization. (a) The rebound for this combination of rebound conductances with a high GNaP density (simulating Neuron 3 in Fig. 3) shows a pronounced increase in firing rate during the prolonged rebound period when the negative current injection (250 ms duration) is increased from −100 pA to −250 pA. The fast rebound due to ICaT is also increased by increasing the negative current injection, but not as much. The peak hyperpolarization during the 250 ms −100 nA cip was −77 mV, whereas it was −97 mV for −250 pA. Note the increase in IHCN activation (blue current trace) with the −250 pA stimulus. (b) Rebound rate histograms show the graded dependence of rebound spiking on the preceding hyperpolarization. The peak rebound rate shown for the fast rebound depends on the shortest inter-spike interval (ISI) present, which lengthens for diminished stimulus amplitudes, but also depends on the number of spikes in the fast rebound (three spikes for −200 and −250 pA, 2 for −150 and −100 pA, 0 for −50 pA) because several spikes at short intervals increase the instantaneous spike rate through local averaging by the addition of Gaussians (see Section 2). (c) The same current injection stimuli as in (a) are shown for our simulation of Neuron 1 (Fig. 3). This simulation has a lower density of GNaP and GHCN, but a higher density of GCaT. Due the presence of less GHCN the hyperpolarization reached in this simulation is larger than that for Neuron 3 and reached −81 mV for −100 pA and −104 mV for −250 pA. (d) Rebound rate histograms showing a robust fast rebound for most current injection levels. There is a small persistent spike rate increase with large negative current injection, which amounts to an increase in spike rate from 12.1 Hz spontaneous activity to 18.8 Hz during the prolonged rebound period following −250 pA current injection (rate averaged over 500 ms). The fast rebound burst in the presence of high GCaT density is robust from −150 to −250 pA current injections. The number of spikes in the fast rebound was 6 for −250 and −200 pA, 5 for −200 pA, 3 for −150 pA, and 0 for −50 pA
The effect of stimulus amplitude was preserved for different stimulus durations, but stimulus duration had important additional effects. Because the de-inactivation time constant of ICaT was much shorter than that of INaP (101 vs 483 ms at −80 mV), a fast rebound could develop already after short hyperpolarizing stimuli of 62.5 ms, whereas it took stimuli of at least 125 ms duration to evoke a strong prolonged rebound (Figs. 7, 8).
Rebound rates as a function of duration and amplitude of negative current injection in simulations of Neuron 3. (a) Rebound rate profiles for 0.5, 0.125, and 0.0625 s duration current injections of varying amplitude. (b, c) Both the fast burst and the prolonged rebound period are reduced by lowering the amplitude of injected current. The prolonged rebound period is sensitive both to duration and amplitude of current injection, and is greatly decreased for the shortest stimulus at all amplitudes. In contrast, the fast burst is maximal at 125 ms duration and is diminished after shorter or longer current injections (see Section 3). (d) Dependence of fast burst and prolonged rebound on the duration of current injections with an amplitude of −250 pA
Rebound rates and latencies for different current injection amplitudes and durations in simulations of Neuron 1. (a) Rebound rate profiles for 0.5 and 0.0625 s duration current injections of varying amplitude. For the longest current injection, even this low density of GNaP leads to a prolonged rebound period from 12.1 Hz baseline to 23.2 Hz after −250 pA current injection (rate averaged over 500 ms). (b) For all durations of current injection, the rebound spike rate increases with the amplitude of injected current. (c) The relationship between current amplitude and rebound latency is more complex. While lowering the amplitude of injected current increases the rebound latency for long current injections, the relationship is reversed for short current injections. This effect is due to IHCN (see Section 3 and Fig. 5)
GHCN had a modulatory influence on the effects of stimulus duration and amplitude on rebound expression. When the density of GHCN was high (Neuron 3, Fig. 7(a–c)), there was a pronounced reduction of fast and slow rebound rates when reducing the level of current injection from −250 pA to −100 pA, with a decrease in fast and slow rebound rates from 193 Hz to 93 Hz and 80 Hz to 8 Hz, respectively. This result can be easily understood by considering the half-inactivation voltages of INaP and ICaT, which are −80 mV in both cases. This level of hyperpolarization was not reached for −100 pA current injection in the presence of the high GHCN density in Neuron 3 due to the voltage sag it introduced.
The effect of GHCN on fast and slow rebound components was strongly dependent on stimulus duration due to the gradual activation of IHCN and ensuing voltage sag. In particular, for the high level of GHCN in Neuron 3 the relationship between fast rebound rate and current injection duration showed a maximum at 125 ms (Fig. 7(d)), because for longer stimuli the voltage sag due to IHCN led to a reduction in ICaT de-inactivation. In contrast, the dependence of slow rebound rate on current injection duration was monotonically increasing. This was due to the slow time course of INaP de-inactivation, which could not take place during short stimuli when IHCN did not dampen responses.
The timing of the fast rebound burst also depended on the duration and depth of hyperpolarization (shown for Neuron 1 in Fig. 8(a, c)). For short current injection pulses (62.5 ms), increasing the current amplitude from −100 pA to −250 pA increased the delay in the fast rebound burst by 12 ms (Fig. 8(c)). In contrast, for long current injections (500 ms), the fast rebound occurred 8 ms earlier when the current injection amplitude was increased by the same amount (Fig. 8(c)). This can be explained by the action of IHCN on shortening rebound delays (Figs. 5, 6): due to the IHCN activation time constant of 400 ms a current injection duration of 62.5 ms led to much less IHCN activation than a current injection duration of 500 ms. Thus, the timing of fast rebounds in response to long current injection pulses is determined by the amount of IHCN activation, while the latency of rebounds for short current pulses is governed by the level of hyperpolarization and the resulting repolarization time.
Overall, these results predict that the fast and slow rebound components are controlled differentially by the duration of a strong inhibitory input burst from Purkinje cells, and that this effect is modulated by IHCN. This would allow different time courses of PC input bursts to DCN neurons to trigger different patterns of post-inhibitory responses, with only long bursts resulting in a prolonged rebound period. Because of some uncertainty as to the precise time constants and voltage-dependence of the NaP and CaT rebound conductances in DCN neurons the detailed numbers for these relationships found in the model are not likely to be fully accurate, however. Our results point out that the functional significance of these parameters could be high and therefore an accurate experimental determination will be important.
3.6 The control of spike rate and pattern by random trains of excitation and inhibition
One mode of operation of DCN neurons in the cerebellar circuit could be that of a rate coding device, in which the relative input rates of excitatory inputs from mossy fibers and inhibitory inputs from Purkinje cells determine the output spike rate. We examined the dynamic range of rate coding and the effect of inhibition on excitatory input–output relationships in our DCN model. Some of the input conditions used were identical to previous stimuli we employed in dynamic current clamping (Gauck and Jaeger 2003), thus allowing a direct comparison with experimental data. Figure 9 shows the effect of random trains of excitatory and inhibitory inputs (see Section 2) on spike rate and coefficient of variation (CV) in the model for different levels of input conductance. For unrealistically small unitary conductance values of 50 pS for Purkinje cell (PC) inhibition and 50 pS AMPA + 43 pS NMDA for mossy fiber (MF) excitation, inputs showed only a small effect on the spontaneous spike cycle even at high input rates (Fig. 9(a)). At this low synaptic conductance level the oscillatory intrinsic spike cycle was preserved as shown by pronounced side-peaks in the autocorrelation function (Fig. 9(a2)). In agreement with our dynamic clamp results for excitatory input that exceeded inhibition (Gauck and Jaeger 2000, 2003), when the synaptic conductances were doubled we saw a reduction in regularity of spiking and an increase in spike rate (Fig. 9(b)). Finally, a further doubling of the synaptic conductance led to a complete loss of autocorrelation side-peaks, a further decrease in regularity, and a further increase in spike rate (Fig. 9(c)). At this strength of input, the timing of individual spikes was determined by transients in the synaptic conductance pattern, and the intrinsic oscillatory spike cycle was overridden (Fig. 9(c2)). The four-fold increase of synaptic conductance levels from 50 pS to 200 pS resulted in a spike rate increase from 17.4 Hz to 37.1 Hz (Fig. 9(d)) and an increase in CV from 0.12 to 0.39 (Fig. 9(e)).
Control of spiking by a background of randomly timed excitatory and inhibitory inputs. a–c The pattern of synaptic input consists of the random activation of excitatory inputs at 30 Hz and inhibitory inputs at 40 Hz (see Section 2) and is identical for all 3 simulations shown. The amplitude of unitary EPSC and IPSC is multiplied by a factor of 2 between low and intermediate and intermediate and high unitary synaptic conductances (Gsyn). For the lowest Gsyn values the GABAA peak conductance is 50 pS, the AMPA peak conductance is also 50 pS, and the NMDA peak conductance (slow + fast, see Section 2) is 43 pS. For this low Gsyn (a) spiking is nearly regular and only mildly increased in frequency (17.5 Hz) from the spontaneous firing at 12.3 Hz. As Gsyn increases (b, c) the spontaneous oscillatory cycle is disrupted, and spiking becomes more irregular (increasing CV). In addition, for this ratio of inhibition and excitation spiking speeds up with increasing Gsyn. The bar graphs in (a2–c2) show ISI histograms, while the grey line shows the autocorrelation plot of the spike train. (d, e) Dependence of spike rate (d) and CV (e) of the simulated spike trains on Gsyn. All plots are constructed from a total data segment of 3.2 s duration. A model with GNaP of 8, GHCN of 0.8, and GCaT of 2 S/m2 was used, however, these conductances have little influence on the response to background inputs (see Fig. 10)
We performed additional control simulations that incorporated a different set of unitary synaptic kinetics suggested by recent publications that most prominently include a shorter decay time constant and larger unitary amplitudes for GABAA IPSCs (Pugh and Raman 2006; Telgkamp et al. 2004). These larger but shorter unitary events led to spike train properties similar to those exhibited by the standard model for the highest unitary synaptic conductances, although the spike rate and the CV were slightly higher (46.2 Hz vs. 37.1 Hz and CV = 0.46 vs. CV = 0.39, see Fig. 9(d, e) and cf. Figure 9(c) with Supplemental Fig. 4). This insensitivity of the firing rate to EPSC and IPSC parameters is not surprising, since the neuron’s spike train is controlled by the total ensemble of thousands of inputs each second, in which temporal conductance fluctuations are dominated by the population statistics of inputs, and not by the size and shape of unitary events (Gauck and Jaeger 2003).
The spike trains and ISI histograms resulting from our simulations with strong synaptic inputs are similar to in vivo DCN recordings from anesthetized rats (Rowland and Jaeger 2005). It is interesting that realistic spike rates much exceeding the spontaneous spike frequency were obtained when the model received 1,800 inhibitory inputs per second compared to 450 excitatory ones. This result can be explained by the much smaller driving force of GABAA than AMPA and NMDA conductance at the membrane potential between spikes and was also observed in our previous dynamic clamp experiments (Gauck and Jaeger 2003). Therefore, the quantitative relationships between synaptic conductance levels and ensuing synaptic currents demonstrated in our simulations help explain the apparent paradox that DCN neurons show fast spike rates in vivo despite much higher inhibitory than excitatory input rates.
When the level of Purkinje cell inhibition was increased, the curves for output spiking vs. input excitation were shifted to the right (Fig. 10(a1–c1)), suggesting that inhibition performed an additive operation on the input–output curve. The additive input modulation performed by inhibitory input is reflected by the nearly perfect overlay of input–output curves that have been shifted along the input axis (Fig. 10(a2–c2), shift = −6.5 n Hz where n = inhibitory input rate/10 Hz). However, the model does not include short-term synaptic plasticity, which can alter the type of operation performed by inhibition (Rothman et al. 2009).
Control of spike rate by varying mean rates of excitatory and inhibitory inputs. (a1) The DCN neuron shows a near-linear relationship between excitatory input rate and output spike rate for a low value of Gsyn. (a2) Inhibitory synaptic input performs an additive operation. This is shown by a nearly perfect overlay of input–output curves that have been shifted my multiples of −6.5 Hz along the input axis (shift = −6.5 n Hz, where n = inhibitory input rate/10 Hz). (b1, c1) At high Gsyn, the relationships between excitatory input rate and output rate become less linear. (b2, c2) Inhibition still performs an additive operation for higher values of Gsyn, but the addition is less clear than for low Gsyn values (shown by the lower quality of the overlay of input–output curves that have been shifted by multiples of −6.5 Hz along the input axis). (d1–2) The control of spiking by intermediate values of Gsyn for a different combination of rebound conductances. There is virtually no effect of rebound conductances on the control of output spiking by random background input (see Section 3)
When the CaT and NaP rebound conductances were halved (Fig. 10(d1–2)) the input–output relationships were virtually unchanged, indicating that the necessary depth of hyperpolarization to de-inactivate ICaT and INaP was not reached. This indicated that rebound conductances played little role in rate coding in the DCN unless their kinetics were modulated to de-inactivate at more depolarized potentials.
Overall, our results suggest that by adjusting the relative rates of excitatory and inhibitory input DCN neurons are capable of performing approximately linear transformations of the rate coded input–output relationship.
3.7 Rebounds in response to strong bursts of Purkinje cell inputs are strongly influenced by the chloride reversal potential
The question of whether the pronounced rebound behavior of DCN neurons plays a significant role for synaptic coding in vivo is currently under active debate (Alvina et al. 2008; Pedroarena 2010; Tadayonnejad et al. 2009). In slice experiments with intracellular current injection neurons are easily driven to −100 mV or below. In contrast, inhibitory synaptic input bursts can only drive neurons close to the reversal potential of chloride (ECl), which can show a wide range of values, but is generally more positive than −90 mV in neurons. This could limit the expression of rebound spiking in DCN neurons following inhibitory input since de-inactivation of rebound conductances might not occur much at ECl. In addition, there is generally a high conductance baseline generated by background synaptic input in vivo (Destexhe et al. 2003; Stern et al. 1998), which could further diminish rebound firing through synaptic shunting of rebound responses. Such a baseline is certainly expected in DCN neurons, since Purkinje cells have a high baseline of tonic activity, and it has been estimated that each DCN neuron receives inputs from over 800 Purkinje cells (Palkovits et al. 1977). Thus it is not at all clear whether the strong rebound behavior of DCN neurons elicited with current injection in slice recordings has much relevance for the dynamics of these neurons with synaptic input in vivo. As already described in the preceding text, a background of randomly timed inputs modulated spiking in our DCN neuron model without any discernible involvement of rebound conductances. To examine whether rebound spiking could be elicited with stronger bursts of inhibitory inputs we subjected our model with different combinations of realistic fast and slow rebound currents to strong increases in inhibitory input rate for 250 ms in the presence of an ongoing background of random input (Figs. 11, 12, and 13). First, we varied ECl between −70 mV and −90 mV to determine its role in eliciting rebound spiking in the presence of synaptic background inputs (Fig. 11(a, e)). We found that fast and prolonged rebound spiking could be generated in the presence of background inputs, but only if ECl was sufficiently negative. The dependence of fast rebound spike rate on ECl in Neurons 2 and 3 is summarized in Fig. 11(d, h). In both Neuron 2 and 3 models, raising ECl from −90 mV to −70 mV led to a reduction of the fast rebound. However, the relationship between ECl and fast rebound spike rate was nearly linear for Neuron 3 with a low GCaT density (1.5 S/m2), while Neuron 2 with a higher GCaT density (4.5 S/m2) was much more robust against raising ECl and showed fast rebound responses at more than 100 Hz above baseline for ECl values of −75 mV and below.
Rebound spiking following inhibitory input bursts during random background inputs: Dependence on chloride reversal potential. (a) Simulation of Neuron 3. A background of 20 Hz excitation and 30 Hz inhibition is present throughout the simulation with varying unitary inhibitory conductances (see below) and unitary excitatory conductances of 100 pS for GAMPA and 86 pS for GNMDA (intermediate gain, see Figs. 9, 10). An intense inhibitory input burst (300 Hz) is added for a 250 ms period. This high-frequency inhibitory input suppresses spiking and pushes the neuron close to the chloride reversal potential. Rebound spiking occurs at the offset of the inhibitory input burst. When the chloride reversal is set to −90 mV, a pronounced rebound is observed. Increasing the chloride reversal potential to −80 mV and −75 mV results in a gradual reduction of the rebound rate. At −70 mV ECl there are no discernible rebounds. The size of the unitary inhibitory conductance was adjusted for different values of ECl to allow comparable spike rates to result from the same input pattern (50 pS for ECl of −90 and −80 mV, 80 pS for ECl of −75 mV, and 120 pS for ECl of −70 mV). (b) Inward and outward currents controlling the rebound. The synaptic currents (IAMPA, INMDA, IGABA) shown present the summed current of all synapses. Similarly, the voltage-gated rebound currents shown (INaP, ICaT) present the summed current over all compartments. Before the hyperpolarization caused by the inhibitory input burst the rebound currents are insignificant compared to the synaptic currents. After the offset of hyperpolarization, the de-inactivated INaP (red trace) now has an amplitude comparable to the synaptic currents and has a dramatic influence on spiking. The CaT current far exceeds synaptic input current during the fast rebound (peak current truncated). Note that due to its voltage dependence the NMDA current is much reduced during hyperpolarization but increased during the rebound depolarization (black trace), while GABA (purple) and AMPA (orange) currents only shift with driving forces. (c) Rebound triggered by a −90 mV voltage clamp stimulus in the absence of synaptic input for the same combination of rebound conductances as used in (a). (d) Relationship between ECl and rebound spike rate in Neuron 3. (e–h) Simulations of Neuron 2 show a similar effect of chloride reversal potential on rebound strength. However, the fast rebound burst in this neuron is more robust and emerges at an ECl of −75 mV. Note that compared to the simulations of Neuron 2 with current injection (Fig. 3) the sag due to IHCN is again largely reduced, as is the pause following the fast rebound burst
Rebound spiking as a function of synaptic input rates and conductance amplitudes in simulations of Neuron 1. (a1–2) Simulated rebounds of Neuron 1 for low and high input Gsyn at different input rates (exr = excitatory input rate, inr = inhibitory GABA input rate in Hz;). The chloride reversal potential is −90 mV throughout. In each case rebounds are elicited by a 250 ms burst of 300 Hz inhibitory input (through all GABA synapses). Insets show an expansion of the fast rebound peak. Negative rates during the inhibitory burst result from the subtraction of the input-driven firing rate without inhibitory input burst from the pause of firing resulting in all cases from the burst of inhibition. (b1–2) Dependence of rebound spike rate on inhibitory input rate for low and high values of Gsyn and low (b1) and high (b2) excitatory input rates. (b1) Robust rebounds in the presence of low inhibitory and excitatory background rates. (b2) High background levels of inhibitory input result in disappearance of rebounds
Simulated rebounds for Neuron 3 under the same input conditions as for Fig. 12 (Neuron 1). (a1–2) Rebound rate profiles for two different sets of synaptic conductances and different background levels of excitatory and inhibitory input. (b1–2) Rebounds are robust in the presence of low inhibitory and excitatory background levels, but disappear in the presence of high inhibitory levels with high Gsyn values
The predicted dependence of rebound spike rate on ECl is clearly related to the half-inactivation voltage of our CaT and NaP conductances of −80 mV. As these half-inactivation voltages are not well characterized for DCN neurons, the potentials described above could well be shifted by values in the order of 10 mV in actual DCN neurons. A recent study determining the activation of ICaT in DCN neurons (Zheng and Raman 2009) found that it activated only to a small degree at −75 mV, but activation rapidly increased after hyperpolarization exceeding this value. The same study also found a modest 200–300 ms lasting spike rate increase following hyperpolarization to −75 mV, suggesting a critical threshold for rebound expression around this level of average ECl. Together, these data and our simulations lead to the prediction that a modulation of ECl on the order of 5–10 mV would have a strong effect on the expression of rebounds in vivo, as would a shift in half-inactivation voltages of rebound conductances. Interestingly, recent work shows that all these parameters are variable and subject to neuromodulation (see Section 4), suggesting that the rebound behavior of DCN neurons could be regulated and/or subject to plasticity mechanisms in vivo.
3.8 Rebound responses are only mildly shunted by synaptic input conductances
When plotting the individual currents summed across all compartments of our DCN model during a post-inhibitory rebound with background synaptic input at intermediate gain, we found that the synaptic and INaP rebound current were of nearly equal amplitudes (Fig. 11(b, e)). However, the inhibitory and excitatory synaptic currents nearly balanced each other, leading to a small net synaptic inward current of −58 pA during baseline firing for the simulation shown in Fig. 11(a) (bottom). In contrast, the inward INaP plateau current during the rebound (300–500 ms after offset of inhibitory burst) had a much larger amplitude of −303 pA. This current is counteracted by an increase in synaptic current to the degree that the depolarization caused by INaP shifts the synaptic driving forces. However, the average membrane potential only depolarized by 6.5 mV during the INaP rebound compared to baseline, resulting in a change in synaptic current of 42 pA. This effect cancelled only 14% of the −303 pA INaP plateau current, and still allowed this current to cause a large increase in spike rate from 19.1 Hz during baseline to 100 Hz after the PC input burst. Because the rebound-elicited shift in synaptic driving force was small, the rebound response observed with a chloride reversal potential of −90 mV in the presence of ongoing synaptic background was very similar to the rebound following a voltage clamp stimulus to −90 mV for 250 ms in the absence of synaptic background conductances (Fig. 11(a, e) vs. 11(c, g)). This illustrates that the shunting effect of background synaptic conductances was overall insufficient to suppress the depolarization caused by activation of rebound currents and concomitant rebound spiking in our models, and the simulated in vivo rebound bursts resembled individual physiological recordings in vitro (Fig. 3).
3.9 Rebounds are modulated by different baseline input conditions
Despite the small amount of shunting present in the example shown in Fig. 11, it is possible that larger synaptic input conductances caused by higher input rates or high values of synaptic conductances would lead to a more significant suppression of rebound activity. We tested this hypothesis for two combinations of rebound conductances (corresponding to Neuron 1 and Neuron 3) at low and high synaptic conductances and input rates ranging from 5 to 20 Hz excitation and 7.5 to 70 Hz inhibition (Figs. 12, 13). In addition we again ran control simulations with higher unitary synaptic conductances and shorter decay times (Supplemental Fig. 5). We found that the rebound patterns were stable against different input combinations and thus different baseline firing rates (Figs. 12(a1–b1) and 13(a1–b1)). Nevertheless, rebound patterns were significantly shaped by the background synaptic conductances. The fast rebound could be delayed by up to 40 ms for high levels of inhibition (Neuron 1 model, Fig. 12(a1) bottom). High background rates of combined excitatory and inhibitory conductances reduced the fast rebound rates in Neuron 1 (Fig. 12(b2)), and the highest levels of inhibition (above the level to suppress baseline spiking) could abolish fast rebounds completely (Fig. 12(b2)). In our Neuron 3 model with a high GNaP density (Fig. 13) we found that the time course of the prolonged spike rate increase was unaffected by the level of background synaptic input, but the amplitude was diminished for high values of synaptic conductances and abolished for combined high values of synaptic conductance and high rates of excitatory and inhibitory input (Fig. 13(b2)). These results indicate that fast rebounds and prolonged spike rate increases can be modulated by synaptic baseline conductances, but that the general temporal pattern of spike rate changes is independent of the level of background synaptic input.
4 Discussion
We have recorded and analyzed the firing properties of an extensive set of DCN neurons and have constructed computer models of DCN neurons with properties that match the spiking behavior including the heterogeneity of pronounced fast and slow post-hyperpolarization rebound components. These models allowed us to characterize the main determinants of the rebound response. We have also used the model to explore the input-output relationship of DCN neurons with complex synaptic input patterns while manipulating and tracking the effect of different active conductances in ways not accessible to physiological recordings. We found that DCN neurons have a large dynamic range of output firing rates and that inhibitory input performs an additive input modulation. Moreover, following strong bursts of inhibitory inputs, rebounds due to the de-inactivation of CaT and NaP conductances could be elicited in the presence of background rates of randomly timed inputs expected in vivo (Destexhe et al. 2003; Gauck and Jaeger 2003; Stern et al. 1998), but this rebound was highly dependent on the value of ECl. Our model suggests that fast and slow components of DCN rebounds could be regulated differentially by the depth and duration of preceding hyperpolarization, and that neurons could be adapted to different rebound profiles by adjusting the density of HCN, CaT, and NaP conductances. Strong inhibitory input transients to DCN neurons could be caused in vivo by tightly correlated climbing fiber inputs to populations of Purkinje cells resulting in simultaneous complex spiking (Lang et al. 1999). Alternatively, correlated increases in Purkinje cell firing rate could be due to mossy fiber activation following sensory stimulation (Jaeger 2003; Shin et al. 2007). The ensuing intrinsic dynamics of rebound conductance activation could shape temporal patterns of DCN neuron activation during behavior. Our results suggest that a fast burst and a prolonged rebound period represent two different phases of such activity patterns that could be modulated by the density of these conductances.
4.1 Critical parameters in the control of DCN neuron rebound dynamics
Our analysis revealed several parameters that proved critical in the expression and control of spike rebounds in DCN neurons. Foremost of these were the values of ECl and the inactivation voltages of rebound currents, since rebounds could only be elicited via synaptic mechanisms if ECl was approaching or negative to the half-inactivation voltages of rebound currents. In neurons, ECl is controlled by the chloride cotransporters NKCC1 and KCC2 (Banke and McBain 2006; Rivera et al. 1999). Hyperpolarizing shifts in ECl occur mostly due to an increase in KCC2, which in many neurons occurs developmentally (Rivera et al. 1999). KCC2 can also be regulated through phosphorylation (Lee et al. 2007) and external potassium concentration (Zhu et al. 2005), and depending on these mechanisms and the density of KCC2 expression ECl can attain a large range of values. The expression of KCC2 and variability of ECl have not been studied in DCN neurons so far, but our modeling study makes a strong prediction that ECl should be relatively hyperpolarized (−75 mV or below) to enable strong rebound spiking. In slices obtained from mature guinea pigs an average reversal of IPSPs was found at −74.3 mV with sharp intracellular recordings (Jahnsen 1986b), a value also supported by a more recent study using perforated patch recordings (Zheng and Raman 2009). Our simulations indicate that this value of ECl is in a critical region where small changes would have a strong influence on rebound strength. Thus, regulation of KCC2 in DCN neurons would have great impact on rebound behavior, and could occur as a mechanism of excitability plasticity. Similar observations hold for the values of activation and inactivation voltages of the rebound conductances. The activation voltage of IHCN in DCN neurons has been found to be fairly hyperpolarized in juvenile mice (Raman et al. 2000). In our own whole cell data from juvenile rats IHCN activation is frequently observed when the membrane potential reaches −70 mV (Fig. 3). Discrepancies in HCN measurements could arise from species and age differences, but could also be due to a different level of cAMP and cGMP modulation of HCN channels in different preparations, which can potentially lead to large shifts in activation voltage (Pape 1996). The half-inactivation voltage of ICaT in thalamus was determined as −80 mV (Destexhe et al. 1998), but again this value can be shifted through modulation (Jagodic et al. 2007; Traboulsie et al. 2006), and may also differ between channel isoforms. The half-inactivation voltage for INaP was set to −80 mV in our model as this value matched our own experimental findings on slow rebounds. Previous studies show generally a somewhat more positive half-inactivation voltage of persistent sodium current, with differing values between cell types, however (Aracri et al. 2006). Our simulation data lead to the prediction that INaP in DCN neurons may have a more negative half-inactivation voltage than in other cell types.
It is important to note that the model performance is not highly sensitive to the specific value for these parameters chosen in the model. A graded change in model parameters for rebound conductances leads to a graded change in rebound behavior. Thus, our simulation results indicate that different levels of rebound conductances and modulation of activation or inactivation kinetics can account for the cell to cell heterogeneity in the rebound strengths and patterns present in our slice recordings. It is also possible, of course, that additional rebound conductances may exist in DCN neurons that are not currently included in our model. One candidate is the L-type calcium current, which for example in subthalamic nucleus neurons slowly inactivates and can produce rebound behavior (Otsuka et al. 2004). This current is unlikely to be of significant amplitude in DCN neurons, however, as the Na channel blocker TTX removes all post-hyperpolarization plateau potentials (Sangrey and Jaeger 2005).
4.2 Possible functional relevance of rebound dynamics in vivo
The cerebellum participates in multiple brain functions, ranging from the regulation of autonomic variables such as blood flow (Çavdar et al. 2001), to the control of balance and motion originating in the vestibular system (Gardner and Fuchs 1975), smooth and saccadic eye movements (Hepp et al. 1982), limb movements (van Kan et al. 1993), and even cognition (Ito 2008; Schmahmann 1991). The cerebellar architecture across different regions of the cerebellum subserving these functions is remarkably uniform, leading to the hypothesis that a common algorithm must underlie these different functions (Houk et al. 1996). However, there is no commonly accepted view as to what this algorithm is, and it is not even clear to what degree popular proposals such as adaptive gain control (Robinson 1976), pattern recognition (Steuber et al. 2007), optimizing sensory data acquisition (Bower 1997), or timing (Ivry and Keele 1989), are compatible with each other or mutually exclusive. The hypothesis that rebound spiking in the DCN contributes to these functions requires that neural activity in the DCN during behavior should show definite pauses in spiking (due to hyperpolarization) before showing excitatory responses. Such pause—excitation patterns are indeed found in some situations in DCN recordings in awake animals, such as saccade related activity (Gardner and Fuchs 1975; Kleine et al. 2003), or eye-blink related activity (Choi and Moore 2003). On the other hand, strong excitatory modulation during limb movement control is generally not preceded by a pause (Gibson et al. 1996; Goodkin and Thach 2003; MacKay 1988). One possible distinction between these behaviors is that the predictive event timing underlying conditioned eye-blink reflexes and saccades makes use of rebound mechanisms, whereas the control of continuous processes does not. Taken together, the recordings from DCN neurons in awake animals suggest that multiple types of codes may be in operation, ranging from analog spike rate control to rebound burst patterns. Some recent evidence suggests that different circuits in the cerebellum may engage a different balance of these coding mechanisms, as the intrinsic properties of DCN neurons in the medial and lateral nuclei in rats show different proportions of fast and slow rebounds (Nejad et al. 2007), which we associate with CaT and NaP conductances, respectively.
One interesting outcome of the present study is that parameters known to undergo modulations such as ECl and ICaT half-inactivation voltages are very effective in controlling the strength and pattern of rebound spike bursting. This leads us to hypothesize that the adjustment of these parameters in biological neurons could be subservient to learning mechanisms through plasticity. Synaptic plasticity specifically dependent on periods of hyperpolarization has already been found in DCN neurons (Pugh and Raman 2006), and a form of excitability plasticity, in which responses to depolarization are enhanced after stimulation, has also been established (Aizenman and Linden 2000; Pugh and Raman 2008). An additional modulation of rebound conductances or ECl could add to the repertoire of plasticity rules that may be relevant to cerebellar-based learning. The presence of a high amount of variability in these properties in vitro also lends itself to the hypothesis that neurons with different rebound properties could be engaged in learning on the basis of a selection algorithm that picks and reinforces the best suited neurons during training (Seth and Edelman 2007).
4.3 Modeling of DCN network activity during behavior and learning
Several efforts have been undertaken in recent years to create system level models of cerebellar function including DCN output (Medina et al. 2000; Quaia et al. 1999; Schweighofer et al. 2004; Wetmore et al. 2007). These models have generally made use of much simplified representations of DCN neuron properties, based on either integrate-and-fire neurons (Medina et al. 2000) or even black box models of signal transfer (Schweighofer et al. 2004). The results with our more biophysically oriented neuron model indicate the presence of important interactions between synaptic input and active conductances. Thus, they suggest that simplified models without such conductances may miss important components of signal processing in the DCN, and in particular may not result in realistic control of rebound patterns. Especially modeling the control of learned timing behaviors such as eye-blink conditioning when rebound behavior is involved (Wetmore et al. 2007) may benefit from the level of biophysical detail included in our model. While our 516 compartment model may not be suited for large network simulations on most platforms, the dynamics can be retained in a reduced model with just six compartments (unpublished results). We anticipate that our model will form the basis for future cerebellar network simulations with more realistic nuclear dynamics, and we are making the code of both the full and the reduced versions available for download from the ModelDB database (http://senselab.med.yale.edu/modeldb/). In addition, the detailed model can be used as a platform to further refine our understanding of conductances present in DCN neurons and to explore signal processing in the DCN. Our model does not contain a full complement of all cellular properties of DCN neurons; it can certainly be refined and improved in the future. Nevertheless, it is already sufficiently advanced to begin to model the natural heterogeneities in cell behaviors in the DCN. We hope that a community effort based on our current first-generation model will ultimately contribute to better delineate detailed DCN neural dynamics and help to unravel the elusive algorithm of cerebellar function.
References
Achard, P., & De Schutter, E. (2006). Complex parameter landscape for a complex neuron model. PLoS Computational Biology, 2, 794–804.
Aizenman, C. D., & Linden, D. J. (1999). Regulation of the rebound depolarization and spontaneous firing patterns of deep nuclear neurons in slices of rat cerebellum. Journal of Neurophysiology, 82, 1697–1709.
Aizenman, C. D., & Linden, D. J. (2000). Rapid, synaptically driven increases in the intrinsic excitability of cerebellar deep nuclear neurons. Nature Neuroscience, 3, 109–111.
Alvina, K., & Khodakhah, K. (2008). Selective regulation of spontaneous activity of neurons of the deep cerebellar nuclei by N-type calcium channels in juvenile rats. Journal of Physiology-London, 586, 2523–2538.
Alvina, K., Walter, J. T., Kohn, A., Ellis-Davies, G., & Khodakhah, K. (2008). Questioning the role of rebound firing in the cerebellum. Nature Neuroscience, 11, 1256–1258.
Alzheimer, C., Schwindt, P. C., & Crill, W. E. (1993). Modal gating of Na+ channels as a mechanism of persistent Na+ current in pyramidal neurons from rat and cat sensorimotor cortex. The Journal of Neuroscience, 13, 660–673.
Anchisi, D., Scelfo, B., & Tempia, F. (2001). Postsynaptic currents in deep cerebellar nuclei. Journal of Neurophysiology, 85, 323–331.
Aracri, P., Colombo, E., Mantegazza, M., Scalmani, P., Curia, G., Avanzini, G., et al. (2006). Layer-specific properties of the persistent sodium current in sensorimotor cortex. Journal of Neurophysiology, 95, 3460–3468.
Banke, T. G., & McBain, C. J. (2006). GABAergic input onto CA3 hippocampal interneurons remains shunting throughout development. The Journal of Neuroscience, 26, 11720–11725.
Baranauskas, G., Tkatch, T., & Surmeier, D. J. (1999). Delayed rectifier currents in rat globus pallidus neurons are attributable to Kv2.1 and Kv3.1/3.2K(+) channels. The Journal of Neuroscience, 19, 6394–6404.
Baranauskas, G., Tkatch, T., Nagata, K., Yeh, J. Z., & Surmeier, D. J. (2003). Kv3.4 subunits enhance the repolarizing efficiency of Kv3.1 channels in fast-spiking neurons. Nature Neuroscience, 6, 258–266.
Bower, J. M. (1997). Is the cerebellum sensory for motor’s sake, or motor for sensory’s sake: the view from the whiskers of a rat? Progress in Brain Research, 114, 483–516.
Bower, J. M., & Beeman, D. (1997). The book of Genesis (2nd ed.). New York: Springer.
Brown, A. M., Schwindt, P. C., & Crill, W. E. (1994). Different voltage-dependence of transient and persistent Na+ currents is compatible with modal-gating hypothesis for sodium-channels. Journal of Neurophysiology, 71, 2562–2565.
Castelfranco, A. M., & Hartline, D. K. (2002). Simulations of space-clamp errors in estimating parameters of voltage-gated conductances localized at different electrotonic distances. Neurocomputing, 44–46, 75–80.
Çavdar, S., San, T., Aker, R., Sehirli, Ü., & Onat, F. (2001). Cerebellar connections to the dorsomedial and posterior nuclei of the hypothalamus in the rat. Journal of Anatomy, 198, 37–45.
Chan-Palay, V. (1977). Cerebellar dentate nucleus. Springer-Verlag.
Choi, J. S., & Moore, J. W. (2003). Cerebellar neuronal activity expresses the complex topography of conditioned eyeblink responses. Behavioral Neuroscience, 117, 1211–1219.
Daniel, H., Billard, J. M., Angaut, P., & Batini, C. (1987). The interposito-rubrospinal system. Anatomical tracing of a motor control pathway in the rat. Neuroscience Research, 5, 87–112.
De Schutter, E., & Bower, J. M. (1994). An active membrane model of the cerebellar Purkinje cell. II. Simulation of synaptic responses. Journal of Neurophysiology, 71, 401–419.
Destexhe, A., Neubig, M., Ulrich, D., & Huguenard, J. (1998). Dendritic low-threshold calcium currents in thalamic relay cells. The Journal of Neuroscience, 18, 3574–3588.
Destexhe, A., Rudolph, M., & Paré, D. (2003). The high-conductance state of neocortical neurons in vivo. Nature Reviews Neuroscience, 4, 739–751.
Fredette, B. J., & Mugnaini, E. (1991). The GABAergic cerebello-olivary projection in the rat. Anatomy and Embryology (Berlin), 184, 225–243.
Gardette, R., Debono, M., Dupont, J.-L., & Crepel, F. (1985a). Electrophysiological studies on the postnatal development of intracerebellar nuclei neurons in rat cerebellar slices maintained in vitro. I. Postsynaptic potentials. Developmental Brain Research, 19, 47–55.
Gardette, R., Debono, M., Dupont, J.-L., & Crepel, F. (1985b). Electrophysiological studies on the postnatal development of intracerebellar nuclei neurons in rat cerebellar slices maintained in vitro. II. Membrane conductances. Developmental Brain Research, 20, 97–106.
Gardner, E. P., & Fuchs, A. F. (1975). Single-unit responses to natural vestibular stimuli and eye movements in deep cerebellar nuclei of the alert rhesus monkey. Journal of Neurophysiology, 38, 627–649.
Gauck, V., & Jaeger, D. (2000). The control of rate and timing of spikes in the deep cerebellar nuclei by inhibition. The Journal of Neuroscience, 20, 3006–3016.
Gauck, V., & Jaeger, D. (2003). The contribution of NMDA and AMPA conductances to the control of spiking in neurons of the deep cerebellar nuclei. The Journal of Neuroscience, 23, 8109–8118.
Gauck, V., Thomann, M., Jaeger, D., & Borst, A. (2001). Spatial distribution of low- and high-voltage-activated calcium currents in neurons of the deep cerebellar nuclei. The Journal of Neuroscience, 21, RC158.
Gibson, A. R., Horn, K. M., Stein, J. F., & VanKan, P. L. E. (1996). Activity of interpositus neurons during a visually guided reach. Canadian Journal of Physiology and Pharmacology, 74, 499–512.
Gleeson, P., Crook, S., Cannon, R. C., Hines, M. L., Billings, G. O., Farinella, M., Morse, T. M., Davison, A. P., Ray, S., Bhalla, U. S., Barnes, S. R., Dimitrova, Y. D., & Silver, R. A. (2010). NeuroML: a language for describing data driven models of neurons and networks with a high degree of biological detail. PLoS Computational Biology 6, e1000815.
Goodkin, H. P., & Thach, W. T. (2003). Cerebellar control of constrained and unconstrained movements. II. EMG and nuclear activity. Journal of Neurophysiology, 89, 896–908.
Gunay, C., Edgerton, J. R., & Jaeger, D. (2008). Channel density distributions explain spiking variability in the globus pallidus: a combined physiology and computer simulation database approach. The Journal of Neuroscience, 28, 7476–7491.
Hepp, K., Henn, V., & Jaeger, J. (1982). Eye movement related neurons in the cerebellar nuclei of the alert monkey. Experimental Brain Research, 45, 253–264.
Hille, B. (2001). Ion channels of excitable membranes (3rd ed.). Sunderland: Sinauer.
Houk, J. C., Buckingham, J. T., & Barto, A. G. (1996). Models of the cerebellum and motor learning. The Behavioral and Brain Sciences, 19, 368–383.
Ito, M. (2008). Opinion—control of mental activities by internal models in the cerebellum. Nature Reviews. Neuroscience, 9, 304–313.
Ivry, R. B., & Keele, S. W. (1989). Timing functions of the cerebellum. Journal of Cognitive Neuroscience, 1, 136–152.
Jaeger, D. (2003). No parallel fiber volleys in the cerebellar cortex: evidence from cross-correlation analysis between Purkinje cells in a computer model and in recordings from anesthetized rats. Journal of Computational Neuroscience, 14, 311–327.
Jaeger, D., & Bower, J. M. (1999). Synaptic control of spiking in cerebellar Purkinje cells: dynamic current clamp based on model conductances. The Journal of Neuroscience, 19, 6090–6101.
Jagodic, M. M., Pathirathna, S., Nelson, M. T., Mancuso, S., Joksovic, P. M., Rosenberg, E. R., et al. (2007). Cell-specific alterations of T-type calcium current in painful diabetic neuropathy enhance excitability of sensory neurons. The Journal of Neuroscience, 27, 3305–3316.
Jahnsen, H. (1986a). Electrophysiological characteristics of neurones in the guinea-pig deep cerebellar nuclei in vitro. Journal de Physiologie, 372, 129–147.
Jahnsen, H. (1986b). Extracellular activation and membrane conductances of neurones in the guinea-pig deep cerebellar nuclei in vitro. Journal de Physiologie, 372, 149–168.
Kleine, J. F., Guan, Y., & Buttner, U. (2003). Saccade-related neurons in the primate fastigial nucleus: what do they encode? Journal of Neurophysiology, 90, 3137–3154.
Lang, E. J., Sugihara, I., Welsh, J. P., & Llinas, R. (1999). Patterns of spontaneous Purkinje cell complex spike activity in the awake rat. The Journal of Neuroscience, 19, 2728–2739.
Lee, H. H. C., Walker, J. A., Williams, J. R., Goodier, R. J., Payne, J. A., & Moss, S. J. (2007). Direct protein kinase C-dependent phosphorylation regulates the cell surface stability and activity of the potassium chloride cotransporter KCC2. The Journal of Biological Chemistry, 282, 29777–29784.
Llinas, R., & Muhlethaler, M. (1988). Electrophysiology of guinea-pig cerebellar nuclear cells in the in vitro brain stem-cerebellar preparation. Journal de Physiologie, 404, 241–258.
MacKay, W. A. (1988). Cerebellar nuclear activity in relation to simple movements. Experimental Brain Research, 71, 47–58.
Magistretti, J., & Alonso, A. (1999). Biophysical properties and slow voltage-dependent inactivation of a sustained sodium current in entorhinal cortex layer-II principal neurons—a whole-cell and single-channel study. The Journal of General Physiology, 114, 491–509.
Medina, J. F., Garcia, K. S., Nores, W. L., Taylor, N. M., & Mauk, M. D. (2000). Timing mechanisms in the cerebellum: testing predictions of a large-scale computer simulation. The Journal of Neuroscience, 20, 5516–5525.
Molineux, M. L., McRory, J. E., McKay, B. E., Hamid, J., Mehaffey, W. H., Rehak, R., et al. (2006). Specific T-type calcium channel isoforms are associated with distinct burst phenotypes in deep cerebellar nuclear neurons. Proceedings of the National Academy of Sciences of the United States of America, 103, 5555–5560.
Muri, R., & Knopfel, T. (1994). Activity induced elevations of intracellular calcium concentration in neurons of the deep cerebellar nuclei. Journal of Neurophysiology, 71, 420–428.
Nejad, R. T., Molineux, M. L., Mehaffey, W. H., & Turner, R. W. (2007). Transient and weak bursting deep cerebellar neurons exhibit differential coding properties for membrane hyperpolarizations. Program No. 409.12. Neuroscience Meeting Planner. San Diego, CA: Society for Neuroscience Online.
Otsuka, T., Abe, T., Tsukagawa, T., & Song, W. J. (2004). Conductance-based model of the voltage-dependent generation of a plateau potential in subthalamic neurons. Journal of Neurophysiology, 92, 255–264.
Palkovits, M., Mezey, E., Hamori, J., & Szentagothai, J. (1977). Quantitative histological analysis of the cerebellar nuclei in the cat. I. Numerical data on cells and synapses. Experimental Brain Research, 28, 189–209.
Pape, H. C. (1996). Queer current and pacemaker: the hyperpolarization-activated cation current in neurons. Annual Review of Physiology, 58, 299–327.
Paulin, M. G. (1995). System identification of spiking sensory neurons using realistically constrained nonlinear time series models. In I. Gath & G. Inbar (Eds.), Advances in processing and pattern analysis of biological signals (pp. 183–194). Plenum: New York.
Pedroarena, C. M. (2010). Mechanisms supporting transfer of inhibitory signals into the spike output of spontaneously firing cerebellar nuclear neurons in vitro. Cerebellum, 9, 67–76.
Prinz, A. A., Billimoria, C. P., & Marder, E. (2003). Alternative to hand-tuning conductance-based models: construction and analysis of databases of model neurons. Journal of Neurophysiology, 90, 3998–4015.
Pugh, J. R., & Raman, I. M. (2006). Potentiation of mossy fiber EPSCs in the cerebellar nuclei by NMDA receptor activation followed by postinhibitory rebound current. Neuron, 51, 113–123.
Pugh, J. R., & Raman, I. M. (2008). Mechanisms of potentiation of mossy fiber EPSCs in the cerebellar nuclei by coincident synaptic excitation and inhibition. The Journal of Neuroscience, 28, 10549–10560.
Purvis, L. K., & Butera, R. J. (2005). Ionic current model of a hypoglossal motoneuron. Journal of Neurophysiology, 93, 723–733.
Quaia, C., Lefevre, P., & Optican, L. M. (1999). Model of the control of saccades by superior colliculus and cerebellum. Journal of Neurophysiology, 82, 999–1018.
Rall, W. (1959). Branching dendritic trees and motoneuron membrane resistivity. Experimental Neurology, 1, 491–527.
Raman, I. M., Gustafson, A. E., & Padgett, D. (2000). Ionic currents and spontaneous firing in neurons isolated from the cerebellar nuclei. The Journal of Neuroscience, 20, 9004–9016.
Rivera, C., Voipio, J., Payne, J. A., Ruusuvuori, E., Lahtinen, H., Lamsa, K., et al. (1999). The K+/Cl- co-transporter KCC2 renders GABA hyperpolarizing during neuronal maturation. Nature, 397, 251–255.
Robinson, D. A. (1976). Adaptive gain control of vestibuloocular reflex by cerebellum. Journal of Neurophysiology, 39, 954–969.
Rothman, J. S., Cathala, L., Steuber, V., & Silver, R. A. (2009). Synaptic depression enables neuronal gain control. Nature, 457, 1015–U1016.
Rowland, N. C., & Jaeger, D. (2005). Coding of tactile response properties in the rat deep cerebellar nuclei. Journal of Neurophysiology, 94, 1236–1251.
Sangrey, T. D., & Jaeger, D. (2005). Currents underlying hyperpolarization-induced rebound spiking in deep cerebellar nuclei neurons. In Program No. 179.10. 2005 Abstract Viewer/Itinerary Planner. Washington, DC: Society for Neuroscience, 2005. Online.
Schmahmann, J. D. (1991). An emerging concept: the cerebellar contribution to higher function. Archives of Neurology, 48, 1178–1187.
Schweighofer, N., Doya, K., & Kuroda, S. (2004). Cerebellar aminergic neuromodulation: towards a functional understanding. Brain Research. Brain Research Reviews, 44, 103–116.
Seth, A. K., & Edelman, G. M. (2007). Distinguishing causal interactions in neural populations. Neural Computation, 19, 910–933.
Shen, G. Y. Y., Chen, W. R., Midtgaard, J., Shepherd, G. M., & Hines, M. L. (1999). Computational analysis of action potential initiation in mitral cell soma and dendrites based on dual patch recordings. Journal of Neurophysiology, 82, 3006–3020.
Shin, S., Hoebeek, F. E., Schonewille, M., De Zeeuw, C. I., Aertsen, A., & De Schutter, E. (2007). Regular patterns in cerebellar Purkinje cell simple spike train. PLoS ONE, 2, e485.
Stern, E. A., Jaeger, D., & Wilson, C. J. (1998). Membrane potential synchrony of simultaneously recorded striatal spiny neurons in vivo. Nature, 394, 475–478.
Steuber, V., De Schutter, E., & Jaeger, D. (2004). Passive models of neurons in the deep cerebellar nuclei: the effect of reconstruction errors. Neurocomputing, 58–60, 563–568.
Steuber, V., Mittmann, W., Hoebeek, F. E., Silver, R. A., De Zeeuw, C. I., Hausser, M., et al. (2007). Cerebellar LTD and pattern recognition by Purkinje cells. Neuron, 54, 121–136.
Sultan, F., Czubayko, U., & Thier, P. (2003). Morphological classification of the rat lateral cerebellar nuclear neurons by principal component analysis. The Journal of Comparative Neurology, 455, 139–155.
Surges, R., Brewster, A. L., Bender, R. A., Beck, H., Feuerstein, T. J., & Baram, T. Z. (2006). Regulated expression of HCN channels and cAMP levels shape the properties of the h current in developing rat hippocampus. The European Journal of Neuroscience, 24, 94–104.
Tadayonnejad, R., Mehaffey, W. H., Anderson, D., & Turner, R. W. (2009). Reliability of triggering postinhibitory rebound bursts in deep cerebellar neurons. Channels, 3, 149–155.
Taylor, A. L., Goaillard, J.-M., & Marder, E. (2009). How multiple conductances determine electrophysiological properties in a multicompartment model. The Journal of Neuroscience, 29, 5573–5586.
Telgkamp, P., Padgett, D. E., Ledoux, V. A., Woolley, C. S., & Raman, I. M. (2004). Maintenance of high-frequency transmission at purkinje to cerebellar nuclear synapses by spillover from boutons with multiple release sites. Neuron, 41, 113–126.
Timmann, D., Citron, R., Watts, S., & Hore, J. (2001). Increased variability in finger position occurs throughout overarm throws made by cerebellar and unskilled subjects. Journal of Neurophysiology, 86, 2690–2702.
Traboulsie, A., Chemin, J., Kupfer, E., Nargeot, J., & Lory, P. (2006). T-type calcium channels are inhibited by fluoxetine and its metabolite norfluoxetine. Molecular Pharmacology, 69, 1963–1968.
Uusisaari, M., Obata, K., & Knopfel, T. (2007). Morphological and electrophysiological properties of GABAergic and non-GABAergic cells in the deep cerebellar nuclei. Journal of Neurophysiology, 97, 901–911.
van Kan, P. L., Houk, J. C., & Gibson, A. R. (1993). Output organization of intermediate cerebellum of the monkey. Journal of Neurophysiology, 69, 57–73.
Wetmore, D. Z., Mukamel, E. A., & Schnitzer, M. (2007). Lock-and-key mechanisms of cerebellar memory recall based on rebound currents. J Neurophysiol. epub in press.
Zheng, N., & Raman, I. M. (2009). Ca currents activated by spontaneous firing and synaptic disinhibition in neurons of the cerebellar nuclei. Journal of Neuroscience, 29, 9826–9838.
Zhu, L., Lovinger, D., & Delpire, E. (2005). Cortical neurons lacking KCC2 expression show impaired regulation of intracellular chloride. Journal of Neurophysiology, 93, 1557–1568.
Acknowledgments
The authors acknowledge Volker Gauck’s contribution to this work by recording some of the physiological data. This work was primarily supported by grant NIMH R01-MH065634 to DJ. Additional support was provided by a Human Frontier Science Program Organization Long-Term Fellowship (VS), the EU Grant QLG3-CT-2001- 01241 (EDS), the FWO (Flanders) (EDS), the MRC (G0400598; RAS), BBSRC (F005490; VS and RAS) and Wellcome Trust. RAS is in receipt of a Wellcome Trust Senior Research Fellowship in Basic Biomedical Science (064413).
Author information
Authors and Affiliations
Corresponding author
Additional information
Action Editor: John Huguenard
Electronic supplementary material
Below is the link to the electronic supplementary material.
ESM 1
(PDF 1075 kb)
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License ( https://creativecommons.org/licenses/by-nc/2.0 ), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Steuber, V., Schultheiss, N.W., Silver, R.A. et al. Determinants of synaptic integration and heterogeneity in rebound firing explored with data-driven models of deep cerebellar nucleus cells. J Comput Neurosci 30, 633–658 (2011). https://doi.org/10.1007/s10827-010-0282-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10827-010-0282-z