1 Introduction

Continuous population growth, industrial revolutions, depletion of fossil fuel reserves, and climate change have led to the increased demand for renewable energy globally. The principle of dye-sensitized solar cell (DSSC) operation depends on photoanodes bound to a wide-bandgap semiconductor material, electrolyte, and counter electrode. DSSCs have many advantages, including low material cost, compatibility with flexible substrates, cost-effectiveness, simplicity, and energy-efficient production methods. However, low efficiency is a major challenge with DSSCs that must be solved to reach commercialization without affecting cell stability. The highest efficiency recorded for DSSCs is approximately 14%, but it is not proven [1]. Improving DSSC parameters [open-circuit voltage (Voc), short-circuit current density (Jsc), efficiency (η), and cell fill factor (FF)] is a vital requirement for solving these challenges. The models most commonly used to represent the equivalent circuit of the DSSC are single- and double-diode models. Different mathematical models are used to simulate the nonlinear relationship of current–voltage characteristics.

Currently, meta-heuristic optimization algorithms are quite attractive due to their distinct advantages over conventional algorithms. Meta-heuristics have the ability to solve multi-objective and nonlinear problems. Despite the random nature of these algorithms, they have the ability to obtain global maxima and avoid local maxima [2,3,4]. Accurate estimation and optimization of DSSC parameters are very important in improving cell quality during fabrication, modeling, and simulation [5,6,7,8,9,10]. This study analyzed the influence of photoanode thickness (d), electron lifetime (τ), electron diffusion coefficient (D), light absorption coefficient (α), and diode ideality factor (m) on the main DSSC parameters. The performance of the proposed optimization algorithms was analyzed by comparing the extracted electrical parameters of the solar cell. Moreover, sensitivity analysis of DSSC performance was carried out for different values of light intensity (φ) and temperature to test the mathematical model used. The variations in physical parameters were also studied.

2 Mathematical modeling of the DSSC

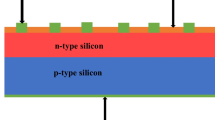
DSSC operation is based on the relative charge kinetics rate. The charge transfer occurs from the dye to the photoanode, from the electrolyte to the dye, and finally from the photoanode to the load. Therefore, it is necessary to understand the charge transfer processes as well as the electronic process at the photoanode. A schematic band diagram of the DSSC is given in Fig. 1 [11,12,13,14,15].

Fig. 1
figure 1

The DSSC band diagram and electron transfer

Full size image

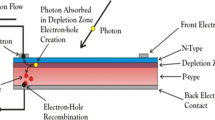
The equivalent electrical circuit of the DSSC based on the single-diode model (SDM) is illustrated in Fig. 2. This circuit contains a photocurrent source, an anti-parallel diode cell, and series and shunt resistance.

Fig. 2
figure 2

DSSC equivalent circuit based on SDM

Full size image

The J–V characteristics model is governed by the physical parameters of the DSSC. The differential diffusion model can be used to describe the electron injection from dye to the photoanode and recombination within the electrolyte at the steady state as [16,17,18]:

$$D \frac{{ \partial }^{2} n\left(x\right)}{\partial {x}^{2}}-\frac{n\left(x\right)-{n}_{o}}{\tau }+\varphi \alpha {e}^{-\alpha x}=0$$
(1)
$${n\left(0\right)=n}_{o} \&\& {\left.\frac{d n}{d x}\right|}_{x=d}=0$$
(2)

where n(x) is the concentration of the excess electrons at position x, no is the concentration of electrons under dark conditions [19, 20], τ describes the electron lifetime, φ is the flux intensity, α is the absorption coefficient of incident light, and D is the electron diffusion coefficient.

By neglecting electron trapping/detrapping in the steady-state case, the electron lifetime is considered constant [21, 22]. The solution equation using open-circuit and short-circuit boundary conditions is given by [11, 23]:

$${J}_{\mathrm{PV}}={J}_{\mathrm{g}}-{J}_{\mathrm{o}} \left[\mathrm{exp}\left(\frac{qV}{ m k T}\right)-1\right]$$
(3)

where JPV is the DSSC current density, Jg is the photocurrent density, Jo is the saturation current density, m describes the DSCC ideality factor, K is the Boltzmann constant, q is the electron charge, and T represents the cell temperature. Solving Eq. (3) with boundary conditions in Eq. (2), the short-circuit current density is calculated by:

$${J}_{\mathrm{sc}}=\frac{q\varphi L\alpha }{1-{L}^{2}{\alpha }^{2}}\left[-L\alpha +\mathrm{tanh}\left(\frac{d}{L}\right)+\frac{L\alpha { e}^{-\alpha d}}{\mathrm{cosh}\left(\frac{d}{L}\right)}\right]$$
(4)

where Jsc is the short-circuit current density, L is the length of electron diffusion, and d is the thickness of the photoanode layer.

Based on the analytical expression for Jsc, the current density under illumination can be obtained as a function of the bias voltage as [23]:

$$J={J}_{\mathrm{sc}}-\frac{q D {n}_{o}}{L} \mathrm{tanh}\left(\frac{d}{L}\right)\left[\mathrm{exp}\left(\frac{qV}{ m k T}\right)-1\right]$$
(5)
$$V=\frac{k m T}{q} \mathrm{ln}\left[\frac{L\left({J}_{\mathrm{sc}}-J\right)}{q D {n}_{o} \mathrm{tanh}\left(\frac{d}{L}\right)}+1\right]$$
(6)
$${I}_{o}=\frac{q D {n}_{o}}{L} \mathrm{tanh}\left(\frac{d}{L}\right)$$
(7)
$$L=\sqrt{D \tau }$$
(8)
$${R}_{\mathrm{s}}=\frac{\frac{m k T}{q} ln\left(1-\frac{{I}_{\mathrm{max}}}{{I}_{\mathrm{sc}}}\right)+{V}_{\mathrm{oc}}- {V}_{\mathrm{max}}}{{I}_{\mathrm{max}}}$$
(9)
$${J}_{\mathrm{max}}={J}_{\mathrm{sc}}\left\{1-\mathrm{exp}\left[\frac{q\left({V}_{\mathrm{max}}-{V}_{oc}+{I}_{\mathrm{max}} {R}_{s}\right)}{m k T}\right]\right\}$$
(10)
$${V}_{\mathrm{oc}}=\frac{m k T}{q} \mathrm{ln}\left[\frac{L{ J}_{\mathrm{sc} }}{q D {n}_{o} \mathrm{tanh}\left(\frac{d}{L}\right)}+1\right]$$
(11)
$$FF=\frac{{P}_{\mathrm{max}}}{{V}_{\mathrm{oc}} {I}_{\mathrm{sc}}}$$
(12)

where Imax is the maximum current density, Pmax is the maximum power, Vmax is the maximum voltage, Rs is series resistance, and FF is the fill factor. Table 1 gives the mathematical modeling parameters definition used for the DSSC.

Table 1 Definitions of mathematical modeling symbols for the DSSC
Full size table

3 Problem formulation

Equations (5–7) are nonlinear transcendental equations that represent the DSSC output current and that have no clear analytical solutions. The problem of parameter identification for the DSSC is to determine the optimal physical parameter values to achieve the highest cell efficiency. The objective function maximizes the DSSC efficiency subject to the minimum and maximum bounds of the required parameters. These parameters are electrode thickness, diffusion coefficient, absorption coefficient, lifetime, and ideality factor. The objective function is as follows:

$$f\left(x\right)=\mathrm{max}\left(\eta \right)$$
(13)

To achieve highly efficient DSSCs, the constraints of the proposed optimization variables are limited within the minimum and maximum bounds, as follows:

$$\begin{gathered} x_{j}^{\min } \le x_{j} \le x_{j}^{\max } j = 1, 2, 3, 4, 5 \hfill \\ x = d, D,\alpha , \tau , m \hfill \\ \end{gathered}$$
(14)

The optimal parameter values are analyzed based on the results of the electric current density–voltage (J–V) characteristics. The photoanode thickness is in the range of 1–100 μm, electron lifetime is 1–100 ms, ideality factor is 2–4.5, absorption coefficient is 1000–50,000 cm−1, and the diffusion coefficient is in range of (1–8) × 10–4 cm2/s. Figure 3 shows the input and output parameters that affected DSSC performance. The input parameters are electrode thickness, diffusion coefficient, absorption coefficient, lifetime, and ideality factor, whereas the output parameters are short-circuit current density, open-circuit voltage, fill factor, cell efficiency, and maximum power. These parameters are taken into consideration during the optimization process [24].

Fig. 3
figure 3

The input and output parameters used for DSSC optimization

Full size image

4 Meta-heuristic optimization methods

Meta-heuristic optimization techniques have become popular for numerous engineering applications due to their simplicity, ease of implementation, and ability to avoid local optima. In nature-inspired algorithms, imitating natural and biological physics phenomena is used to solve the objective functions. They are divided into three main groups: evolutionary, physical, and swarm. Evolutionary methods are controlled by the concepts of natural evolution, the most familiar of which is the genetic algorithm (GA) [25], whereas swarm techniques simulate the group behavior of animals. Using meta-heuristic algorithms to search for an optimal solution through J–V data for the DSSC, the cell parameters can be obtained with high accuracy and convergence rate. The meta-heuristic parameters used are the population size and the maximum number of iterations [26, 27]. Figure 4 presents a flowchart of the proposed optimization algorithms.

Fig. 4
figure 4

Flowchart of proposed optimization algorithms

Full size image

4.1 GA optimization

The GA is an algorithm inspired by the evolutionary process [28], and consists of three main steps: selection process, crossover process, and mutation process [29, 30]. The main concept is to generate a population, and for each individual of the population, calculate the fitness function, then the next generation by applying selection, recombination, and mutation. The process is repeated until the required stop criteria are reached [31]. The pseudo-code of GA optimization is shown in Fig. 5.

Fig. 5
figure 5

The pseudo-code of GA optimization

Full size image

4.2 GWO algorithm

The grey wolf optimization (GWO) algorithm was first used by Mirjalili [32] and is inspired by the hunting behavior of the grey wolf. To mathematically model the GWO, the hunting and social hierarchies are used. The grey wolf leader is called the alpha (\(\alpha\)), which is considered the fittest solution in the algorithm. The second best solution is called beta (\(\beta\)), and the third is called delta (\(\delta\)), whereas all the other possible solutions are called omegas (\(\omega\)). The three leading grey wolves \((\alpha , \beta , and \delta )\) will lead all \(\omega\) during the optimization process of searching and hunting. When the prey is found, the iterations start, and the \((\alpha , \beta , and \delta )\) wolves will lead, monitor, and finally surround the target. The surrounding behavior is as follows [32]:

$$\overrightarrow{D}=\left|\overrightarrow{C}.\overrightarrow{{X}_{P}}(\mathrm{t})-\overrightarrow{X}(t)\right|$$
(15)
$$\overrightarrow{X}(t+1)=\overrightarrow{{X}_{P}}(t)+\overrightarrow{A}.\left(\overrightarrow{D}\right)$$
(16)

where \(\overrightarrow{X}(t)\) is the grey wolf position vector at the current iteration (t), while \(\overrightarrow{{X}_{P}}(\mathrm{t})\) is the prey position vector.

The vectors \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{C}}\) coefficient can be modeled as:

$$\overrightarrow{A}=2\overrightarrow{a}.\overrightarrow{{r}_{1}}-\overrightarrow{a}$$
(17)
$$\overrightarrow{C}=2.\overrightarrow{{r}_{2}}$$
(18)

where \(\overrightarrow{a}\) decreases linearly from 2 to 0 throughout iterations, and \(\overrightarrow{{r}_{1}}\), \(\overrightarrow{{r}_{2}}\) are random vectors in the range [0, 1]. The mathematical modeling of \((\alpha , \beta , and , \delta )\) grey wolf hunting processes are given by:

$$\begin{array}{c}\overrightarrow{{D}_{\alpha }}=\left|\overrightarrow{{C}_{1}}.\overrightarrow{{X}_{\alpha }}-\overrightarrow{X}\right|\\ \overrightarrow{{D}_{\beta }}=\left|\overrightarrow{{C}_{2}}.\overrightarrow{{X}_{\beta }}- \overrightarrow{X}\right|\\ \overrightarrow{{D\delta}_{\ }}=\left|\overrightarrow{{C}_{3}}.\overrightarrow{{X}_{\delta }}- \overrightarrow{X}\right|\end{array}$$
(19)
$$\begin{array}{c}\overrightarrow{{X}_{1}}=\overrightarrow{{X}_{\alpha }}+\overrightarrow{{A}_{1}}.\left(\overrightarrow{{D}_{\alpha }}\right)\\ \overrightarrow{{X}_{2}}=\overrightarrow{{X}_{\beta }}+\overrightarrow{{A}_{2}}.\left(\overrightarrow{{D}_{\beta }}\right)\\ \overrightarrow{{X}_{3}}=\overrightarrow{{X}_{\delta }}+\overrightarrow{{A}_{3}}.\left(\overrightarrow{{D}_{\delta }}\right)\end{array}$$
(20)
$$\overrightarrow{X}(t+1)=\frac{\overrightarrow{{X}_{1}}+\overrightarrow{{X}_{2}}+\overrightarrow{{X}_{3}}}{3}$$
(21)

where \(\overrightarrow{{X}_{1}},\overrightarrow{{X}_{2}}\) and \(\overrightarrow{{X}_{3}}\) are the α, β, and δ position vectors.

After gaining the three best solutions (α, β, and δ), then the other agents (\(\omega\)) will be obliged to update their positions based on the best solutions and compute the fitness function value up to the determined stopping criteria. The pseudocode of GWO is given by Fig. 6.

Fig. 6
figure 6

The pseudocode of GWO

Full size image

4.3 MFO algorithm

The MF is another type of nature-inspired algorithm that was first presented by Mirjalili [33]. MFO is simple, flexible, and robust, has a fast searching speed, and is easy to use with the other algorithms at the same time [34]. Moths are a type of insect that has peregrination behavior called transverse orientation based on moonlight navigation. The flying technique of a moth maintains a fixed angle with respect to the moon, which is considered a very effective method for traveling long distances in an upward line. MFO steps can be outlined as follows. Firstly, moths are randomly generated in the search space, and then their position is calculated, adopting the best position using a flame. Finally, to achieve the best positions, the positions of moths are updated by a spiral movement as [33]:

$${M}_{i}=S\left({M}_{i},{F}_{j}\right)$$
(22)
$$S\left({M}_{i},{F}_{j}\right)={XD}_{i} {e}^{by}\mathrm{cos}\left(2\pi y\right)+{F}_{j}$$
(23)
$${XD}_{i}=\left|{F}_{j}-{M}_{i}\right|$$
(24)

where \({M}_{i},{F}_{j}\) are the ith moth and the jth flame, b is the variability of the model of the logarithmic maturation pattern, y is a random number in the range of [−1, 1], and XDi is the distance between the ith moth and the jth flame.

The number of flames is updated by:

$$\mathrm{flame}\_\mathrm{No}=\mathrm{round}\left(N-t\times \frac{N-t}{{\mathrm{iter}}_{\mathrm{max}}}\right)$$
(25)

where \(N\) is the maximum number of flames, \(t\) is the current iteration, and \({iter}_{max}\) is the maximum iterations. Finally, the new best positions of moths are updated and the previous steps are repeated until the termination criteria are reached. Figure 7 gives the pseudocode of the MFO algorithm.

Fig. 7
figure 7

The pseudocode of the MFO algorithm

Full size image

4.4 ALO algorithm

Ant-lion optimization (ALO) is another type of nature-inspired algorithm introduced by Mirjalili [35] that simulates the hunting behavior of ant-lions in catching their prey. AL have five steps in their hunting process, which include random walk, trap construction, ant (prey) entrapment, prey capture, and finally, trap reconstruction. ALO steps are summarized as follows. Firstly, an initial population of ants given by XAnt = (x1, x2, …, xN) and ant-lions given by XAntlion = (x1, x2, …, xN) are generated in the search space of the parameters. For each ant, using a roulette wheel, an AL is selected based on the best fitness to construct a trap for the ants, and then the ants' random walk is mathematically presented as [35, 36]:

$$X\left(\mathrm{iter}\right)=\left[\begin{array}{c}0, cumsum\left(2r\left({\mathrm{iter}}_{1}\right)-1\right), cumsum\left(2r\left({\mathrm{iter}}_{2}\right)-1\right),\dots \\ cumsum\left(2r\left({\mathrm{iter}}_{\mathrm{max}}\right)-1\right)\end{array}\right]$$
(26)

where cumsum is the cumulative sum, itermax is the maximum number of iterations, iter is the random walk steps, and r(iter) is a stochastic function defined as:

$$ r({\text{iter}})=\left\{\begin{array}{ll} 1 &{\text{if }} r {\text{ and}} > 0.5 \\ 0 & {\text{if }} r {\text{ and}} \le 0.5 \end{array} \right. $$
(27)

where rand is a number generated randomly in [0, 1]. The normalized random walk formula is used to keep the ants’ position in the search space as:

$$\it \it \it {x}^{\mathrm{iter}}=\frac{\left({x}^{\mathrm{iter}}-{\mathrm{mi}}^{\mathrm{iter}}\right)+ \left(U-L\right)}{\left({\mathrm{mx}}^{\mathrm{iter}}-{\mathrm{mi}}^{\mathrm{iter}}\right)}+L$$
(28)

where mi and mx are the minimum and maximum of a random walk, and L and U are the lower and upper bounds of the variable, respectively. Trapping of ants is expressed as:

$${L}_{i}^{\mathrm{iter}}={\mathrm{Antlion}}_{j}^{\mathrm{iter}}+{L}^{\mathrm{iter}}$$
(29)
$${U}_{i}^{\mathrm{iter}}={\mathrm{Antlion}}_{j}^{\mathrm{iter}}+{U}^{\mathrm{iter}}$$
(30)

where i is the selected ant index, and j is the selected ant-lion index. This sliding mechanism is expressed as:

$${L}^{\mathrm{iter}}=\frac{{L}^{\mathrm{iter}}}{\mathrm{I}}$$
(31)
$${U}^{\mathrm{iter}}=\frac{{U}^{\mathrm{iter}}}{\mathrm{I}}$$
(32)
$$I={10}^{\omega }\frac{\mathrm{iter}}{\mathrm{iter}\_\mathrm{max}}$$
(33)

where ω is a constant defined as:

$$\omega = \left\{ {\begin{array}{*{20}c} 2 & {{\text{when}}} & {{\text{iter}} > 0.10} & {{\text{iter}}_{\max } } \\ 3 & {{\text{when}}} & {{\text{iter}} > 0.50} & {{\text{iter}}_{\max } } \\ 4 & {{\text{when}}} & {{\text{iter}} > 0.70} & {{\text{iter}}_{\max } } \\ 5 & {{\text{when}}} & {{\text{iter}} > 0.90} & {{\text{iter}}_{\max } } \\ 6 & {{\text{when}}} & {{\text{iter}} > 0.95} & {{\text{iter}}_{\max } } \\ \end{array} } \right.$$
(34)

The fitness of the ants’ new position is expressed by:

$${x}_{ALj}^{\mathrm{iter}}={x}_{\mathrm{Ai}}^{\mathrm{iter}}\, \mathrm{if}\, f\left({x}_{\mathrm{Ai}}^{\mathrm{iter}}\right)>f\left({x}_{ALj}^{\mathrm{iter}}\right)$$
(35)

where xAi is the ant-lion position. Elitism is the process that keeps the best ant-lion position by using:

$${x}_{\mathrm{A}}^{\mathrm{iter}}=\frac{{R}_{\mathrm{A}}^{\mathrm{iter}}+{R}_{\mathrm{E}}^{\mathrm{iter}}}{2}$$
(36)

where \({x}_{\mathrm{A}}^{\mathrm{iter}}\) is the position of the ant, RA is the ant random walk for an ant-lion selected using a roulette wheel, and RE is an elite ant-lion. The elite is updated, and if termination criteria are reached, the process is stopped or the next iteration is begun. Figure 8 explains the pseudocode of the ALO algorithm.

Fig. 8
figure 8

The pseudocode of the ALO algorithm

Full size image

4.5 DA optimization

The dragonfly algorithm (DA) was proposed by Mirjalili in 2015 [37]. The inspiration for DA is based on dragonfly swarming behaviors. There are two important behaviors of dragonflies in nature, which are static and dynamic. In the static case, dragonflies create a very small group to fly a small distance and hunt small insects. On the other hand, in the dynamic case, dragonflies create a large group and travel in one specific direction for long distances, which agree with the two optimization phases of exploration and exploitation. The main goals of dragonfly swarms are attraction to food sources and distracting enemies. According to these two behaviors, there are five factors for position updating of individuals, namely separation, alignment, cohesion, attraction to food sources, and distracting enemies [37]. The mathematical model of the separation is calculated as [37]:

$$S_{i} = - \mathop \sum \limits_{j = 1}^{N} X - X_{j}$$
(37)

where X indicates the current position, Xj shows the jth neighboring individual position, and N is the number of neighboring individuals. Alignment (A) is represented as:

$${\mathrm{A}}_{i}=\frac{\sum_{j=1}^{N}{ X}_{j}}{N}$$
(38)

where Xj is the jth neighboring individual velocity. The cohesion (C) is calculated as:

$${\mathrm{C}}_{i}=\frac{\sum_{j=1}^{N}{ X}_{j}}{N}-X$$
(39)

The attraction towards a food source (F) is determined by:

$${\mathrm{F}}_{i}={X}^{+}-X$$
(40)

Distracting an enemy (E) outwards is determined by:

$${\mathrm{E}}_{i}={X}^{-}+X$$
(41)

where X+ is the food source position and X− is the enemy position.

Updating the dragonfly's position in a search space and analyzing their movements takes into account step vectors (ΔX) and position (X) vectors. The step vector of the DA is similar to particle swarm optimization (PSO), so the DA step vector shows the direction of movement as given by:

$${\Delta X}_{t+1}=\left(s{S}_{i}+a{\mathrm{A}}_{i}+c{\mathrm{C}}_{i}+f{\mathrm{F}}_{i}+e{\mathrm{E}}_{i}\right)+w\Delta {X}_{t}$$
(42)

where s is the weight of separation, a is the weight of alignment, A is the alignment of the ith individual, c is the weight of cohesion, f is the food factor, e is the enemy factor, w is the weight of inertia, and t is the iteration count. The position vectors are computed as:

$${X}_{t+1}={X}_{t}+{\Delta X}_{t+1}$$
(43)

To improve the randomness, Lévy flight random walk is used for dragonflies to fly when there are no neighboring solutions. Thus, the dragonfly's position is updated by:

$${X}_{t+1}={X}_{t}+Levy\left(d\right)\times {X}_{t}$$
(44)
$$\mathrm{Levy}\left(x\right)=0.01\times \frac{\sigma {r}_{1}}{{\left|{r}_{2}\right|}^{\frac{1}{\beta }}}$$
(45)
$$\sigma ={\left(\frac{\Gamma \left(1+\beta \right)\times \mathrm{sin}\left(\frac{\pi \beta }{2}\right)}{\Gamma \left(\frac{1+\beta }{2}\right)\times \beta \times {2}^{\left(\frac{\beta -1}{2}\right)}}\right)}^{1/{\beta}}$$
(46)
$$\Gamma \left(x\right)=\left(x-1\right)$$
(47)

where d indicates the dimension of position vectors, r1 and r2 are random numbers in [0, 1], and β is a constant (= 1.5) [38, 39]. Figure 9 gives the pseudocode for the DA.

Fig. 9
figure 9

The pseudo-code of the DA

Full size image

4.6 WO algorithm

The whale optimization algorithm (WOA) is a new optimization algorithm based on meta-heuristics that simulates the hunting behavior of the humpback whale [40,41,42]. Humpback whales use random search strategies for finding prey through the transfer of data with the others. Figure 10 gives the pseudo-code of the WOA. The mathematical model of encirclement of prey, net of the bubble method for hunting, and the prey behavior are as follows [43]:

$$\overrightarrow{D}= \left|\overrightarrow{C} . \overrightarrow{{X}^{*}}\left(t\right)-\overrightarrow{X}\left(t\right)\right|$$
(48)
$$\overrightarrow{X}\left(t+1\right)=\overrightarrow{{X}^{*}}\left(t\right)-\overrightarrow{A} . \overrightarrow{D}$$
(49)

where D represents the distance between the whale and the prey, t is the iteration, A and C are vector coefficients, X* is the best solution position vector gained, and X is the position vector. Vectors \(\overrightarrow{A}\) and \(\overrightarrow{C}\) are presented by:

$$\overrightarrow{A}=\left(2\overrightarrow{a}.\overrightarrow{r}\right)-\overrightarrow{a}$$
(50)
$$\overrightarrow{C}=2 \overrightarrow{r}$$
(51)

where \(\overrightarrow{a}\) decreases linearly from 2 to 0 for iterations, and \(\overrightarrow{r}\) is a random vector in [0, 1]. To update the positions of whale and prey, the spiral equation is used to simulate the spiral-shaped movement of humpback whales as:

$$\overrightarrow{X} \left(t+1\right)=\overrightarrow{{D}^{^{\prime}}}. {e}^{bi}\mathrm{cos}\left(2 \pi l\right)+\overrightarrow{{X}^{*}} (t)$$
(52)
$$\overrightarrow{{D}^{^{\prime}}} \left(t\right)=\left|\overrightarrow{{X}^{*}} \left(t\right)-\overrightarrow{X} \left(t\right)\right|$$
(53)

where b is a constant for the shape definition, and l is a random number in [−1, 1].

Fig. 10
figure 10

The pseudo-code of the WOA

Full size image

The humpback whales swim around the prey in a shrinking circle and a spiral simultaneously. The mathematical model of this behavior has a 50% probability (p) of choosing between them during the optimization process, expressed as:

$$\overrightarrow{X}\left(t+1\right)=\left\{\begin{array}{c}\overrightarrow{{X}^{*}}\left(t\right)-\overrightarrow{A} . \overrightarrow{D} \,if\, p<0.5\\ \overrightarrow{{D}^{^{\prime}}}. {e}^{bi}\mathrm{cos}\left(2 \pi l\right)+\overrightarrow{{X}^{*}} \left(t\right)\, if\, p\ge 0.5\end{array}\right.$$
(54)

According to the random searching of humpback whales, \(\overrightarrow{A}\) is used with the random values [−1, 1] based on the exploration and exploitation for updating the position of the search agent. This mechanism and |\(\overrightarrow{A}\)| > 1 emphasize exploration and allow the WOA to perform a global search. The mathematical model representing this mechanism is as follows:

$$\overrightarrow{D}=\left|\overrightarrow{C} . \overrightarrow{{X}_{\mathrm{rand} }}\left(t\right)-\overrightarrow{X}\left(t\right)\right|$$
(55)
$$\overrightarrow{X}\left(t+1\right)= \overrightarrow{{X}_{\mathrm{rand} }}\left(t\right)-\overrightarrow{A} . \overrightarrow{D}$$
(56)

where \(\overrightarrow{{X}_{rand}}\) is a random position vector chosen from the current population [43].

5 Results and discussion

Convergence curves for the best run of the six proposed algorithms are shown in Fig. 11. It is evident that all the optimization algorithms have the ability to reach an optimal objective function value in less than 20 iterations. Comparisons of the extracted optimal DSSC parameters using different optimization techniques are presented in Table 2. Figure 12 shows the J–V characteristic curve of the DSSC based on optimal parameter values obtained.

Fig. 11
figure 11

Convergence curves of the proposed optimization algorithms

Full size image
Table 2 Optimal DSSC parameters obtained for different optimization algorithms
Full size table
Fig. 12
figure 12

J–V characteristic curve of DSSC based on optimal parameter values

Full size image

5.1 Sensitivity analysis

As presented, the increase in temperature causes an increase in the photocurrent density and the voltage and, therefore, the conversion efficiency. According to the results achieved with this simulation, with increasing temperature, the open-circuit voltage, the power, and the conversion efficiency of the DSSC increase. Two contrastingly changing factors affect the open-circuit voltage. The first is that as the charge diffusion and mobility increase with increasing temperature, the open-circuit voltage increases. The other factor is the decrease in open-circuit voltage due to the increase in the charge recombination with temperature that results in a directly proportional relationship between temperature and open-circuit voltage, as shown in Fig. 13.

Fig. 13
figure 13

J–V characteristic curve of DSSC with temperature variation

Full size image

Voc increases due to the increase in chemical potential caused by the increased charge generation with increasing solar radiation. On the other hand, the charge lifetime decreases with increasing solar radiation intensity, resulting in a reduction in chemical potential, which leads to lowering of the Voc. However, the dominant process is the increase in charge generation and hence the increase in open-circuit voltage as given by Fig. 14. Also, short-circuit current density increases significantly with the increase in solar radiation. As shown in Fig. 15, the lifetime affected mainly the open-circuit voltage; as τ increases, Voc increases due to the decrease in the recombination rate, hence resulting in higher electron density in the photoanode. The photocurrent density is not affected by the lifetime variation.

Fig. 14
figure 14

J–V characteristic curve of DSSC with the variation in solar radiation

Full size image
Fig. 15
figure 15

J–V characteristic curve of DSSC with variation in electron lifetime

Full size image

Figure 16 presents the variation in the DSSC Jsc, Voc and Pmax with the variation in electron lifetime. Lifetime Voc and Pmax increase while Jsc is approximately constant. The variation in fill factor and efficiency with electron lifetime is given by Fig. 17.

Fig. 16
figure 16

DSSC parameter variation (Jsc, Voc, and Pmax) with electron lifetime variation

Full size image
Fig. 17
figure 17

DSSC efficiency and fill factor variation with electron lifetime variation

Full size image

The variation in the J–V characteristics with various absorption coefficients is presented in Fig. 18. It is observed that both the current density and potential difference increase with the increase in the absorption coefficient. This behavior can be interpreted as follows: with the increase in the absorption coefficient, more photons are absorbed by the dye molecules on the surface of the photoanode, resulting in the generation of more electrons and consequently enhancing the conversion efficiency. Both Jsc and Voc increase with increasing absorption coefficient values, as more photons can be absorbed to enhance the photoelectric conversion. Figure 19 displays the variation in the output parameters of the DSSC (Jsc, Voc, and Pmax) with the variation in the absorption coefficient. The variation in the efficiency and fill factor with the absorption coefficient is presented in Fig. 20. Both the efficiency and fill factor increase with an increase in the absorption coefficient due to the increase in photon absorption by the DSSC and hence the collection of more electrons.

Fig. 18
figure 18

J–V characteristic curve of the DSSC with absorption coefficient variation

Full size image
Fig. 19
figure 19

DSSC parameter variation (Jsc, Voc, and Pmax) with absorption coefficient variation

Full size image
Fig. 20
figure 20

DSSC efficiency and fill factor variation with absorption coefficient variation

Full size image

The thickness of photoanode film is an important technological parameter for the design and optimization of the dye cell. The effect of the variation in photoanode thickness on the J–V curves can be clearly seen in Fig. 21. The range of variation taken into consideration is between 0.1 and 30 μm.

Fig. 21
figure 21

J–V characteristic curve variation of DSSC with photoanode film thickness

Full size image

Figure 22 presents the effect of the variation in thickness on Jsc. The current increases up to a certain value, and after the optimal point, the current starts to decrease.

Fig. 22
figure 22

DSSC parameter variation (Jsc, Voc, and Pmax) with electrode thickness variation

Full size image

This effect can lead to an increase in the area of the internal surface and the absorption of more photons by the photoanode, but if the thickness is greater than the light penetration depth, the number of photons will reach the limit, and Jsc will start to decrease because more recombination occurs, causing electron loss. This behavior can be explained as follows: the increase in the thickness of the photoanode increases the dye absorbance in the photoanode porous voids, thus enhancing its light absorbance and further increasing the density of photogenerated carriers. Hence, photocurrent density increases, but at the same time, the series resistance of the electrode also tends to increase, affecting the cell performance. In addition, Voc decreases with the increase in thickness due to the high series resistance.

Figure 23 presents the effect of the variation in thickness on the fill factor and efficiency. Increasing thickness leads to an increase in the internal resistance of the cell.

Fig. 23
figure 23

DSSC efficiency and fill factor variation with electrode thickness variation

Full size image

The results indicate that finding the optimal value of thickness leads to high efficiency, and the maximum values of the DSSC electrical parameters can be obtained.

The effect of the variation in the diffusion coefficient on DSSC performance is indicated in Fig. 24. There is a directly proportional relationship between the diffusion coefficient and the current density, but the converse is seen with its voltage. This is because increasing the value of the diffusion coefficient leads to an increase in electron diffusion length. This means that a greater diffusion coefficient causes a decrease in the recombination rate, and thus more electrons can be collected. This increases the current density. However, the greater electron extraction results in a smaller value of electron density. The small electron density decreases the potential difference. Figure 25 displays the effect of D on the J–V characteristics. With increasing D, Jsc increases but Voc decreases. The variations can be understood by the fact that an increase in D increases the diffusion length, and subsequently more electrons are taken out to the external circuit, resulting in higher electrical current. Consequently, the electron density is reduced, causing a lower Voc.

Fig. 24
figure 24

Variation in DSSC J–V characteristic curve with different electron diffusion coefficients

Full size image
Fig. 25
figure 25

DSSC parameter variation (Jsc, Voc, and Pmax) with diffusion coefficient variation

Full size image

The variations in DSSC parameters Jsc, Voc, FF, and η with the electron diffusion coefficient is demonstrated in Figs. 25 and 26. A clear tendency can be detected, where both Voc and FF decrease while Jsc increases with the increase in the electron diffusion coefficient.

Fig. 26
figure 26

DSSC efficiency and fill factor variation with diffusion coefficient variation

Full size image

6 Conclusion

DSSCs have received extensive attention from many scientists over the past three decades. Fast theoretical and practical studies have been undertaken to enhance the performance of DSSCs. To identify the DSSC intrinsic parameters, we need to tune each component and determine the appropriate conditions in optimizing the performance of complete cells. Meta-heuristic optimization techniques are applied to extract the DSSC parameters using semiconductor thin-film electron diffusion modeling. MATLAB software is used to investigate the influence of various physical and environmental parameters on DSSC characteristics and to perform sensitivity analysis. The electrode thickness, electron lifetime, diffusion coefficient, absorption coefficient, radiation, and air temperature are the parameters under consideration. Jsc, Voc, Pmax, FF, and efficiency are the DSSC performance indicators. The suggested optimization algorithms have been verified as offering superior characteristics, including good solutions, stable and fast convergence to the best solution, and high computational performance.