Subdomain-based exponential integrators for quantum Liouville-type equations

Abstract

In order to describe quantum mechanical effects, the use of the von-Neumann equation is apparent. In this work, we present a unified numerical framework so that the von-Neumann equation in center-of-mass coordinates leads to a Quantum Liouville-type equation when choosing a suitable basis. In particular, the proposed approach can be related to the conventional Wigner equation when a plane wave basis is used. The drawback of the numerical methods is the high computational cost. Our presented approach is extended to allow reducing the dimension of the basis, which leads to a computationally efficient and accurate subdomain approach. Not only the steady-state behavior is of interest, but also the dynamic behavior. In order to solve the time-dependent case, suitable approximation methods for the time-dependent exponential integrator are necessary. For this purpose, we also investigate approximations of the exponential integrator based on Faber polynomials and Krylov methods. In order to evaluate and justify our approach, various test cases, including a resonant tunnel diode as well as a double-gate field-effect transistor, are investigated and validated for the stationary and the dynamic device behavior.

1 Introduction

For the analysis of quantum transport, the focus has been on the study of numerical methods for solving Quantum Liouville-type equations in recent years, because interaction effects could be appropriately integrated in these models. Above all, there is the possibility of numeric and efficient analysis of not only stationary but also dynamic processes [1,2,3]. As an alternative, the non-equilibrium Green’s function (NEGF) formalism is very widespread, but is associated with difficulties when dynamic or transient algorithms are implemented, especially with regard to memory requirements [4]. Therefore, the study of numerical methods for solving time-dependent Quantum Liouville-type equations is of particular interest.

The Wigner formalism provides a broad basis in terms of a phase space formulation [5]. The investigation of electronic properties is inherently combined with the numerical solution of the Wigner equation, which results in a quasi-distribution function known as the Wigner function [2, 3]. Along with the quasi-distribution function, the electronic properties can be efficiently determined.

The approximation of Quantum Liouville-type equations has hitherto been associated with some difficulties, which were linked with the integration of boundary conditions [6,7,8,9,10] and the discretization methodologies [6, 11] used. As a consequence, the results deviate on a large scale from reference approaches such as the NEGF approach [10,11,12,13]. Additionally, highly oscillating functions within the phase space [14, 15] occur, which hinder the computationally efficient solution of the Wigner equation depending on the quality of the numerical approximation. The latter aspect is of particular interest, when quantum effects are prominent. Unfortunately, to resolve all the features within the Wigner methodology by the use of conventional numerical approaches, an extremely fine computational grid is needed resulting in large linear systems of equations. Even worse, the linear system has to be solved several times along with the Poisson equation for quantum self-consistency.

To overcome these limitations, a real space formulation of the Liouville equation is preferable [12, 16, 17]. With these new approaches, such as the introduction of a complex absorbing potential (CAP) and a spatial discretization based on a norm conserving approximation of the spatial exponential integrator, the previous problems of unphysical reflections and an overestimation of diffusion effects are avoided [10, 13]. Consequently, the investigations herein are carried out with the approach presented in [10, 13]. The approaches presented in [12, 16] are based on the expansion of the statistical density matrix in terms of the eigenvectors of the diffusion matrix for the case of a simplified Hamiltonian assuming a spatially constant effective mass distribution, which seems to be the standard model for numerical investigations of the Wigner equation, e.g. [14, 17,18,19,20,21,22]. In [23, 24], the approach has been analyzed with regard to plane wave functions spanning the numerical basis, which become particular important when multiband transport has to be considered or the spatially varying effective mass has to be taken into account.

In this paper, we show that after a spatial discretization and subsequent transformations, the von-Neumann equation in center-mass coordinates is transformed into a Quantum Liouville-type equation. We show that a formal relation to the Wigner equation can be established when using a transformation with basis functions representing plane waves. Moreover, a subdomain approach based on [23] is investigated by successively reducing the set of basis functions used to expand the statistical density matrix. This approach is necessary so that together with a suitable subset of the original complete set of basis functions, the solution procedure can be significantly improved in terms of computational efficiency. In order to describe high-frequency behavior or switching processes of components, dynamic calculations are needed. To this end, this paper also examines approaches for the dynamic solution of the Quantum Liouville-type equation that allow a parallelization of the algorithms.

The manuscript is organized as follows. The proposed methodology is presented in chapter 2. Herein, the von-Neumann equation is introduced (2.1) followed by the presentation of the expansion technique (2.2). Afterward, the connection with the Wigner approach is discussed in detail in Sect. 2.3. Finally, the structure of the system matrix and the required boundary conditions are briefly discussed (2.4). Based on these aspects, the subdomain approach is validated in chapter 3 using several simulation examples in the stationary regime, covering different devices such as a GaAs-based resonant tunnel diode (RTD) (3.1) and a GaInAs-based double-gate field-effect transistor (DGFET) (3.2). The results are compared with those of a Green’s function approach, which serves as a reference method. Efficient and accurate methods for the time-dependent solution are discussed in chapter 4. First, the scheme with its time-dependent exponential integrator is presented (4.1). Special attention is paid to methods that allow numerically stable and, most importantly, explicit methods (4.2). Thus, such methods can be implemented allowing parallelized algorithms. The eigenvector expansion method is presented, which serves as a reference method since it is based on an analytical solution of the matrix exponential (4.2.1). Since the eigenvectors and eigenvalues of the system matrix must be calculated, this approach leads to an accurate evaluation of the matrix exponential. Next, a Crank–Nicolson scheme is presented (4.2.2). This implicit method is widely used and is included for completeness. In particular, explicit approaches based on Faber polynomials (4.2.3) and commonly used Krylov approaches (4.2.4) are presented and evaluated with regard to their potential to solve Quantum Liouville-type equations. After a detailed presentation of their approximation, a brief validation is performed using test examples (4.3). An analysis of the dynamic regime is then undertaken in chapter 5 by examining a class-C operation of a DGFET (5.1) and also considering a simplified electron–phonon scattering mechanism to show that non-ballistic effects can also be included when using the proposed concept (5.2). The presentation ends with a summary and conclusion in chapter 6.

2 Quantum transport theory

2.1 Von-Neumann equation

For demonstration purposes, the one-dimensional transport behavior is investigated utilizing an effective mass Hamiltonian. In addition, the effective mass is assumed to be spatially constant with regard to the comparison of the proposed approach to the conventional Wigner equation, where the homogeneous effective mass case seems to be the standard, see, e.g. [3, 18].

The von-Neumann equation, i.e., based on the coordinates r and $r'$ is transformed introducing center-mass coordinates according to $\chi =(r'+r)/2$ and $\xi =r'-r$. Then, the von-Neumann equation in center-mass coordinates reads as

$$\begin{aligned} \dfrac{\partial }{\partial t}\rho (\chi ,\xi ,t)&=\mathrm {j}\dfrac{\hbar }{m}\dfrac{\partial }{\partial \chi }\dfrac{\partial }{\partial \xi }\rho (\chi ,\xi ,t) \nonumber \\&\quad -\mathrm {j}\dfrac{q}{\hbar }B(\chi ,\xi ,t)\rho (\chi ,\xi ,t), \end{aligned}$$

(1)

where the function $B(\chi ,\xi ,t)$ contains the potential energy and $\rho$ represents the statistical density matrix. The potential energy includes the static conduction band, the self-consistent Hartree potential and the externally applied bias all of them contained in V as well as the complex absorbing potential (CAP) $\mathrm {j}W$

$$\begin{aligned} B(\chi ,\xi ,t) = V\left( \chi +\dfrac{1}{2}\xi ,t\right) - V\left( \chi -\dfrac{1}{2}\xi ,t\right) -\mathrm {j}W(\xi ). \end{aligned}$$

(2)

The CAP is introduced in order to suppress artificial reflections caused by the finiteness of the computational domain with regard to the $\xi$-direction [12]. The use of the CAP can be explained as follows. After the Wigner transformation related to a finite space is carried out, a surface term is obtained [12]. The neglect of the surface term corresponds to the mathematical formulation of Dirichlet boundary conditions for the statistical density matrix. This boundary condition corresponds to a termination of the computational domain with a perfectly reflective layer. As a result, the portions of the statistical density matrix incident on the boundary are reflected and subsequently superimposed on the original solution leading to unphysical solutions. The basic idea behind the complex potential is the introduction of an artificial layer at the edges of the computational domain. Within these layers, an additional term is added onto the potential, which contains a complex potential $\mathrm {j}W(\xi )$. This complex potential causes a decaying behavior of the statistical density matrix within the layers, so that reflections at the edges of the computational domain can be significantly reduced.

Following the approach in [12], an equidistant standard finite volume scheme with regard to the $\xi$-direction is utilized to discretize the von-Neumann equation (1). Hereby, the interval $[-L_\xi /2, +L_\xi /2]$ is subdivided into $N_\xi$ cells with a volume $\varDelta \xi$. Finally, the von-Neumann equation results in a semi-discrete system of coupled partial differential equations

$$\begin{aligned} \dfrac{\partial }{\partial t}{\varvec{\rho }}(\chi ,t)=c_{A}{\varvec{A}}\dfrac{\partial }{\partial \chi }{\varvec{\rho }}(\chi ,t)-c_B{\varvec{B}}(\chi ,t){\varvec{\rho }}(\chi ,t), \end{aligned}$$

(3)

where the abbreviations $c_A=\mathrm {j}\hbar /(2m\varDelta \xi )$ and $c_B=\mathrm {j}q/\hbar$ are introduced. The vector ${\varvec{\rho }}(\chi ,t)$ contains the values of the discretized locations $\xi _j$. For the evaluation of the so-called diffusion matrix ${\varvec{A}}$, the central flux is chosen with regard to coherence effects [12] so that the nonzero matrix elements $A_{i,j}$ of the matrix ${\varvec{A}}$ are defined by $A_{i,i+1} = 1$ and $A_{i,i-1} = -1$. The application of the trapezoidal rule leads to a tridiagonal drift matrix ${\varvec{B}}(\chi )$, with the nonzero elements $B_{i,i}$ given by $B_{i,i}(\chi ,t)=1/4\left( B(\chi ,\xi _{i-\frac{1}{2}},t)+B(\chi ,\xi _{i+\frac{1}{2}},t)\right)$ and $B_{i,i\pm 1}(\chi ,t)=1/4\cdot B(\chi ,\xi _{i\pm \frac{1}{2}},t)$, where the values $\xi _{i\pm \frac{1}{2}}$ represent the locations of the interfaces of the i-th cell. Furthermore, for the comparison with the Wigner equation, the midpoint rule is also considered leading to a diagonal drift matrix, where the diagonal element functions are $B_{i,i}(\chi ,t)= B(\chi ,\xi _{i},t)$.

2.2 Quantum Liouville-type equations

Unfortunately, the open boundary conditions required for quantum transport described by the von-Neumann Eq. (3) are unknown in real space. To address this aspect, the proposed approach adopts the inflow boundary condition scheme stemming from the Wigner formalism. The distinction between forward and backward waves within the Wigner formalism emerges naturally. To establish such distinction within the von-Neumann equation, a basis transformation is needed. Along with this basis transformation, the Quantum Liouville-type equations arise.

Introducing the basis vectors ${\varvec{\varPhi }}_n$ as well as the corresponding expansion coefficients $c_n$, the semi-discrete statistical density matrix can be expanded on the basis of N basis vectors ${\varvec{\varPhi }}_n$ defined by

$$\begin{aligned} {\varvec{\rho }}(\chi ,t) = \sum _{n=1}^N {\varvec{\varPhi }}_n\cdot c_n(\chi ,t)={\varvec{\varPhi }}\cdot {\varvec{c}}(\chi ,t). \end{aligned}$$

(4)

The matrix ${\varvec{\varPhi }}$ contains the discretized basis functions column wise and ${\varvec{c}}$ includes the corresponding expansion coefficients. The choice of the expansion order N is discussed later on. The basis functions can always be chosen such that they are orthonormal ${\varvec{\varPhi }}_n^{\dagger }\cdot {\varvec{\varPhi }}_m = \delta _{n,m}$ so that the vector of expansion coefficients ${\varvec{c}}(\chi ,t)$ can be easily determined by solving

$$\begin{aligned} {\varvec{c}}(\chi ,t) = {\varvec{\varPhi }}^{\dagger }\cdot {\varvec{\rho }}(\chi ,t). \end{aligned}$$

(5)

To summarize, the system is discretized with regard to the $\xi$-direction within the real space. As a consequence, interface conditions can be spatially local considered in terms of numerical flux functions.

In order to arrive at the Quantum Liouville-type equations, the basis expansion (4) is applied onto the semi-discrete von-Neumann Eq. (3). Then, this equation is multiplied with the Hermitian conjugate of the matrix of the basis functions ${\varvec{\varPhi }}^{\dagger }$ resulting in

$$\begin{aligned} \dfrac{\partial }{\partial t}{\varvec{c}}(\chi ,t)=c_{A}{\varvec{\varPhi }}^{\dagger }{\varvec{A}}{\varvec{\varPhi }}\dfrac{\partial }{\partial \chi }{\varvec{c}}(\chi ,t)-c_B{\varvec{\varPhi }}^{\dagger }{\varvec{B}}(\chi ,t){\varvec{\varPhi }}\cdot {\varvec{c}}(\chi ,t). \end{aligned}$$

(6)

The diffusion matrix ${\varvec{A}}$ as well as the drift matrix ${\varvec{B}}$ have a dimension of $N_\xi \times N_\xi$, whereas the matrix of the basis vectors ${\varvec{\varPhi }}$ shows a dimension of $N_\xi \times N$. As a result, the transformed matrices ${\varvec{\varPhi }}^{\dagger }{\varvec{A}}{\varvec{\varPhi }}$ and ${\varvec{\varPhi }}^{\dagger }{\varvec{B}}(\chi ){\varvec{\varPhi }}$ show a dimension of $N\times N$, which constitutes the subdomain formulation.

Along with the approaches presented in [12, 16], the basis is spanned utilizing all eigenvectors of the diffusion matrix ${\varvec{A}}$ so that no reduction in the computational effort can be expected if the expansion order N could be chosen according to $N=N_\xi$. For the particular case of a constant effective mass, they can be analytically determined and are given by [16]

$$\begin{aligned} {\varvec{\varPhi }}_n = \left( \mathrm {j}^{1/2}\sin \left( \dfrac{1 \pi n}{N_\xi +1}\right) ,\dots ,\mathrm {j}^{N_\xi /2}\sin \left( \dfrac{ N_\xi \pi n}{N_\xi +1}\right) \right) ^{T}. \end{aligned}$$

(7)

This transformation matrix diagonalizes the diffusion matrix leading to the corresponding eigenvalues

$$\begin{aligned} \lambda _n = 2\mathrm {j}\cos \left( \dfrac{\pi n}{N_\xi +1}\right) . \end{aligned}$$

(8)

As mentioned, the value $N_\xi$ indicates the number of cells within the $\xi$-direction. In case, a symmetric discretization pattern is chosen, in which the discretized mean value of ${\varvec{\rho }}(\chi , t)$ at the location $\xi =0$ is included, $N_\xi$ represents an odd number.

A major prerequisite for the application of the inflow boundary condition scheme [1] is the assignment of the flow characteristic [16]. For this purpose, a symmetrically distributed eigenvalue spectrum is constructed on the basis of the signs of the eigenvalues. Herein, the value zero within the symmetrically distributed eigenvalue spectrum in $\lambda _n$ as well as $k_n$ has to be excluded as usual in order to avoid singularity issues [21]. Accordingly, the number of basis functions N utilized to expand the semi-discrete statistical density matrix has to be even.

Besides, the transformation matrix $\varvec{\varPhi }$ can be spanned by discretized plane wave basis functions, which then transform the von-Neumann equation into some kind of phase space representation. Here, the basis functions are defined as

$$\begin{aligned} {\varvec{\varPhi }}_n = \varPhi _n({\varvec{\xi }}) = \sqrt{\dfrac{\varDelta \xi }{L_\xi }}\exp \left( \mathrm {j}k_n {\varvec{\xi }}\right) \end{aligned}$$

(9)

with the variable k given by

$$\begin{aligned} k_n = -\dfrac{2\pi }{L_\xi }\left( n-\dfrac{1}{2}\left( N+1\right) \right) \end{aligned}$$

(10)

to fulfill the orthogonality requirement. Along with this plane wave basis, the implementation of scattering mechanisms becomes naturally facilitated. The variable k can be readily identified with the quantum mechanical momentum such that the flow behavior can be linked to the sign of k, which is, as aforementioned, a major prerequisite for the application of the inflow boundary condition scheme. On this basis, the advantages of the real space discretization can, therefore, be combined with the advantages of a direct phase space approach. Apart from that, subdomain approaches can be established.

Since the major quantum transport takes only place within a narrow energy window near the Fermi level, it is convenient to include just this region in the numerical calculations. Within the recognized methods based on the NEGF formalism [4], a constant energy is added to the band edge energy in the simplest case at each contact of interest conceptually leading to the value $E_\text {max}$. Along with the energy dispersion, this leads to an upper limit $k_\text {max}$, as well, which can be determined by using the relation

$$\begin{aligned} k_\text {max} =\frac{\sqrt{2 m_{\text {eff}} E_{\text {max}}}}{\hbar }. \end{aligned}$$

(11)

Now, the expression (10) is exploited to establish an interrelationship between the length $L_\xi$ and the corresponding value of $k_\text {max}$ by

$$\begin{aligned} L_{\xi }=\frac{\pi }{k_{\text {max}}} (N-1). \end{aligned}$$

(12)

2.3 Relation to the Wigner equation

The proposed approach can be linked to the conventional Wigner Eq. [3], for which the matrix elements have to be evaluated analytically for the case of the basis spanned by plane wave functions.

The elements of the transformed diffusion matrix are given by

$$\begin{aligned} c_A{\varvec{\varPhi }}_m^{\dagger }{\varvec{A}}{\varvec{\varPhi }}_n = \dfrac{\hbar }{m}\left( -\dfrac{\delta _{m,n}}{\varDelta \xi } + (-1)^{(m-n)}\dfrac{2}{L_\xi }\right) \sin (k_n\varDelta \xi ). \end{aligned}$$

(13)

From the physical point of view, the matrix elements correspond to the velocities. These velocities consist of two different portions as apparent from (13). The first term can be assigned to the numerical dispersion of the underlying finite volume scheme. In particular, it can be interpreted as the velocity of the eigenvector excluding external effects. The second term can be regarded as a crosstalk due to the remaining eigenvectors. This term is in addition strongly coupled to the boundaries of the computational domain in terms of the length $L_\xi$. In the limit $L_\xi \rightarrow \infty$, the latter term is zero-valued and the theoretical error due to the finite computational domain is zero-valued, too. When the limit $\varDelta \xi \rightarrow 0$ is additionally considered, the overall term converges toward

$$\begin{aligned} \lim _{L_\xi \rightarrow \infty }\lim _{\varDelta \xi \rightarrow 0}c_A{\varvec{\varPhi }}_m^{\dagger }{\varvec{A}}{\varvec{\varPhi }}_n = -\dfrac{\hbar k_n}{m}\delta _{m,n}, \end{aligned}$$

(14)

which exactly coincides with the values of the discretized diffusion matrix within the conventional Wigner formalism [3].

Furthermore, the transformed drift matrix can be related to the discretized drift operator within the Wigner formalism according to

$$\begin{aligned} \begin{aligned} c_B{\varvec{\varPhi }}_m^{\dagger }{\varvec{B}}{\varvec{\varPhi }}_n&= \dfrac{\varDelta \xi }{L_\xi }\sum _j \exp \left( \mathrm {j}(k_n-k_m)\xi _j\right) B(\chi ,\xi _j,t)\\ {}&=\dfrac{\varDelta k}{2\pi }\sum _j \exp \left( \mathrm {j}(k_n-k_m)\xi _j\right) B(\chi ,\xi _j,t)\varDelta \xi . \end{aligned} \end{aligned}$$

(15)

For simplicity, the midpoint rule is considered for the evaluation of the discretized drift operator. Exploiting the interrelationship of (10), namely $\varDelta k= 2\pi /L_\xi$, the matrix element coincides exactly with the approximated integral kernel within the drift operator [3].

As a consequence, the vector of expansion coefficients ${\varvec{c}}(\chi ,t)$ can be formally related to the semi-discrete Wigner function and the properties of the Wigner formalism can be retained. But, the proposed scheme is combined with a more flexible discretization of the real space, as aforementioned.

Nonetheless, these advantages come at a price, due to the numerical dispersion, which is proportional to $\sin (k\varDelta \xi )$. This proportionality represents a periodical projecting of the basis vectors onto their corresponding velocity.

With regard to the continuum solution given by (15), the numerical dispersion should be at least restricted to allow only one specific basis vector per velocity. As a result, the following condition $|\sin (k_\text {max}\varDelta \xi )|<1$ should hold for the maximum value $k_\text {max}$ included within the plane wave functions. Utilizing (10), an expression for $k_\text {max}=\pi /L_\xi (N-1)$ is found leading to

$$\begin{aligned} \left| \sin \left( \dfrac{\pi }{N_\xi }(N-1)\right) \right| <1. \end{aligned}$$

(16)

To fulfill this condition, the argument must be smaller than $\pi /2$ in its absolute value so that

$$\begin{aligned} N-1\le \dfrac{N_\xi }{2} \end{aligned}$$

(17)

holds. When this condition is violated, numerical instabilities arise. To avoid this restriction, higher order methods with regard to the discretization of the $\xi$-direction proved to be successful. However, that aspect is beyond the scope of this work and represents a topic for future discussions.

2.4 Matrix assembly and boundary conditions

To solve the Quantum Liouville-type equations, the $\chi$-direction must be discretized and boundary conditions have to be included. Although, the procedure is discussed in depth in [12], the fundamentals are briefly outlined in the following.

To start with, the discretization with regard to the $\chi$-direction is carried out. The computational domain with regard to the $\chi$-direction is subdivided into $N_\chi$ cells within the interval $[0, L_\chi ]$. The interface values of the i-th cell are given by $\chi _i$ and $\chi _{i+1}$. Furthermore, the abbreviations

$$\begin{aligned} {\varvec{\mathcal {A}}}=c_{A}{\varvec{\varPhi }}^{\dagger }{\varvec{A}}{\varvec{\varPhi }}~\text {and}~{\varvec{\mathcal {B}}}(\chi ,t)=c_B{\varvec{\varPhi }}^{\dagger }{\varvec{B}}(\chi ,t){\varvec{\varPhi }} \end{aligned}$$

are introduced enabling a compact notation. Herewith, the discretization procedure results in

$$\begin{aligned} \begin{aligned} \dfrac{\partial }{\partial t}\dfrac{{\varvec{c}}_{i+1}(t)+{\varvec{c}}_{i}(t)}{2}&={\varvec{\mathcal {A}}}\dfrac{{\varvec{c}}_{i+1}(t)-{\varvec{c}}_{i}(t)}{\varDelta \chi }\\ {}&-{\varvec{\mathcal {B}}}_{i+\frac{1}{2}}(t)\dfrac{{\varvec{c}}_{i+1}(t)+{\varvec{c}}_{i}(t)}{2}\\ \end{aligned} \end{aligned}$$

(18)

for the i-th cell, where ${\varvec{c}}_i$ is located at the value $\chi _i$. This equation can be applied onto each cell, which are connected by the neighbored interfaces. Finally, this procedure results in a system of linear equations. When rewriting the system of linear equations (18), the system matrix is obtained [12, 16]. For this purpose, a supervector ${\mathbf {F}}$ containing the vectors ${\mathbf {c}}$ at the discretized locations $\chi _i$ is formed. Taking into account the term on the right-hand side of (18) for each value $\chi _i$, a sparse matrix $\mathbf {\Lambda }$ results. In the same manner, along with the approximation of the left-hand side of (18), the elements of a sparse matrix $\mathbf {\Omega }$ can be determined. So, along with the supervector ${\mathbf {F}}$, the matrices $\mathbf {\Omega }$ and $\mathbf {\Lambda }$ can be defined including the corresponding discretized operators within the phase space. Finally, the system of linear equations can be written as

$$\begin{aligned} \mathbf {\Omega }\dfrac{\text {d}}{\text {d} t}{\mathbf {F}}(t)=\mathbf {\Lambda }\cdot {\mathbf {F}}(t). \end{aligned}$$

(19)

Along with this definition, the discretization procedure conceptually results in

$$\begin{aligned} \dfrac{\text {d}}{\text {d} t}{\mathbf {F}}(t)=\mathbf {\Gamma }\cdot {\mathbf {F}}(t) \end{aligned}$$

(20)

with the overall system matrix $\mathbf {\Gamma }=\mathbf {\Omega }^{-1}\cdot \mathbf {\Lambda }$, which represents a non-sparse matrix. Utilizing $N_\chi$ discretization points, the matrices show a dimension of $\mathbf {\Omega }, \mathbf {\Lambda }\in {\mathbb {C}}^{M \times M}$ with $M=N_\chi \cdot N$.

With regard to the formulation of the boundary conditions for the Quantum Liouville-type equations, the concept of inflow boundary conditions from the Wigner formalism [1] is adopted, as aforementioned. The Fermi–Dirac statistics $f_c(k)$, which are usually utilized for the inflow boundary conditions for each contact c, reads

$$\begin{aligned} f_\text {FD}(k) = \dfrac{mk_BT}{\pi \hbar ^2}\cdot \log \left( 1+\exp \left( \dfrac{q(\mu _c-E_c(k))}{k_BT}\right) \right) . \end{aligned}$$

(21)

The chemical potential is represented by $\mu$, and the energy $E_c(k)$ contains the energy dispersion as well as the potential energy effects arising from external sources and the Hartree potential at each contact c.

For the proposed approach, the inflow boundary conditions must be transformed to the discretized real space presentation for each contact c, resulting in [16]

$$\begin{aligned} \rho _c({\varvec{\xi }}) = \int \dfrac{\text {d}k}{2\pi } \cos (k{\varvec{\xi }})\cdot f_c(k). \end{aligned}$$

(22)

Now, this inflow boundary condition is expanded in terms of the basis functions leading to the corresponding vector of expansion coefficient

$$\begin{aligned} {\varvec{c}}_c = {\varvec{\varPhi }}^{\dagger }\rho _c({\varvec{\xi }}). \end{aligned}$$

(23)

Finally, the inflow boundary conditions for the Quantum Liouville-type equations can be formulated with regard to $k_n$ or $\lambda _n$ according to ${\varvec{c}}_{i=1}(t) = {\varvec{c}}_1$ for $k_n/\lambda _n>0$ and ${\varvec{c}}_{i=N_\chi }(t) ={\varvec{c}}_2$ for $k_n/\lambda _n<0$. Once the system of equations is solved, the discretized expansion coefficients are utilized to rewrite the statistical density matrix (4). Then, the statistical density matrix is utilized to calculate the carrier density n as well as the current density j, which are given by

$$\begin{aligned} n(\chi ,t) = \rho (\chi ,\xi ,t)\biggr |_{\xi =0} \end{aligned}$$

(24)

and

$$\begin{aligned} j(\chi , t) = \dfrac{\mathrm {j}q\hbar }{m}\dfrac{\partial }{\partial \xi }\rho (\chi ,\xi ,t)\biggr |_{\xi =0}, \end{aligned}$$

(25)

respectively.

Table 1 Parameters of the AlGaAs/GaAs Resonant Tunneling Diode

3 Numerical evaluation for the stationary case

For the evaluation of the proposed approach, different test scenarios are investigated in the stationary regime. At first, a RTD is investigated. Secondly, a DGFET is analyzed. For the validation of the proposed approach, the results for both devices are compared to the results obtained from the NEGF formalism. Herein, a finite differences approximation is implemented for the same Hamiltonian as in (1). The discretization widths are chosen accordingly to the parameters used for the proposed approach.

The self-consistent Hartree potential is determined by coupling the transport equation along with the Poisson equation. To account for the corresponding nonlinearity, a standard Newton–Raphson method [19] is applied in both cases.

The stop criterion for the i-th iteration is defined as

$$\begin{aligned} \dfrac{||{\varvec{V}}_H^{i}-{\varvec{V}}_H^{i-1}||}{N_p} < 10^{-5}, \end{aligned}$$

(26)

where the vector ${\varvec{V}}_H^{i}$ contains the $N_p$ discretized values of the Hartree potential at the i-th iteration.

3.1 AlGaAs resonant tunneling diode

The investigated resonant tunneling diode within the material system of Al$_{0.3}$Ga$_{0.7}$As/GaAs consists of seven different layers. The corresponding parameters for each layer utilized for the simulations can be found in Table 1. As mentioned, the effective mass is assumed to be constant and set to $0.063\cdot m_0$. For the numerical investigations, a length $L_\xi =120\text { nm}$ with regard to the $\xi$-direction is presumed. The corresponding interval is subdivided into $N_\xi =401$ cells. The $\chi$-direction with the parameters defined in Table 1 is subdivided into $N_\chi =361$ cells ($\varDelta \chi =0.25$ nm). The discrete basis functions are either given by the set of plane waves (EXP-basis) or by the eigenvectors of the diffusion matrix (EIG-basis). Both are analyzed for the different values of the subspace dimension N. An increasing number of the value N leads to the inclusion of larger absolute values of $\lambda _n$ and $k_n$ corresponding to higher energy scattering states.

3.1.1 Investigation of the carrier density

In Fig. 1, the carrier densities n are shown in dependency of $\chi$-direction for different dimensions N of the subspace and an externally applied bias of $U=0.3$ V.

Fig. 1

Carrier densities $n(\chi )$ for different subspace dimensions $N=40,~80$ and 120 for an applied bias $U=0.3$ V. The black dots indicate the values of the reference solution obtained from the NEGF formalism. The solid black line represents the overall potential distribution. The numbers within the legend entries indicate the subspace dimension N

In Fig. 1a, the case of the EIG-basis is depicted, whereas in Fig. 1b the case of the EXP-basis is shown. As can be observed from these figures, the results converge toward the reference solution obtained from the NEGF formalism with an increasing subspace dimension N. However, for $N=40$ basis functions the EXP-basis is superior in comparison with the EIG-basis, because a remarkable deviation of the carrier densities can be observed at $\chi \approx 50$ nm for the EIG-basis with respect to the reference solution as depicted in Fig. 1a.

3.1.2 Investigation of the current density

Now, the current densities are investigated in dependence of the subspace dimension N and externally applied biases in the range $[0\text { V},~0.6\text { V}]$ ($\varDelta U=0.02$ V) for the two different basis function types.

Fig. 2

Current densities j dependence on the applied bias U for different subspace dimensions $N=40,~80$ and 120. The black dots represent the values of the reference solution obtained from the NEGF formalism. The numbers within the legend entries represent the subspace dimension N

For the case of the EIG-basis, the current density is depicted in Fig. 2a. It can be seen from this figure, that the deviation with respect to the reference solution given by the NEGF formalism decreases with an increasing number of basis functions N. A qualitative coincidence with the reference current density is found for $N=120$.

Utilizing the EXP-basis, a qualitative coincidence with the reference solution is found for all investigated dimensions of the subspace $N=40,~80$ and 120, as can be observed from Fig. 2b.

3.1.3 Investigation of the relative error

So far only qualitative considerations have been carried out. Therefore, we pay particular attention to quantitative investigations in the following. In this regard, the relative error with respect to reference solution given by the NEGF formalism is determined according to

$$\begin{aligned} \epsilon _2 = \dfrac{||{\varvec{n}}-{\varvec{n}}_\text {NEGF}||}{||{\varvec{n}}_\text {NEGF}||} \end{aligned}$$

(27)

on the basis of the spatial carrier density ${\varvec{n}}$. The relative error in dependence of the subspace dimension N is shown in Fig. 3 for both cases, the EIG-basis as well as the EXP-basis.

Fig. 3

Relative error dependence on the subspace dimension N for both cases, the EXP-basis (blue line) and the EIG-basis (red line) (Color figure online)

For the calculations, the thermal equilibrium case is considered. As can be seen from this figure, the relative error converges rapidly toward an error plateau of approximately $2\cdot 10^{-3}$ for an increasing subspace dimension N for the case of the EIG-basis. For the case of the EXP-basis, this plateau is reached for all considered subspace dimensions N. Since there is an error plateau, the inclusion of further basis vectors does not provide additional physical information, but increases the overall computation time, because the system matrix increases along with N.

The small deviations in the error plateau between the proposed approach and the NEGF approach can be traced back to the fact, that two distinct numerical methods are investigated, and, therefore, different errors are apparent as well. Especially, the formulation of boundary conditions differs distinctly since the inflow boundary condition applying the semi-classical Fermi–Dirac statistic is only valid infinitely far away from the device structure [6]. As a consequence, these deviations could be attributed to model errors.

3.2 GaInAs double gate field effect transistor

For the numerical simulation of a Ga$_{0.47}$In$_{0.53}$As DGFET, which is schematically depicted in Fig. 4, the methodology presented is combined with the so-called mode space approach as described in [25,26,27]. Of course, the presented methodology can be applied to the analysis of multidimensional transport by carrying out the expansion in the ${\varvec{k}}$-space. For reasons of reducing the required computation time, a combination with other suited methods should be applied. In many applications nowadays, the carrier transport is dominant in a specific direction, so the carrier transport problem should be mapped onto this particular direction. The use of the mode space approach is appropriate for exactly this purpose. A demonstration also shows that the methodology presented can be combined with other methods in a versatile way.

Fig. 4

Schematic diagram of the GaInAs-DGFET with the corresponding length parameters as defined in the following: $w_\text {ox}=1$ nm, $w_\text {ch}=3$ nm, $L_\text {source/drain}=15$ nm and $L_\text {gate/channel}=10$ nm

Finally, the mode space approach is based on the projection of a multidimensional transport problem onto a one-dimensional transport problem, for which the proposed methodology is applied. Therefore, for the example under investigation, the corresponding equations are projected onto the eigenvector basis of the lateral direction, in which the electrons are confined between the oxide layers. These eigenvectors are referred to as modes. Intermodal coupling effects have been neglected. The distribution of eigenenergies forms the potential energy for the one-dimensional transport.

The source and drain contact extensions are highly doped $2\cdot 10^{19}$ cm$^{-3}$, whereas the channel is assumed to be intrinsic. For the Ag gate-contacts, a workfunction of $\varphi _m=4.74$ eV is assumed and the electron affinity of the GaInAs is set to $\chi _\text {GaInAs}=4.72$ eV, which are needed to formulate the boundary conditions for the 2D-Poisson equation [25, 28]. Other relevant material parameters are also taken from [25]. A discrete step width $\varDelta \chi =0.25$ nm regarding the transport direction is applied, and three modes are taken into account. Regarding the $\xi$-direction, the same set of parameters has been applied as in the previous section. The results are presented for a subdomain dimension of $N=80$.

Fig. 5

Drain current density in dependence of the applied drain-source bias for different applied gate voltages. The blue dots represent the values of the reference solution obtained from the NEGF approach, whereas the solid red line shows the results obtained from the proposed approach

In Fig. 5, the drain current density in dependence of the source-drain-voltage $U_{DS}$ is depicted for different applied gate voltages. To calculate this current density, the current density given by (25) is accumulated for each mode.

As can be seen from the results, the current densities coincide with the results obtained from the NEGF reference method.

4 Numerical evaluation for the dynamic case

4.1 Matrix exponential integrators

To introduce the concept of the matrix exponential integrators [29], (20) is formally integrated resulting in

$$\begin{aligned} {\mathbf {F}}(t_0+\varDelta t)=\exp \left( \mathbf {\Gamma }\varDelta t\right) \cdot {\mathbf {F}}(t_0), \end{aligned}$$

(28)

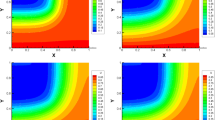
with $t_0$ being the initial time and $\varDelta t$ the time step size, respectively. In order to implement transient algorithms, particular information regarding the eigenvalue spectrum of the system matrix $\mathbf {\Gamma }$ is required, whereby a time-independent system matrix $\mathbf {\Gamma }$ is assumed first for clarity. Consequently, the eigenvalue spectrum for the system matrix $\mathbf {\Gamma }$ is investigated by evaluating the complete eigenvalue spectrum for the AlGaAs resonant tunneling diode introduced in the last chapter. Therefore, the contour of the eigenvalue spectrum depending on the Hartree potential, on the band conduction energy as well as on the CAP is examined for practically important values and schematically depicted in Fig. 6.

Fig. 6

Eigenvalue distribution $\lambda$ of the matrix $\mathbf {\Gamma }$ for the non-equilibrium case applying an external bias of $U=0.2$ V. The contours needed for further discussions are as well depicted, as there are the rectangle (-.-.-) with its length and width, on which basis the semi-axes a and b of the ellipse (...) are defined, and the circle (—) with a radius of $r=\sqrt{a^2+b^2}$

From Fig. 6 can be seen that the area of existing eigenvalues lies entirely in the left half-plane of the eigenvalue spectrum containing negative real parts, only. This particular characteristic ensures stability for appropriately validated algorithms. The non-hermiticity of the Wigner operator can also be seen from this illustration.

In addition to the eigenvalues on the real negative axis, there are conjugated complex eigenvalue pairs with a negative real part. The investigations regarding the maximum absolute eigenvalue show that for parameters relevant in practice with regard to the Hartree potential and the conduction band energy, this eigenvalue is purely real and is located on the negative real axis. With increasing values for those parameters, conjugated complex eigenvalue pairs appear to be the maximum absolute eigenvalues. Hence, the contour does not essentially change its characteristics.

4.2 Approximation of the matrix exponential

Unfortunately, methods are used for the analysis of the dynamic behavior for time-dependent solutions of Quantum Liouville-type equations, which are not computationally efficient. Implicit methods such as Crank–Nicolson schemes [1, 19, 30, 31] are very time-consuming due to the solution of large scale linear equation systems and are difficult to parallelize. Instead, explicit methods such as Euler schemes [1, 3] or Runge–Kutta schemes [15] are based on the calculation of matrix-vector multiplications, so that they are predestined for parallelization. However, these are limited by stability criteria, so the necessary time step sizes are small leading to high computing times. These methods are, therefore, very time-consuming and consequently inefficient, particularly for analyzing components in which multiband effects occur. The difficulties will increase, if interaction effects have to be included. Among the several methods utilized to calculate the matrix exponential function [32], especially the Faber polynomial-based approximation [33] and the Krylov subspace approach [32, 34, 35] are suitable and, therefore, analyzed to compute the action of the matrix exponential function since they combine efficiency and accuracy.

The appropriate approximation of an exponential integrator is decisive for the analysis of the dynamic behavior, which, in the approximated case, is converted into a matrix-valued exponential. For the approximation, methods come into play, which build up a basis in a subspace adapted to the problem. The approximation includes the conventional Krylov space methods [34, 35], herein combined with Padé approximants [36, 37], but also methods based on the expansion of the exponential integrator dependent on Faber polynomials [33]. Depending on the characteristics of the eigenvalue spectrum, there are advantages for one or the other method. Krylov space methods are particularly useful when the parameters describing the eigenvalue spectrum, such as the maximum possible eigenvalue, are not known. Faber polynomial-based methods are interesting if and only if the eigenvalue spectrum and its characteristic parameters are known.

The structure of the present eigenvalue spectrum is also important. Krylov methods are particularly predestined when the eigenvalues differ only slightly from the largest absolute eigenvalue. Faber-polynomial-based methods are particularly interesting in the contrary case. In practice, both methods must be compared with one another in order to be able to carry out an evaluation for the respective application. The results obtained herein are important because they form the basis for nonlinear methods in which interaction effects are to be included, but are based on the knowledge of the linear behavior of the exponential integrators [29]. The Crank–Nicolson scheme is included in the investigations for the sake of completeness.

4.2.1 Eigenvector expansion method

For the purpose of the evaluation of approximated matrix exponential functions, the matrix exponential can be analytically reformulated utilizing the transformation onto the principal axis. Formally, the matrix exponential can then be determined by

$$\begin{aligned} \exp \left( \mathbf {\Gamma }\varDelta t\right) = {\mathbf {V}}\exp \left( \mathbf {\Lambda }\varDelta t\right) {\mathbf {V}}^{-1} \end{aligned}$$

(29)

utilizing the matrix of eigenvectors ${\mathbf {V}}$ as well as the diagonal matrix of eigenvalues $\mathbf {\Lambda }$ containing the corresponding eigenvalues $\lambda _i$ of each eigenvector $V_i$. Due to the requirement of determining the eigenvalues and eigenvectors, this procedure is impractical in realistic device simulations. In addition, the eigenvectors ${\mathbf {V}}$ are not orthogonal in general so that the matrix-inversion increases the computational burden, too. Here, the method is utilized to determine the reference solution with regard to the transient propagation.

4.2.2 Crank–Nicolson scheme

In the following, the Crank–Nicolson scheme is presented briefly as they are the mainly utilized transient approximation schemes applied onto the WTE [1, 3, 19, 30, 31]. The Crank–Nicolson scheme is an unconditionally stable scheme, but implicit scheme. Consequently, to proceed in time within the WTE, an inverse matrix has to be calculated according to

$$\begin{aligned} {\mathbf {F}}(t_0+\varDelta t) = \left( 1-\dfrac{\varDelta t}{2}\mathbf {\Gamma }\right) ^{-1}\left( 1+\dfrac{\varDelta t}{2}\mathbf {\Gamma }\right) \cdot {\mathbf {F}}(t_0). \end{aligned}$$

(30)

In the worst case, this inversion has to be carried out each time step, i.e., in the selfconsistent transient case.

4.2.3 Faber polynomial-based expansion

The matrix exponential in (28) can be approximated by the use of Faber polynomials [33, 38,39,40]. For this purpose, the matrix exponential is expanded dependent on the Faber polynomials $P_m(\mathbf {\Gamma })$ as proposed in [33] according to

$$\begin{aligned} \text {exp}(\mathbf {\Gamma } \varDelta t)= \sum _{m=0}^{M} c_m \cdot P_m(\mathbf {\Gamma }), \end{aligned}$$

(31)

where M denotes the order of the expansion and the coefficients $c_m$ represent the expansion coefficients given by

$$\begin{aligned} c_m= \frac{1}{2\pi \mathrm {j}} \int _{|w|=R} \frac{f(\psi (w))}{w^{m+1}} \ \text {d}w. \end{aligned}$$

(32)

The Faber polynomials $P_m(\mathbf {\Gamma })$ are evaluated by using the relation [40, 41]

$$\begin{aligned} P_{m+1}(z)=zP_{m}(z)-\sum _{k=0}^{m} \gamma _k P_{m-k}(z)-m \gamma _0. \end{aligned}$$

(33)

Hereby, the eigenvalue spectrum of the matrix $\mathbf {\Gamma }$ in the z-plane is mapped on an inner circle with a radius of $\rho$ in the w-plane. A conformal mapping $z=\psi (w)$ introducing the mapping function $\psi$ has to be identified [39]. In order to ultimately carry out the exact mapping and to determine the Faber polynomials $P_m(\mathbf {\Gamma })$ and its corresponding coefficients $c_m$, the area of the present eigenvalue spectrum and the curve shapes R defining it have to be utilized. The coefficients $\gamma _k$ and the parameter m depend on the characteristics of the curve shape. The choice of suitable curve shapes and the related values for $\gamma _k$ as well as for the parameter m are discussed in the next section.

Methods based on Faber polynomial expansions of an exponential integrator are particularly advantageous in terms of their efficiency, if the eigenvalue spectrum of the system matrix ${\varvec{\Gamma }}$ under consideration is known and the parameters of the contour comprising the eigenvalue spectrum can be determined as precisely as possible. Based on the characteristics of the contour, the Faber polynomial-based expansion can be carried out.

The parameters of the contour will be important for the expansion of the exponential integrator based on Faber polynomials. Due to the contour of the area of the existing eigenvalues in the eigenvalue spectrum, the choice of an ellipse or a circle is appropriate. For both forms of representation, the knowledge of its center is important, which is located on the negative real semi-axis. Based on the conclusions above, the following approximations can be evaluated on the basis of the contour and its related characteristics.

To ensure that all eigenvalues are located within an ellipse or a circle, a rectangle is defined with the maximum possible real part as well as the maximum possible imaginary part of the eigenvalues obtained as shown in Fig. 6. The specific sizes define the sides of the rectangle. Either an ellipse or a circle containing the corner points of the rectangle can be placed around this rectangle. When choosing a circle, the radius can be defined by the distance from the center to one of the corner points of the rectangle. For the parameters of the ellipse, a method described in [38] is utilized and explained later on.

The intervals have to be determined, in which, on the one hand, the real parts of the eigenvalues $[-R_\text {max}, 0]$ and, on the other hand, the imaginary parts of the eigenvalues $[-I_\text {max}, I_\text {max}]$ can be found. These limits can be used to define a circle or an ellipse surrounding the eigenvalue spectrum as shown in Fig. 6. The parameters c and l are introduced and linked with the values of $R_\text {max}$ and $I_\text {max}$ by the relations $l=R_\text {max}/2$ as well as $c=I_\text {max}$. Therefore, for all cases, the value $z_0=-l$ indicates the center of the comprising shape. When the maximum absolute eigenvalue is located on the real axis, the center $\gamma _0$ of the area can be determined with the maximum absolute eigenvalue by simply taking the half of the maximum absolute eigenvalue $\gamma _0/2$. The semi-axes of an ellipse, for which the mapping is designed, are defined by the parameters a and b as depicted in Fig. 6. Obviously, the ellipse turns out to be a circle for $a=b$. The choice of the parameters a and b is discussed in the following.

Further discussions are firstly addressing the general case of an ellipse, which is constructed on the basis of a rectangle as shown in Fig. 6. The radius $\rho$ in the w-plane should be 1 to allow stability [42]. For this purpose, a scaling factor $\lambda _s$ is introduced according to [42] and defined along with the considerations above by choosing

$$\begin{aligned} \lambda _s=\frac{(l^{2/3}+c^{2/3})^{3/2}}{2}. \end{aligned}$$

(34)

to allow stability [42]. With the information given, the mapping can be designed for each of the above enumerated options. An ellipse in the z-plane, which of course implicitly includes the case of a circle in the z-plane and which comprises the eigenvalue spectrum in the z-plane, is mapped onto a circle in the w-plane via the transformation [42, 43]

$$\begin{aligned} \psi (w)=w+\gamma _0+\gamma _1/w. \end{aligned}$$

(35)

The system matrix $\mathbf {\Gamma }$ and the time step size $\varDelta t$ are normalized according to $\mathbf {\Gamma }_s=\mathbf {\Gamma }/\lambda _s$ and $\varDelta t_s=\varDelta t \lambda _s$ to allow stability. The parameters c and l are normalized as well resulting in the normalized parameters $c_s=c/\lambda _s$ and $l_s=l/\lambda _s$. With the help of these parameters, the semi-axes of the ellipse can be specified as follows

$$\begin{aligned} b=\sqrt{l_s^2+(c_s l_s^2)^{3/2}} \quad \text {and}\quad a=2-b. \end{aligned}$$

(36)

The parameters $\gamma _0$ and $\gamma _1$ as introduced in (35) are given by [42]

$$\begin{aligned} \gamma _0=-l/\lambda _s \quad ,\quad \gamma _1=(a-b)/2, \end{aligned}$$

(37)

whereby the value $z_0=-l$ indicates the center of the ellipse. When considering a circle, the value of $\gamma _1$ vanishes as the condition $a=b$ holds. In general, the Faber polynomials $P_m(z)$ can be determined by using the recursive relation

$$\begin{aligned} P_{m+1}(z)=(z-\gamma _0)P_{m}(z)-\gamma _1 P_{m-1}(z); m > 2 \end{aligned}$$

(38)

applying the initial conditions $F_{0}(z)=1$ and $F_{1}(z)=z-\gamma _0$ [39]. Accordingly, after replacing z by the matrix $\mathbf {\Gamma }$, the propagation in time can be realized by a recursive relation. The expansion coefficients are given by [42, 43]

$$\begin{aligned} c_m=\text {exp}(\varDelta t_s \gamma _0) (\frac{1}{\mathrm {j}\sqrt{\gamma _1}})^m J_m(\mathrm {j}2\varDelta t_s\sqrt{\gamma _1}). \end{aligned}$$

(39)

For the case of a circle, this relation can be rearranged leading to

$$\begin{aligned} c_m= \frac{1}{m!} \text {exp}(\varDelta t_s \gamma _0). \end{aligned}$$

(40)

Along with (40) a stop criterion, the corresponding order m of the expansion can be defined. When the expansion coefficient $c_m$ is getting smaller than $10^{-15}$, then the expansion is stopped. All different concepts require the determination of the eigenvalue spectrum with its maximum absolute eigenvalue. The limits of the eigenvalue spectrum can only be insufficiently estimated with commonly applied methods, such as the Gershgorin method, spectral methods or perturbation methods. The limits are overestimated by factors up to an order of magnitude. The exact knowledge is crucial to ensure stability and to develop efficient methods with regard to computing time, especially when the advantages of the Faber polynomial expansion shall be exploited. With these methods, however, a first estimate is possible on the basis of which the actual spectrum of eigenvalues can be determined. The eigenvalue range can be limited with this known spectrum of eigenvalues. Therefore, also to identify whether conjugate complex pairs of values occur, a subspace is built up by a set of vectors resulting from the Faber polynomial expansion applied onto an initial vector. The expansion according to (31) forms a subspace of the n-th order as defined by

$$\begin{aligned} \mathcal {L}_{n}(\mathbf {\Gamma }, {\mathbf {F}}(t_i))=\text {span}\left\{ {\mathbf {F}}(t_i), {\mathbf {P}}_{1}{\mathbf {F}}(t_i),\dots ,{\mathbf {P}}_{n-1}{\mathbf {F}}(t_i)\right\} \end{aligned}$$

(41)

and when considering a circle, the subspace $\mathcal {L}_{n}$ turns into a space, which is similar to the Krylov space approach. An orthogonal basis is calculated by using the standard Gram–Schmidt orthogonalization. The vectors ${\mathbf {f}}_k$ of the new basis are stored within the matrix ${\mathbf {F}}_n\in {\mathbb {F}}^{N\times n}$ given by

$$\begin{aligned} {\mathbf {F}}_n=\left[ {\mathbf {f}}_1,{\mathbf {f}}_2,\dots ,{\mathbf {f}}_n\right] , \end{aligned}$$

(42)

so that the original matrix $\mathbf {\Gamma }$ can be transformed into a matrix ${\mathbf {S}} \in {\mathbb {S}}^{n\times n}$ according to

$$\begin{aligned} {\mathbf {S}}={\mathbf {F}}_{n}^{-1}\mathbf {\Gamma } {\mathbf {F}}_{n}. \end{aligned}$$

(43)

This procedure allows the computation of the dominant eigenvalues of $\mathbf {\Gamma }$ by the use of a matrix ${\mathbf {S}}$ of lower order with which the contour of the eigenvalue spectrum can be defined.

4.2.4 Krylov based expansion

Faber polynomial-based approaches require the knowledge of the eigenvalue spectrum in contrast to conventional methods based on approximations in the Krylov space. The latter methods are of particular interest and efficiency, if the eigenvalues in the eigenvalue spectrum deviate only slightly from the maximum absolute eigenvalue. The conventional Krylov subspace of the n-th order is defined by

$$\begin{aligned} \mathcal {K}_{n}(\mathbf {\Gamma }, {\mathbf {F}}(t_i))=\text {span}\left\{ {\mathbf {F}}(t_i), \mathbf {\Gamma }\cdot {\mathbf {F}}(t_i),\dots ,\mathbf {\Gamma }^{n-1}\cdot {\mathbf {F}}(t_i)\right\} . \end{aligned}$$

(44)

Unfortunately, the vectors $\mathbf {\Gamma }^{k}\cdot {\mathbf {F}}(t_i)$ converge rapidly toward the eigenvector of $\mathbf {\Gamma }$ with the largest absolute eigenvalue. As a consequence, the vectors become progressively linear dependent. To overcome these limitations, the so-called Arnoldi process is utilized to build an orthogonal basis of the Krylov subspace [34]. The orthogonal basis vectors ${\mathbf {q}}_k$ are stored within the matrix ${\mathbf {Q}}_n\in {\mathbb {C}}^{N\times n}$ according to

$$\begin{aligned} {\mathbf {Q}}_n=\left[ {\mathbf {q}}_1,{\mathbf {q}}_2,\dots ,{\mathbf {q}}_n\right] , \end{aligned}$$

(45)

which satisfies the so-called Arnoldi decomposition

$$\begin{aligned} \mathbf {\Gamma }{\mathbf {Q}}_n={\mathbf {Q}}_{n+1}{\mathbf {H}}_{n+1,n}. \end{aligned}$$

(46)

The matrix ${\mathbf {H}}_{n+1,n}\in {\mathbb {R}}^{n+1\times n}$ is upper-Hessenberg being directly obtained by the Arnoldi process. Exploiting the characteristics of the upper-Hessenberg matrix ${\mathbf {H}}_{n+1,n}$, the expression (46) can be rewritten

$$\begin{aligned} \mathbf {\Gamma }{\mathbf {Q}}_n={\mathbf {Q}}_{n+1}{\mathbf {H}}_{n,n}+h_{n+1,n}{\mathbf {q}}_{n+1}{\mathbf {e}}_n^{T}, \end{aligned}$$

(47)

because the elements $h_{i,j}$ of the matrix ${\mathbf {H}}_{n+1,n}$ are equal to zero for $i>j+1$. The vector ${\mathbf {e}}_{n}^{T}$ is the n-th canonical basis vector given by $\left[ 0,0,\dots ,1\right] \in {\mathbb {R}}^{n}$. Consequently, the action of $\mathbf {\Gamma }$ onto a vector of the Krylov subspace $\mathcal {K}_{n}$ can be re-expressed in terms of vectors belonging to the same Krylov subspace $\mathcal {K}_{n}$ and a multiple of the next Krylov basis vector ${\mathbf {q}}_{n+1}$. Especially, when the last term on the right-hand side of (47) becomes extremely small for a certain order n of the Krylov subspace, the Krylov subspace nearly represents an invariant subspace of the matrix $\mathbf {\Gamma }$.

Following the Arnoldi process, the first vector of the Krylov subspace is defined by ${\mathbf {q}}_1={\mathbf {F}}(t_0)/||{\mathbf {F}}(t_0)||$, so that the time propagation (20) can be easily rewritten

$$\begin{aligned} \begin{aligned} {\mathbf {F}}(t_0+\varDelta t)&= \exp \left( \mathbf {\Gamma }\cdot \varDelta t\right) \cdot \mathbf {Q_n}\cdot ||{\mathbf {F}}(t_0)||{\mathbf {e}}_1\\&\approx {\mathbf {Q}}_{n}\exp \left( {\mathbf {H}}_{n,n}\varDelta t\right) \cdot ||{\mathbf {F}}(t_0)||{\mathbf {e}}_1 \end{aligned} \end{aligned}$$

(48)

where ${\mathbf {e}}_{1}$ is the first canonical basis vector $\left[ 1,0,\dots ,0\right] \in {\mathbb {R}}^{n}$. The evaluation of the matrix exponential of the upper-Hessenberg matrix ${\mathbf {H}}_{n,n}$ is computationally much cheaper than the evaluation of the original matrix exponential function of $\mathbf {\Gamma }$ due to $n\lll N$. Additionally, an a priori stopping criterion based on the residual [35] can be defined

$$\begin{aligned} \begin{aligned} {\mathbf {r}}_n(t)&=\dfrac{d}{dt}{\mathbf {F}}_n(t)-\mathbf {\Gamma }\cdot {\mathbf {F}}_n(t)\\&=-\left( h_{n+1,n}{\mathbf {e}}_m^{T}\exp \left( {\mathbf {H}}_{n,n}\varDelta t\right) \cdot ||{\mathbf {F}}(t_0)||{\mathbf {e}}_1\right) {\mathbf {q}}_{n+1} \end{aligned} \end{aligned}$$

(49)

utilizing (46) and (48). Along with the stopping criterion, the residual of the approximant ${\mathbf {F}}_n(t)$ with regard to discretized transient WTE in (20) can be controlled. As a consequence, the dimension of the Krylov subspace can be determined adaptively in a computationally efficient manner.

The remaining task is the evaluation of the matrix exponential function of the Hessenberg matrix, which can be efficiently approximated by using the Padé approximation as discussed in the following. A commonly utilized and highly accurate method to approximate the matrix exponential function is given by the (n, m)-Padé approximation with n, m being the degrees of the polynomials. To reduce the computational costs, this technique is combined with the scaling and squaring method. For the case of (n, n)-Padé approximations, the matrix exponential of the Hessenberg matrix ${\mathbf {H}}={\mathbf {H}}_{n,n}$ can be approximated by

$$\begin{aligned} \exp \left( {\mathbf {H}}\varDelta t\right) \approx \dfrac{P_n({\mathbf {H}}\varDelta t)}{P_n(-{\mathbf {H}}\varDelta t)}, \end{aligned}$$

(50)

where the polynomial $P_n({\mathbf {H}}\varDelta t)$ is defined according to

$$\begin{aligned} P_n(\Gamma \varDelta t)=\sum \limits _{i=0}^{n}c_i\cdot \left( {\mathbf {H}}\varDelta t\right) ^{i}. \end{aligned}$$

(51)

The expansion coefficient $c_i$ fulfills the recurrence relation

$$\begin{aligned} c_i =\left\{ \begin{array}{cl} 1, &{} \text {if~}i=0\\ \dfrac{n-i+1}{(2n-i+1)i}\cdot c_{i-1}, &{}\text {if~}i>0\\ \end{array} \right. . \end{aligned}$$

(52)

The scheme is unconditionally stable. Nonetheless, the matrix-inversion needed to compute the approximant represents a serious bottleneck of the scheme. As a consequence, the Padé approximation seems to be impractical for large-scale applications.

4.3 Numerical simulation results

The evaluation takes place with regard to the relative error, the computation time and computational efficiency. For the transient analysis, different time steps $\varDelta t$ subdividing the interval $I_t=[0\text { fs},~5\text { fs}]$ are chosen. For all methods and time steps, the transient evolution of the Wigner function is carried out in an iterative manner until the final time $t_\text {f}=5\text { fs}$ is reached. At the initial time $t=0$ fs, the Wigner function is set to be in the thermal equilibrium state. Hereby, the Wigner function for the thermal equilibrium state is obtained from the numerical solution of the stationary WTE applying the commonly utilized inflow boundary condition scheme. Then, for $t>0$ the device is driven toward the non-equilibrium situation applying a constant external bias of $U = 0.2$ V. The Wigner function for the thermal equilibrium state is evolved in time utilizing the different methods.

Hereby, the relative error e is defined by

$$\begin{aligned} e = \dfrac{||{\mathbf {F}}_\text {ref}(t_\text {f})-{\mathbf {F}}(t_\text {f})||_\infty }{||{\mathbf {F}}_\text {ref}(t_\text {f})||_\infty }, \end{aligned}$$

(53)

where ${\mathbf {F}}_\text {ref}(t_\text {f})$ is the reference solution obtained from the eigenvalue-decomposition method. As discussed, this method computes the matrix exponential function without resulting in any error, theoretically. In practice, the internal CPU accuracy as well as the errors combined with the computation of the eigenvalues and eigenvectors have to be taken into account. Nonetheless, since these errors are negligible small, the method serves as an excellent basis for the evaluation of the reference solution. The discretized Wigner function ${\mathbf {F}}(t_\text {f})$ represents the solution obtained from the corresponding scheme under investigation.

Table 2 Relative Error for different time steps for the Faber approximation of the exponential integrator on the basis of different contours

The relative error and the computation time for all presented options are enlisted in Table 2 for different time step sizes covering a large range of orders of magnitude. From the results shown can be concluded that the relative error and the computation time differ slightly from each other, only. This conclusion can be drawn as the ellipses obtained do not deviate much from being a circle so the eccentricity of the ellipses is close to zero. The optimum approach is the option choosing a circle, which is defined by the corner points of the rectangle. As a consequence, for clarity, this particular option is considered further on.

All the relevant parameters are then calculated for the cases of an adaptive Faber approximation, an adaptive Krylov method, and non-adaptive Krylov approaches of different orders $N=20, 60, 120$. As can be seen from Fig. 7, the relative error with respect to the non-adaptive Krylov approaches increases accordingly with increasing time step sizes.

Fig. 7

Relative errors for the different time integration techniques in comparison

In such cases, the dimension N of the Krylov space is smaller than the dimension of the space needed to represent the solution. As a characteristic of the Krylov approach, the overall accuracy increases with an increasing dimension N of the Krylov space. This characteristic can be seen in Fig. 7. The application of adaptive approaches, for which the order of expansion is determined by a stop criterion, leads to a very small relative error, whereby the relative error of both approaches deviates slightly from each other, only. However, the order of the approximation increases with increasing time step size.

Furthermore, comparing the different dimensions of the Krylov subspace $N=10,30$, it can be concluded that along with an increasing number of basis functions the relative error decreases as long as $\mathcal {K}_n$ is no invariant subspace of $\mathbf {\Gamma }$ as depicted in Fig. 7. With regard to extremely small time step sizes, a slightly increasing behavior of the relative error can be observed from Fig. 7, which can be assigned to the increasing round-off error due to the massive matrix-vector multiplications needed to propagate in time. The Faber and Krylov approaches allow arbitrary time step sizes combined with a predefined accuracy without the expense calculation of the eigenvalue spectrum.

The computation times for each method in dependence of the time step $\varDelta t$ are depicted in Fig. 8.

Fig. 8

Computation time dependent on the discretized time step $\varDelta t$ for the different time integration techniques in comparison

The dependency between computing time and time step size shows a linear behavior for the non-adaptive Faber and Krylov-based methods. Naturally, the computing time for the lower orders is less compared to the higher orders. The adaptive Faber and Krylov based methods do not have this linear behavior, since the order of the approximation also increases with an increased time step size. The simulations have been performed on a standard PC with 16GB RAM with a proprietary OS assuming the flat-band case. Furthermore, the underlying situation analyzing the flat-band case favors the computation time as discussed in the following. Normally, the transport equation has to be solved selfconsistently along with the Poisson equation, so that the drift operator changes at each time step (assuming no steady state has reached). Due to the drift operator changing at every time step, the system matrix $\mathbf {\Gamma }$ as part of the transient-related operator changes at each time step, too. Here, the transient related operator has to be evaluated only once, because the flat-band case is considered due to an additional error occurring by the inclusion of the Poisson equation as aforementioned.

For the further investigation of the efficiency, the relative errors are depicted in Fig. 9 dependent on the corresponding computing time for each time step $\varDelta t$.

Fig. 9

Relative error in dependence of the computation time for the different time integration techniques in comparison

The pairs of values are taken from Figs. 7 and 8. The conclusion is obvious. The adaptive methods have a clear advantage with the difference between both methods being minor. The adaptive methods are equivalent in terms of their efficiency. It can be seen that the adaptive schemes are superior. On the one hand, for the same computation time highly accurate results can be obtained; on the other hand, when the same accuracy is needed, the computation time can be highly reduced. Furthermore, the adaptive schemes enable a far more fast reaching of the plateau of the relative error, where the scheme is presumed to be converged. The slight increase in the relative error toward larger computational times for the Krylov based scheme is accounted to the increasing round off error, due to massive matrix vector multiplications needed to advance in time.

Of course, when analyzing time-dependent problems, the matrix exponential in (28) becomes a time-ordered integral, which can be approximated by a successive application of matrix exponentials. One has to note that the calculation of the eigenvalue spectrum in the subspace needs only a very small proportion of the total computing time. Essentially, the efficiency of all approaches is influenced by the evaluation of the occurring matrix-vector multiplications when approximating the matrix exponential. The contribution of the computing time for the calculation of the eigenvalue spectrum is less than 1% in relation to the total computing time. Furthermore, the calculation of the eigenvalue spectrum is not needed when applying Krylov-based methods. For Faber polynomial-based methods, only an estimation of the eigenvalue spectrum at the start of the algorithm is mandatory. To sum up, the calculation of the eigenvalue spectrum is of minor importance with regard to the computing time.

From all results can be concluded that Faber and Krylov-based methods are superior compared to Crank–Nicolson-based approaches with respect to all evaluated parameters.

5 Device modeling for the dynamic case

5.1 Class-C analysis of a GaInAs-based DGFET

In the following, a GaInAs-based DGFET as introduced before is investigated with regard to its dynamic behavior with the same methodology as presented before. The modeling of the time-dependent voltage at the gate contact can be interesting in many technically relevant applications, e.g. [25, 26, 44]. On the one hand, an application as a simple amplifier is possible. On the other hand, an application as a mixer is conceivable. While nonlinearities often result in unwanted intermodulation effects for the first application case, these just allow the second application case as a mixer. In the following, the dynamic application as an amplifier will be demonstrated for mixer applications. For this purpose, a time-dependent control voltage is applied to the gate contacts according to

$$\begin{aligned} U_G(t)=1.0 V+0.4 V \cdot (\sin (2 \pi f_1 t)+\sin (2 \pi f_2 t)). \end{aligned}$$

(54)

The operating point of 1.0 V corresponds to a C-mode operation. The modulation around the operating point is performed with harmonic carrier signals of frequencies $f_1 = 180$ GHz and $f_2 = 220$ GHz. The drain-source voltage is assumed to be constant in time with a value of $U_{DS}=1.0$ V. The time integration is performed using the Crank–Nicolson method, assuming a discrete time step size of $\varDelta t = 5$ fs. Under the given operating parameters, the output signal of the DGFET is shown in Fig. 10. In addition, the control voltage is depicted. Because of the C operation, only a part of the positive half-wave above the operating point of 1 V of the control voltage is passed as can be seen from Fig. 10 and the enlarged time Sect. Fig. 11.

Fig. 10

Current density $j_D(t)$ at the output of the DGFET for a time-dependent voltage at the gate $U_G(t)$ for a constant drain-source voltage $U_{DS}$ of 1.0 V: whole period

Fig. 11

Current density $j_D(t)$ at the output of the DGFET for a time-dependent voltage at the gate $U_G(t)$ for a constant drain-source voltage $U_{DS}$ of 1.0 V: section of the whole period

With the present operating point within the C-mode, the system behavior of the DGFET is highly nonlinear. This nonlinearity results in intermodulation products $f_\text {IM}$ in the output signal at frequencies

$$\begin{aligned} f_\text {IM}=a \cdot f_1 + b \cdot f_2 \quad \text {with} \quad a,b \in Z. \end{aligned}$$

(55)

The resulting intermodulation products can be used for additive mixing. Figure 12 shows the spectrum of the output signal.

Fig. 12

Spectrum of the current density $j_D$ at the output of the DGFET for a time-dependent voltage applied at the gate contact $U_G(t)$. The drain-source bias is kept constant $U_{DS} = 1$ V

In addition to the intermodulation products relevant for additive mixers for a frequency conversion to $f_1 + f_2 =400$ GHz, potentially interfering intermodulation products exist for the amplification process at the frequencies $2f_{1} - f_{2}$ and $2f_{2} - f_{1}$, i.e., 140 GHz and 260 GHz. The time-dependent behavior of the electron density n(x, z, t) is shown in Fig. 13 for different times from $t = 0$ ps to $t = 2.0$ ps in 1 ps intervals. This curve represents the switching operation of the DGFET as shown in Fig. 13 for the first time. As can be seen from Fig. 13, the formulation of Dirichlet boundary conditions at the drain and source junctions allows a violation of carrier neutrality within the transient regime.

Fig. 13

Electron densities n(z, x, t) at different times

In this strong non-equilibrium situation, this boundary condition thus allows a charge carrier injection from the contacts into the device and vice versa to establish steady-state flow equilibrium corresponding to the Fermi levels [28].

5.2 Resonant AlGaAs/GaAs tunneling diode

In the following example, the dynamic behavior of a RTD with parameters given in Table 3 is investigated. As the effective mass is no longer invariant along the transport direction, the spatially varying effective mass has to be taken into account. For this purpose, the discretization scheme with respect to the $\chi$-direction as described in [24] is adopted. THz oscillations of the current density are observed as previously described by [45,46,47].

Table 3 Parameters of the AlGaAs/GaAs resonant tunneling diode

Interactions mechanisms can be incorporated as well. As an example, the electron–phonon interaction mechanism is considered. To demonstrate that scattering can be conceptually integrated within the methodology, finally a simplified model is used. The starting point for the modeling of electron–phonon interaction mechanisms is the Hamiltonian operator applying the Born–Oppenheimer approximation and assuming a Bravais lattice. To account for the lattice oscillation, the additional linear deviation around the equilibrium position is modeled according to $\hat{{\mathcal {H}}}_{el,p}$ which in the second quantization can be conceptually written as

$$\begin{aligned} \hat{{\mathcal {H}}}_{el,p}=\sum _{k,q} M_{k,q} (b_{-q}^{\dagger }+b_{q}) c_{k+q}^{\dagger } c_{k,q}. \end{aligned}$$

(56)

Here, $b^{\dagger }$ represents the phonon generation operator and b the annihilation operator and $c^{\dagger }$ represents the electron generation operator and c the annihilation operator. The matrix element $M_{k,q}$ describes the strength of the electron–phonon coupling. To determine the dynamics, the Heisenberg equation of motion for the entire Hamiltonian operator must be solved. Then, equations of motion for the expectation values $\langle b_q \rangle$ as well as $\langle c_{k}^{\dagger }c_{k} \rangle$ can be set up. This methodology immediately results in a hierarchy problem for the phonon-assisted density matrix $\langle c_{k+q}^{\dagger }b_{q}c_{k} \rangle$, which can be simplified with the help of the correlation expansion as well as bath assumption, Hartree factorization, and random phase approximation [48] leading to an equation of motion for the distribution function $\langle c_{k}^{\dagger }c_{k} \rangle$. After analytical integration, the differential equation for the phonon-assisted density matrix can be substituted into the equation of motion for the distribution function $f_k=\langle c_{k}^{\dagger }c_{k} \rangle$. This equation represents the so-called quantum kinetic Boltzmann equation. In the Markov approximation, this expression finally yields the semi-classical formulation conceptually given in [1] as

$$\begin{aligned} \begin{aligned} \left( \frac{\partial }{\partial t} f_k\right) _\text {coll}=&-\sum _q W_{k,k+q} (1-f_{k+q}) f_k\\&+\sum _q W_{k+q,k} (1-f_{k}) f_{k+q}, \end{aligned} \end{aligned}$$

(57)

where $W_{k,k+q}$ represents the transition probability from state $|k\rangle$ to $|k+q\rangle$ per unit time and $W_{k+q,k}$ represents the transition probability from state $|k+q\rangle$ to $|k\rangle$ per unit time, respectively.

Assuming a small deviation from the thermodynamic equilibrium, a perturbation calculation according to the equilibrium distribution $f_{eq,k}$ allows a further simplification [48]. Second-order terms are neglected, while zero-order terms are considered. Here, the relaxation time $\tau _k$ can be introduced as defined in [19, 49]

$$\begin{aligned} \frac{1}{\tau _k}=-\sum _q W_{k,k+q} (1-f_{eq, k+q})+\sum _q W_{k+q,k} f_{eq,k+q}. \end{aligned}$$

(58)

Finally, the collision operator for the description of the electron–phonon interaction results in [50, 51]

$$\begin{aligned} \left( \frac{\partial }{\partial t} f_k\right) _\text {coll}=-\frac{1}{\tau }\left\{ f(\chi ,k,t)-\frac{n(\chi ,t)}{n_{eq}(\chi )} f_{eq}(\chi ,k)\right\} . \end{aligned}$$

(59)

The equilibrium distribution $f_{eq,k}$ is still weighted with the local ratio defined by the charge carrier density $n(\chi ,t)$ and the charge carrier density of the equilibrium $n_{eq}(\chi )$ at each location $\chi$.

Fig. 14

Current density j as a function of the applied voltage U and different time constants $\tau$ for the forward (forw.) voltage sweep as well as backward (backw.) voltage sweep

For the application of (59), the expression still has to be transformed into the local space. These expressions can be incorporated into the discretization matrices in an additive manner. The equilibrium distribution $f_{eq}$ is assumed to be the distribution function of the thermodynamic equilibrium and, therefore, has to be calculated beforehand. Of course, with such an relaxation time approach neither nonelastic and anisotropic scattering effects are considered, which have an effect on a device performance when considering polar optical phonons. In principle, other models can also be integrated in this manner, such as those presented in [52,53,54,55]. Since scattering approaches may lead to unphysical results, one must pay attention on the proper choice of models, i.e., by modeling the collision integral with terms describing energy dissipation, momentum relaxation, and the decay of spatial coherence [52] or by a quantum-mechanical generalization of relaxation-time and Boltzmann-like models resulting in nonlocal scattering superoperators [54].

To analyze the hysteresis behavior, the self-consistent I-V-characteristic curve of the RTD is determined with the device parameters given in the previous section. For this purpose, a forward voltage sweep from 0 V up to 0.5 V is applied followed by a reverse voltage sweep, allowing the hysteresis effect to take place. The electron–phonon interaction is accounted for by the collision operator (59), and the hysteresis is determined for various relaxation time constants $\langle \tau \rangle$. To model the electron–phonon interaction within the AlGaAs/GaAs material system, the relaxation time constants $\tau _k$ can be assumed to be constant as $\tau =525$ fs [56]. Furthermore, in order to evaluate the physical influence of the collision operator in terms of the device behavior, the relaxation time constants $\tau =55$ fs, $\tau =255$ fs as well as $\tau =1050$ fs are also considered. The corresponding I-V characteristics for the different time constants $\tau$ are shown in Fig. 14a–d. The I–V characteristic for the physically based relaxation time constant of $\tau =525$ fs [56] is shown in Fig. 14c. As it can be seen from this Fig. 14c, the I–V characteristic exhibits a bistable behavior within the voltage range of 0.31–0.36 V. The values of the current density j for the forward (forw.) voltage sweep differ significantly from those for the reverse (backw.) voltage sweep. The result shows a clear hysteresis behavior, which is also known from relevant experiments [57]. In particular, in the forward voltage sweep, two so-called plateaus occur between the voltage ranges 0.31–0.32 as well as 0.34–0.36 V. Within these plateaus, the RTD operates as an oscillator in the technically relevant THz frequency range [45, 46]. If the influence of the scattering mechanisms is artificially increased by reducing the relaxation time constant to the value $\tau =255$ fs a single narrow plateau exists, only. However, the hysteresis is still maintained as shown in Fig. 14b.

For a relaxation time constant of $\tau =55$ fs, the electron–phonon coupling increases even more. As it can be seen from Fig. 14a, the I–V characteristic no longer exhibits a hysteresis. Compared to the other curves, a decrease in the peak current density from about 6 to about $5\text { GA/m}^{2}$ as well as an increase in the valley current density from about 1 to about $2\text { GA/m}^{2}$ can be observed. The other limiting case is the artificial reduction in the influence of the electron–phonon interaction. For this purpose, the I–V characteristic is shown for a time constant of $\tau =1050$ fs in Fig. 14d. In this case, in addition to the plateau in the forward voltage sweep in the range of about 0.31 V, another narrow plateau exists in the reverse voltage sweep at about 0.3 V. In the overall context of all Fig. 14d, for a decreasing time constant $\tau$, there is a decrease in the ripple of the current density. This system behavior is due to the increase in the electron–phonon coupling, which increasingly smears the sharp resonant transitions.

Within the plateaus of the I–V characteristic shown in Fig. 14d, the RTD exhibits an unstable time-dependent behavior. This results from the interaction between the emitter state and the resonant state of the double barrier structure [45]. This allows the possibility to use the RTD as a source of THz oscillations [45, 46]. To generate the THz oscillations, the RTD is excited starting from a voltage $U = 0.313$ V before the hysteresis region is reached with a linear voltage slope of 5 V/ns over the period of 14 ps. For the dynamic calculation, the Crank–Nicolson method is used with a time step size of $\varDelta t=2.5$ fs and the average value of the current density j is calculated. The results are plotted in Fig. 15a dependent on the time as well as the corresponding applied voltage.

Fig. 15

Analysis of the excited THz oscillations for a time-dependent forward voltage sweep with a slope of 5 GV/s from 0.31 to 0.38 V

As it can be seen from Fig. 15a, persistent self-exciting oscillations of the current densities are present in both, the first plateau between 0.31 and 0.32 V and the second plateau between 0.34 and 0.36 V. These are characteristics of the unstable system behavior of the RTD [46]. In the first plateau, the current density oscillates with a frequency of $f_1 = 14.8$ THz. Here, a relatively weak amplitude of about $0.1\text { GA/m}^{2}$ around the DC component of $5.775\text { GA/m}^{2}$ can be observed from Fig. 15b. In the second plateau, the oscillation of the current density is comparatively strong with an amplitude of $0.75\text { GA/m}^{2}$ at frequency of $f_2=2.89$ THz around the mean value of about $4.75\text { GA/m}^{2}$, which is shown in Fig. 15c. An analogous behavior is observed in [46].

6 Summary and conclusion

In essence, the proposed approach includes ballistic effects and also allows integration of interaction mechanisms for the description of non-ballistic effects. Furthermore, band models can be integrated so that not only intraband effects but also interband effects can be described.

An essential conclusion is that with the inclusion of the CAP particular device properties, such as the spatially dependent effective mass distribution, can be adequately considered along with the von Neumann-equation, which is not possible via a direct approximation of the Wigner equation commonly used in the literature. The introduction of a complex potential leads to a physically reasonable and in numerical terms effective limitation of the computational domain. Furthermore, the use of the von Neumann-equation allows the application of various approximation techniques such as the finite volume technique. The resulting system equations can be solved numerically efficient and scalable in combination with subspace methods and the CAP. It was shown in this context that for the dynamic analysis of the matrix exponential operator both, Faber polynomial-based and Krylov subspace-based approximations, have proven to be computationally efficient.

Therefore, the formulation of a modified Wigner equation with an expansion based on a plane wave basis succeeds. This avoids the previously mentioned disadvantages, such as highly oscillating functions within the phase space or the overestimation of diffusion effects in the conventional procedures for the approximation of the Wigner equation.