Open quantum dynamics theory on the basis of periodical system-bath model for discrete Wigner function

Abstract

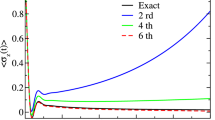
Discretizing a distribution function in a phase space for an efficient quantum dynamics simulation is a non-trivial challenge, in particular for a case in which a system is further coupled to environmental degrees of freedom. Such open quantum dynamics is described by a reduced equation of motion (REOM), most notably by a quantum Fokker–Planck equation (QFPE) for a Wigner distribution function (WDF). To develop a discretization scheme that is stable for numerical simulations from the REOM approach, we employ a two-dimensional (2D) periodically invariant system-bath (PISB) model with two heat baths. This model is an ideal platform not only for a periodic system but also for a non-periodic system confined by a potential. We then derive the numerically “exact” hierarchical equations of motion (HEOM) for a discrete WDF in terms of periodically invariant operators in both coordinate and momentum spaces. The obtained equations can treat non-Markovian heat-bath in a non-perturbative manner at finite temperatures regardless of the mesh size. As demonstrations, we numerically integrate the discrete QFPE for a 2D free rotor and harmonic potential systems in a high-temperature Markovian case using a coarse mesh with initial conditions that involve singularity.

Appendices

A Canonical commutation relation in the large N limit

In this Appendix, we show that our coordinate and momentum operators satisfy the canonical commutation relation in the large N limit.

First we consider a non-periodic case, $dx = x_0 \sqrt{2 \pi /(2N + 1)}$ and $dp = p_0 \sqrt{2 \pi /(2N + 1)}$ with $x_0 p_0 = \hbar$. We employ the relationship between the displaced operator, ${\hat{U}}_x {\hat{U}}_p - {\hat{U}}_p {\hat{U}}_x \omega ^{-1} = 0$. Assuming large N, we express ${\hat{U}}_x$ and ${\hat{U}}_p$ in Taylor expansion forms as

$$\begin{aligned}&\left[ 1 + \frac{i dp {\hat{x}}}{\hbar } + \frac{(i dp)^2}{2 \hbar ^2} {\hat{x}}^2\right] \left[ 1 + \frac{i {\hat{p}} dx}{\hbar } + \frac{(i dx)^2}{2 \hbar ^2} {\hat{p}}^2 \right] \nonumber \\&\quad - \left[ 1 + \frac{i {\hat{p}} dx}{\hbar } + \frac{(i dx)^2}{2 \hbar ^2} {\hat{p}}^2\right] \left[ 1 + \frac{i dp {\hat{x}}}{\hbar } + \frac{(i dp)^2}{2 \hbar ^2} {\hat{x}}^2\right] \left[ 1 - \frac{i dx dp}{\hbar }) + O( (N^{\frac{-3}{2}})\right] \nonumber \\&\quad = \frac{dx dp}{\hbar ^2}({\hat{x}} {\hat{p}} - {\hat{p}} {\hat{x}}) - \frac{i dx dp}{\hbar } + O( N^{\frac{-3}{2}} ). \end{aligned}$$

(35)

This indicates that the canonical commutation relation $[{\hat{x}} , {\hat{p}}] = i \hbar$ satisfies to an accuracy of $O( N^{\frac{-3}{2}} )$.

In the $2 \pi$-periodic case, we set $dx = {2 \pi }/{(2 N + 1)}$ and $dp = \hbar$. Then, we obtain

$$\begin{aligned}&(\cos {\hat{x}} + i \sin {\hat{x}}) \left( 1 - \frac{i dx}{\hbar } {\hat{p}} \right) - \left( 1 - \frac{i dx}{\hbar } {\hat{p}}\right) (\cos {\hat{x}} + i \sin {\hat{x}}) (1 - i dx) + O(N^{-2}) \nonumber \\&\quad = \frac{dx}{\hbar }(\sin {\hat{x}} {\hat{p}} - {\hat{p}} \sin {\hat{x}} - i \hbar \cos {\hat{x}}) + \frac{i dx}{\hbar }(\cos {\hat{x}} {\hat{p}} - {\hat{p}} \cos {\hat{x}} + i \hbar \sin {\hat{x}}) + O(N^{-2}). \end{aligned}$$

(36)

The first and second terms of the RHS in Eq. (36) are the anti-Hermite and Hermite operators. Therefore, the contributions from these terms are zero. Thus, for large N, we obtain the canonical commutation relations for a periodic case as [70]

$$\begin{aligned} {[}\sin {\hat{x}} , {\hat{p}}]&= i \hbar \cos {\hat{x}}, \end{aligned}$$

(37)

and

$$\begin{aligned} {[}\cos {\hat{x}} , {\hat{p}}]&= - i \hbar \sin {\hat{x}}, \end{aligned}$$

(38)

to an accuracy of $O(N^{-2})$.

B QME for 2D PISB model and counter term

To demonstrate a role of the counter term, here we employ the QME for the 2D PISB model. As shown in [62], the QME for the reduced density matrix of the system, ${\hat{\rho }}(t)$, is derived from the second-order perturbation approach as

(39)

where

$$\begin{aligned} {{\hat{\varGamma }}}_\alpha (\tau ) {\hat{\rho }}(t - \tau )&\equiv C(\tau ) [{\hat{V}}_{\alpha } , {\hat{G}}_S(\tau ) {\hat{V}}_{\alpha } {\hat{\rho }}(t - \tau ) {\hat{G}}_S^{\dagger }(\tau )] \nonumber \\&- C(-\tau )[ {\hat{V}}_{\alpha } , {\hat{G}}_S(\tau ) {\hat{\rho }}(t - \tau ) {\hat{V}}_{\alpha } {\hat{G}}_S^{\dagger }(\tau )] \end{aligned}$$

(40)

is the damping operator for $\alpha = x$ or y, in which

$$\begin{aligned} C(\tau )&= \hbar \int ^{\infty }_0 \frac{d \omega }{\pi } J (\omega ) \left[ \coth \left( \frac{\beta \hbar \omega }{2}\right) \cos (\omega \tau ) - i \sin (\omega \tau )\right] \end{aligned}$$

(41)

is the bath correlation function and ${\hat{G}}_S(\tau )$ is the time-evolution operator of the system. For the Ohmic SDF $J(\omega )=\eta \omega$, $C(\tau )$ reduces to the Markovian form as

$$\begin{aligned} C(\tau ) = \eta \left( \frac{2 }{\beta } + i \hbar \frac{d}{d\tau } \right) \delta (\tau ). \end{aligned}$$

(42)

Using the relation $\int ^{t}_{0} d \tau {{\hat{\varGamma }}}_{\alpha }(\tau ) {\hat{\rho }}(t - \tau ) = \hat{{{\bar{\varGamma }}}}_{\alpha } {\hat{\rho }}(t)+{i \hbar \eta }\delta (0) [({\hat{V}}_{\alpha })^2, {\hat{\rho }}(t)]$, we can rewrite the damping operator, Eq. (40), as

$$\begin{aligned} \hat{{{\bar{\varGamma }}}}_{\alpha } {\hat{\rho }}(t)&= \frac{\eta }{\beta } \left( [{\hat{V}}_{\alpha }, {\hat{V}}_{\alpha } {\hat{\rho }}(t) ] - [ {\hat{V}}_{\alpha } , {\hat{\rho }}(t ) {\hat{V}}_{\alpha }] \right) +\frac{i\hbar \eta }{2 } \left[ ({\hat{V}}_{\alpha })^2 , \frac{d {\hat{\rho }}(t - \tau )}{d \tau }|_{\tau = 0} \right] \nonumber \\&- \frac{\eta }{2 } \left( [{\hat{V}}_{\alpha } , {\hat{H}}_S {\hat{V}}_{\alpha } {\hat{\rho }}(t ) ] + [ {\hat{V}}_{\alpha } , {\hat{H}}_S {\hat{\rho }}(t ) {\hat{V}}_{\alpha } ] - [{\hat{V}}_{\alpha } , {\hat{V}}_{\alpha } {\hat{\rho }}(t ) {\hat{H}}_S] - [ {\hat{V}}_{\alpha } , {\hat{\rho }}(t ) {\hat{V}}_{\alpha } {\hat{H}}_S] \right) . \end{aligned}$$

(43)

In the case if there is only ${{\hat{V}}}_{y} =\hbar \sin ({{\hat{x}} dp}/{\hbar } )/dp$ interaction in the PISB model, (i.e., ${\hat{V}}_{x}=0$), we encounter the divergent term ${i \hbar \eta }\delta (0) [({\hat{V}}_{y})^2, {\hat{\rho }}(t)]$ that arises from the second term in the RHS of Eq. (43). Because ${\hat{V}}_{y}$ reduces to the linear operator of the coordinate ${\hat{V}}_{y} \approx {{\hat{x}}}$ in the large N limit, the PISB model under this condition corresponds to the Caldeira–Leggett model without the counter term: Divergent term arises because we exclude the counter term in the bath Hamiltonian, Eq. (3). (See also [64].) If we include ${{\hat{V}}}_{x} =\hbar \cos ({{\hat{x}} dp}/{\hbar } )/dp$, this divergent term vanishes, because, by using the relation $\sin ^2({{\hat{x}} dp}/{\hbar } ) + \cos ^2({{\hat{x}} dp}/{\hbar } )=1$, we have

$$\begin{aligned} {i \hbar \eta }\delta (0) [({\hat{V}}_{x})^2, {\hat{\rho }}(t)] + {i \hbar \eta }\delta (0) [({\hat{V}}_{y})^2, {\hat{\rho }}(t)]&= {i \hbar \eta }\delta (0)[{\hat{I}}, {\hat{\rho }}(t)] \nonumber \\&= 0. \end{aligned}$$

(44)

This implies that the interaction ${\hat{V}}_{y}$ plays the same role as the counter term. This fact indicates the significance of constructing a system-bath model with keeping the same symmetry as the system itself. If we ignore this point, the system dynamics are seriously altered by the bath even if the system-bath interaction is feeble [64].

C Discrete Moyal bracket

Using the kinetic term (the first term in the RHS of Eq. (32)) as an example, here we demonstrate the evaluation of the discrete Moyal bracket defined as Eq. (30). The kinetic energy in a finite Hilbert space representation is expressed as

$$\begin{aligned} \varvec{T}(p_j, q_k)&= \frac{\hbar ^2}{dx^2} \left( 1 - \sum _{l = -N}^{N} \exp \left( i \frac{-2 q_k (p_j - p_l)}{\hbar } \right) \langle P, l | \cos \left( \frac{{\hat{p}} dx}{\hbar } \right) | P, 2 j - l \rangle \right) \nonumber \\&= \frac{\hbar ^2}{dx^2} \left( 1 - \sum _{l = -N}^{N} \exp \left( i \frac{-2 q_k (p_j - p_l)}{\hbar } \right) \cos \left( \frac{p_l dx}{\hbar } \right) \delta _{l, 2j - l } \right) \nonumber \\&= \frac{\hbar ^2}{dx^2} \left( 1 - \cos \left( \frac{p_j dx}{\hbar } \right) \right) . \end{aligned}$$

(45)

Because the Moyal bracket with $\varvec{A_1} = \hbar ^2/dx^2$ and $\varvec{A_2} = \varvec{W}$ is zero, we focus on the $\cos \left( {p_j dx}/{\hbar } \right)$ term. Let $\varvec{A_1} = \exp \left( \pm i{p_j dx}/{\hbar }\right)$ and $\varvec{A_2} = \varvec{W}$ in Eq. (30). Then we have

$$\begin{aligned}&\left[ \exp \left( \pm i\frac{p_j dx}{\hbar }\right) \star \varvec{W} \right] (p_j, q_k) = \frac{1}{(2 N + 1)^2} \sum _{j_1, j_2, k_1, k_2 = -N}^N \exp \left( i \frac{2 p_{j_2} q_{k_1} - 2 p_{j_1} q_{k_2}}{\hbar } \right) \nonumber \\&\quad \times \exp \left( \pm i\frac{(p_j + p_{j_1}) dx}{\hbar }\right) \varvec{W}( p_j + p_{j_2}, q_k + q_{k_2})\nonumber \\&\quad = \frac{1}{(2 N + 1)} \sum _{j_1, k_2 = -N}^N \exp \left( i \frac{(\pm 1 - 2 k_2) p_{j_1} dx}{\hbar } \right) \exp \left( \pm i\frac{p_j dx}{\hbar }\right) \varvec{W}( p_j , q_k + q_{k_2}) \nonumber \\&\quad = \sum _{k_2 = -N}^N \delta '_{\pm 1 - 2 k_2, 0} \exp \left( \pm i\frac{p_j dx}{\hbar }\right) \varvec{W}( p_j , q_k + q_{k_2}) \nonumber \\&\quad = \exp \left( \pm i\frac{p_j dx}{\hbar } \right) \varvec{W}( p_j , q_{k \pm (N + 1)}). \end{aligned}$$

(46)

Similarly, for $\varvec{A_1} = \varvec{W}$ and $\varvec{A_2} = \exp \left( \pm i{p_j dx}/{\hbar }\right)$, we have

$$\begin{aligned}&\left[ \varvec{W} \star \exp \left( \pm i\frac{p_j dx}{\hbar }\right) \right] (p_j, q_k) = \exp \left( \mp i\frac{p_j dx}{\hbar }\right) \varvec{W}( p_j , q_{k \pm (N + 1)}). \end{aligned}$$

(47)

Thus, the discrete Moyal product of the kinetic energy is expressed as

$$\begin{aligned}&-\frac{i}{\hbar }[ \varvec{T} \star \varvec{W}](p_j, q_k) = - \hbar \sin \left( \frac{p_j dx}{\hbar } \right) \frac{\varvec{W}( p_j , q_{k + N + 1}) - \varvec{W}( p_j , q_{k - N - 1})}{dx^2}. \end{aligned}$$

(48)

For example, for $q_0$, the above expression involves the contributions from $q_{N + 1 \equiv -N (mod \ 2N + 1)}$ and $q_{-N - 1 \equiv N (mod \ 2N + 1)}$, which are the elements near the boundary of the periodic state. Note that $N + 1$ arises from $\delta '_{1 - 2 k_2, 0}$ that is the inverse element of 2 modulo $2N + 1$. For large N, the above expression reduces to the kinetic term of the conventional QFPE by regarding the finite difference near the boundary as the derivative of the coordinate.

D Discrete quantum Fokker–Planck equation for large N

For a large N, Eq. (33) reduces to

$$\begin{aligned} \frac{\partial }{\partial t} W(p, q)&= -p \frac{\partial }{\partial q} W(p, q) -\frac{i}{\hbar } \{ \varvec{U} , \varvec{W} \}_M + \frac{\eta }{ \beta } \frac{\partial ^2}{\partial p^2}W(p, q) \nonumber \\&+\frac{\eta }{2} \left( {\hat{M}}^2_p {\hat{M}}_x W(p, q) + p {\hat{M}}_x \frac{\partial }{\partial p} W(p, q) \right) , \end{aligned}$$

(49)

where

$$\begin{aligned}&\frac{\partial W(p, q)}{\partial q} \equiv \frac{W(p_j, q_{k + N + 1)} - W(p_j, q_{k - N - 1})}{dx}, \end{aligned}$$

(50)

$$\begin{aligned}&\frac{\partial W(p, q)}{\partial p} \equiv \frac{W(p_{j + N + 1}, q_k) - W(p_{j - N - 1}, q_k)}{dp}, \end{aligned}$$

(51)

$$\begin{aligned}&{\hat{M}}_x W(p, q) \equiv \frac{W(p_j, q_{k + N + 1)} + W(p_j, q_{k - N - 1})}{2} , \end{aligned}$$

(52)

and

$$\begin{aligned} {\hat{M}}_p W(p, q) \equiv \frac{W(p_{j + N + 1}, q_k) + W(p_{j - N - 1}, q_k)}{2}. \end{aligned}$$

(53)

Although the above expression has a similar form to the QFPE, the finite difference operators for the discrete WDF are defined by the elements near the periodic boundary, i.e., for $W(p_0, q_0)$, $\partial /\partial q$ is evaluated from $W(p_0, q_{-(N+1)} )$, and $W(p_0, q_{N+1})$. Thus, the appearance of the discrete WDF can be different from the regular WDF, as depicted in Fig. 5 even for large N.